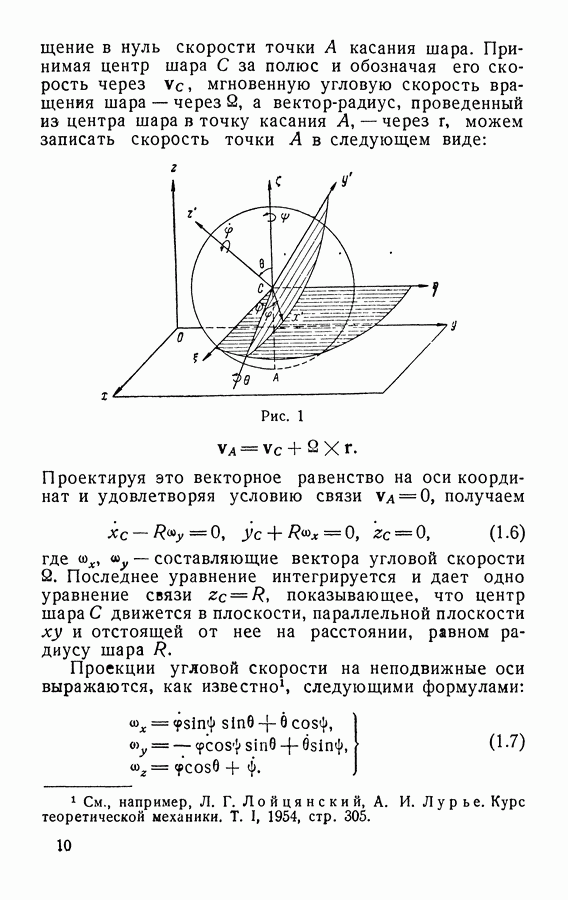
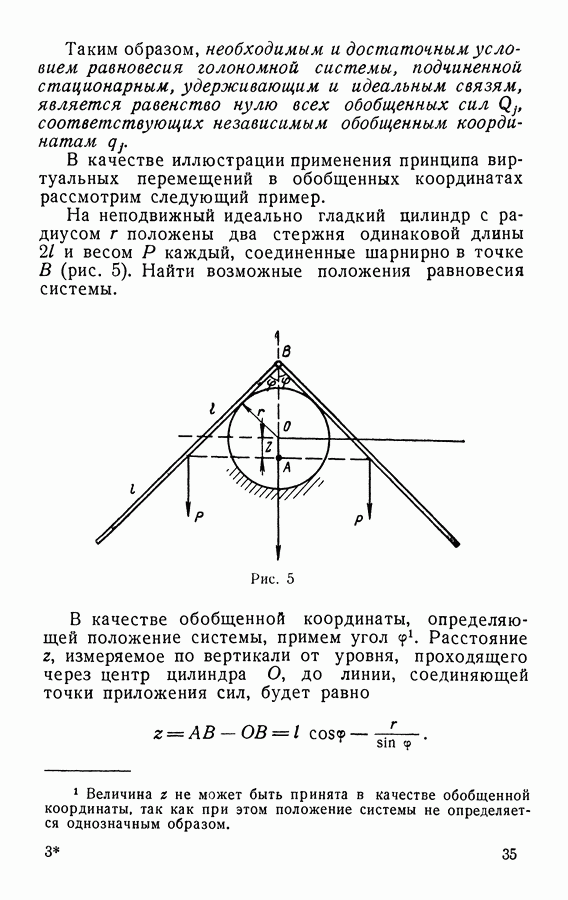
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Скобки Пуассона
Пусть  суть некоторые функции, зависящие от переменных, определяющих состояние механической системы, а именно, от обобщенных координат
суть некоторые функции, зависящие от переменных, определяющих состояние механической системы, а именно, от обобщенных координат  обобщенных импульсов
обобщенных импульсов  и времени
и времени 

Скобками Пуассона для функций  называется выражение вида
называется выражение вида

Из определения скобок Пуассона вытекают следующие их свойства:
1) свойство антикоммутативности

2) если функции совпадают, то скобки Пуассона обращаются в нуль:

3) если одна из функций равна постоянной, то скобки Пуассона обращаются в нуль:

где а — постоянная;
4) свойство распределительности

5) частная производная по времени  (или по какому-либо другому параметру) от скобок Пуассона равна
(или по какому-либо другому параметру) от скобок Пуассона равна

Если рассматривать три функции  то можно составить и двойные скобки Пуассона. Например, если скобку Пуассона
то можно составить и двойные скобки Пуассона. Например, если скобку Пуассона  обозначить через
обозначить через  то, составляя скобку Пуассона
то, составляя скобку Пуассона  получим двойную скобку Пуассона
получим двойную скобку Пуассона  . Аналогично можно составить и другие двойные скобки Пуассона. Имеет место следующее замечательное равенство, которое выполняется тождественно (тождество Якоби-Пуассона):
. Аналогично можно составить и другие двойные скобки Пуассона. Имеет место следующее замечательное равенство, которое выполняется тождественно (тождество Якоби-Пуассона):

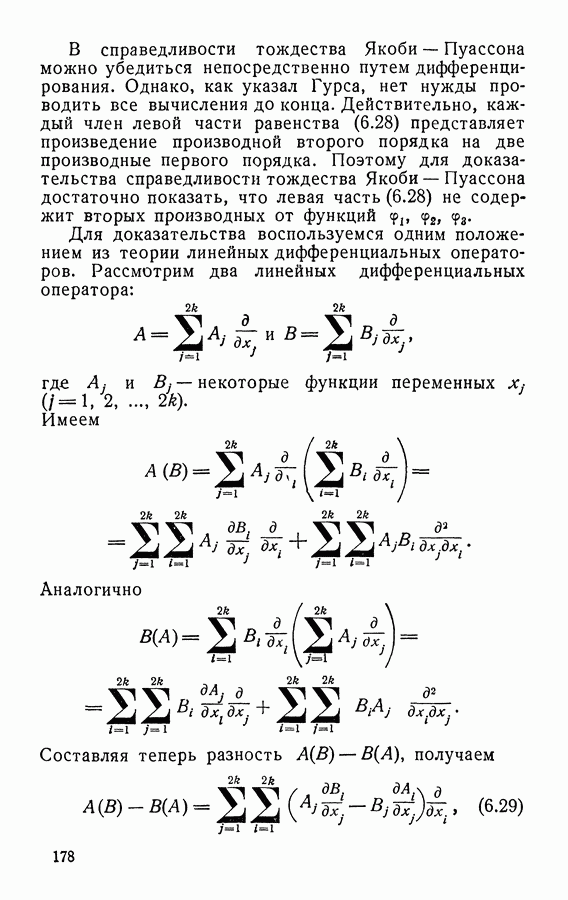
В справедливости тождества Якоби — Пуассона можно убедиться непосредственно путем дифференцирования. Однако, как указал Гурса, нет нужды проводить все вычисления до конца. Действительно, каждый член левой части равенства (6.28) представляет произведение производной второго порядка на две производные первого порядка. Поэтому для доказательства справедливости тождества Якоби — Пуассона достаточно показать, что левая часть (6.28) не содержит вторых производных от функций 
Для доказательства воспользуемся одним положением из теории линейных дифференциальных операторов. Рассмотрим два линейных дифференциальных оператора:

где  — некоторые функции переменных
— некоторые функции переменных  .
.
Имеем

Аналогично

Составляя теперь разность  , получаем
, получаем

т. е. снова получаем линейный оператор, не содержащий вторых производных.
Пользуясь полученным результатом, можно доказать тождество Якоби — Пуассона. Покажем, что левая часть (6.28) не содержит вторых производных от функции  .
.
Вторые производные от функции  получаются из скобок Пуассона
получаются из скобок Пуассона

что можно представить так:

Скобки Пуассона  можно рассматривать как некоторый линейный дифференциальный оператор, действующий на одну из функций
можно рассматривать как некоторый линейный дифференциальный оператор, действующий на одну из функций  или
или  Тогда выражение (6.30) с помощью этих операторов можно представить следующим образом.
Тогда выражение (6.30) с помощью этих операторов можно представить следующим образом.
Рассмотрим два линейных оператора:

Равенство (6.30) тогда можно представить так:

Это выражение на основании (6.29) не содержит вторых производных от функции Аналогичным способом можно показать, что левая часть равенства (6.28) не содержит вторых производных от функций  Таким образом, тождество Якоби—Пуассона доказано.
Таким образом, тождество Якоби—Пуассона доказано.
Рассмотрим теперь связь между скобками Пуассона и уравнениями движения. Для этого составим скобки Пуассона от функции Гамильтона  и некоторой функции
и некоторой функции  Имеем
Имеем

Если теперь воспользоваться уравнениями Гамильтона 

то

Но так как

то окончательно получаем

Если функция  является интегралом уравнений движения, то
является интегралом уравнений движения, то  и, следовательно,
и, следовательно,  , а это на основании (6.31) приводит к соотношению
, а это на основании (6.31) приводит к соотношению

Таким образом, для того чтобы функция  была интегралом канонической системы уравнений Гамильтона, необходимо чтобы выполнялось условие (6.32).
была интегралом канонической системы уравнений Гамильтона, необходимо чтобы выполнялось условие (6.32).
Если же интеграл уравнений движения не зависит явным образом от времени  , следовательно, соответствующее условие принимает вид
, следовательно, соответствующее условие принимает вид

С помощью скобок Пуассона можно находить интегралы канонической системы уравнений Гамильтона. Имеет место следующая теорема Пуассона: если функции  являются интегралами канонической системы, то и их скобки Пуассона
являются интегралами канонической системы, то и их скобки Пуассона  также будут интегралом.
также будут интегралом.
Для того чтобы показать, что функция  также будет интегралом канонической системы, воспользуемся тождеством Якоби — Пуассона, составленным для трех функций:
также будет интегралом канонической системы, воспользуемся тождеством Якоби — Пуассона, составленным для трех функций:  Имеем:
Имеем:

Так как  являются интегралами канонической системы, то имеют место следующие равенства:
являются интегралами канонической системы, то имеют место следующие равенства:

С помощью этих соотношений равенство (6.34) можно представить в следующей форме:

Пользуясь свойствами скобок Пуассона, находим

или

и, окончательно,

а это означает, что функция  является интегралом канонической системы уравнений Гамильтона.
является интегралом канонической системы уравнений Гамильтона.
Таким образом, зная два независимых интеграла канонической системы, можно найти третий интеграл. Однако таким путем не всегда удается получить новый интеграл, не зависящий от первых двух.
Будем говорить, что функции  от переменных
от переменных  находятся в инволюции, если их скобки Пуассона тождественно равны нулю, т. е.
находятся в инволюции, если их скобки Пуассона тождественно равны нулю, т. е.  Пусть известна система
Пусть известна система  независимых интегралов
независимых интегралов  канонической системы уравнений Гамильтона такая, что каждая пара интегралов находится в инволюции, т. е.
канонической системы уравнений Гамильтона такая, что каждая пара интегралов находится в инволюции, т. е.

Такая система интегралов называется инволюционной системой интегралов или якобиевой системой. Легко видеть, что из якобиевой системы интегралов нового независимого интеграла с помощью теоремы Пуассона получить нельзя.
Пример 1. Показать, что для каждой пары координат (аналогично для каждой пары импульсов) скобки Пуассона обращаются в нуль:

а

где  — символ Кронекера:
— символ Кронекера:

Указание. Воспользоваться определением скобок Пуассона.
Пример 2. Показать, что если  — компоненты момента количества движения материальной точки, то имеют место следующие соотношения:
— компоненты момента количества движения материальной точки, то имеют место следующие соотношения:

Для доказательства воспользуемся известными соотношениями

Скобка Пуассона  как в этом нетрудно убедиться, сведется к двум слагаемым:
как в этом нетрудно убедиться, сведется к двум слагаемым:

Аналогично доказываются остальные два соотношения.
Пример 3. Показать, что если функция Гамильтона Н не зависит явным образом от времени а функция  является интегралом уравнений движения, то новые интегралы тех же уравнений движения можно получить, положив
является интегралом уравнений движения, то новые интегралы тех же уравнений движения можно получить, положив

Если функция Гамильтона Н не зависит явным образом от времени  то
то  является интег
является интег
ралом уравнений движения. На основании теоремы Пуассона  есть также интеграл. Но так как функция
есть также интеграл. Но так как функция  есть интеграл канонической системы уравнений Гамильтона, то на основании (6.32) имеем
есть интеграл канонической системы уравнений Гамильтона, то на основании (6.32) имеем

Следовательно,

также есть интеграл канонической системы уравнений Гамильтона.
Аналогично доказывается, что

тоже будет интегралом.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ
- § 1. Механическая система. Связи и их классификация
- § 2. Обобщенные координаты
- § 3. Обобщенные скорости и ускорения
- § 4. Вариация координат
- § 5. Виртуальные перемещения. Число степеней свободы
- § 6. Принцип освобождаемости. Идеальные связи
- Глава II. ДИФФЕРЕНЦИАЛЬНЫЕ ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- § 2. Выражение принципа виртуальных перемещений в обобщенных координатах
- § 3. Силы, имеющие потенциал
- § 4. Принцип Даламбера
- § 5. Общее уравнение динамики
- § 6. Общее уравнение динамики для случая сил, имеющих потенциал
- § 7. Уравнения Лагранжа первого рода
- § 8. Принцип наименьшего принуждения (принцип Гаусса)
- § 9. Принцип Журдена
- § 10. Совместность дифференциальных принципов. Перемещения по Четаеву
- Глава III. ИНТЕГРАЛЬНЫЕ ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ
- § 1. Траектория механической системы. Прямой и окольный путь
- § 2. Принцип стационарного действия Гамильтона
- § 3. Вывод принципа Гамильтона из общего уравнения динамики
- § 4. Другая формулировка принципа Гамильтона
- § 5. Принцип стационарного действия Мопертюи—Лагранжа
- § 6. Принцип стационарного действия в форме Якоби
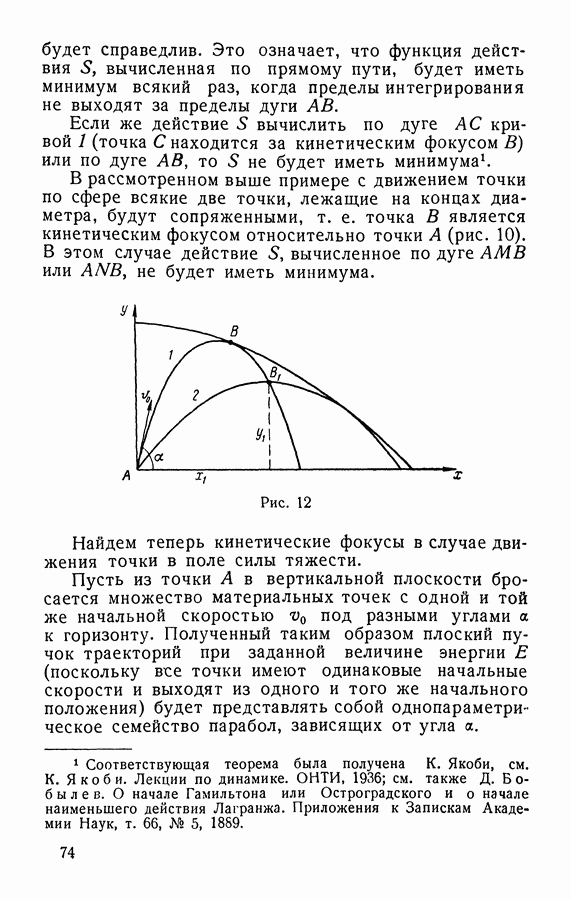
- § 7. Кинетические фокусы
- Глава IV. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ПРИНЦИПА СТАЦИОНАРНОГО ДЕЙСТВИЯ
- § 1. Задача о траекториях
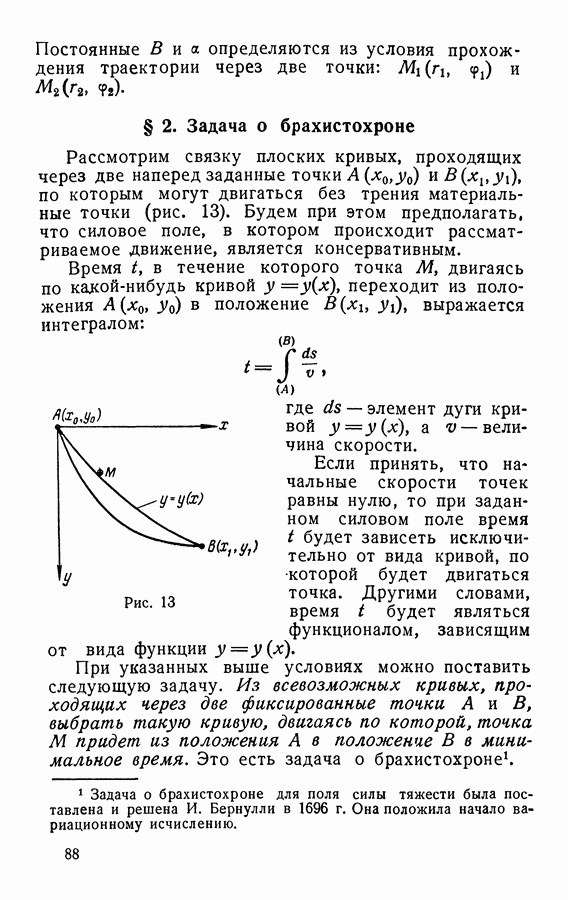
- § 2. Задача о брахистохроне
- § 3. Движение системы по инерции (спонтанные движения)
- § 4. Движение точки по инерции
- § 5. Задача о геодезических линиях
- Глава V. УРАВНЕНИЯ ДВИЖЕНИЯ
- § 1. Уравнения Лагранжа второго рода
- § 2. Инвариантность уравнений Лагранжа
- § 3. Кинетическая энергия системы
- § 4. Теорема об изменении кинетической энергии системы
- § 5. Гироскопические системы
- § 6. Диссипативные системы
- § 7. Интеграл энергии
- § 8. Циклические координаты. Циклические интегралы
- § 9. О разрешимости уравнений Лагранжа
- § 10. Уравнения Аппеля
- Глава VI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА
- § 1. Функция Гамильтона
- § 2. Уравнения Гамильтона
- § 3. Вывод уравнений Гамильтона из принципа Гамильтона
- § 4. Функция Рауса. Уравнения движения в форме Рауса
- § 5. Скобки Пуассона
- Глава VII. МЕТОД ЯКОБИ—ГАМИЛЬТОНА
- § 1. Главная функция Гамильтона
- § 2. Принцип переменного действия
- § 3. Общая формула для вариации функции действия
- § 4. Производные главной функции Гамильтона
- § 5. Дифференциальное уравнение Гамильтона — Якоби
- § 6. Теорема Якоби о нахождении полной системы независимых интегралов уравнений движения
- § 7. Случай консервативной системы
- § 8. Метод разделения переменных
- § 9. Оптико-механическая аналогия
- Глава VIII. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
- § 1. Преобразование Лежандра
- § 2. Канонические преобразования
- § 3. Различные виды канонических преобразований
- § 4. Вполне канонические преобразования
- § 5. Бесконечно малые канонические преобразования
- Глава IX. ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ
- § 1. Интегральный инвариант Пуанкаре
- § 2. Интегральный инвариант Пуанкаре — Картана
- § 3. Абсолютные интегральные инварианты
- § 4. Системы уравнений, имеющие интегральные инварианты
- § 5. Принцип сохранения количества движения и энергии
- § 6. Уравнения Уиттекера
- § 7. Понижение порядка системы уравнений Гамильтона с помощью интеграла энергии
- Глава X. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- § 2. Уравнения в вариациях
- § 3. Теорема Ляпунова об устойчивости движения
- § 4. Теорема Ляпунова об асимптотической устойчивости
- § 5. Теоремы Ляпунова и Четаева о неустойчивости движения
- § 6. Устойчивость равновесия. Теорема Лагранжа
- § 7. Устойчивость линейных систем
- § 8. Критерий асимптотической устойчивости Рауса — Гурвица
- ЛИТЕРАТУРА