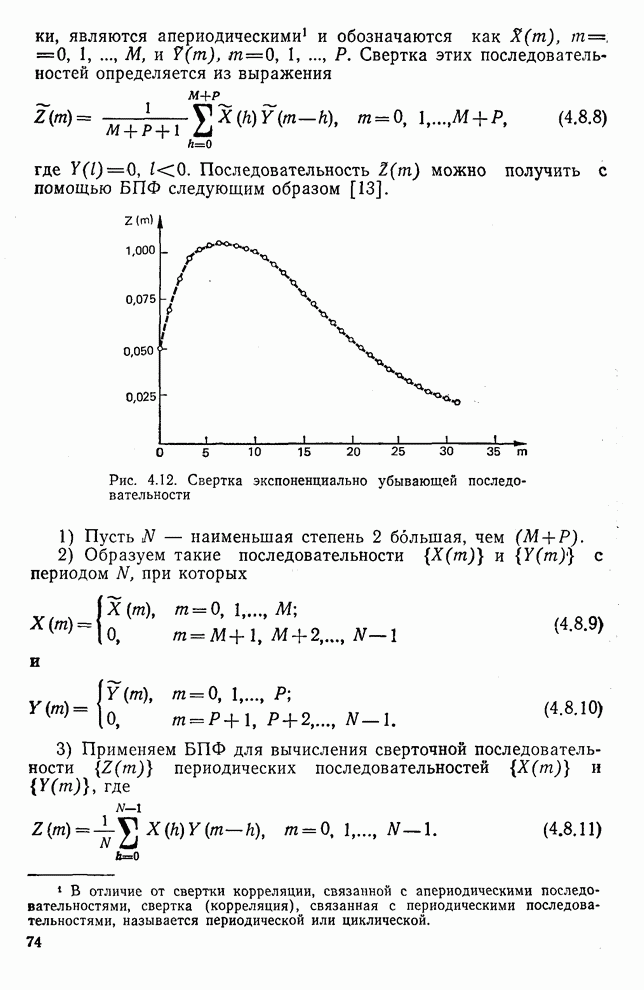
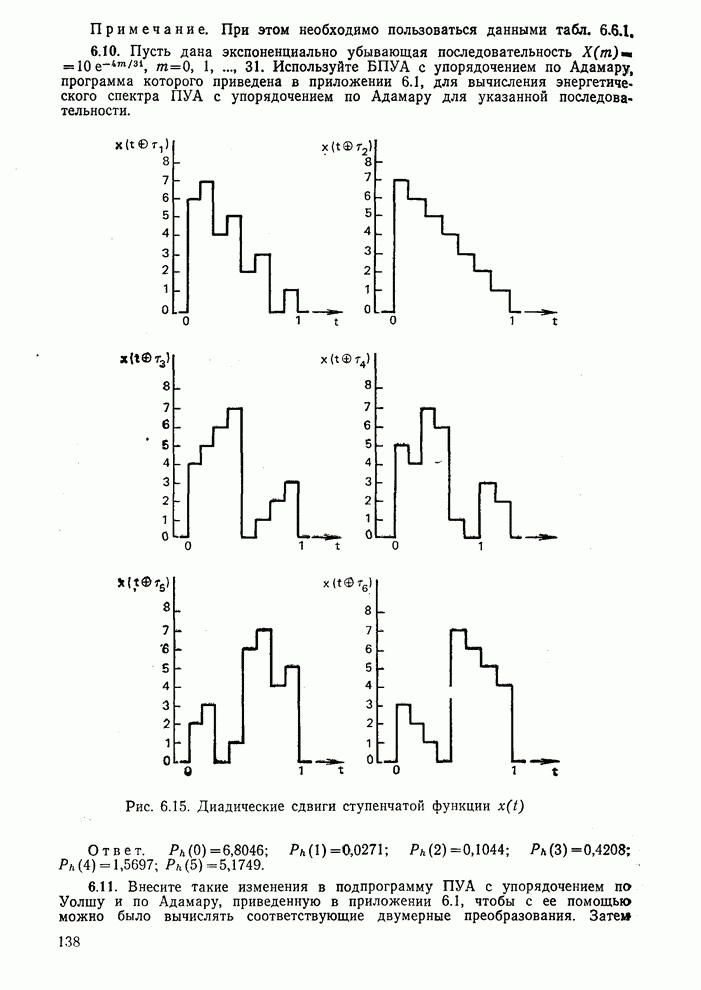
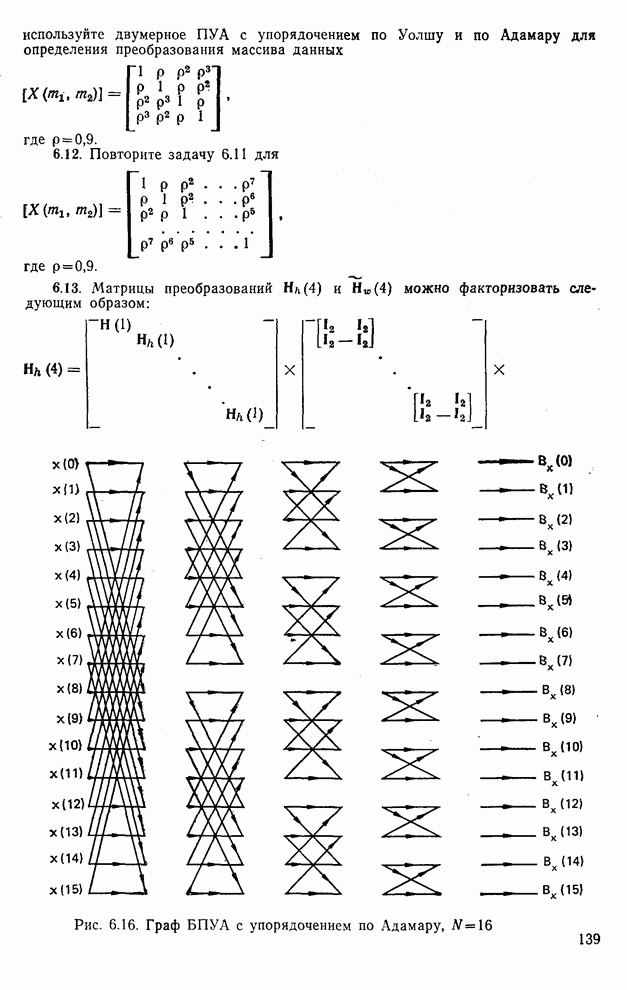
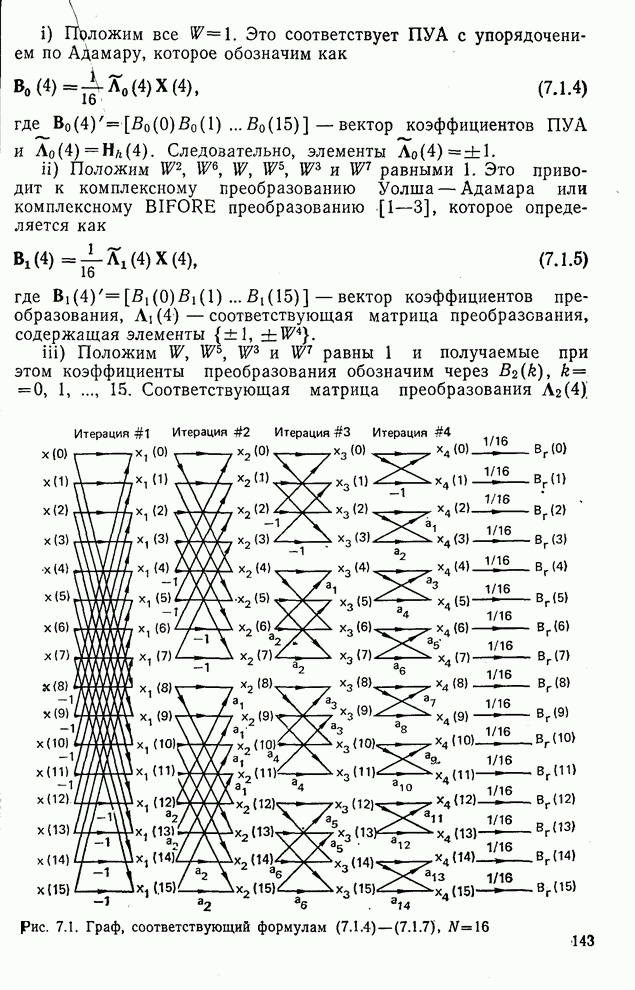
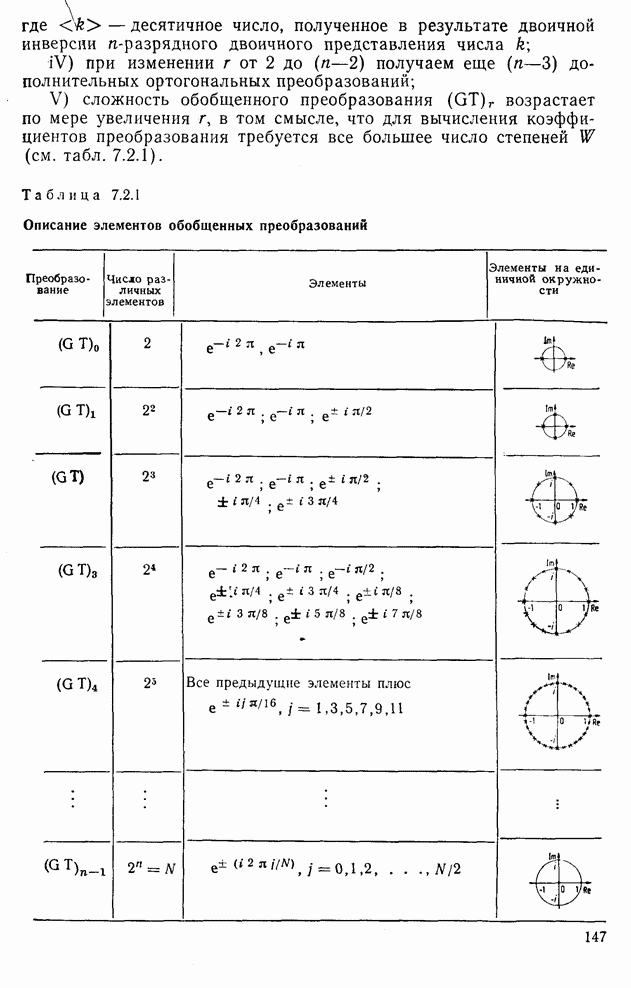
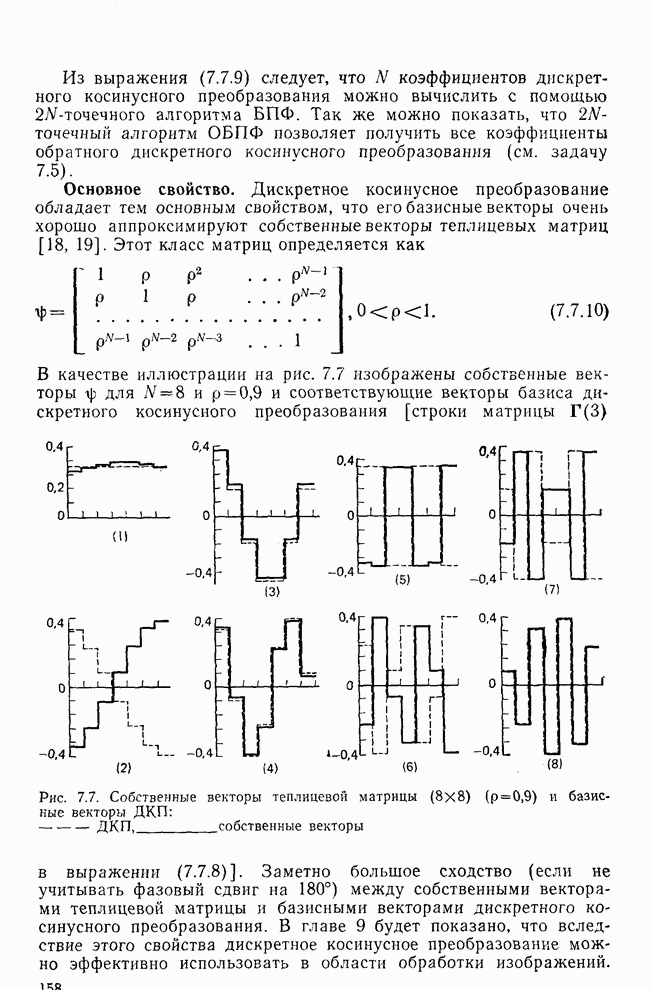
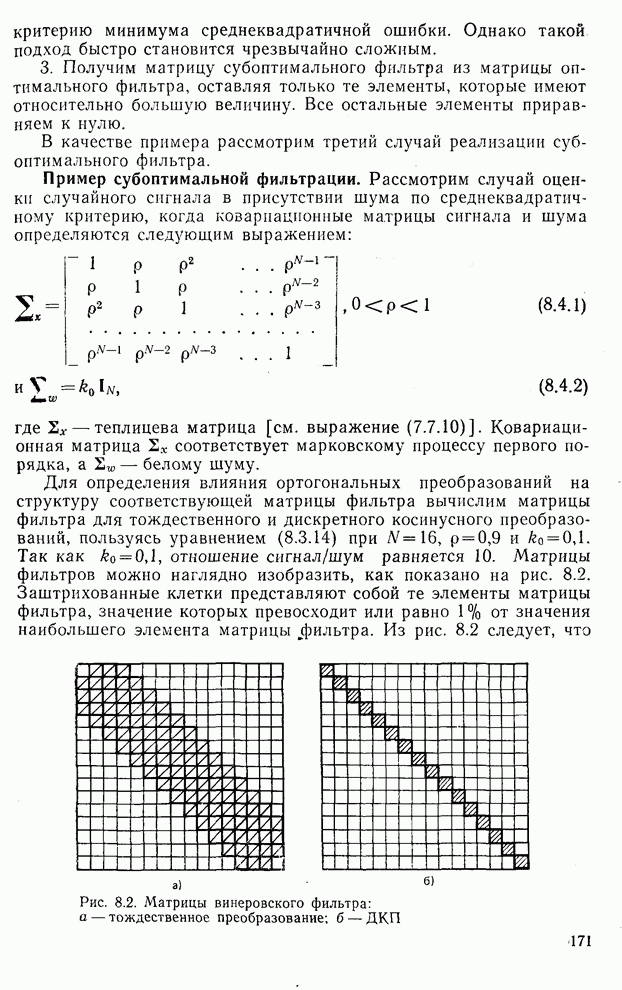
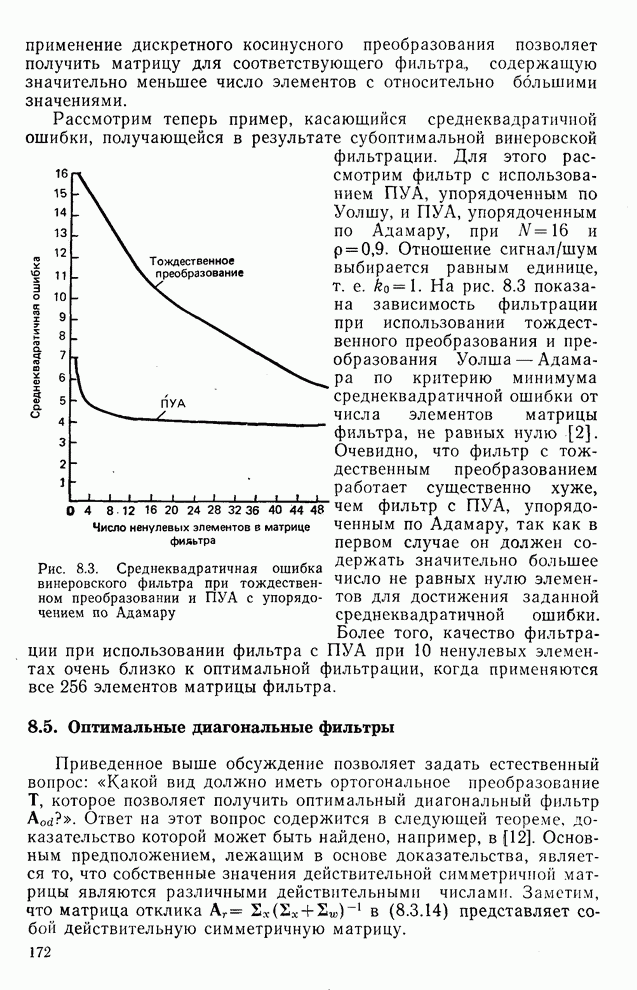
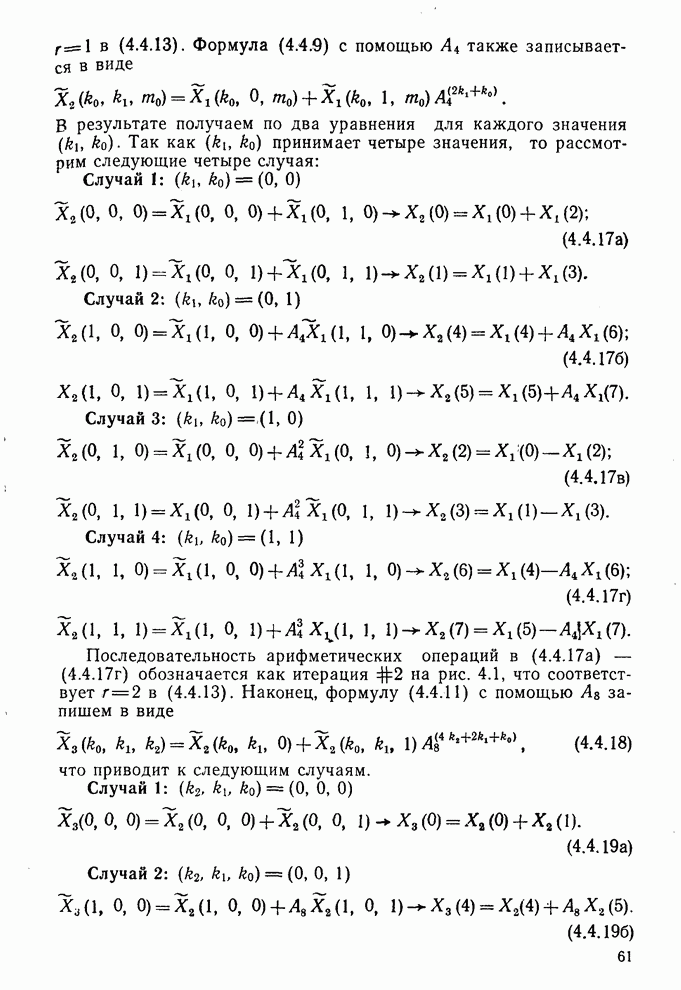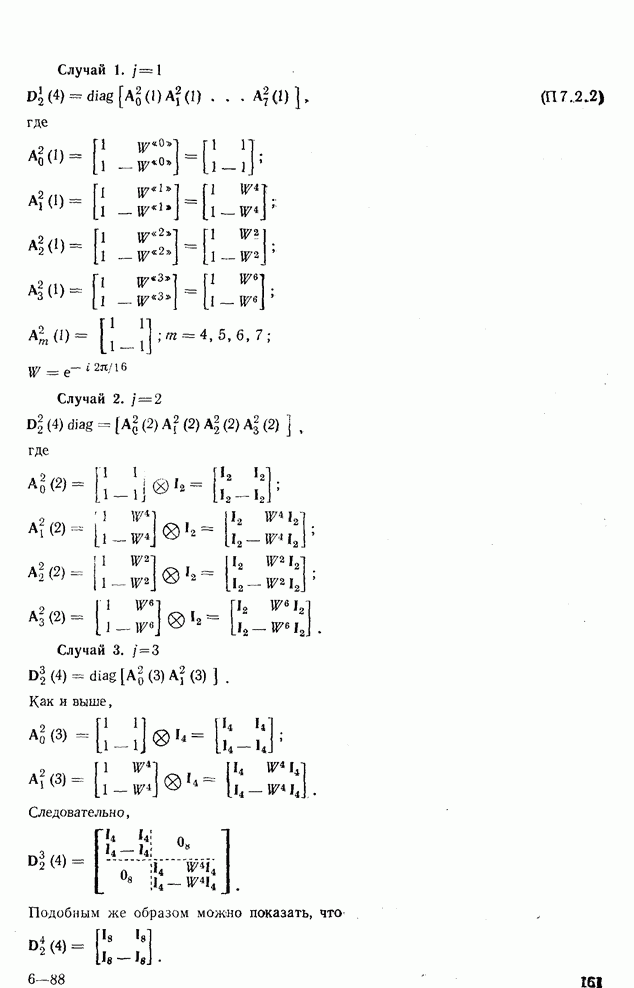| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ЗАДАЧИ
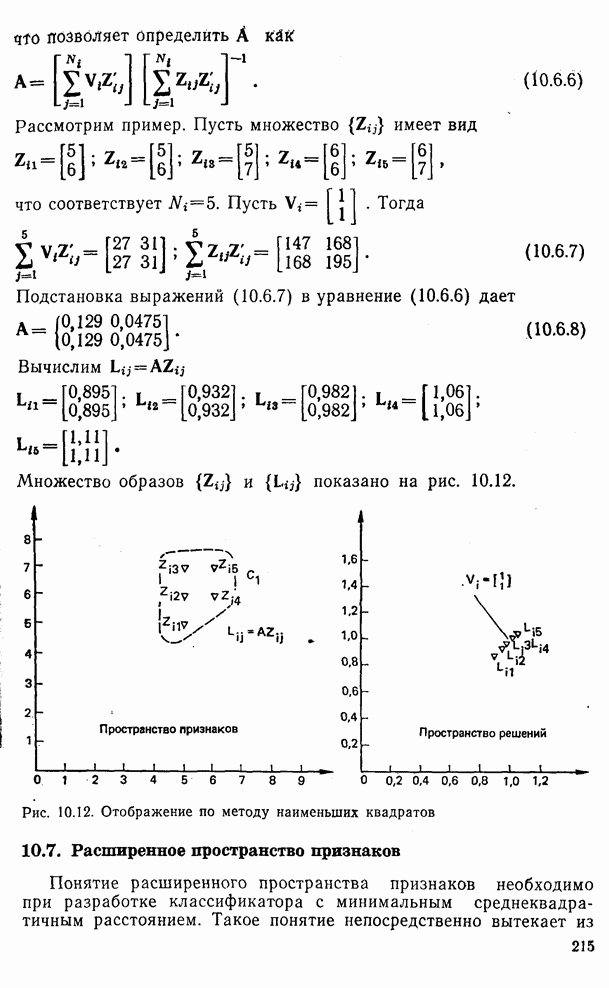
10.1. а) Средние образы, соответствующие множеству трехмерных обучающих образов, равны  и
и  . Найдите уравнение плоскости, перпендикулярной к прямой, которая соединяет
. Найдите уравнение плоскости, перпендикулярной к прямой, которая соединяет  и
и  и делит ее пополам.
и делит ее пополам.
Ответ.  .
.
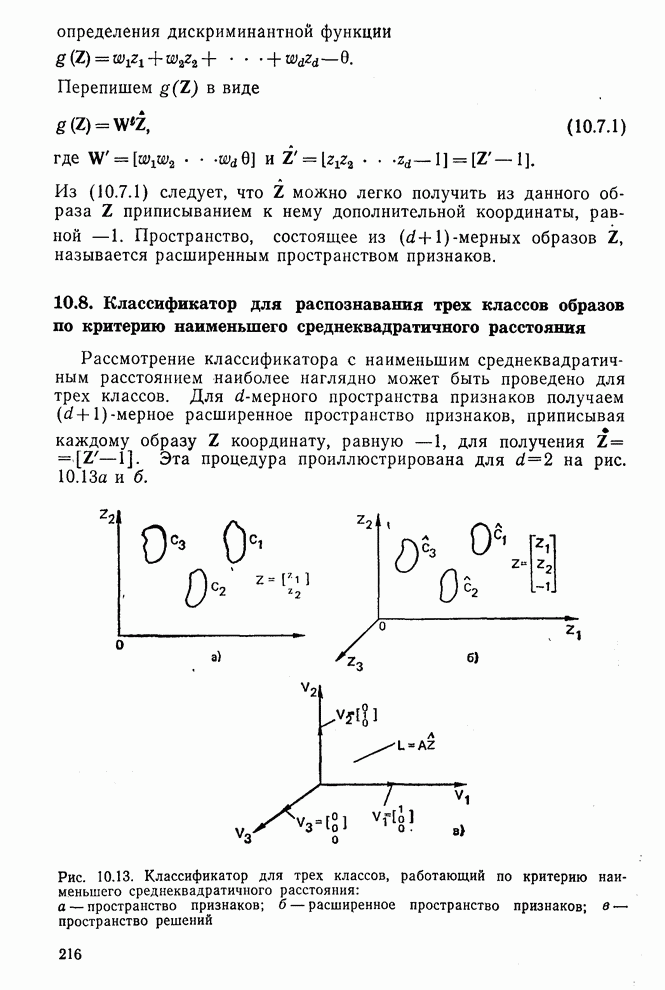
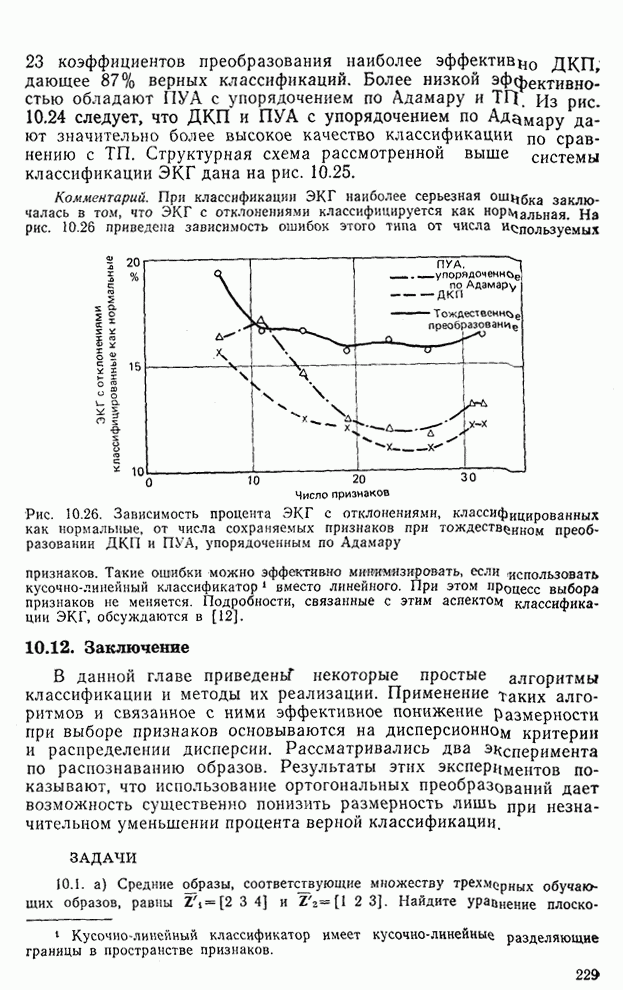
б) При решении некоторой задачи для трех классов получаем следующие дискриминантные функции:

Найдите уравнения для разделяющих границ  и точку их пересечения.
и точку их пересечения.
Примечание. Точка пересечения получается в результате решения любых двух из трех уравнений для разделяющих границ.
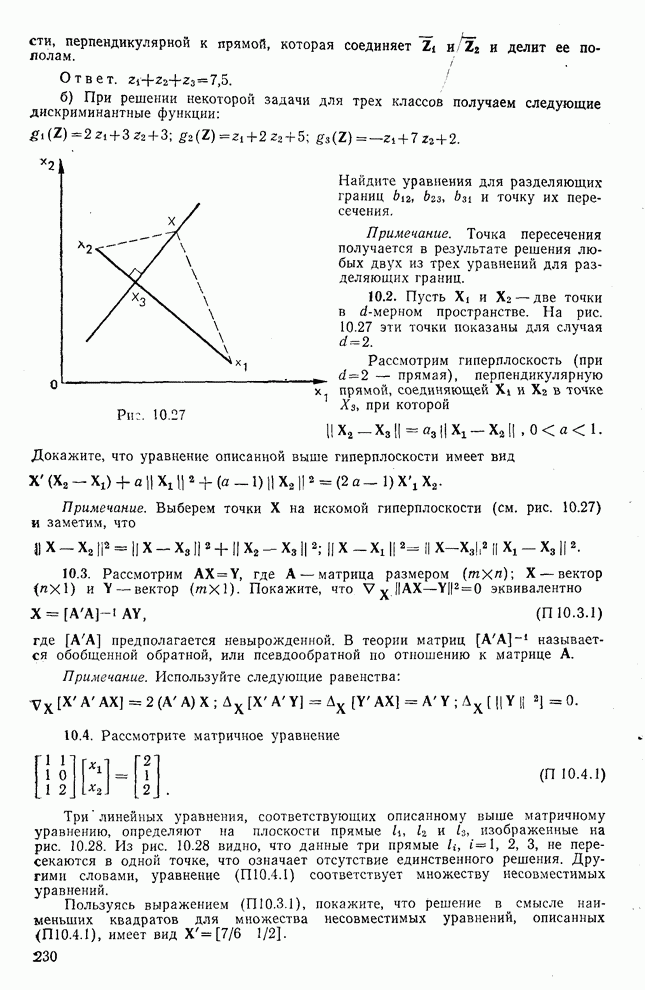
10.2. Пусть  и
и  — две точки в
— две точки в  -мерном пространстве. На рис. 10.27 эти точки показаны для случая
-мерном пространстве. На рис. 10.27 эти точки показаны для случая  .
.

Рис. 10.27
Рассмотрим гиперплоскость (при  — прямая), перпендикулярную прямой, соединяющей
— прямая), перпендикулярную прямой, соединяющей  и
и  в точке
в точке  , при которой
, при которой

Докажите, что уравнение описанной выше гиперплоскости имеет вид

Примечание. Выберем точки X на искомой гиперплоскости (см. рис. 10.27) и заметим, что

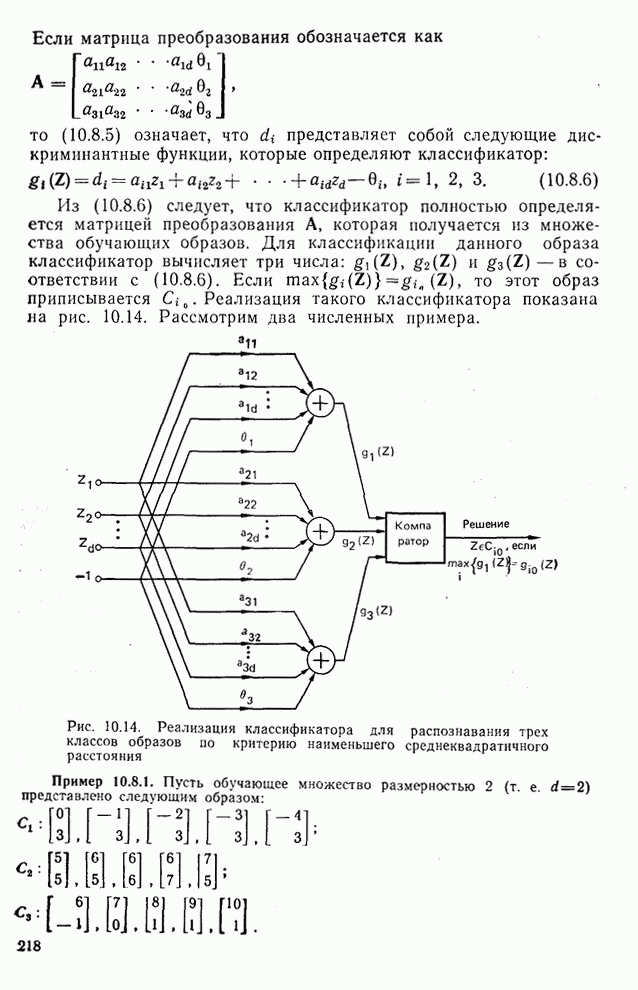
10.3. Рассмотрим  , где А — матрица размером
, где А — матрица размером  — вектор
— вектор  и Y —вектор
и Y —вектор  . Покажите, что
. Покажите, что  эквивалентно
эквивалентно

где  предполагается невырожденной. В теории матриц
предполагается невырожденной. В теории матриц  называется обобщенной обратной, или псевдообратной по отношению к матрице А.
называется обобщенной обратной, или псевдообратной по отношению к матрице А.
Примечание. Используйте следующие равенства:

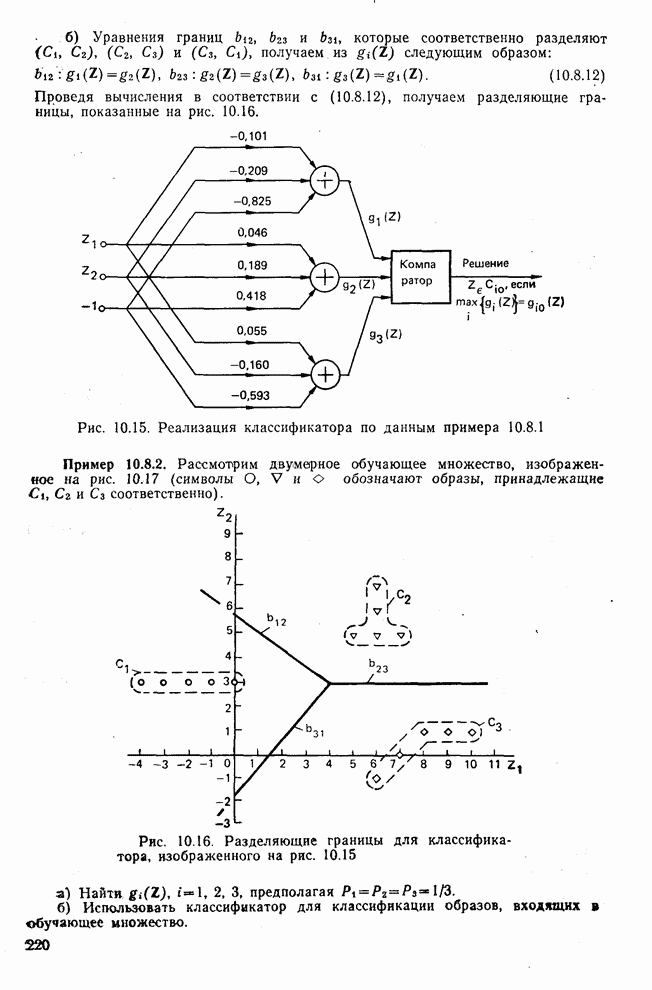
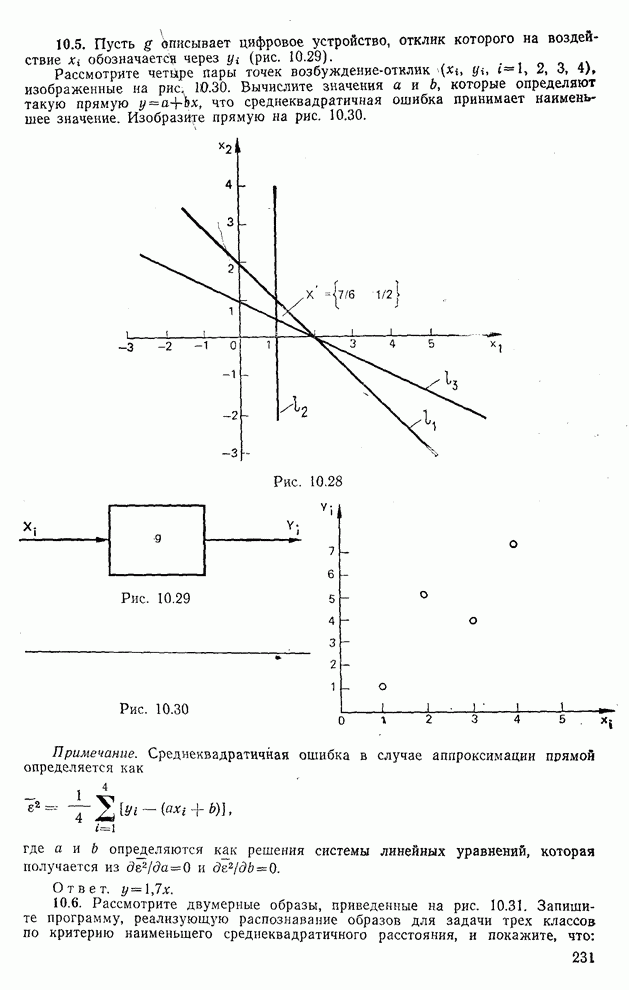
10.4. Рассмотрите матричное уравнение

Три линейных уравнения, соответствующих описанному выше матричному уравнению, определяют на плоскости прямые  и
и  , изображенные на рис. 10.28. Из рис. 10.28 видно, что данные три прямые
, изображенные на рис. 10.28. Из рис. 10.28 видно, что данные три прямые  не пересекаются в одной точке, что означает отсутствие единственного решения. Другими словами, уравнение
не пересекаются в одной точке, что означает отсутствие единственного решения. Другими словами, уравнение  соответствует множеству несовместимых уравнений.
соответствует множеству несовместимых уравнений.
Пользуясь выражением  , покажите, что решение в смысле наименьших квадратов для множества несовместимых уравнений, описанных
, покажите, что решение в смысле наименьших квадратов для множества несовместимых уравнений, описанных  , имеет вид
, имеет вид  .
.
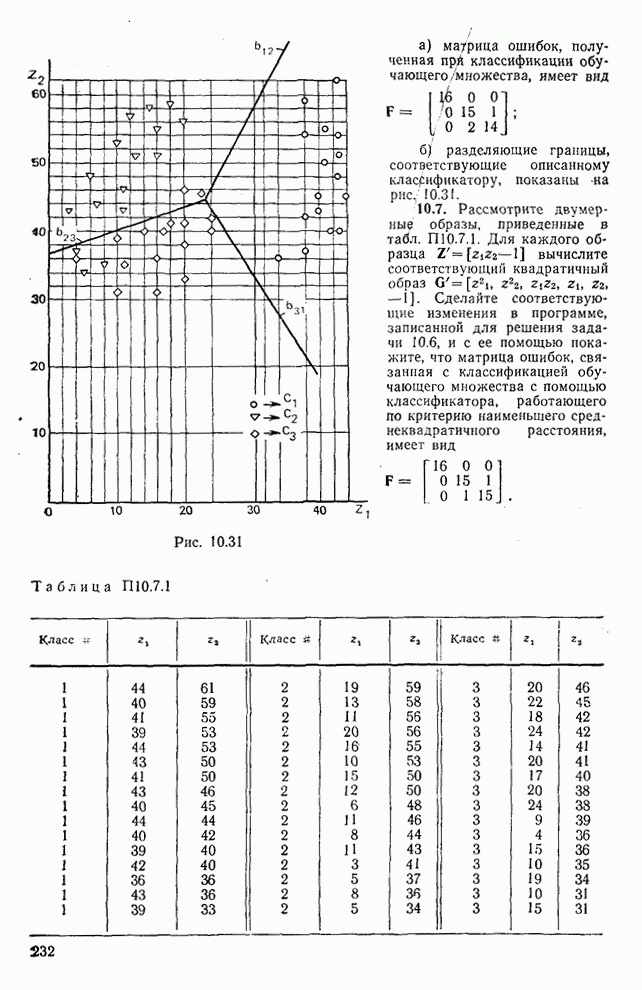
10.5. Пусть g описывает цифровое устройство, отклик которого на воздействие  обозначается через (рис. 10.29).
обозначается через (рис. 10.29).
Рассмотрите четыре пары точек возбуждение-отклик  , изображенные на рис. 10.30. Вычислите значения а и b, которые определяют такую прямую
, изображенные на рис. 10.30. Вычислите значения а и b, которые определяют такую прямую  , что среднеквадратичная ошибка принимает наименьшее значение. Изобразите прямую на рис. 10.30.
, что среднеквадратичная ошибка принимает наименьшее значение. Изобразите прямую на рис. 10.30.

Рис. 10.28.

Рис. 10.29.

Рис. 10.30.
Примечание. Среднеквадратичная ошибка в случае аппроксимации прямой определяется как

где а и b определяются как решения системы линейных уравнений, которая получается из  и
и  .
.
Ответ.  .
.
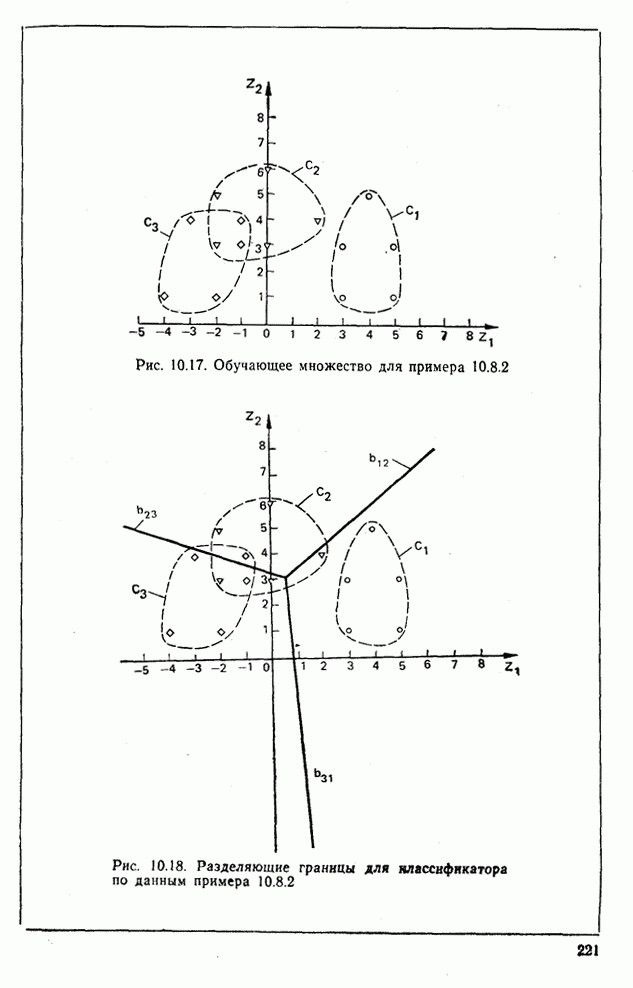
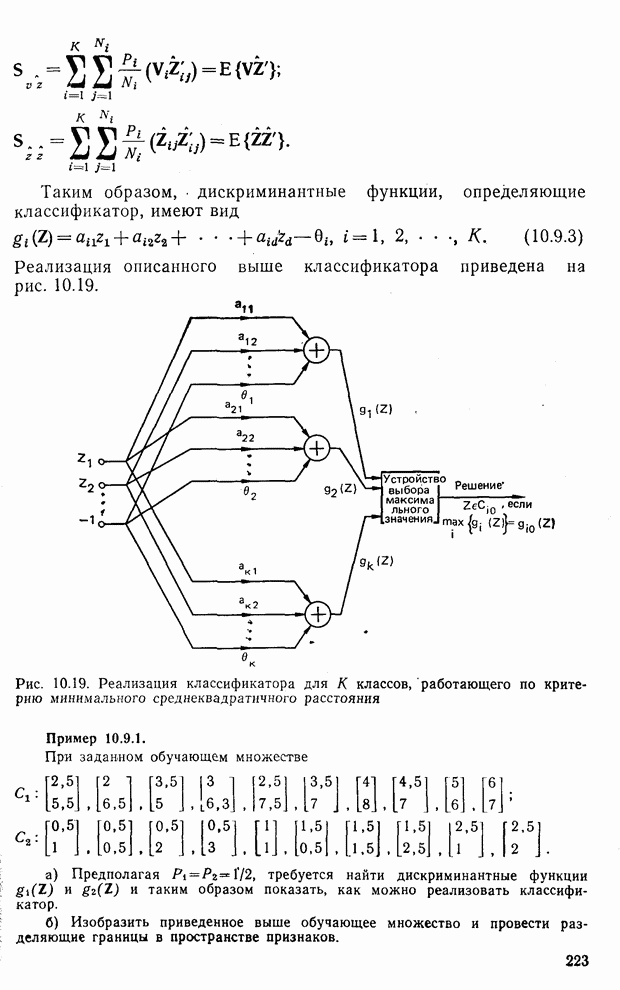
10.6. Рассмотрите двумерные образы, приведенные на рис. 10.31. Запишите программу, реализующую распознавание образов для задачи трех классов по критерию наименьшего среднеквадратичного расстояния, и покажите, что:
а) матрица ошибок, полученная при классификации обучающего множества, имеет вид

б) разделяющие границы, соответствующие описанному классификатору, показаны на  .
.
10.7. Рассмотрите двумерные образы, приведенные в табл. П10.7.1. Для каждого образца  вычислите соответствующий квадратичный образ
вычислите соответствующий квадратичный образ  . Сделайте соответствующие изменения в программе, записанной для решения задачи 10.6, и с ее помощью покажите, что матрица ошибок, связанная с классификацией обучающего множества с помощью классификатора, работающего по критерию наименьшего среднеквадратичного расстояния, имеет вид
. Сделайте соответствующие изменения в программе, записанной для решения задачи 10.6, и с ее помощью покажите, что матрица ошибок, связанная с классификацией обучающего множества с помощью классификатора, работающего по критерию наименьшего среднеквадратичного расстояния, имеет вид


Рис. 10.31
Таблица П10.7.1
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
- 2.4. Связь между рядом Фурье и преобразованием Фурье
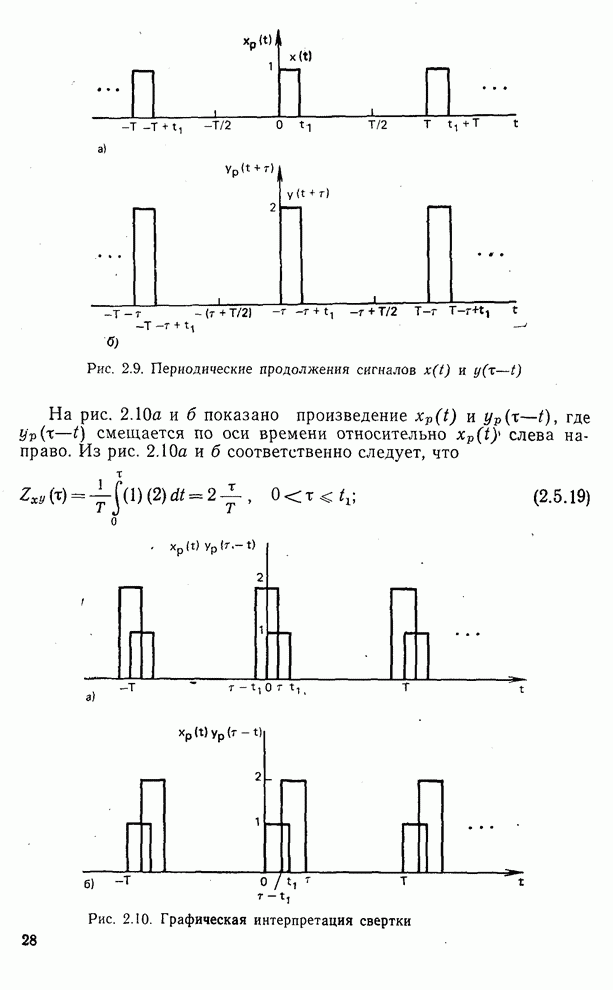
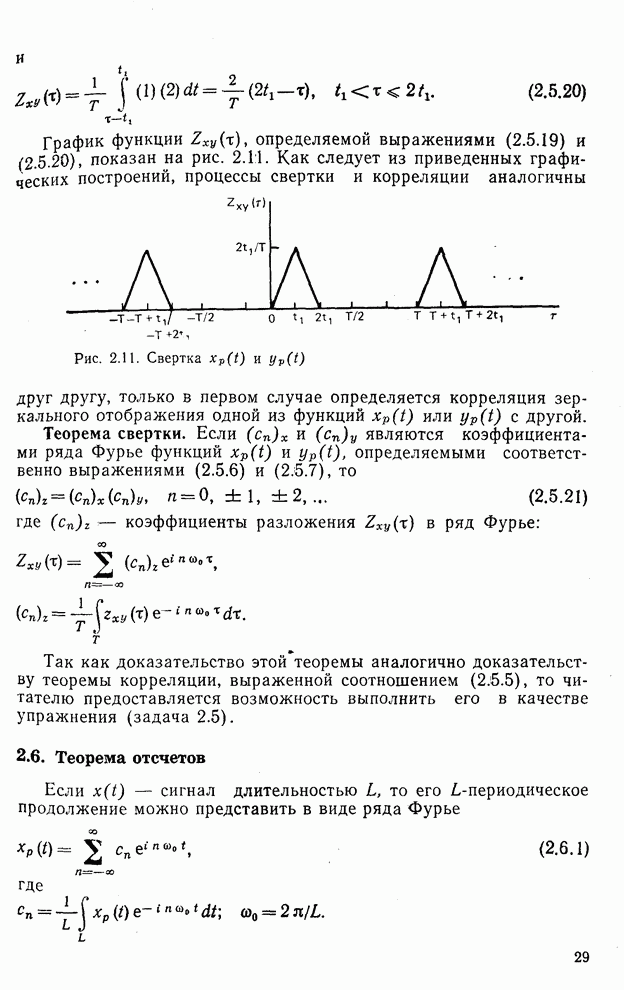
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
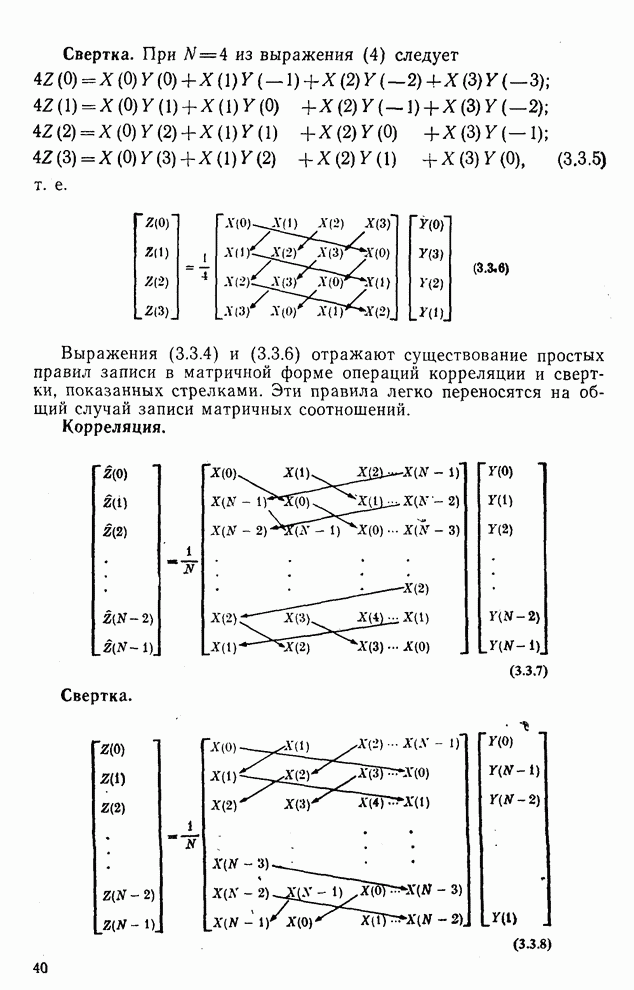
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
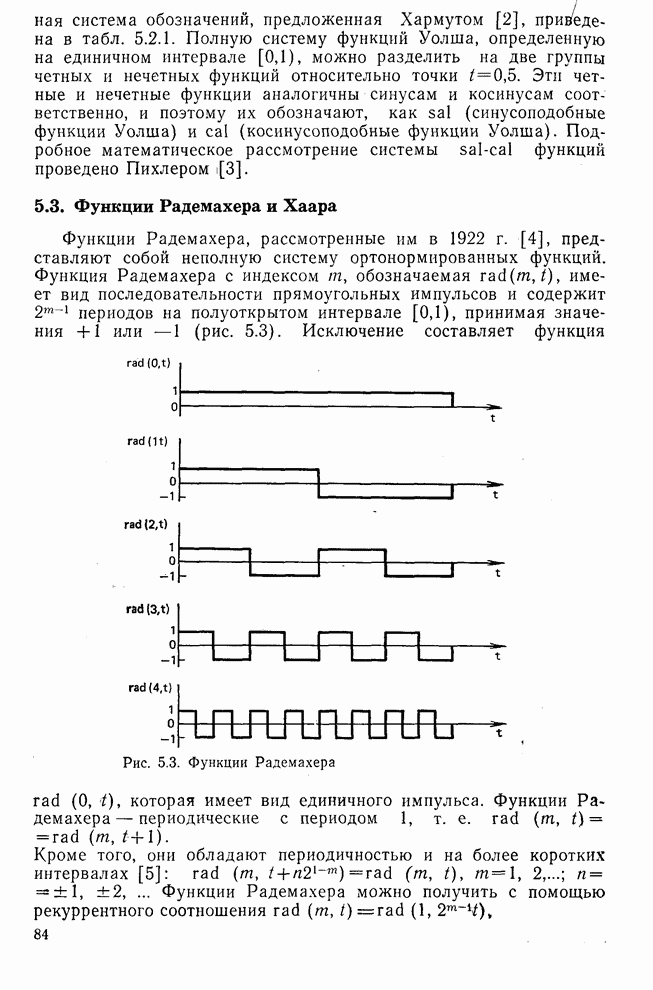
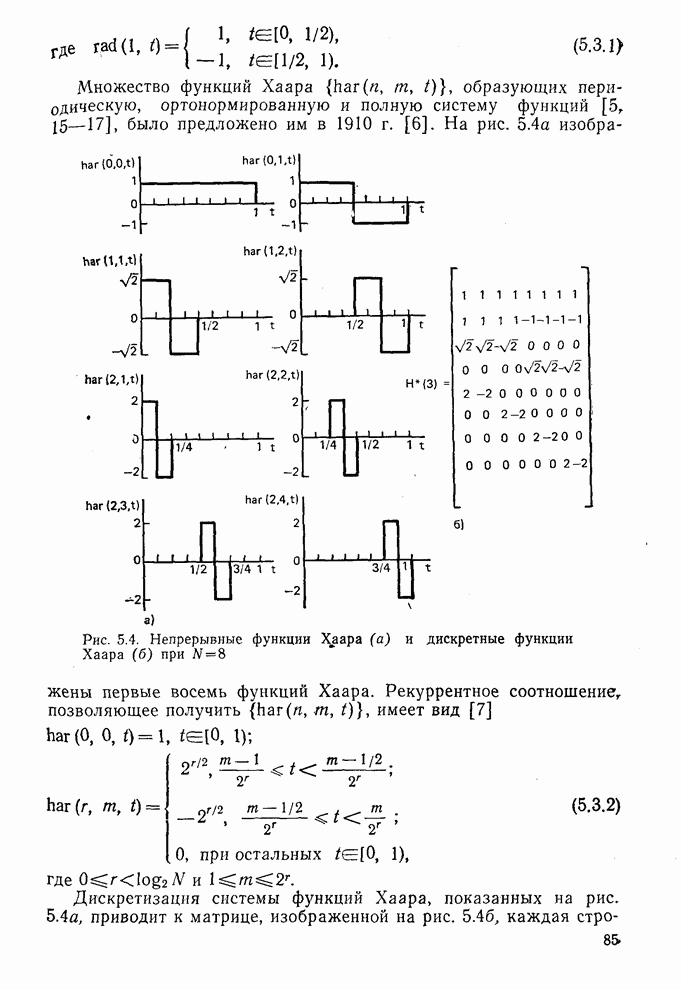
- 5.3. Функции Радемахера и Хаара
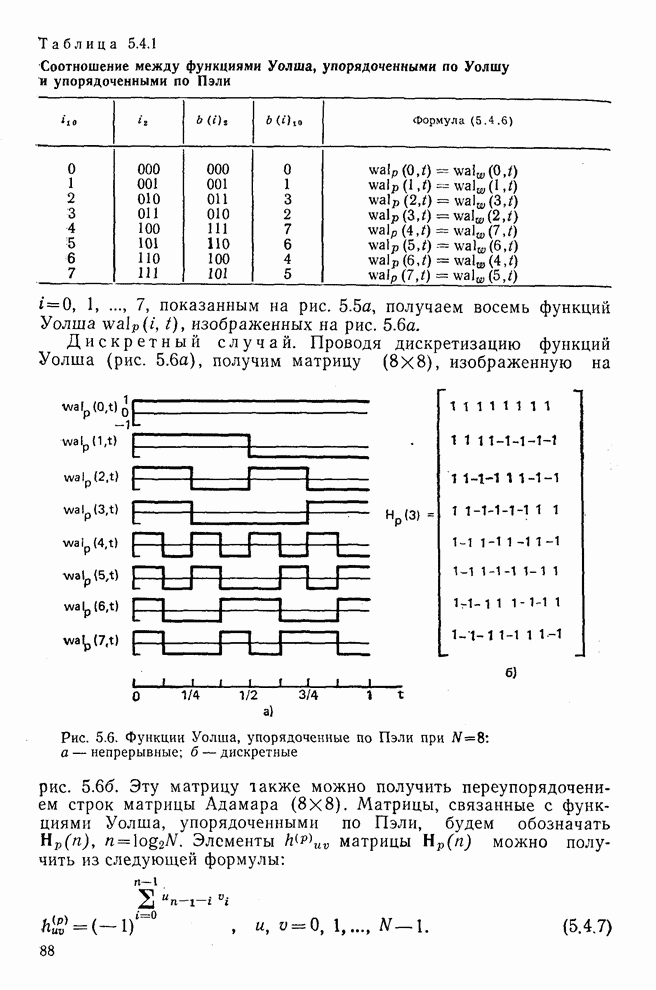
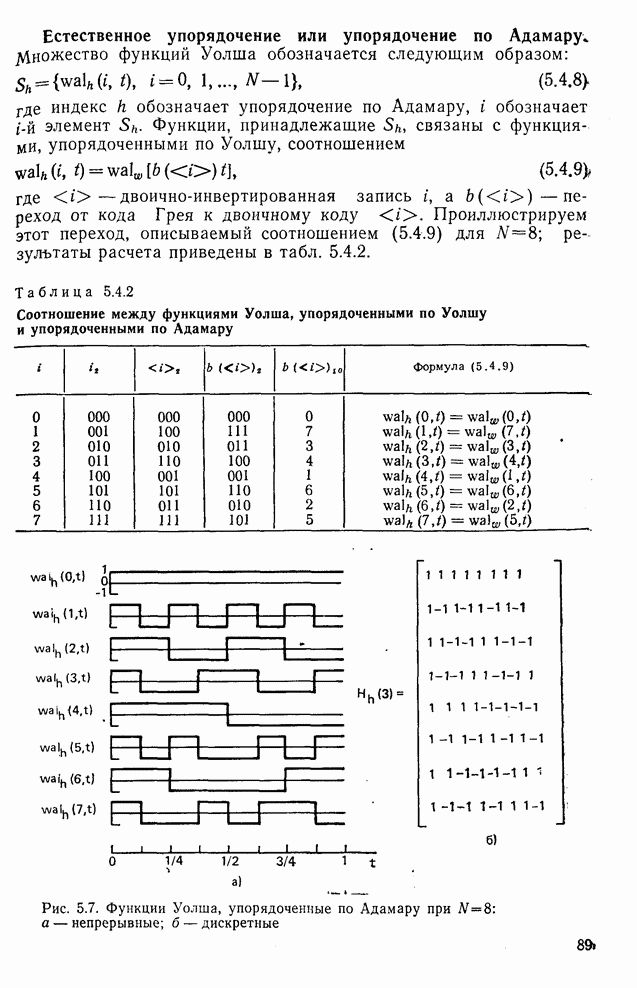
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
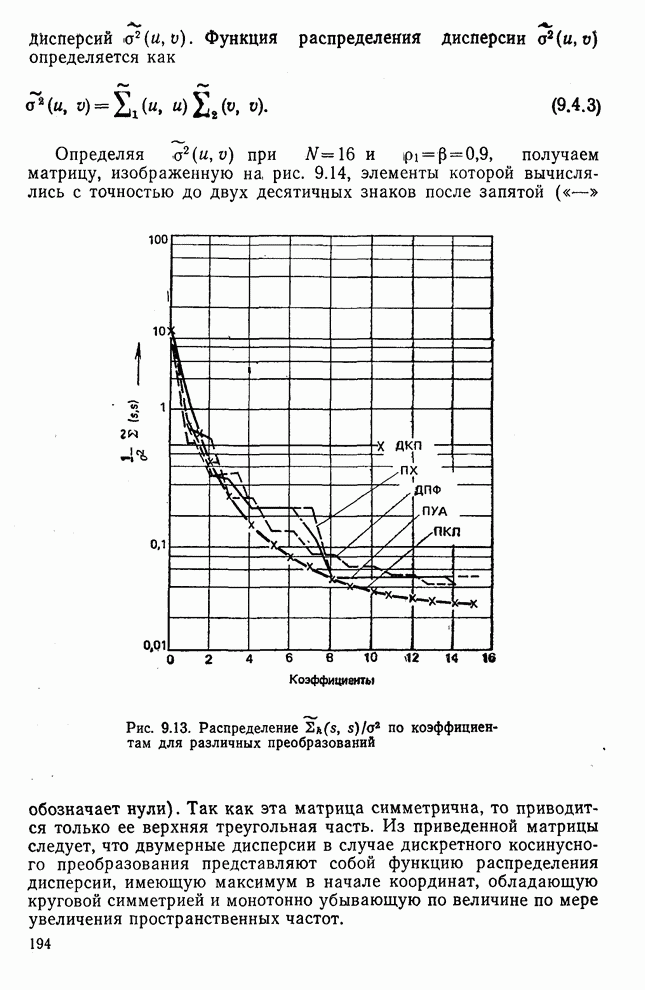
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
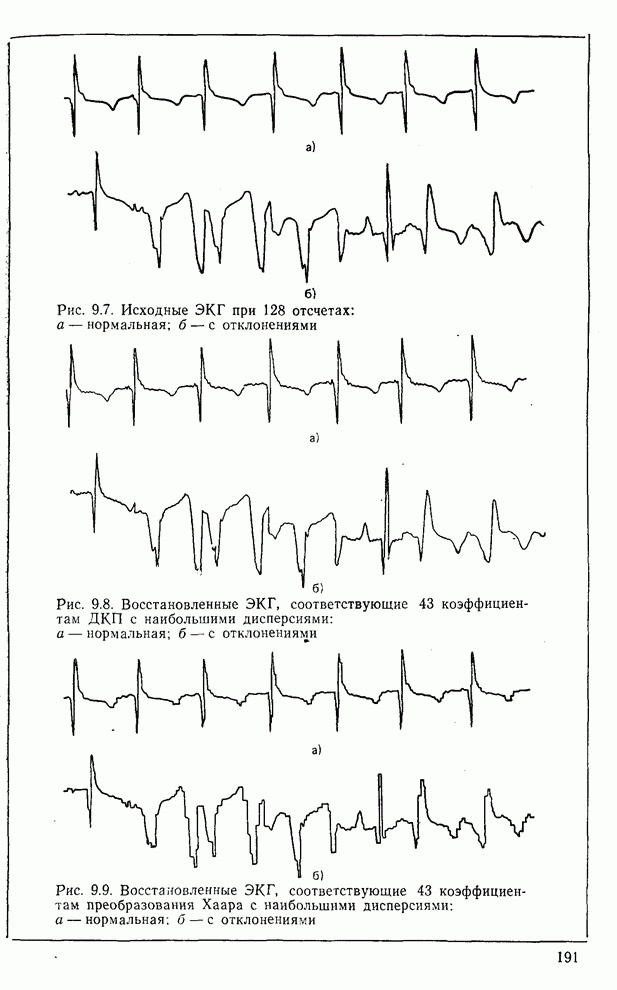
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
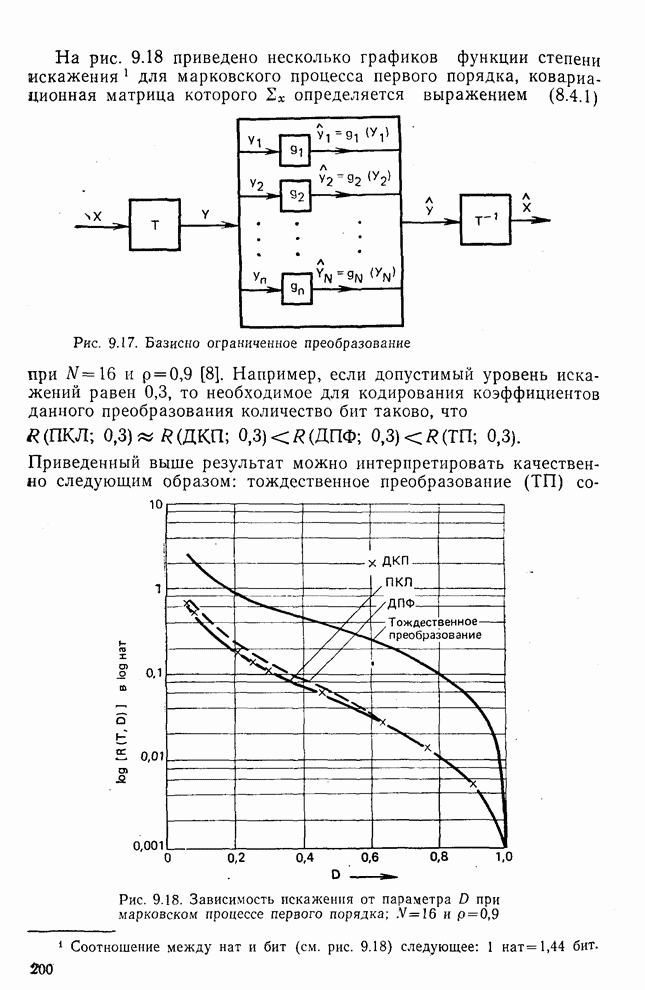
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
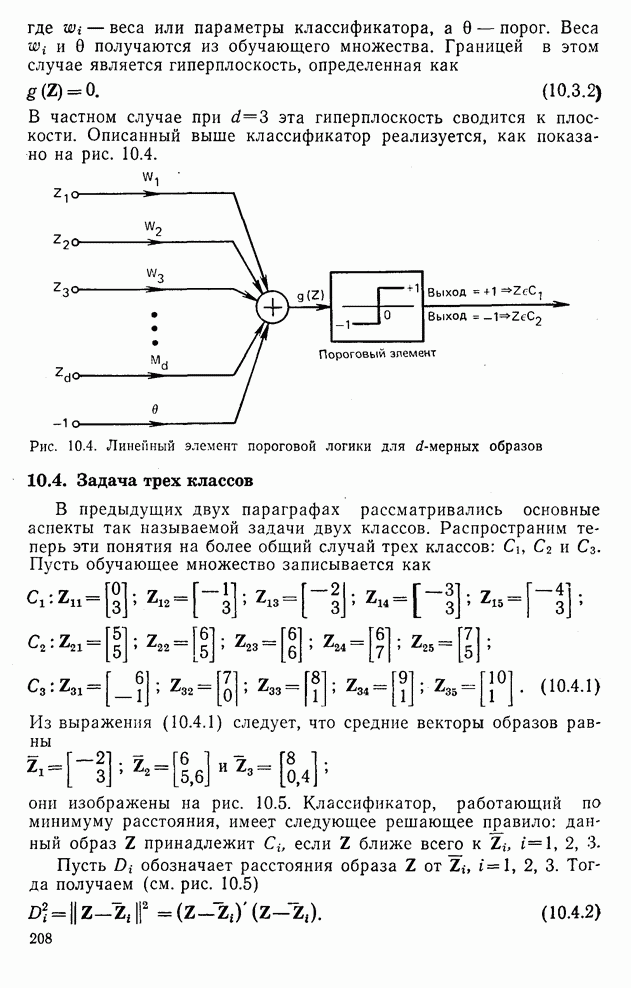
- 10.3. d-мерные образы
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
- 10.6. Метод отображения по методу наименьших квадратов
- 10.7. Расширенное пространство признаков
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
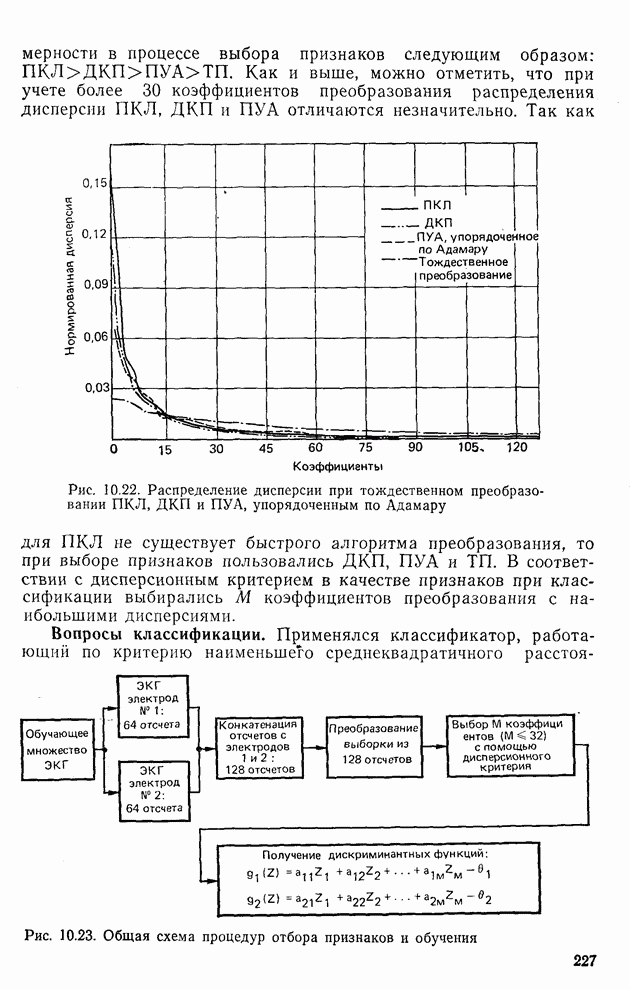
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ