| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.7. Мгновенный спектр Фурье
Если  — сигнал с полосой В Гц, то соответствующий ему дискретный сигнал
— сигнал с полосой В Гц, то соответствующий ему дискретный сигнал  определяется как
определяется как

где  отсчет и
отсчет и  . Преобразование Фурье сигнала
. Преобразование Фурье сигнала  определяется как
определяется как
 (3.7.1)
(3.7.1)
Теперь покажем, что спектр мощности и фазовый спектр, соответствующие  , могут быть вычислены реккурентно в моменты времени
, могут быть вычислены реккурентно в моменты времени  . Следовательно, спектр, полученный в результате такого вычисления, можно называть мгновенным спектром Фурье [7—9]. Будем предполагать, что необходимо знать спектры на множестве частот
. Следовательно, спектр, полученный в результате такого вычисления, можно называть мгновенным спектром Фурье [7—9]. Будем предполагать, что необходимо знать спектры на множестве частот  . Допустим,
. Допустим,
что  означает сигнал, который является зеркальным отображением
означает сигнал, который является зеркальным отображением  т. е.
т. е.
 (3.7.2)
(3.7.2)
Преобразование Фурье  при
при  определяется как
определяется как
 (3.7.3)
(3.7.3)
Можно показать [см. приложение 3.1], что спектры мощности и фазовые спектры сигналов  и
и  связаны следующими соотношениями:
связаны следующими соотношениями:

и
 (3.7.4)
(3.7.4)
Рекуррентный способ вычисления спектров  и
и  . Из (3.7.3) имеем
. Из (3.7.3) имеем
 (3.7.5)
(3.7.5)
где

и

Запишем  в виде вектора
в виде вектора  размером
размером 
 (3.7.6)
(3.7.6)
Теперь рассмотрим матрицу размером 

Можно показать, что матрица  является ортогональной (см. задачу 3.9) и, следовательно, обладает следующим свойством:
является ортогональной (см. задачу 3.9) и, следовательно, обладает следующим свойством:

где  означает
означает  степень
степень  . Таким образом, из
. Таким образом, из
Из этого выражения следует, что
 (3.7.16)
(3.7.16)
где  коэффициент ДПФ. Объединяя выражения (3.7.15) и (3.7.16), получаем следующие выражения для мгновенного спектра мощности и фазового спектра ДПФ:
коэффициент ДПФ. Объединяя выражения (3.7.15) и (3.7.16), получаем следующие выражения для мгновенного спектра мощности и фазового спектра ДПФ:
 (3.7.17)
(3.7.17)
и

где  . Полученное выше выражение для мгновенного спектра позволяет проследить характер изменения спектра, дискретного
. Полученное выше выражение для мгновенного спектра позволяет проследить характер изменения спектра, дискретного

Рис. 3.4. Мгновенный энергетический спектр затухающей синусоиды с частотой 4 Гц
сигнала по мере обработки соответствующей временной последовательности данных  .
.
Это можно проиллюстрировать с помощью следующего конкретного числового примера.
Пример 3.7.1. Рассмотрим последовательность данных

которая получается в результате дискретизации по времени со скоростью 26 отсчетов в секунду затухающей синусоиды частотой 4 Гц, т. е.  с. Необходимо определить мгновенный спектр мощности
с. Необходимо определить мгновенный спектр мощности  , на множестве из 20 частот, которые равномерно отстоят друг от друга по логарифмической шкале и определяются набором чисел:
, на множестве из 20 частот, которые равномерно отстоят друг от друга по логарифмической шкале и определяются набором чисел:  1,55; 1,74; 1,96; 2,20; 2,48; 2,79; 3,14; 3,53; 3,97, 4,47; 5,03; 5,65; 6,36; 7,15; 8,05; 9,06; 10,19; 11,46; 12,89}. Результаты вычислений
1,55; 1,74; 1,96; 2,20; 2,48; 2,79; 3,14; 3,53; 3,97, 4,47; 5,03; 5,65; 6,36; 7,15; 8,05; 9,06; 10,19; 11,46; 12,89}. Результаты вычислений  в виде двумерной таблицы «время—частота—амплитуда» приведены на рис. 3.4. Представленные в таблице значения
в виде двумерной таблицы «время—частота—амплитуда» приведены на рис. 3.4. Представленные в таблице значения  сначала были пронумерованы с помощью некоторого нормирующего множителя, а затем выражены в децибелах. Полученные таким образом значения обозначены
сначала были пронумерованы с помощью некоторого нормирующего множителя, а затем выражены в децибелах. Полученные таким образом значения обозначены  . Пояснение таблицы лучше всего провести с помощью следующих примеров:
. Пояснение таблицы лучше всего провести с помощью следующих примеров:
i)  и
и  означает, что
означает, что  больше
больше  на 6 дБ.
на 6 дБ.
ii)  и
и  означает, что
означает, что  больше
больше  на 13 дБ.
на 13 дБ.
Для удобства минимальное значение  было ограничено величиной
было ограничено величиной  . На частоте 3,97 Гц и примыкающих к ней частотах мощность значительно выше мощности на других частотах. Очевидно, это и следовало ожидать, поскольку дискретный сигнал является затухающей синусоидой с частотой 4 Гц.
. На частоте 3,97 Гц и примыкающих к ней частотах мощность значительно выше мощности на других частотах. Очевидно, это и следовало ожидать, поскольку дискретный сигнал является затухающей синусоидой с частотой 4 Гц.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
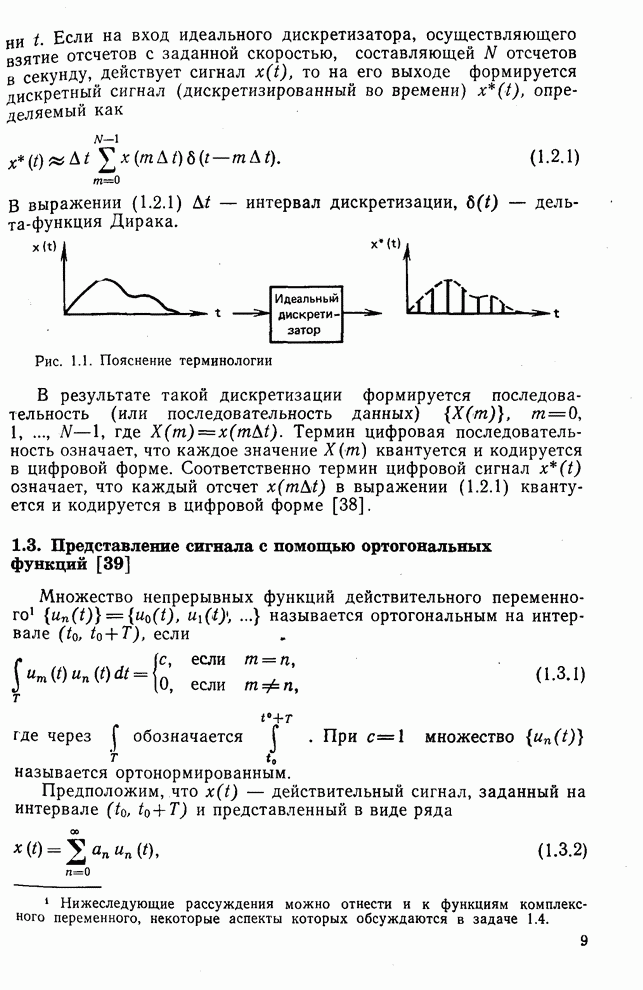
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
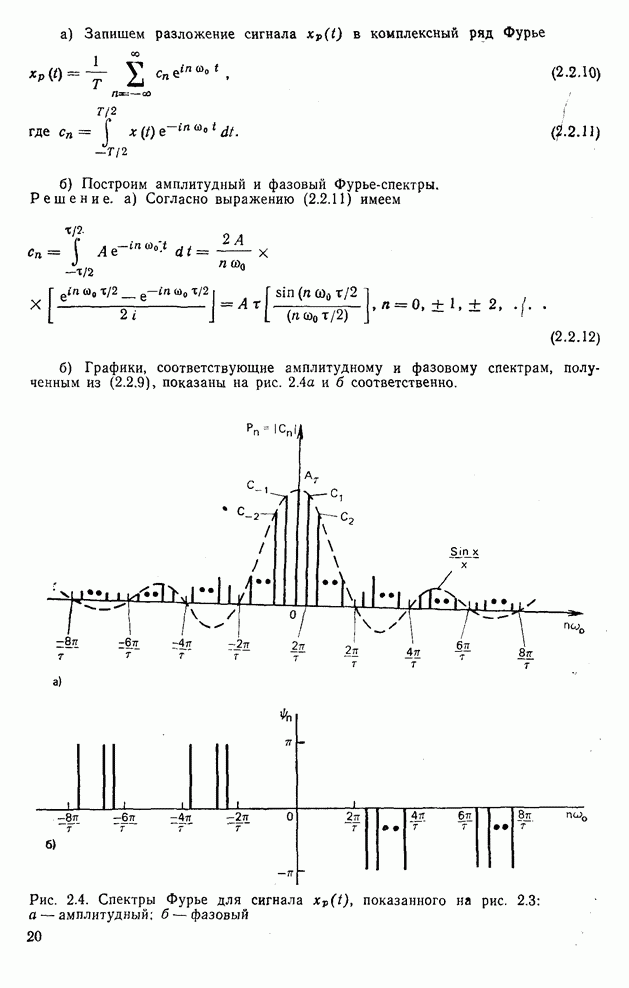
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
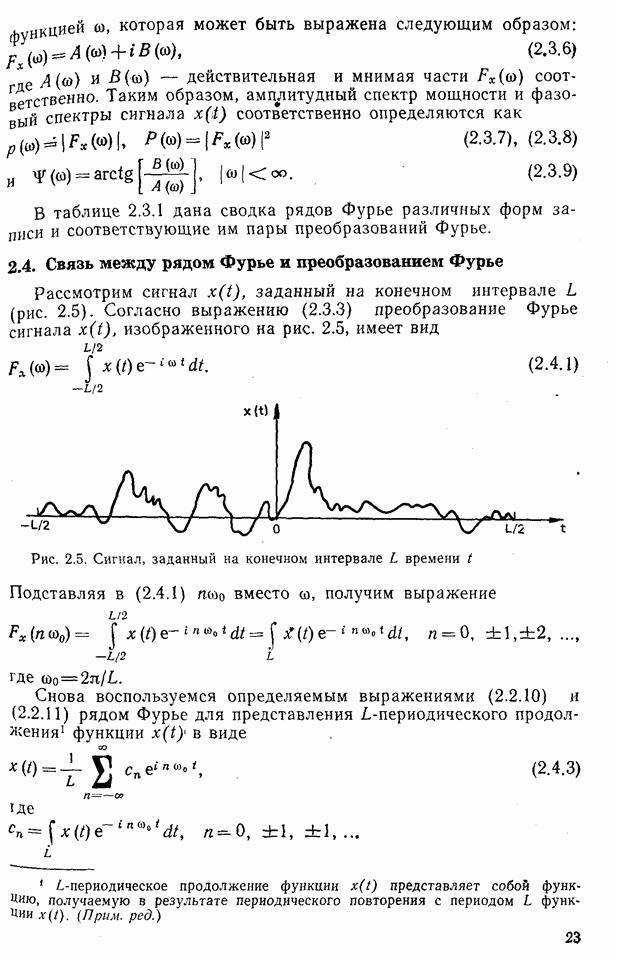
- 2.4. Связь между рядом Фурье и преобразованием Фурье
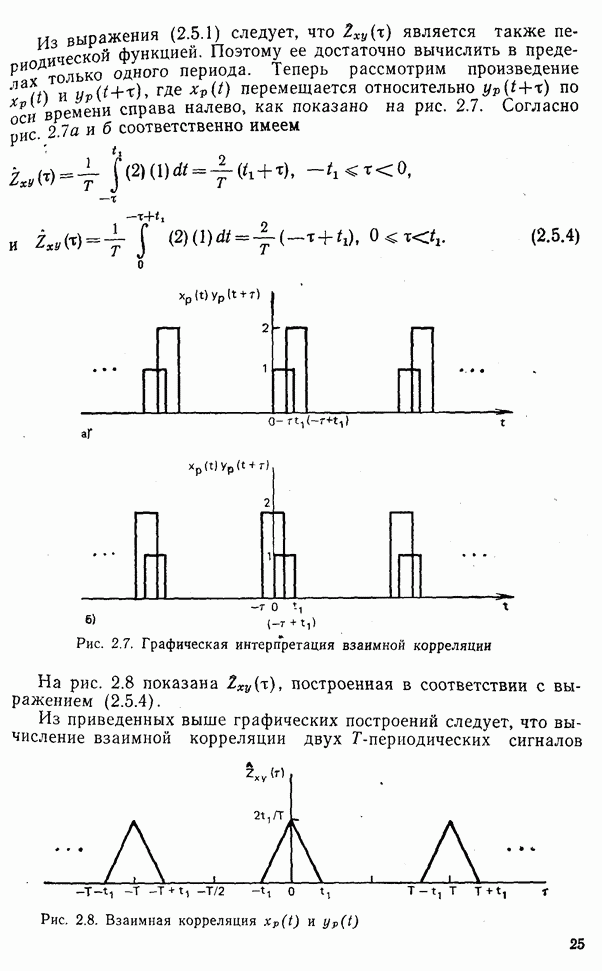
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
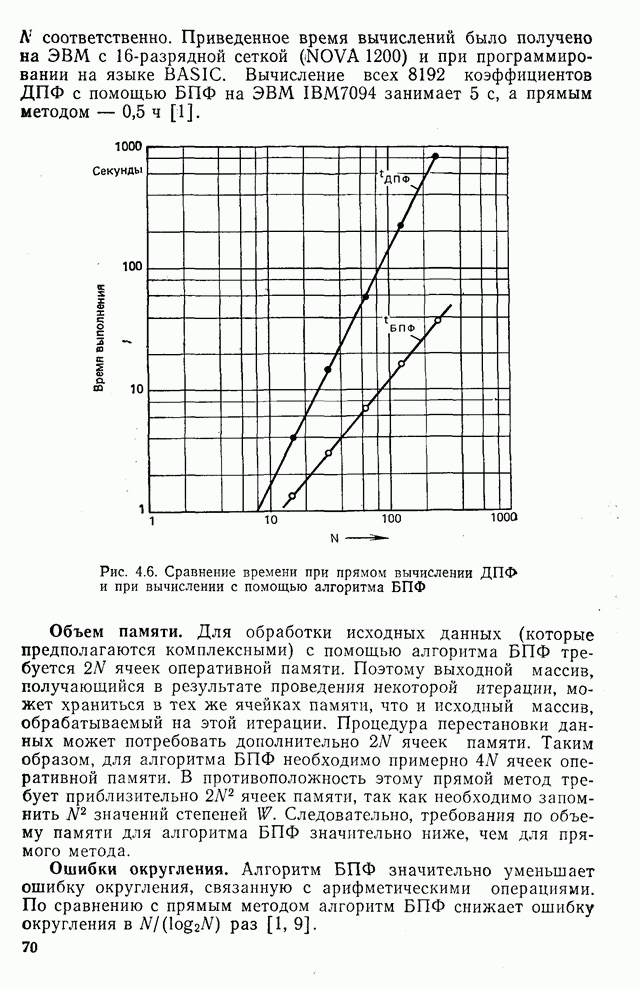
- 4.7. Объем вычислений и памяти
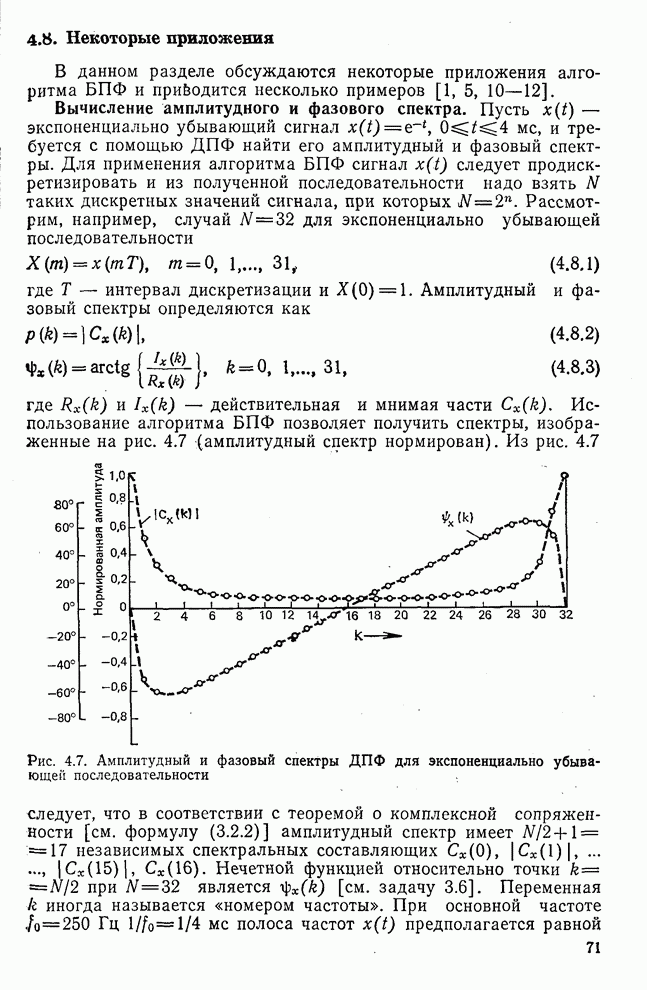
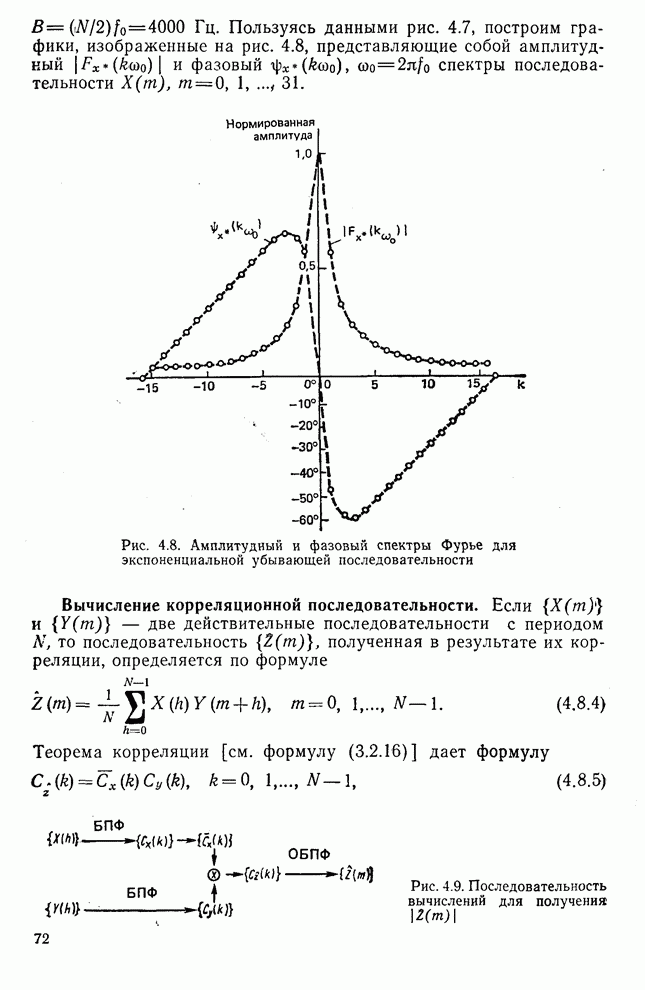
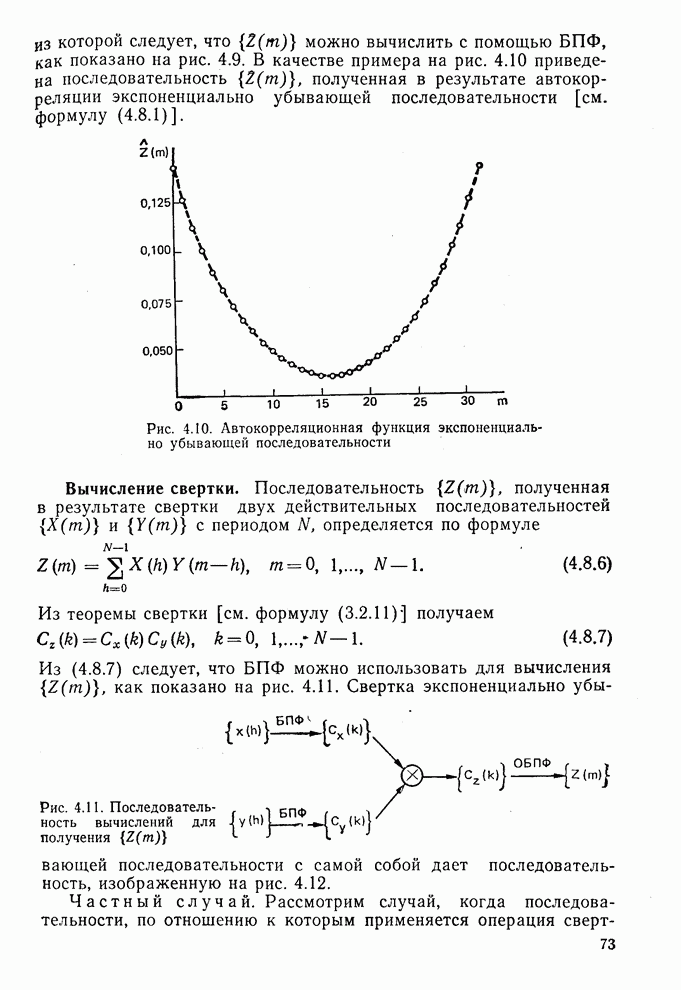
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
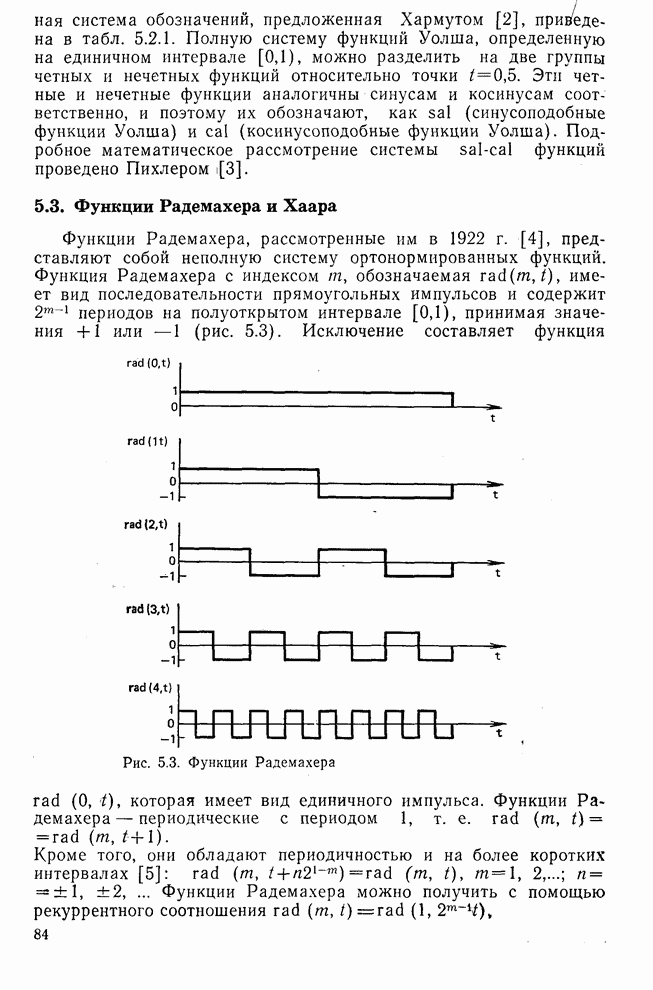
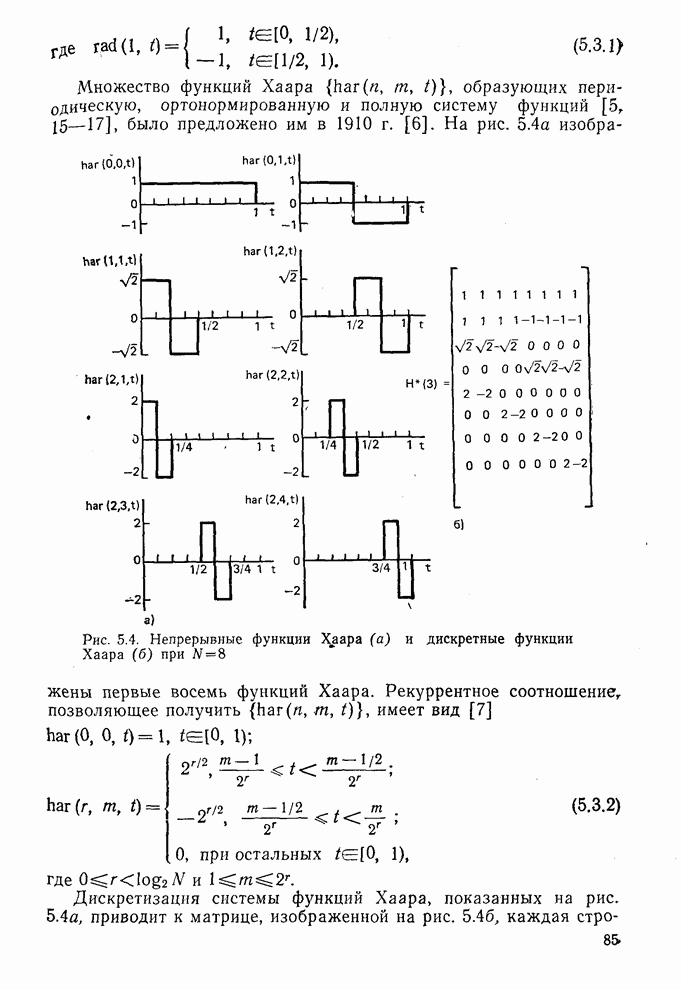
- 5.3. Функции Радемахера и Хаара
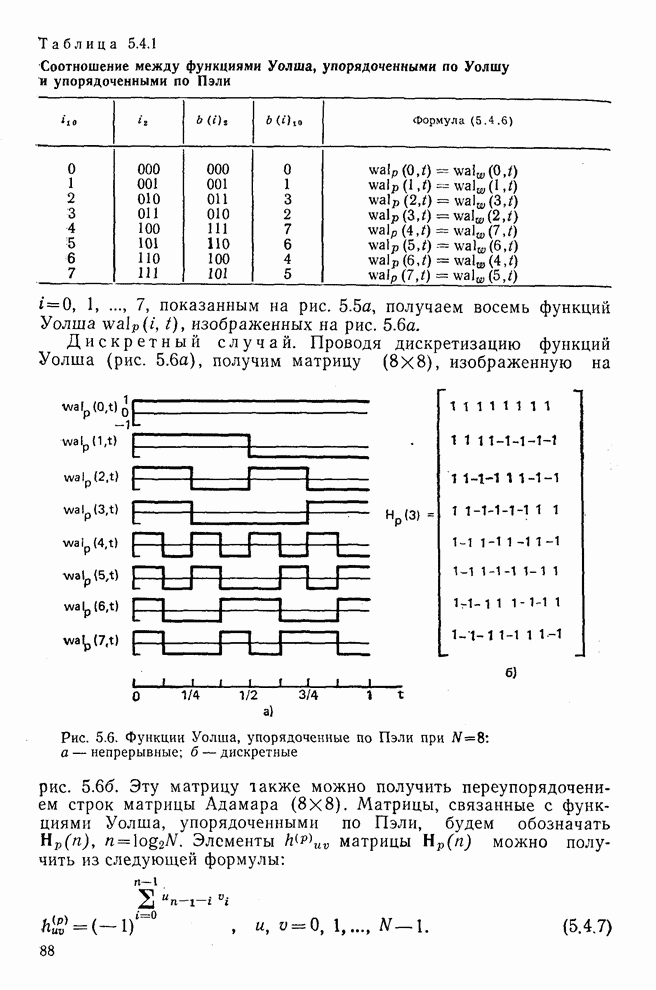
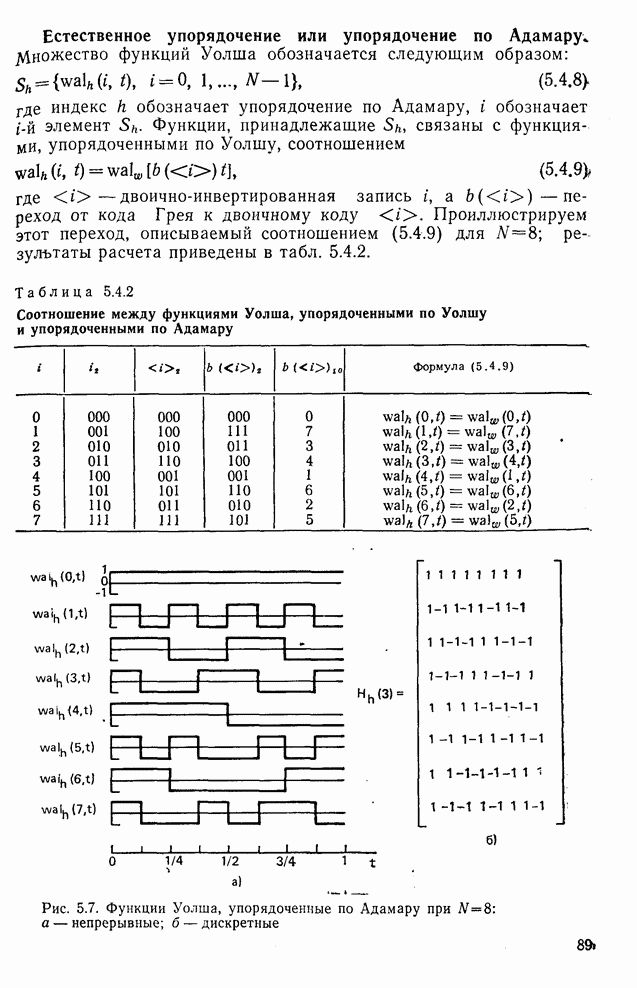
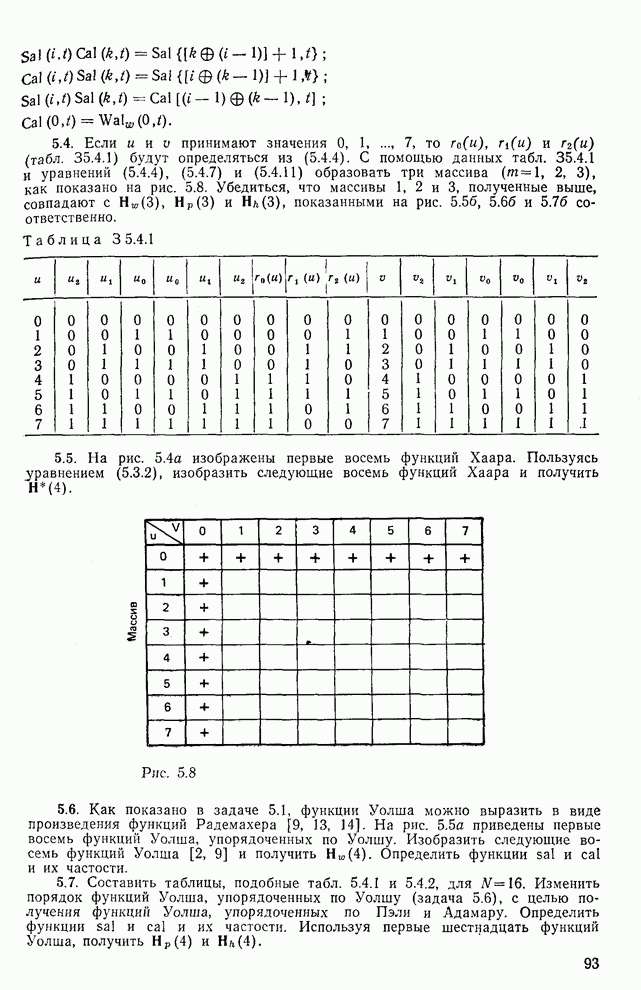
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
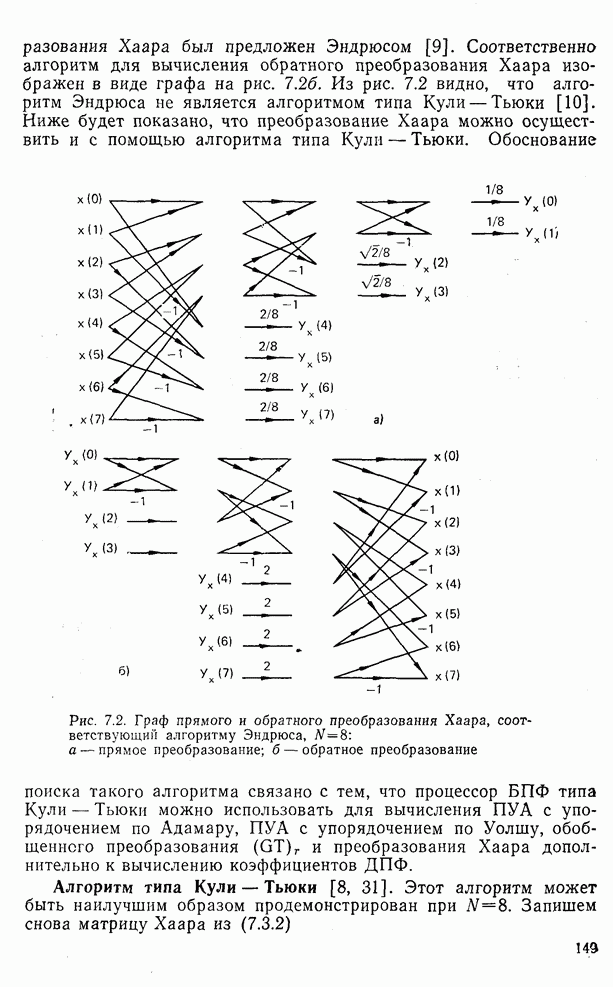
- 7.3. Преобразование Хаара [ПХ]
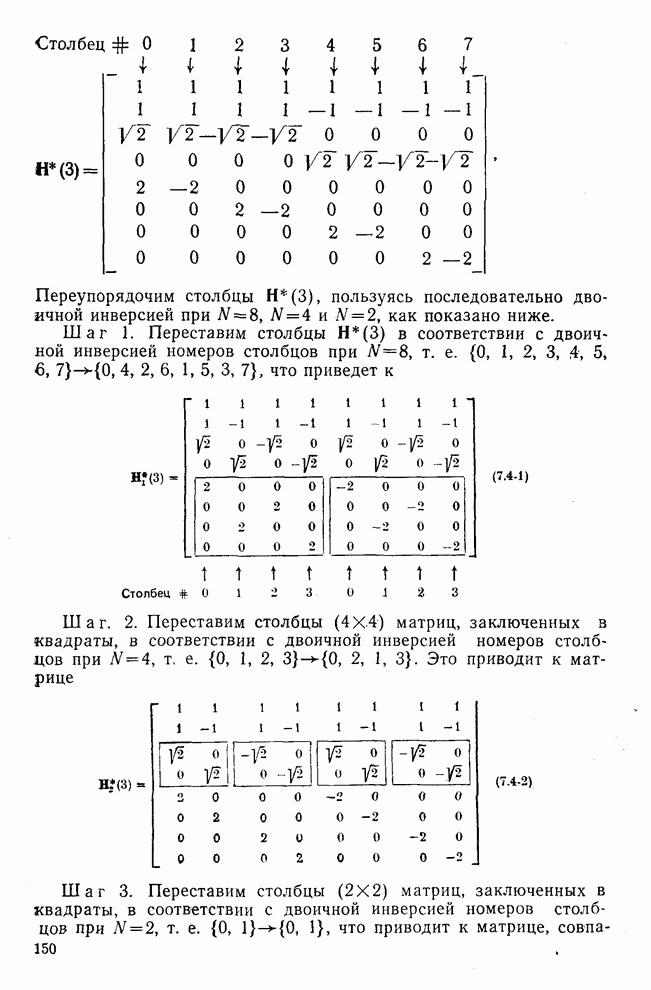
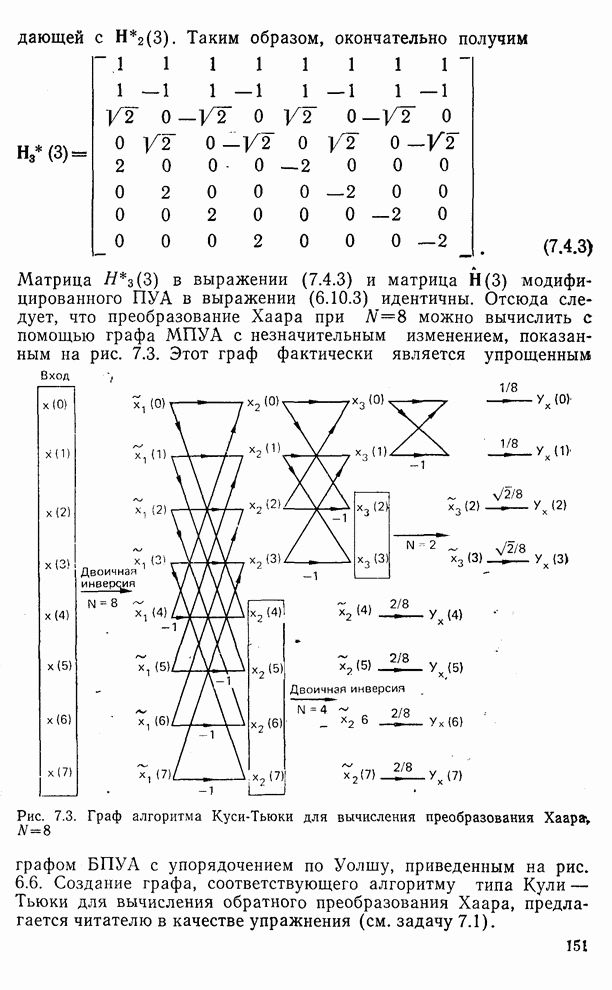
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
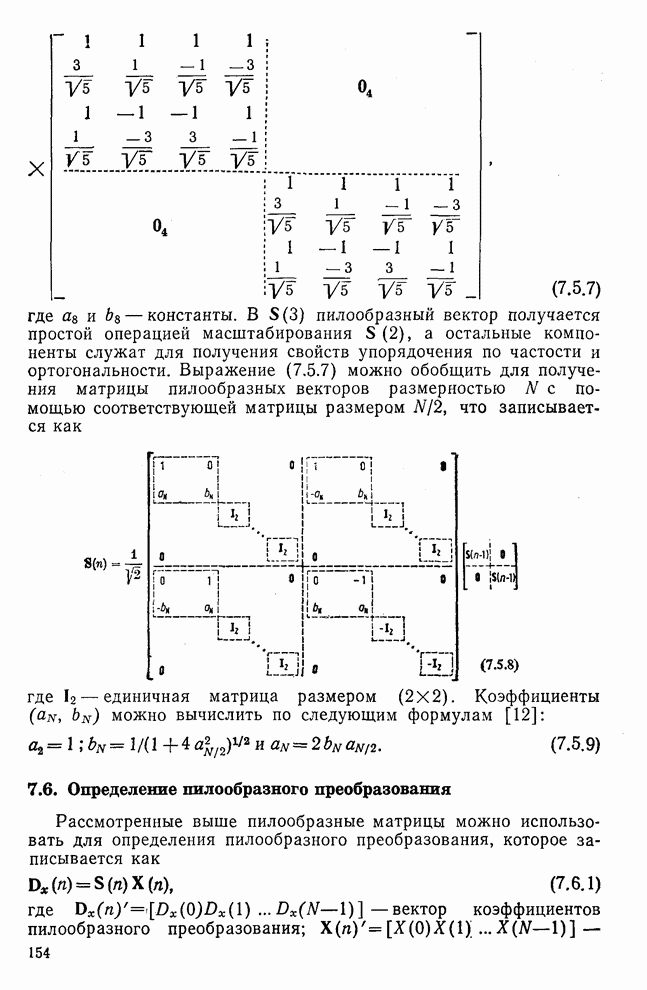
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
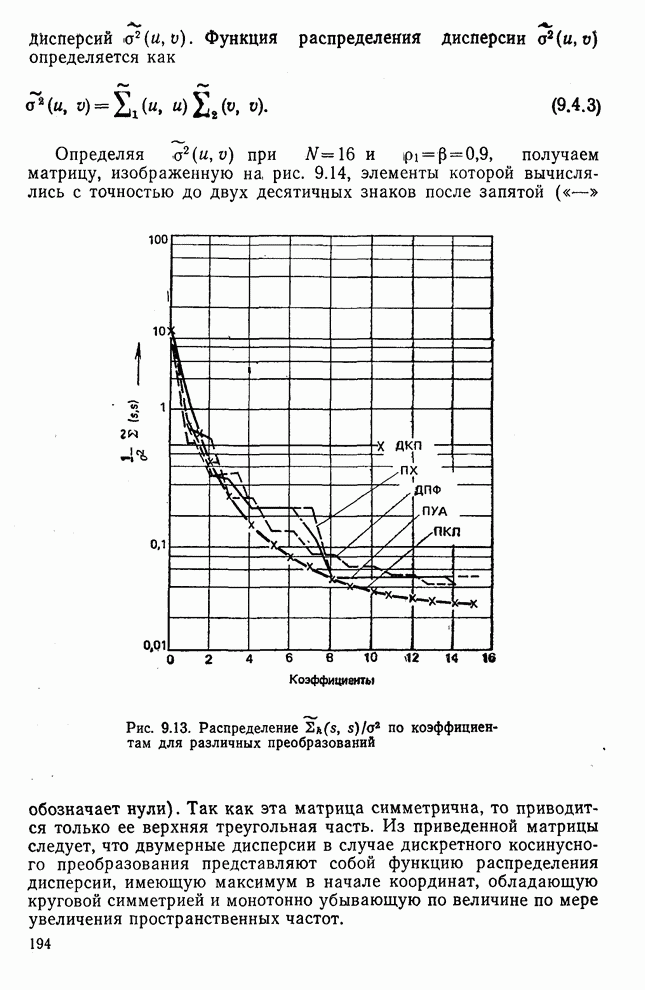
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
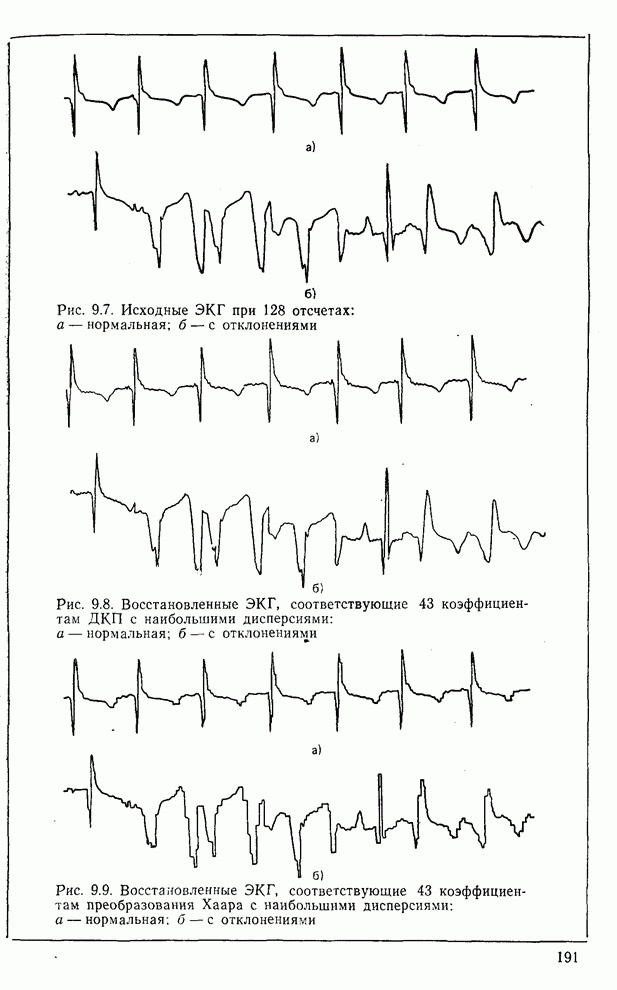
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
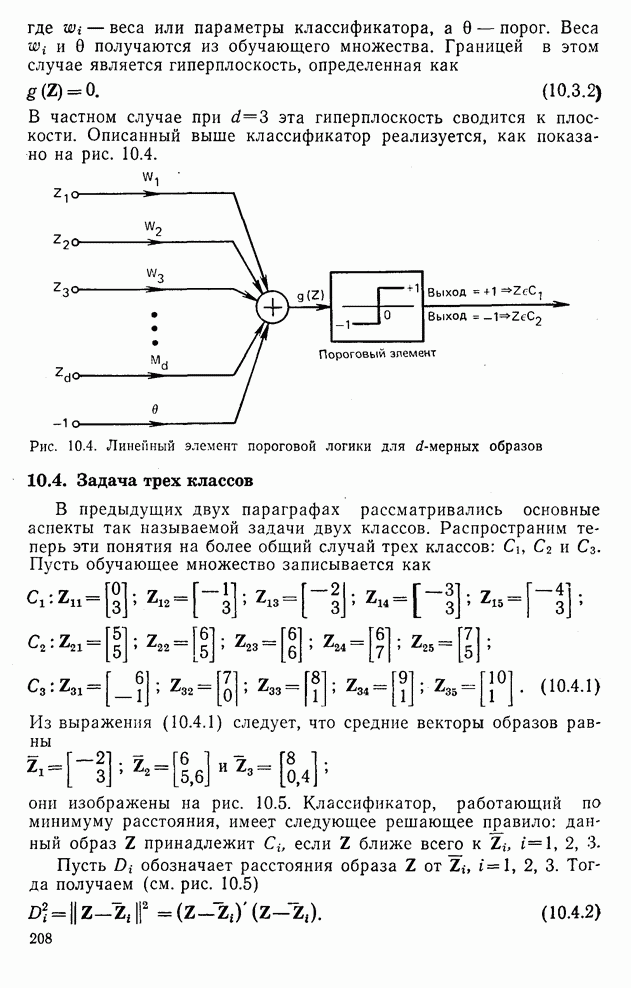
- 10.3. d-мерные образы
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
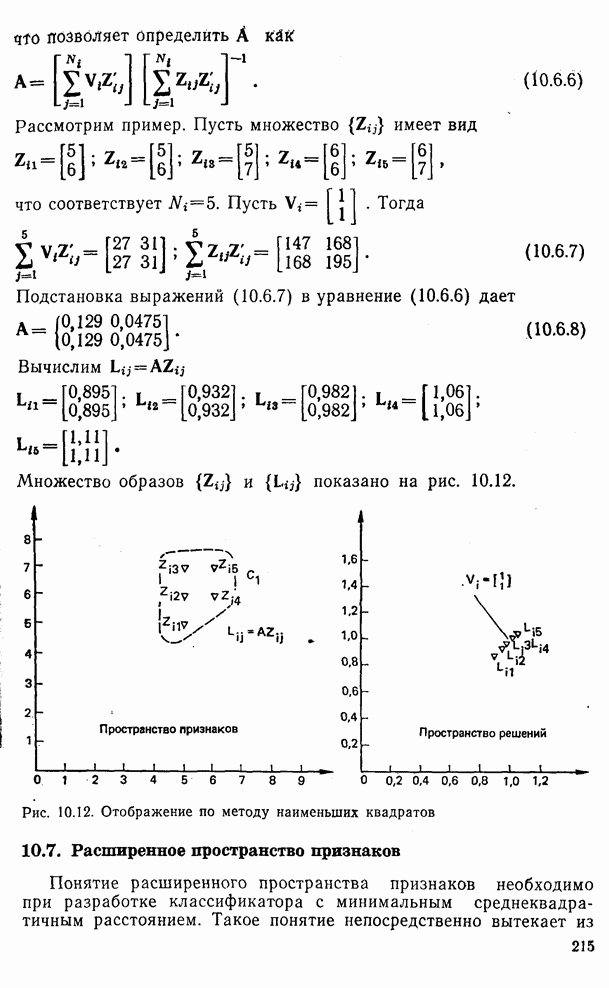
- 10.6. Метод отображения по методу наименьших квадратов
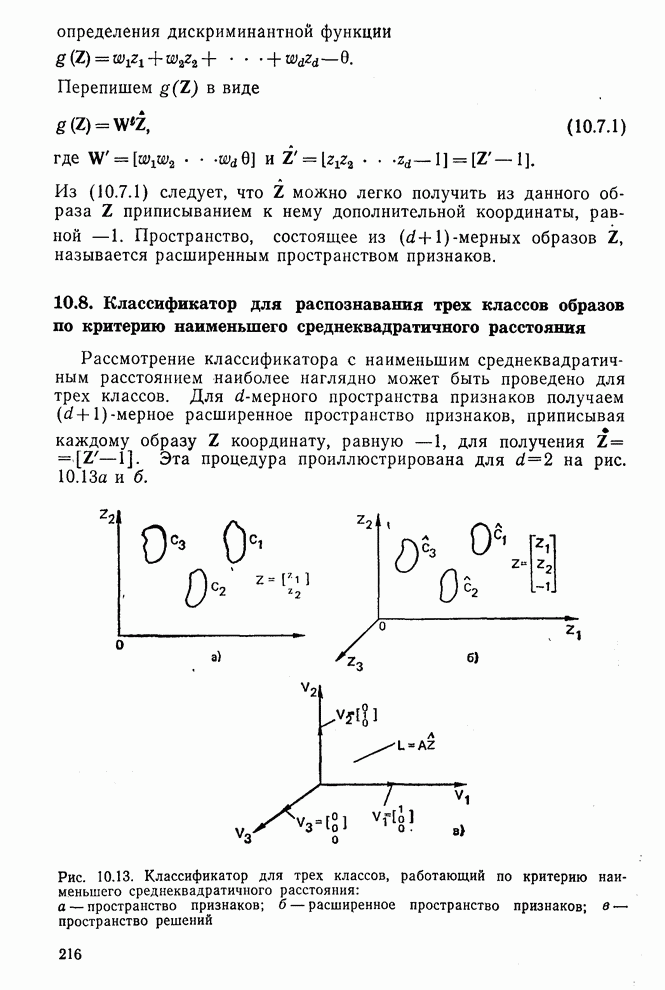
- 10.7. Расширенное пространство признаков
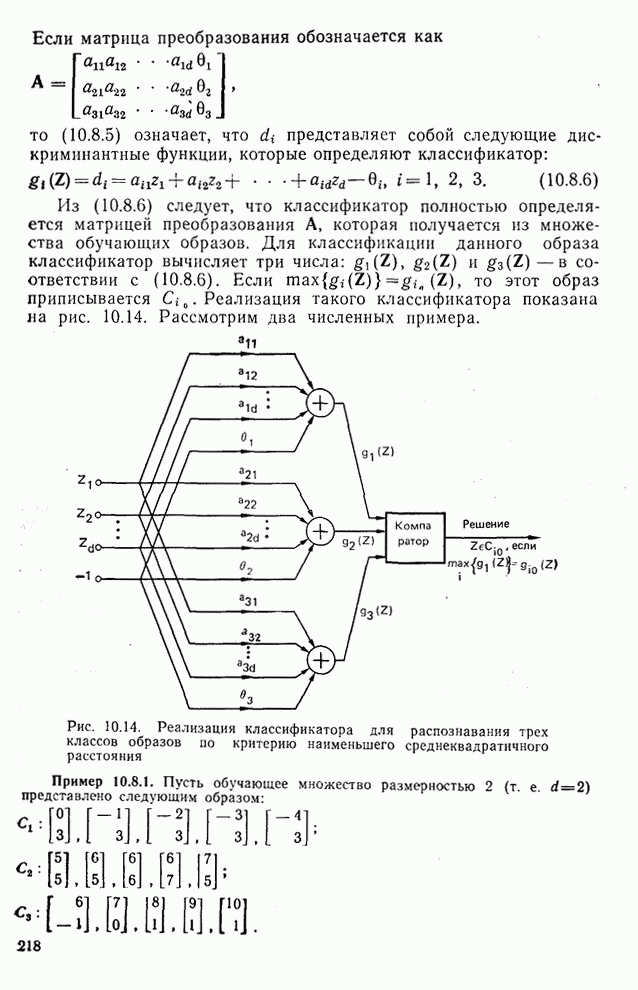
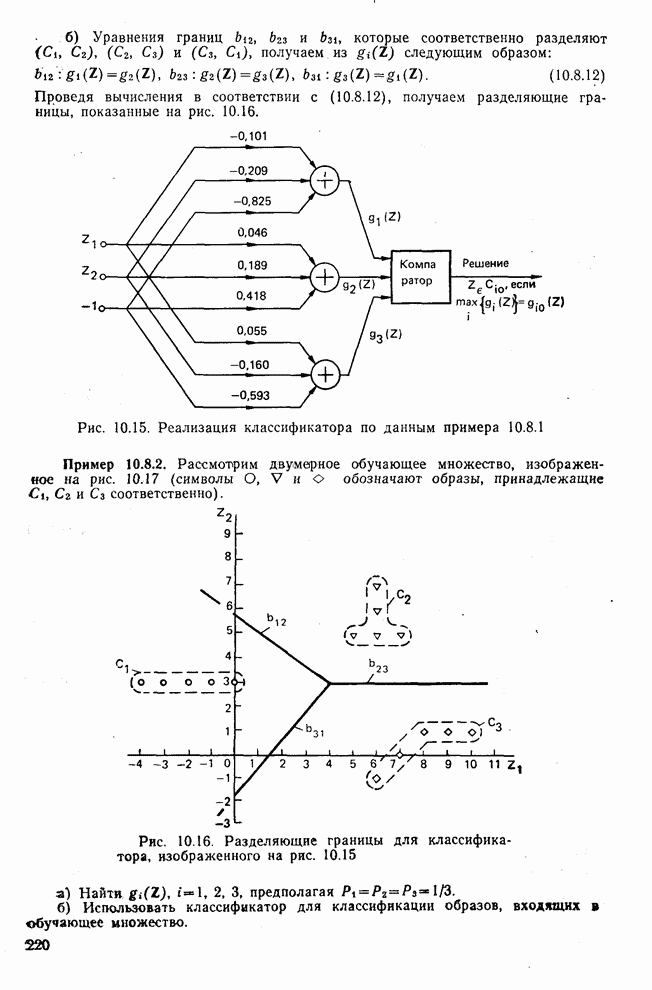
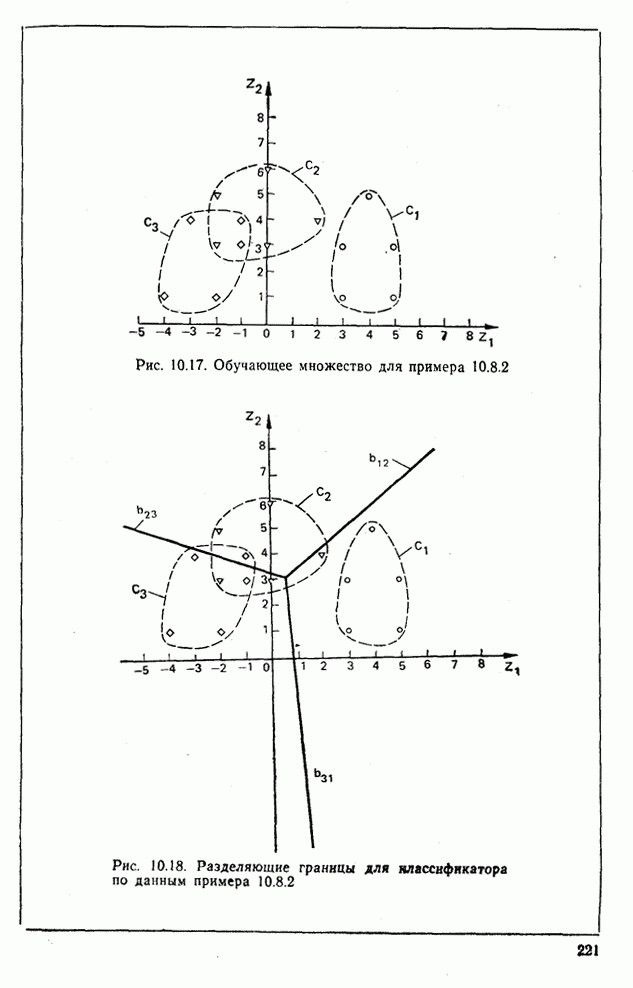
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
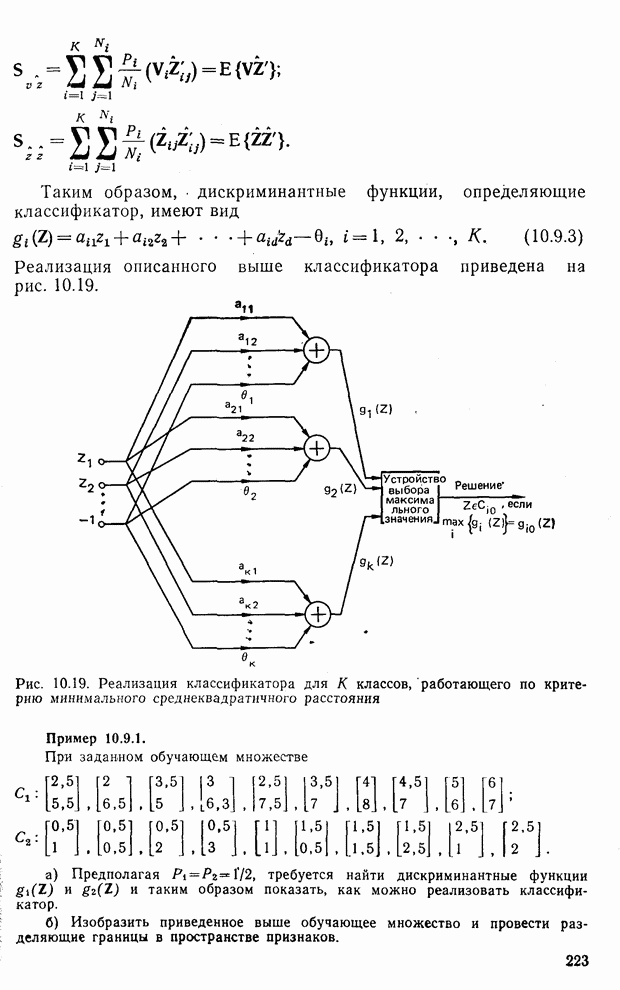
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
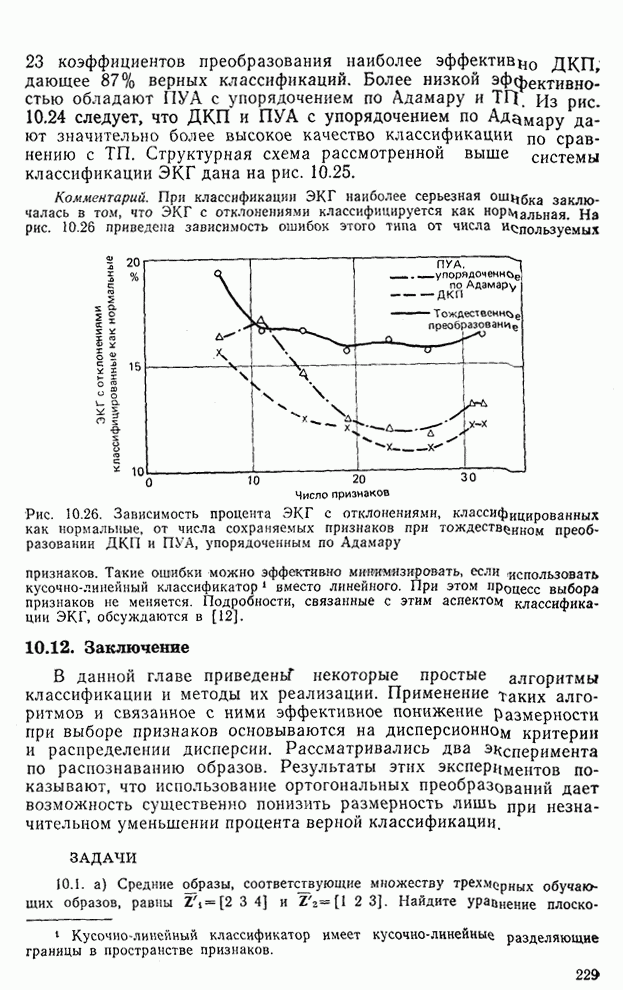
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
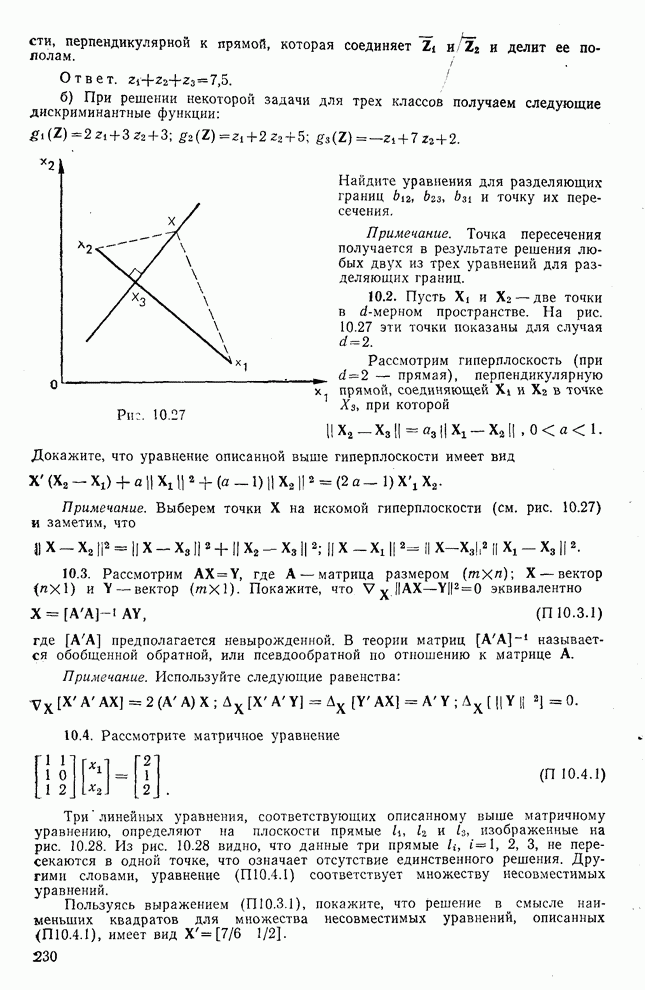
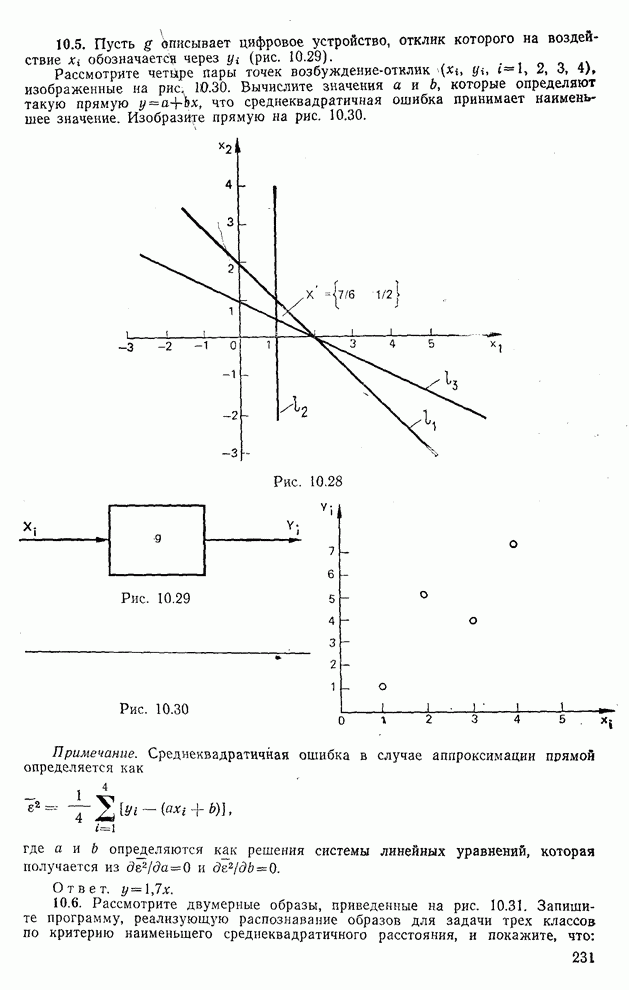
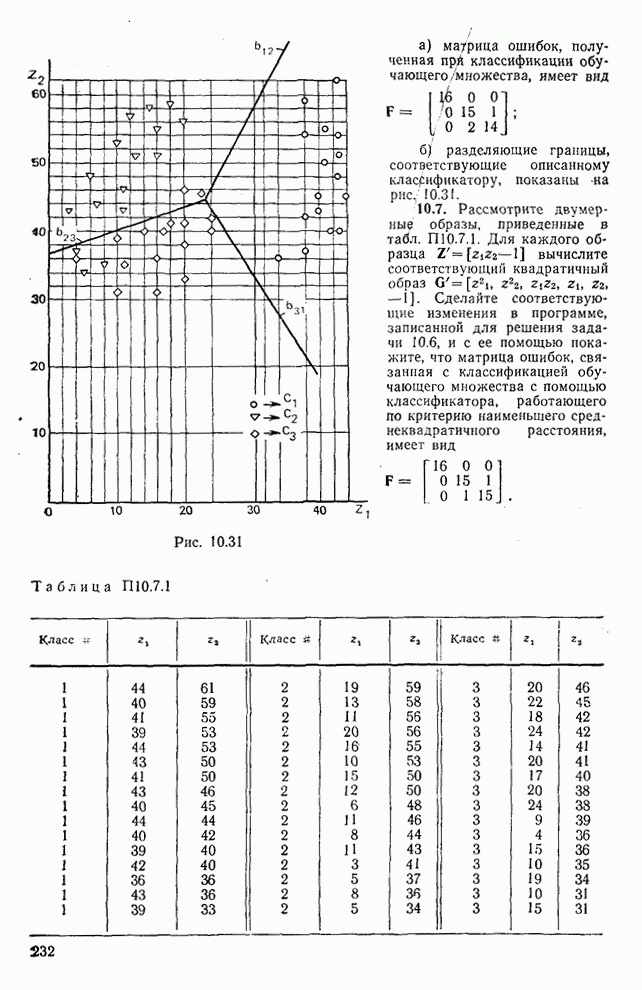
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ