| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.1. Поиск оптимального преобразования
Найдем ортогональное преобразование, которое, с одной стороны, будет обеспечивать представление сигнала, а с другой стороны, будет оптимальным в смысле среднеквадратичного критерия. Пусть I — ортогональное преобразование, заданное в виде
 (9.1.1)
(9.1.1)
где  — есть
— есть  -векторы. Для удобства базисные векторы
-векторы. Для удобства базисные векторы  будем считать вещественнозначными и ортонормированными, т. е.
будем считать вещественнозначными и ортонормированными, т. е.

Для каждого вектора X, принадлежащего к данному классу векторов исходных данных, получаем
 (9.1.3)
(9.1.3)
где  и
и  . Из выражений (9.1.1) и (9.1.2) следует, что
. Из выражений (9.1.1) и (9.1.2) следует, что  и, следовательно,
и, следовательно,  , что можно записать как
, что можно записать как

Желательно сохранить подмножество  координат Y и при этом получить оценку X. Это может быть осуществлено заменой остальных
координат Y и при этом получить оценку X. Это может быть осуществлено заменой остальных  координат Y заранее выбранными константами
координат Y заранее выбранными константами  , что приводит к
, что приводит к
 (9.1.5)
(9.1.5)
где  обозначает оценку X. Ошибку, возникающую при отбрасывании
обозначает оценку X. Ошибку, возникающую при отбрасывании  координат, можно представить в виде
координат, можно представить в виде  , где
, где  — вектор ошибки, т. е.
— вектор ошибки, т. е.
 (9.1.6)
(9.1.6)
Из выражений (9.1.4) и (9.1.6) следует, что
 (9.1.7)
(9.1.7)
Таким образом, среднеквадратичная ошибка  определяется в виде
определяется в виде
 (9.1.8)
(9.1.8)
Подстановка (9.1.7) в (9.1.8) приводит к

что в упрощенном виде можно записать как
 (9.1.9)
(9.1.9)
Из выражения (9.1.9) следует, что для каждого выбора  и
и  получаем определенное значение
получаем определенное значение  . Требуется определить такую комбинацию этих величин, чтобы минимизировать
. Требуется определить такую комбинацию этих величин, чтобы минимизировать  . Процедура выбора оптимальных
. Процедура выбора оптимальных  и
и  , разбивается соответственно на два этапа.
, разбивается соответственно на два этапа.
Первый этап. Оптимальное значение  , определяем из выражения
, определяем из выражения
 ,
,
что приводит к
 (9.1.10)
(9.1.10)
Затем из выражений (9.1.2) и (9.1.4) получаем
 (9.1.11)
(9.1.11)
Таким образом,  , где
, где  . Так как разность
. Так как разность  в (9.1.9) является скалярной величиной, то
в (9.1.9) является скалярной величиной, то  можно записать как
можно записать как
 (9.1.12)
(9.1.12)
Подстановка  и
и  выражение (9.1.12) приводит к
выражение (9.1.12) приводит к

Так как  является ковариационной матрицей X, получаем
является ковариационной матрицей X, получаем

Второй этап. Для нахождения оптимального  следует не только минимизировать
следует не только минимизировать  по отношению к
по отношению к  , но и удовлетворить ограничению
, но и удовлетворить ограничению  . При этом воспользуемся методом множителей Лагранжа и минимизируем
. При этом воспользуемся методом множителей Лагранжа и минимизируем
 (9.1.14)
(9.1.14)
по отношению к  , где
, где  — множители Лагранжа. Можно показать, что (см. задачу 9.1)
— множители Лагранжа. Можно показать, что (см. задачу 9.1)

Таким образом, из выражения (9.1.14) получаем

что приводит к

По определению выражение (9.1.15) означает, что  собственный вектор ковариационной матрицы а
собственный вектор ковариационной матрицы а  — соответствующее
— соответствующее  собственное значение. Обозначая
собственное значение. Обозначая  через
через  и подставляя (9.1.15) в (9.1.13), получаем минимальное значение среднеквадратичной ошибки в виде
и подставляя (9.1.15) в (9.1.13), получаем минимальное значение среднеквадратичной ошибки в виде
 (9.1.16)
(9.1.16)
Таким образом, разложение, записанное в (9.1.4), представляет собой разложение по собственным векторам ковариационной матрицы. Это разложение называется разложением Карунена—Лоэва. Векторы  , которые образуют Т в (9.1.1), являются собственными векторами Поэтому преобразование
, которые образуют Т в (9.1.1), являются собственными векторами Поэтому преобразование  называется преобразованием Карунена—Лоэва (ПКЛ). Напомним, что ПКЛ уже упоминалось в § 8.5.
называется преобразованием Карунена—Лоэва (ПКЛ). Напомним, что ПКЛ уже упоминалось в § 8.5.
В литературе по статистике задача минимизации  называется факторным анализом или анализом главных компонент. Из приведенного выше рассмотрения можно сделать два важных вывода:
называется факторным анализом или анализом главных компонент. Из приведенного выше рассмотрения можно сделать два важных вывода:
1. Преобразование Карунена—Лоэва является оптимальным преобразованием для представления сигналов по отношению к критерию среднеквадратичной ошибки.
2. Поскольку  , то ковариационная матрица в области изображений определяется как [см. выражение (8.2.4)]
, то ковариационная матрица в области изображений определяется как [см. выражение (8.2.4)]

Так как Т состоит из собственных векторов  , то [см. выражение (8.5.1)]
, то [см. выражение (8.5.1)]
 (9.1.17)
(9.1.17)
где  — собственные значения
— собственные значения  . Так как
. Так как  — диагональная матрица, то приходим к выводу, что координаты вектора преобразованных данных
— диагональная матрица, то приходим к выводу, что координаты вектора преобразованных данных  в выражении (9.1.11) некоррелированны.
в выражении (9.1.11) некоррелированны.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
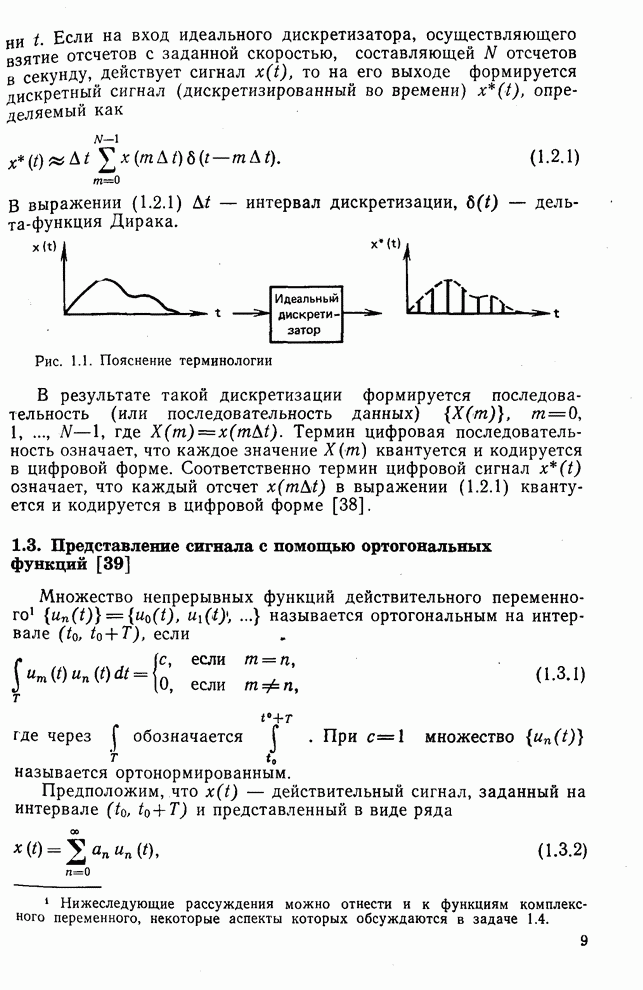
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
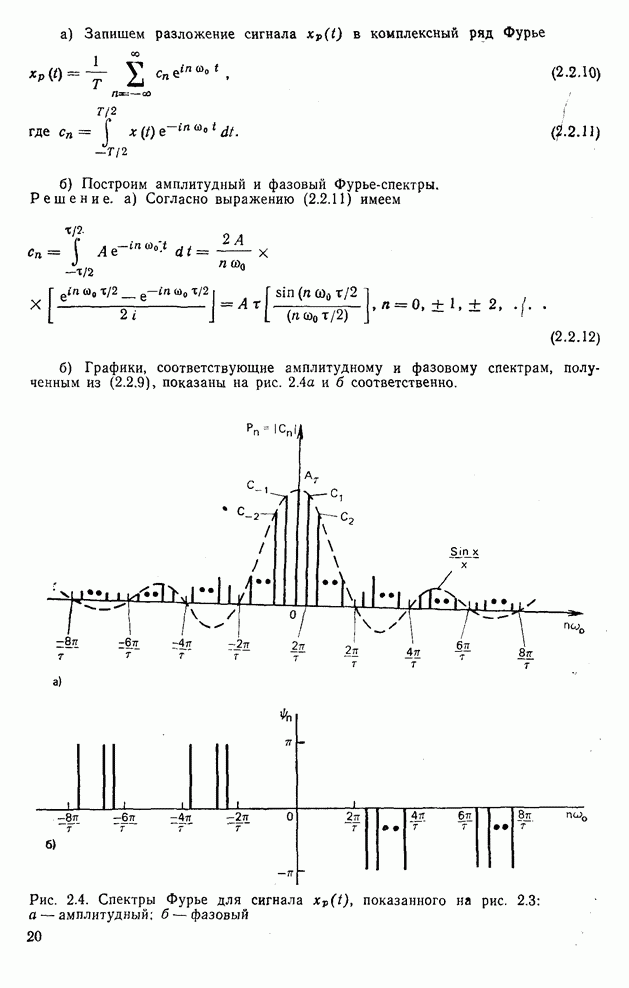
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
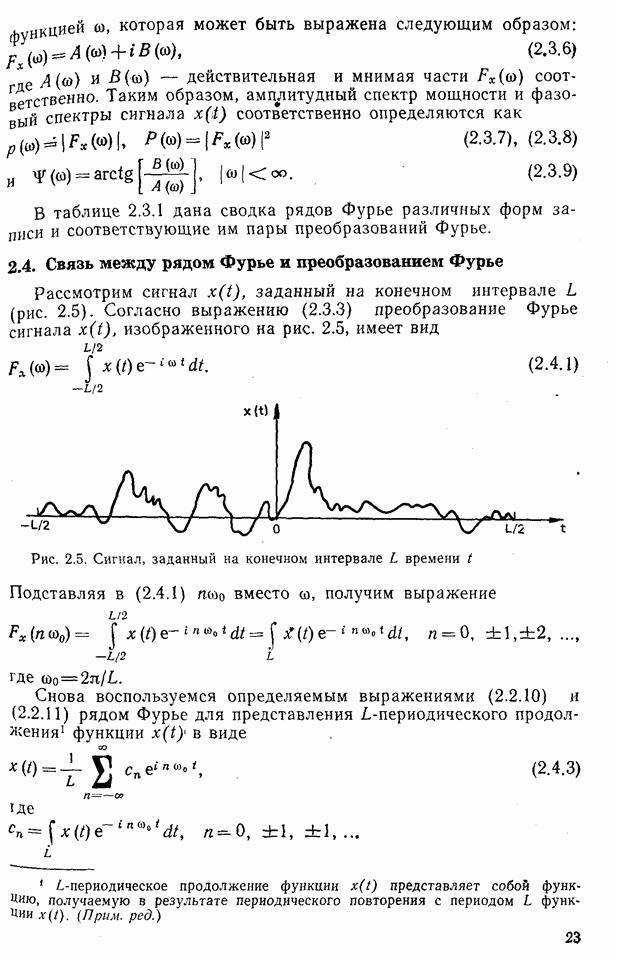
- 2.4. Связь между рядом Фурье и преобразованием Фурье
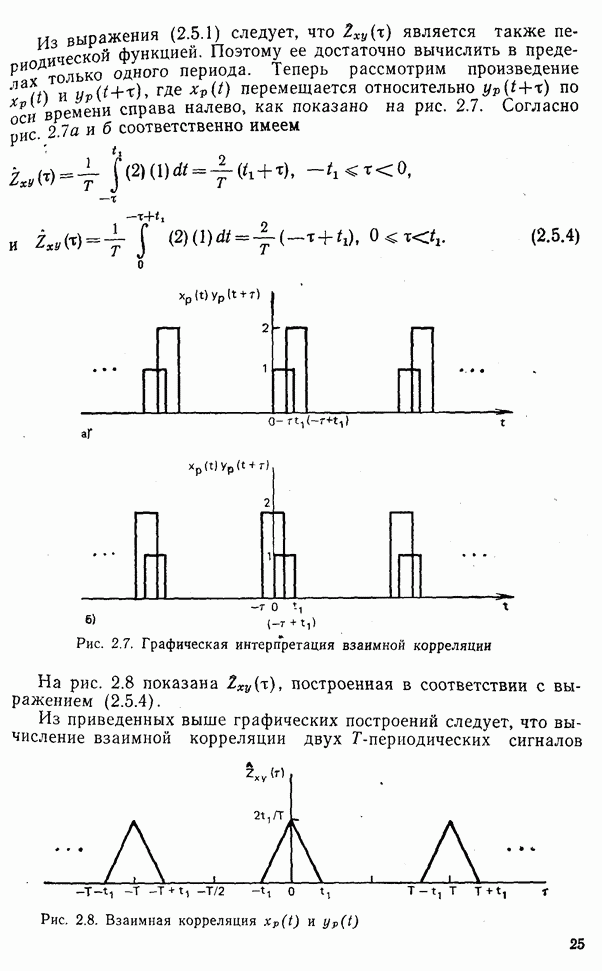
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
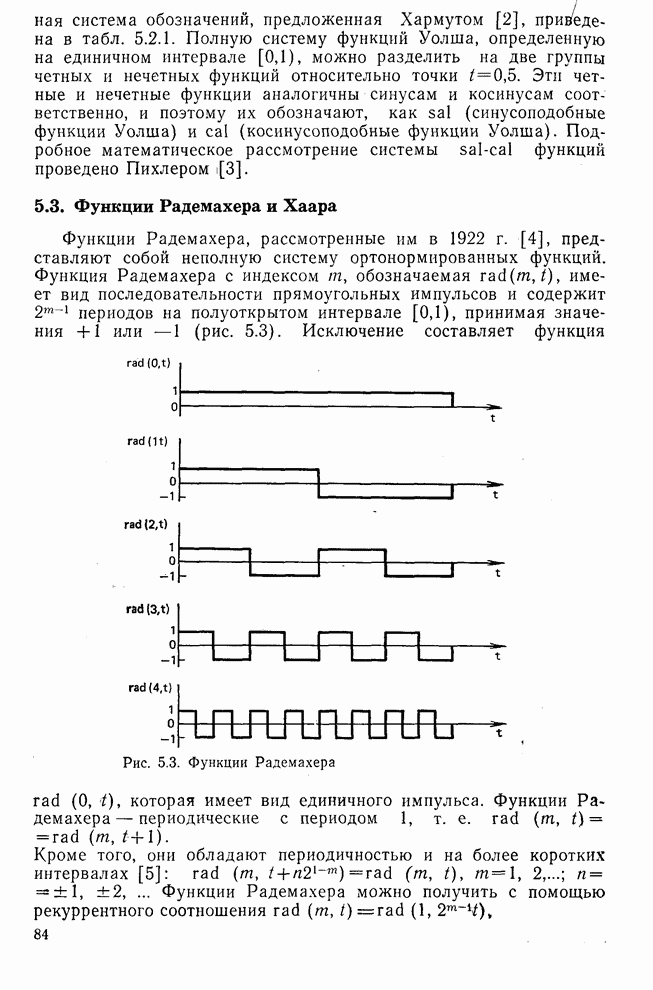
- 5.3. Функции Радемахера и Хаара
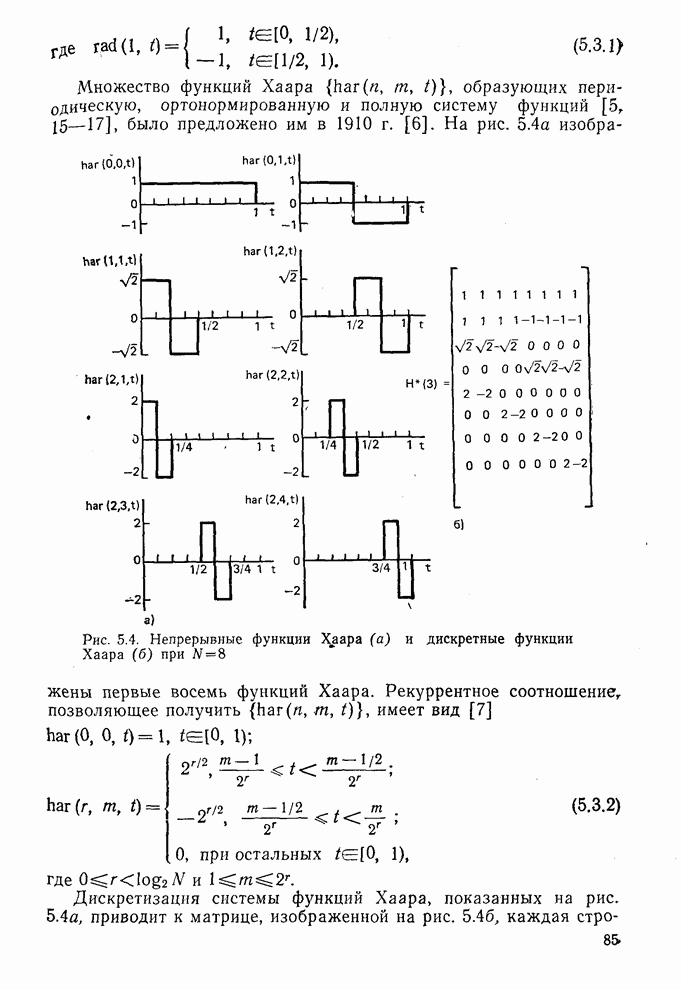
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
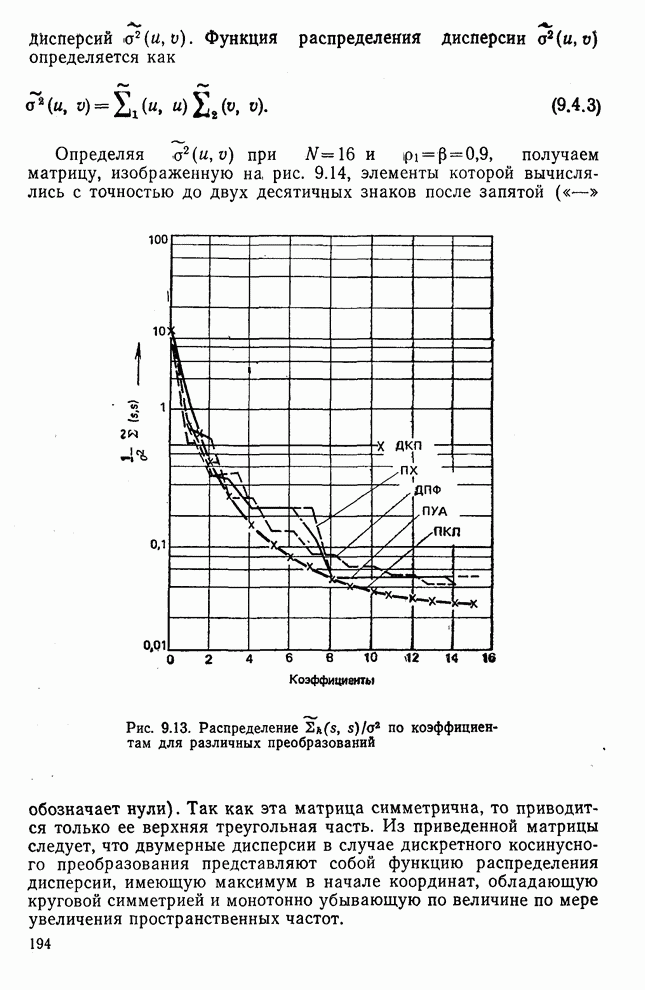
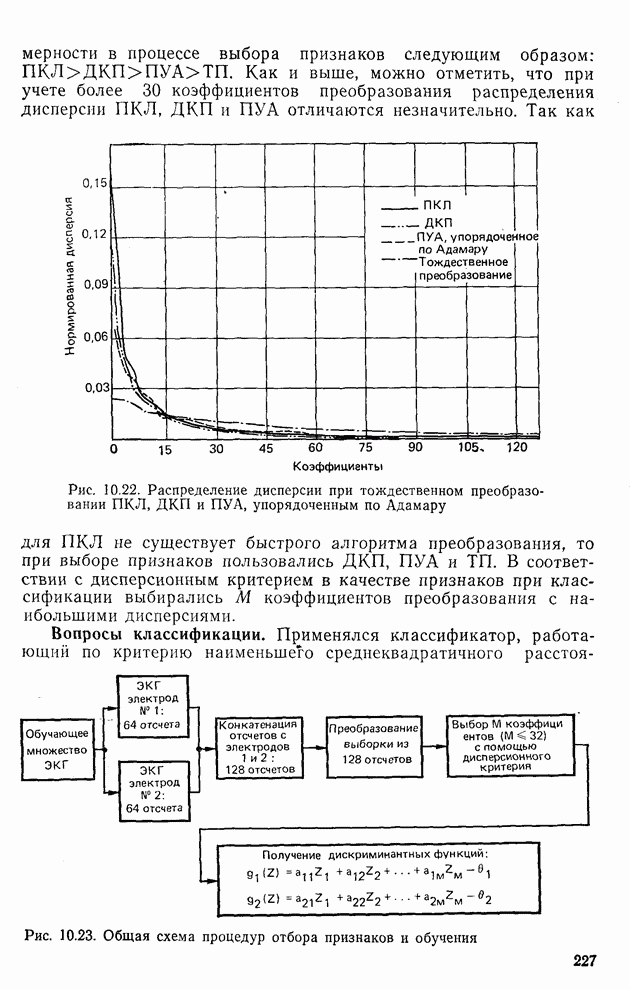
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
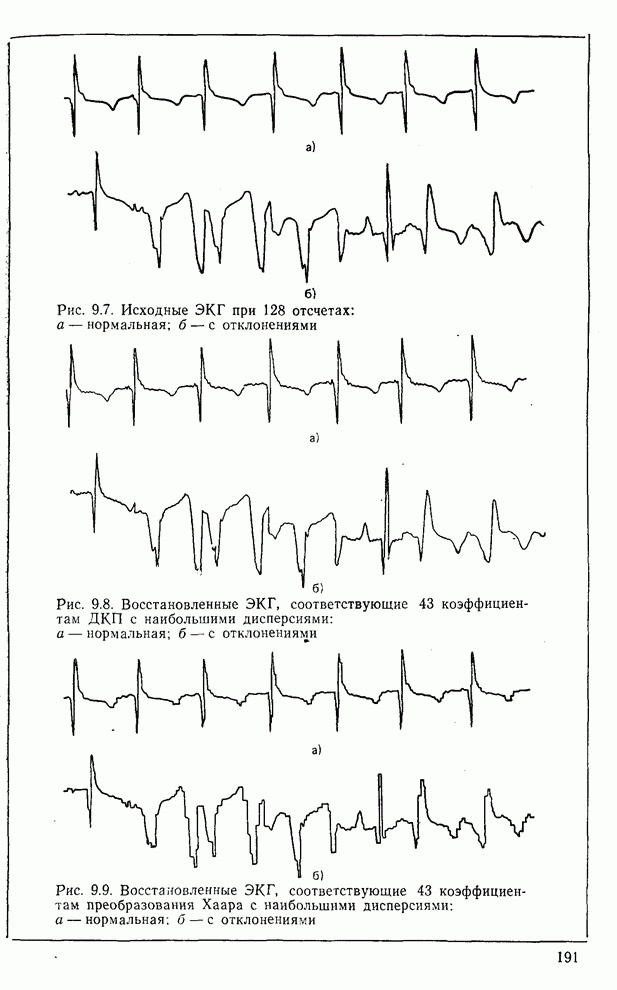
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
- 10.3. d-мерные образы
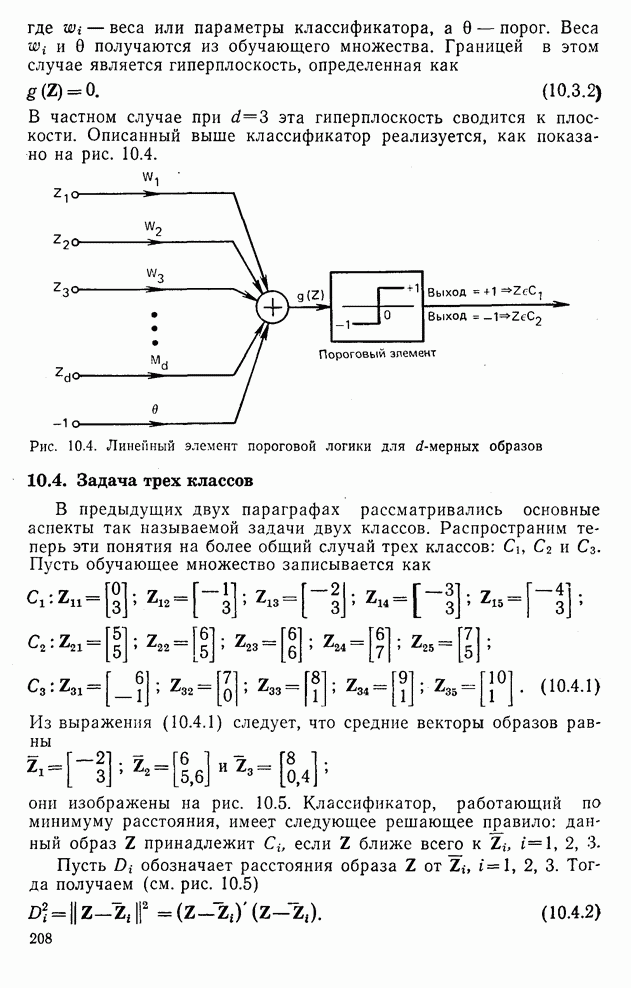
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
- 10.6. Метод отображения по методу наименьших квадратов
- 10.7. Расширенное пространство признаков
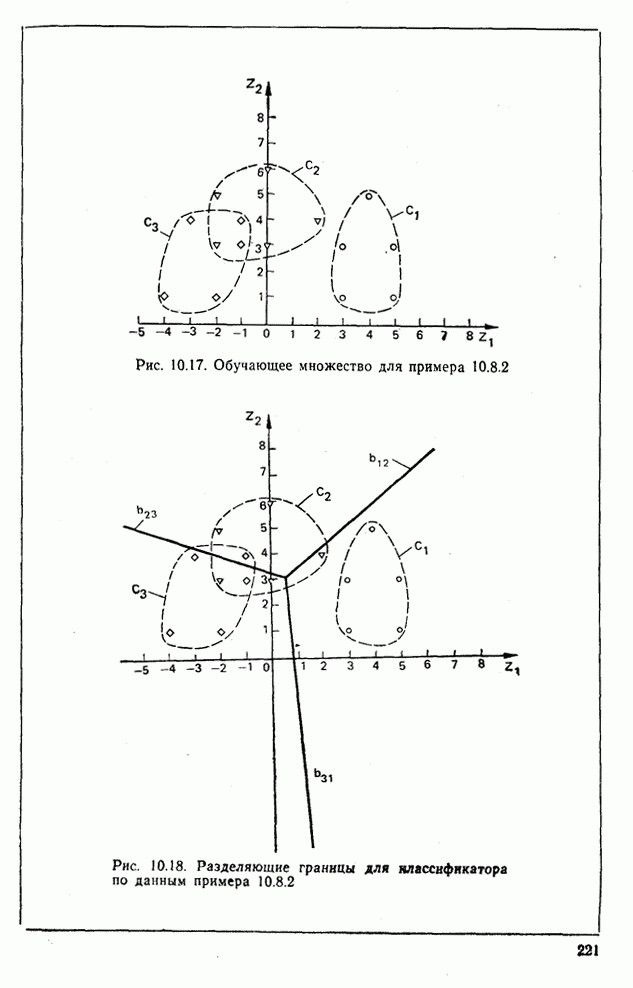
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
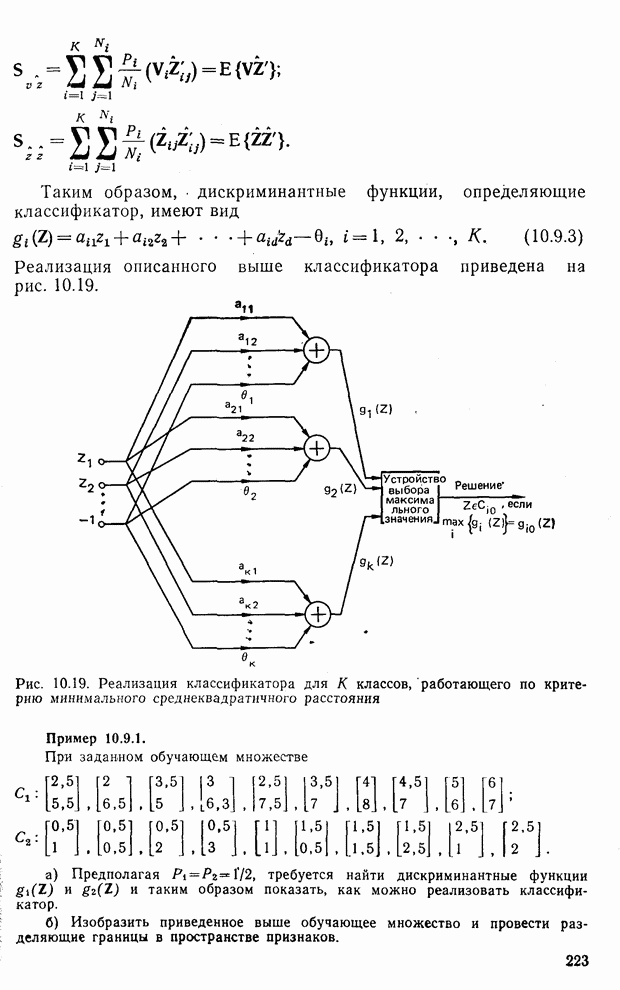
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
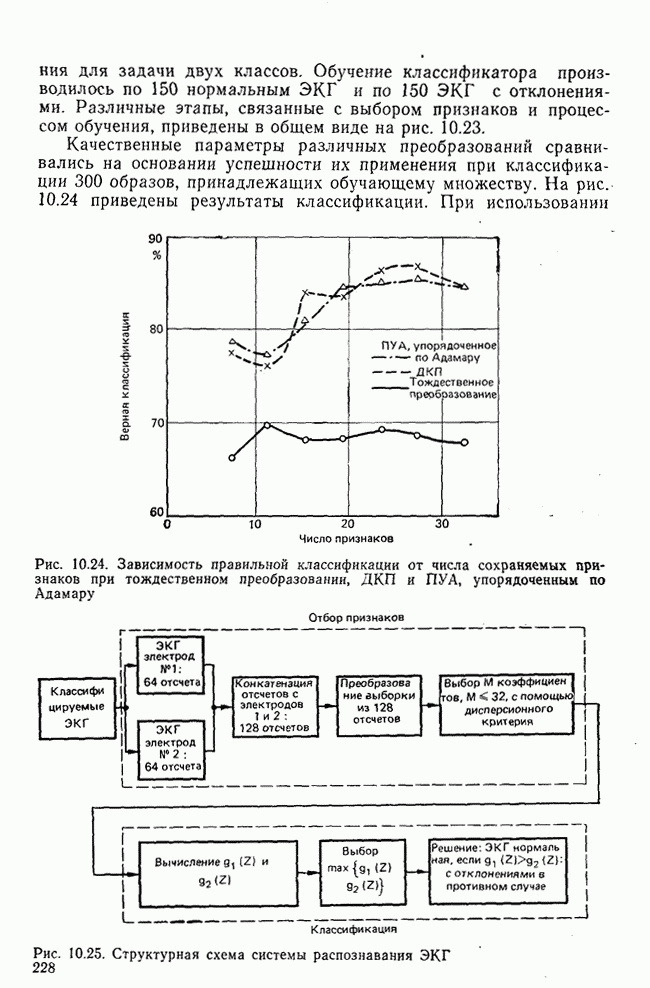
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ