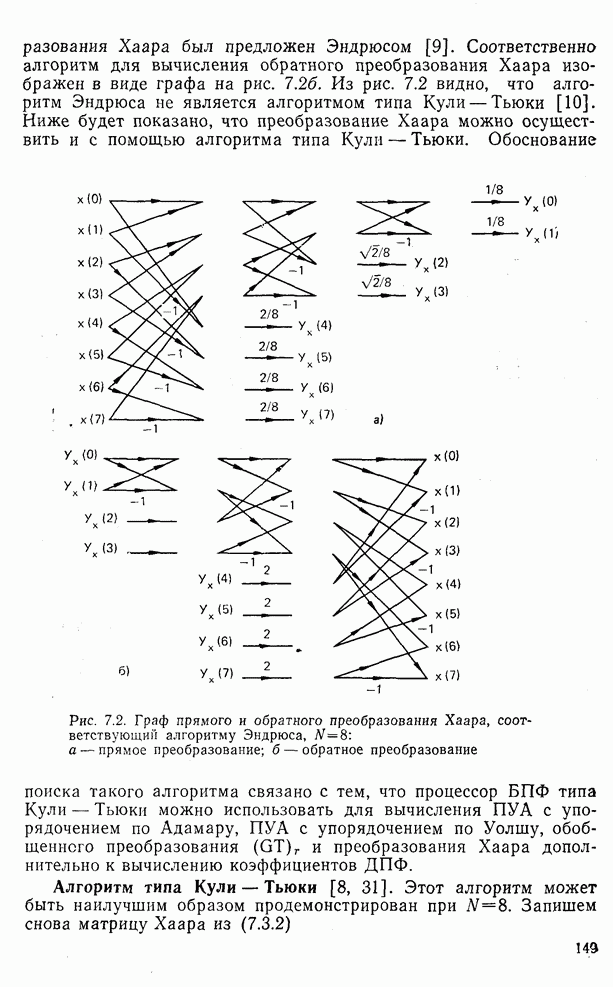
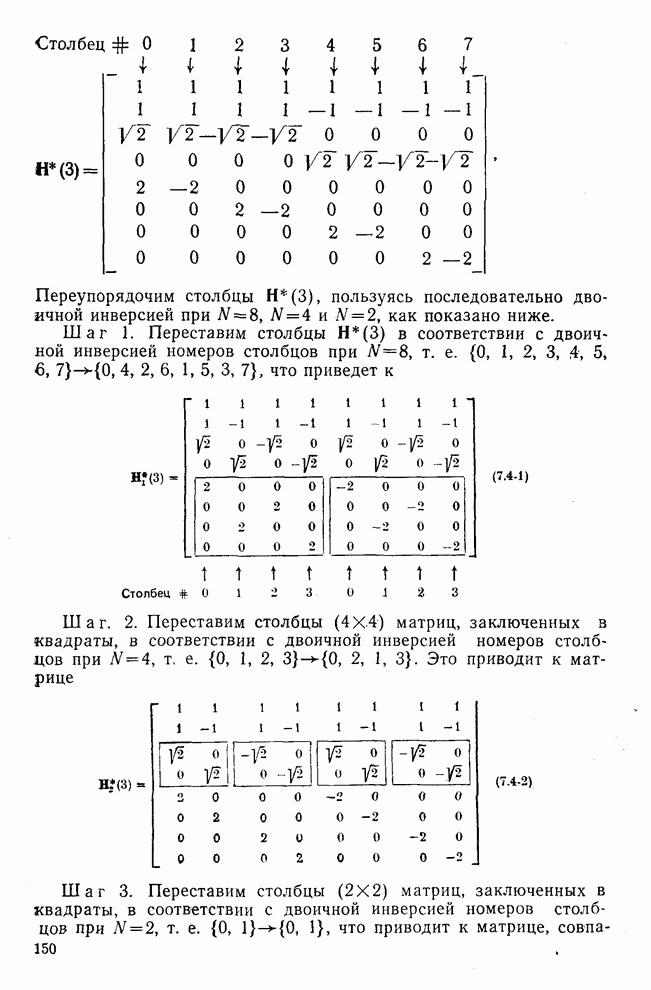
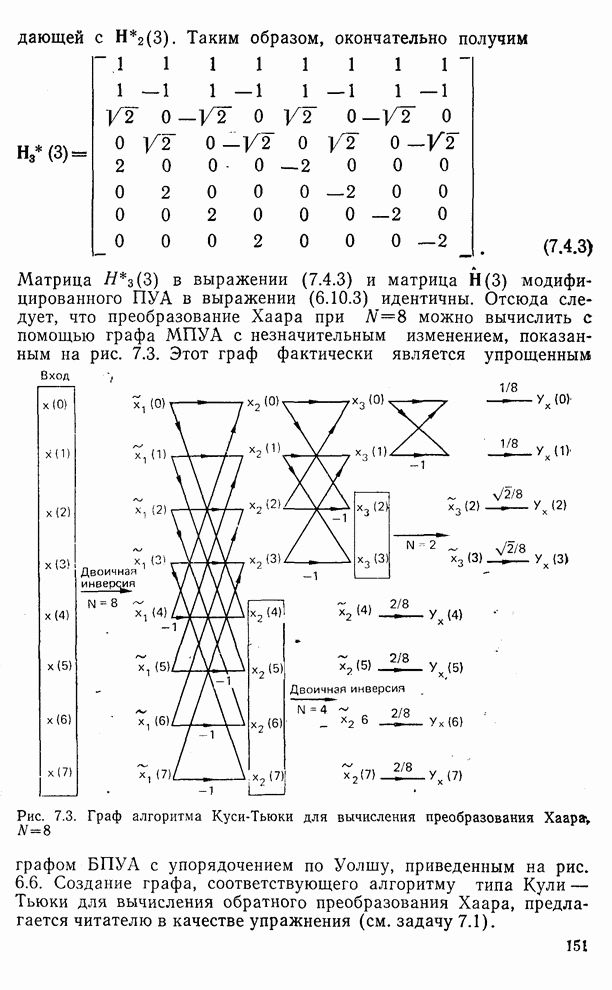
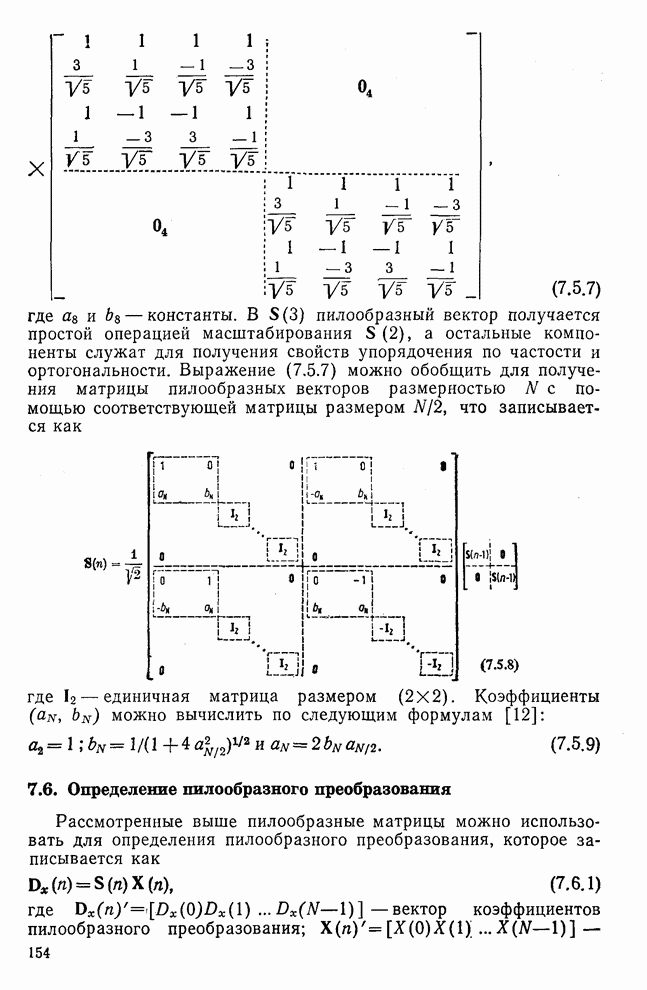
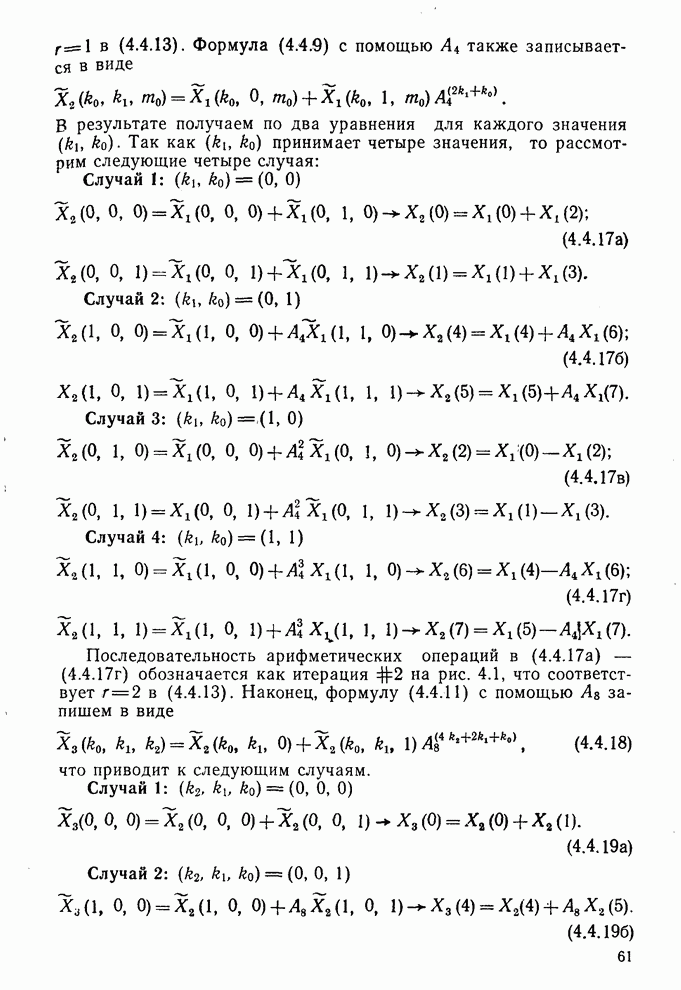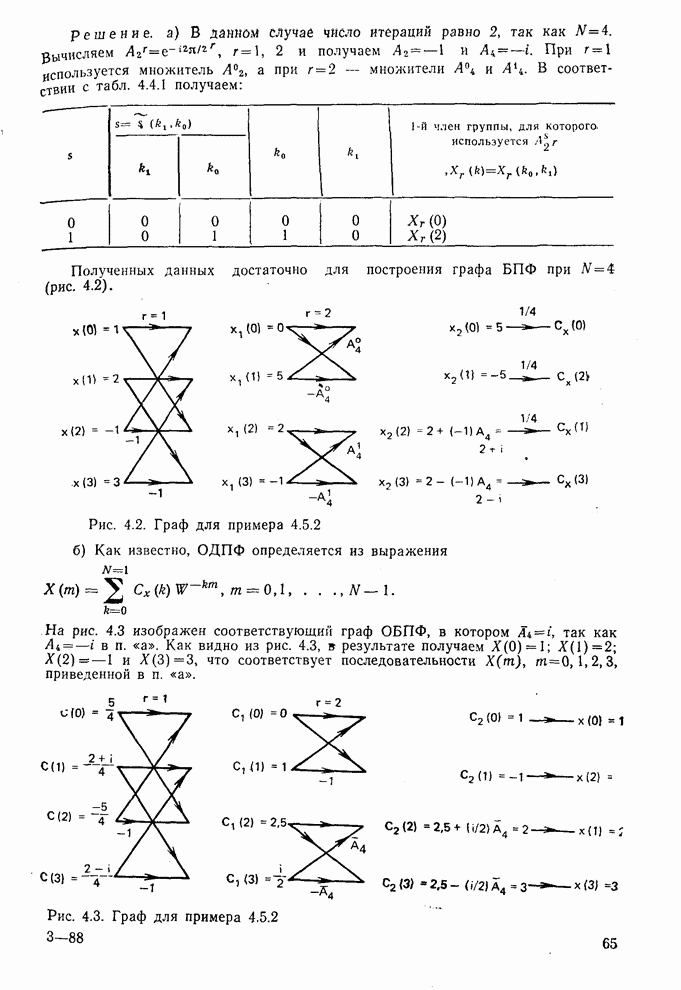| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.4. Вывод алгоритма
Вывод алгоритма [7, 8] наиболее нагляден при  , поэтому запишем
, поэтому запишем
 (4.4.1)
(4.4.1)
где  . Выразим
. Выразим  в двоичной системе счисления
в двоичной системе счисления
 (4.4.2)
(4.4.2)
Из (4.3.2), (4.4.1) и (4.4.2) следует, что
 (4.4.3)
(4.4.3)
В выражении (4.4.3) внутреннее суммирование по  обозначим через
обозначим через  , что записывается как
, что записывается как

Подставляя в это выражение двоичное представление k и учитывая, что  , получим
, получим

Поскольку  значение
значение  можно записать в виде
можно записать в виде
 (4.4.4)
(4.4.4)
В выражении (4.4.4) суммирование по  приводит к величине, которая является функцией
приводит к величине, которая является функцией  и
и  . Поэтому вводится обозначение
. Поэтому вводится обозначение
 (4.4.5)
(4.4.5)
Подстановка (4.4.5) в выражение (4.4.3) дает
 (4.4.6)
(4.4.6)
Вновь рассмотрим внутреннее суммирование в (4.4.6) и обозначим его через  что запишем в виде
что запишем в виде
 (4.4.7)
(4.4.7)
В выражении (4.4.7)  , и поэтому запись упрощается:
, и поэтому запись упрощается:
 (4.4.8)
(4.4.8)
Суммирование по  в (4.4.8) приводит к функции, зависящей от
в (4.4.8) приводит к функции, зависящей от  , т.е.
, т.е.
 (4.4.9)
(4.4.9)
Подставляя (4.4.9) в (4.4.6), получаем

Обозначим суммирование по  через
через  , что можно записать в виде
, что можно записать в виде

Рассмотрение формулы (4.4.10) приводит к выводу, что дальнейшее упрощение невозможно. Суммирование по  , как и ранее, приводит к функции, зависящей от
, как и ранее, приводит к функции, зависящей от  и
и  , которую обозначим через
, которую обозначим через  , т. е.
, т. е.
 (4.4.11)
(4.4.11)
Это означает, что
 (4.4.12)
(4.4.12)
и, следовательно, (4.4.5), (4.4.9) и (4.4.11) позволяют выполнить действия, необходимые для получения коэффициентов ДПФ  . Однако остается неясным, как в дальнейшем пользоваться этими формулами. В качестве первого шага для ответа на этот вопрос сделаем два замечания.
. Однако остается неясным, как в дальнейшем пользоваться этими формулами. В качестве первого шага для ответа на этот вопрос сделаем два замечания.
1. При  получаем
получаем  такие формулы.
такие формулы.
2. Коэффициенты  и
и  в этих формулах выражаются через корень из единицы,
в этих формулах выражаются через корень из единицы,  . Очевидно, что
. Очевидно, что  и
и  являются соответственно корнями 2, 4 и 8-й степени из единицы. Поэтому введем обозначение
являются соответственно корнями 2, 4 и 8-й степени из единицы. Поэтому введем обозначение
 (4.4.13)
(4.4.13)
где  является
является  -м первообразным корнем из единицы. Непосредственно можно показать, что
-м первообразным корнем из единицы. Непосредственно можно показать, что  обладают следующими свойствами:
обладают следующими свойствами:
 (4.4.14а)
(4.4.14а)
 (4.4.14б)
(4.4.14б)
где  ;
;
 (4.4.14в)
(4.4.14в)
Теперь выражение (4.4.5) можно записать с помощью 

Откуда
 (4.4.15)
(4.4.15)
В (4.4.15)  может принимать значение 0 или 1. Соответственно для каждого значения
может принимать значение 0 или 1. Соответственно для каждого значения  запишем по четыре уравнения при переменных
запишем по четыре уравнения при переменных  и
и  .
.
Случай 1: 
 (4.4.16а)
(4.4.16а)
Случай 2: 
 (4.4.16б)
(4.4.16б)
Приведенная последовательность сложений и вычитаний, показанная на рис. 4.1, обозначена как итерация  , что соответствует
, что соответствует

Рис. 4.1. Граф БПФ при N=8
 в (4.4.13). Формула (4.4.9) с помощью
в (4.4.13). Формула (4.4.9) с помощью  также записывается в виде
также записывается в виде

В результате получаем по два уравнения для каждого значения  . Так как
. Так как  принимает четыре значения, то рассмотрим следующие четыре случая:
принимает четыре значения, то рассмотрим следующие четыре случая:
Случай 1: 
 (4.4.17а)
(4.4.17а)

Случай 2: 
 (4.4.17б)
(4.4.17б)

Случай 3: 


Случай 4: 


Последовательность арифметических операций в  обозначается как итерация
обозначается как итерация  на рис. 4.1, что соответствует
на рис. 4.1, что соответствует  в (4.4.13). Наконец, формулу (4.4.11) с помощью
в (4.4.13). Наконец, формулу (4.4.11) с помощью  запишем в виде
запишем в виде
 (4.4.18)
(4.4.18)
что приводит к следующим случаям.
Случай 1: 

Случай 2: 
 (4.4.19б)
(4.4.19б)
Случай 3: 

Случай 4: 

Случай 5: 

Последовательность арифметических операций в (4.4.19а)-(4.4.19), показанная на рис. 4.1, обозначена как итерация #3, что соответствует  в (4.4.13). Для получения желаемых значений
в (4.4.13). Для получения желаемых значений  вспомним, что
вспомним, что
 (4.4.20)
(4.4.20)
Двоичные коэффициенты  и
и  появляются в
появляются в  в инвертированном порядке, в отличие от
в инвертированном порядке, в отличие от  , где они появляются в естественном порядке. Такой порядок называется двоичной инверсией. Итак,
, где они появляются в естественном порядке. Такой порядок называется двоичной инверсией. Итак,  связаны с
связаны с  следующим образом:
следующим образом:
 (4.4.21)
(4.4.21)
Остальные коэффициенты  могут быть получены как
могут быть получены как  , т. е.
, т. е.  и
и  . Коэффициенты
. Коэффициенты  и
и  могут быть вычислены по (4.4.22) и (4.4.18) следующим образом:
могут быть вычислены по (4.4.22) и (4.4.18) следующим образом:
 (4.4.22)
(4.4.22)
Арифметические операции, приведенные в (4.4.22), показаны в итерации #3 на рис. 4.1 штриховыми линиями. Рисунок 4.1 представляет собой граф БПФ для  .
.
Примечания. В отношении приведенного выше графа БПФ можно сделать следующие выводы.
1. Максимальное значение индекса итерации  определяется как
определяется как  при
при  .
.
2. В  итерации,
итерации,  , используются следующие множители
, используются следующие множители  .
.
 (4.4.23)
(4.4.23)
При  в итерации
в итерации  используются множители
используются множители  . Так как
. Так как  , то в этой итерации осуществляются только сложения и вычитания. При
, то в этой итерации осуществляются только сложения и вычитания. При  в итерации
в итерации  используются множители
используются множители  и
и  при
при  в итерации
в итерации  — множители
— множители  и
и  .
.
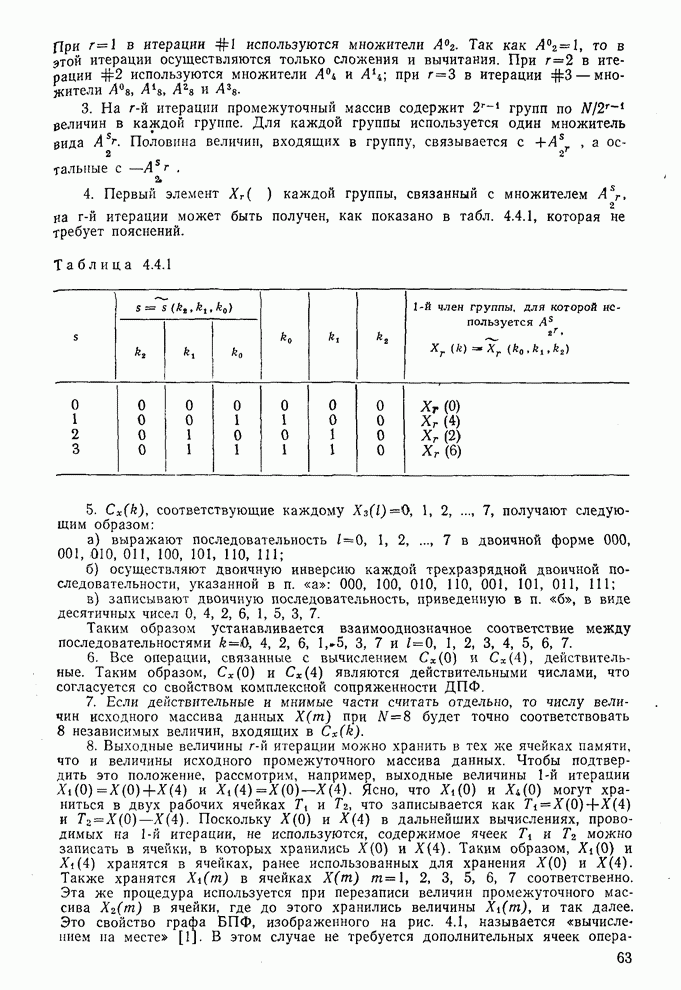
3. На  итерации промежуточный массив содержит
итерации промежуточный массив содержит  групп по
групп по  величин в каждой группе. Для каждой группы используется один множитель вида
величин в каждой группе. Для каждой группы используется один множитель вида  . Половина величин, входящих в группу, связывается с
. Половина величин, входящих в группу, связывается с  , а остальные с
, а остальные с  .
.
4. Первый элемент  каждой группы, связанный с множителем
каждой группы, связанный с множителем  , на
, на  итерации может быть получен, как показано в табл. 4.4.1, которая не требует пояснений.
итерации может быть получен, как показано в табл. 4.4.1, которая не требует пояснений.
Таблица 4.4.1
5.  , соответствующие каждому
, соответствующие каждому  , получают следующим образом:
, получают следующим образом:
а) выражают последовательность  в двоичной форме 000, 001, 010, 011, 100, 101, 110, 111;
в двоичной форме 000, 001, 010, 011, 100, 101, 110, 111;
б) осуществляют двоичную инверсию каждой трехразрядной двоичной последовательности, указанной в п. "а": 000, 100, 010, 110, 001, 101, 011, 111;
в) записывают двоичную последовательность, приведенную в п. "б", в виде десятичных чисел 0, 4, 2, 6, 1, 5, 3, 7.
Таким образом устанавливается взаимооднозначное соответствие между последовательностями  и
и  .
.
6. Все операции, связанные с вычислением  и
и  , действительные. Таким образом,
, действительные. Таким образом,  и
и  являются действительными числами, что согласуется со свойством комплексной сопряженности ДПФ.
являются действительными числами, что согласуется со свойством комплексной сопряженности ДПФ.
7. Если действительные и мнимые части считать отдельно, то числу величин исходного массива данных  при будет точно соответствовать 8 независимых величин, входящих в
при будет точно соответствовать 8 независимых величин, входящих в  .
.
8. Выходные величины  итерации можно хранить в тех же ячейках памяти, что и величины исходного промежуточного массива данных. Чтобы подтвердить это положение, рассмотрим, например, выходные величины
итерации можно хранить в тех же ячейках памяти, что и величины исходного промежуточного массива данных. Чтобы подтвердить это положение, рассмотрим, например, выходные величины  итерации
итерации  и
и  . Ясно, что
. Ясно, что  и
и  могут храниться в двух рабочих ячейках
могут храниться в двух рабочих ячейках  и
и  , что записывается как
, что записывается как  и
и  . Поскольку
. Поскольку  и
и  в дальнейших вычислениях, проводимых на
в дальнейших вычислениях, проводимых на  итерации, не используются, содержимое ячеек
итерации, не используются, содержимое ячеек  и
и  можно записать в ячейки, в которых хранились
можно записать в ячейки, в которых хранились  и
и  . Таким образом,
. Таким образом,  и
и  хранятся в ячейках, ранее использованных для хранения
хранятся в ячейках, ранее использованных для хранения  и
и  . Также хранятся
. Также хранятся  в ячейках
в ячейках  соответственно. Эта же процедура используется при перезаписи величин промежуточного массива
соответственно. Эта же процедура используется при перезаписи величин промежуточного массива  в ячейки, где до этого хранились величины
в ячейки, где до этого хранились величины  , и так далее. Это свойство графа БПФ, изображенного на рис. 4.1, называется «вычислением на месте» [1]. В этом случае не требуется дополнительных ячеек оперативной памяти для хранения различных промежуточных массивов.
, и так далее. Это свойство графа БПФ, изображенного на рис. 4.1, называется «вычислением на месте» [1]. В этом случае не требуется дополнительных ячеек оперативной памяти для хранения различных промежуточных массивов.
Общее число ячеек оперативной памяти, необходимых для осуществления БПФ, равно  , если исходный массив данных является комплексным. Кроме того, требуется еще
, если исходный массив данных является комплексным. Кроме того, требуется еще  ячеек для выполнения двоичной инверсии.
ячеек для выполнения двоичной инверсии.
9. Общее число арифметических операций (т. е. умножений с последующим сложением или вычитанием), необходимых для получения всех  , равно примерно
, равно примерно  .
.
10. Алгоритм БПФ не зависит от того, являются исходные величины действительными или комплексными. Следовательно, он может быть использован для вычисления ОДПФ с незначительными изменениями, которые следуют из (3.1.4) и (4.1.1):
W заменяется на  ;
;
опускается множитель  , стоящий после последней итерации.
, стоящий после последней итерации.
Такая модификация алгоритма БПФ будет в дальнейшем именоваться обратным быстрым преобразованием Фурье (ОБПФ).
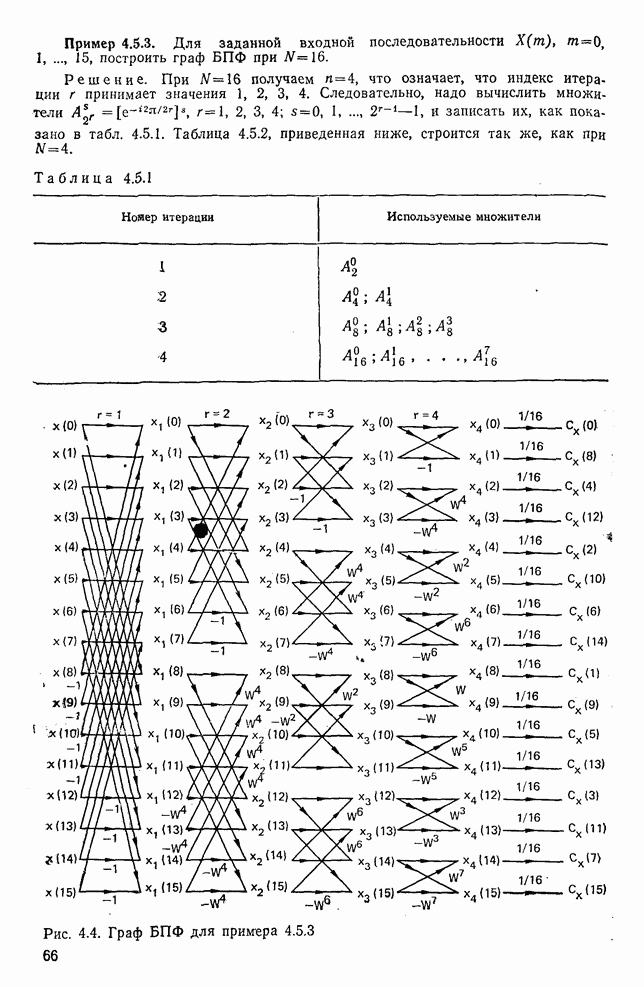
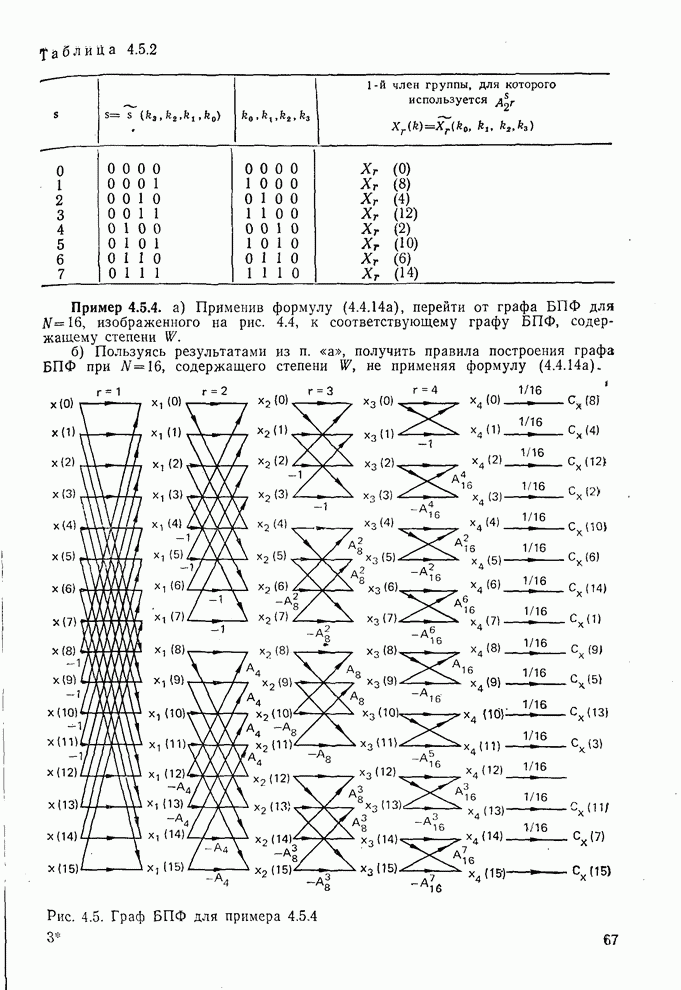
11. Множители, используемые в графе БПФ, могут быть выражены непосредственно через степени W в соответствии с тем, что  . Ниже (пример 4.5.4) показано, что соответствующий граф БПФ может быть построен непосредственно с использованием степеней W с помощью простого правила.
. Ниже (пример 4.5.4) показано, что соответствующий граф БПФ может быть построен непосредственно с использованием степеней W с помощью простого правила.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
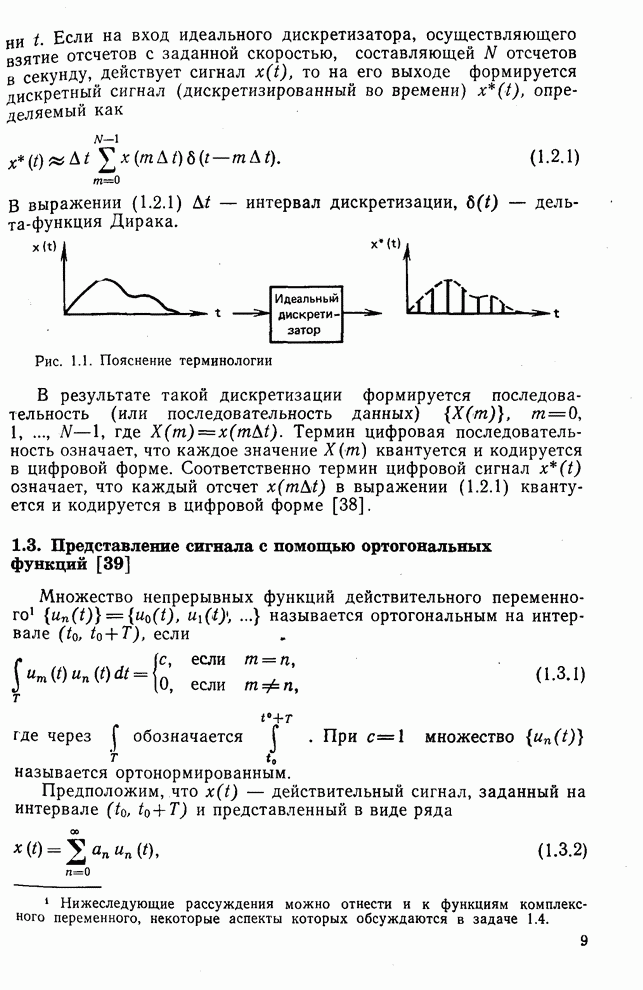
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
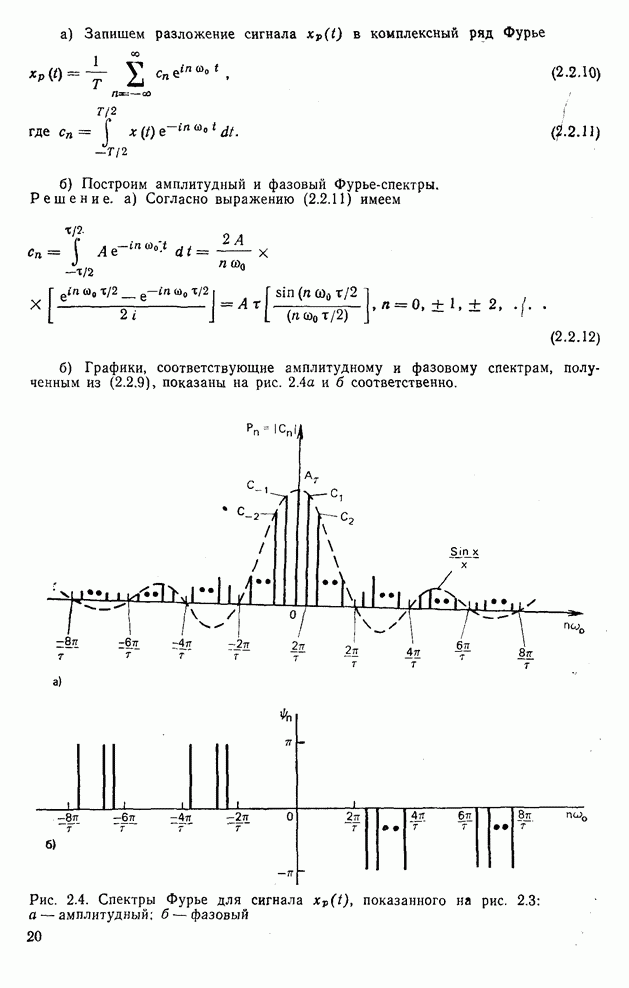
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
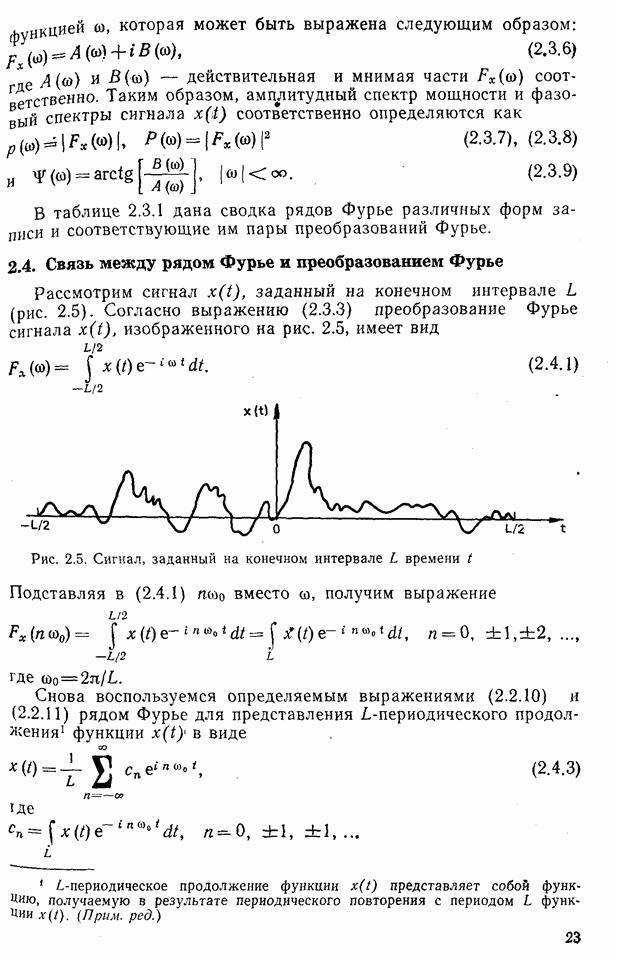
- 2.4. Связь между рядом Фурье и преобразованием Фурье
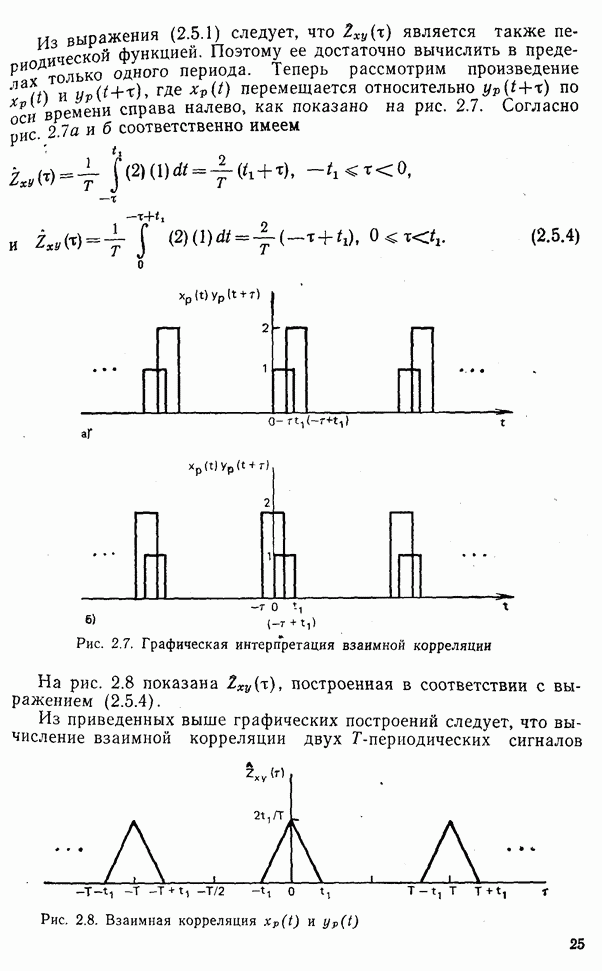
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
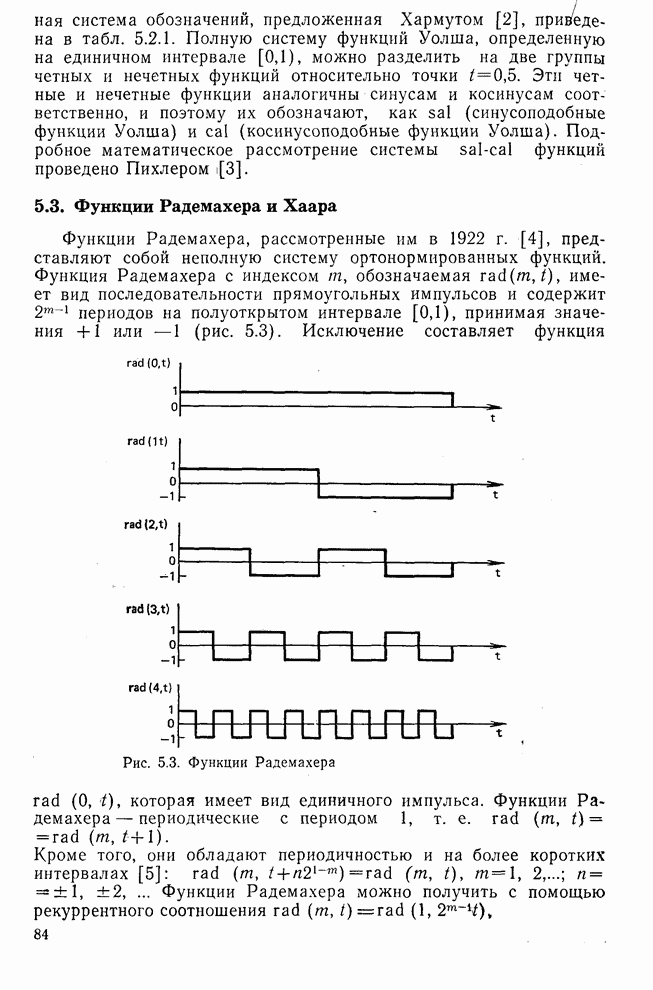
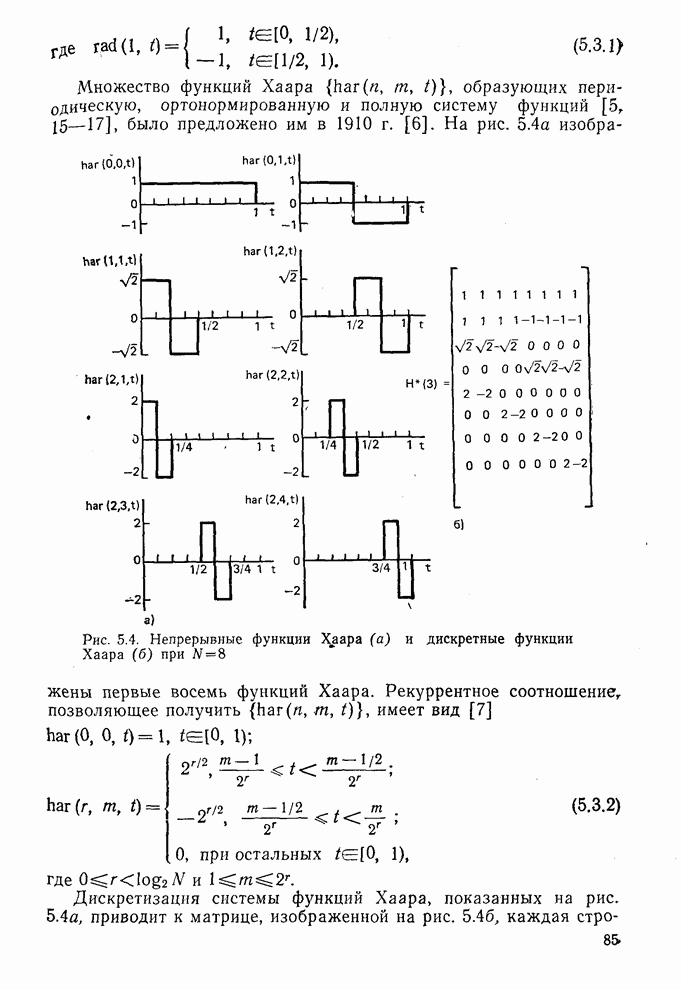
- 5.3. Функции Радемахера и Хаара
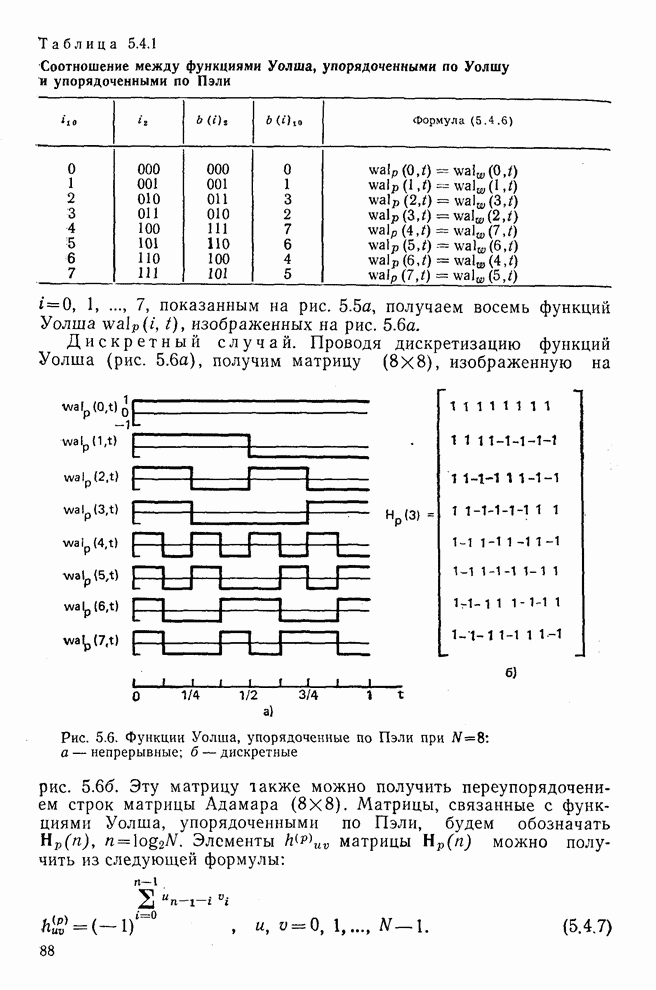
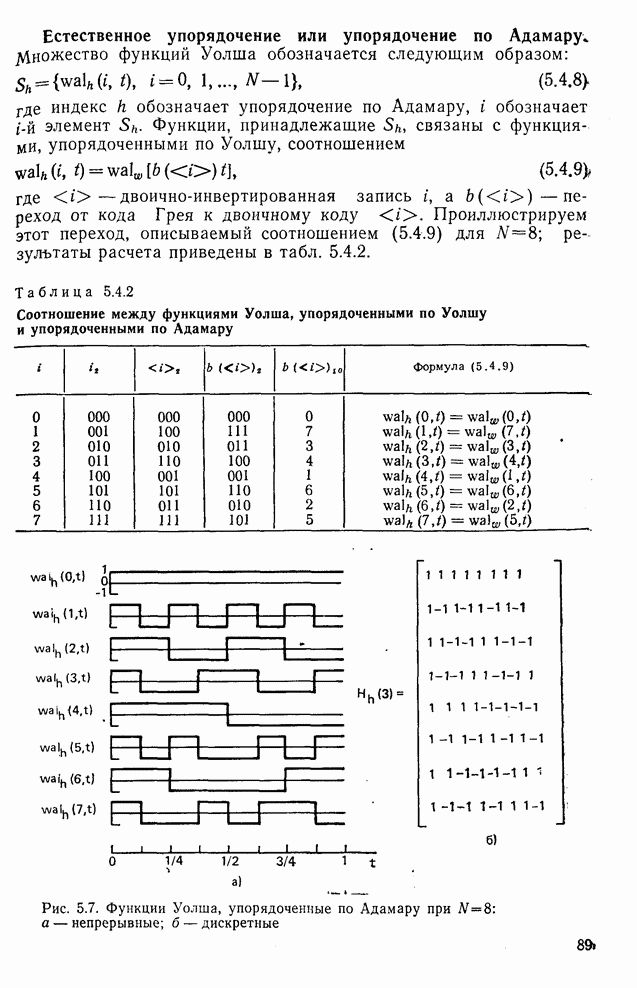
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
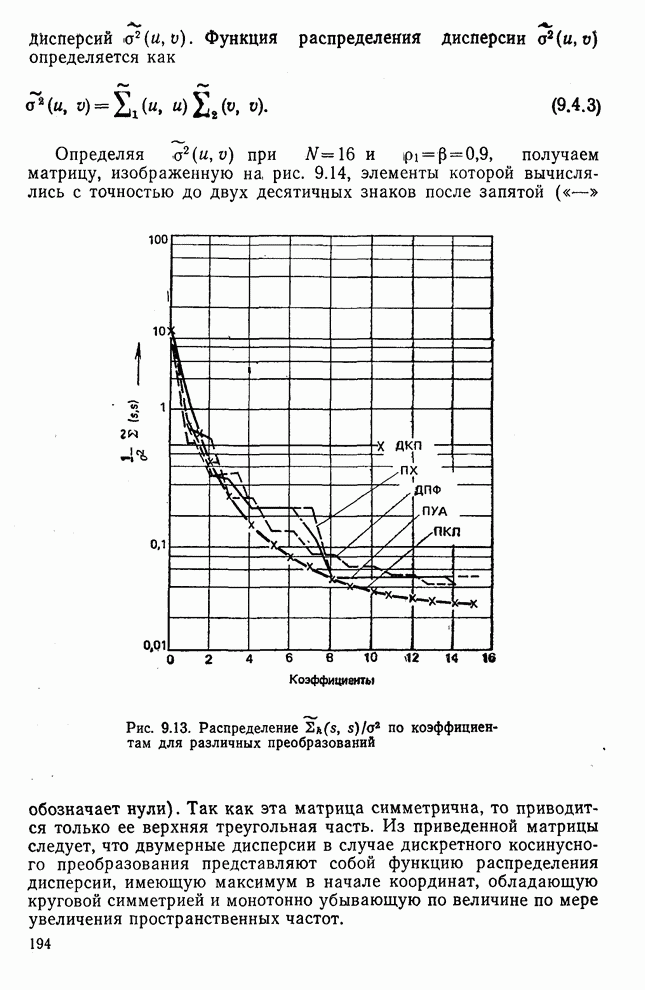
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
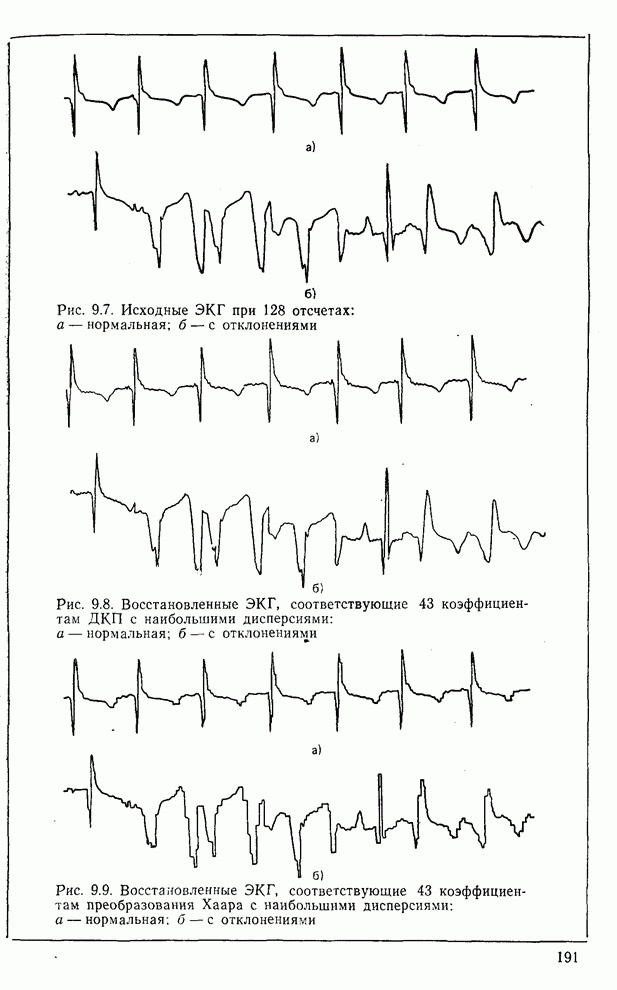
- 9.3. Сжатие электрокардиограмм [2]
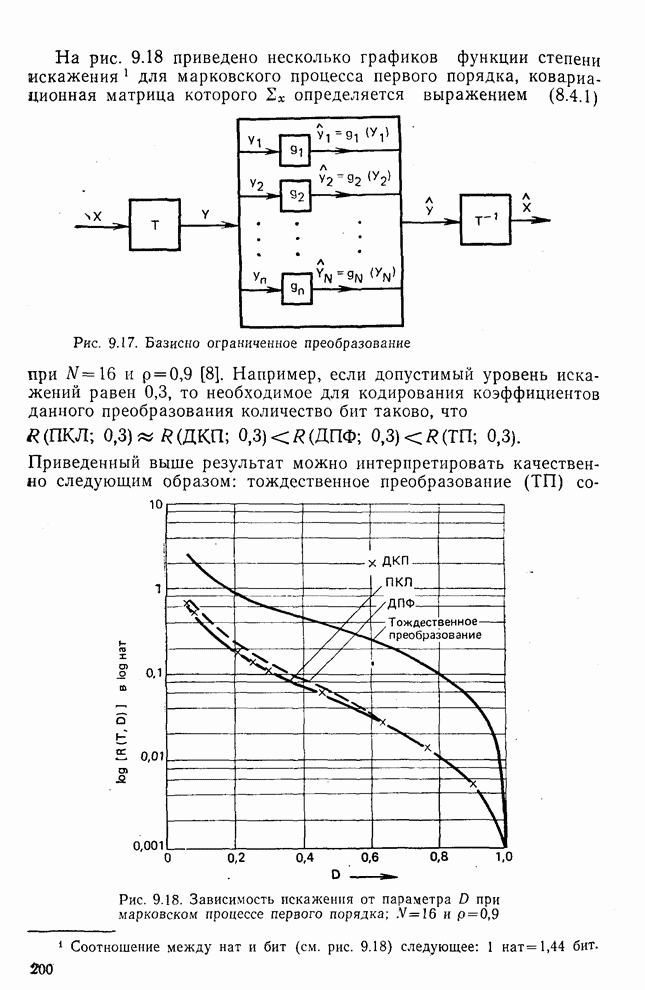
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
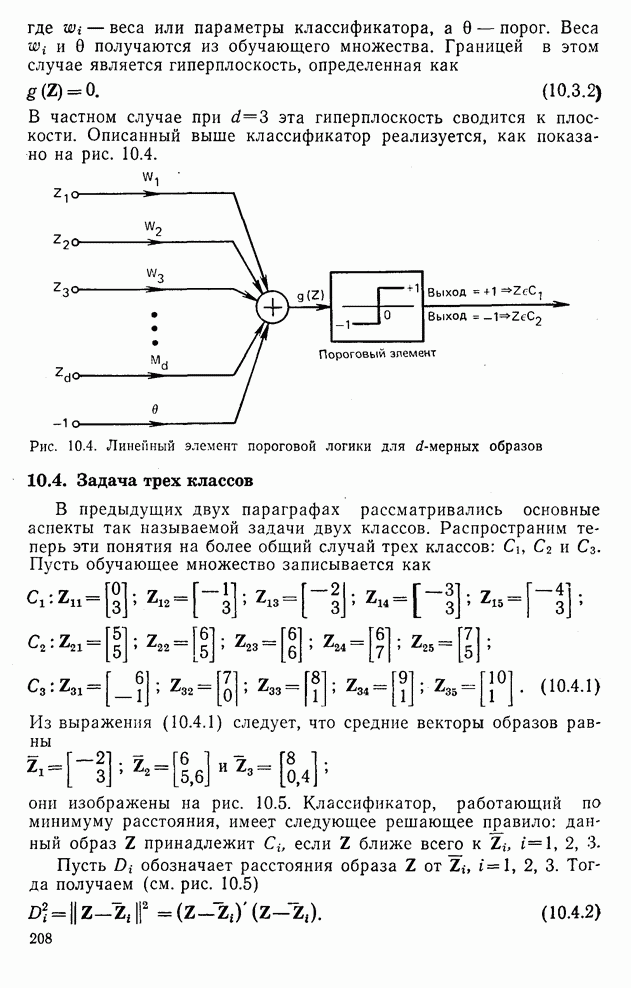
- 10.3. d-мерные образы
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
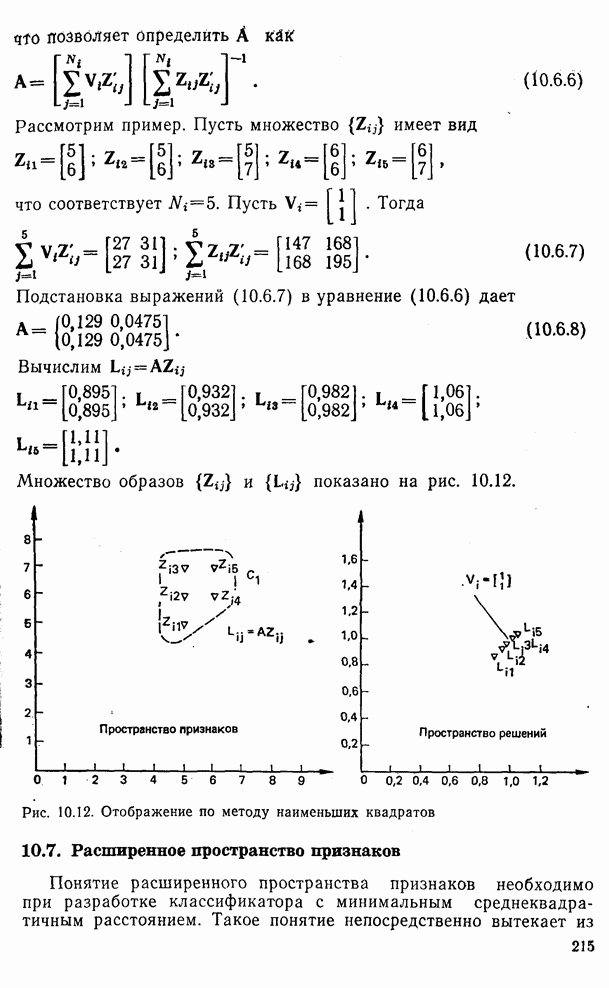
- 10.6. Метод отображения по методу наименьших квадратов
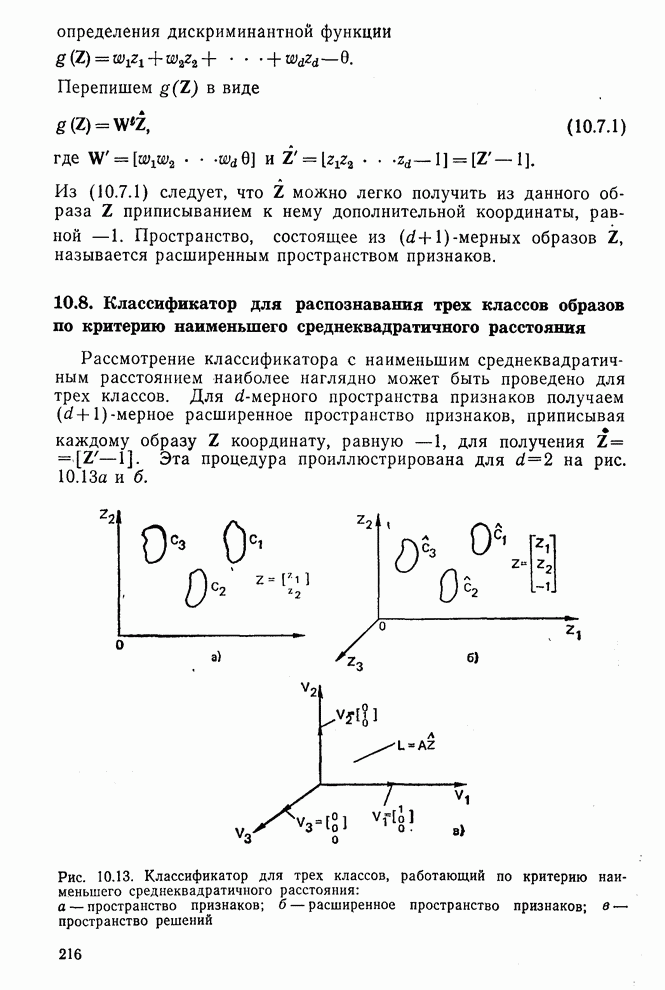
- 10.7. Расширенное пространство признаков
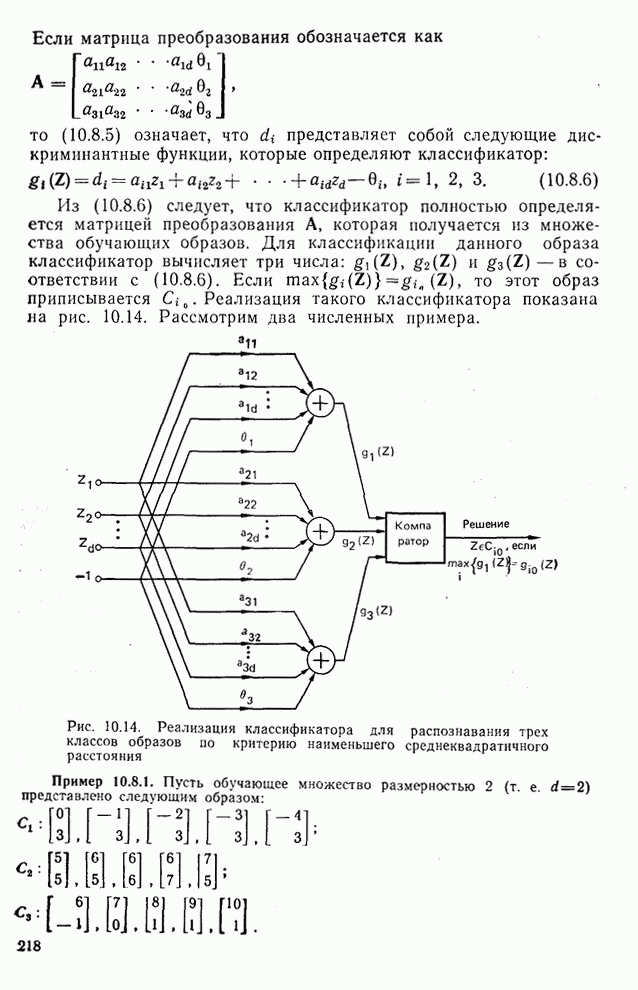
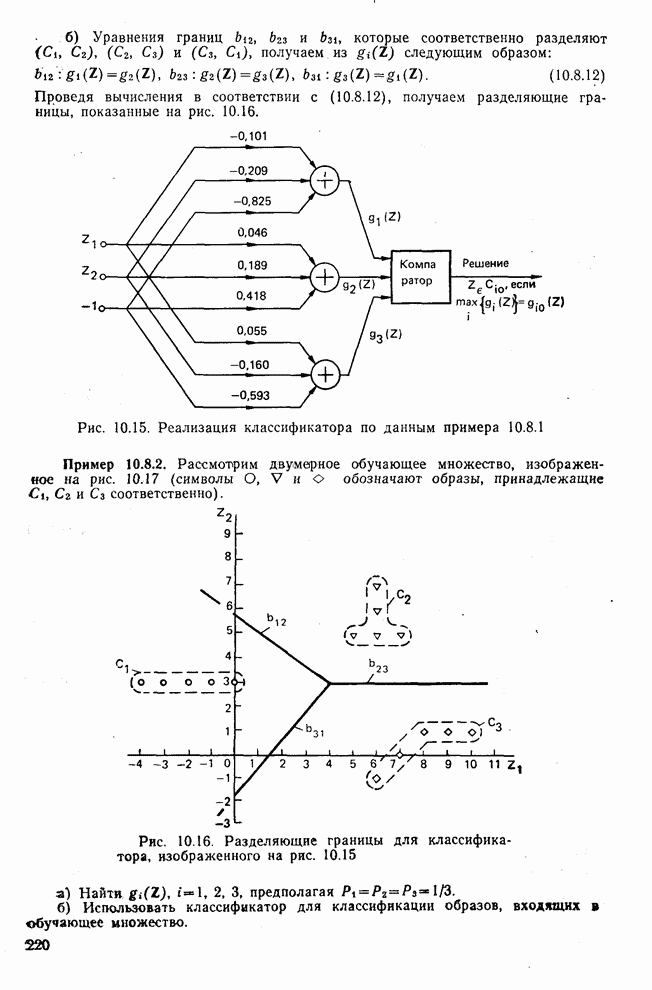
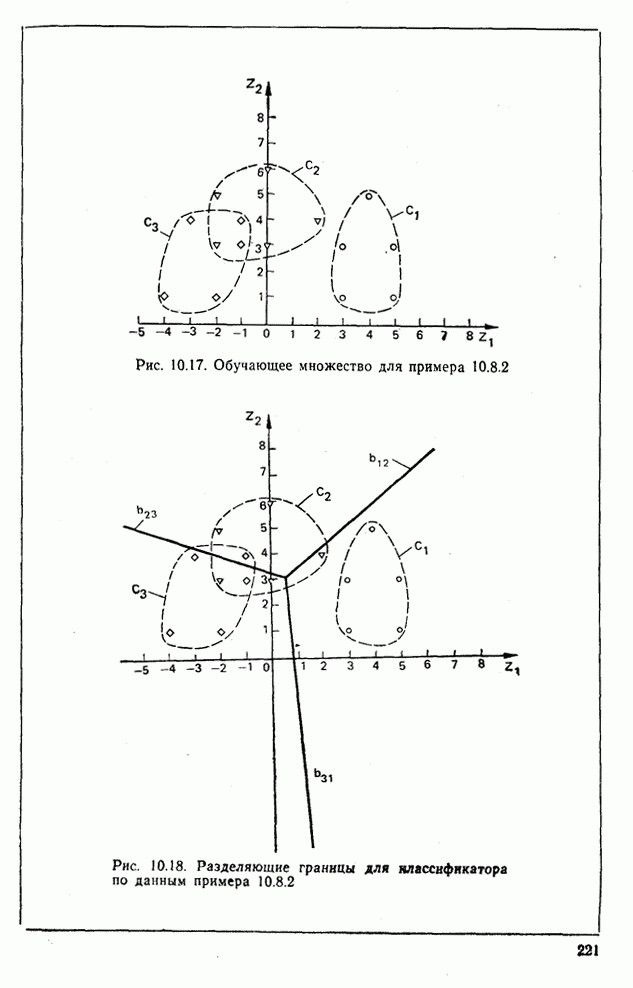
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
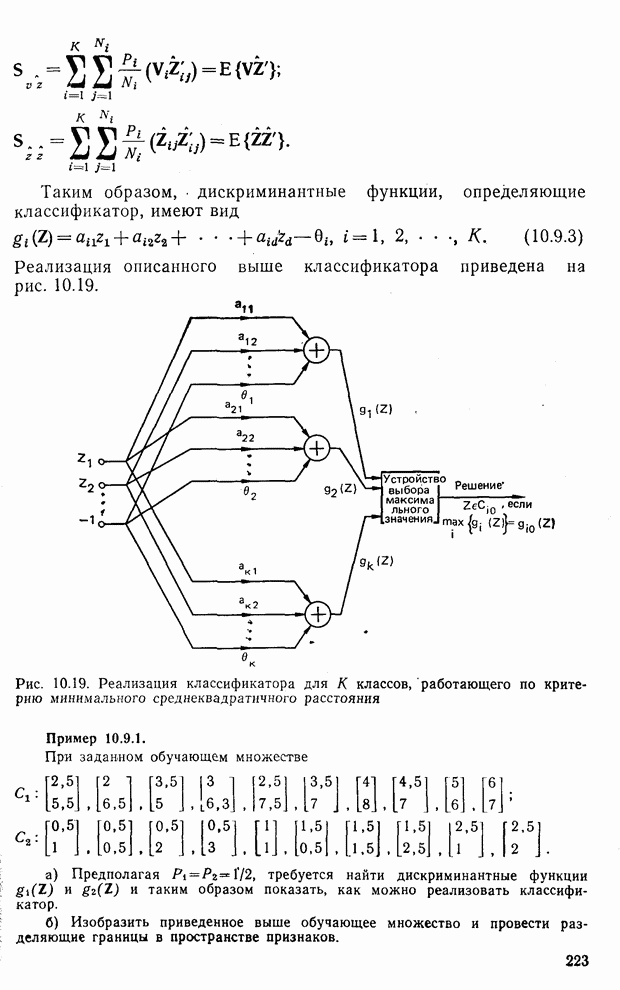
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
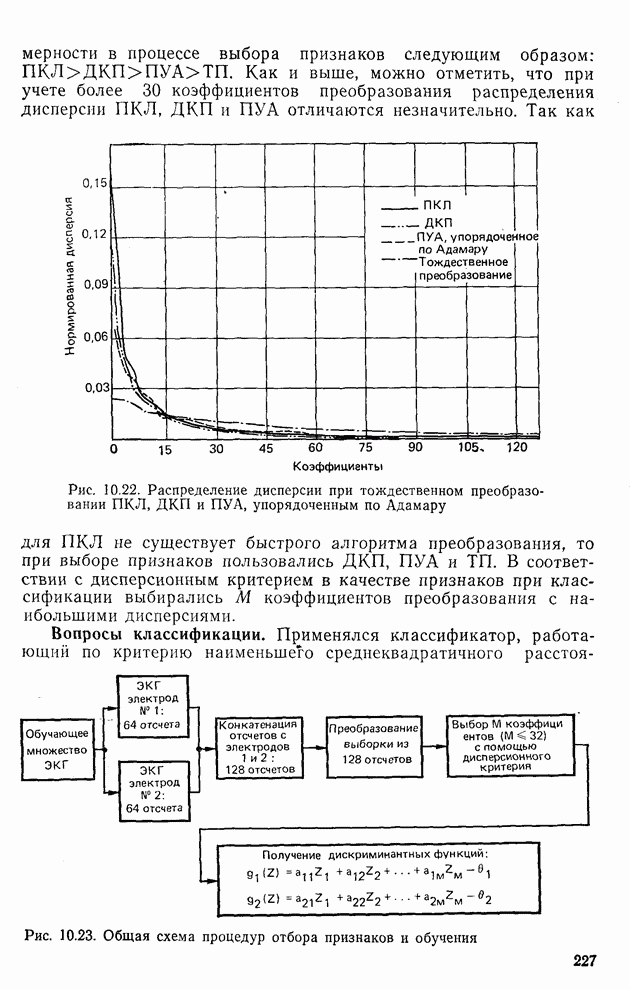
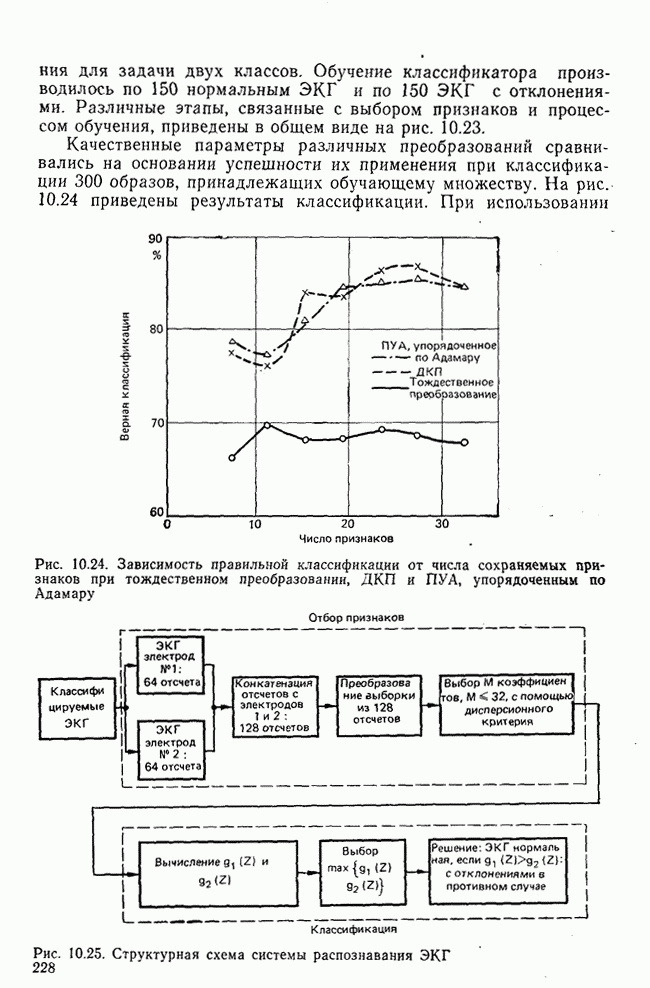
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ