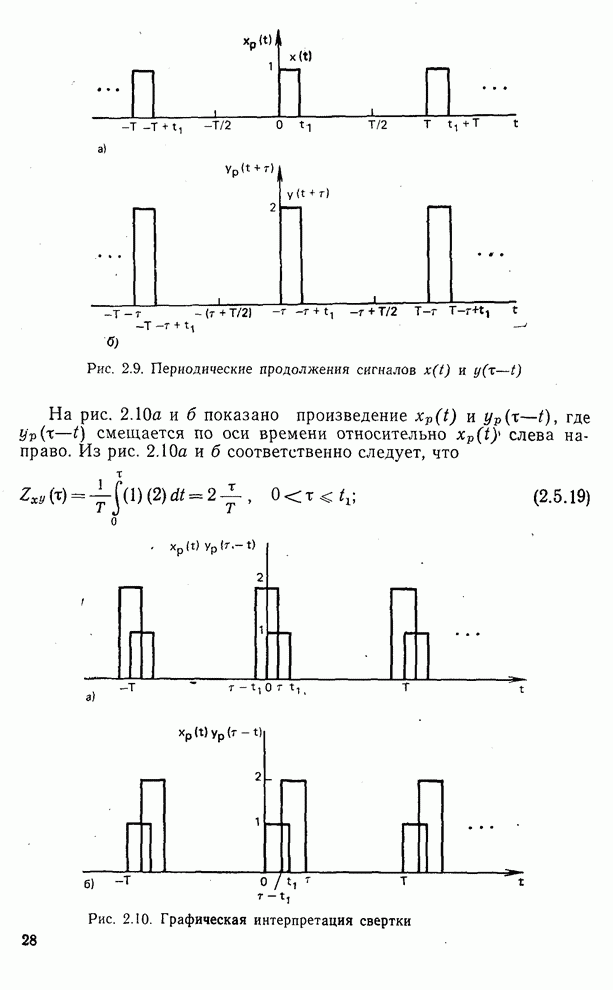
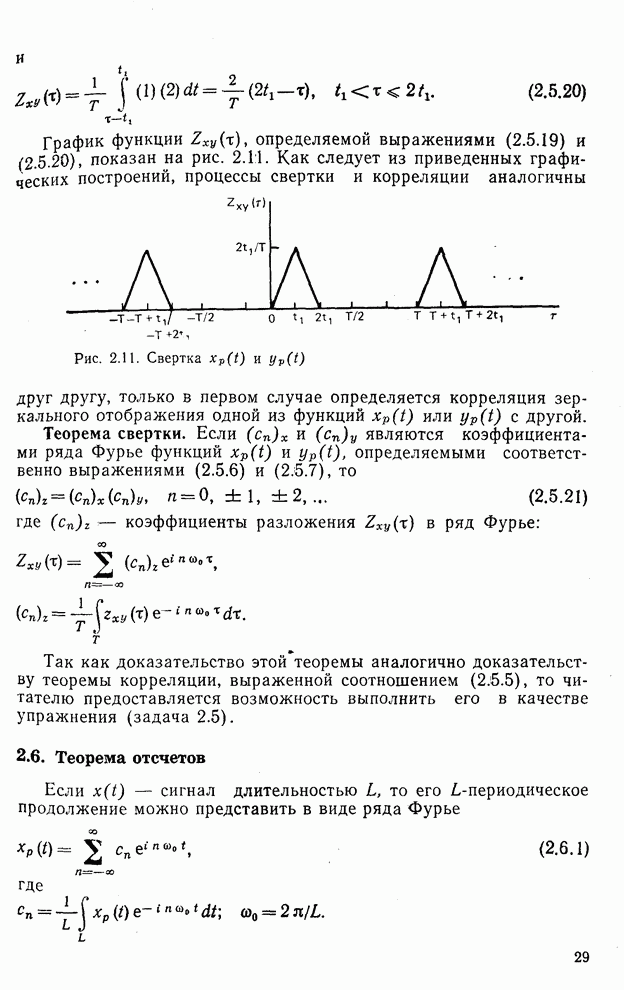
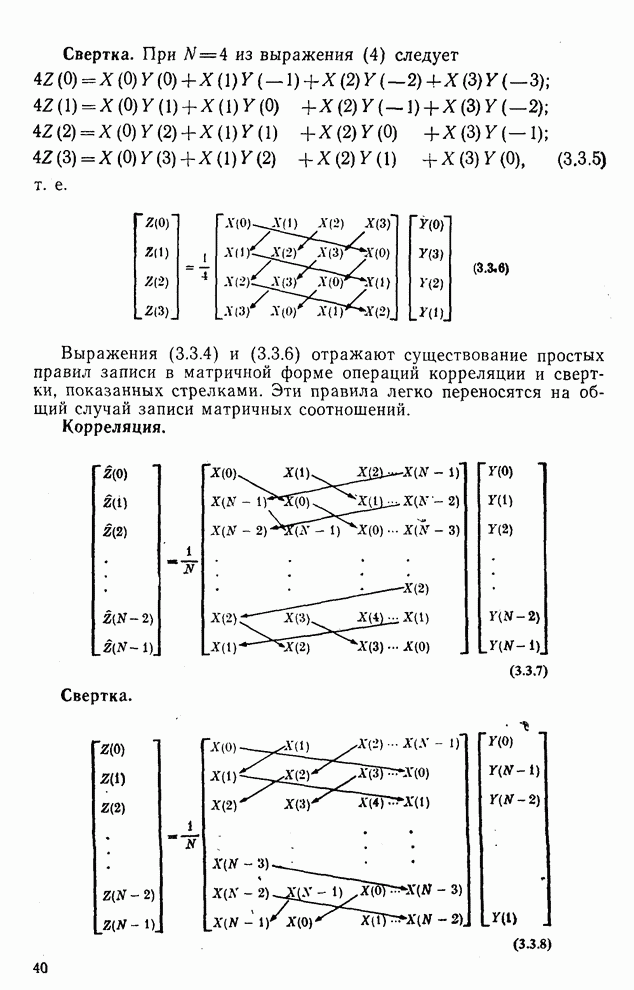
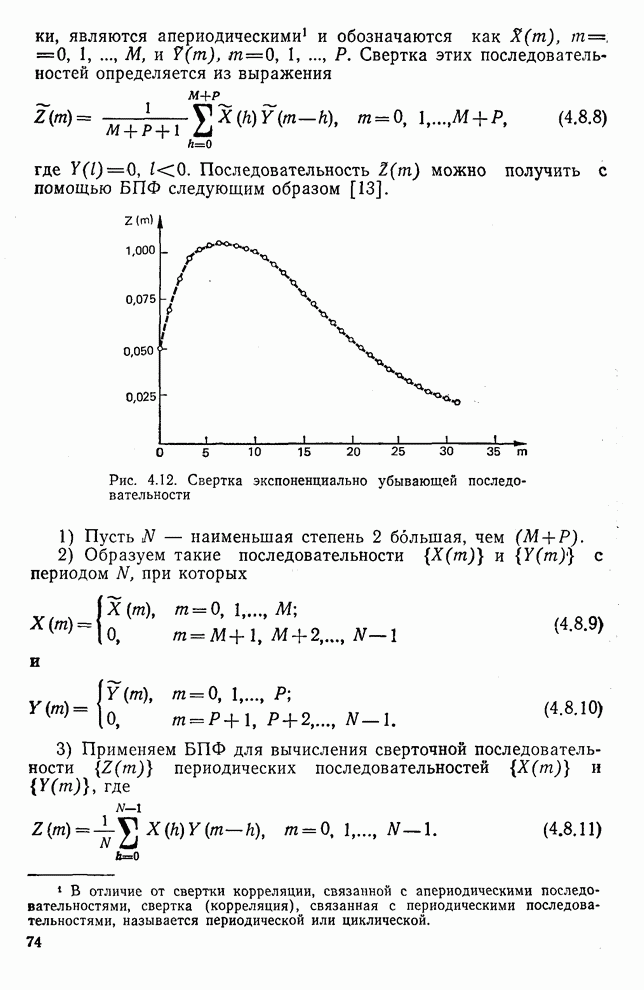
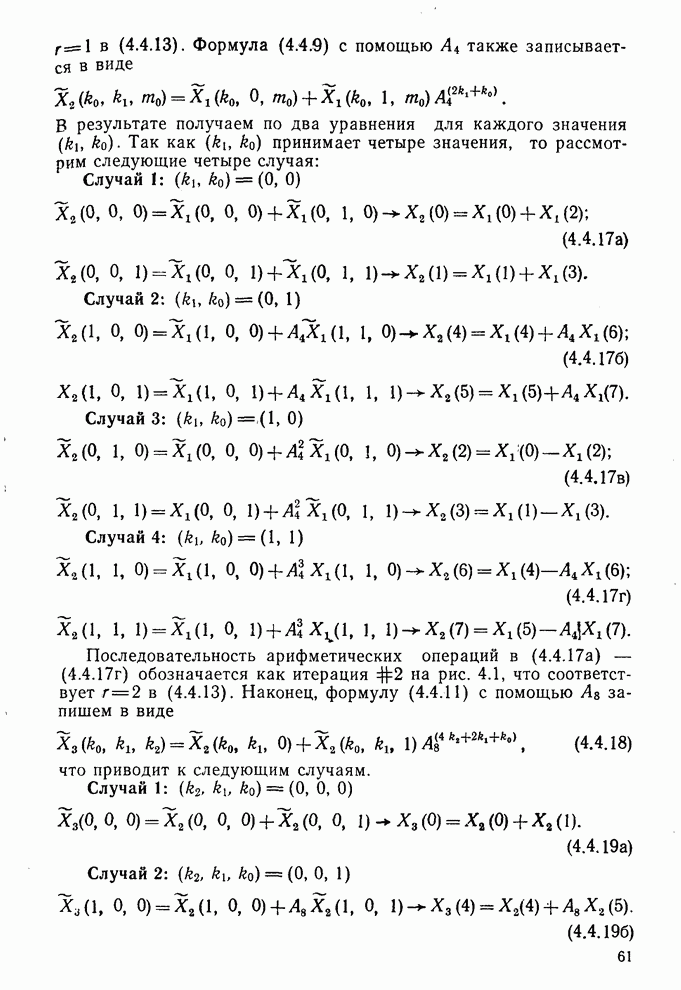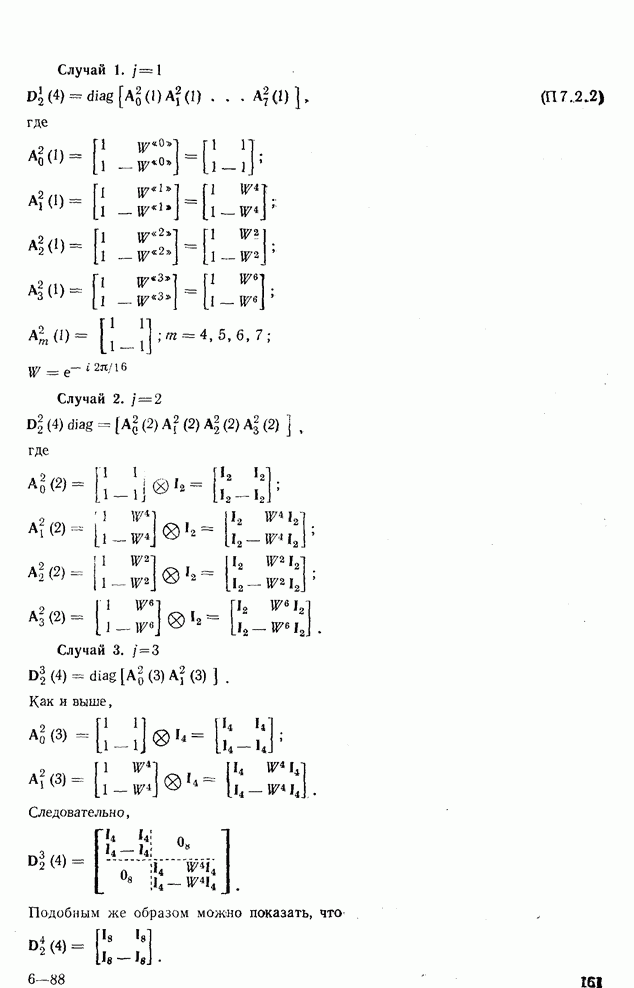| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.6. Дополнительные соображения
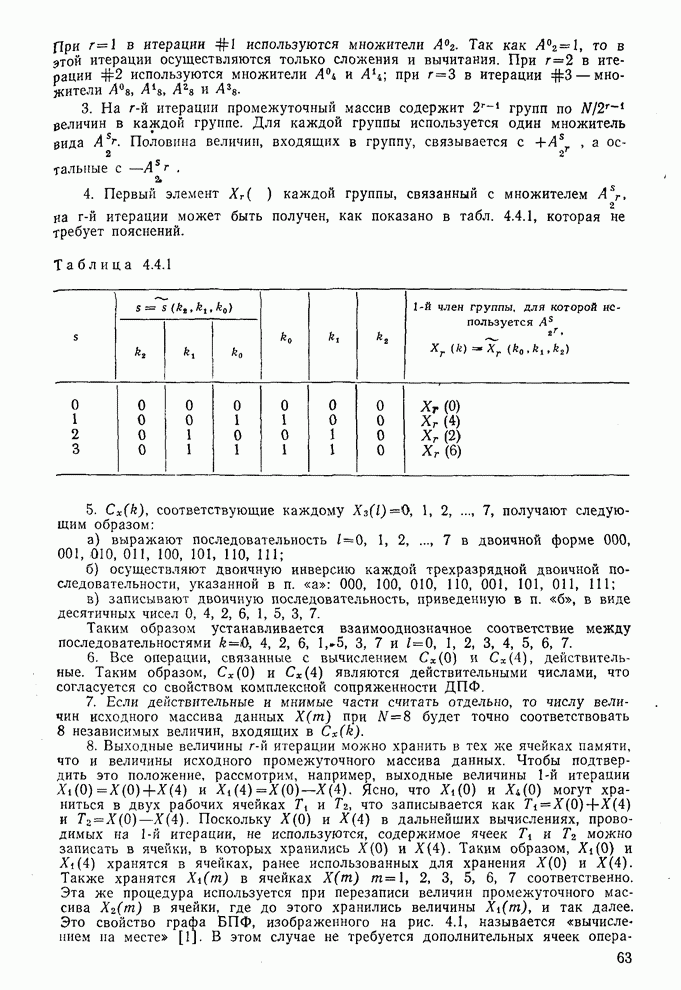
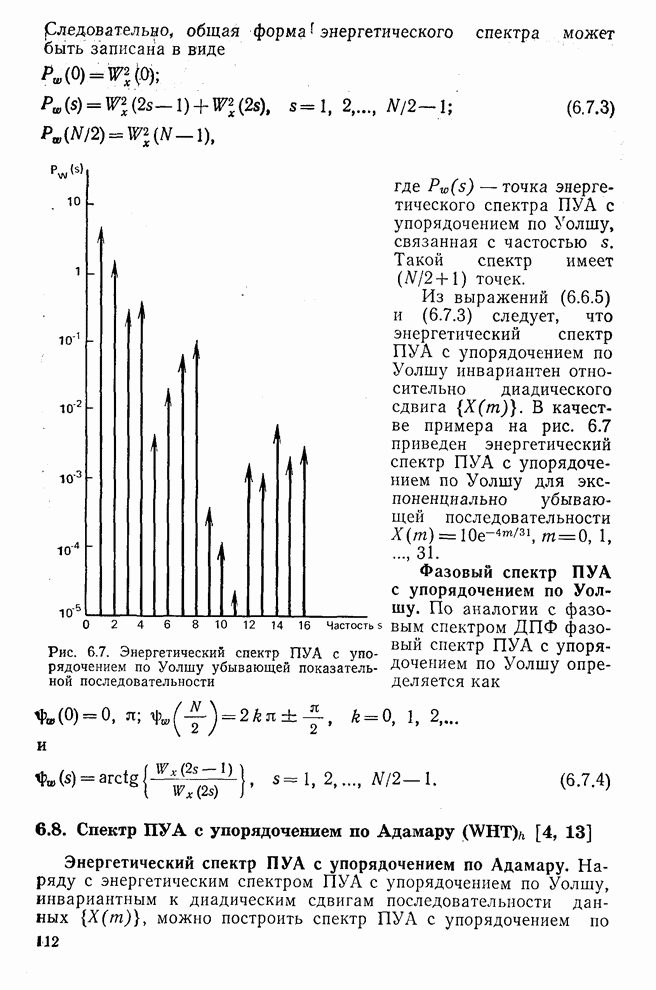
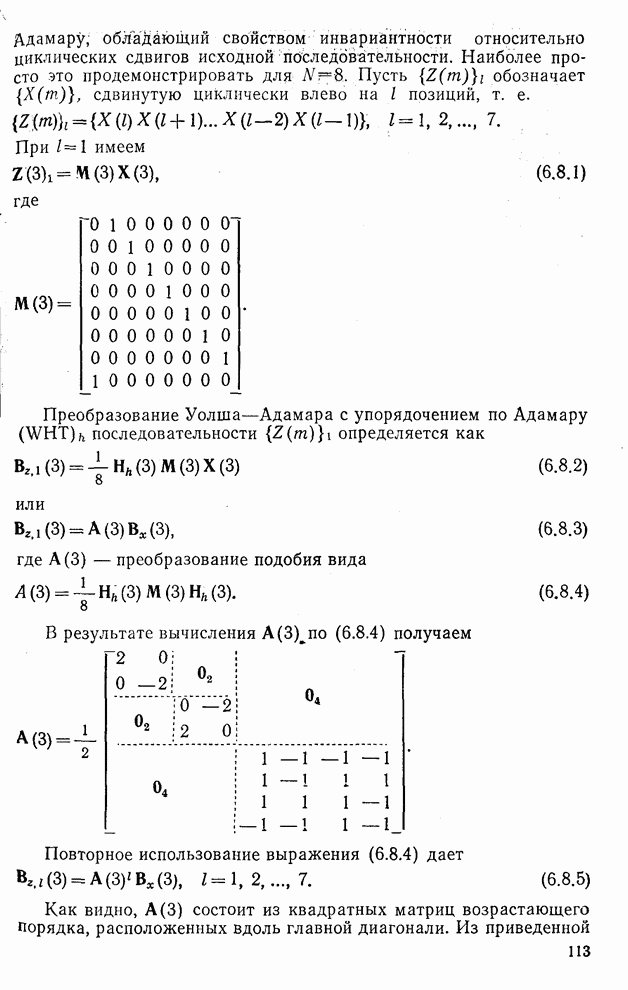
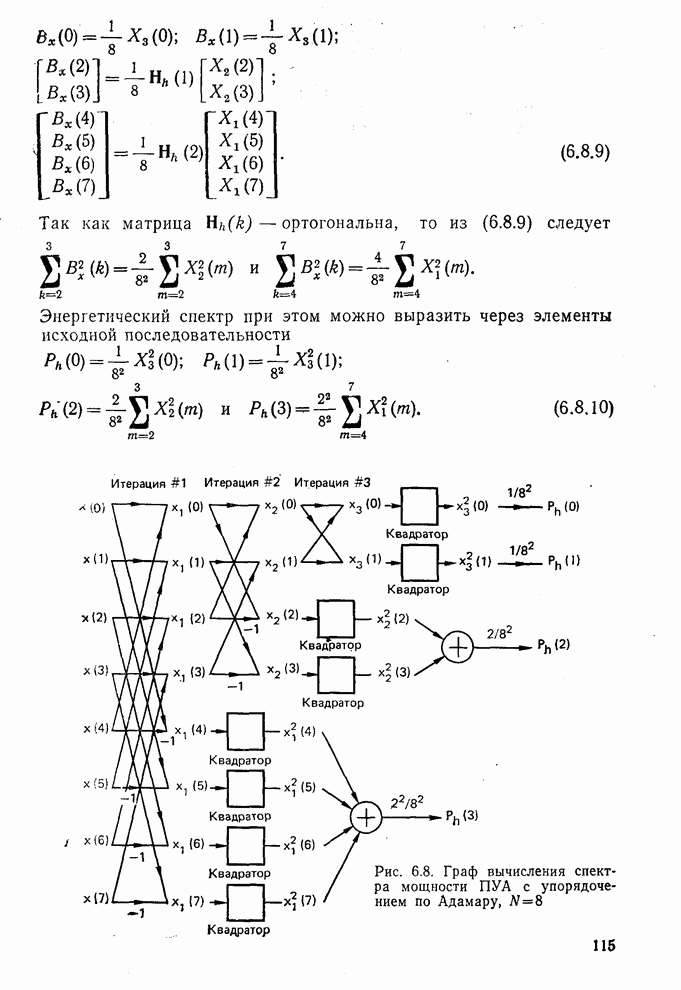
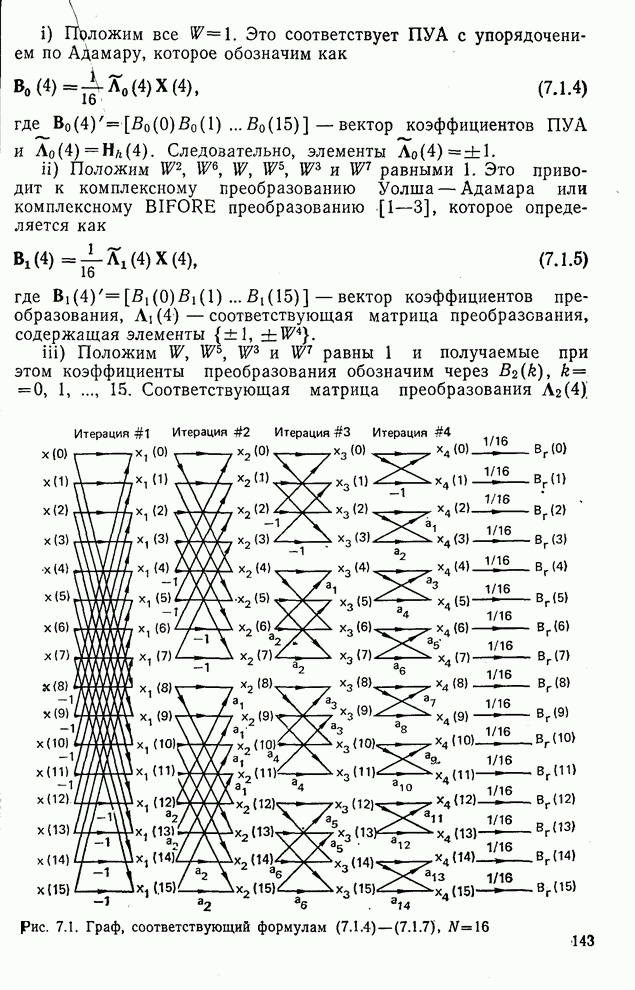
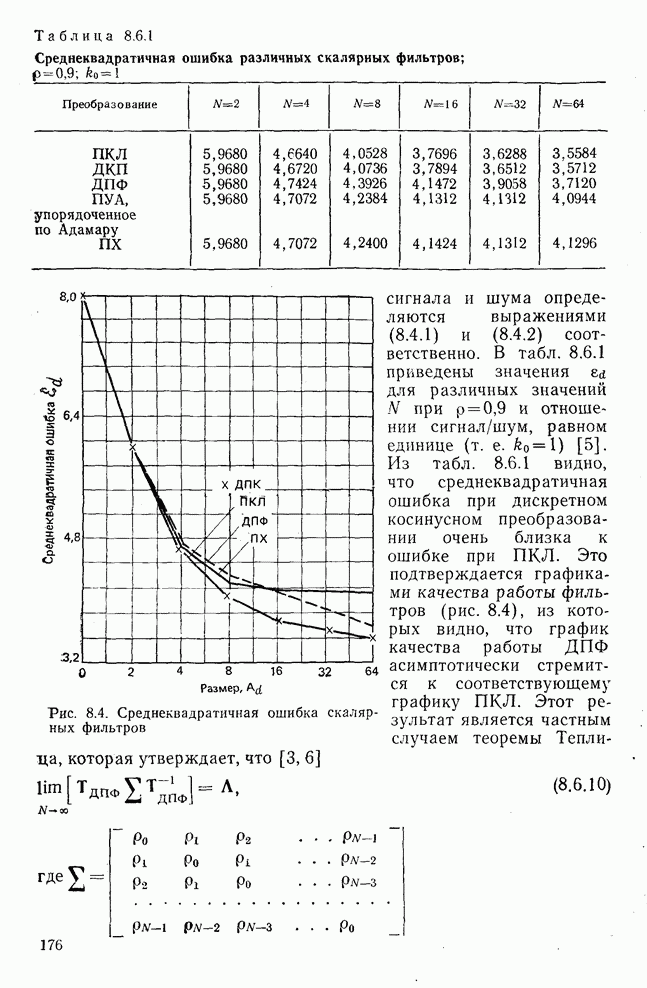
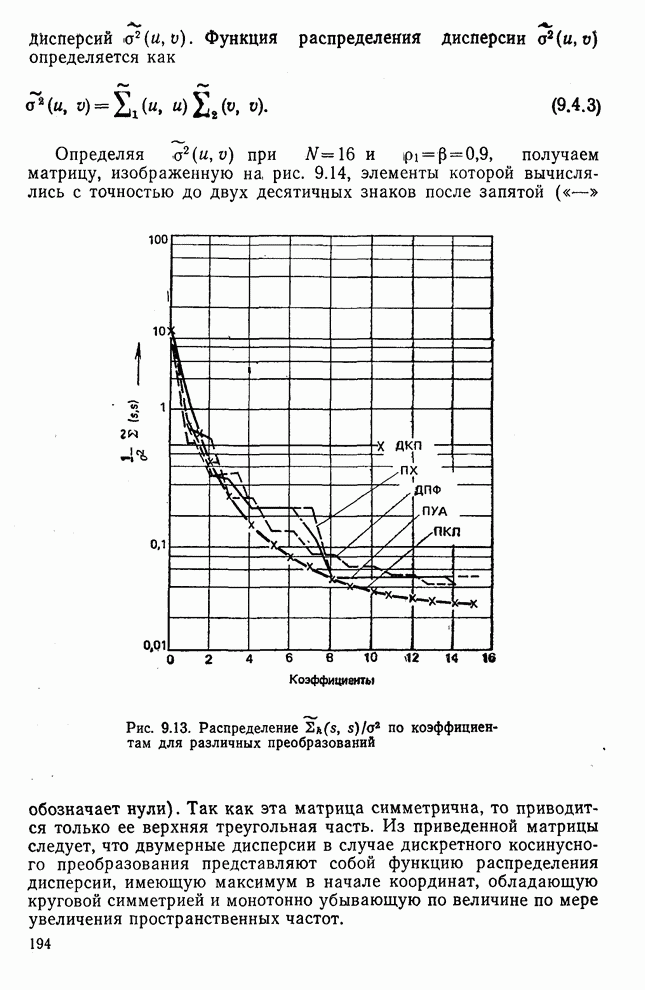
Выше было показано, что дисперсионный критерий дает возможность предсказать относительное качество различных преобразований при сжатии данных. В соответствии с дисперсионным критерием сохраняется множество коэффициентов преобразования, обладающих наибольшими дисперсиями, а остальные коэффициенты не учитываются. Такой подход может быть также объяснен с помощью функции степени искажения, связанной с базисно ограниченными (БО) преобразованиями. Понятие базисно ограниченного преобразования ввел Пирл [5, 6]. Такое преобразование (рис. 9.17) включает в себя преобразование Т, операцию Q (не обязательно линейную), определенную на множестве коэффициентов преобразования  , и обратное преобразование
, и обратное преобразование  .
.

Приведенная структура имеет очевидное ограничение, заключающееся в том, что Q действует на каждый коэффициент  , отдельно. Например, при
, отдельно. Например, при  БО преобразование сводится к скалярной винеровской фильтрации, которая рассматривалась в § 8.4. Если же
БО преобразование сводится к скалярной винеровской фильтрации, которая рассматривалась в § 8.4. Если же  и
и  , то БО преобразование соответствует модели сжатия данных, изображенной на рис. 9.10.
, то БО преобразование соответствует модели сжатия данных, изображенной на рис. 9.10.
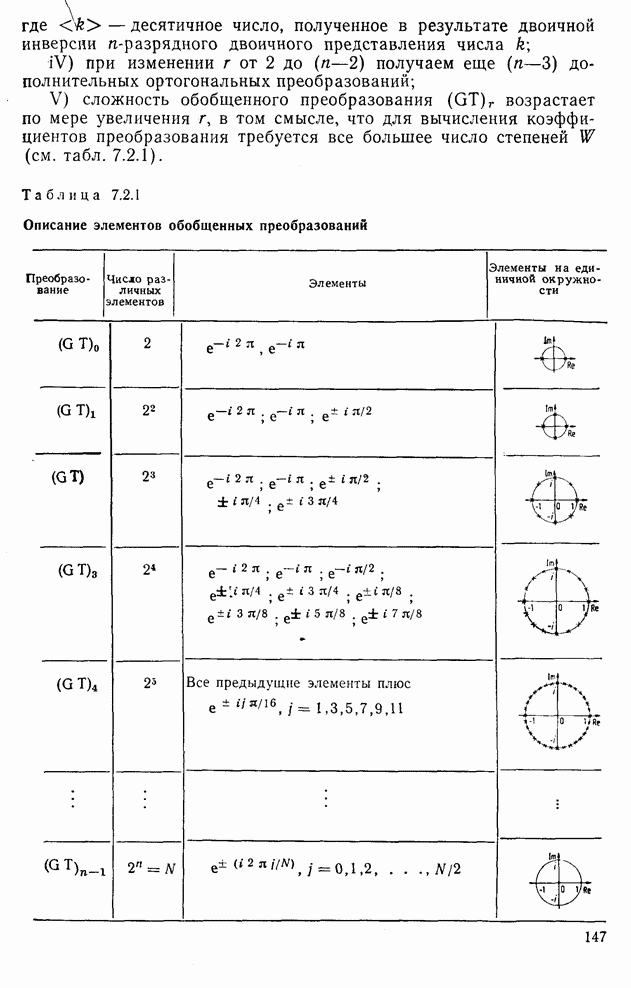
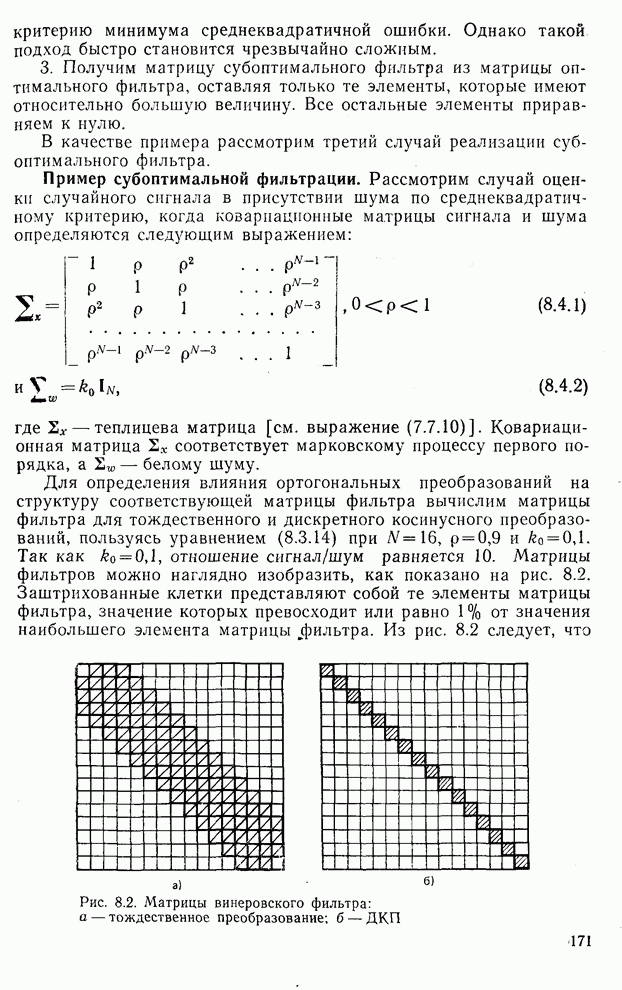
По существу функция степени искажения определяет минимум информации в битах, необходимый для такого кодирования коэффициента преобразования, при котором среднее искажение меньше или равно заданной величине D. Обычно стремятся распределить искажение по всем коэффициентам так, чтобы число бит на коэффициент (т. е. количество) было минимальным. Рассмотрим случай, когда коэффициенты преобразования имеют нормальное распределение, а искажение измеряется в соответствии с критерием среднеквадратичной ошибки. Тогда, как показано в [5—7], функция степени искажения определяется из выражения

Рис. 9.16. Примеры сжатия изображения:
а — оригинал; 8 бит на элемент изображения; б — ПКЛ; 2 бита на элемент изображения; в — ДКП; 2 бита на элемент изображения; г — пилообразное преобразование; 2 бита на элемент изображения; д — ДПФ; 2 бита на элемент изображения; е — ПУА, упорядоченное по Адамару; 2 бита на элемент изображения;  — преобразование Хаара; 2 бита на элемент изображения
— преобразование Хаара; 2 бита на элемент изображения

где R — минимальное количество бит на коэффициент преобразования;  собственное значение, если Т представляет собой ПКЛ или
собственное значение, если Т представляет собой ПКЛ или  диагональный элемент ковариационной матрицы в области преобразований
диагональный элемент ковариационной матрицы в области преобразований  , если Т представляет собой любое другое преобразование, и
, если Т представляет собой любое другое преобразование, и  — параметр, удовлетворяющий равенству
— параметр, удовлетворяющий равенству
 (9.6.2)
(9.6.2)
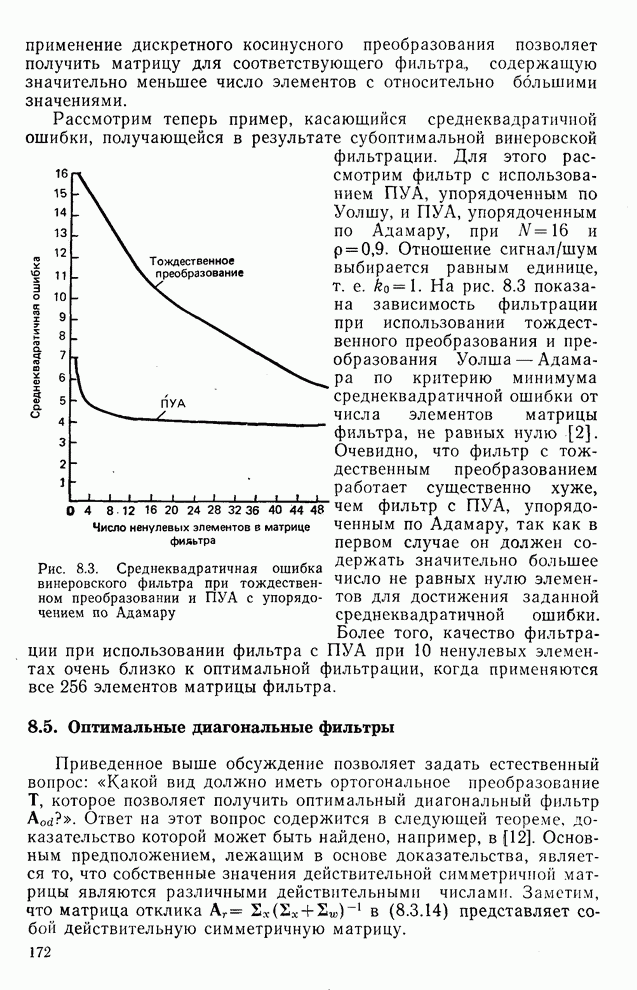
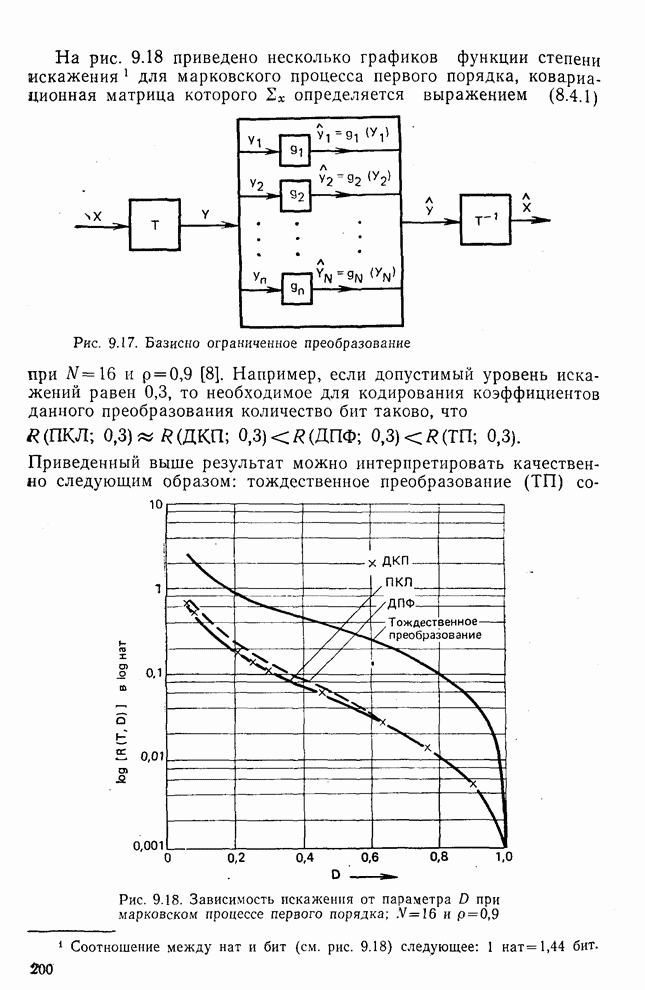
На рис. 9.18 приведено несколько графиков функции степени искажения для марковского процесса первого порядка, ковариационная матрица которого  определяется выражением (8.4.1) при
определяется выражением (8.4.1) при  и
и  0,9 [8]. Например, если допустимый уровень искажений равен 0,3, то необходимое для кодирования коэффициентов данного преобразования количество бит таково, что
0,9 [8]. Например, если допустимый уровень искажений равен 0,3, то необходимое для кодирования коэффициентов данного преобразования количество бит таково, что


Рис. 9.17. Базисно ограниченное преобразование
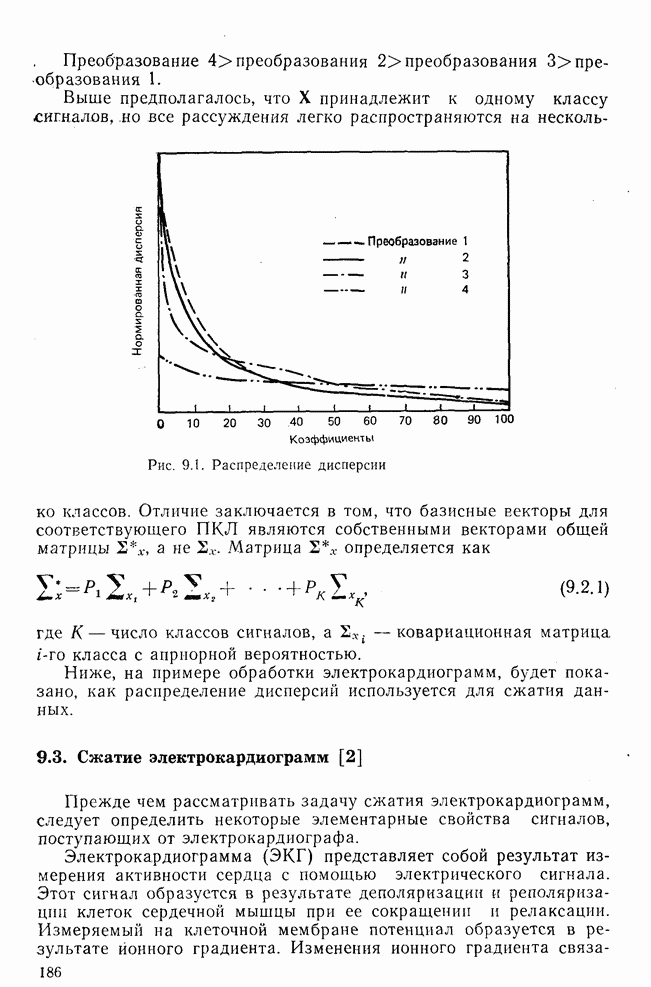
Приведенный выше результат можно интерпретировать качественно следующим образом: тождественное преобразование (ТП) сохраняет всю корреляцию в исходных данных; преобразование ДГТФ декоррелирует исходные данные, но не полностью;

Рис. 9.18. Зависимость искажения от параметра D при марковском процессе первого порядка:  и
и 
преобразование ПКЛ декоррелирует исходные данные полностью, а дискретное косинусное преобразование очень близко в этом отношении к ПКЛ. Таким образом, декорреляция с помощью преобразований приводит к значительно меньшим искажениям, чем непосредственное кодирование данных, состоящих из некоррелированных отсчетов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
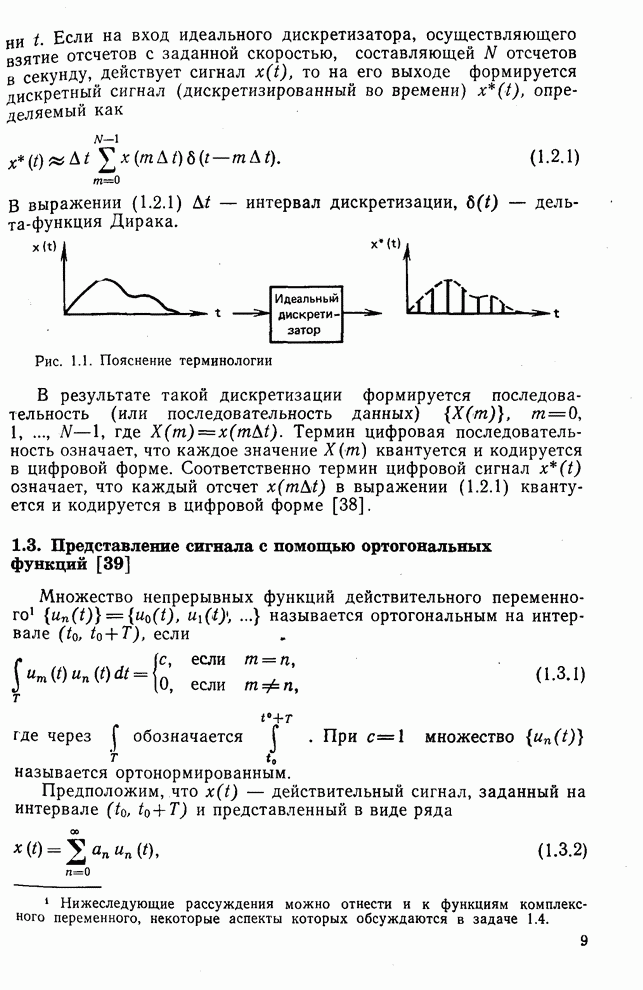
- 1.1. Общие замечания
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
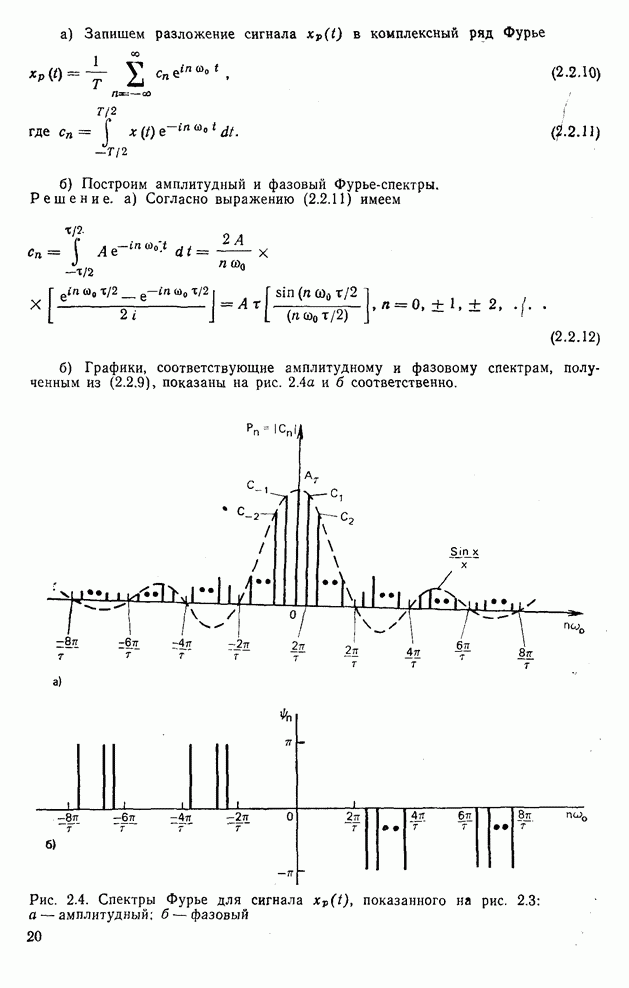
- 2.1. Фурье-представление
- 2.2. Спектр мощности, амплитудный и фазовый спектры
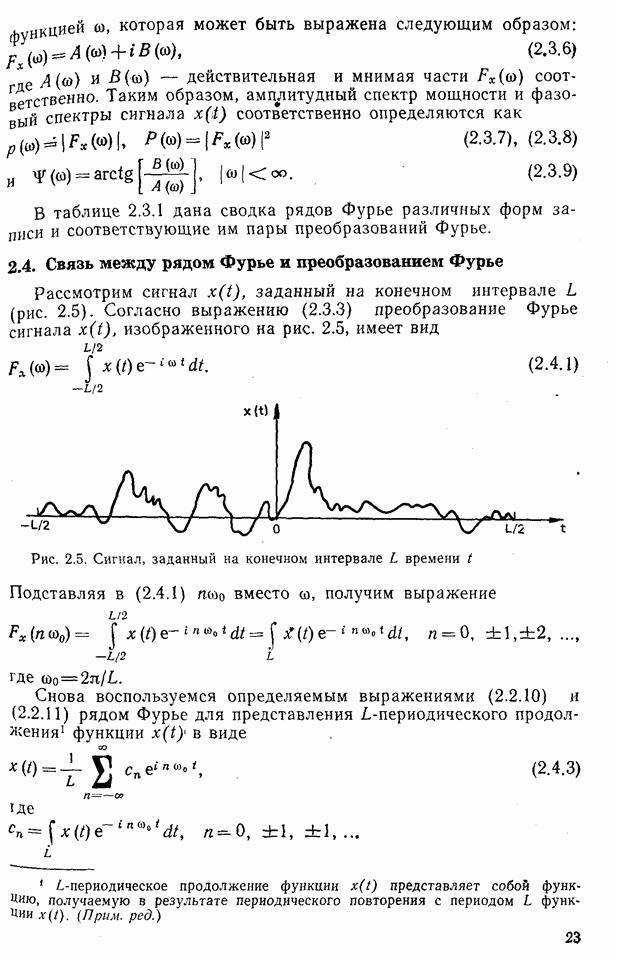
- 2.3. Преобразование Фурье
- 2.4. Связь между рядом Фурье и преобразованием Фурье
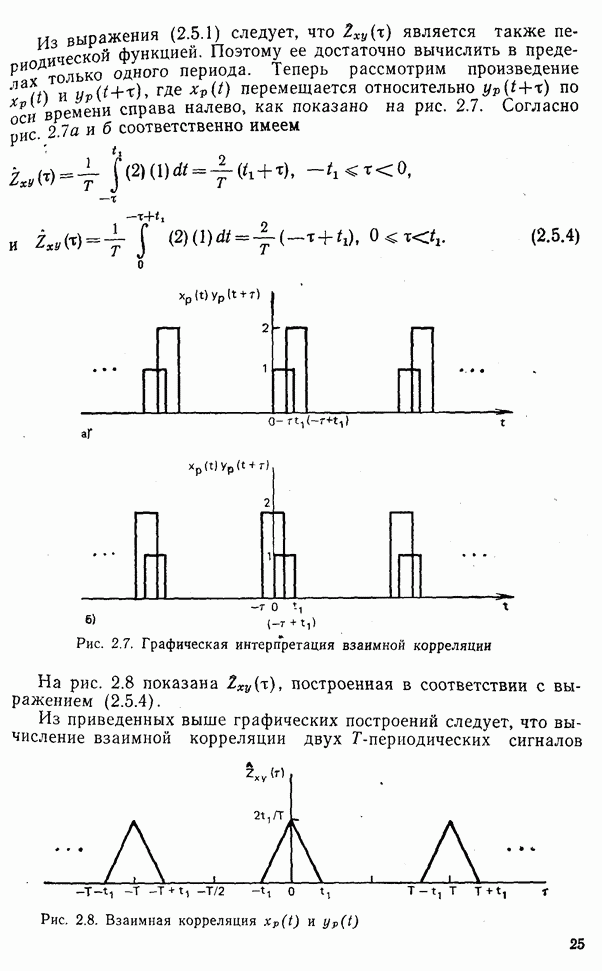
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
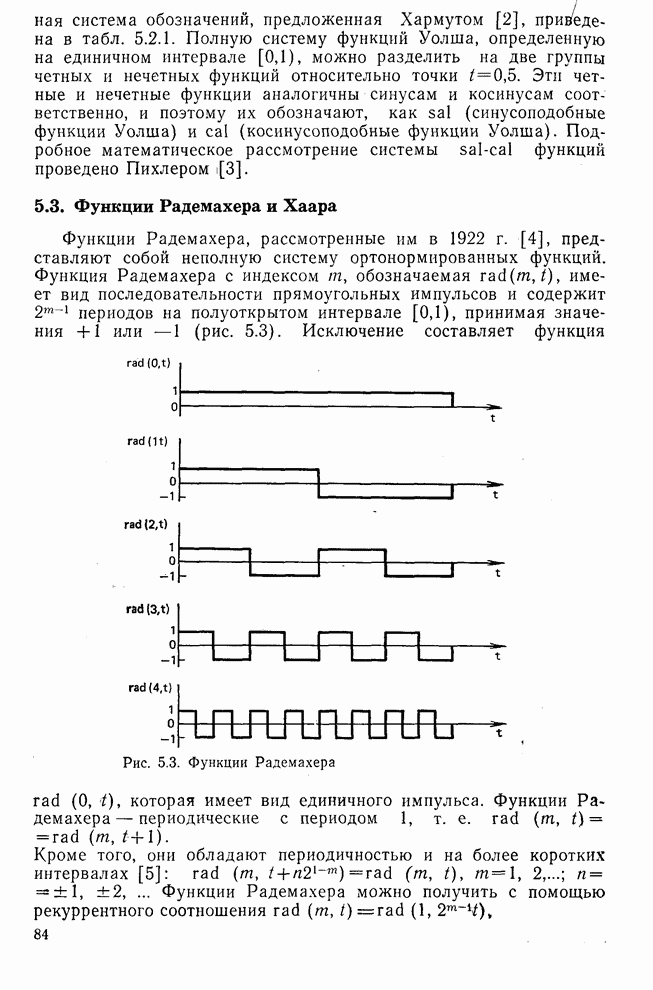
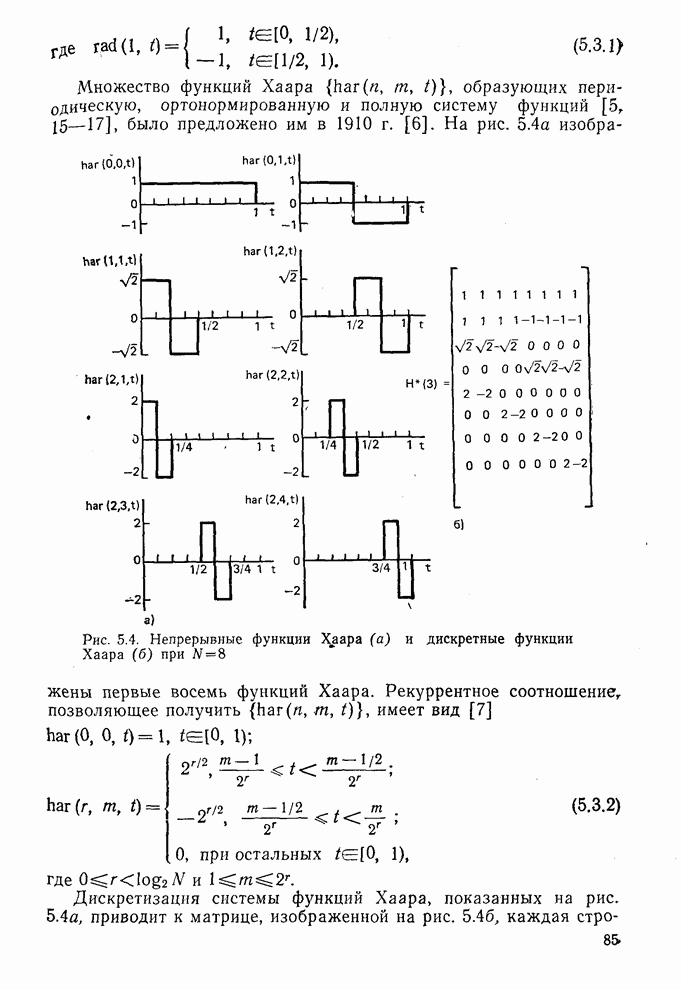
- 5.3. Функции Радемахера и Хаара
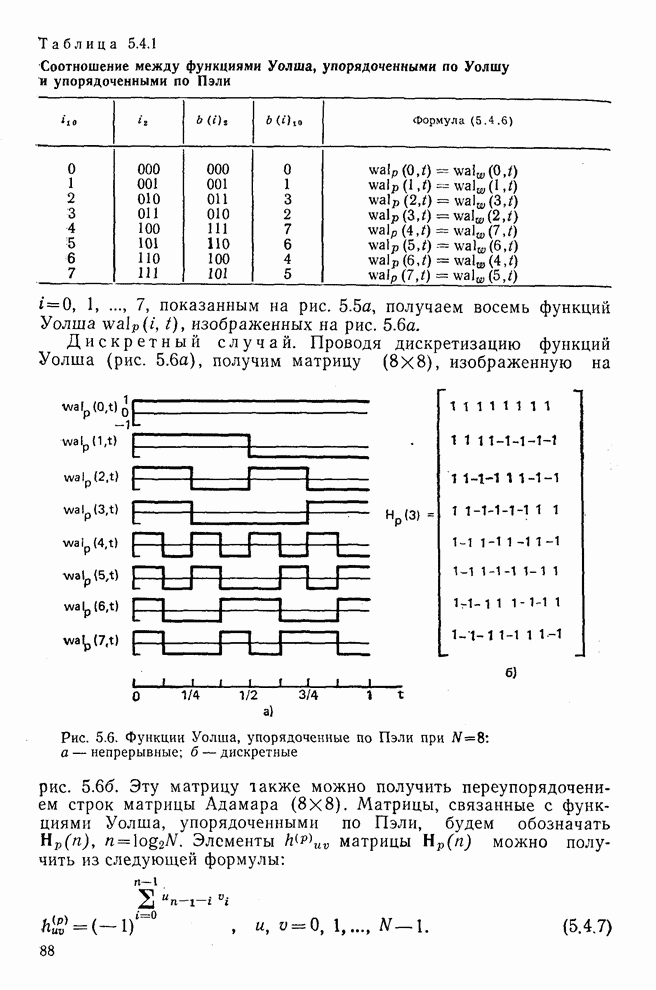
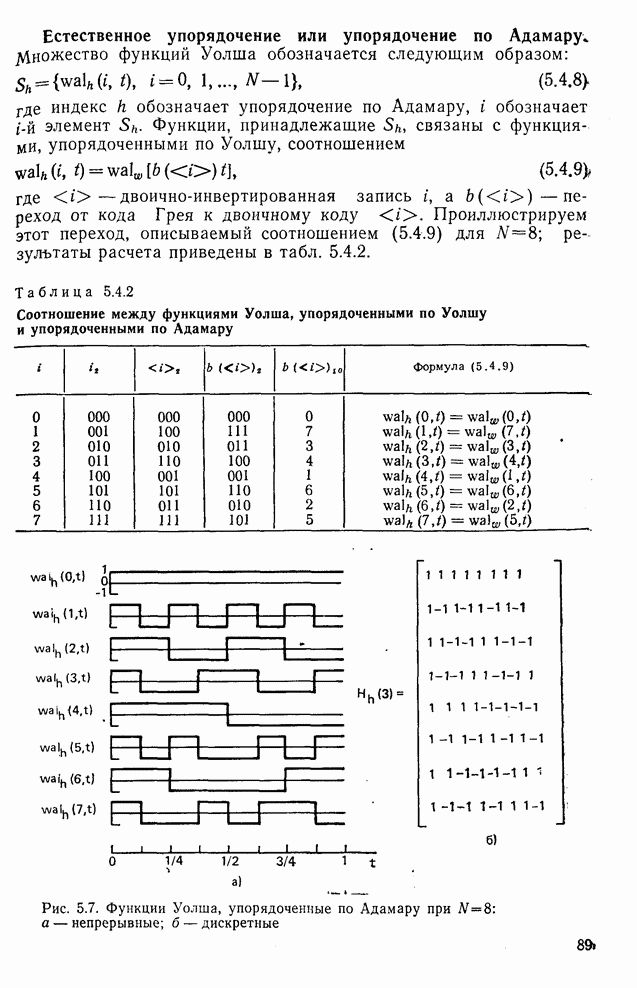
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
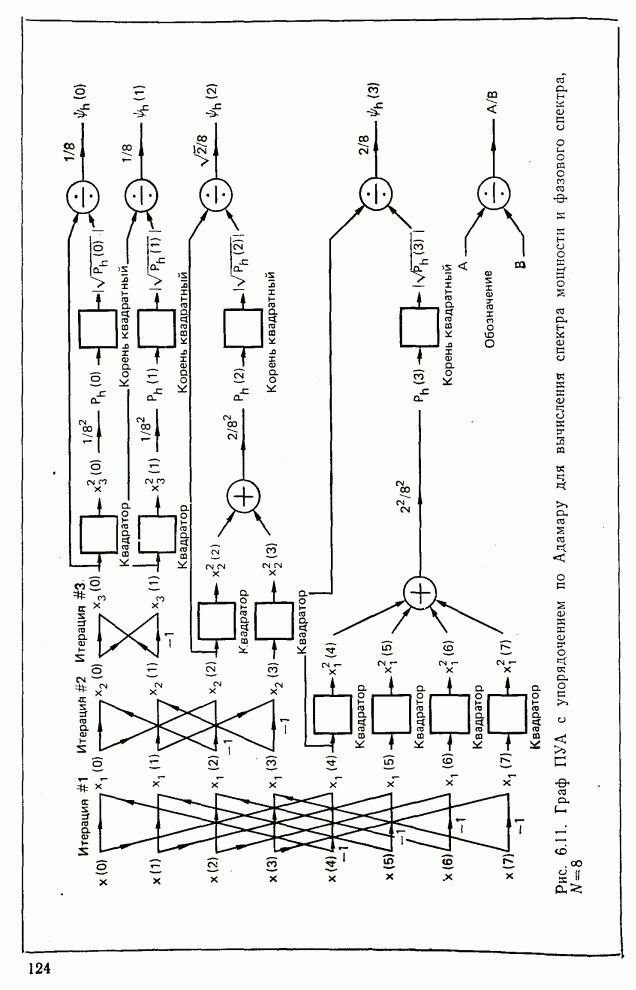
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
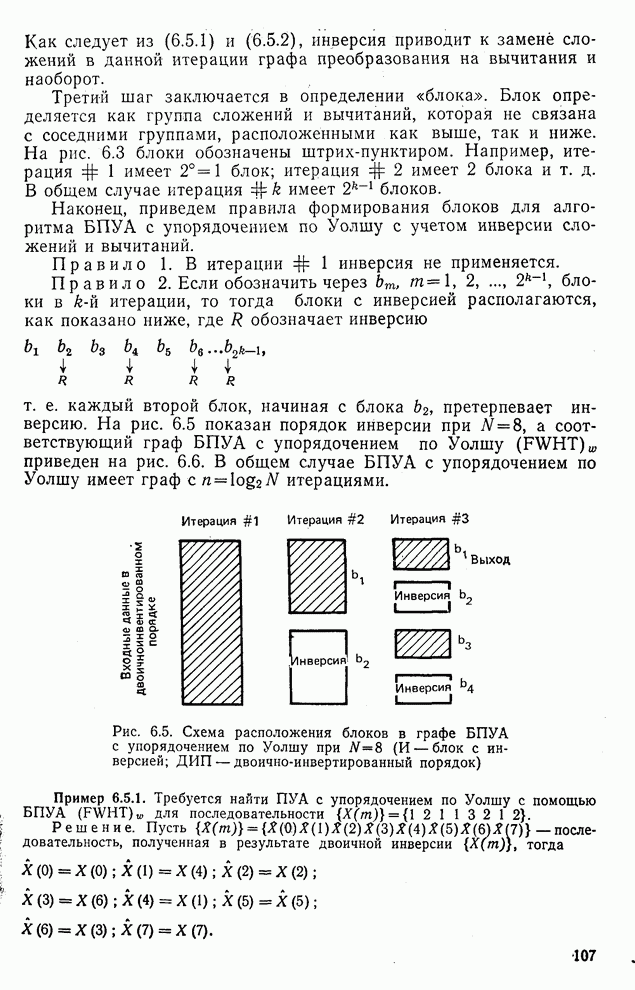
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
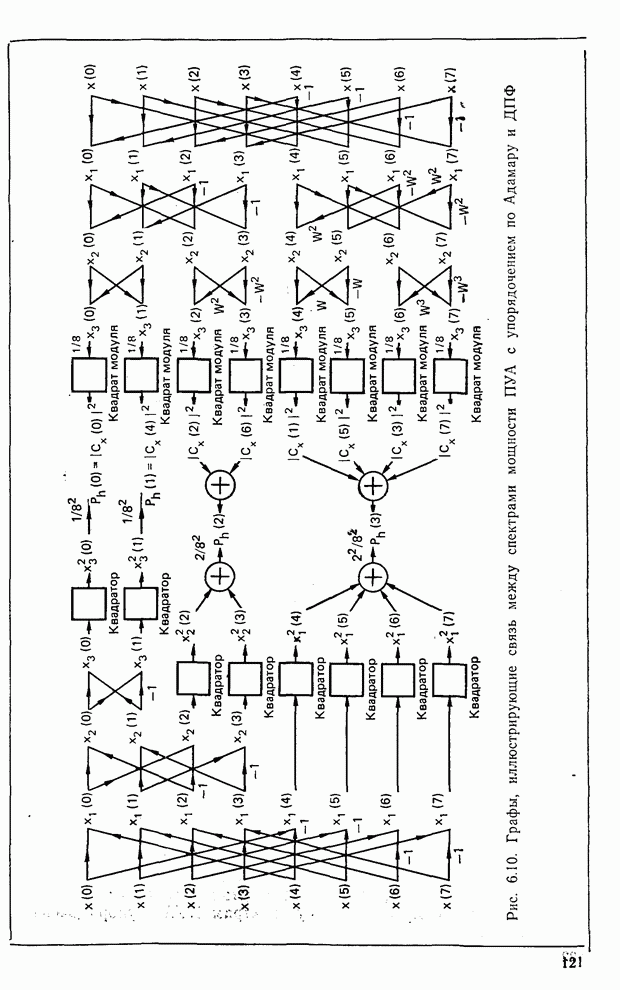
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
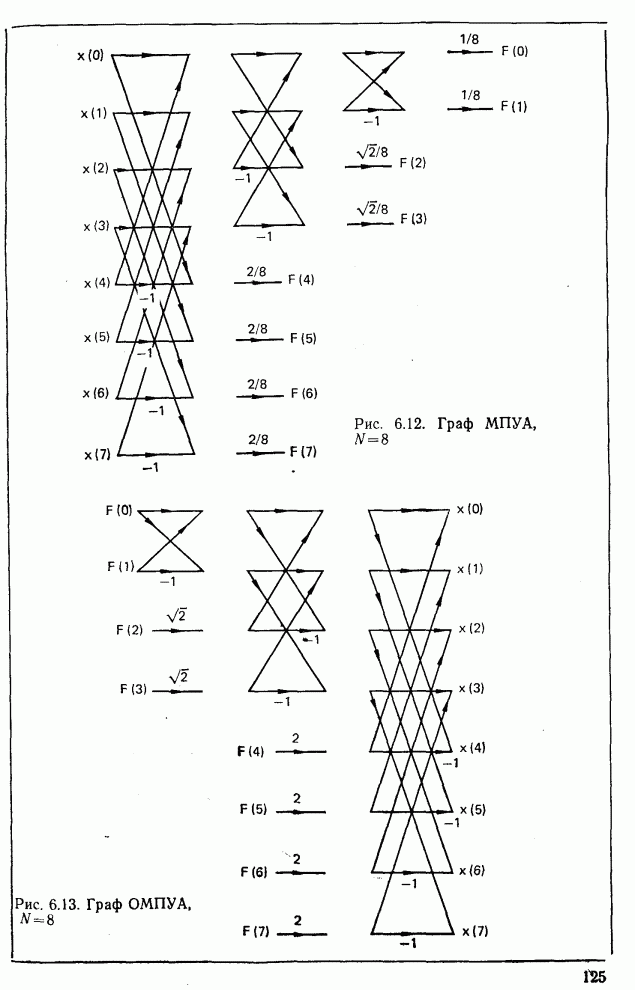
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
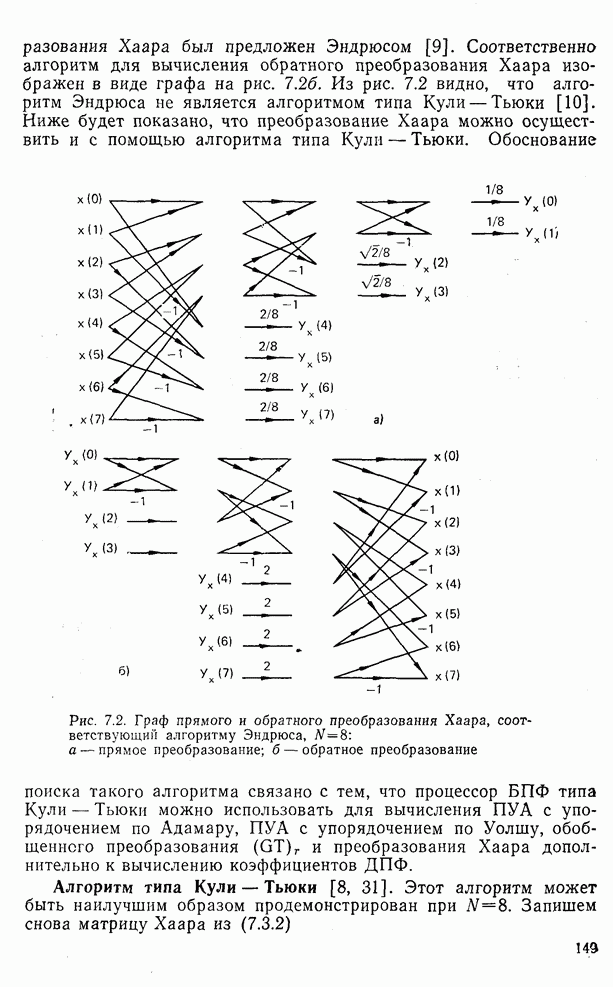
- 7.3. Преобразование Хаара [ПХ]
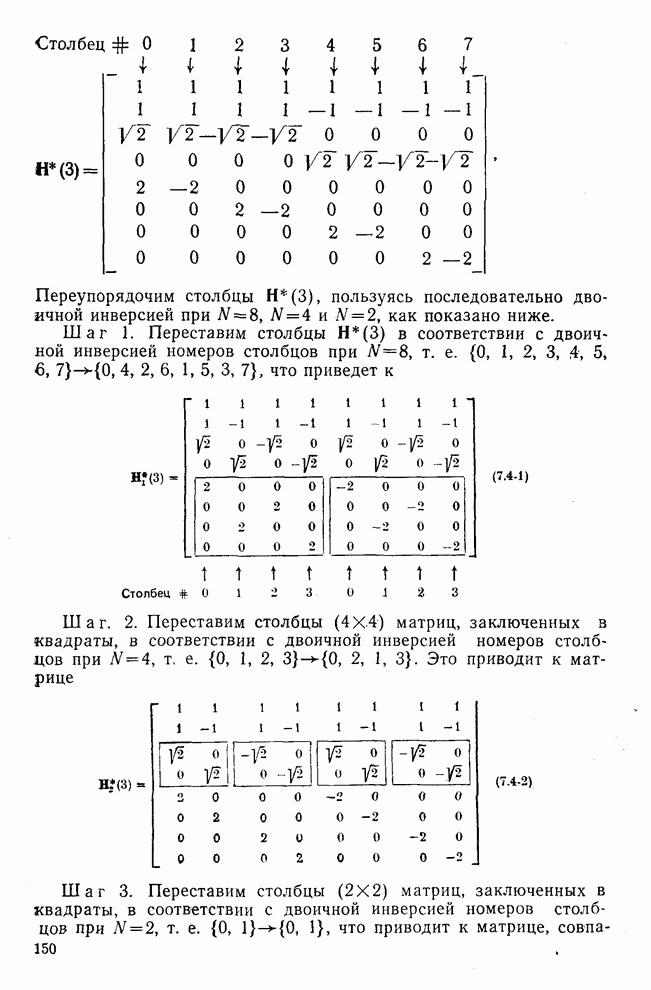
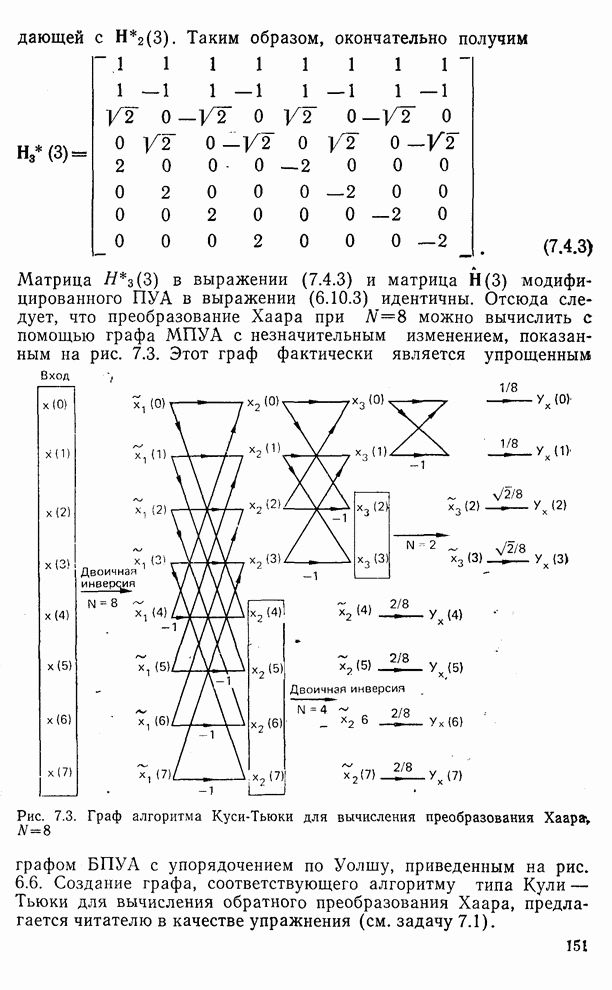
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
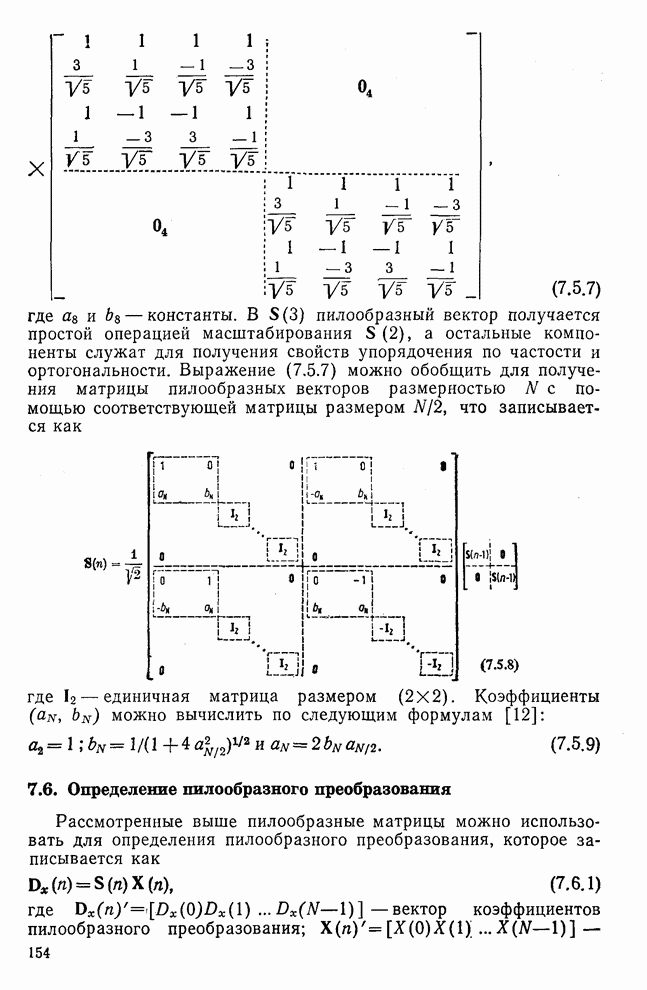
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
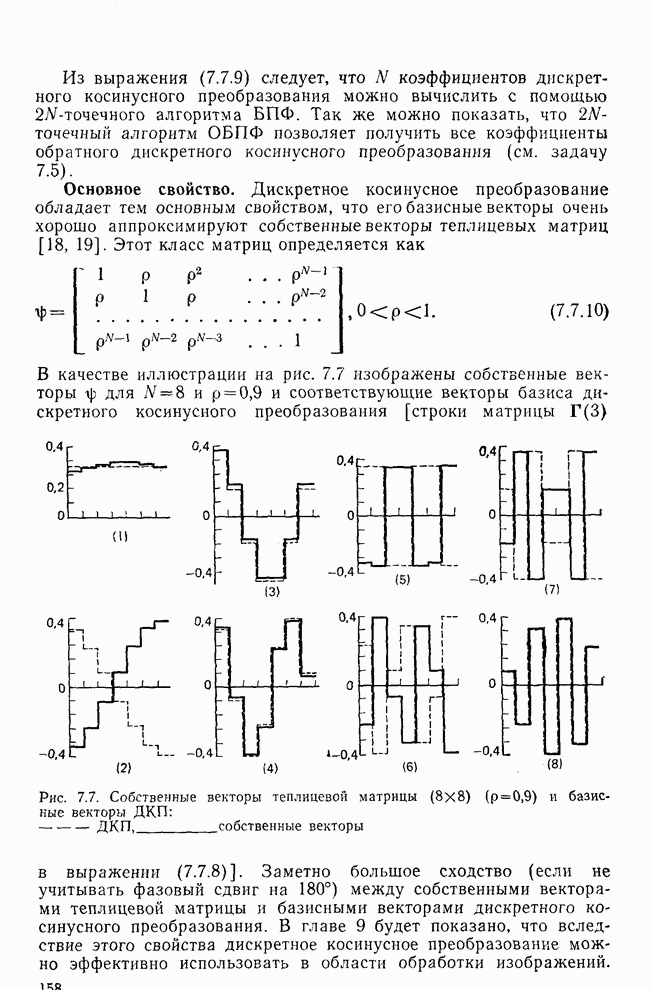
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
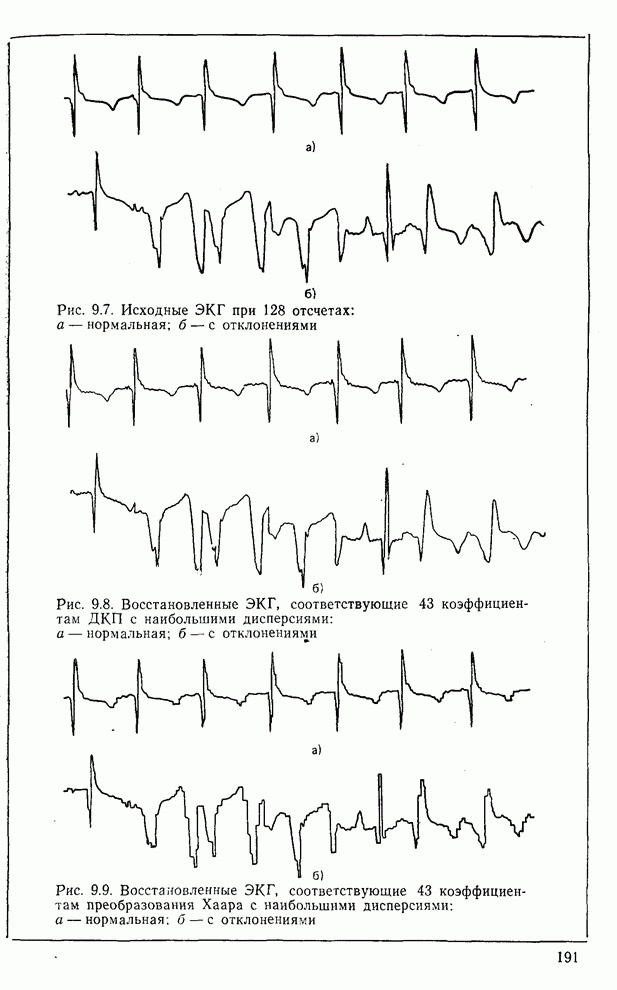
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
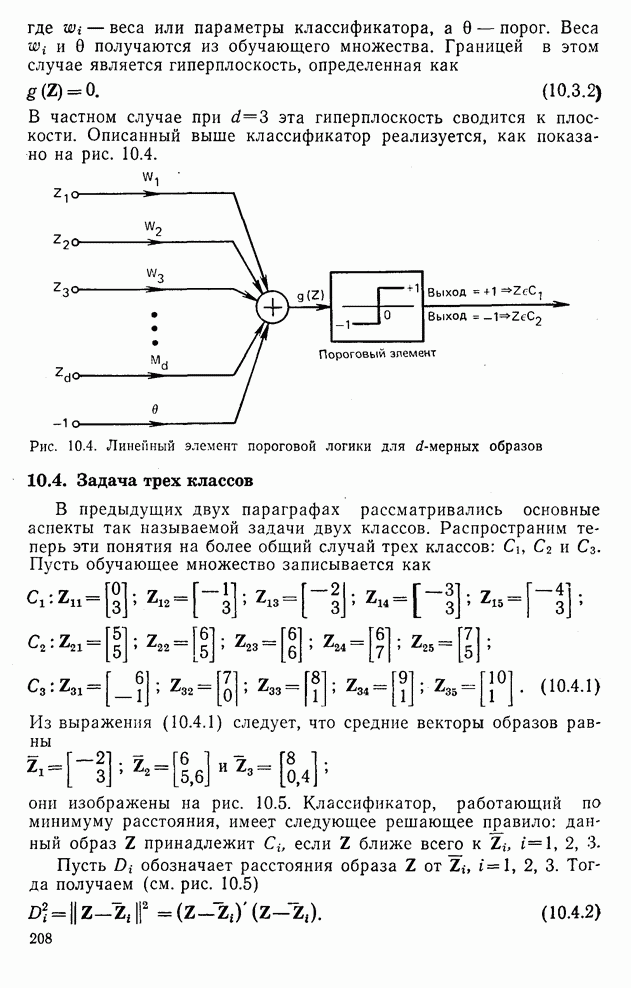
- 10.3. d-мерные образы
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
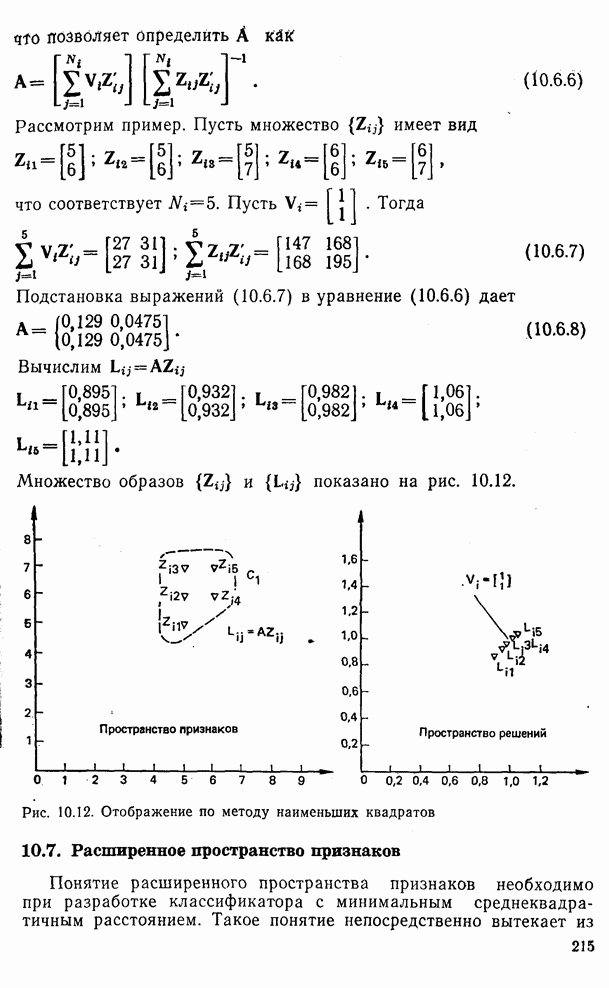
- 10.6. Метод отображения по методу наименьших квадратов
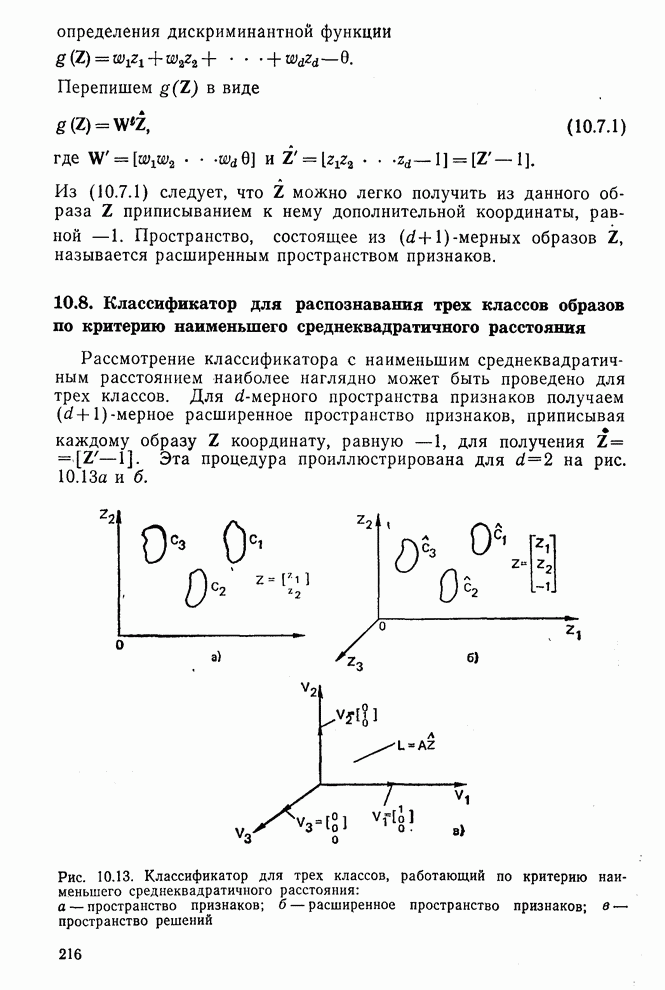
- 10.7. Расширенное пространство признаков
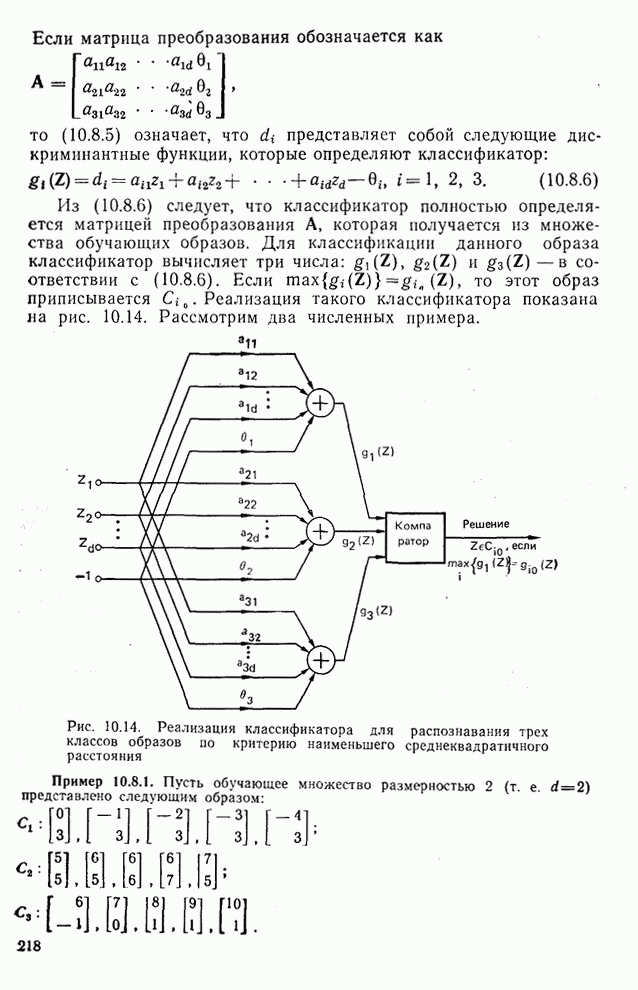
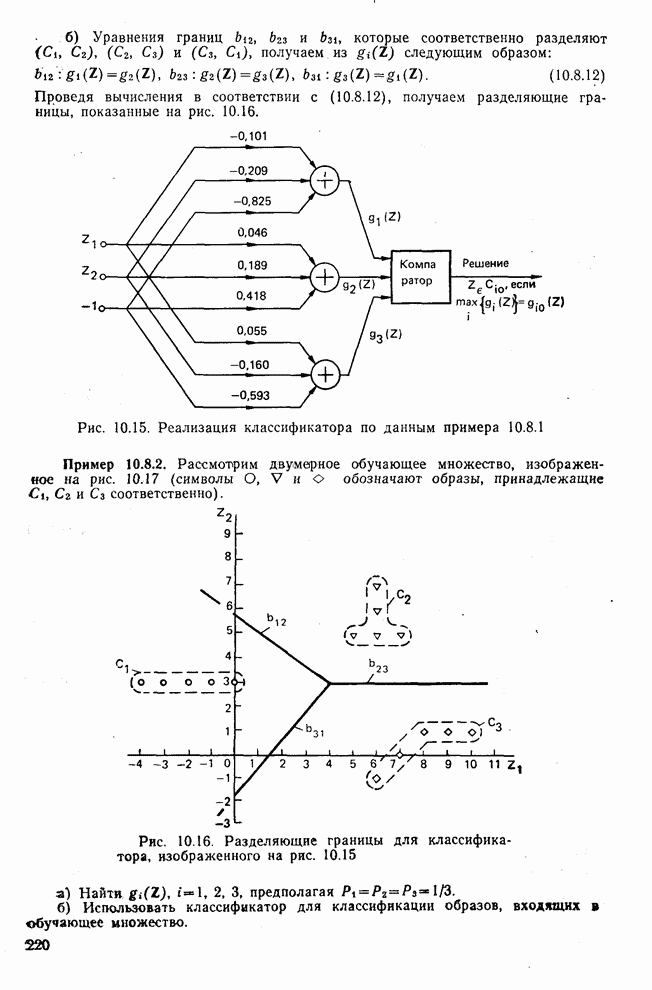
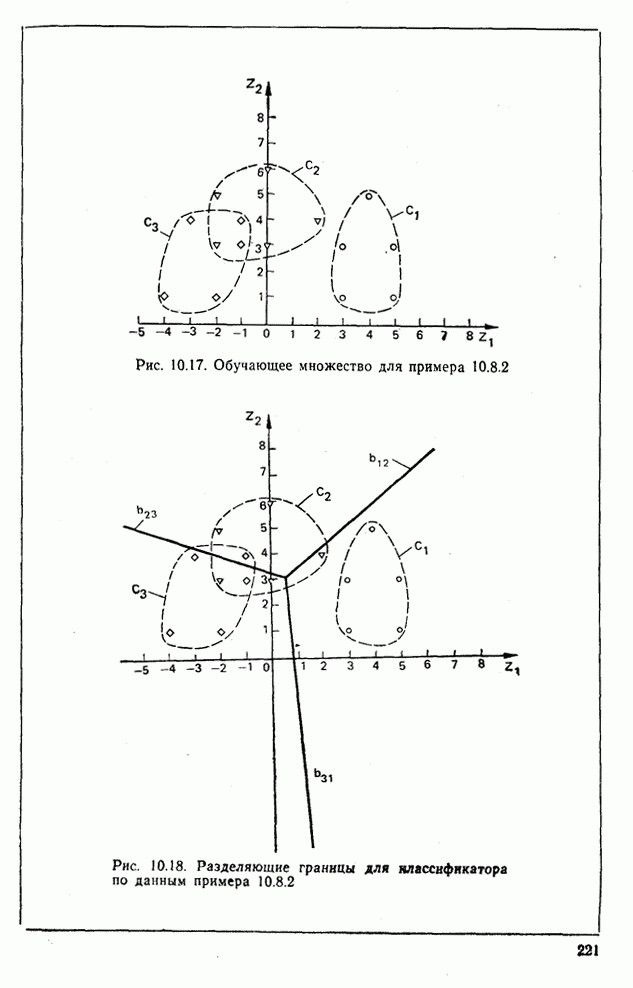
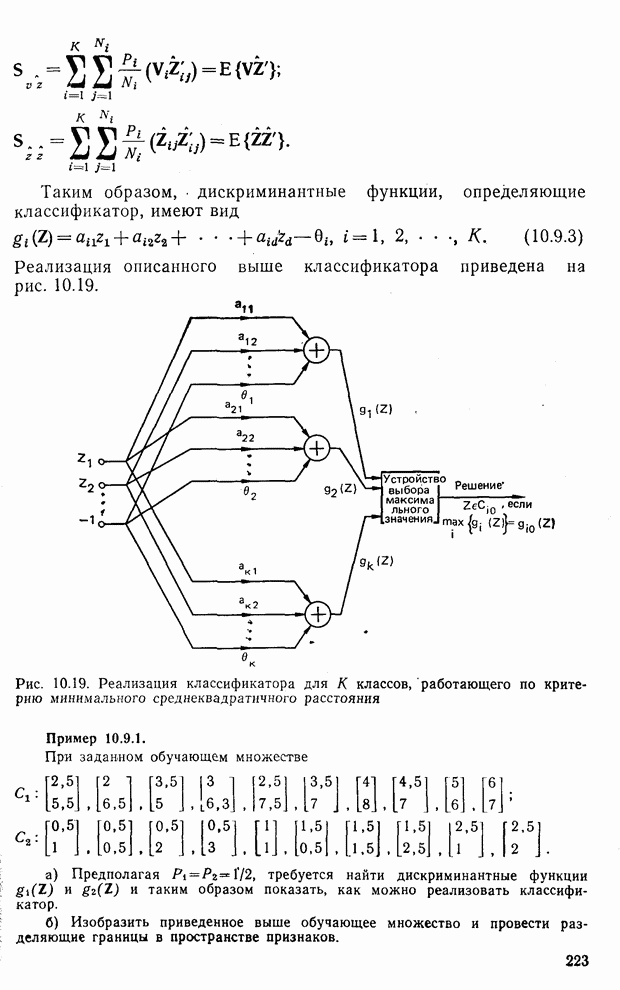
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
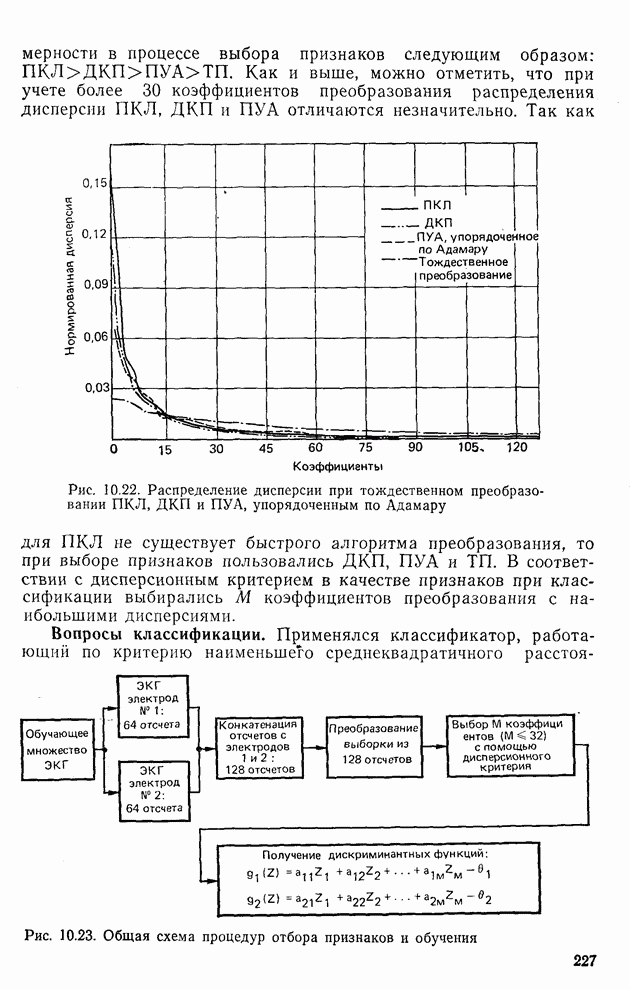
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
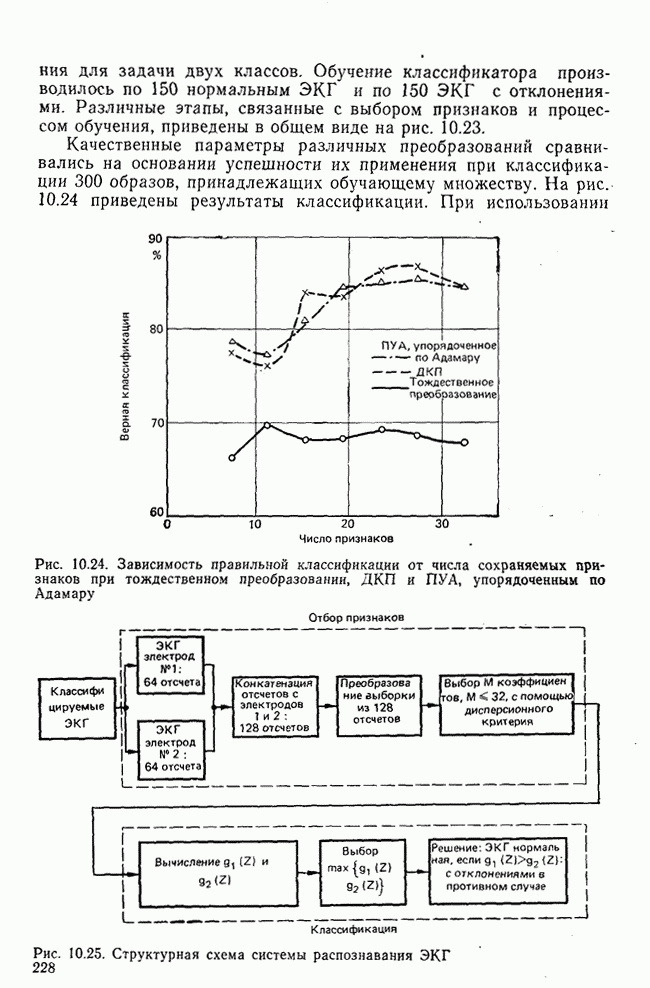
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ