| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
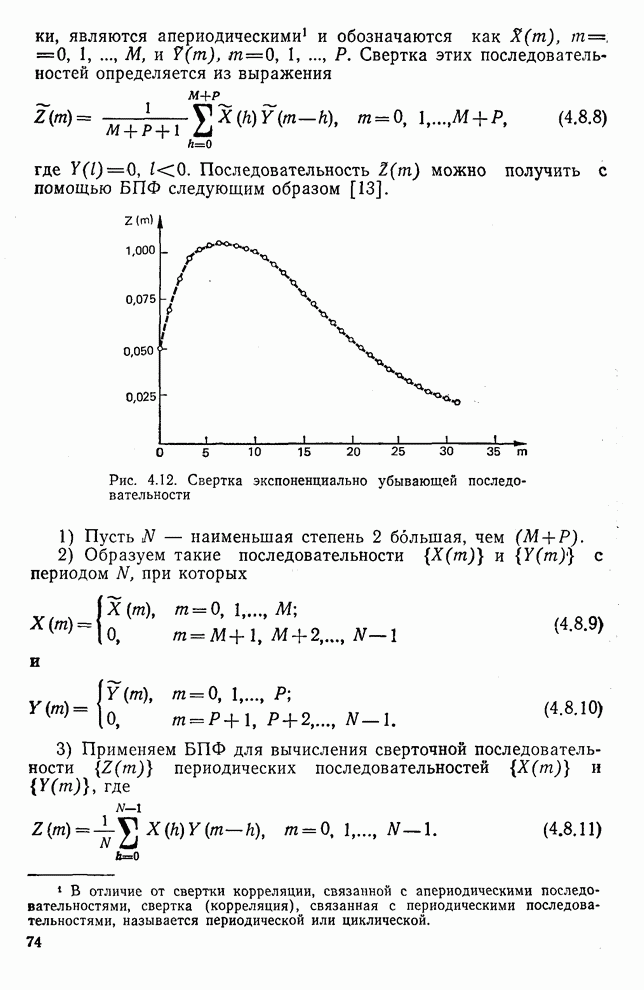
6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
Энергетический спектр ПУА, упорядоченного по Адамару, имеет следующие физические интерпретации:
1) спектральные точки  представляют собой средние энергии множества
представляют собой средние энергии множества  взаимно ортогональных подпоследовательностей;
взаимно ортогональных подпоследовательностей;
2) каждая точка  представляет собой энергетическое содержание группы частостей, а не одной частости, как в случае энергетического спектра ПУА с упорядочением по Уолшу.
представляет собой энергетическое содержание группы частостей, а не одной частости, как в случае энергетического спектра ПУА с упорядочением по Уолшу.
Чтобы продемонстрировать первое толкование энергетического спектра, воспользуемся тем, что последовательность  периода N можно представить в виде суммы
периода N можно представить в виде суммы  (
( -периодической последовательности
-периодической последовательности  и
и  последовательности
последовательности  т. е.
т. е.

где

и  .
.
После этого последовательность  можно представить в виде
можно представить в виде  -периодической последовательности
-периодической последовательности  и
и  -косопериодической последовательности
-косопериодической последовательности  , т. е.
, т. е.

где

и  .
.
Продолжая далее указанный выше процесс, получаем, что  можно разложить в сумму следующих
можно разложить в сумму следующих  последовательностей:
последовательностей:
 (6.9.1)
(6.9.1)
где  представляет собой
представляет собой  -периодическую последовательность, а
-периодическую последовательность, а  последовательность,
последовательность,  .
.
Описанный выше процесс разложения иллюстрируется рис. 6.9 при  . Последовательность
. Последовательность  разлагается в сумму
разлагается в сумму

в которой  является
является  -периодической,
-периодической,  представляют собой 1-, 2- и
представляют собой 1-, 2- и  -периодическую последовательность соответственно.
-периодическую последовательность соответственно.

Рис. 6.9. Граф, преображающий разложение  на подпоследовательности,
на подпоследовательности, 
Следовательно, эти последовательности можно представить в виде векторов:
 (6.9.2)
(6.9.2)
где коэффициенты  могут быть выражены через коэффициенты ПУА, упорядоченного по Уолшу.
могут быть выражены через коэффициенты ПУА, упорядоченного по Уолшу.
Из рассмотрения векторов в записи (6.9.2) можно сделать вывод, что они все взаимно ортогональны и, следовательно,
 (6.9.3)
(6.9.3)
где  обозначает норму вектора. Кроме того,
обозначает норму вектора. Кроме того,
 (6.9.4)
(6.9.4)
Вспомним теперь, что средняя энергия  записывается в
записывается в

Подставляя выражение (4.9.4) в формулу (4.9.3), получаем
 (6.9.5)
(6.9.5)
Чтобы связать коэффициенты  с соответствующими коэффициентами
с соответствующими коэффициентами  , запишем ПУА с упорядочением по Адамару последовательности
, запишем ПУА с упорядочением по Адамару последовательности  , в котором сама последовательность
, в котором сама последовательность  выражается в виде суммы подпоследовательностей. При этом получаем следующее матричное выражение:
выражается в виде суммы подпоследовательностей. При этом получаем следующее матричное выражение:
 (6.9.6)
(6.9.6)
Из выражения (6.9.6) следует, что

 (6.9.7)
(6.9.7)
Так как  и
и  — ортогональные матрицы, то формулы (6.9.7) приводят к следующему результату:
— ортогональные матрицы, то формулы (6.9.7) приводят к следующему результату:

Таким образом,
 (6.9.8)
(6.9.8)
где  -средняя мощность
-средняя мощность  -периодической последовательности
-периодической последовательности  и
и  - средние мощности последовательностей
- средние мощности последовательностей  и
и  , которые являются 1-, 2- и
, которые являются 1-, 2- и  -косопериодическими соответственно.
-косопериодическими соответственно.
Из приведенного выше анализа можно сделать следующие выводы:
1)  представляют собой среднюю мощность Апериодической последовательности
представляют собой среднюю мощность Апериодической последовательности  ;
;
2)  представляет собой среднюю мощность
представляет собой среднюю мощность  -косопериодической последовательности
-косопериодической последовательности  .
.
Для иллюстрации второго физического толкования энергетического спектра ПУА с упорядочением по Адамару рассмотрим как входят частости в энергетический спектр этого преобразования при  . Из (6.8.8) имеем
. Из (6.8.8) имеем
 (6.9.9)
(6.9.9)
Затем из табл. 6.3.1 находим
 (6.9.10)
(6.9.10)
Если через  обозначить частости, входящие в состав спектральной точки
обозначить частости, входящие в состав спектральной точки  , то из (6.9.9) и (6.9.10) следует, что
, то из (6.9.9) и (6.9.10) следует, что
 (6.9.11)
(6.9.11)
Можно показать, что в общем случае выражение (6.9.11) будет иметь вид

 (6.9.12)
(6.9.12)
Каждая спектральная точка  представляет собой энергетическое содержание труппы частостей, а не одной единственной частости, как в случае энергетического спектра ПУА с упорядочением по Уолшу. Однако группирование частостей не является произвольным. Каждая группа состоит из основной частости и множества всех нечетных частостей относительно основной.
представляет собой энергетическое содержание труппы частостей, а не одной единственной частости, как в случае энергетического спектра ПУА с упорядочением по Уолшу. Однако группирование частостей не является произвольным. Каждая группа состоит из основной частости и множества всех нечетных частостей относительно основной.
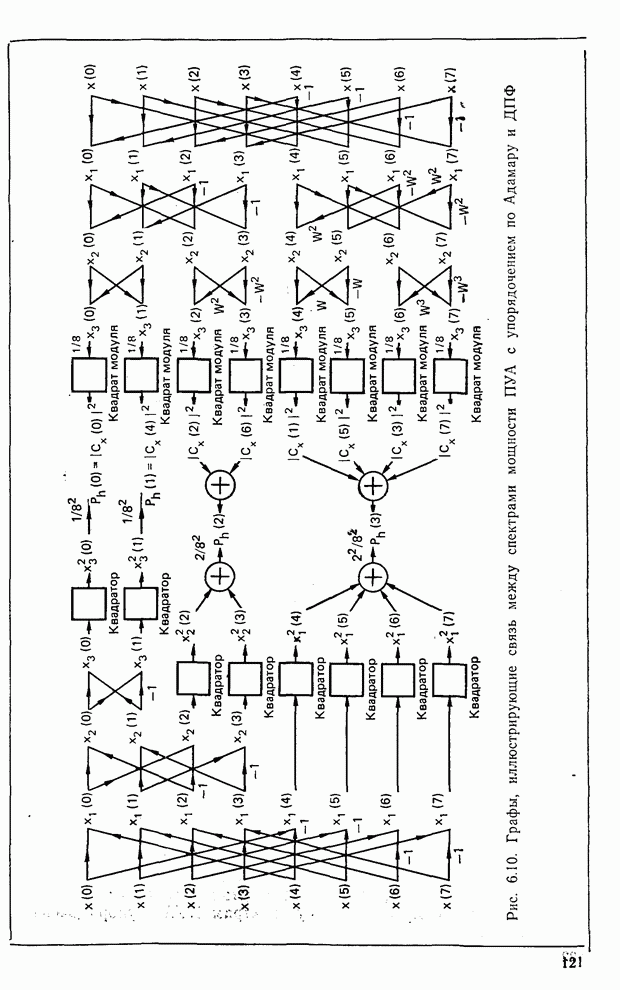
Связь со спектром ДПФ. Естественным следствием приведенного выше обсуждения является установление взаимосвязи между энергетическими спектрами ПУА с упорядочением по Адамару и ДПФ. Рассмотрим случай  . Графы, соответствующие вычислению энергетического спектра ПУА с упорядочением по Адамару и энергетического спектра ДПФ, приведены на рис. 6.10. Из графа БПФ следует, что
. Графы, соответствующие вычислению энергетического спектра ПУА с упорядочением по Адамару и энергетического спектра ДПФ, приведены на рис. 6.10. Из графа БПФ следует, что

или
 (6.9.13)
(6.9.13)
Так как матрица  в выражении (6.9.13) ортогональна, то
в выражении (6.9.13) ортогональна, то
 (6.9.14)
(6.9.14)
При рассмотрении (6.8.10) можно сделать вывод, что правая часть выражения (6.9.14) равняется  . Таким образом,
. Таким образом,

Подобным же образом получаем

Из приведенного выше анализа можно сделать следующий вывод: взаимосвязь между энергетическими спектрами ПУА, упорядоченным по Адамару, и ДПФ

Рис. 6.10. Графы, иллюстрирующие связь между спектрами мощности ПУА с упорядочением по Адамару и ДПФ
 (6.9.15)
(6.9.15)
где  -десятичное число, полученное в результате двоичной инверсии двоичного представления числа
-десятичное число, полученное в результате двоичной инверсии двоичного представления числа  , представленного
, представленного  битами.
битами.
Фазовый спектр ПУА с упорядочением по Адамару. Так же,
как энергетический спектр ПУА с упорядочением по Адамару, можно определить и фазовый спектр ПУА или спектр «положения». Фазовый спектр определяется в многомерном пространстве с помощью эталонного вектора и понятий «средняя мощность» и «фазовый угол». Можно показать [14], что
 (6.9.16)
(6.9.16)
где  — фазовый спектр ПУА с упорядочением по Адамару в
— фазовый спектр ПУА с упорядочением по Адамару в  точке. Для
точке. Для  8 выражение (6.9.16) дает
8 выражение (6.9.16) дает

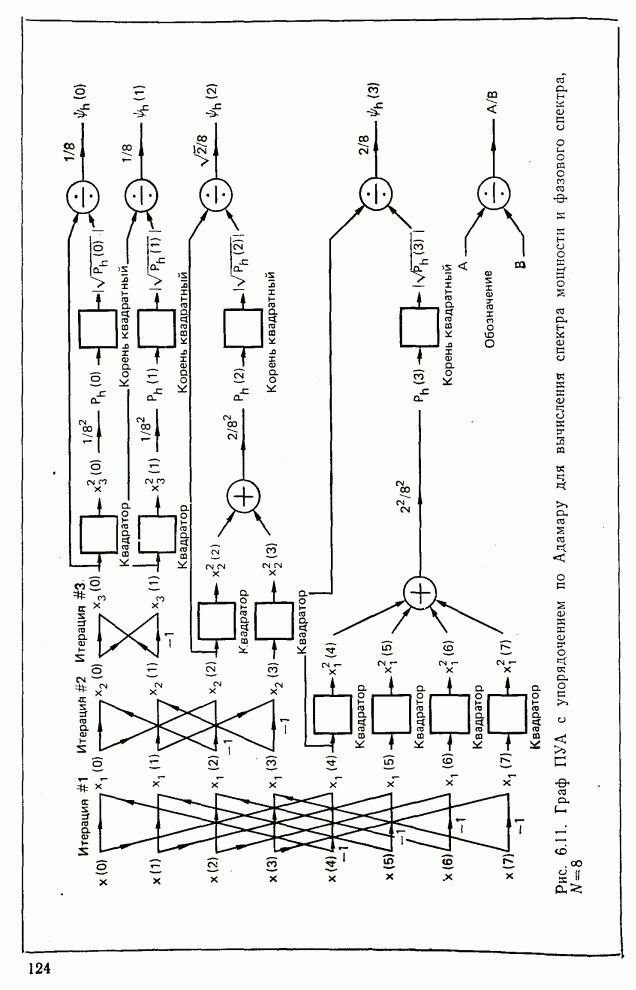
Определенный выше фазовый спектр можно быстро оценить совместно с энергетическим спектром с помощью графа, приведенного на рис. 6.11. Можно показать, что фазовый спектр ПУА с упорядочением по Адамару инвариантен к умножению исходной последовательности  на действительное число. Кроме того, он изменяется определенным образом (см. задачу 6.7) при циклическом сдвиге
на действительное число. Кроме того, он изменяется определенным образом (см. задачу 6.7) при циклическом сдвиге  . Отсюда и название — спектр «положения». Ясно, что эти свойства аналогичны подобным же свойствам фазового спектра ДПФ. В отличие от фазового спектра ДПФ, каждая спектральная точка которого определяется по отношению к одной частоте, фазовый спектр ПУА, упорядоченного по Адамару, определяется по отношению к группе частостей. Группировка частостей в этом случае такая же, как и у энергетического спектра ПУА с упорядочением по Адамару. Вследствие указанной группировки частостей и последующего сжатия данных исходная последовательность
. Отсюда и название — спектр «положения». Ясно, что эти свойства аналогичны подобным же свойствам фазового спектра ДПФ. В отличие от фазового спектра ДПФ, каждая спектральная точка которого определяется по отношению к одной частоте, фазовый спектр ПУА, упорядоченного по Адамару, определяется по отношению к группе частостей. Группировка частостей в этом случае такая же, как и у энергетического спектра ПУА с упорядочением по Адамару. Вследствие указанной группировки частостей и последующего сжатия данных исходная последовательность  не может быть восстановлена по заданным энергетическому и фазовому спектрам ПУА с упорядочением по Адамару.
не может быть восстановлена по заданным энергетическому и фазовому спектрам ПУА с упорядочением по Адамару.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
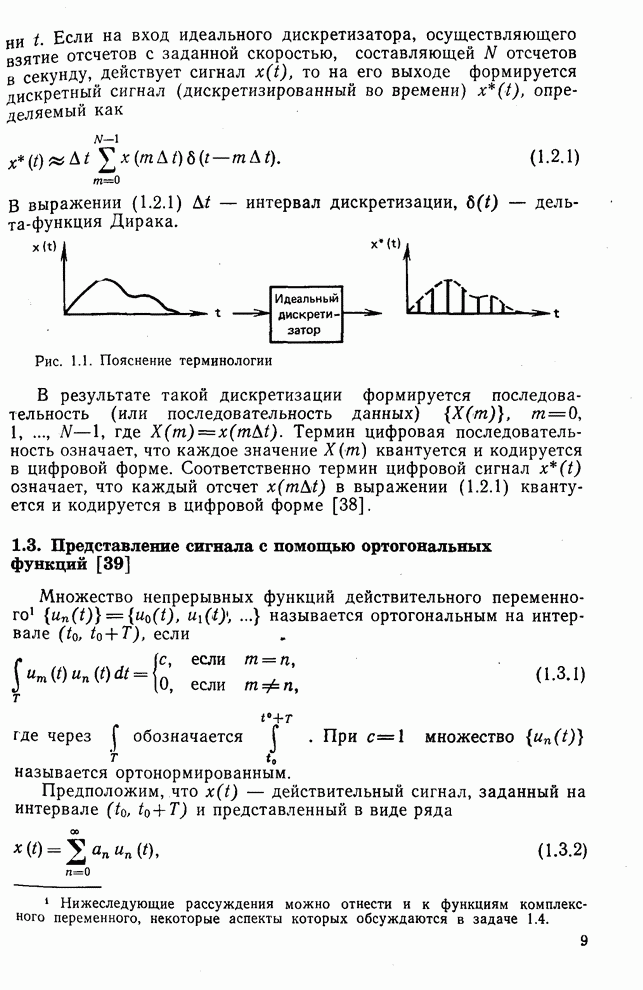
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
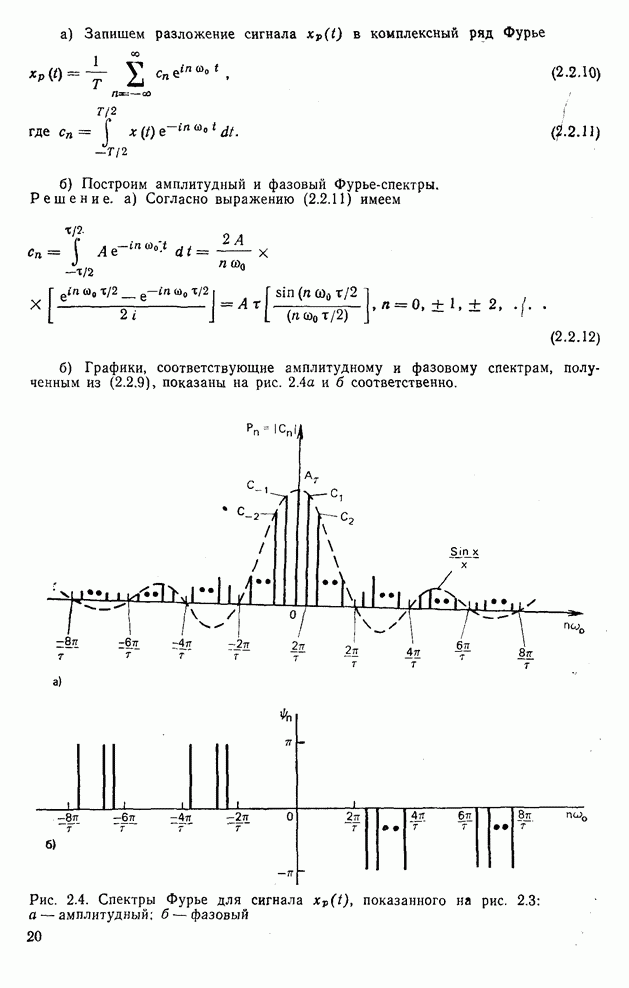
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
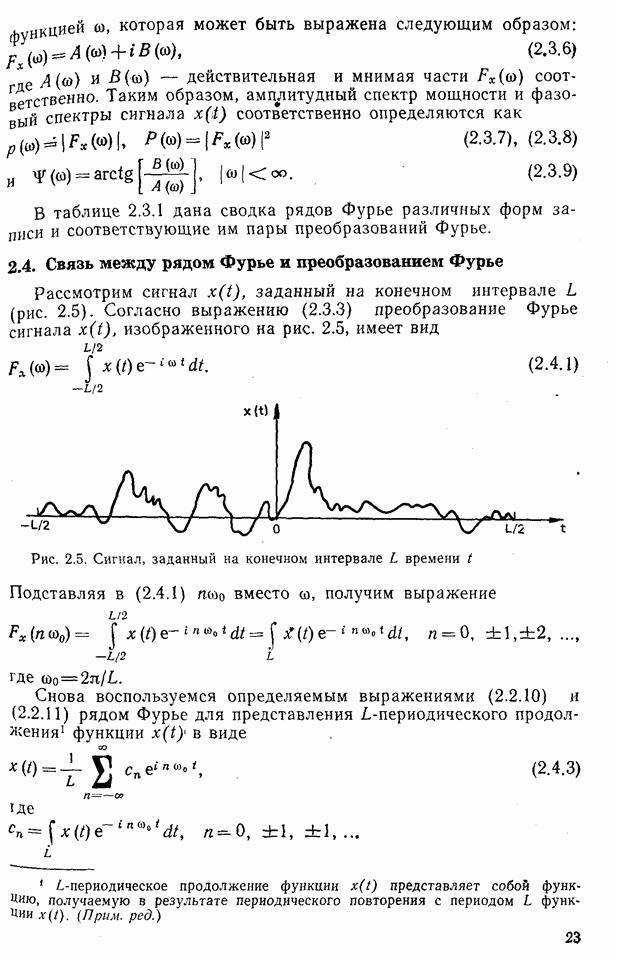
- 2.4. Связь между рядом Фурье и преобразованием Фурье
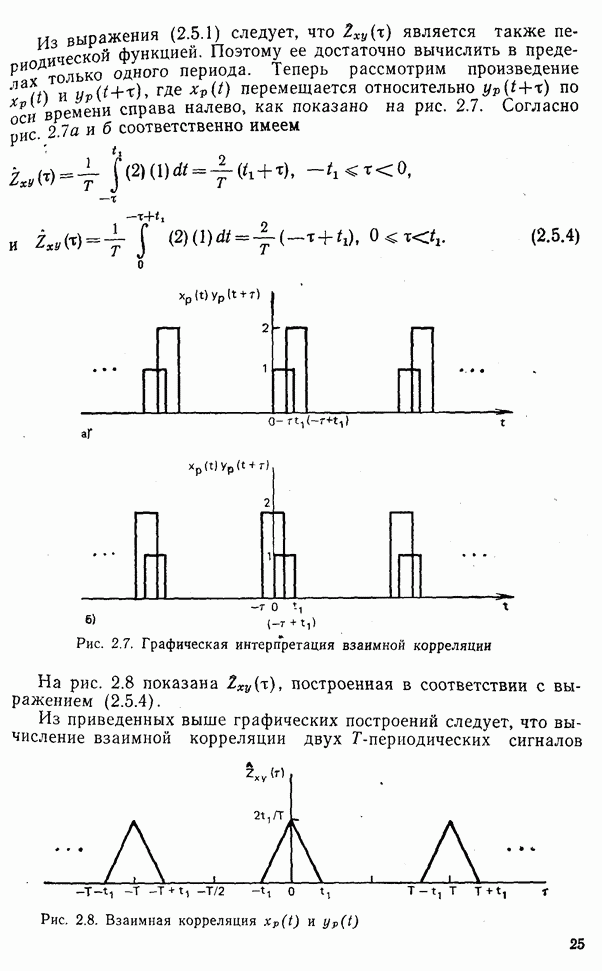
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
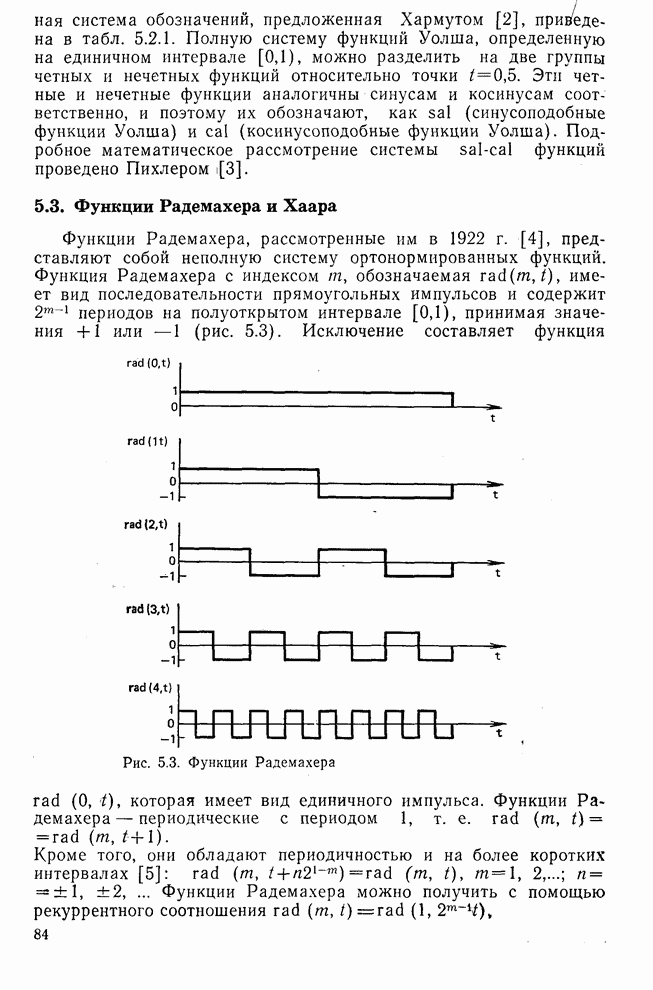
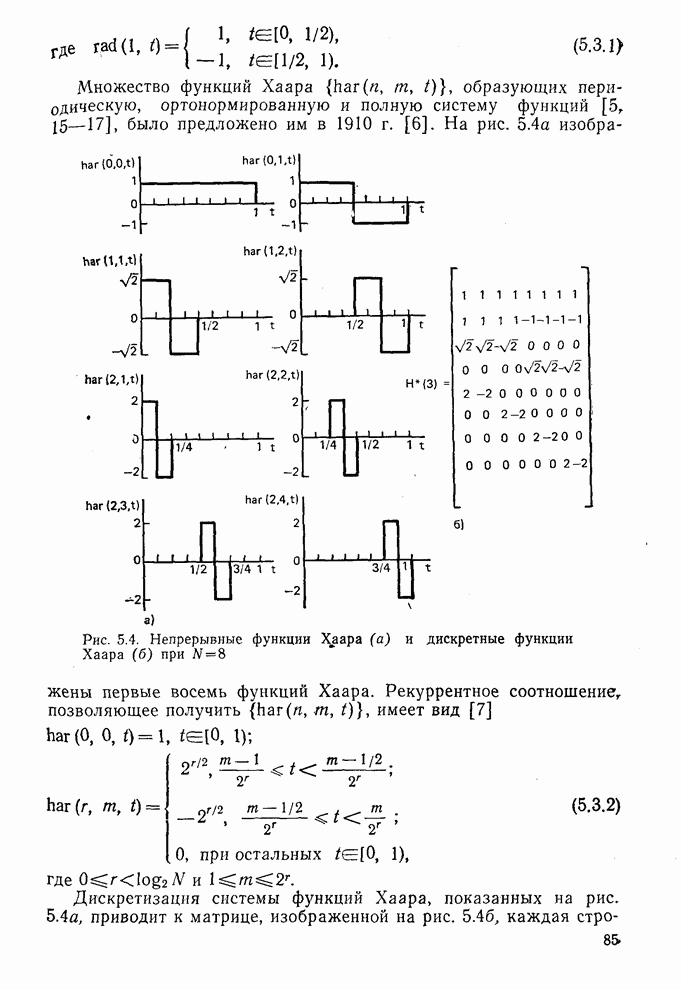
- 5.3. Функции Радемахера и Хаара
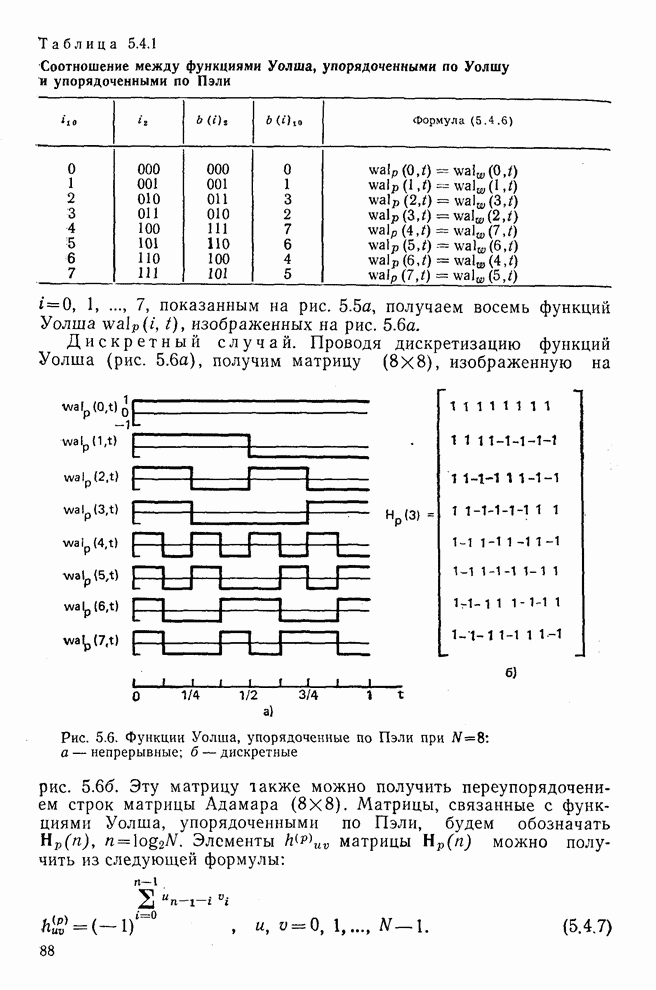
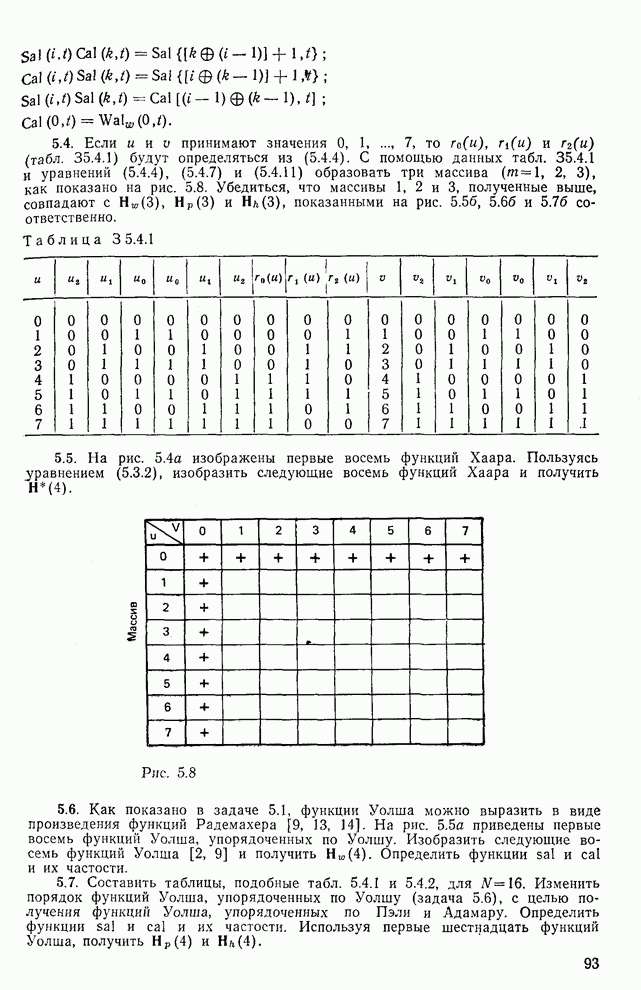
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
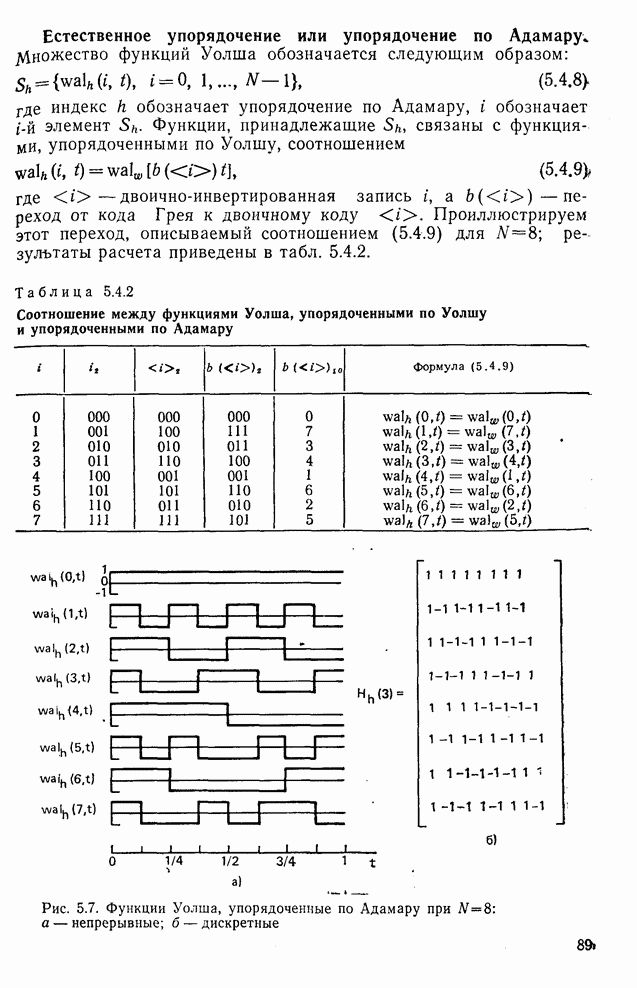
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
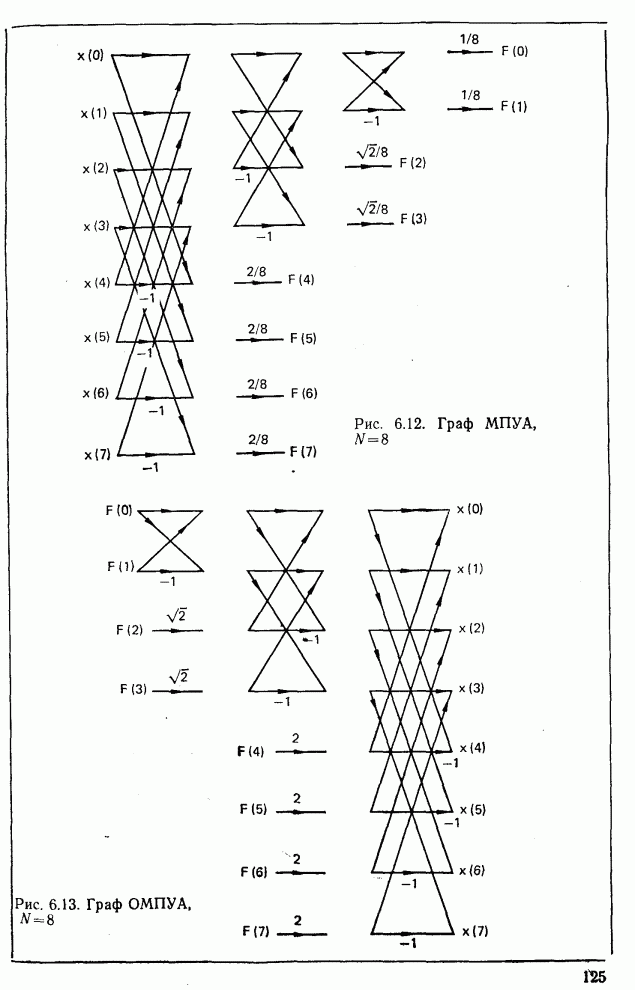
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
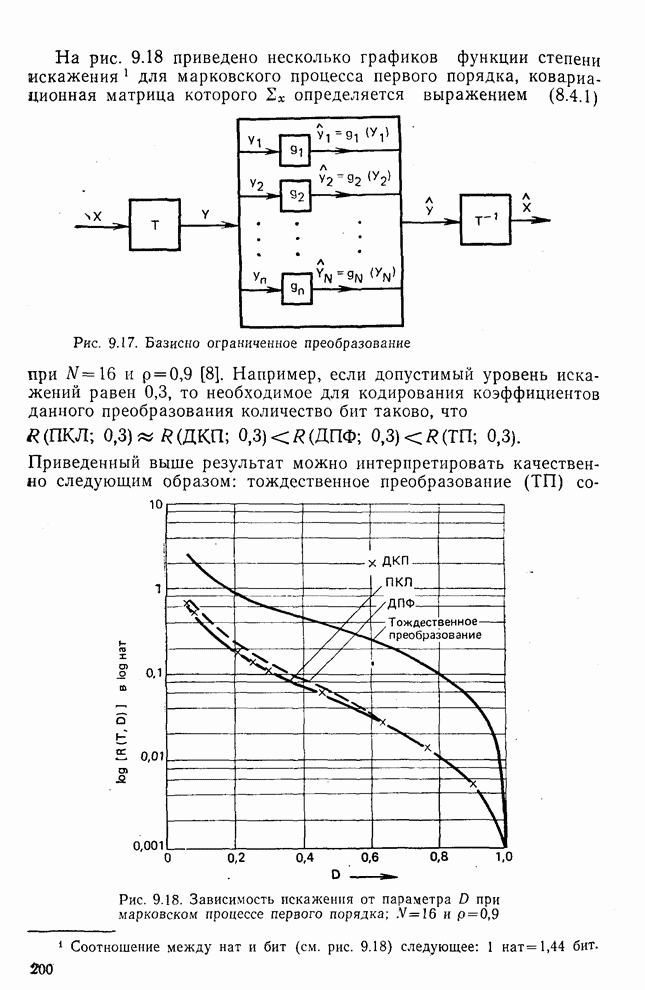
- 9.1. Поиск оптимального преобразования
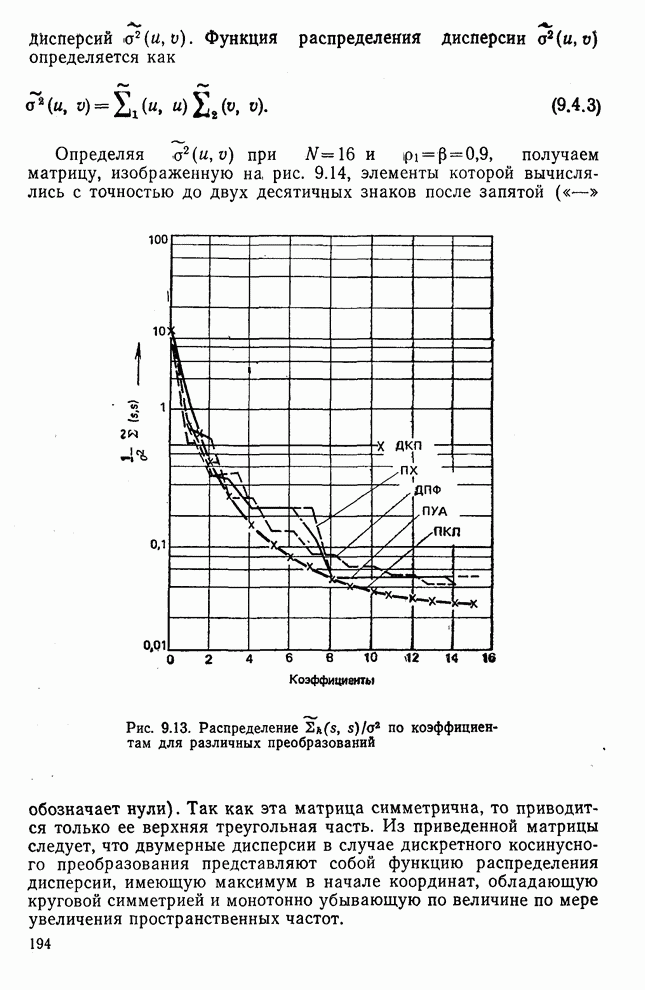
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
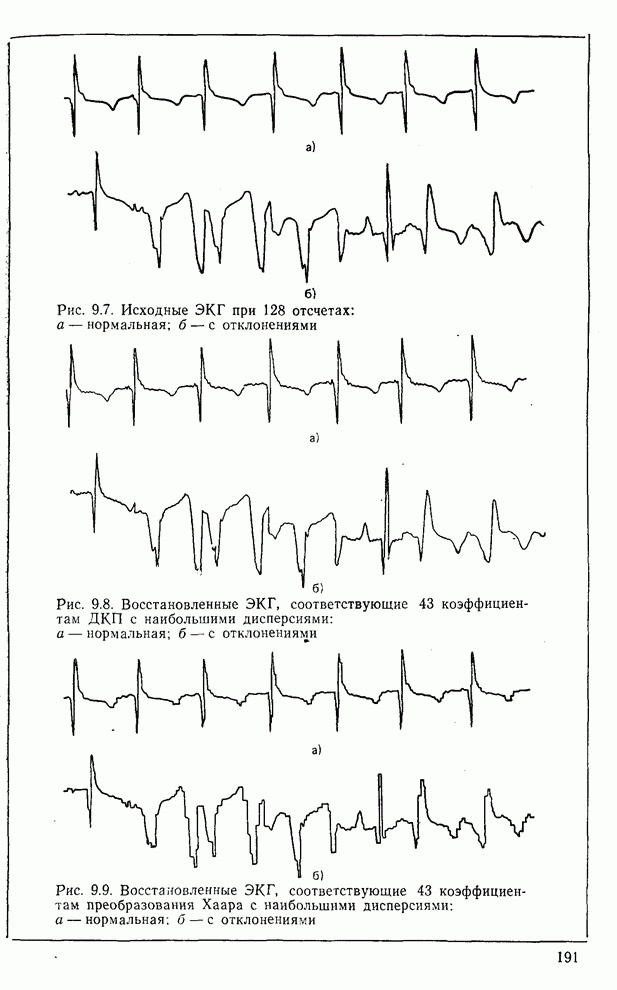
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
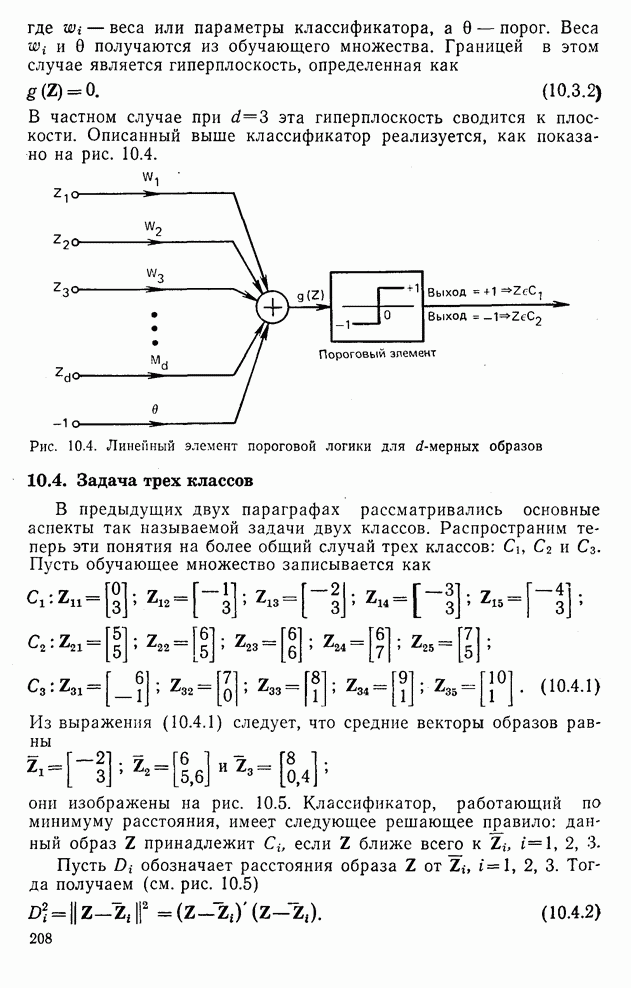
- 10.3. d-мерные образы
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
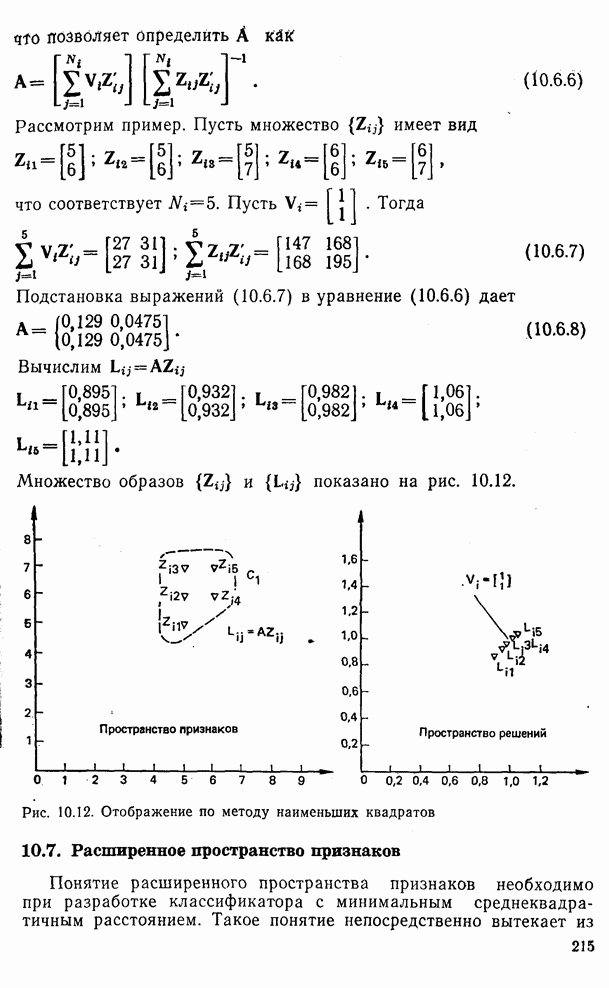
- 10.6. Метод отображения по методу наименьших квадратов
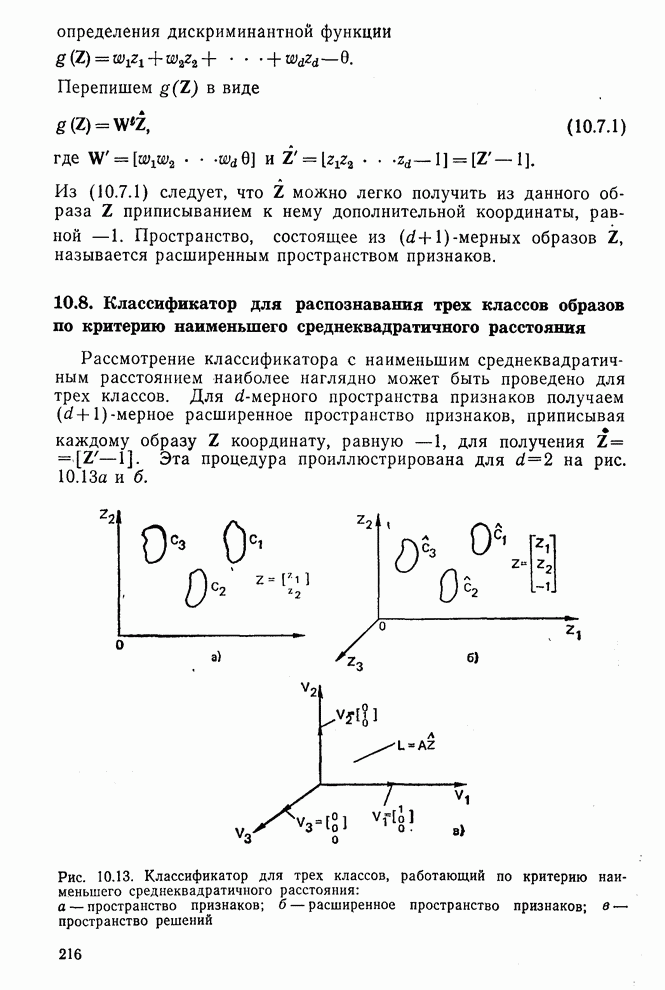
- 10.7. Расширенное пространство признаков
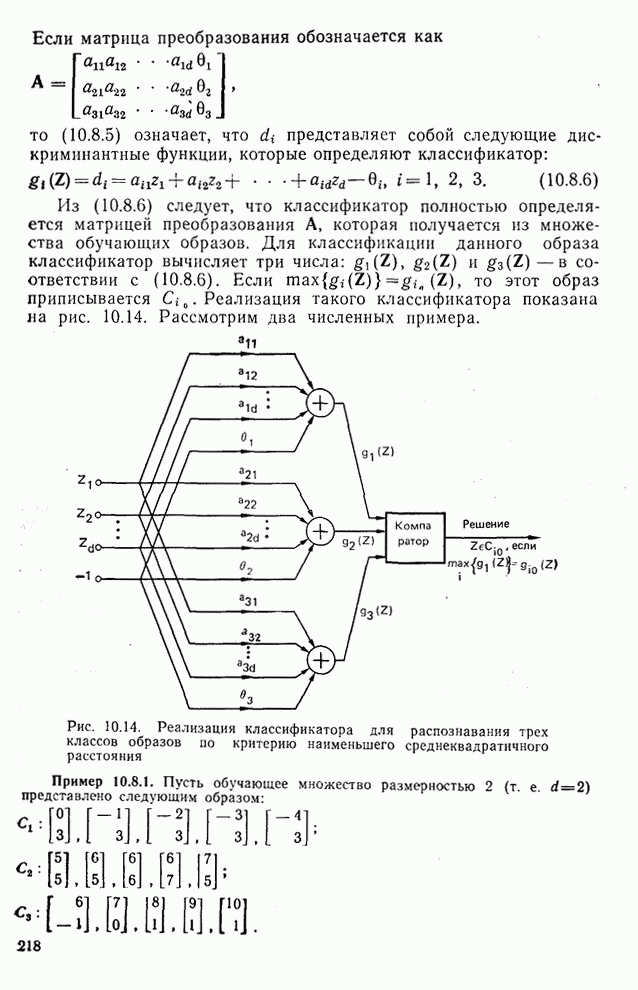
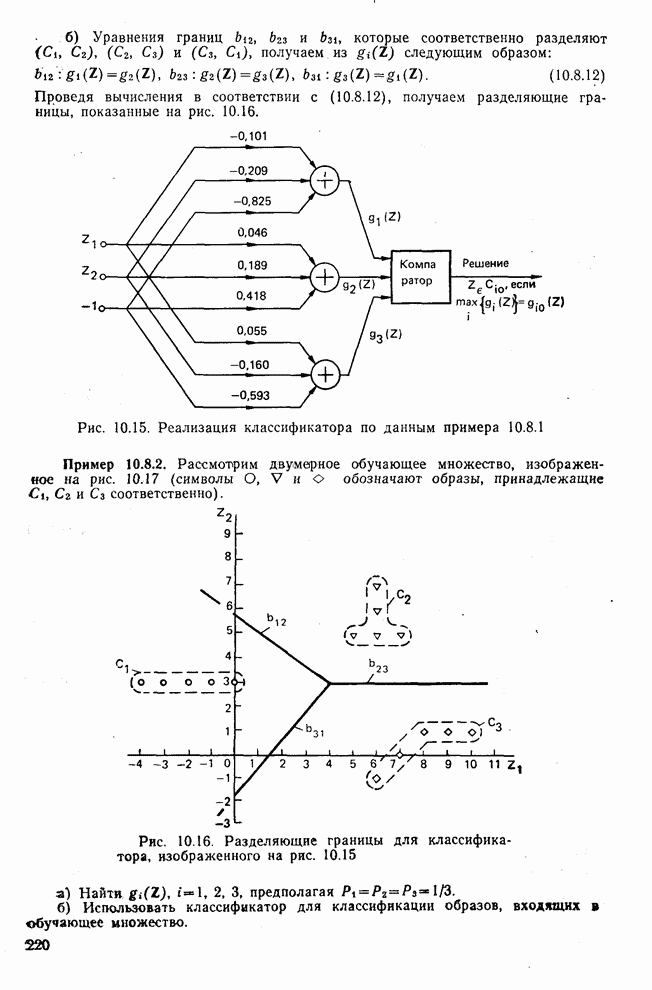
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
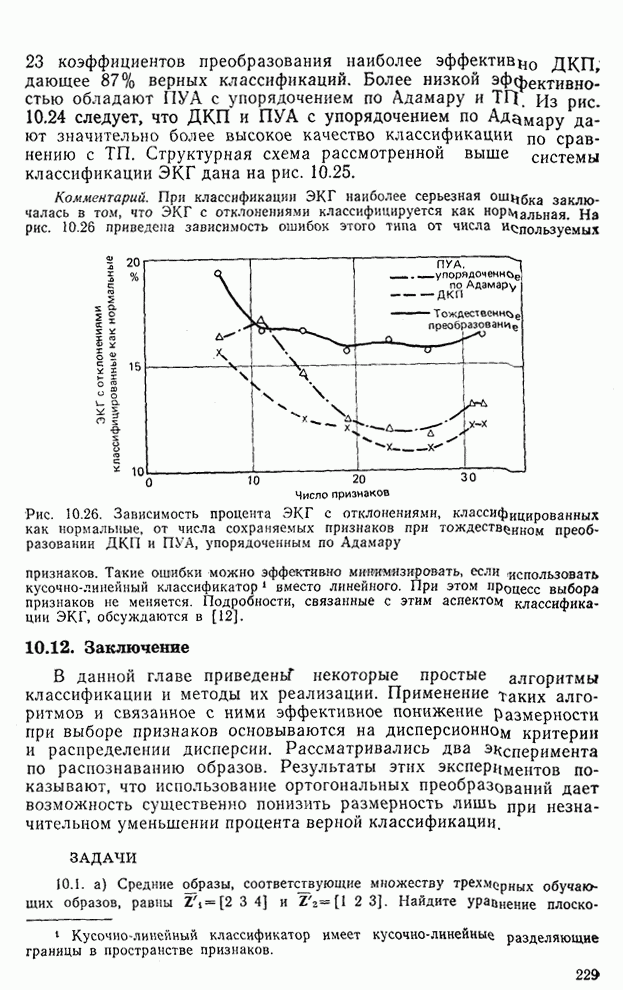
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
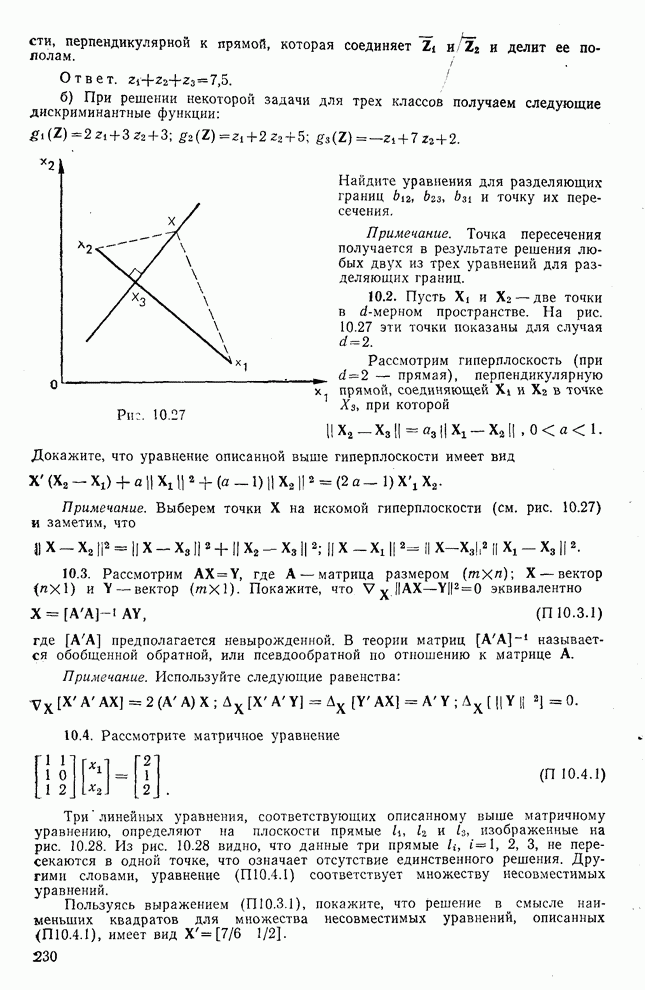
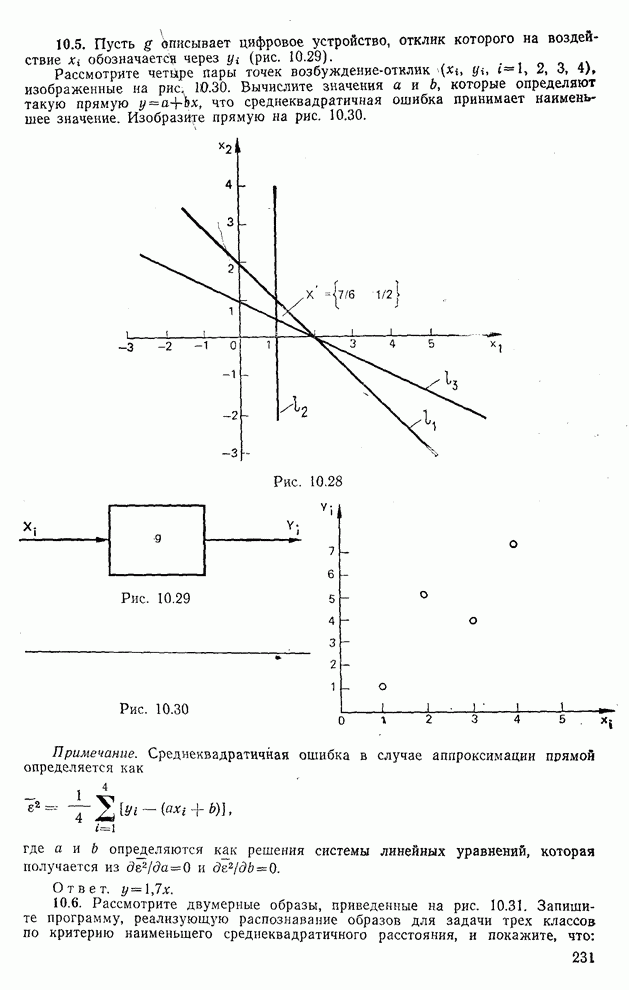
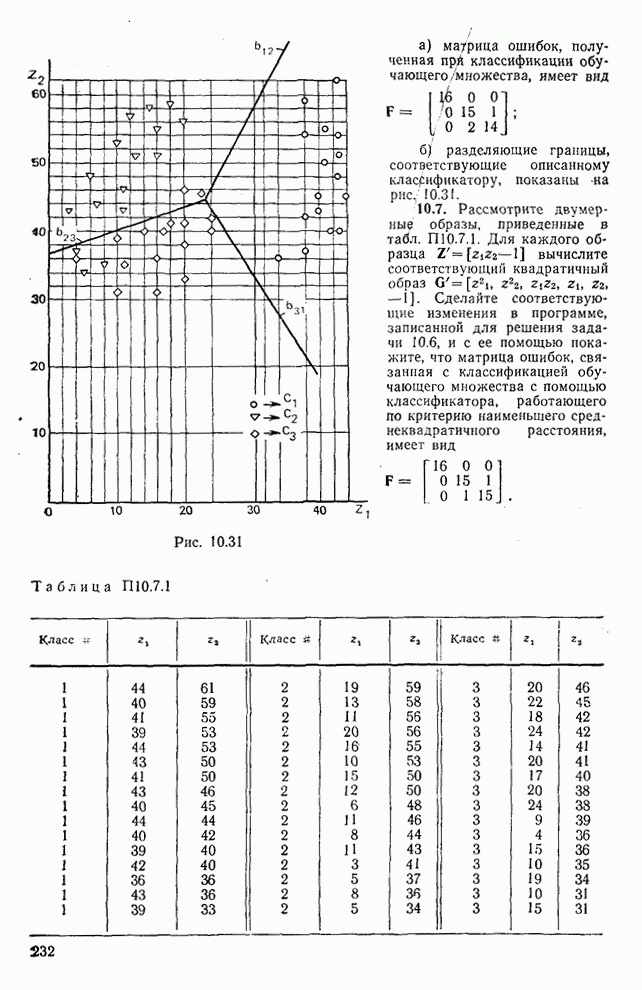
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ