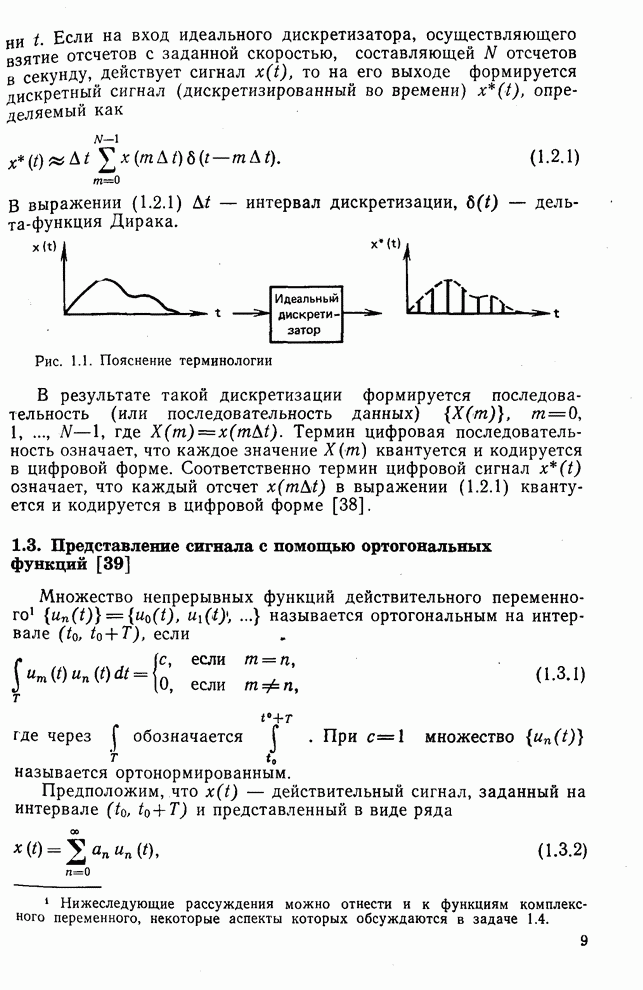
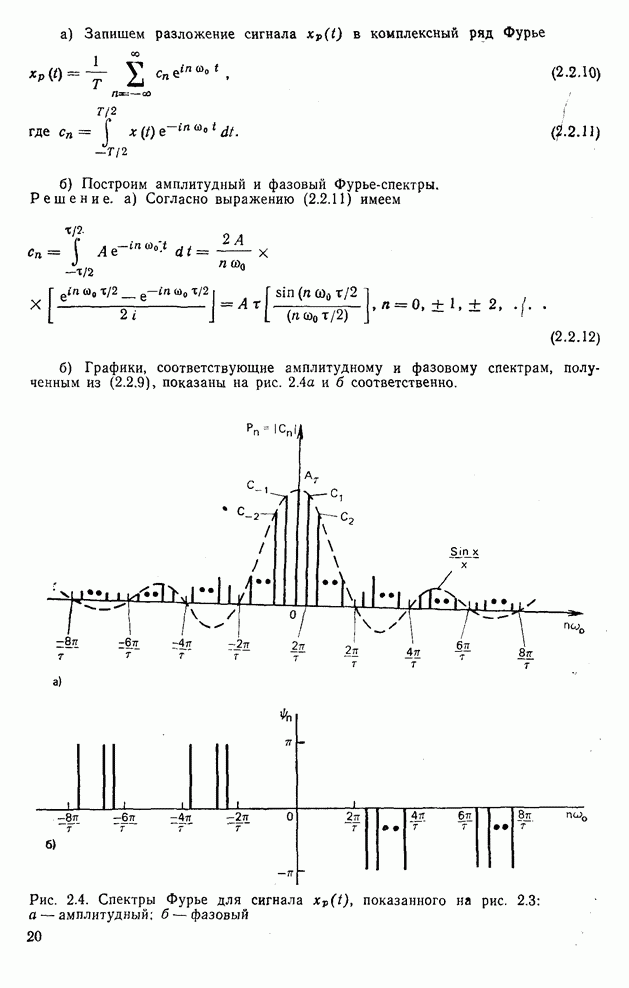
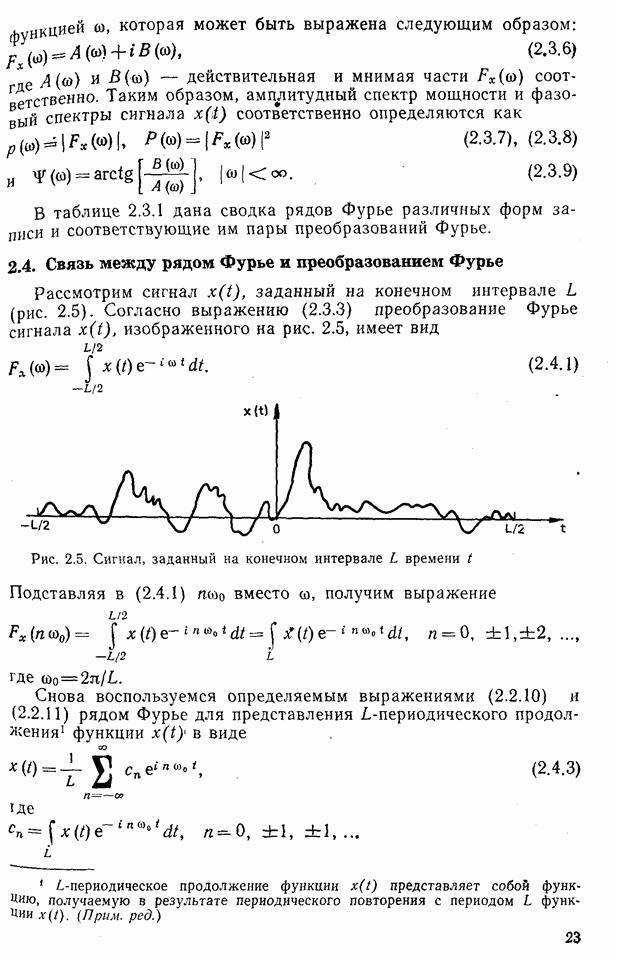
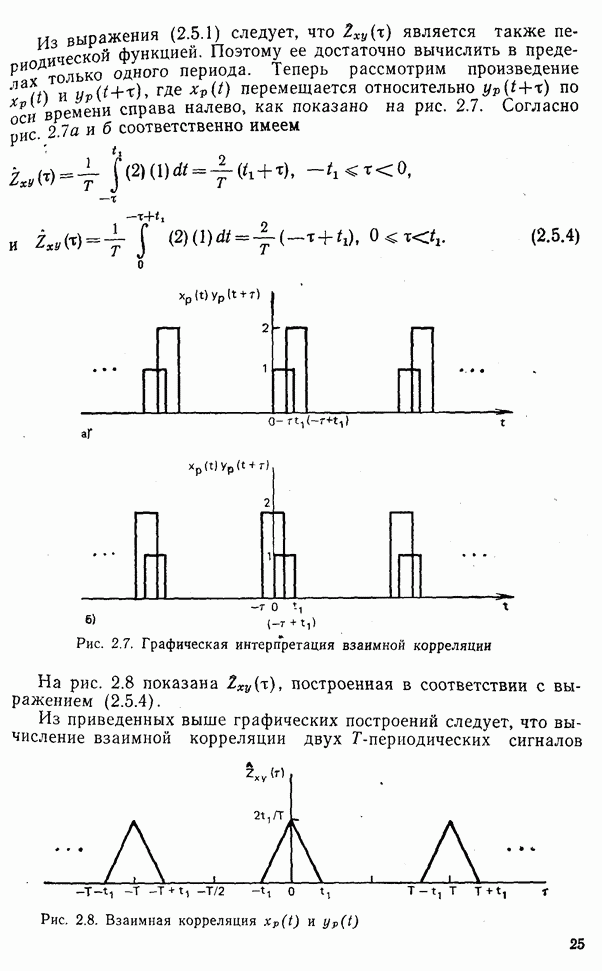
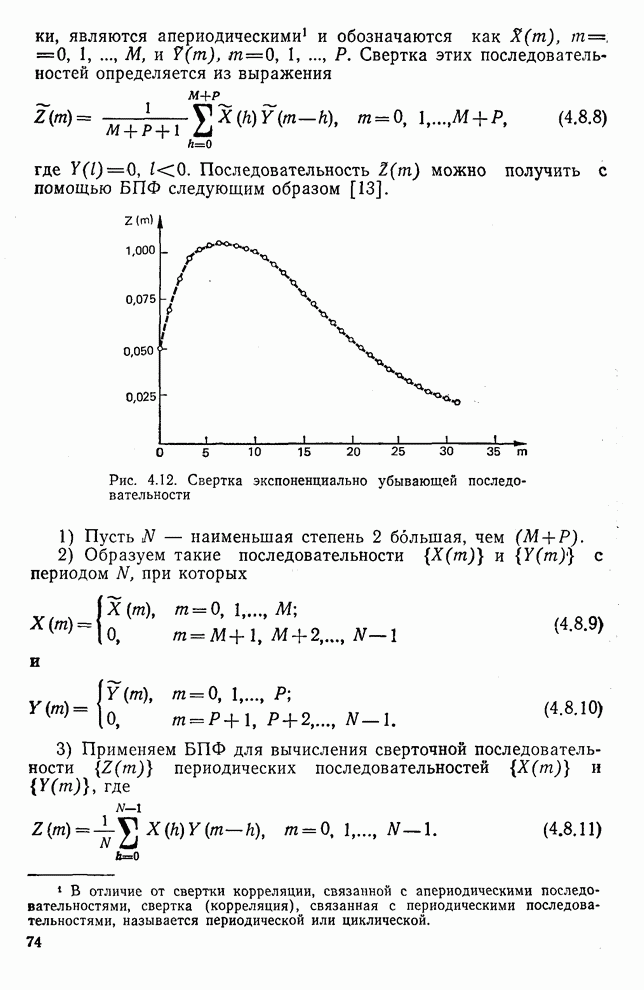
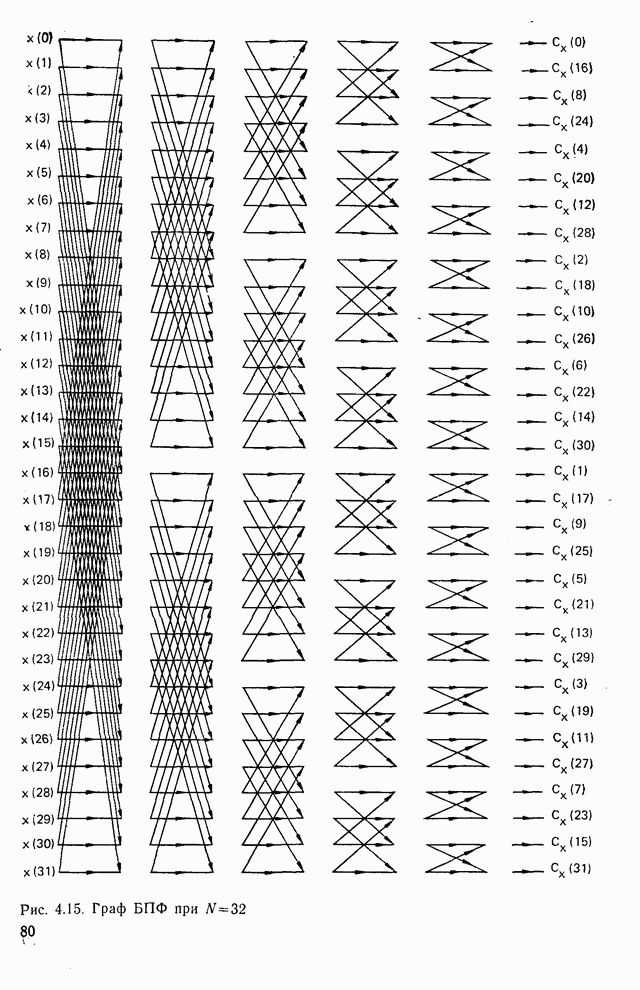
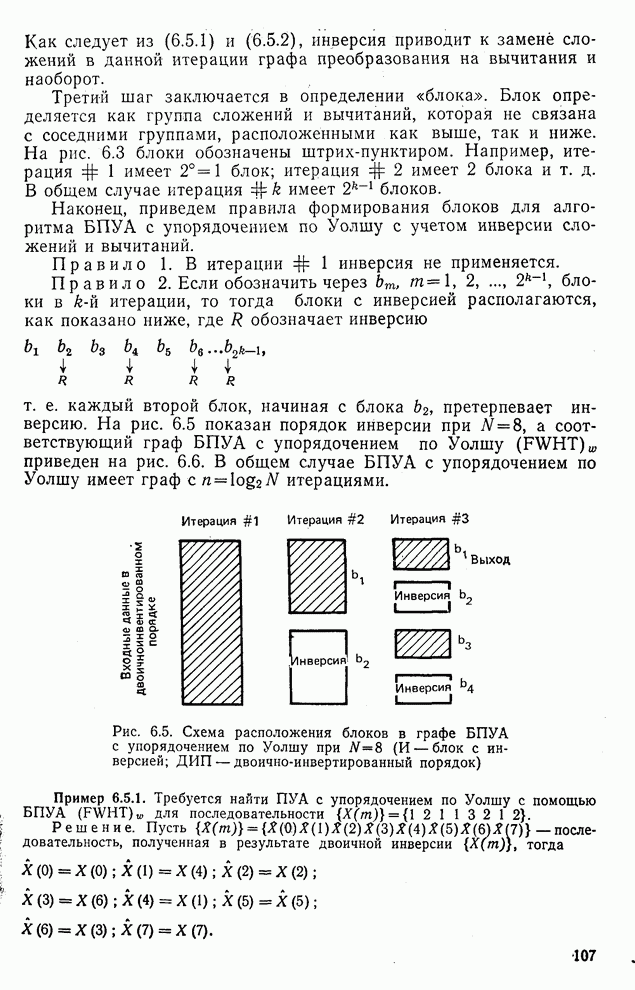
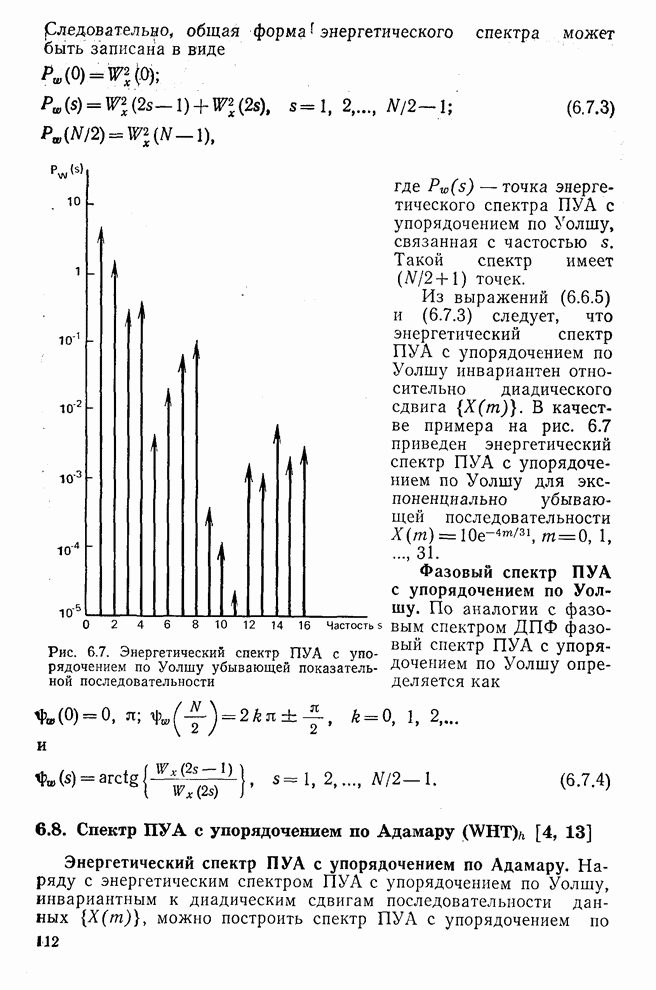
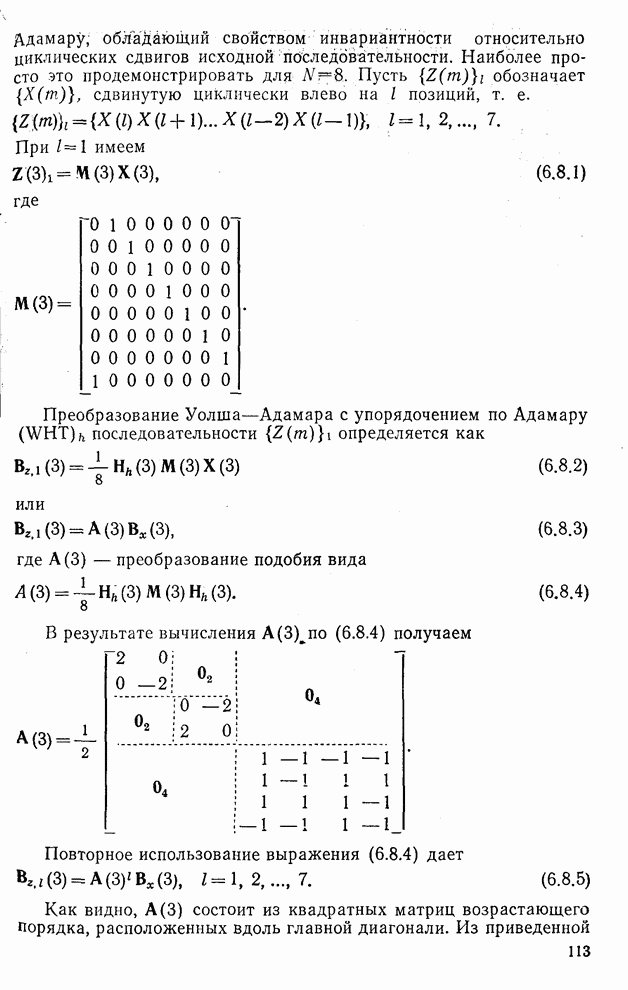
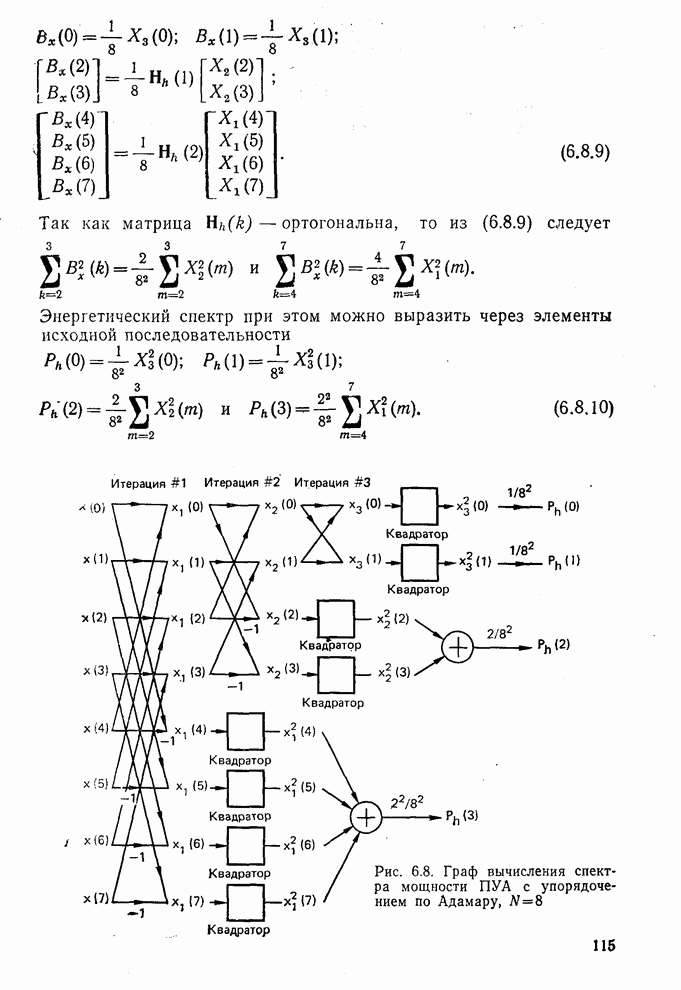
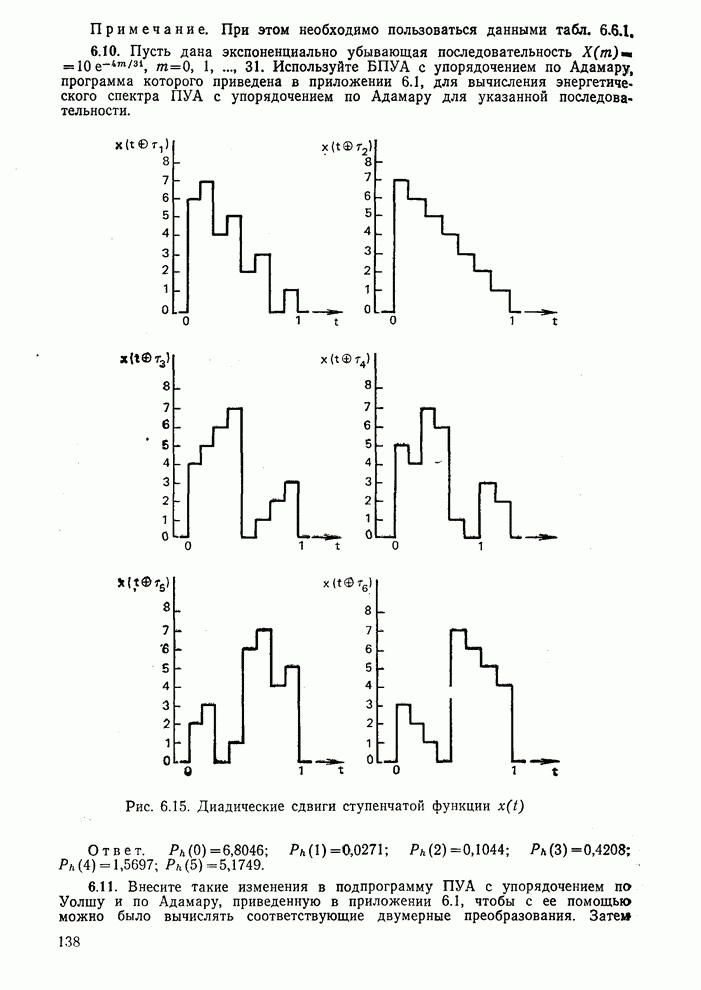
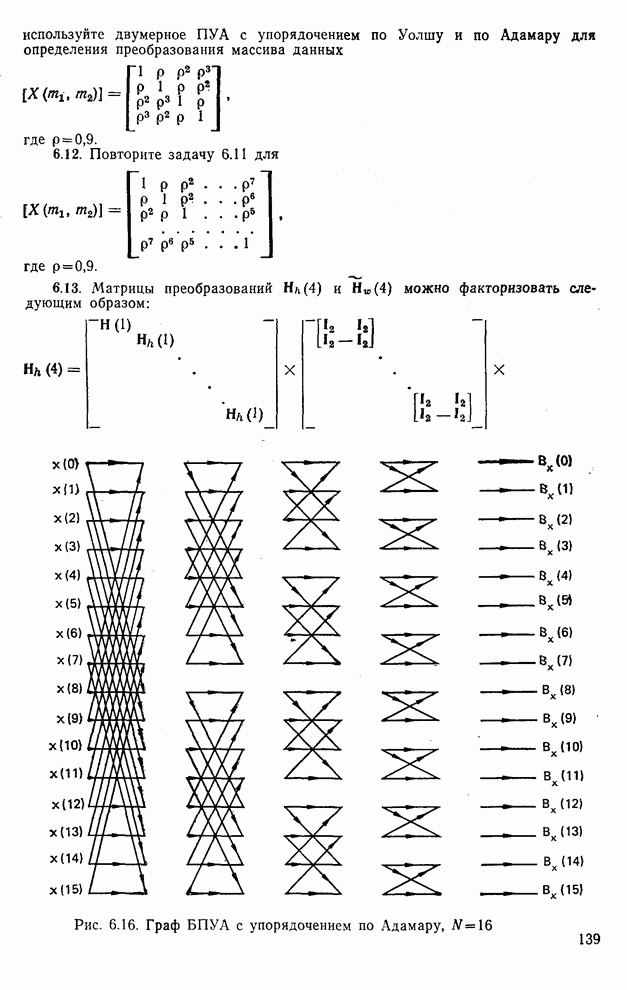
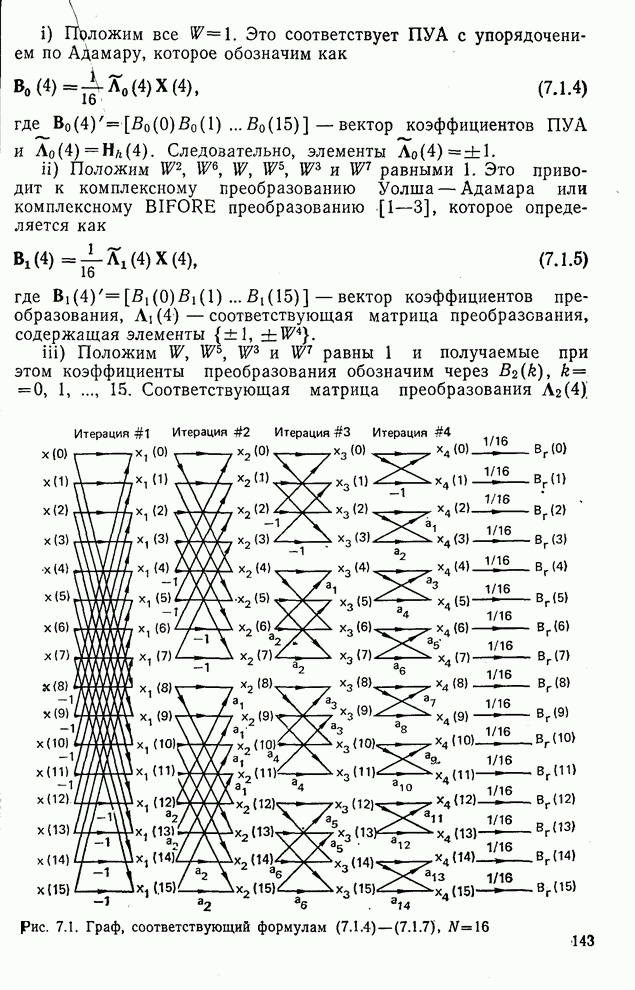
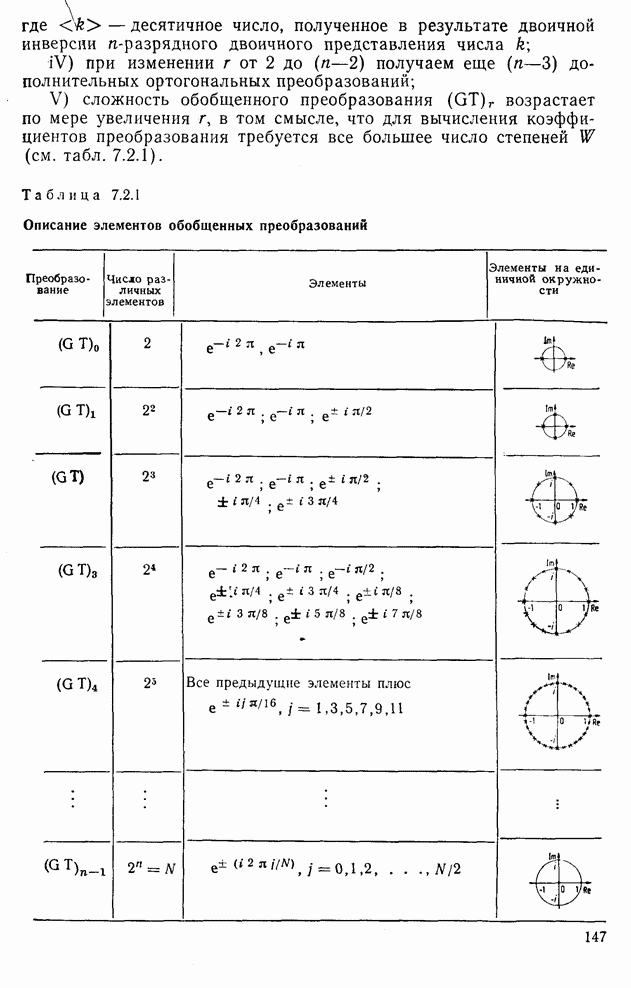
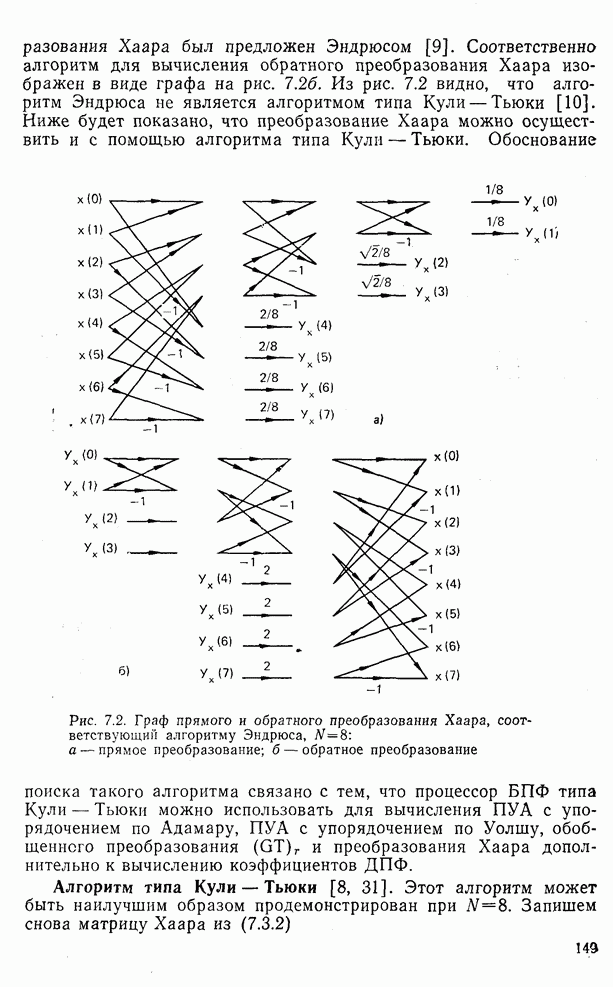
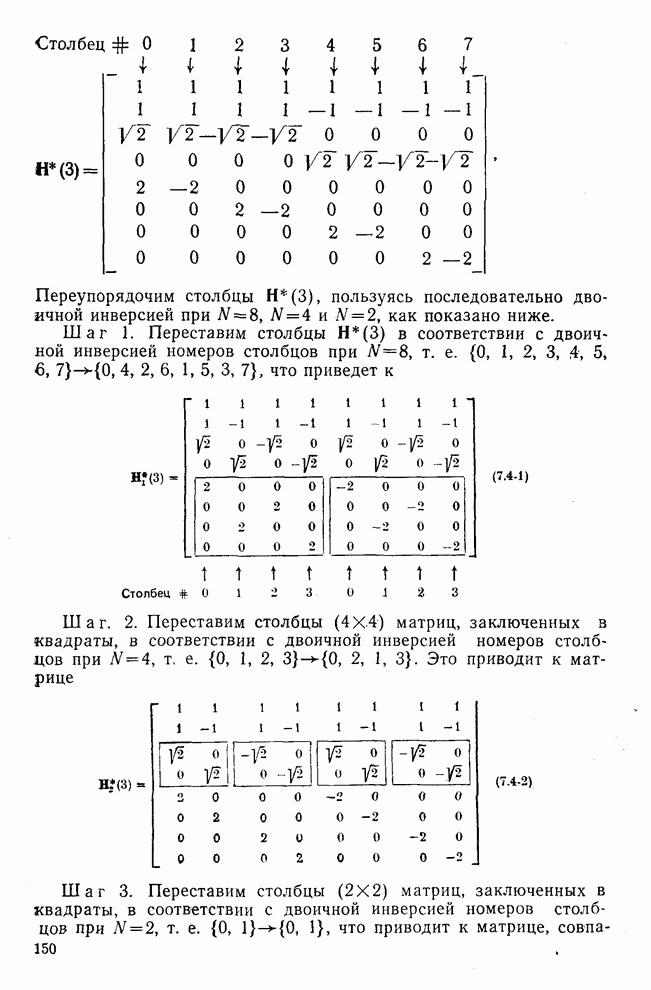
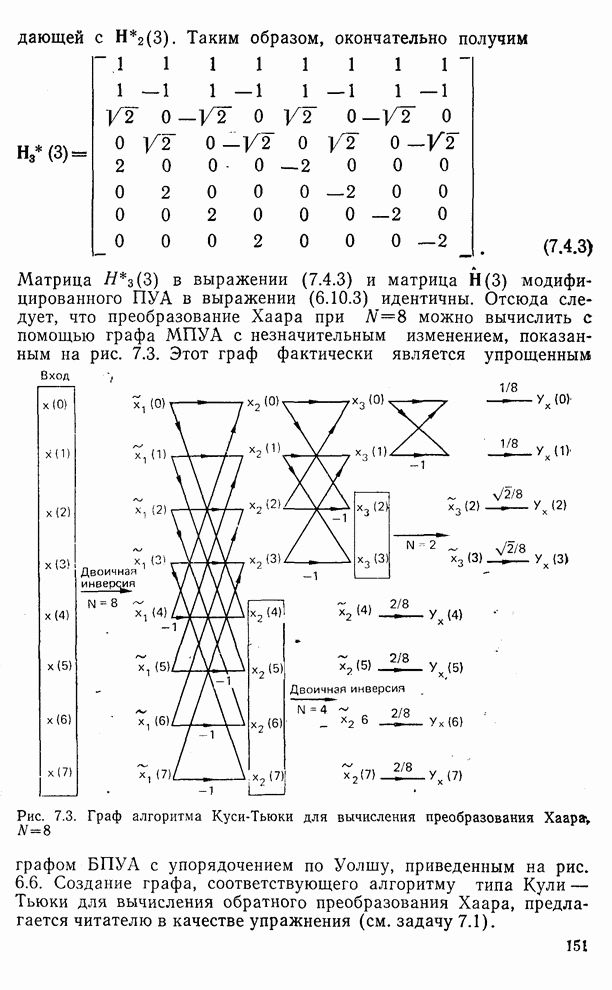
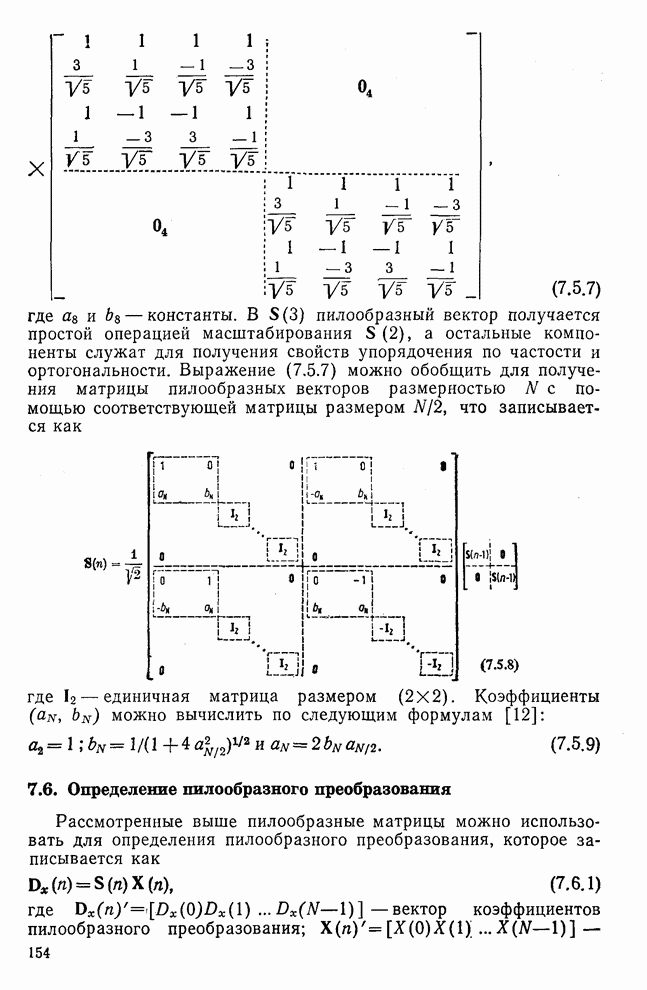
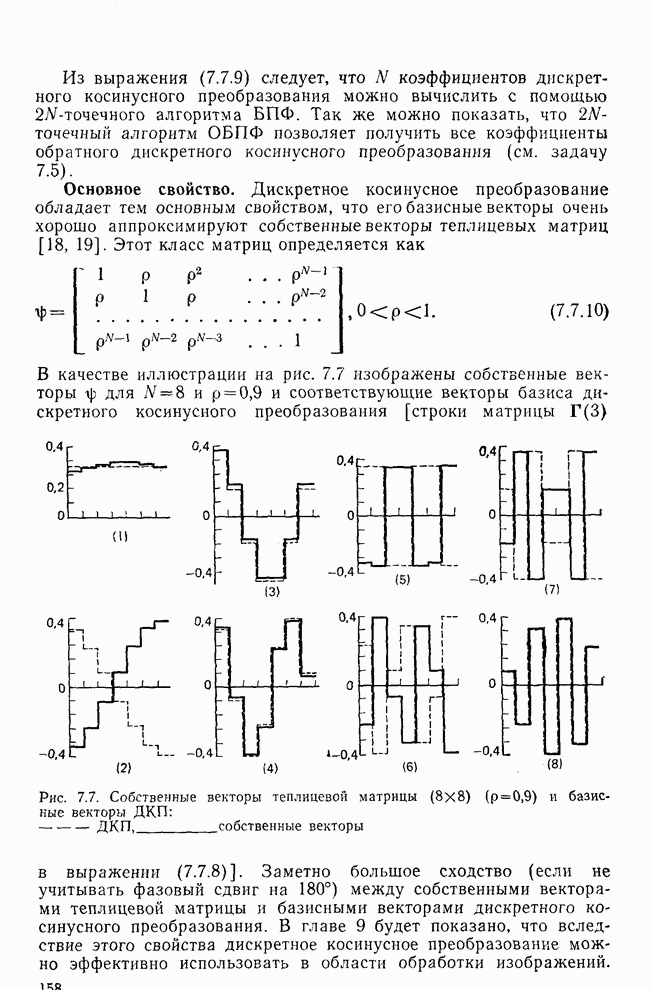
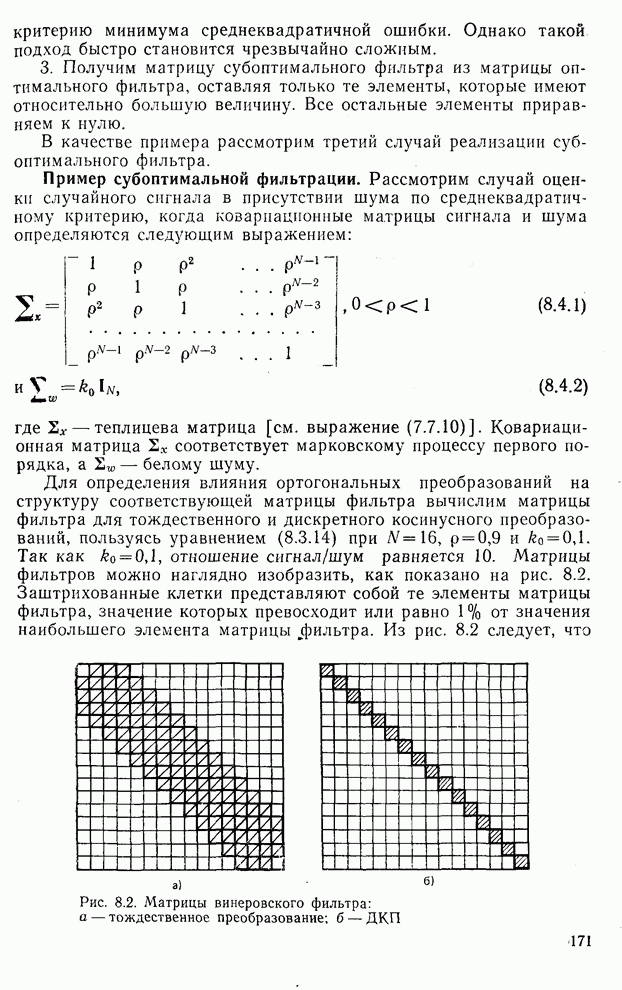
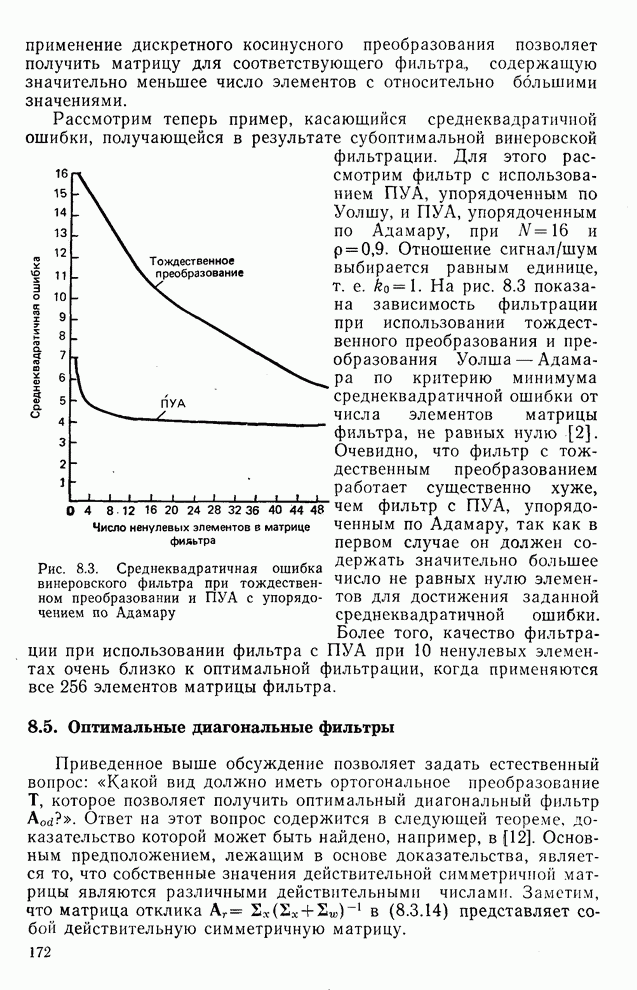
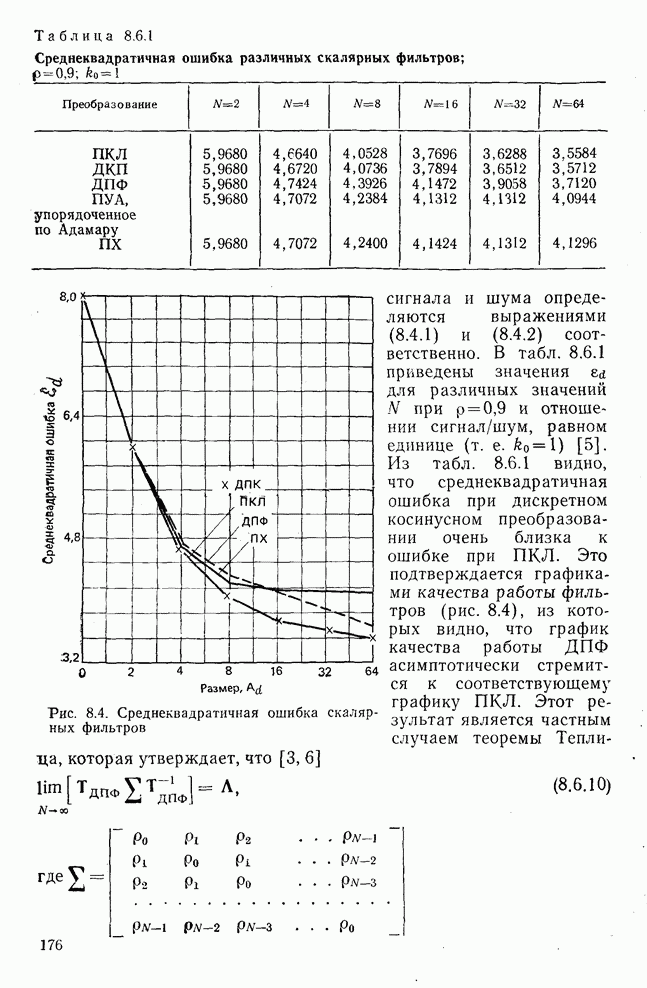
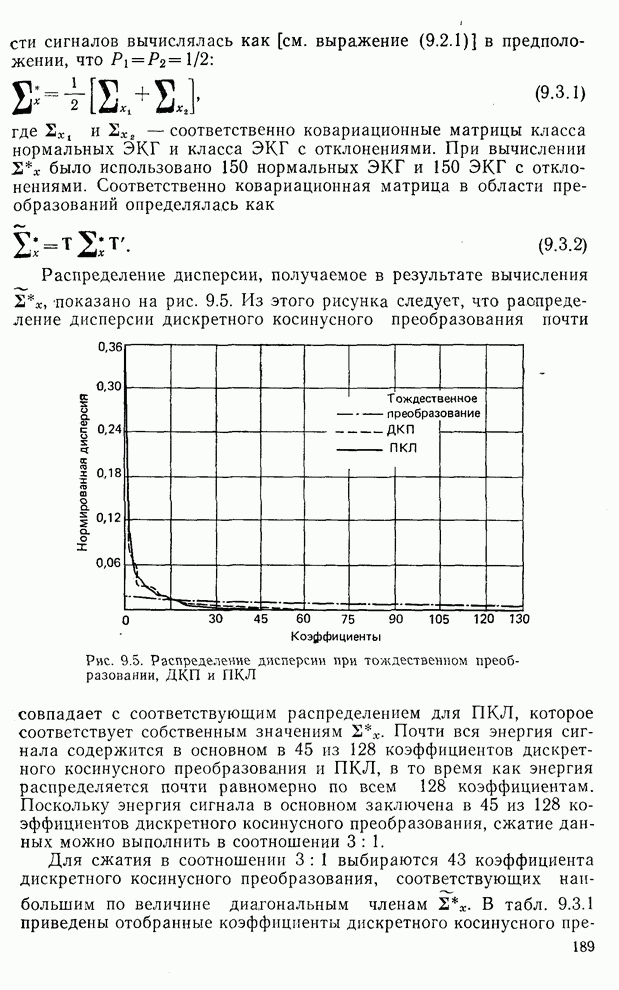
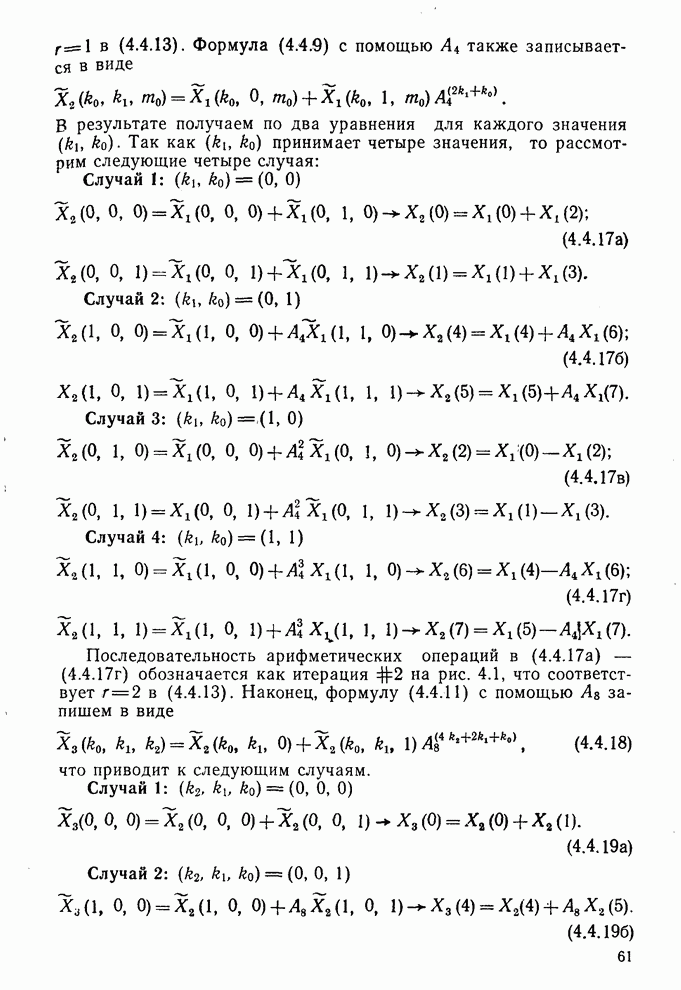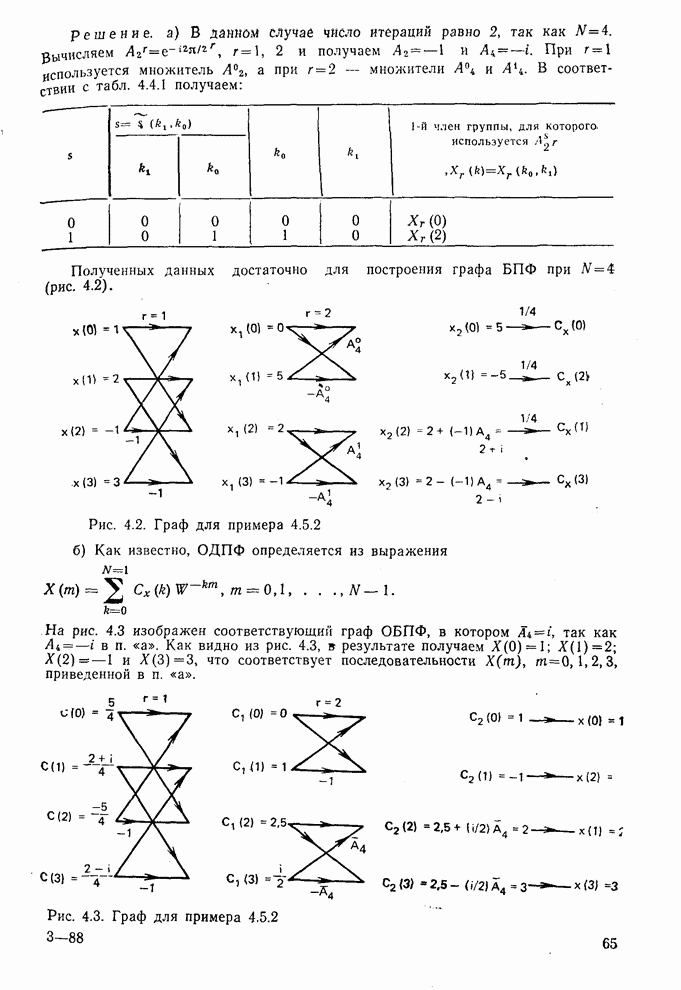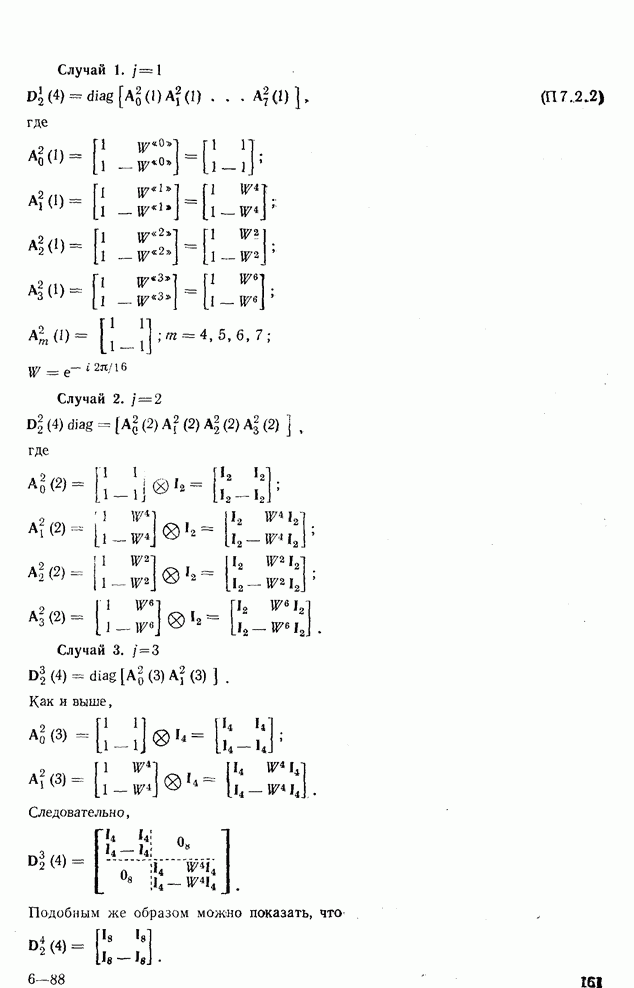| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
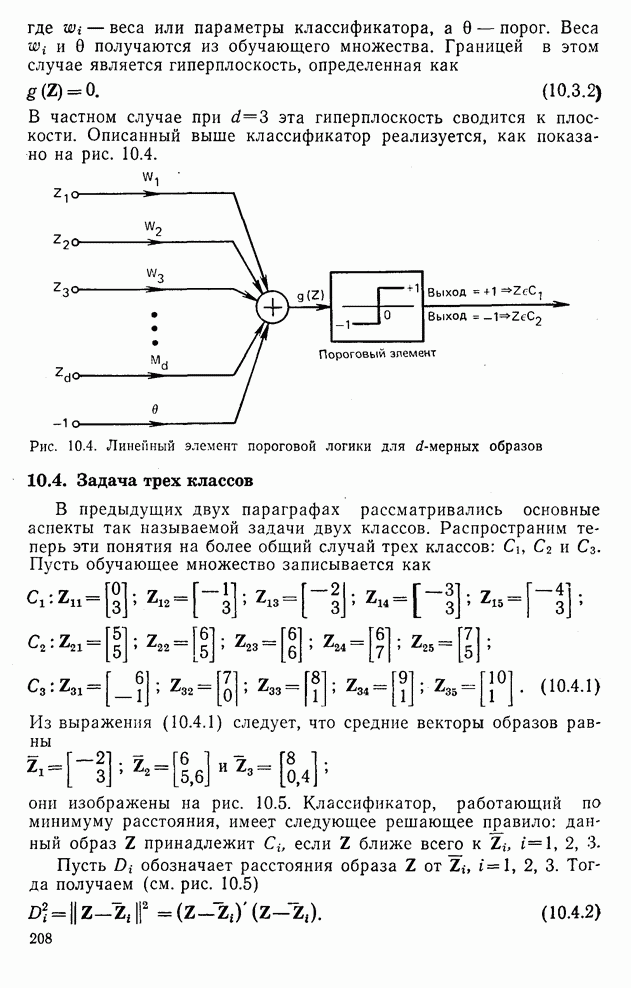
10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
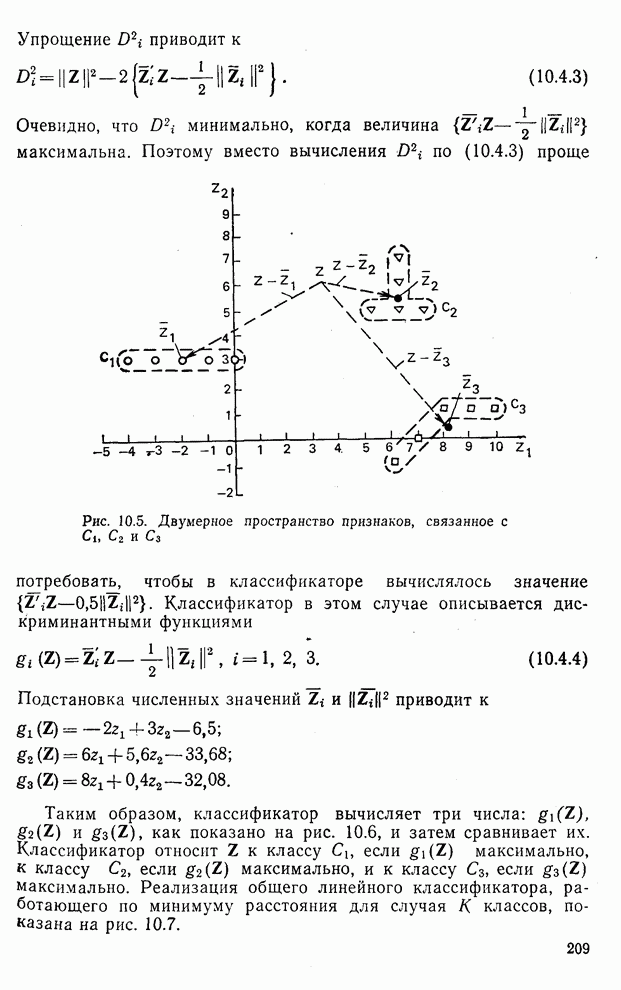
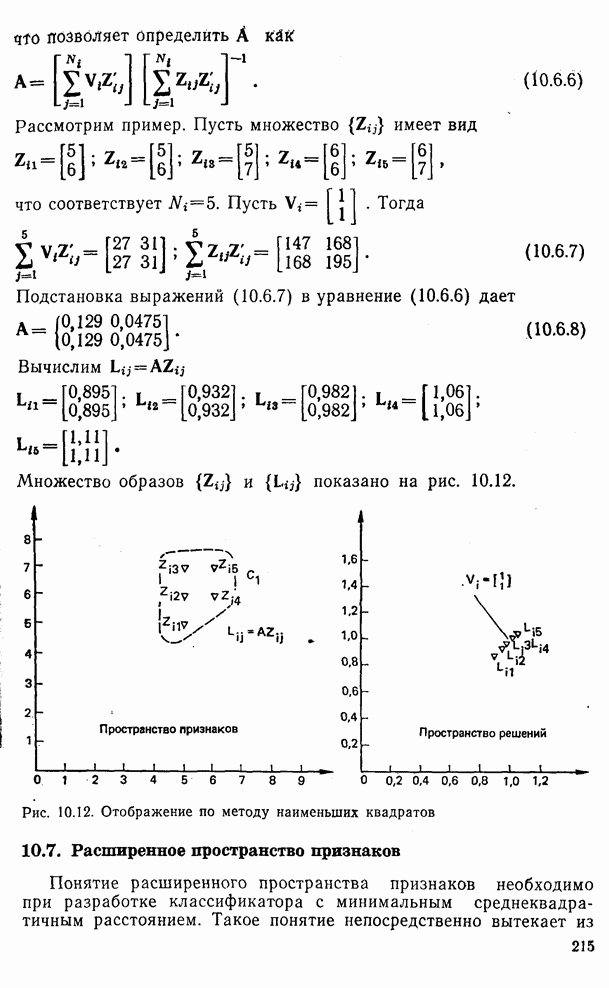
Рассмотрение классификатора с наименьшим среднеквадратичным расстоянием наиболее наглядно может быть проведено для трех классов. Для  -мерного пространства признаков получаем (
-мерного пространства признаков получаем ( )-мерное расширенное пространство признаков, приписывая каждому образу Z координату, равную
)-мерное расширенное пространство признаков, приписывая каждому образу Z координату, равную  , для получения
, для получения  . Эта процедура проиллюстрирована для
. Эта процедура проиллюстрирована для  на рис. 10.13а и б.
на рис. 10.13а и б.

Рис. 10.13. Классификатор для трех классов, работающий по критерию наименьшего среднеквадратичного расстояния:
а — пространство признаков; б — расширенное пространство признаков; в — пространство решений
Определяем преобразование А, отображающее  в
в  в смысле наименьших квадратов. Выберем в качестве
в смысле наименьших квадратов. Выберем в качестве  вершины трех единичных векторов, как показано на рис. 10.13в. Обозначим априорные вероятности классов
вершины трех единичных векторов, как показано на рис. 10.13в. Обозначим априорные вероятности классов  через
через  . Преобразование можно непосредственно найти в соответствии с рассуждениями, приведенными в § 10.6. В частности, в соответствии с выражением (10.6.5) получаем
. Преобразование можно непосредственно найти в соответствии с рассуждениями, приведенными в § 10.6. В частности, в соответствии с выражением (10.6.5) получаем

Решая это уравнение относительно А, получаем
 , (10.8.2)
, (10.8.2)
где

Очевидно, что  матрицами взаимной корреляции и автокорреляции соответственно [см. выражение
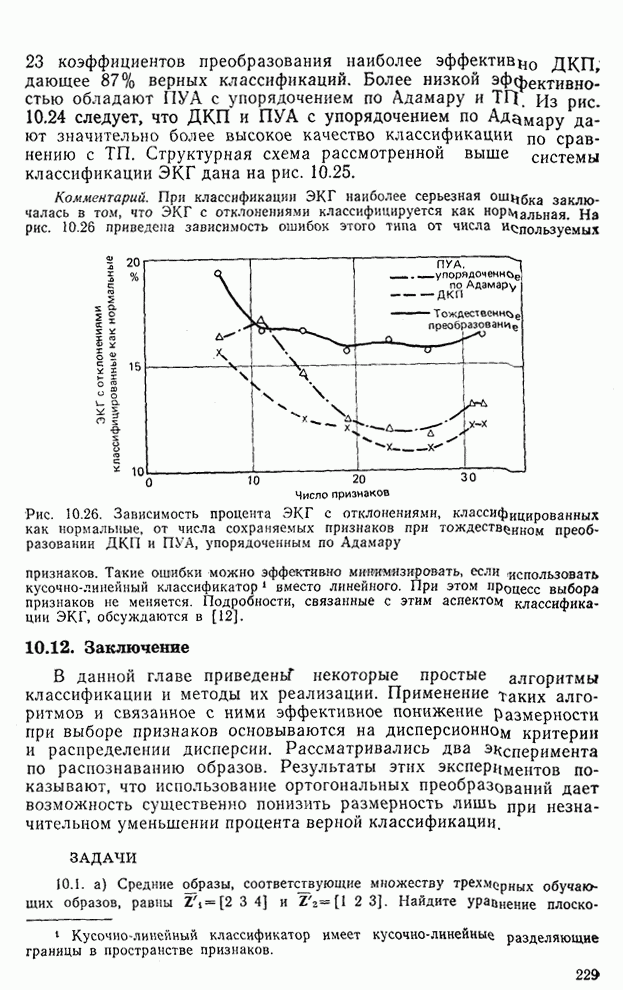
матрицами взаимной корреляции и автокорреляции соответственно [см. выражение  ]. Из.
]. Из.
(10.8.2) следует, что А — матрица размером  . Для классификации образа
. Для классификации образа  классификатор в первую очередь вычисляет
классификатор в первую очередь вычисляет  , а затем отображает Z в пространство решений (рис. 10.13). При этом применяется следующее решающее правило по критерию минимума, расстояния: если L наиболее близок
, а затем отображает Z в пространство решений (рис. 10.13). При этом применяется следующее решающее правило по критерию минимума, расстояния: если L наиболее близок  , то Z классифицируется как принадлежащий
, то Z классифицируется как принадлежащий  . Расстояния, которые вычисляет классификатор, определяются как
. Расстояния, которые вычисляет классификатор, определяются как  , т. е.
, т. е.
 (10.8.3)
(10.8.3)
В выражении (10.8.3)  , и, следовательно,
, и, следовательно,  -минимально, когда
-минимально, когда  максимально. Поэтому вместо
максимально. Поэтому вместо  в (10.8.3) достаточно, чтобы классификатор вычислил
в (10.8.3) достаточно, чтобы классификатор вычислил
 (10.8.4)
(10.8.4)
Подставляя  и
и  в (10.8.4), получаем
в (10.8.4), получаем
 (10.8.5)
(10.8.5)
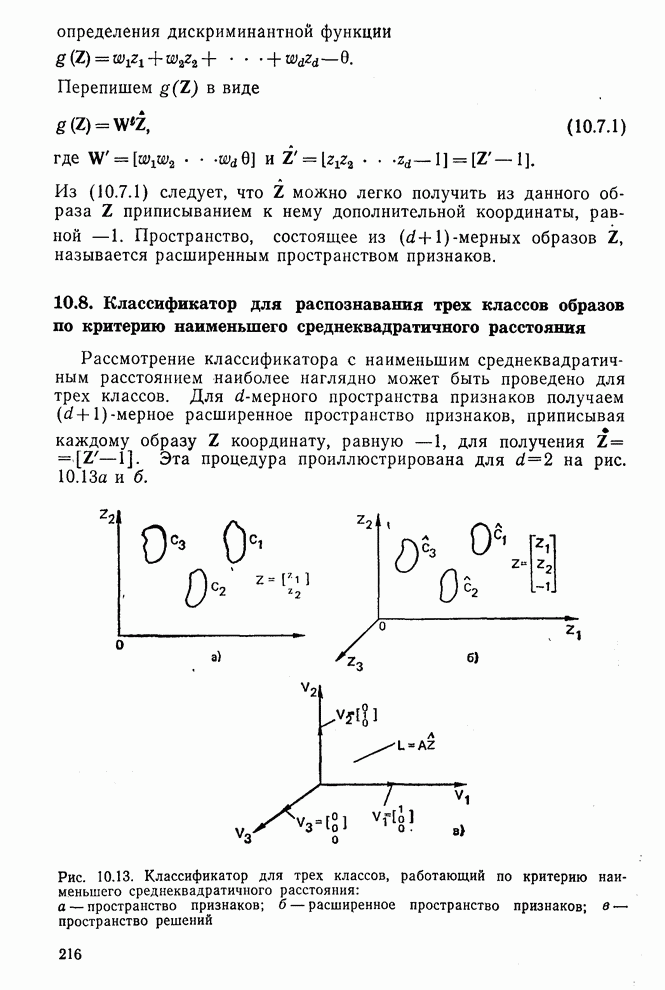
Если матрица преобразования обозначается как

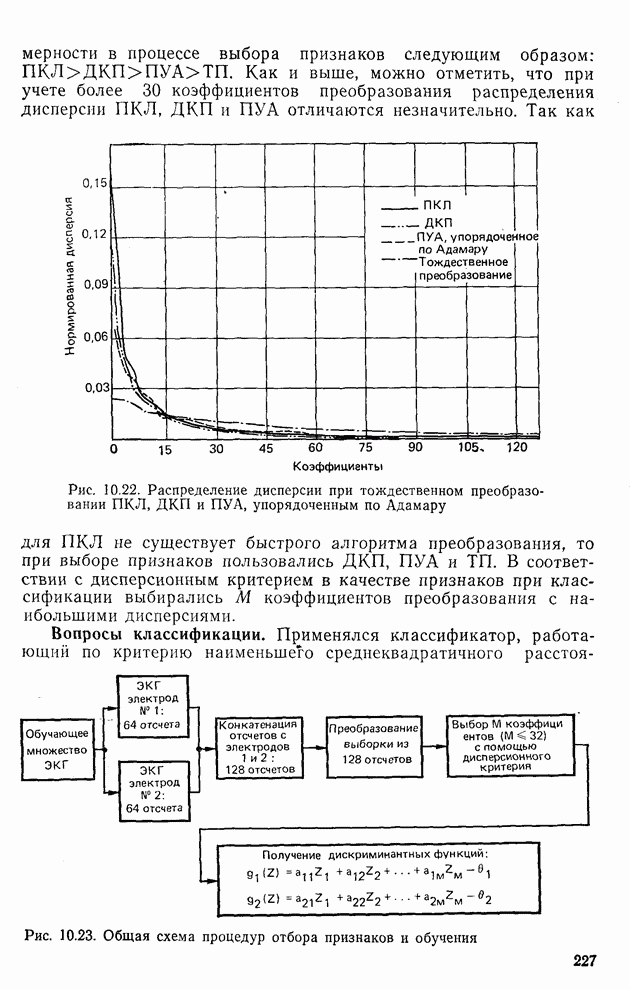
то (10.8.5) означает, что  представляет собой следующие дискриминантные функции, которые определяют классификатор:
представляет собой следующие дискриминантные функции, которые определяют классификатор:
 (10.8.6)
(10.8.6)
Из (10.8.6) следует, что классификатор полностью определяется матрицей преобразования А, которая получается из множества обучающих образов. Для классификации данного образа классификатор вычисляет три числа:  и
и  — в соответствии с (10.8.6). Если
— в соответствии с (10.8.6). Если  , то этот образ приписывается
, то этот образ приписывается  . Реализация такого классификатора показана на рис. 10.14. Рассмотрим два численных примера.
. Реализация такого классификатора показана на рис. 10.14. Рассмотрим два численных примера.

Рис. 10.14. Реализация классификатора для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
Пример 10.8.1. Пусть обучающее множество размерностью 2 (т. е.  ) представлено следующим образом:
) представлено следующим образом:

а) Предполагая  , требуется найти дискриминантные функции, которые определяют классификатор.
, требуется найти дискриминантные функции, которые определяют классификатор.
б) С помощью  , требуется определить уравнения разделяющих границ и изобразить их в пространстве признаков.
, требуется определить уравнения разделяющих границ и изобразить их в пространстве признаков.
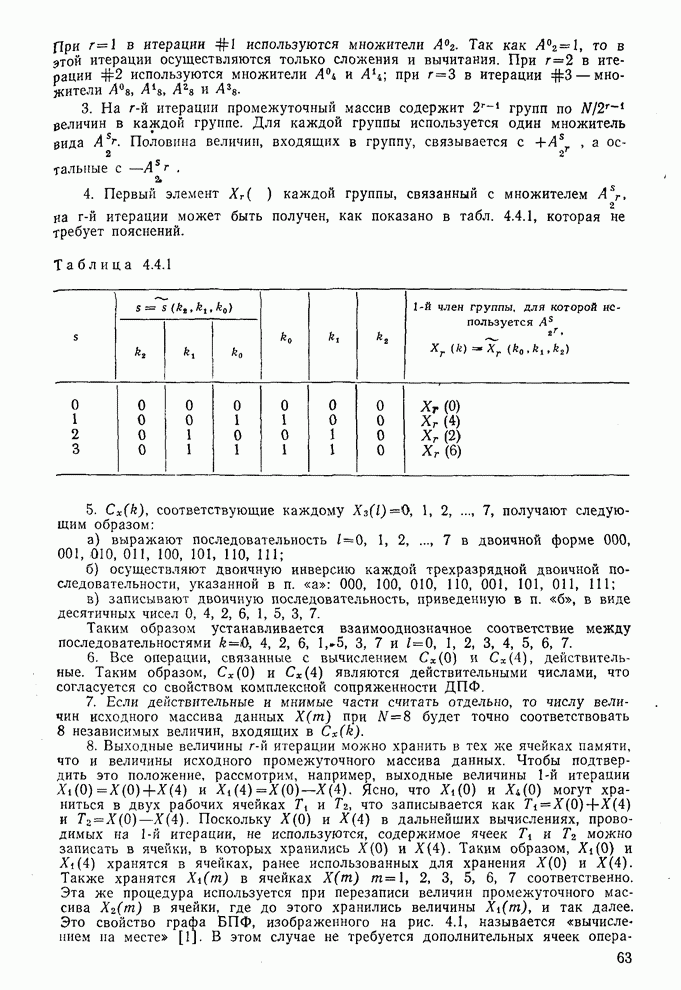
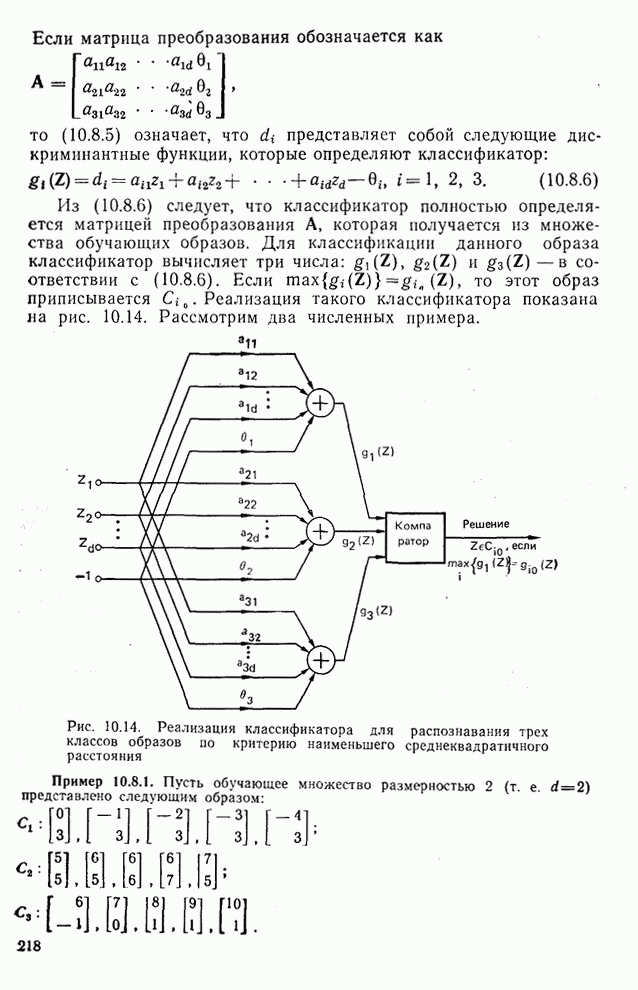
Решение. а) А вычисляют в соответствии с (10.8.2) следующим образом:

что дает
 (10.8.7)
(10.8.7)
в результате получаем
 (10.8.8)
(10.8.8)
Матрица, обратная  равна
равна

Подставляя (10.8.7) и (10.8.9) в выражение (10.8.2), получаем
 (10.8.10)
(10.8.10)
Таким образом, дискриминантные функции, которые определяют классификатор, имеют вид [см. выражение (10.8.6)]

Реализация полученного классификатора показана на рис. 10.15.
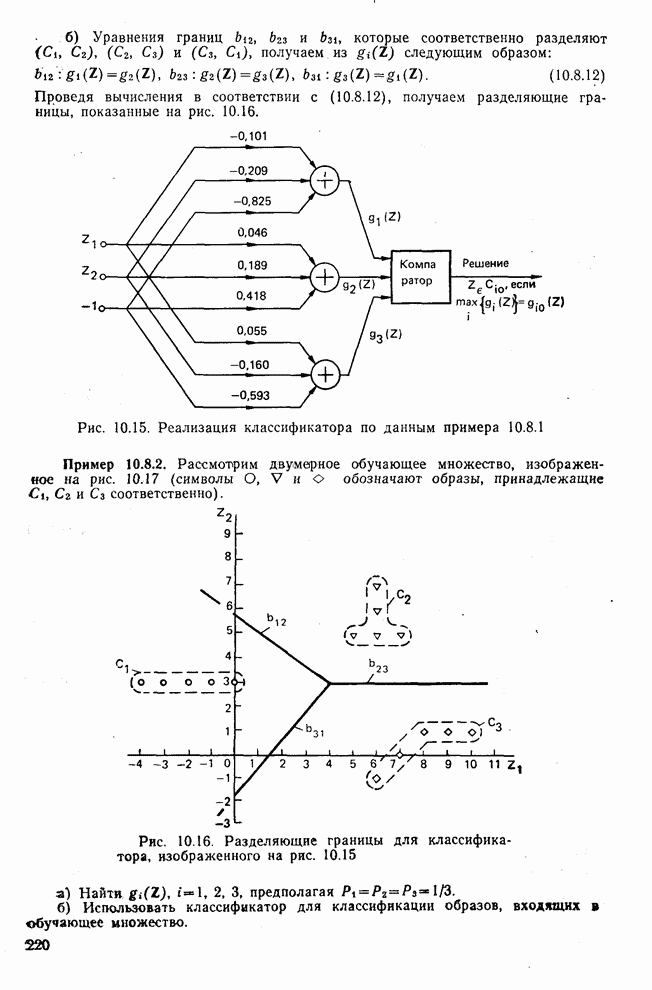
б) Уравнения границ  и
и  , которые соответственно разделяют
, которые соответственно разделяют  и
и  , получаем из
, получаем из  следующим образом:
следующим образом:
 (10.8.12)
(10.8.12)
Проведя вычисления в соответствии с (10.8.12), получаем разделяющие границы, показанные на рис. 10.16.

Рис. 10.15. Реализация классификатора по данным примера 10.8.1
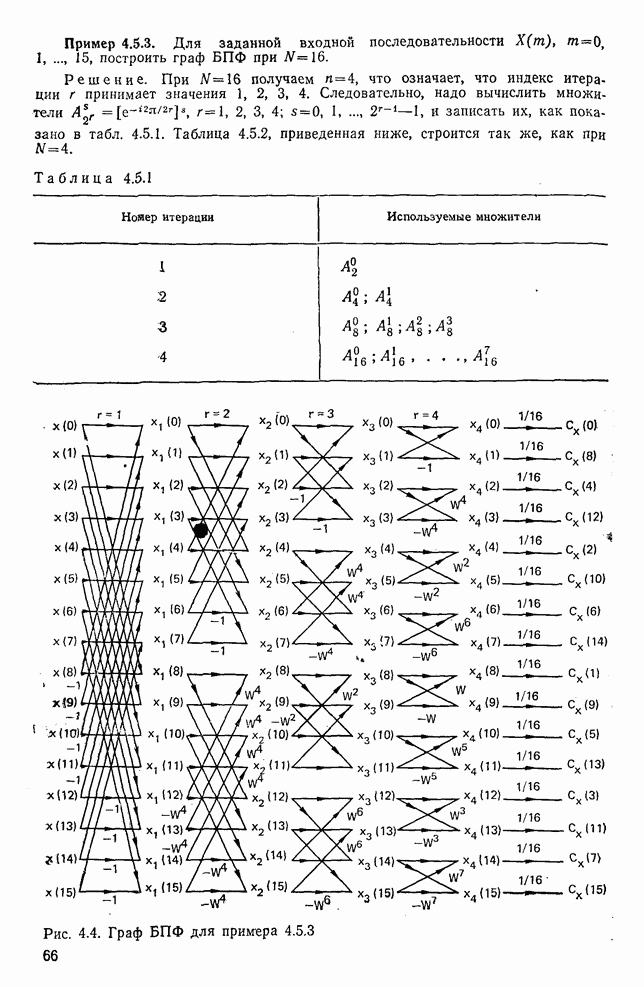
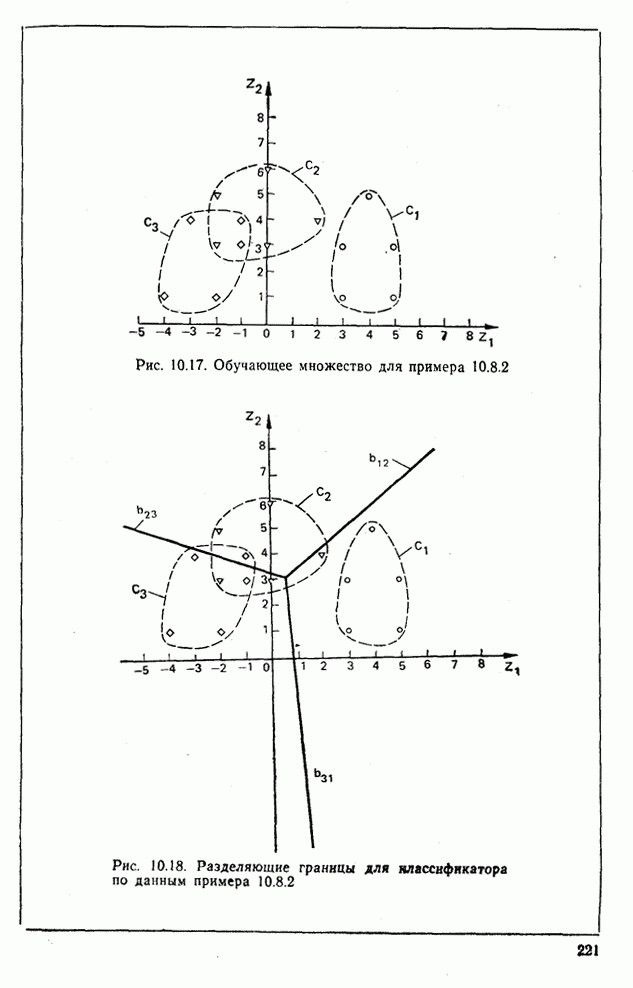
Пример 10.8.2. Рассмотрим двумерное обучающее множество, изображенное на рис. 10.17 (символы  и
и  обозначают образы, принадлежащие
обозначают образы, принадлежащие  и
и  соответственно).
соответственно).

Рис. 10.16. Разделяющие границы для классификатора, изображенного на рис. 10.15
а) Найти  , предполагая
, предполагая  .
.
б) Использовать классификатор для классификации образов, входящих обучающее множество.

Рис. 10.17. Обучающее множество для примера 10.8.2

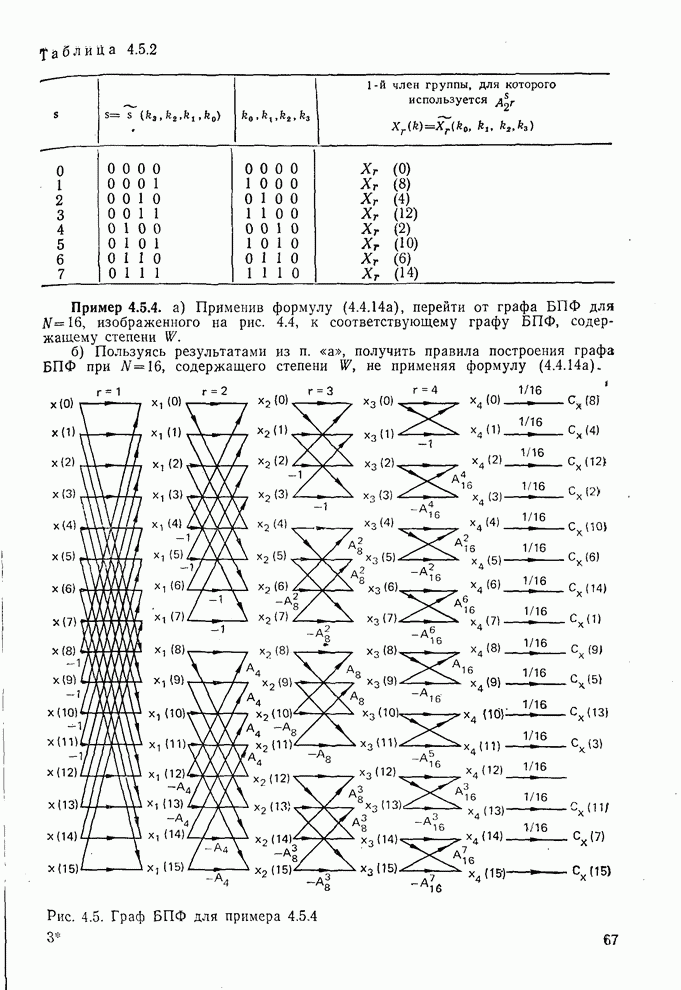
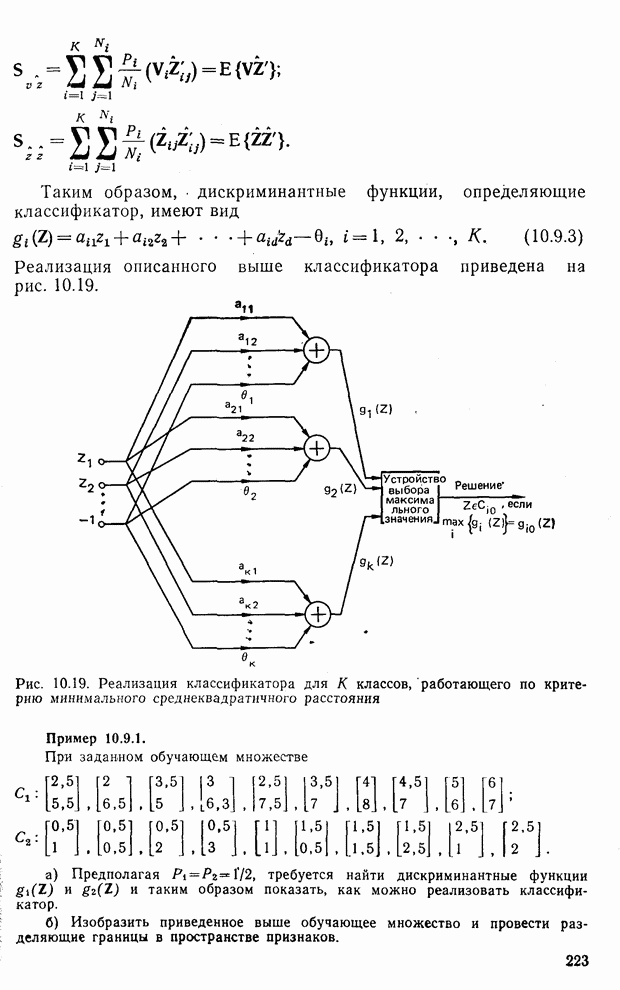
Рис. 10.18. Разделяющие границы для классификатора по данным примера 10.8.2
Решение, а) Вычисления проводим по той же схеме, что и в примере 10.8.1. В результате получаем

Соответственно дискриминантные функции определяются как

б) Классификация образов, принадлежащих обучающему множеству, осуществляется в результате вычисления  для каждого Z, принадлежащего множеству. Затем Z приписывается
для каждого Z, принадлежащего множеству. Затем Z приписывается  если
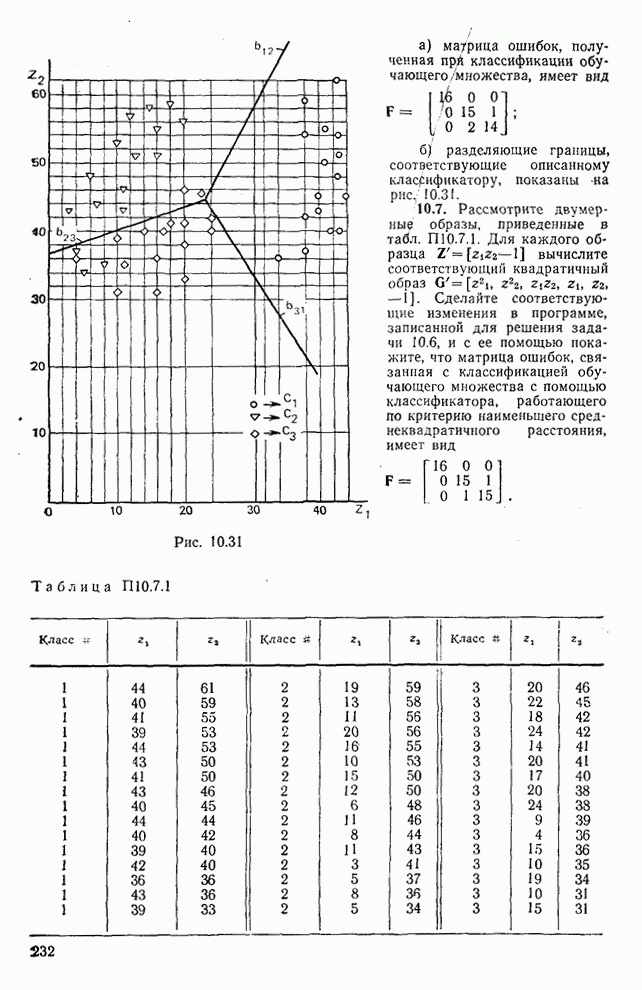
если  . Результаты классификации обычно суммируются в виде следующей матрицы ошибок классификации:
. Результаты классификации обычно суммируются в виде следующей матрицы ошибок классификации:
 (10.8.14)
(10.8.14)
В матрице F ненулевые элементы, стоящие не на главной диагонали, соответствуют ошибкам классификатора, т. е. если элемент в  строке и
строке и  столбце матрицы F обозначить как
столбце матрицы F обозначить как  и
и  , то s образов, принадлежащих
, то s образов, принадлежащих  , были ошибочно классифицированы как принадлежащие
, были ошибочно классифицированы как принадлежащие  .
.
Примечание. Полезно рассмотреть ошибки, которые отображены в матрице ошибок классификации. Это можно сделать, изобразив разделяющие границы, которые соответствуют приведенному классификатору. На рис. 10.18 показаны разделяющие границы  и
и  . Процедура их получения опущена, так как она полностью повторяет процедуру, приведенную в примере 10.8.1. Из рассмотрения рис. 10.18 следует, что два треугольника ошибочно классифицируются как принадлежащие
. Процедура их получения опущена, так как она полностью повторяет процедуру, приведенную в примере 10.8.1. Из рассмотрения рис. 10.18 следует, что два треугольника ошибочно классифицируются как принадлежащие  , а один треугольник ошибочно приписывается
, а один треугольник ошибочно приписывается  . Это соответствует второй строке F. Таким же образом один квадрат ошибочно приписывается
. Это соответствует второй строке F. Таким же образом один квадрат ошибочно приписывается  , что соответствует третьей строке F. Наконец, все образы
, что соответствует третьей строке F. Наконец, все образы  классифицируются правильно, что отображено в первой строке
классифицируются правильно, что отображено в первой строке  .
.
В заключение заметим, что любой классификатор, обладающий линейными границами, будет совершать ошибки при классификации обучающего множества типа, изображенного на рис. 10.18, так как  и
и  нельзя разделить линейными границами.
нельзя разделить линейными границами.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
- 2.4. Связь между рядом Фурье и преобразованием Фурье
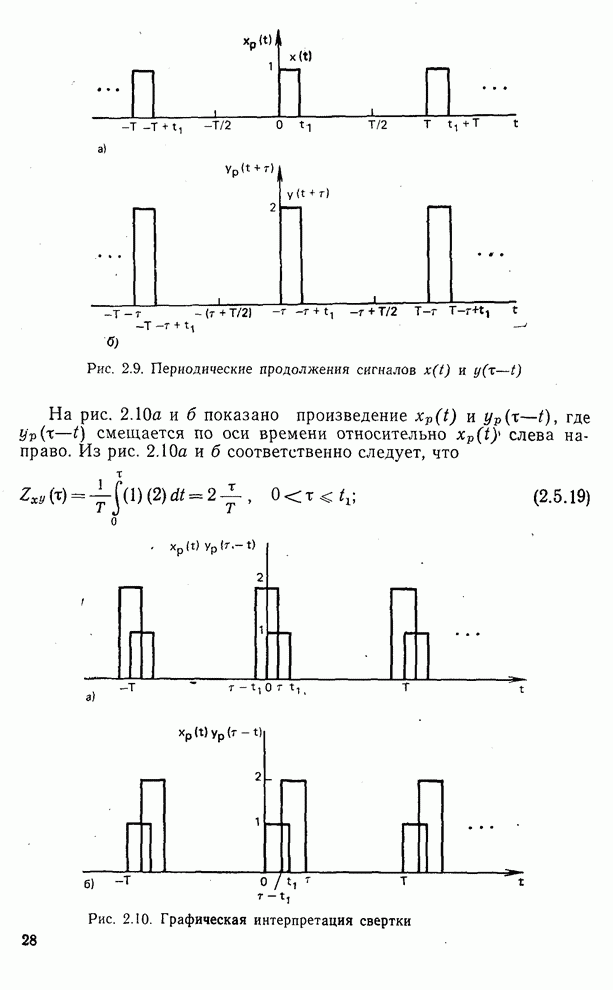
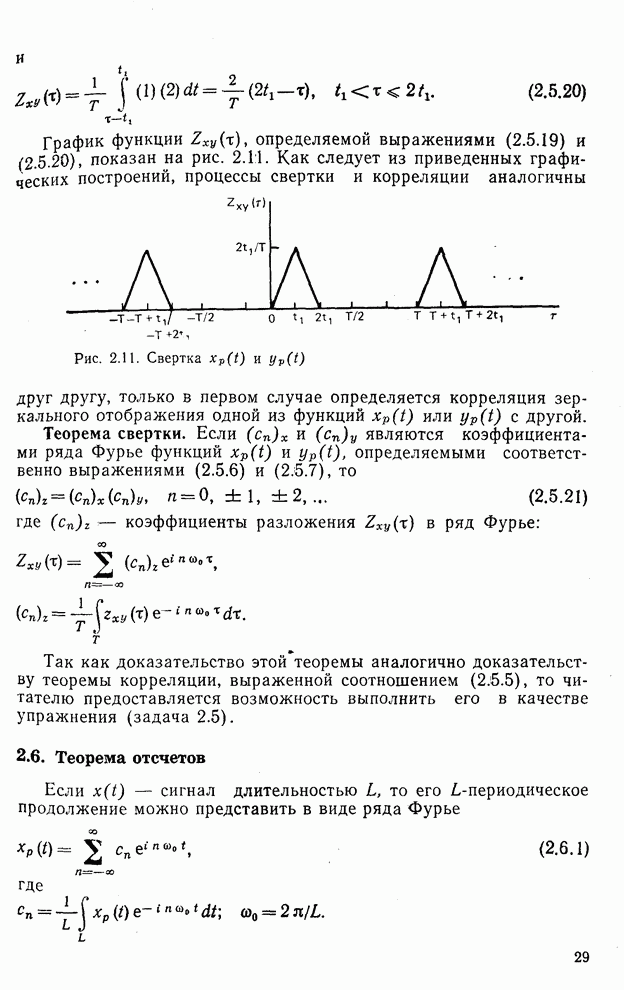
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
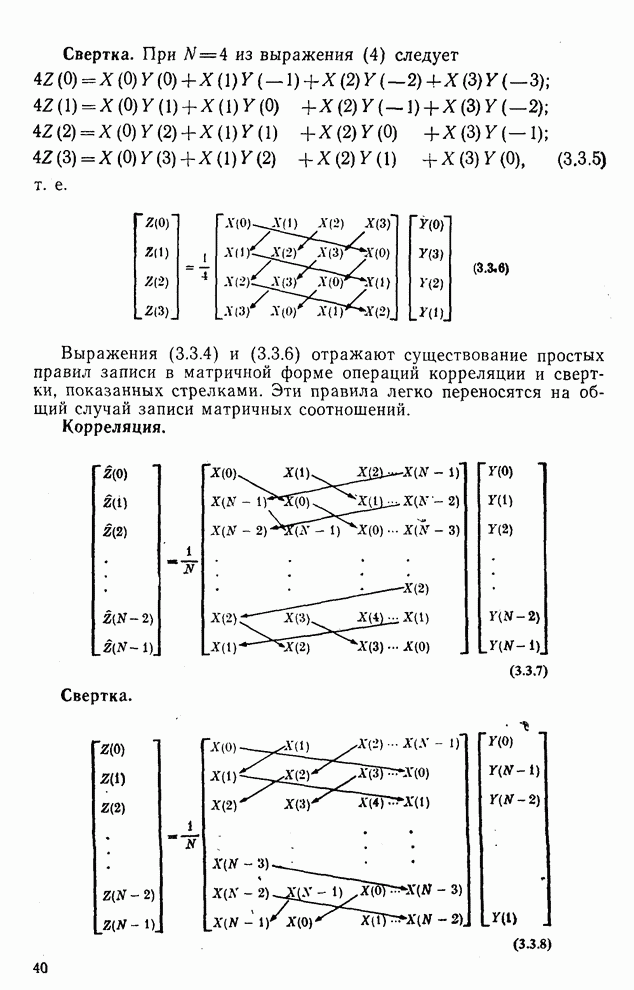
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
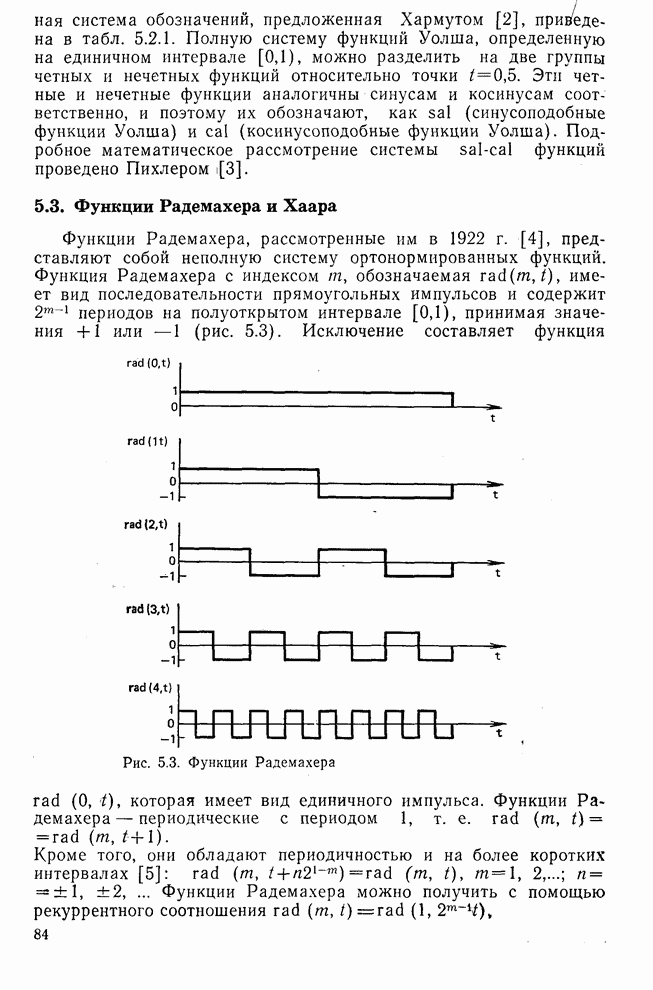
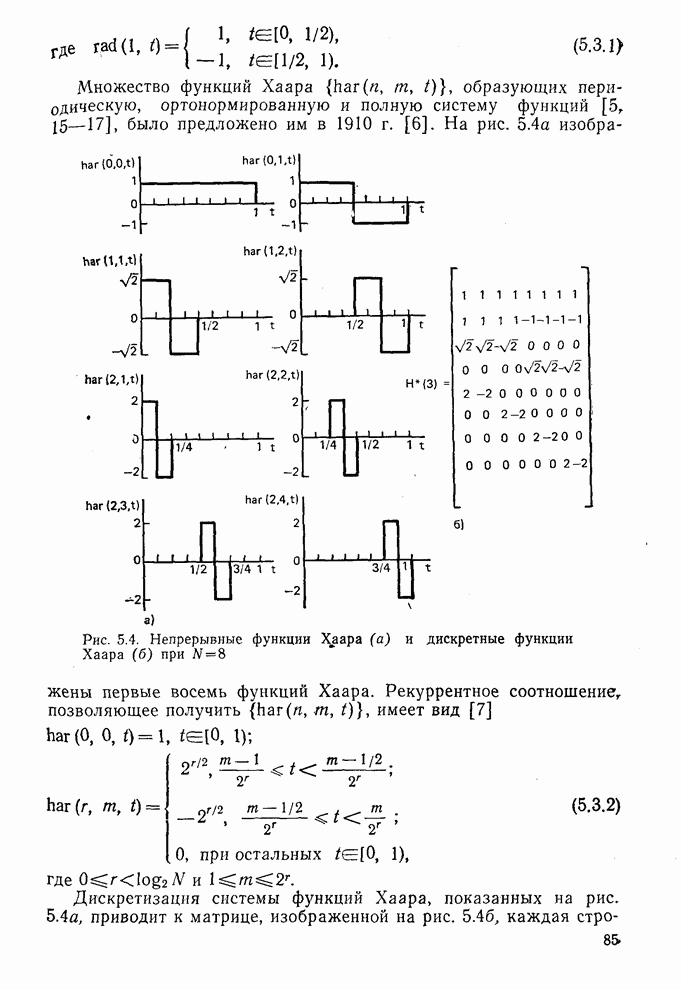
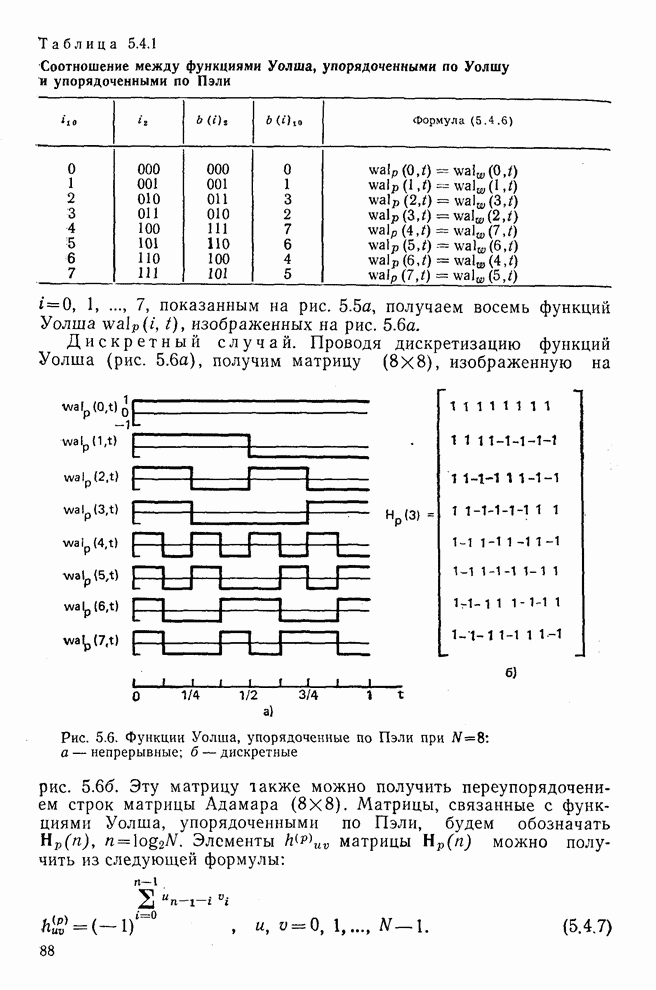
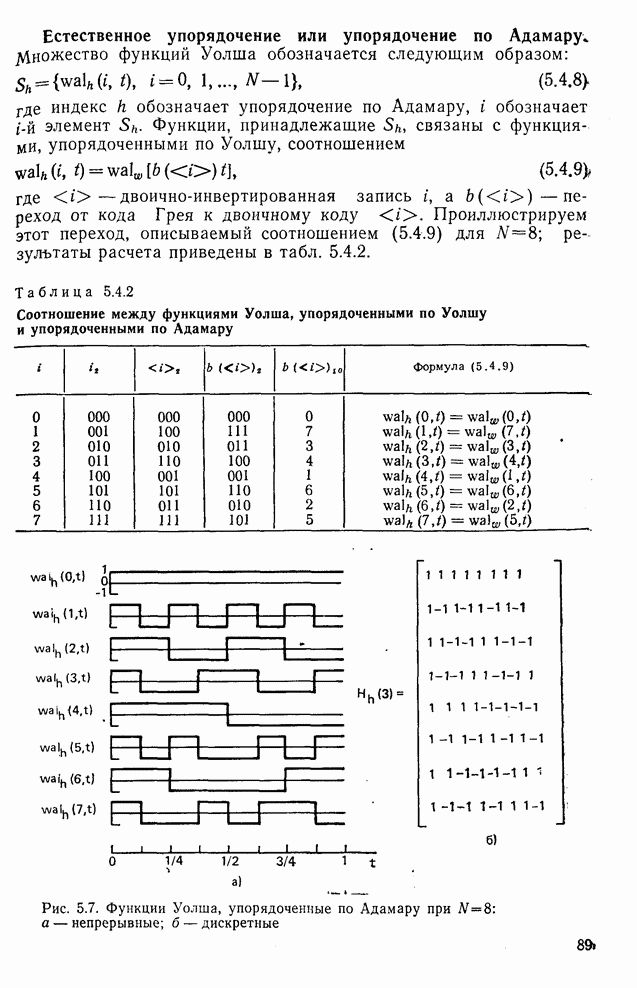
- 5.3. Функции Радемахера и Хаара
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
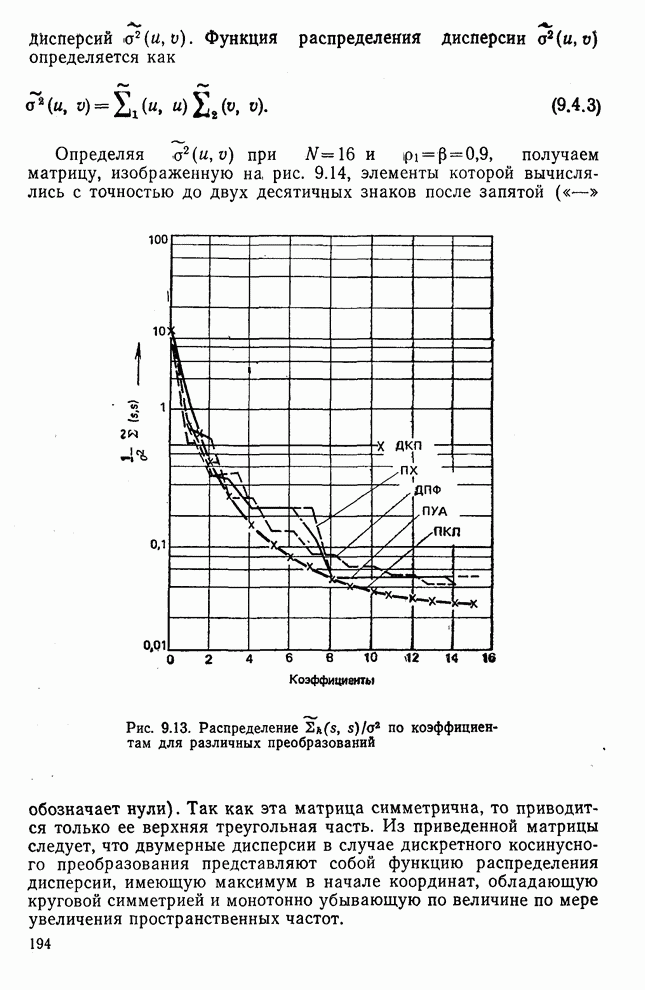
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
- 9.3. Сжатие электрокардиограмм [2]
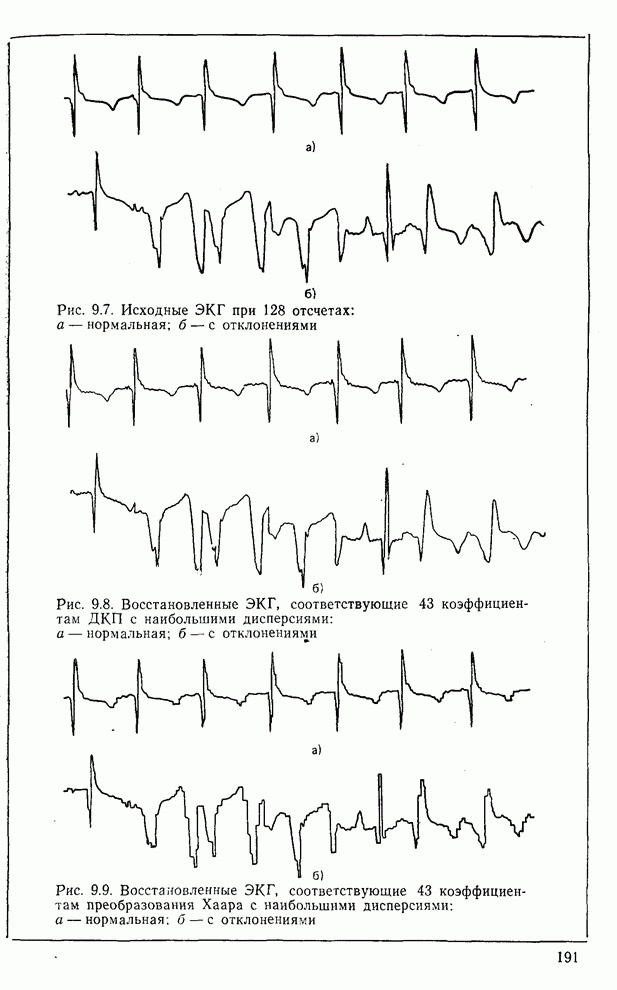
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
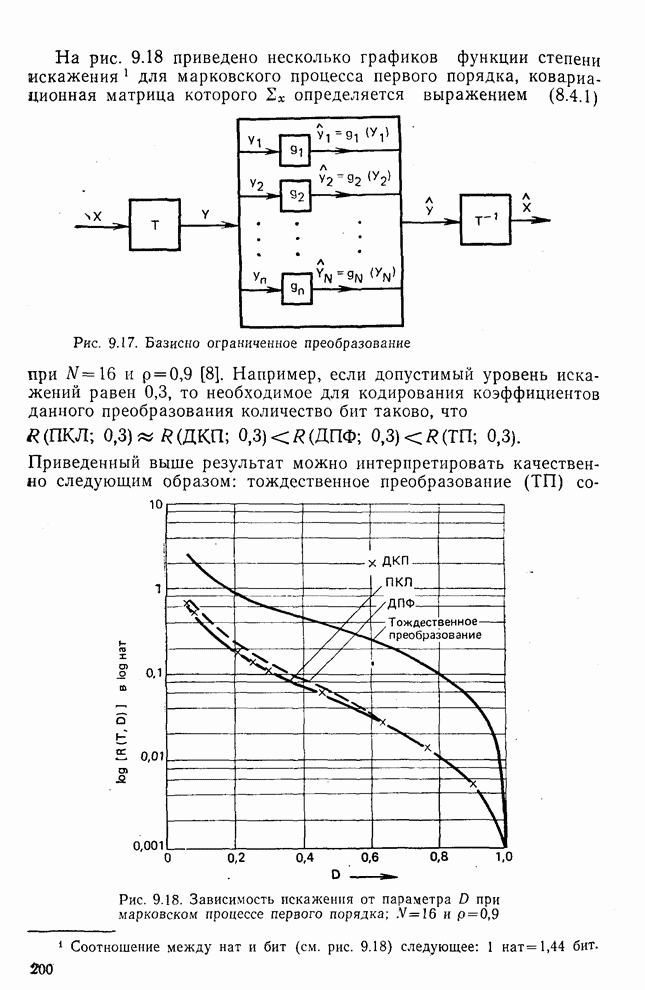
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
- 10.3. d-мерные образы
- 10.4. Задача трех классов
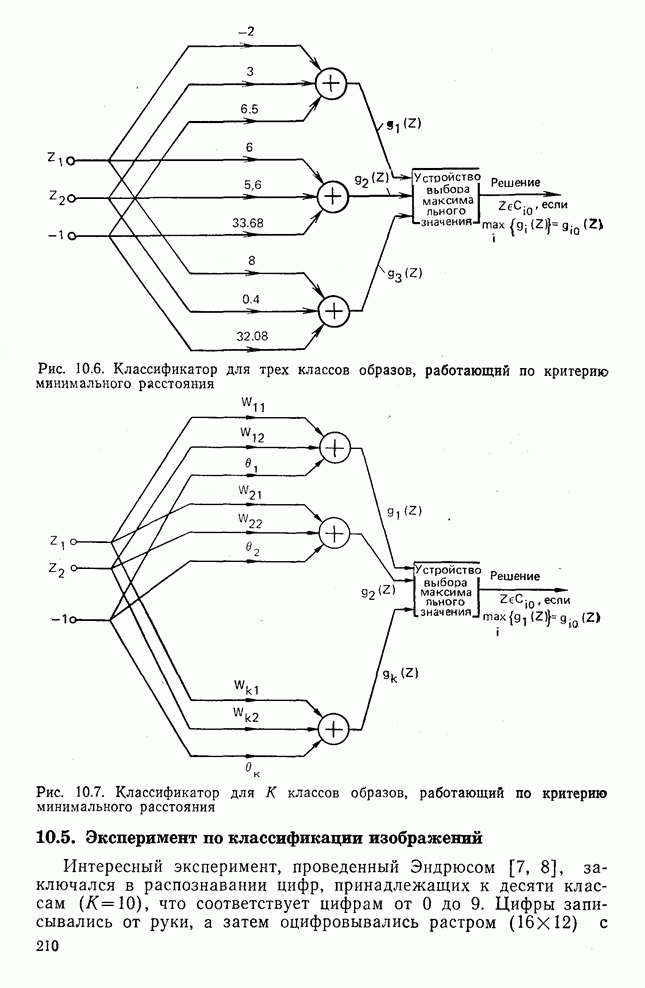
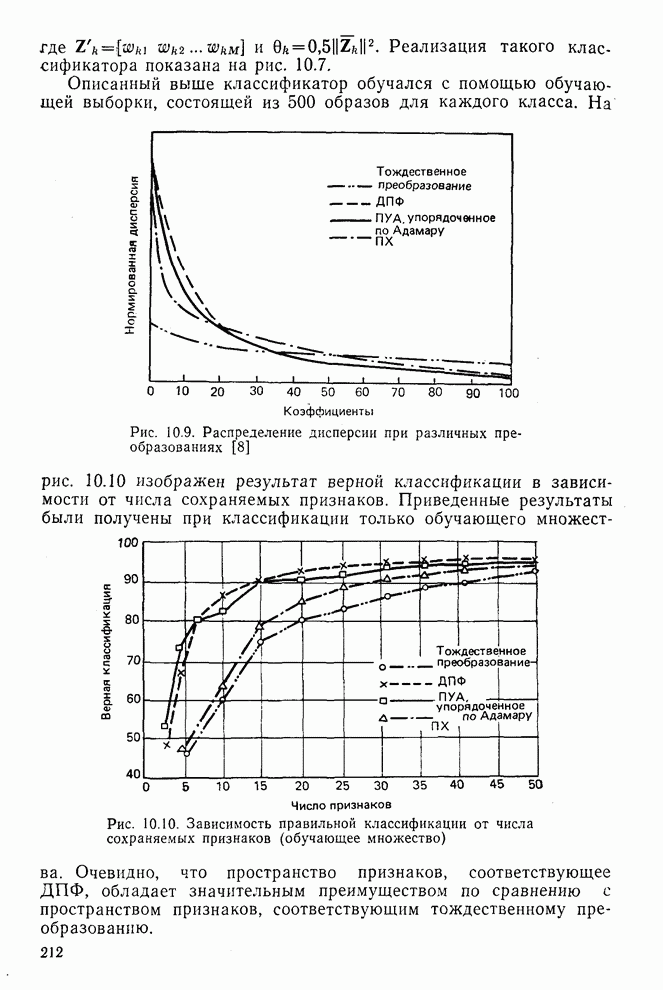
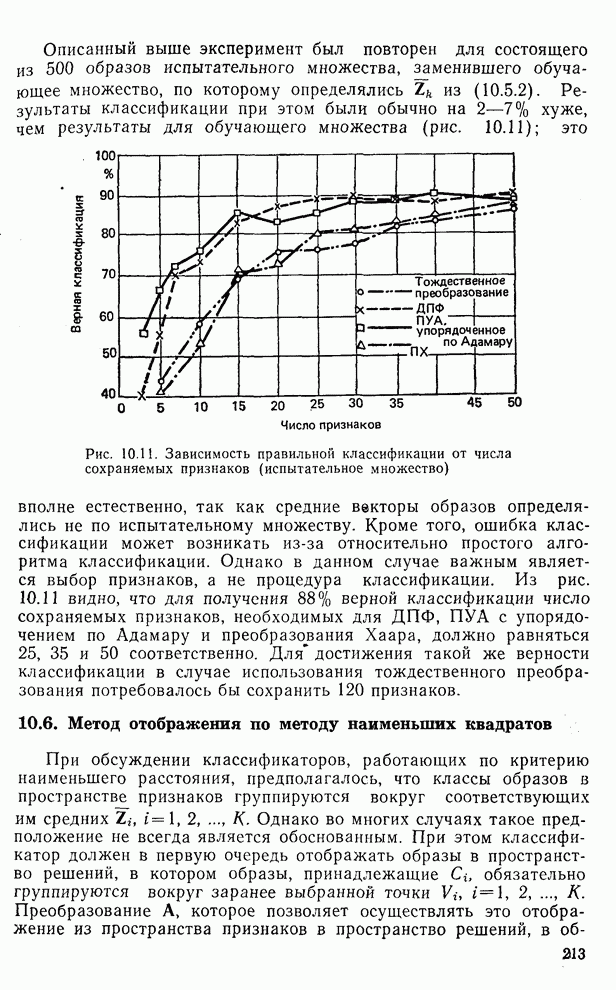
- 10.5. Эксперимент по классификации изображений
- 10.6. Метод отображения по методу наименьших квадратов
- 10.7. Расширенное пространство признаков
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ