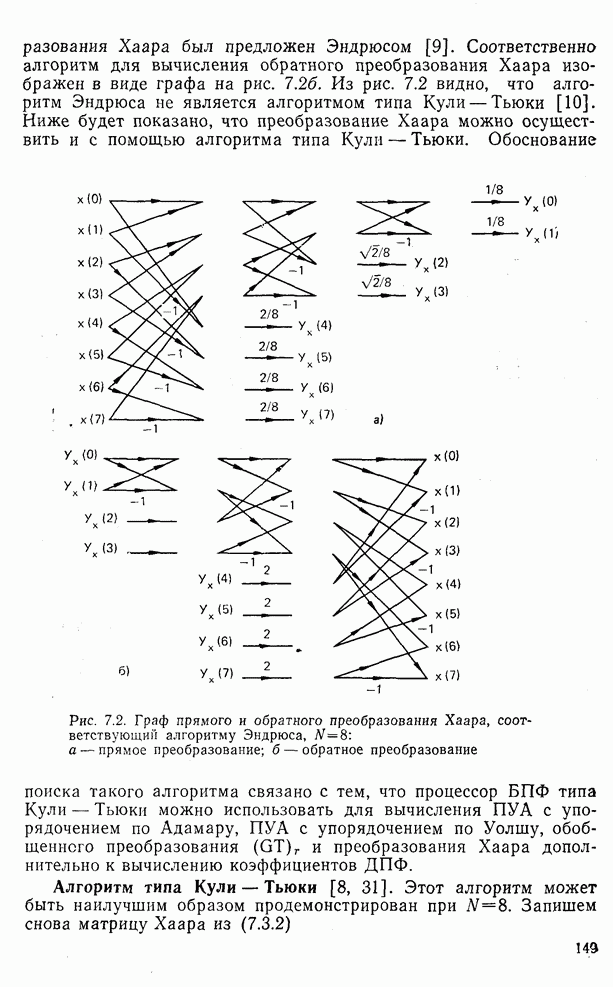
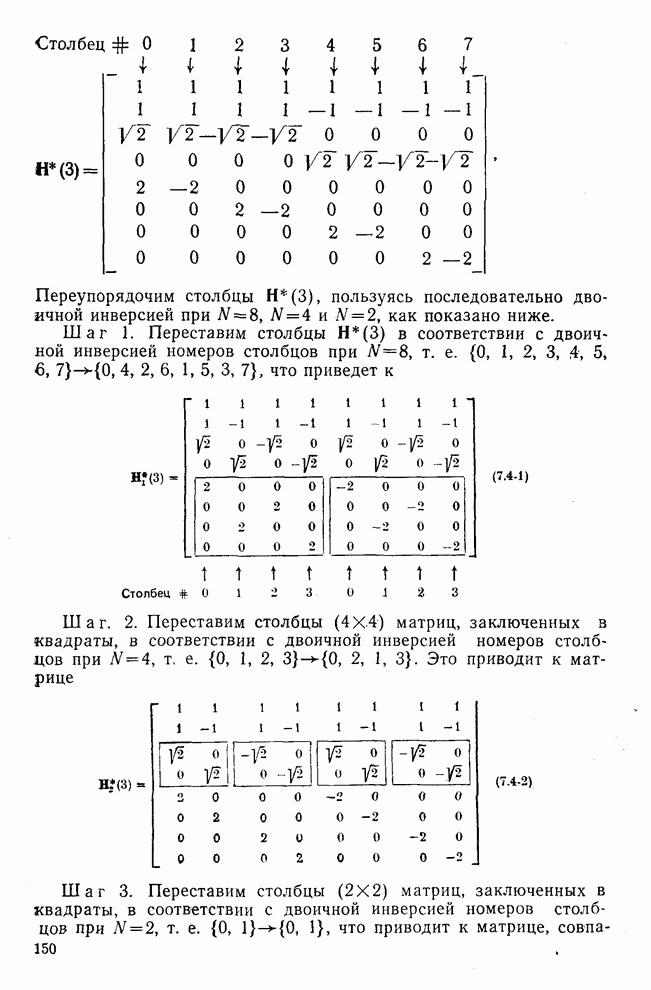
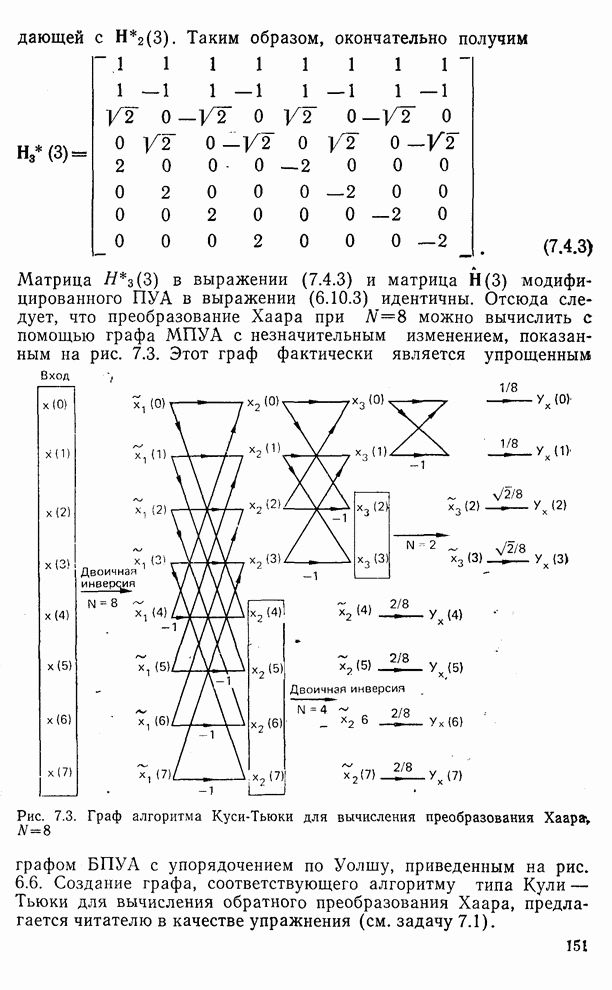
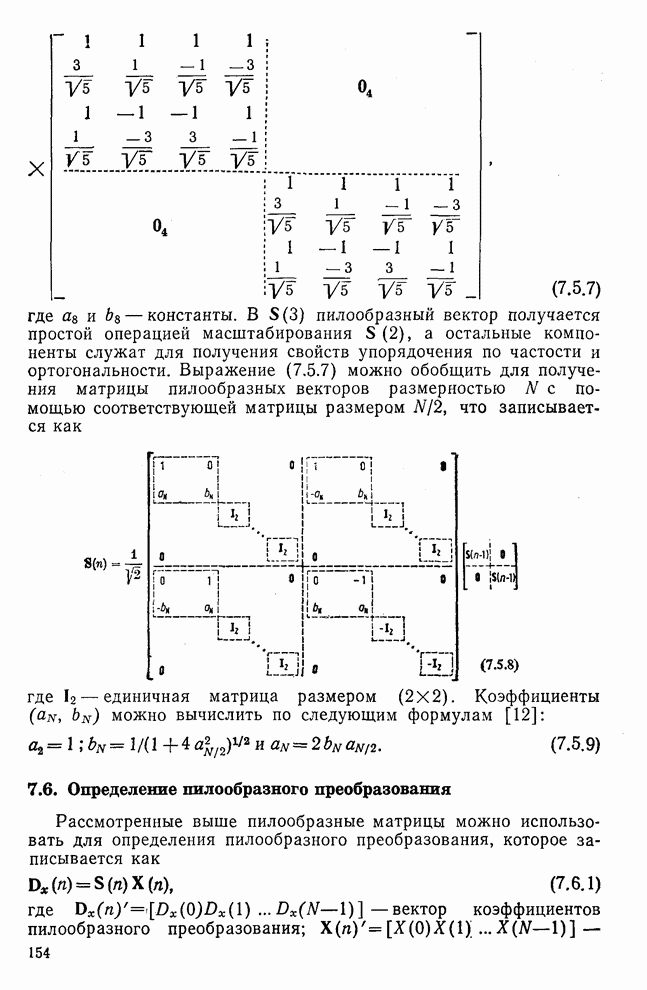
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
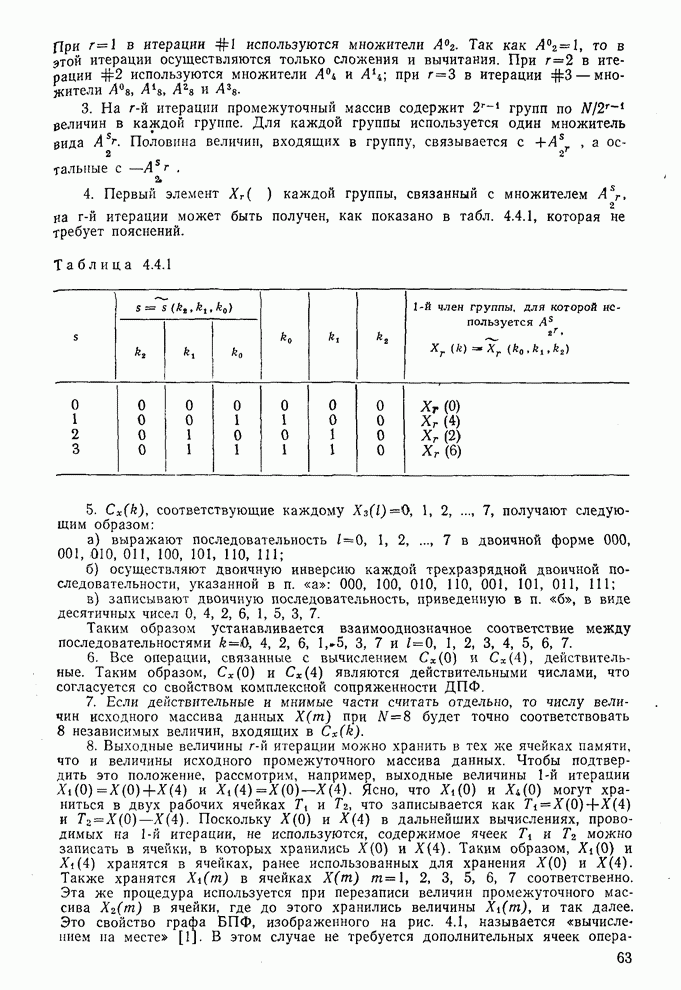
5.4. Функции Уолша
В 1923 г. Уолш [8] получил полную систему  прямоугольных функций, которая дополняет систему функций Радемахера и известна теперь как система функций Уолша. Множество функций Уолша обычно разделяется на три группы,
прямоугольных функций, которая дополняет систему функций Радемахера и известна теперь как система функций Уолша. Множество функций Уолша обычно разделяется на три группы,  порядком расположения отдельных функций в системе. Общеприняты следующие упорядочения: 1) упорядочение по частости (по Уолшу); 2) диадическое упорядочение (по Пэли); 3) естественное упорядочение (по Адамару). Ниже каждое из этих упорядочений рассмотрено отдельно.
порядком расположения отдельных функций в системе. Общеприняты следующие упорядочения: 1) упорядочение по частости (по Уолшу); 2) диадическое упорядочение (по Пэли); 3) естественное упорядочение (по Адамару). Ниже каждое из этих упорядочений рассмотрено отдельно.
Упорядочение по частости или по Уолшу. Это упорядочение  предложено Уолшем [8]. Будем обозначать множество функций Уолша, упорядоченных таким образом через
предложено Уолшем [8]. Будем обозначать множество функций Уолша, упорядоченных таким образом через

где  нижний индекс w обозначает упорядочение по Уолшу, a i соответствует
нижний индекс w обозначает упорядочение по Уолшу, a i соответствует  -му элементу
-му элементу  . Если через
. Если через  обозначить частость
обозначить частость  , то
, то  определяется как
определяется как

Функции  и
и  , соответствующие
, соответствующие  , описываются следующим образом:
, описываются следующим образом:

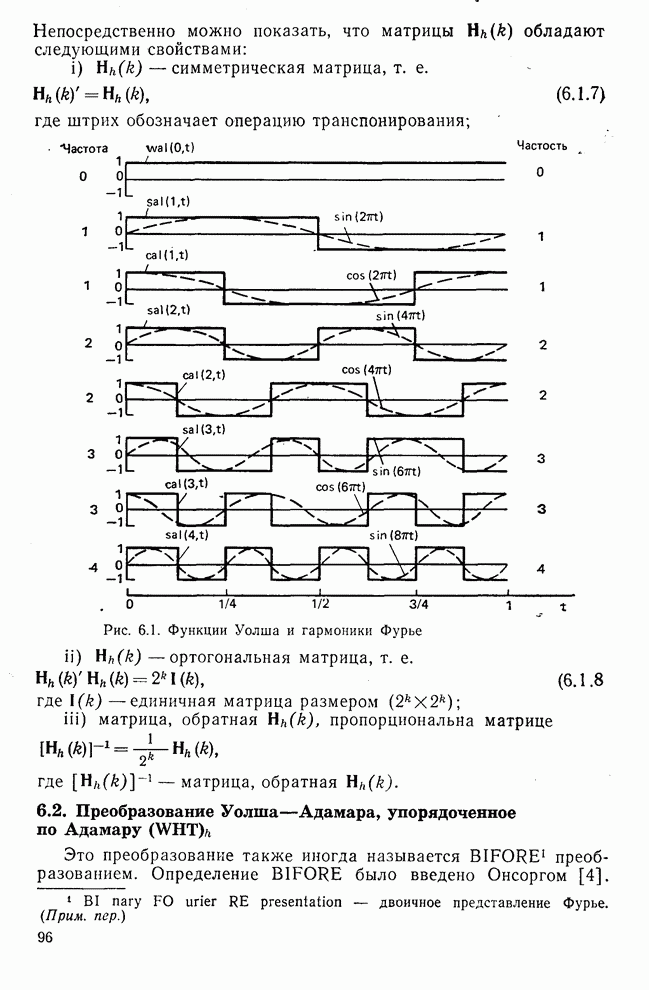
Первые восемь функций Уолша в указанных выше обозначениях приведены на рис. 5.5а, из которого видно, что частость следующей функции Уолша больше или равняется частости предыдущей функции Уолша и имеет точно на одно пересечение нулевого уровня больше в открытом интервале  . Отсюда и следует название упорядочение по частости. Элемент
. Отсюда и следует название упорядочение по частости. Элемент  можно получить из множества функций Радемахера при использовании кода Грея [9] (см. задачу 5.1).
можно получить из множества функций Радемахера при использовании кода Грея [9] (см. задачу 5.1).
Дискретный случай. Дискретизация функций Уолша, изображенных на рис. 5.5а, в восьми равноотстоящих точках приводит к матрице  , показанной на рис. 5.5б. В общем случае получается матрица
, показанной на рис. 5.5б. В общем случае получается матрица  . Такие матрицы будем обозначать
. Такие матрицы будем обозначать  , так как они получаются в результате переупорядочения строк матриц Адамара.
, так как они получаются в результате переупорядочения строк матриц Адамара.
Пусть  и
и  цифры
цифры  -го разряда в двоичном представлении целых чисел и
-го разряда в двоичном представлении целых чисел и  соответственно, т. е.
соответственно, т. е.

Тогда элементы  матрицы
матрицы  имеют вид
имеют вид
 (5.4.4)
(5.4.4)
где


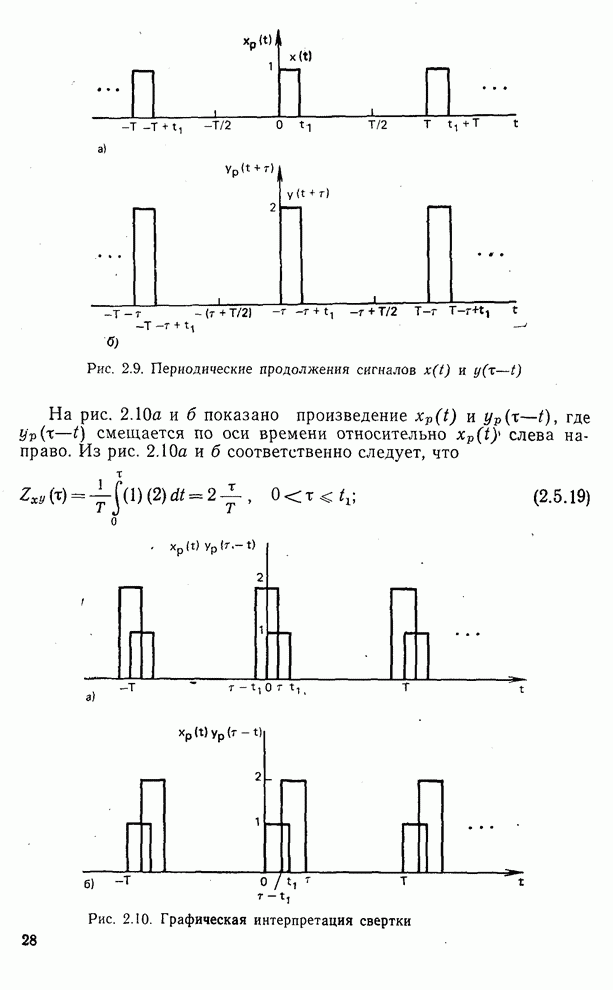
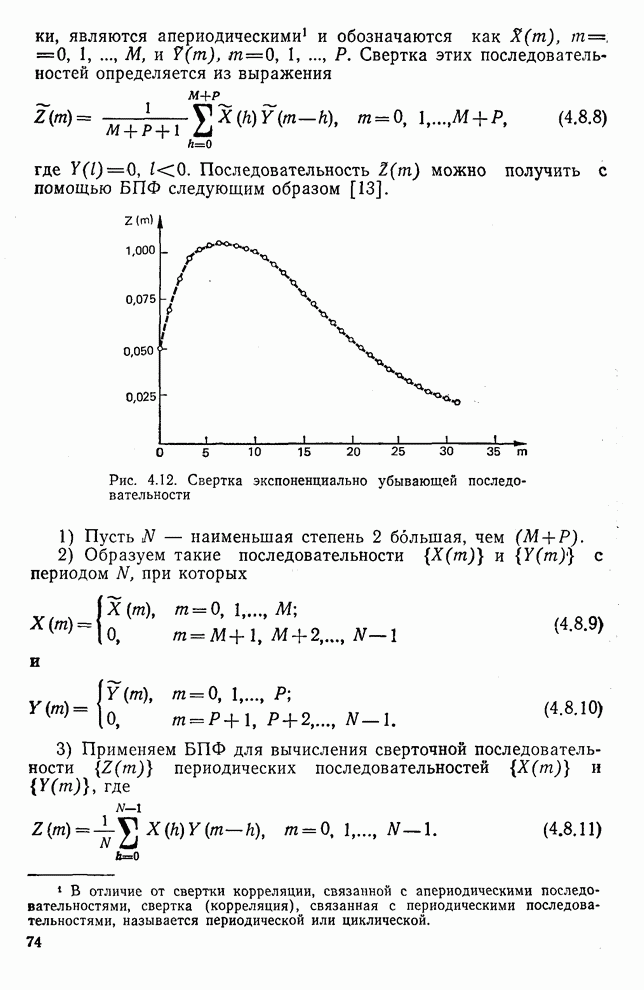
Рис. 5.5. Функции Уолша, упорядоченные по Уолшу, при  : а — непрерывные; б — дискретные
: а — непрерывные; б — дискретные
Диадическое упорядочение или упорядочение по Пэли. Диадическое упорядочение было введено Пэли [11]. Функции Уолша являются элементами диадической группы и могут быть упорядочены с помощью кода Грея [9, 12]. Данное множество функций Уолша обозначается как
 (5.4.5)
(5.4.5)
где индекс  обозначает упорядочение по Пэли, a i обозначает
обозначает упорядочение по Пэли, a i обозначает  элемент
элемент  . Множество
. Множество  связано с множеством
связано с множеством  , упорядоченным по Уолшу, соотношением
, упорядоченным по Уолшу, соотношением
 (5.4.6)
(5.4.6)
где  — переход от кода Грея к двоичному коду с индексом Алгоритм преобразования, соответствующий (5.4.6), и его осуществление рассмотрены в [12]. Проиллюстрируем соотношение (5.4.6) на примере
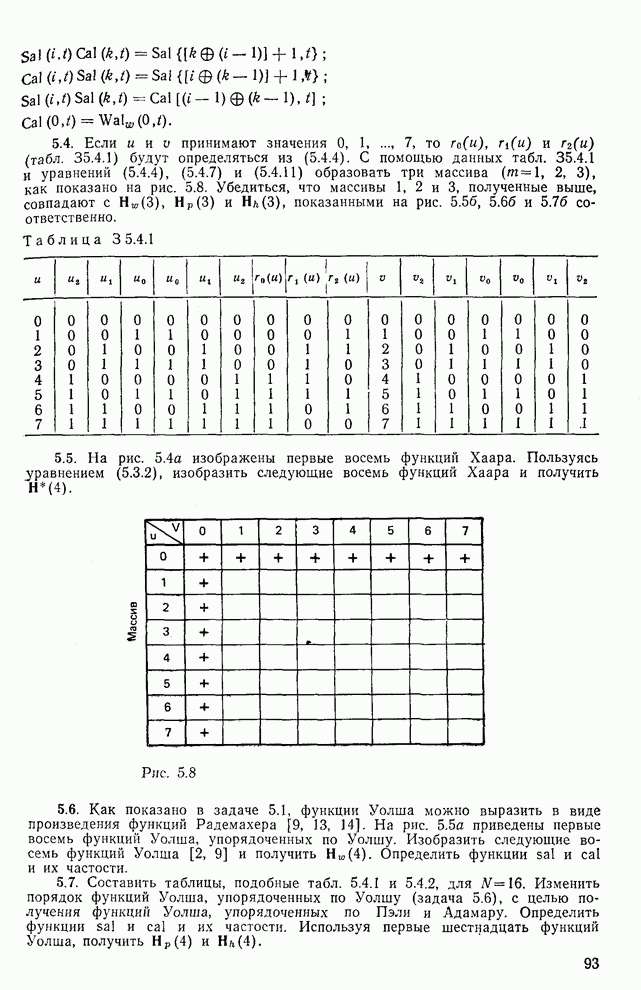
— переход от кода Грея к двоичному коду с индексом Алгоритм преобразования, соответствующий (5.4.6), и его осуществление рассмотрены в [12]. Проиллюстрируем соотношение (5.4.6) на примере  . Соответствующие результаты приведены в табл. 5.4.1. Применяя данные табл. 5.4.1 к функциям
. Соответствующие результаты приведены в табл. 5.4.1. Применяя данные табл. 5.4.1 к функциям  ,
,  , показанным на рис. 5.5а, получаем восемь функций Уолша
, показанным на рис. 5.5а, получаем восемь функций Уолша  , изображенных на рис. 5.6а.
, изображенных на рис. 5.6а.
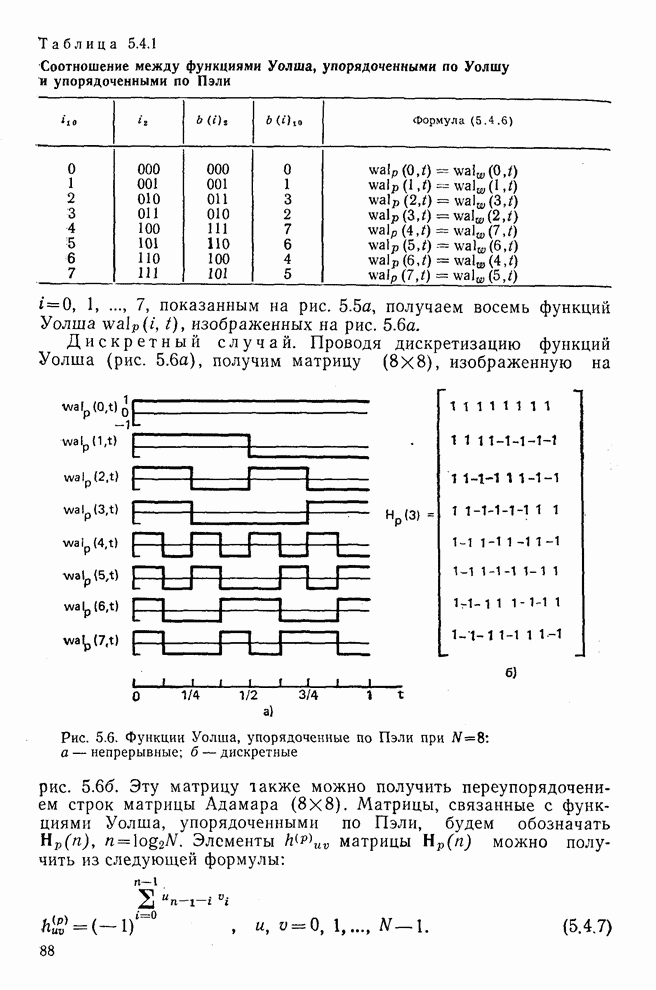
Таблица 5.4.1. Соотношение между функциями Уолша, упорядоченными по Уолшу и упорядоченными по Пэли
Дискретный случай. Проводя дискретизацию функций Уолша (рис. 5.6а), получим матрицу  , изображенную на рис. 5.6б.
, изображенную на рис. 5.6б.

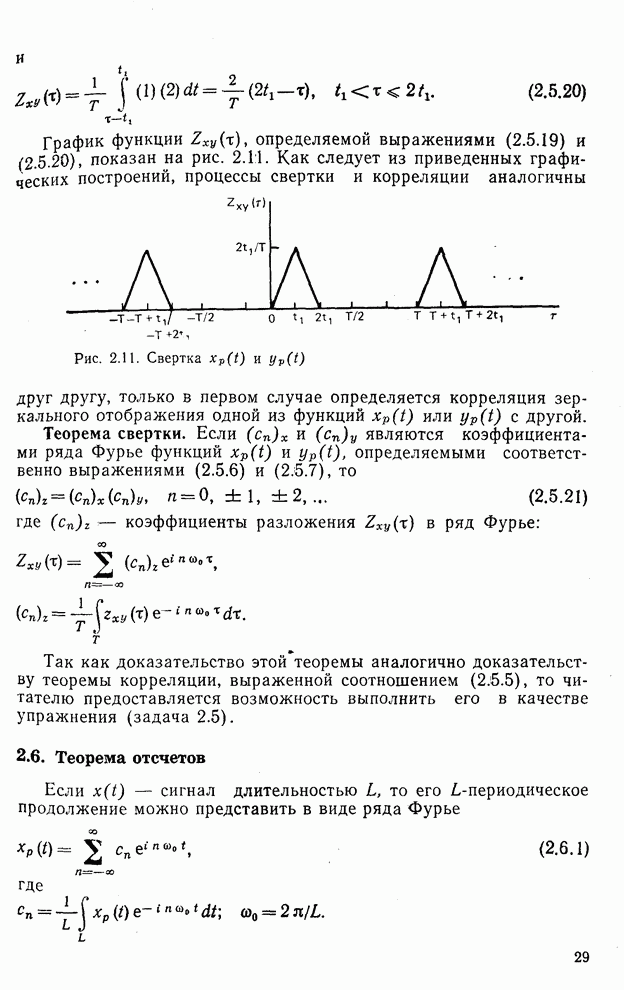
Рис. 5.6. Функции Уолша, упорядоченные по Пэли при  : а — непрерывные; б — дискретные
: а — непрерывные; б — дискретные
Эту матрицу также можно получить переупорядочением строк матрицы Адамара  . Матрицы, связанные с функциями Уолша, упорядоченными по Пэли, будем обозначать
. Матрицы, связанные с функциями Уолша, упорядоченными по Пэли, будем обозначать  . Элементы
. Элементы  матрицы
матрицы  можно получить из следующей формулы:
можно получить из следующей формулы:
 (5.4.7)
(5.4.7)
Естественное упорядочение или упорядочение по Адамару.
Множество функций Уолша обозначается следующим образом:

где индекс h обозначает упорядочение по Адамару, i обозначает  элемент
элемент  . Функции, принадлежащие
. Функции, принадлежащие  , связаны с функциями, упорядоченными по Уолшу, соотношением
, связаны с функциями, упорядоченными по Уолшу, соотношением

где  -инвертированная запись i, a
-инвертированная запись i, a  - переход от кода Грея к двоичному коду
- переход от кода Грея к двоичному коду  . Проиллюстрируем этот переход, описываемый соотношением (5.4.9) для
. Проиллюстрируем этот переход, описываемый соотношением (5.4.9) для  результаты расчета приведены в табл. 5.4.2.
результаты расчета приведены в табл. 5.4.2.
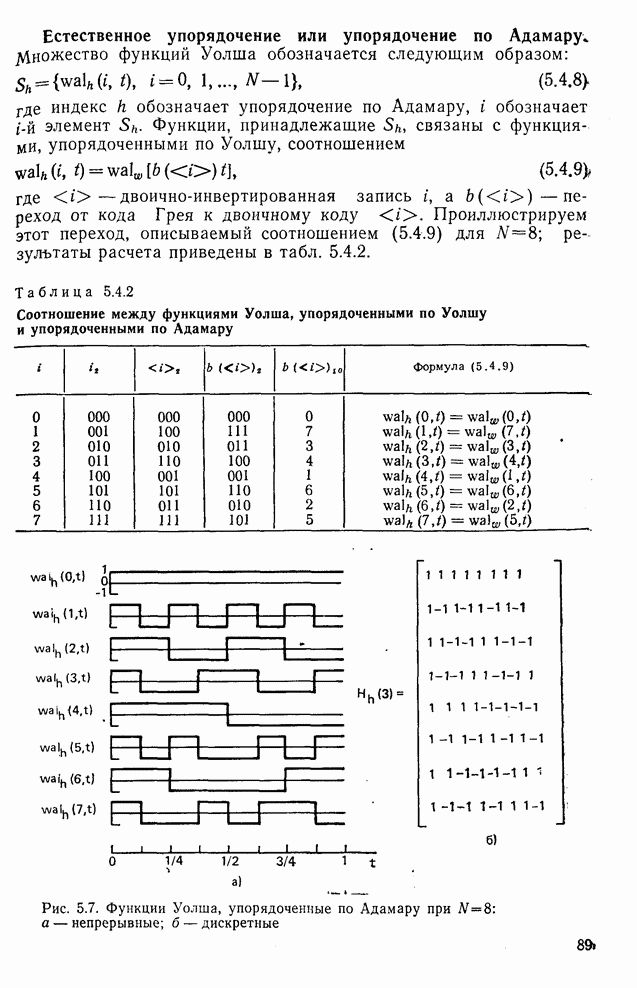
Таблица 5.4.2. Соотношение между функциями Уолша, упорядоченными по Уолшу и упорядоченными по Адамару

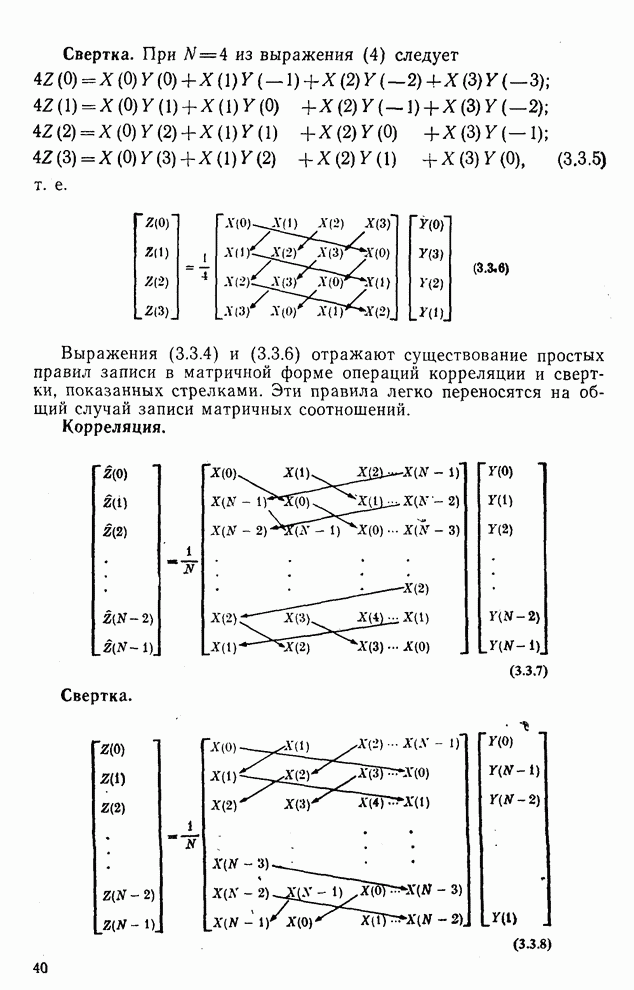
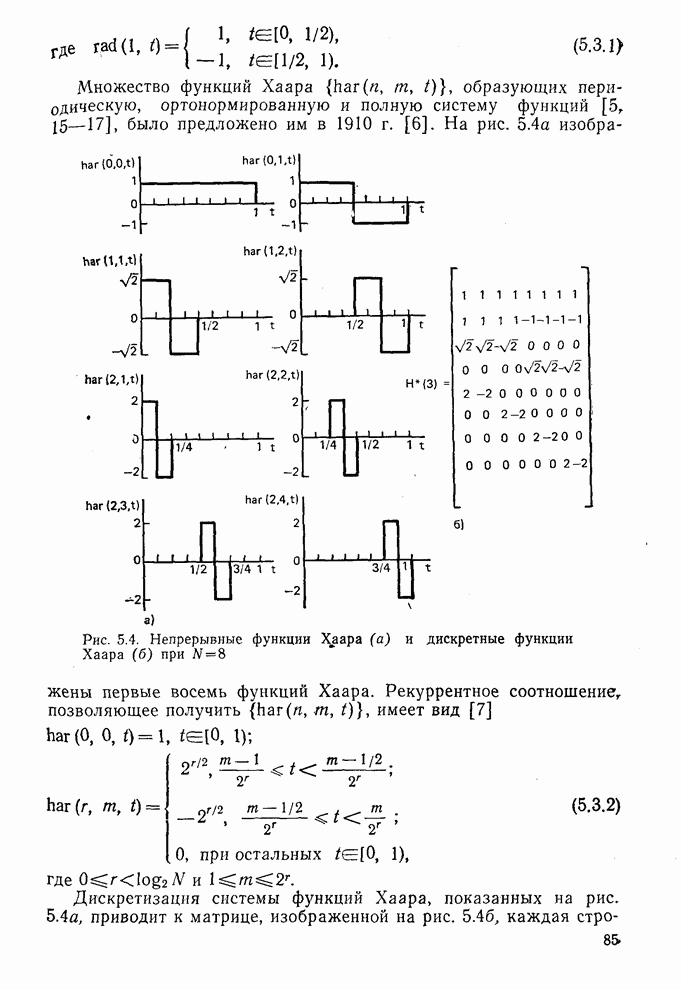
Рис. 5.7. Функции Уолша, упорядоченные по Адамару при  : а — непрерывные; б — дискретные
: а — непрерывные; б — дискретные
Используя данные табл. 5.4.2 и функции  (см. рис. 5.5а), получаем первые восемь функций Уолша (рис. 5.7а).
(см. рис. 5.5а), получаем первые восемь функций Уолша (рис. 5.7а).
случай. Дискретизация функций Уолша (см. рис. 5.7а) приводит к матрице Адамара  , изображенной на рис. 5.7б. В общем случае получается матрица
, изображенной на рис. 5.7б. В общем случае получается матрица  размером
размером  , где
, где  . Для этого класса матриц Адамара справедливо разбиение на подматрицы вида
. Для этого класса матриц Адамара справедливо разбиение на подматрицы вида

Такие матрицы соответствуют естественному упорядочению [10]. Элементы  матрицы
матрицы  можно получить из следующей формулы:
можно получить из следующей формулы:
 (5.4.11)
(5.4.11)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
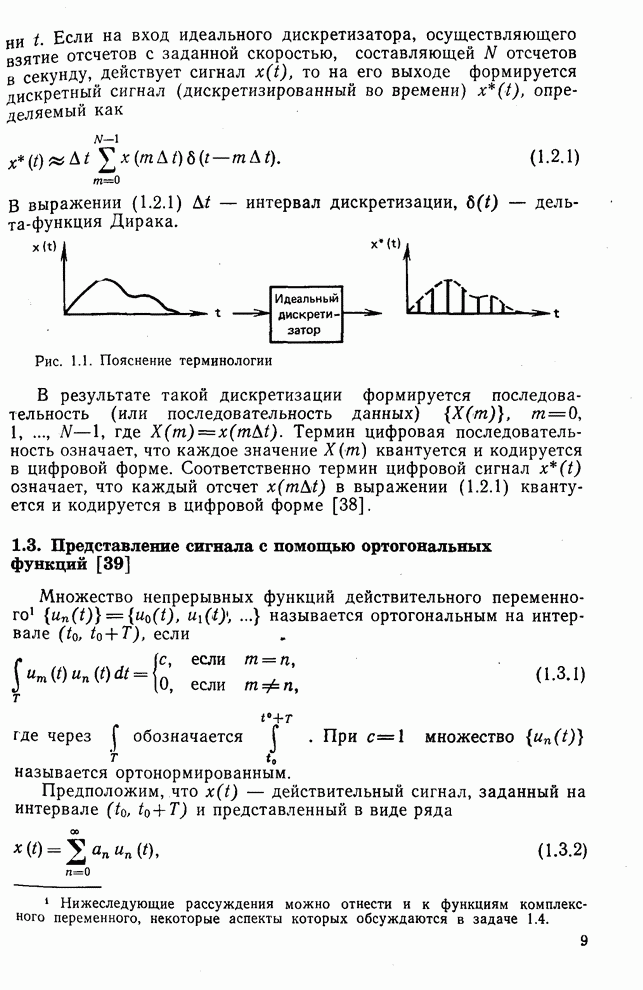
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
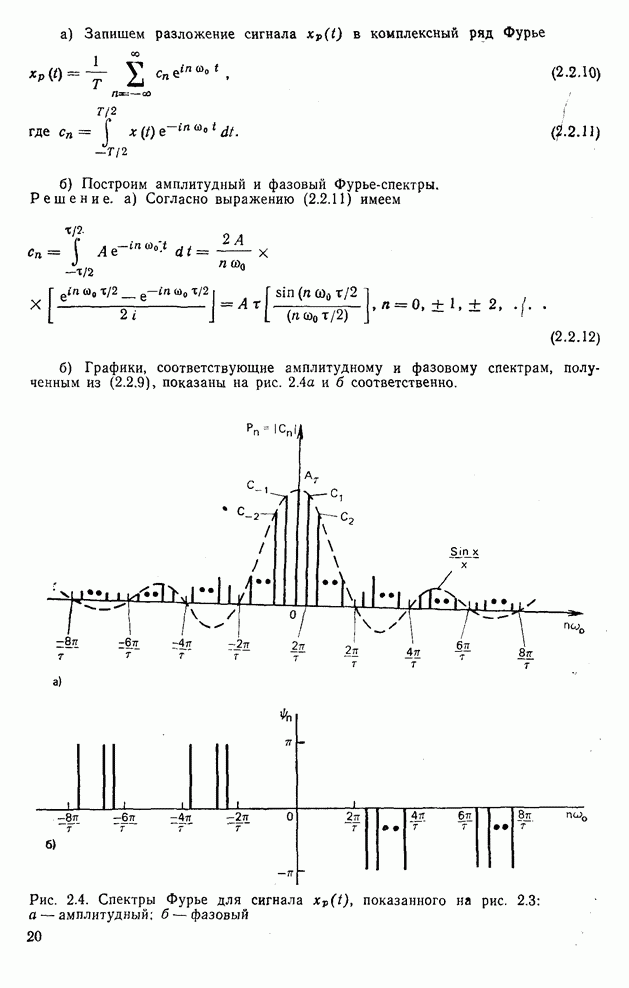
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
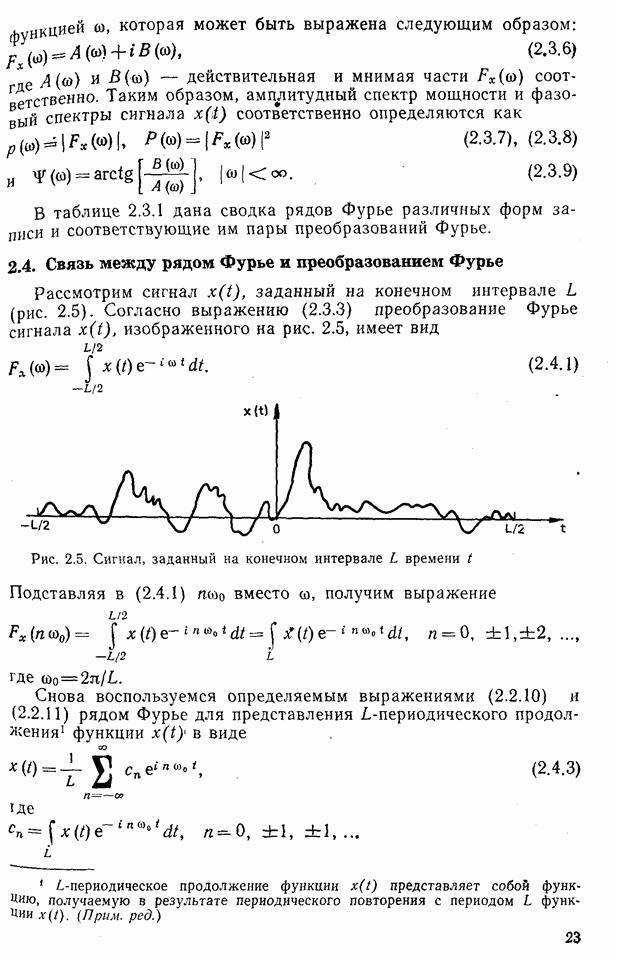
- 2.4. Связь между рядом Фурье и преобразованием Фурье
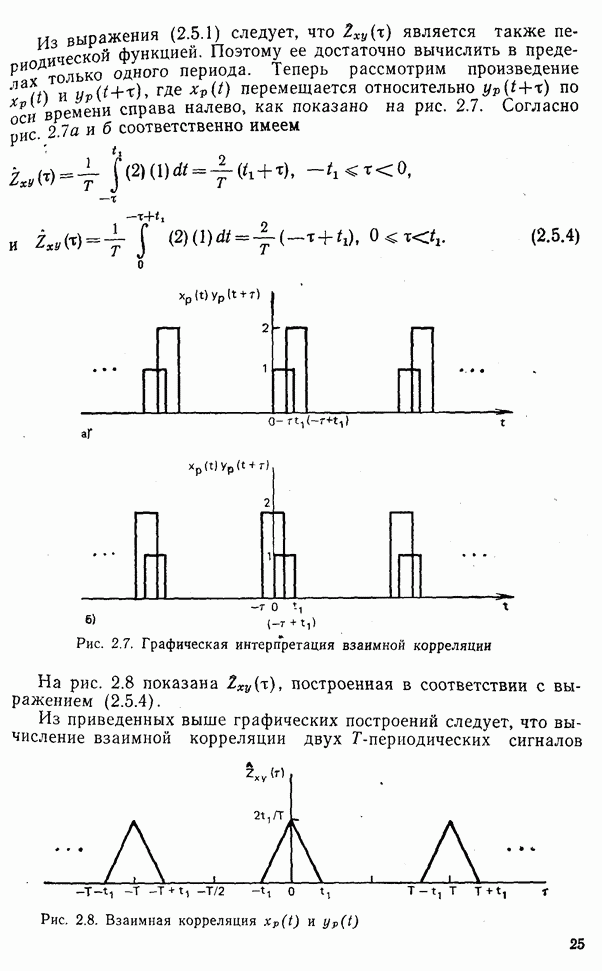
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
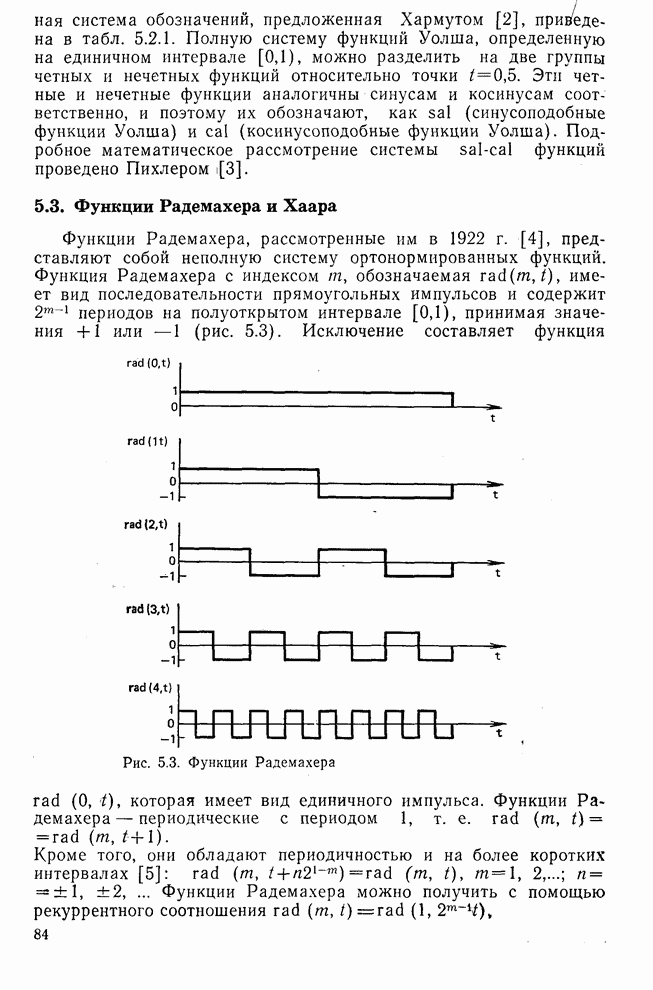
- 5.3. Функции Радемахера и Хаара
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
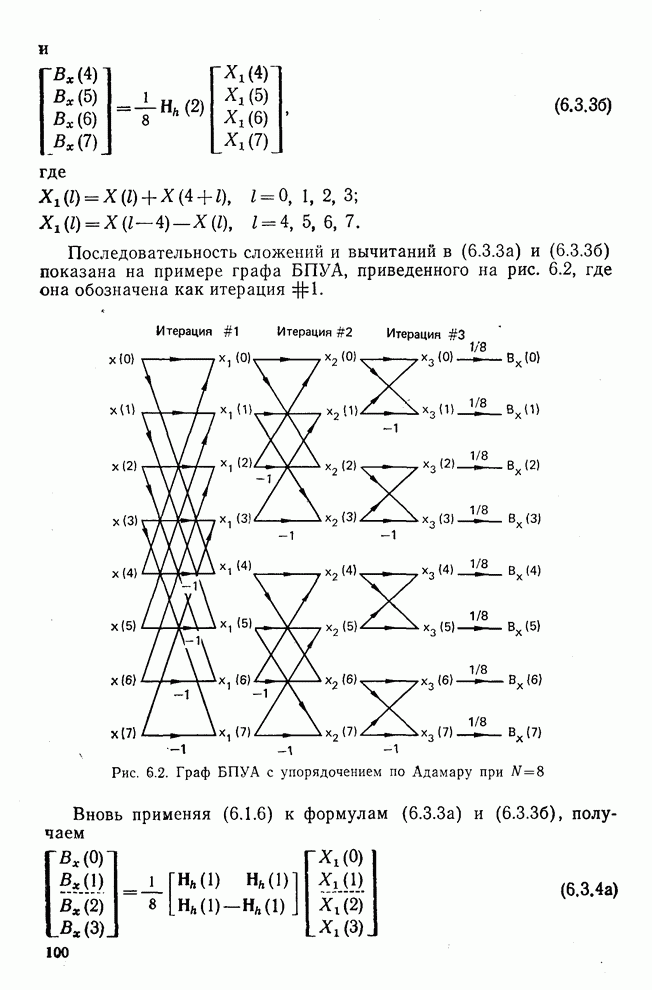
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
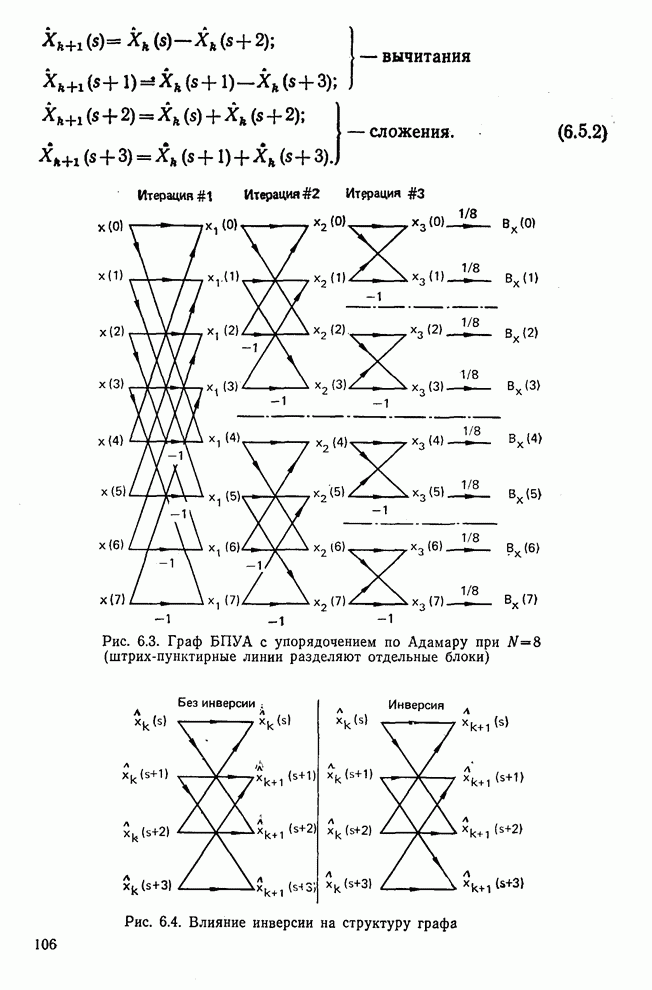
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
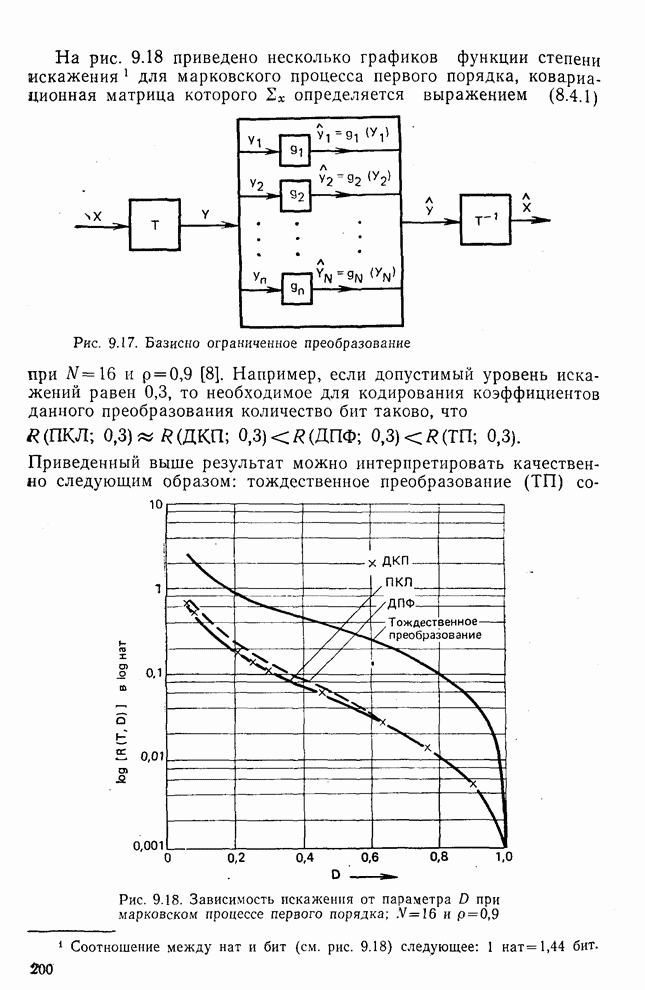
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
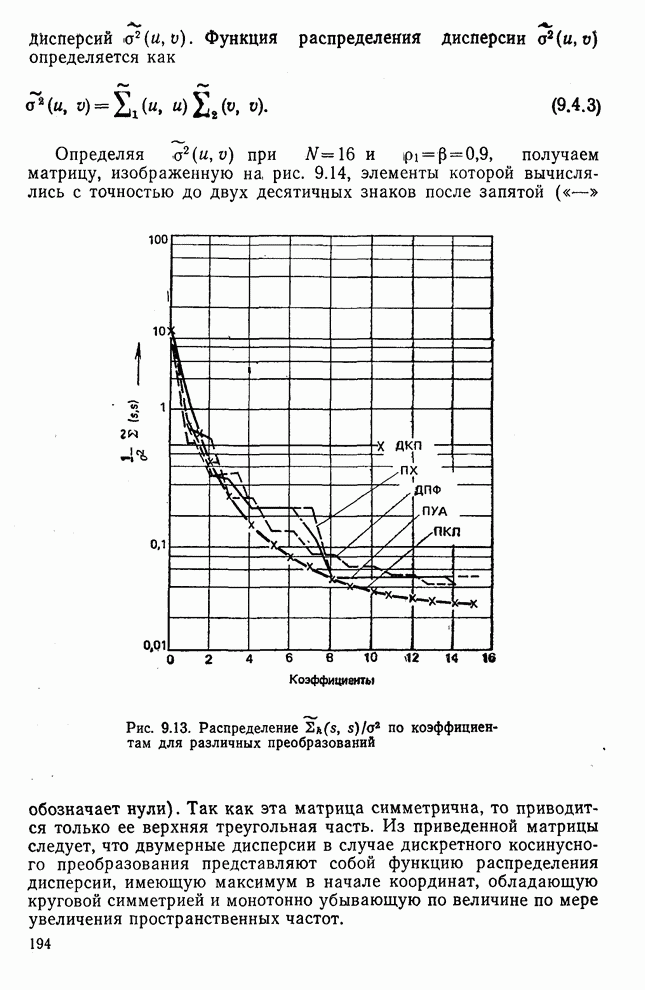
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
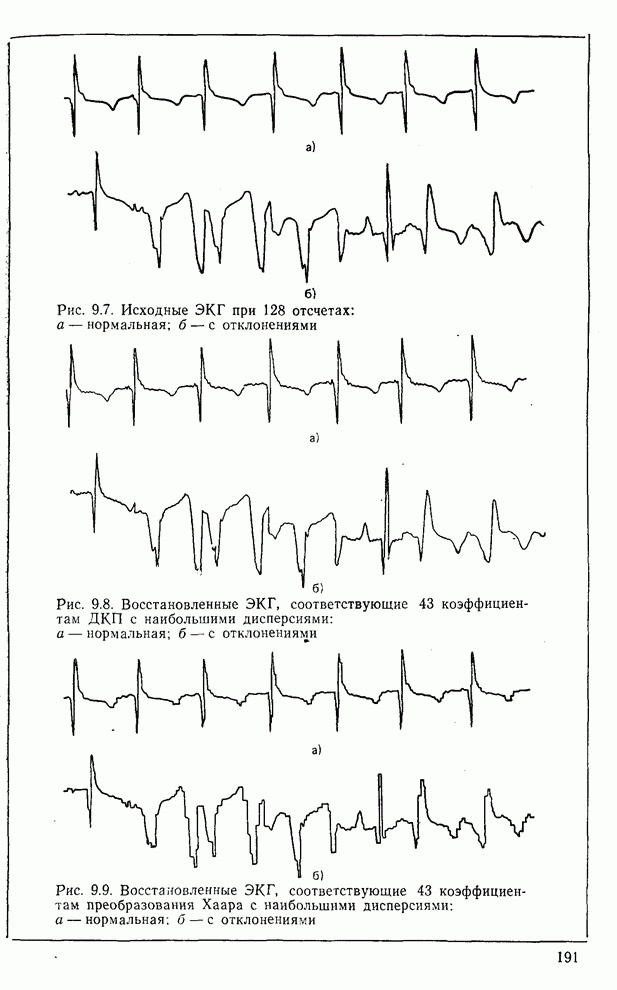
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
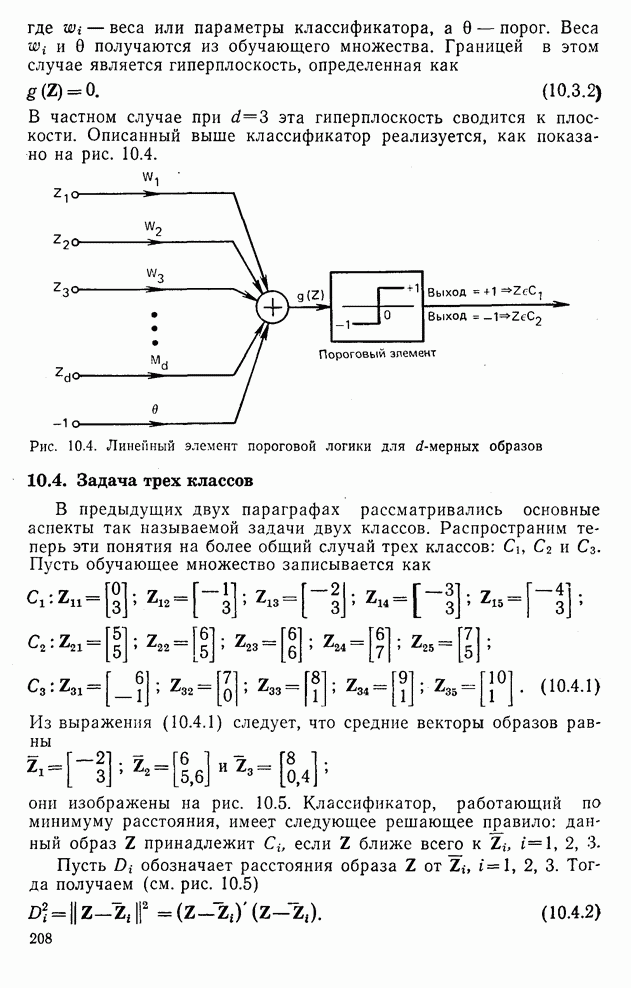
- 10.3. d-мерные образы
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
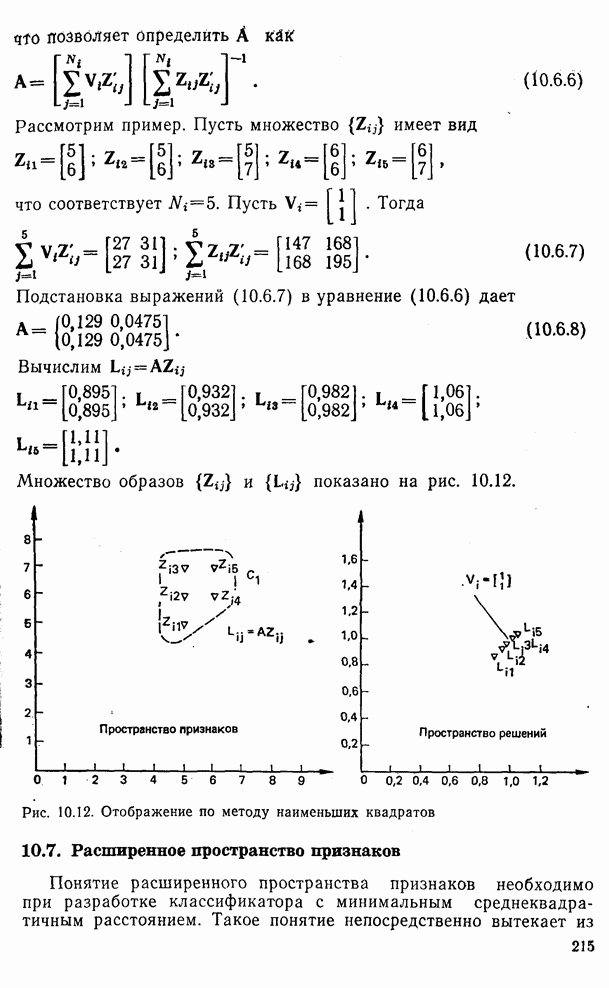
- 10.6. Метод отображения по методу наименьших квадратов
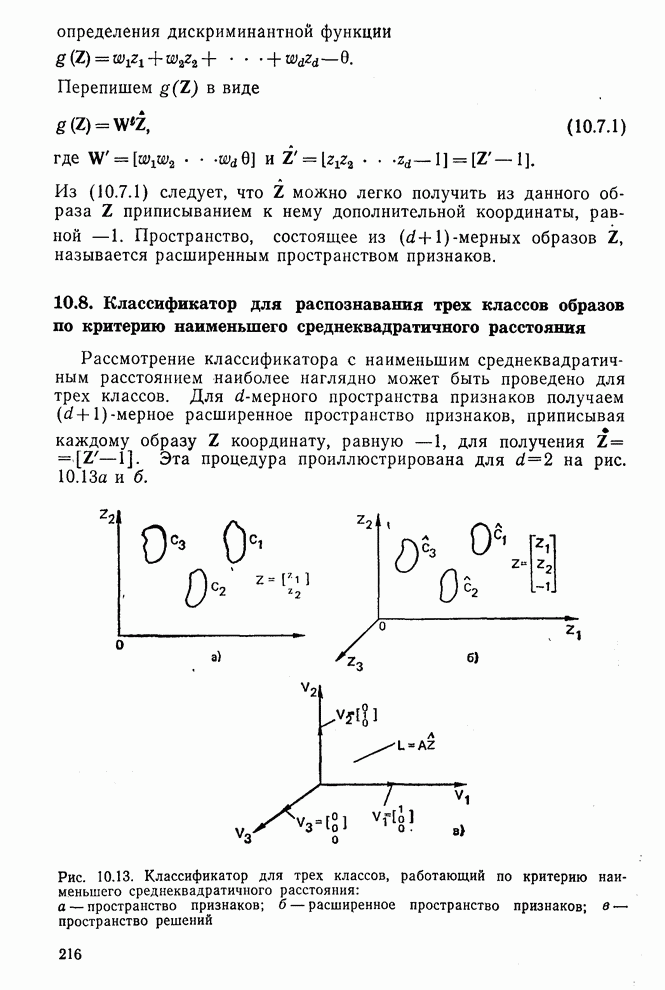
- 10.7. Расширенное пространство признаков
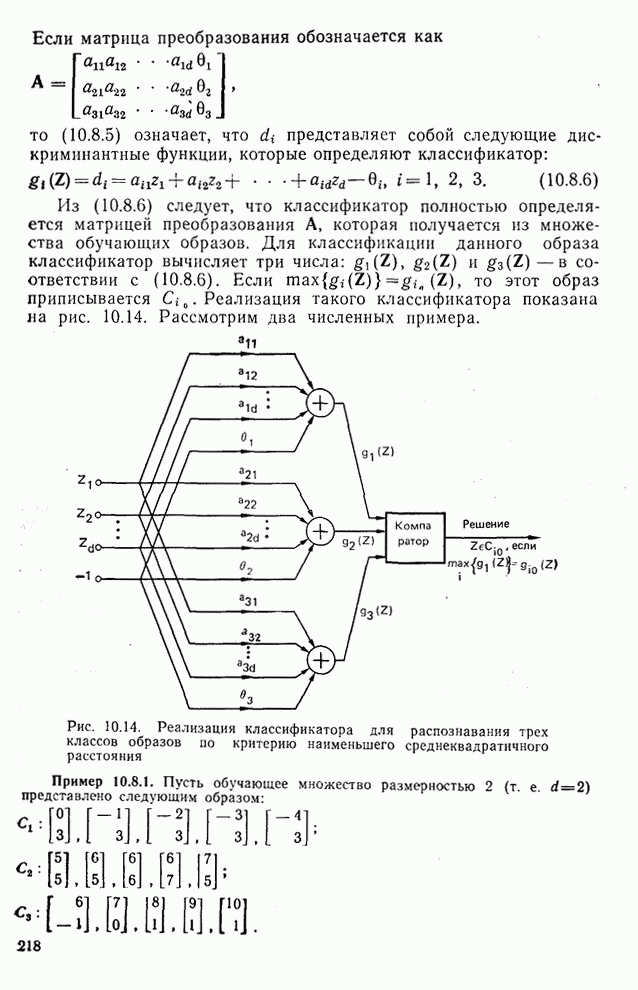
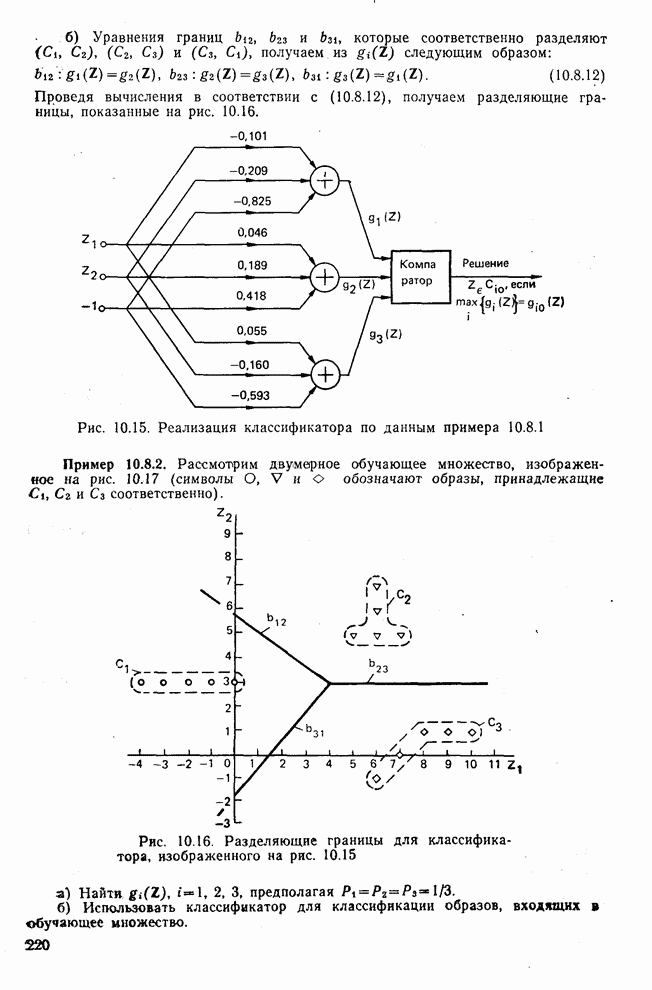
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
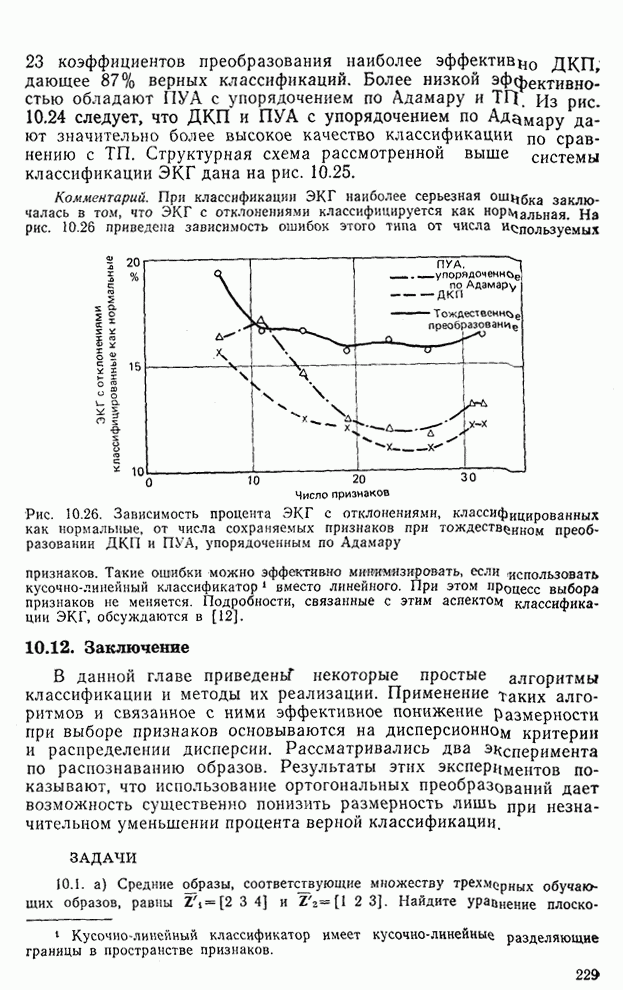
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ