| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.6. Теорема отсчетов
Если  — сигнал длительностью L, то его
— сигнал длительностью L, то его  -периодическое продолжение можно представить в виде ряда Фурье
-периодическое продолжение можно представить в виде ряда Фурье
 (2.6.1)
(2.6.1)
где

Из выражения (2.6.1) следует, что для точного описания  необходимо бесконечное число коэффициентов ряда
необходимо бесконечное число коэффициентов ряда  . Поэтому в строгом математическом смысле не существует сигнала
. Поэтому в строгом математическом смысле не существует сигнала  конечной длительности L, для которого
конечной длительности L, для которого
 (2.6.2)
(2.6.2)
где N — некоторое конечное положительное число. Однако известно, что во всех реальных ситуациях передаточная функция любой физически реализуемой системы спадает до нуля «на очень высоких» частотах. Примерами таких систем являются механизмы речеобразования, слуха и зрения человека, различные системы связи. Поэтому можно предположить, что для достаточно больших N условие (2.6.2) выполняется. Сигналы такого типа называются ограниченными по полосе и имеют полосу, равную 
По существу, теорема отсчетов утверждает, что сигнал  с ограниченной полосой, равной В, Гц, может быть однозначно восстановлен по отсчетам, взятым с частотой
с ограниченной полосой, равной В, Гц, может быть однозначно восстановлен по отсчетам, взятым с частотой  отсчетов в секунду, где
отсчетов в секунду, где  . Таким образом, эта теорема дает возможность оперировать с цифровым сигналом
. Таким образом, эта теорема дает возможность оперировать с цифровым сигналом  , соответствующим непрерывному сигналу
, соответствующим непрерывному сигналу  . Ниже приводится доказательство теоремы отсчетов.
. Ниже приводится доказательство теоремы отсчетов.
Теорема. Если  — такой сигнал длительности L, что разложение в ряд Фурье его
— такой сигнал длительности L, что разложение в ряд Фурье его  -периодического продолжения не содержит гармоник выше номера
-периодического продолжения не содержит гармоник выше номера  , то
, то  полностью определяется множеством значений
полностью определяется множеством значений
 (2.6.3)
(2.6.3)
Кроме того, он может быть восстановлен по этим значениям следующим образом:
 (2.6.4)
(2.6.4)
Доказательство. Представление  рядом Фурье имеет вид
рядом Фурье имеет вид
 (2.6.5)
(2.6.5)
Подставляя  в выражение (2.6.5), получаем
в выражение (2.6.5), получаем

где  . Умножая обе части выражения (2.6.6) на
. Умножая обе части выражения (2.6.6) на  по и суммируя по k в пределах от 0 до N, получаем
по и суммируя по k в пределах от 0 до N, получаем
 (2.6.7)
(2.6.7)
Теперь можно показать, что множество функций  является ортогональным, т. е.
является ортогональным, т. е.

Таким образом, из выражений (2.6.7) и (2.6.8) следует, что

т.е.
 (2.6.9)
(2.6.9)
Из выражения (2.6.9) следует, что  определяется N отсчетными значениями
определяется N отсчетными значениями  , взятыми согласно выражению (2.6.3). Подставляя выражение (2.6.9) в выражение (2.6.5), получаем
, взятыми согласно выражению (2.6.3). Подставляя выражение (2.6.9) в выражение (2.6.5), получаем

Так как  , то из (2.6.10) вытекает
, то из (2.6.10) вытекает

Пусть  , тогда выражение
, тогда выражение  можно переписать в следующем виде:
можно переписать в следующем виде:

В выражении (2.6.11б)
 (2.6.12)
(2.6.12)
Если теперь воспользоваться тригонометрическим тождеством
 (2.6.13)
(2.6.13)
и подставить (2.6.12) и (2.6.13) в выражение (2.6.11б), то получим

Подставляя  и
и  в (2.6.14), получаем результат, который требовалось доказать:
в (2.6.14), получаем результат, который требовалось доказать:

На основании этого можно сделать следующие выводы.
1. Теорема отсчетов устанавливает минимальную частоту отсчетов, которая гарантирует сохранение всей информации, содержащейся в сигнале  любая частота отсчетов выше минимальной также сохраняет информацию. Поскольку минимальное количество отсчетов на интервале времени L равно
любая частота отсчетов выше минимальной также сохраняет информацию. Поскольку минимальное количество отсчетов на интервале времени L равно  , то временной интервал
, то временной интервал  между двумя соседними отсчетами должен удовлетворять условию
между двумя соседними отсчетами должен удовлетворять условию
 (2.6.15)
(2.6.15)
2. Так как  — полоса сигнала, где
— полоса сигнала, где  — основная частота, то неравенство (2.6.15) можно записать в следующем виде:
— основная частота, то неравенство (2.6.15) можно записать в следующем виде:
 (2.6.16)
(2.6.16)
3. Выражение (2.6.16) означает, что частота отсчетов  должна удовлетворять условию
должна удовлетворять условию  , которое при
, которое при  принимает следующий вид:
принимает следующий вид:  выборок в секунду (2.6.17).
выборок в секунду (2.6.17).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
- 2.4. Связь между рядом Фурье и преобразованием Фурье
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
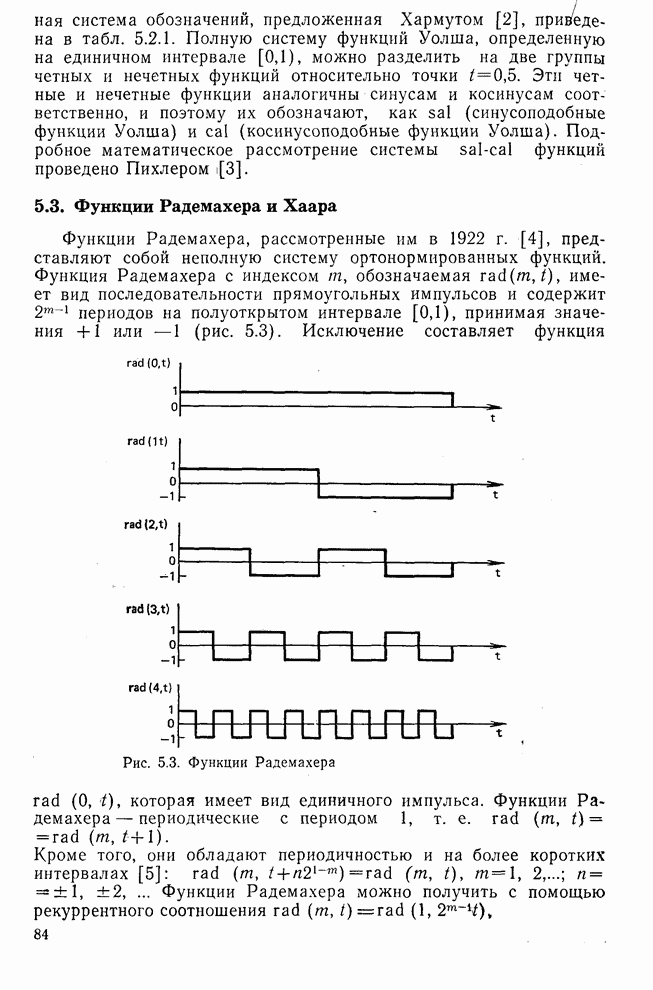
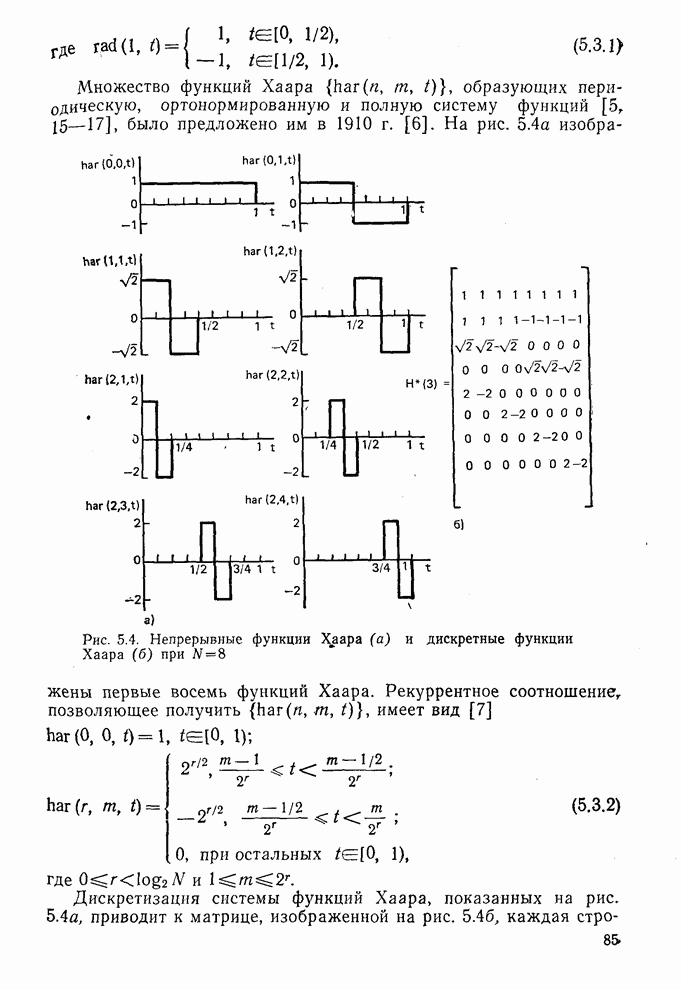
- 5.3. Функции Радемахера и Хаара
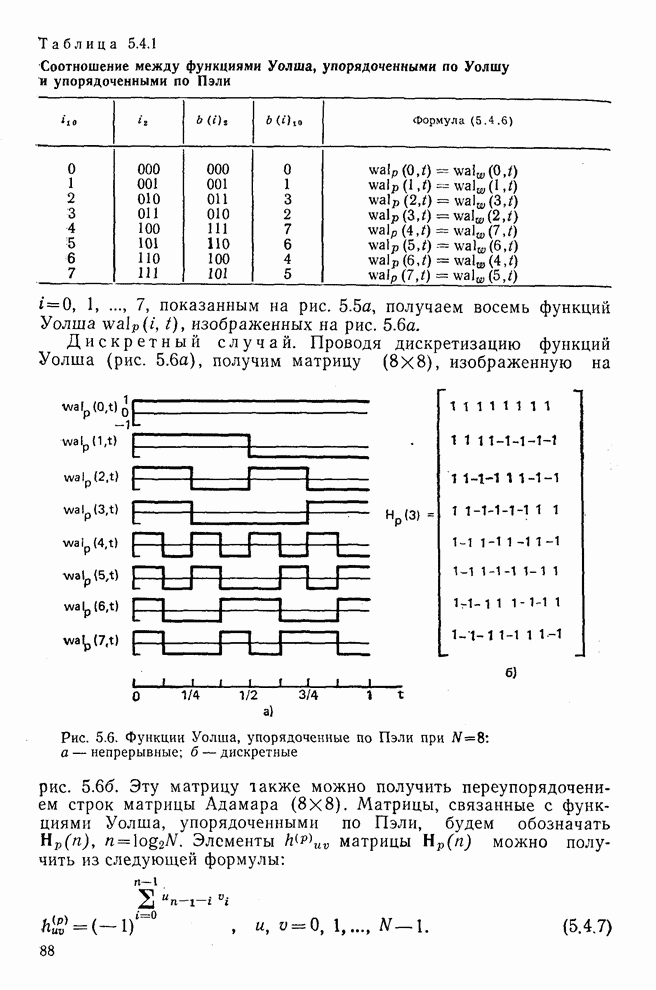
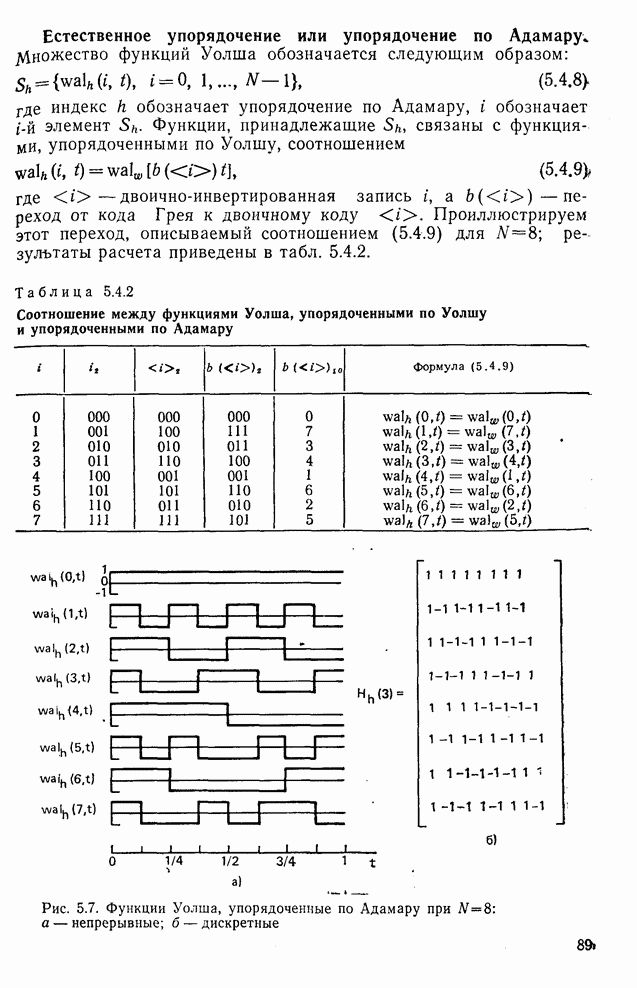
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
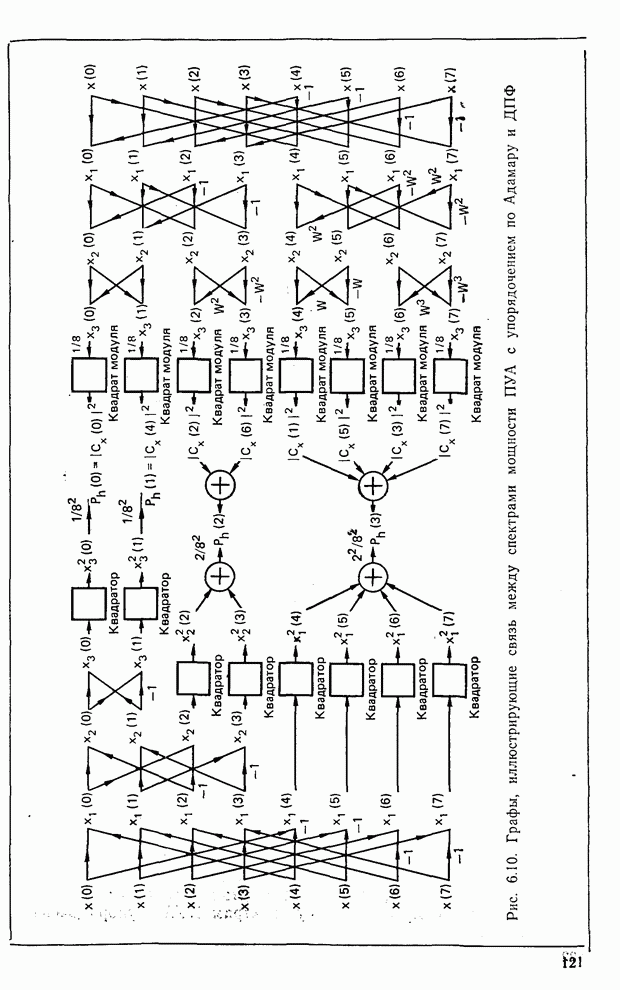
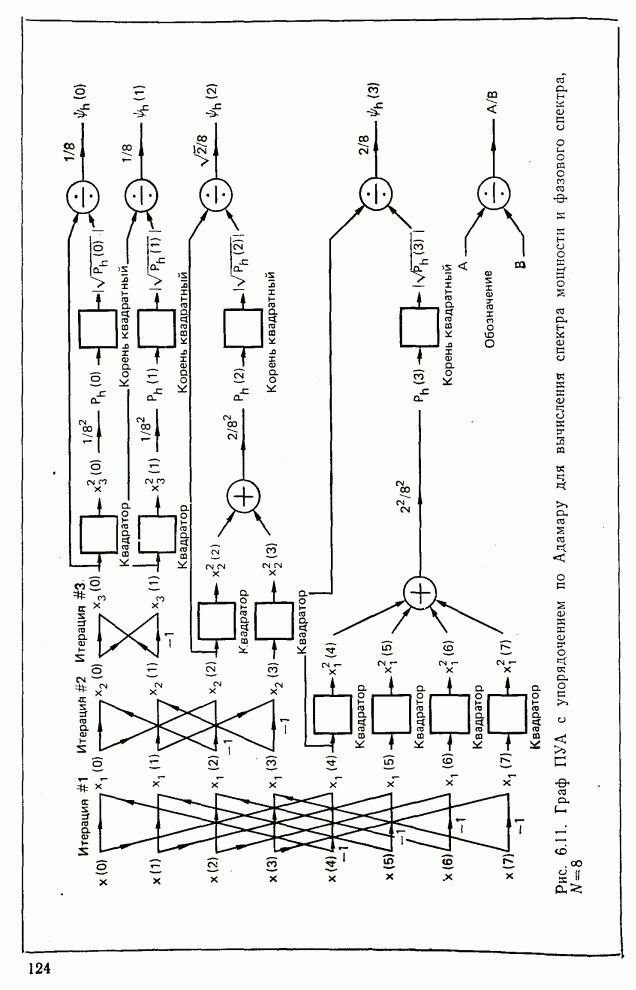
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
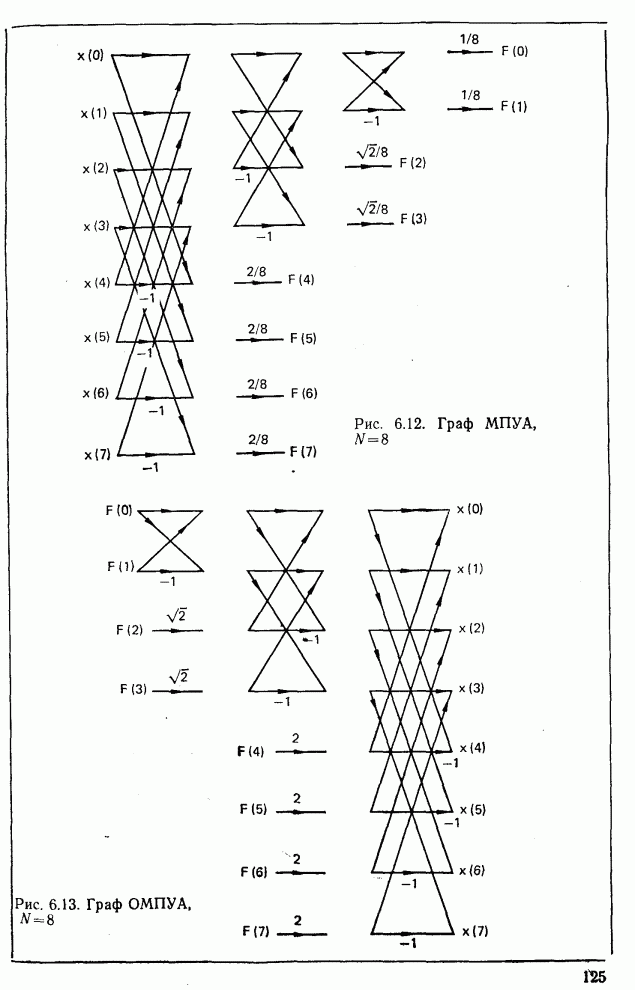
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
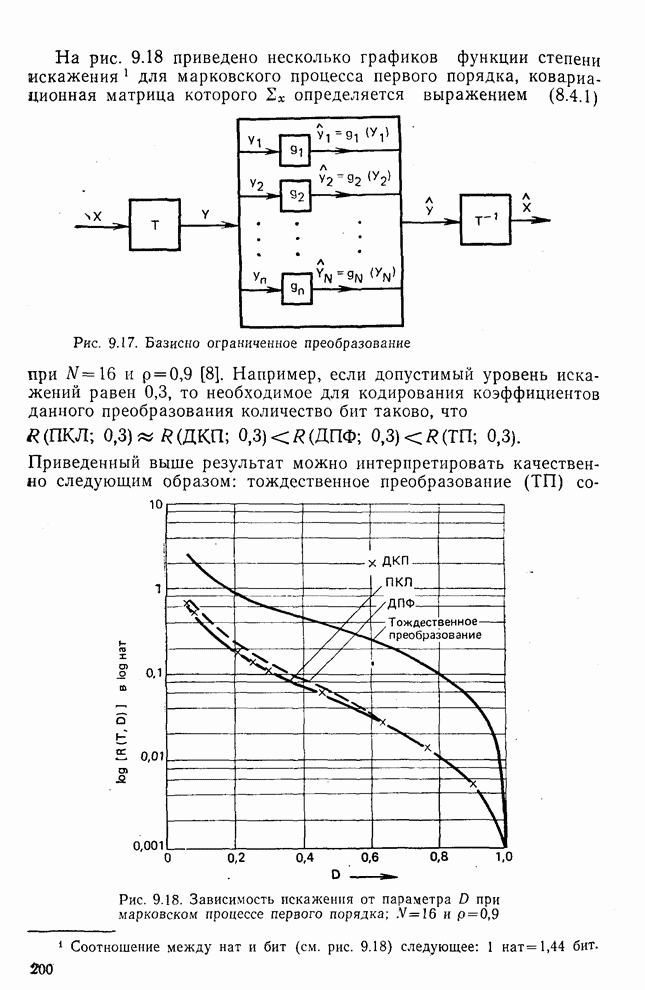
- 9.1. Поиск оптимального преобразования
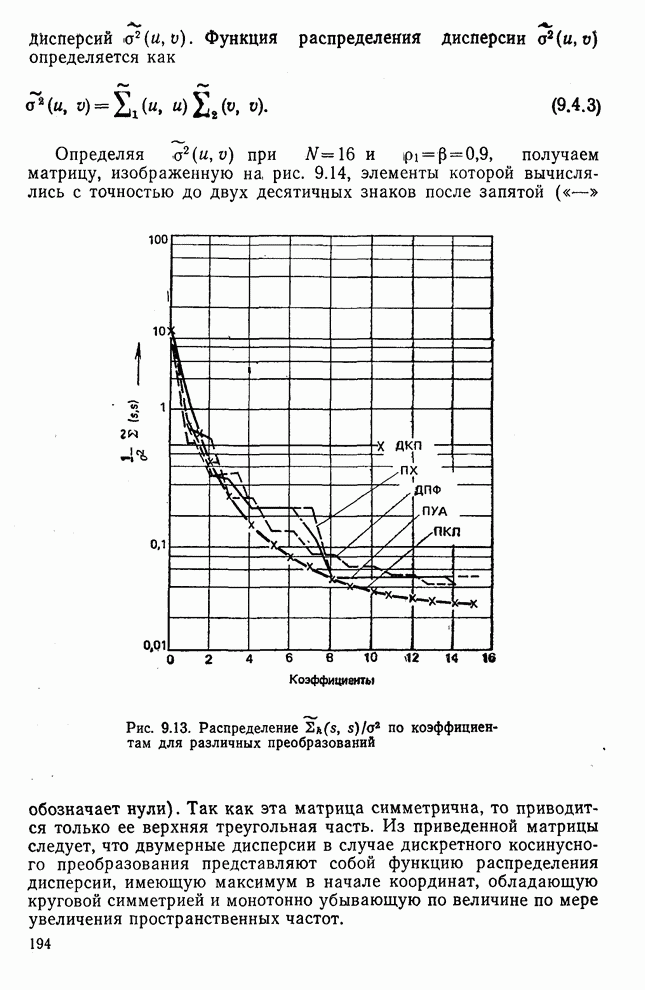
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
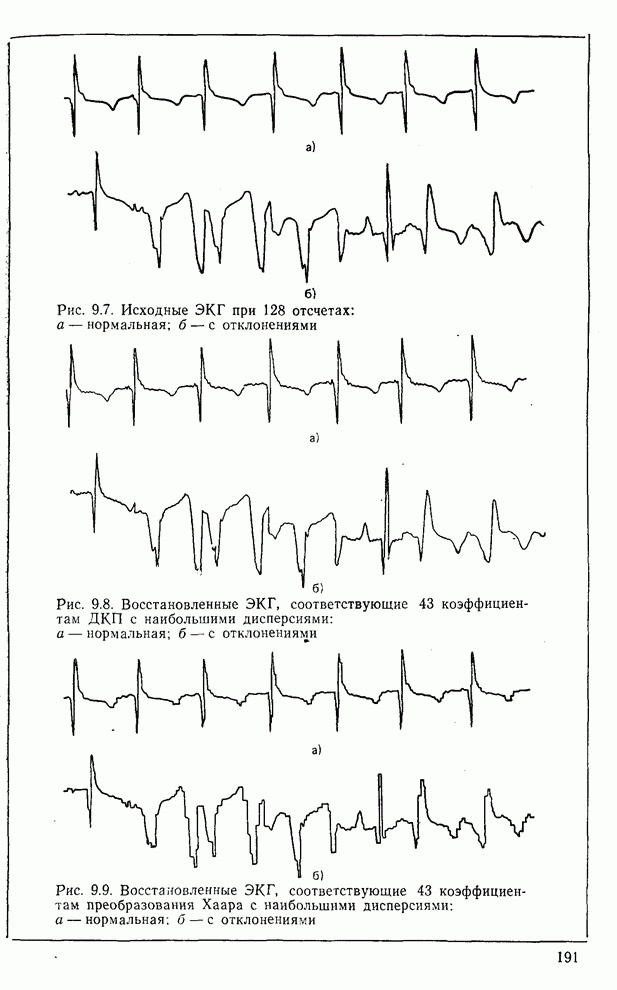
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
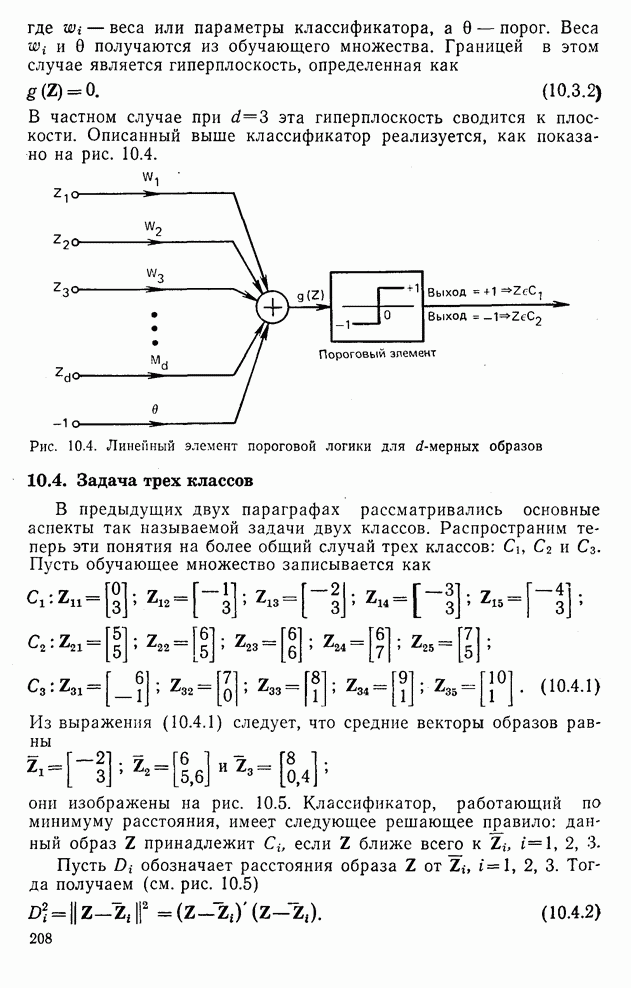
- 10.3. d-мерные образы
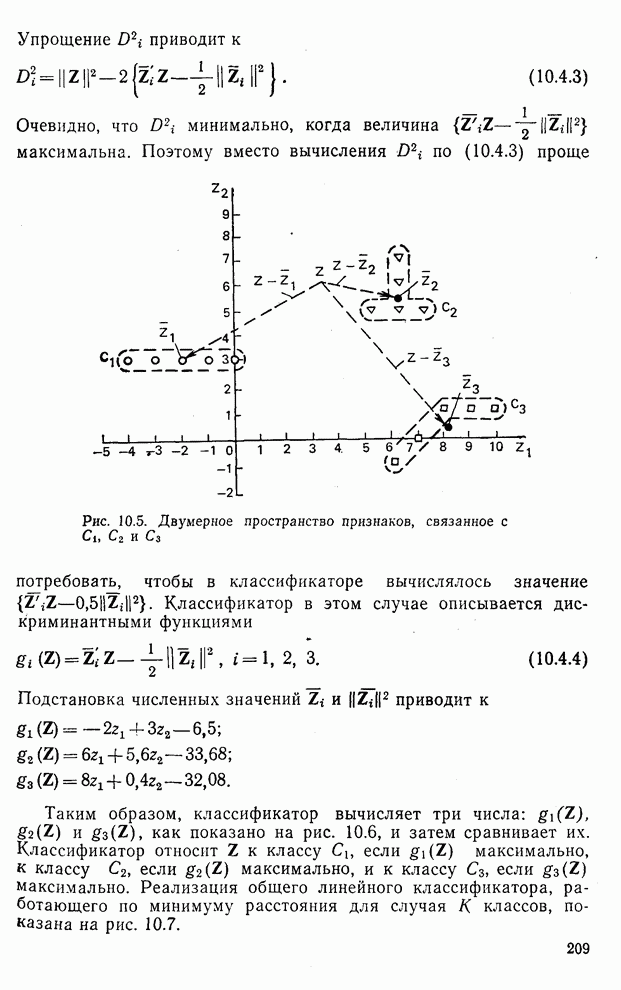
- 10.4. Задача трех классов
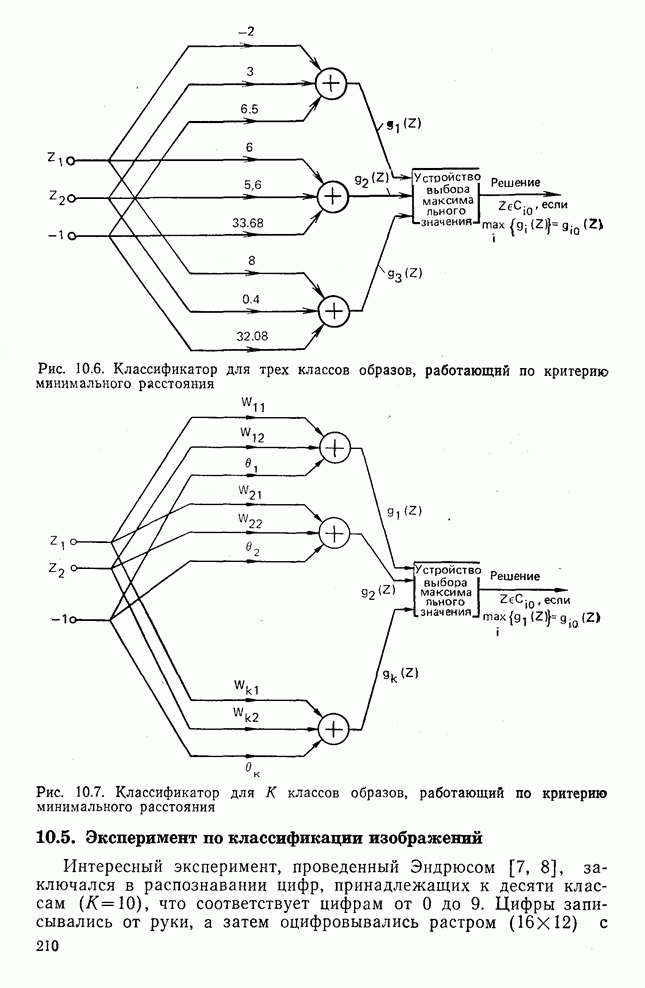
- 10.5. Эксперимент по классификации изображений
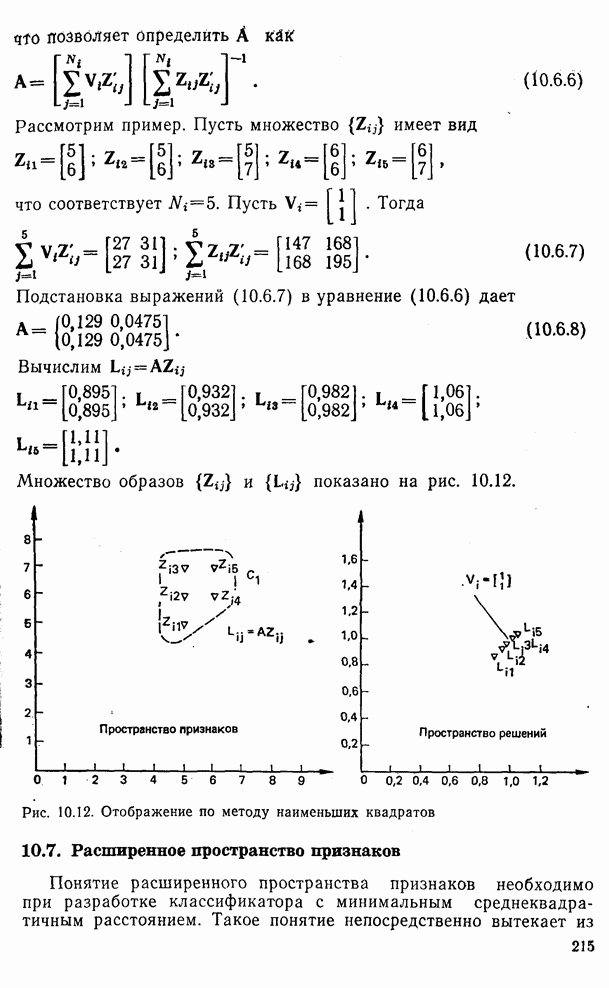
- 10.6. Метод отображения по методу наименьших квадратов
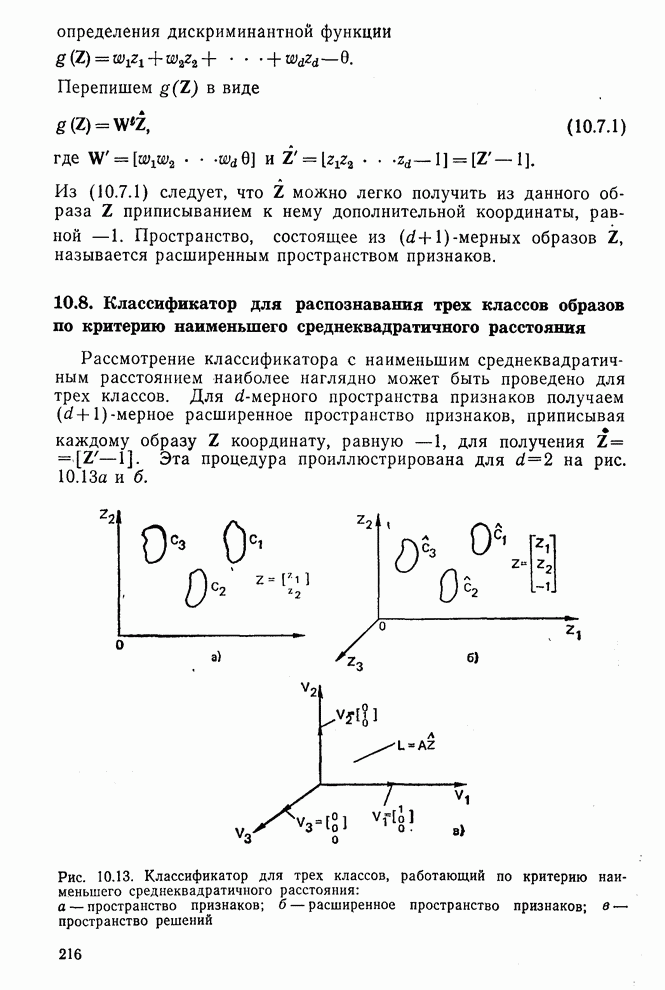
- 10.7. Расширенное пространство признаков
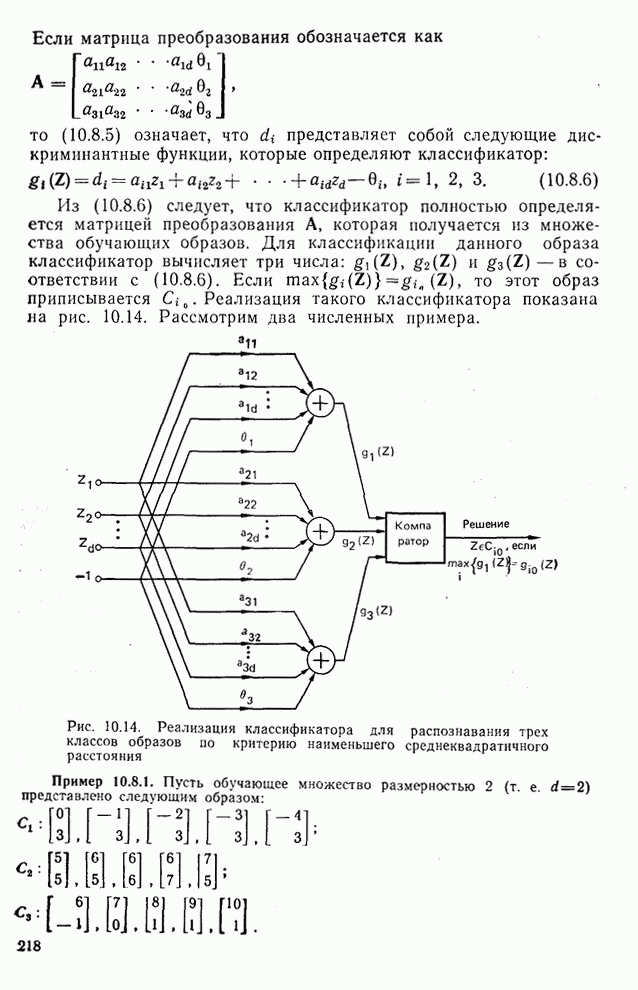
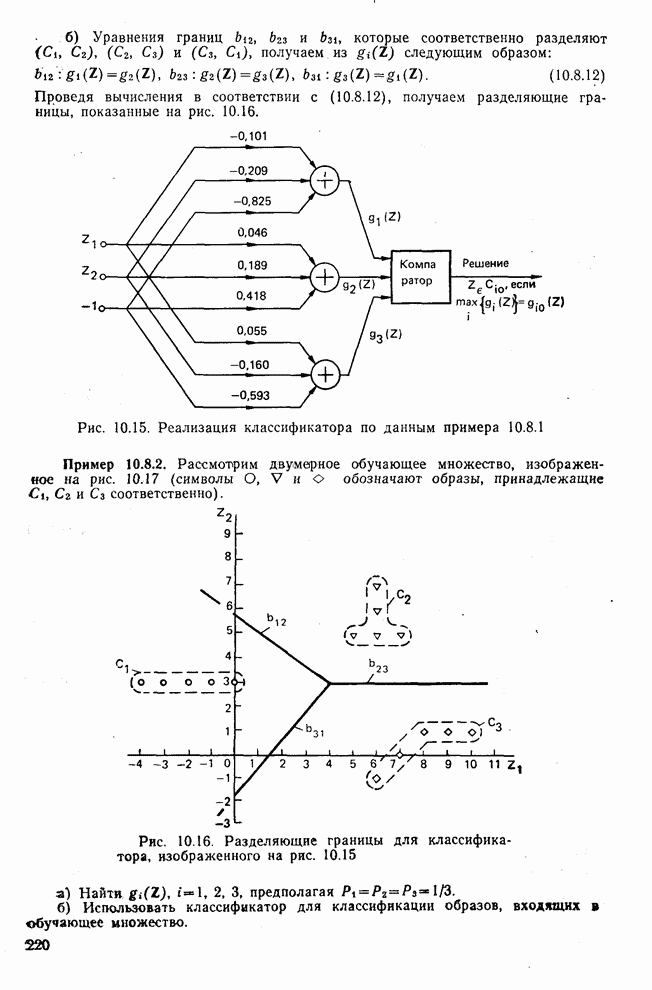
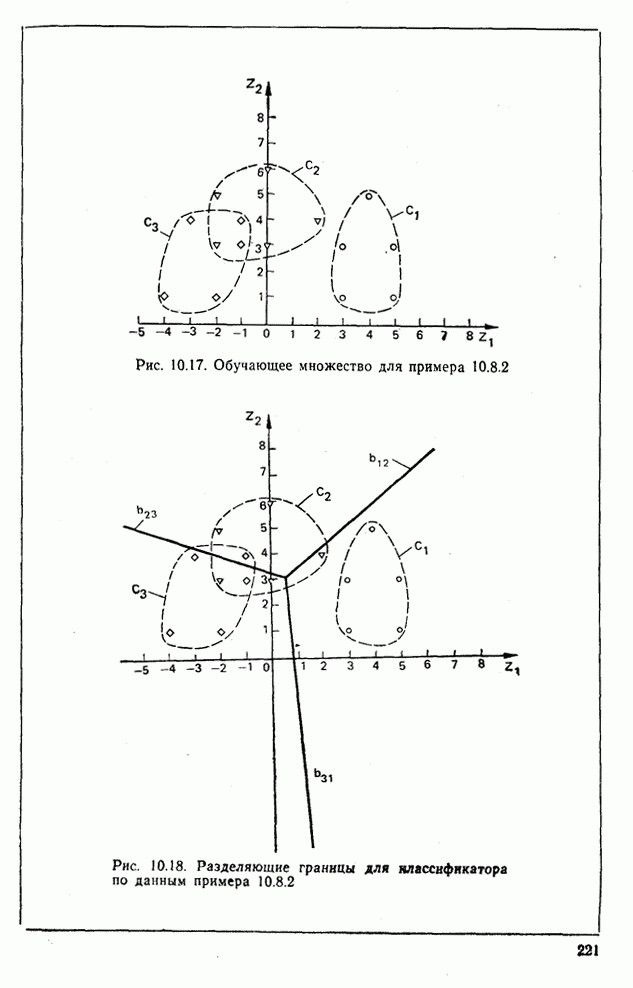
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
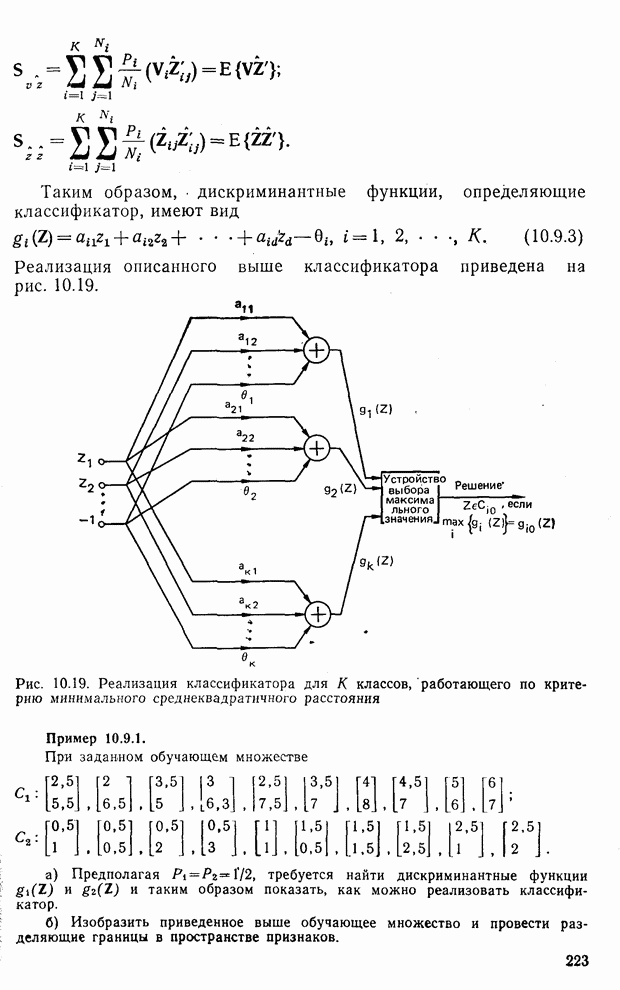
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
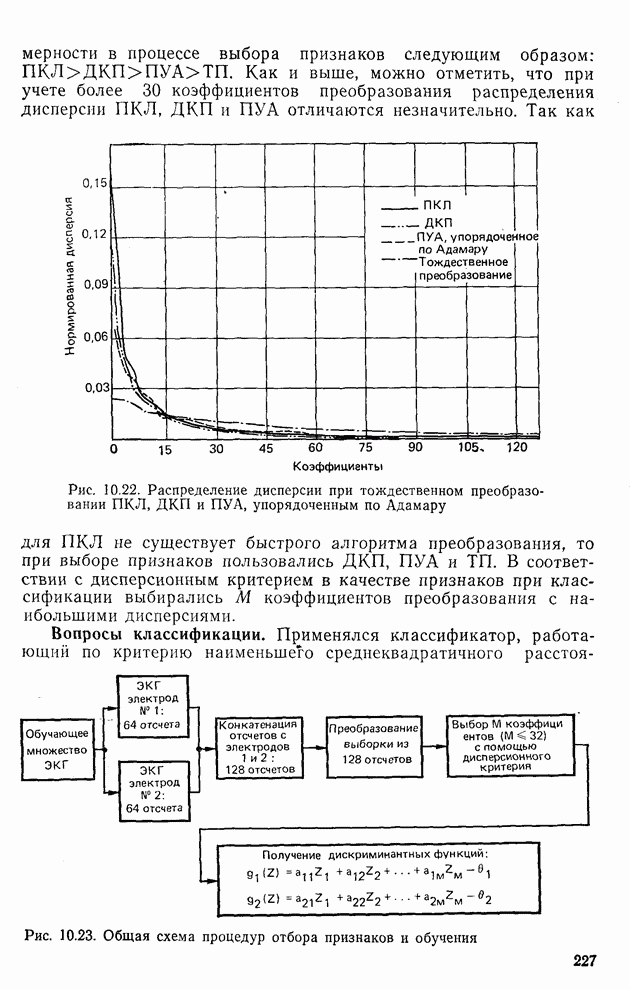
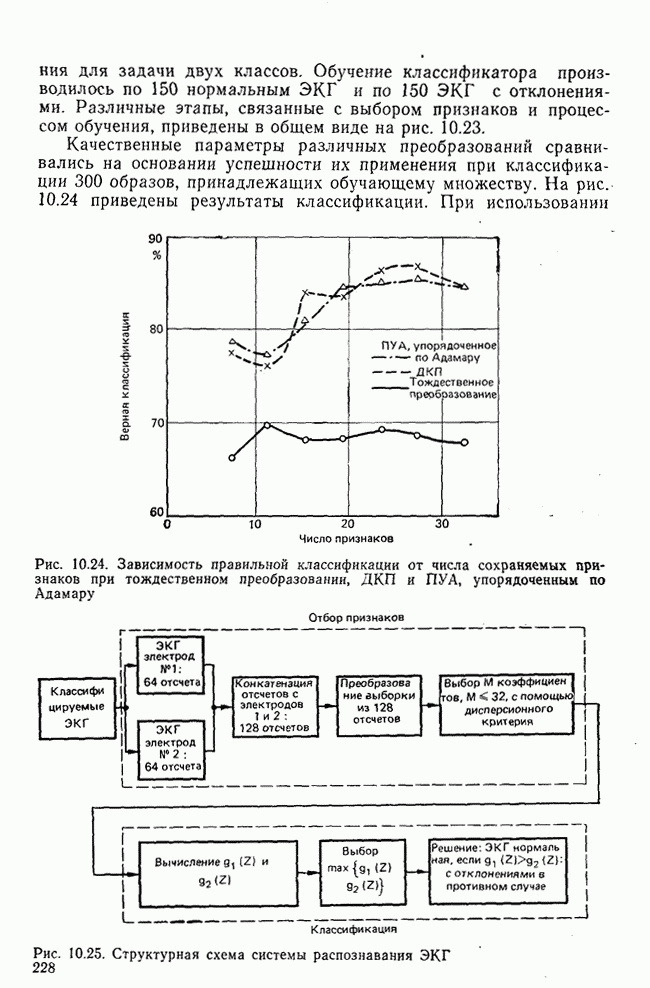
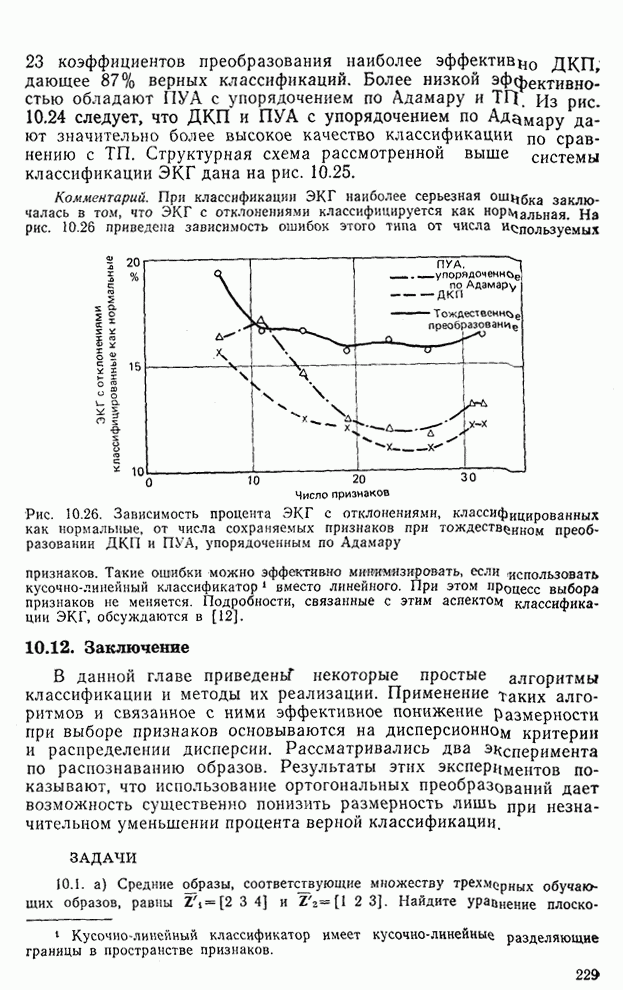
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
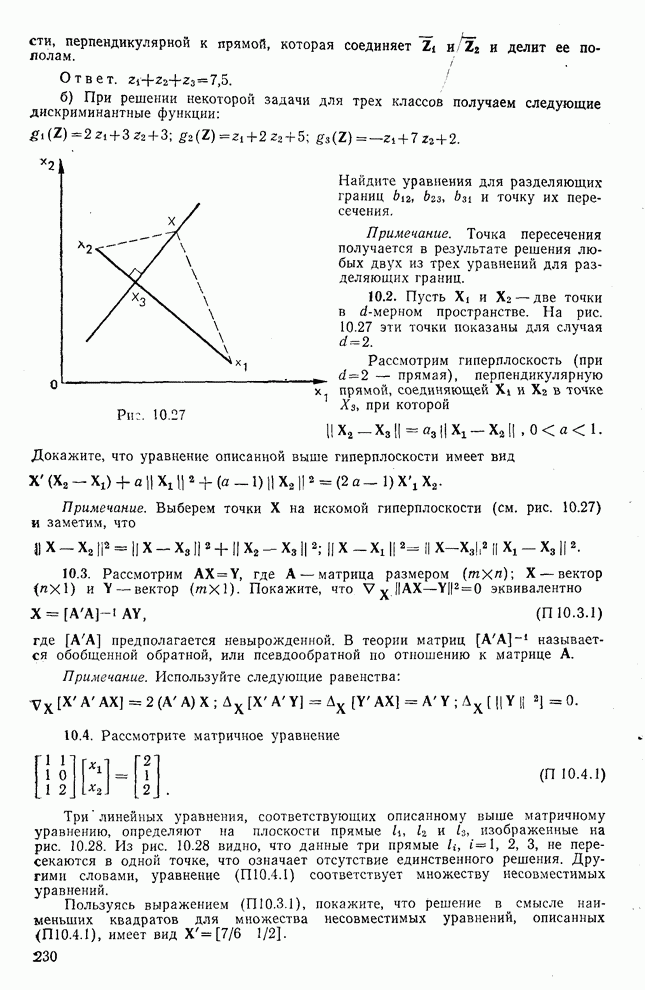
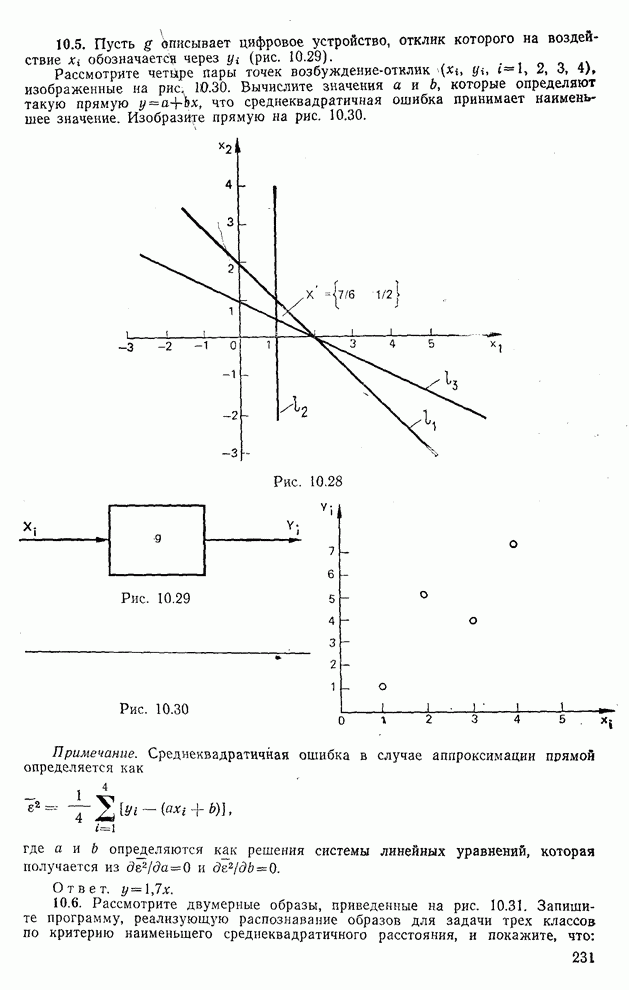
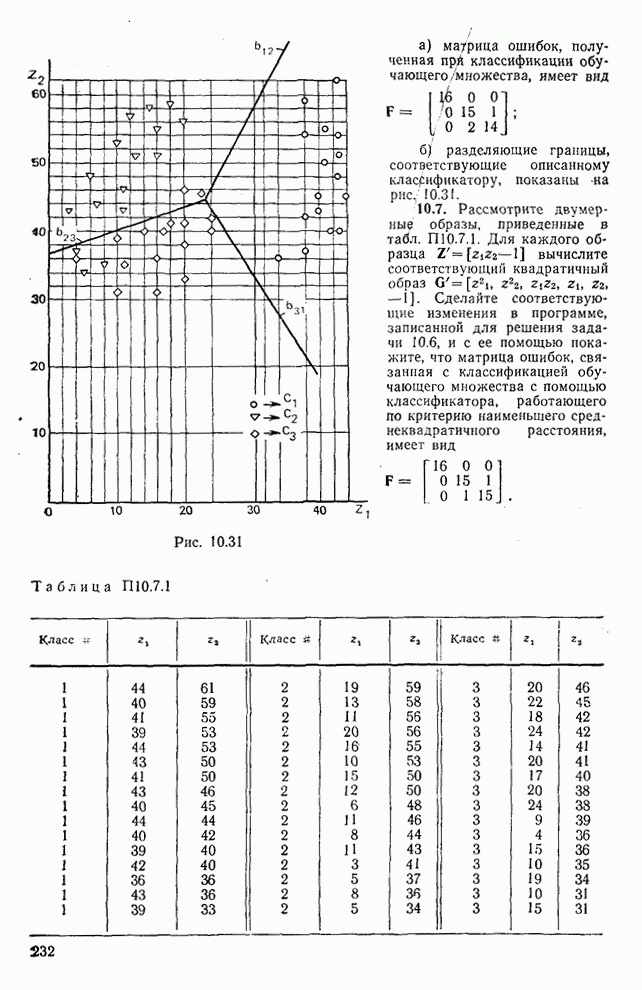
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ