| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
Ограничимся рассмотрением двумерного случая, который используется при обработке изображений. Обобщение для г-мерно-го случая может быть получено непосредственно. Определение двумерного ПУА с упорядочением по Адамару следует непосредственно из выражения (6.2.8):
 (6.12.1)
(6.12.1)
где  —входной массив,
—входной массив,  —коэффициент преобразования,
—коэффициент преобразования,  . Выражения
. Выражения  и
и  представляют собой двоичные представления
представляют собой двоичные представления  и
и  соответственно, т. е.
соответственно, т. е.  .
.
Входной массив  можно однозначно восстановить, выполняя обратное двумерное ПУА с упорядочением по Адамару, которое определяется как
можно однозначно восстановить, выполняя обратное двумерное ПУА с упорядочением по Адамару, которое определяется как
 (6.12.2)
(6.12.2)
Входной массив данных может быть записан в виде матрицы  размером
размером  :
:
 (6.12.3)
(6.12.3)
В выражении (6.12.1) рассмотрим внутреннее суммирование, которое записывается как
 (6.12.4)
(6.12.4)
В правой части приведенного выше выражения записано ПУА с упорядочением по Адамару каждого столбца матрицы входных данных  . Введем следующее обозначение:
. Введем следующее обозначение:
 (6.12.5)
(6.12.5)
Коэффициенты  можно записать в матричном виде
можно записать в матричном виде

Подстановка (6.12.5) в (6.12.1) дает

что можно записать в следующем виде:
 (6.12.7)
(6.12.7)
Выражение (6.12.7) означает, что коэффициенты  можно получить, выполняя ПУА с упорядочением по Адамару для каждой строки
можно получить, выполняя ПУА с упорядочением по Адамару для каждой строки  в выражении (6.12.6). В результате получаем
в выражении (6.12.6). В результате получаем  коэффициентов, которые в матричной форме записываются как
коэффициентов, которые в матричной форме записываются как
 (6.12.8)
(6.12.8)
Приведенное выше рассмотрение позволяет сделать вывод, что двумерное ПУА с упорядочением по Адамару можно вычислить с помощью алгоритма одномерного БПУА с упорядочением по Адамару следующим образом:
i) при  выполняется БПУА с упорядочением по Адамару для каждого из
выполняется БПУА с упорядочением по Адамару для каждого из  столбцов
столбцов  при получении
при получении  из выражения (6.12.6);
из выражения (6.12.6);
ii) при  выполняется БПУА с упорядочением по Адамару для каждой из
выполняется БПУА с упорядочением по Адамару для каждой из  строк
строк  при получении
при получении  из выражения (6.12.8).
из выражения (6.12.8).
Таким образом, одномерный алгоритм БПУА с упорядочением по Адамару применяется  раз.
раз.
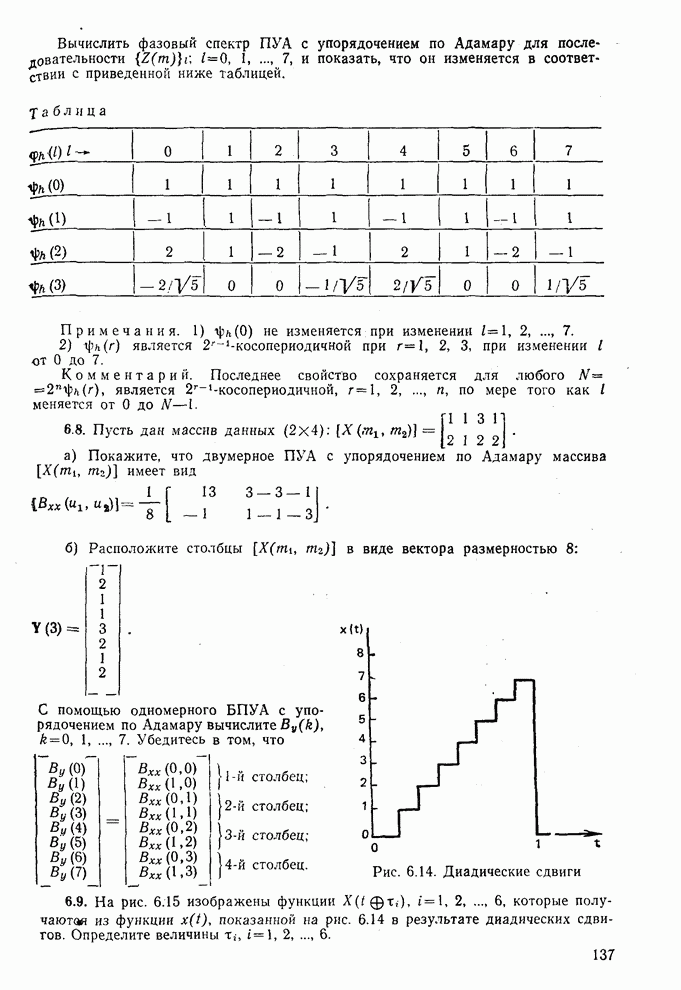
Другой путь для вычисления двумерного ПУА с упорядочением по Адамару заключается в вычислении одномерного ПУА с упорядочением по Адамару при условии, что матрица входных .данных преобразуется в  -вектор [см. задачу (6.8)]. Вычисление
-вектор [см. задачу (6.8)]. Вычисление  ПУА с упорядочением по Адамару и определение соответствующего энергетического спектра рассматриваются в [24],
ПУА с упорядочением по Адамару и определение соответствующего энергетического спектра рассматриваются в [24],  .
.
В заключение отметим, что двумерное ПУА с упорядочением это Адамару и обратное преобразование могут быть записаны в матричной форме:
 (6.12.9)
(6.12.9)
Таким же образом можно показать, что матричная форма ПУА с упорядочением по Уолшу и его обратное преобразование при двумерном ПУА можно записать как

и
 (6.12.10)
(6.12.10)
где

Из выражения (6.12.10) следует, что двумерное ПУА с упорядочением по Уолшу и обратное преобразование можно выполнить с помощью одномерного БПУА с упорядочением по Уолшу, которое применяется  раз так же, как и в случае ПУА с упорядочением по Адамару.
раз так же, как и в случае ПУА с упорядочением по Адамару.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ АВТОРОВ
- ГЛАВА 1. Введение
- 1.1. Общие замечания
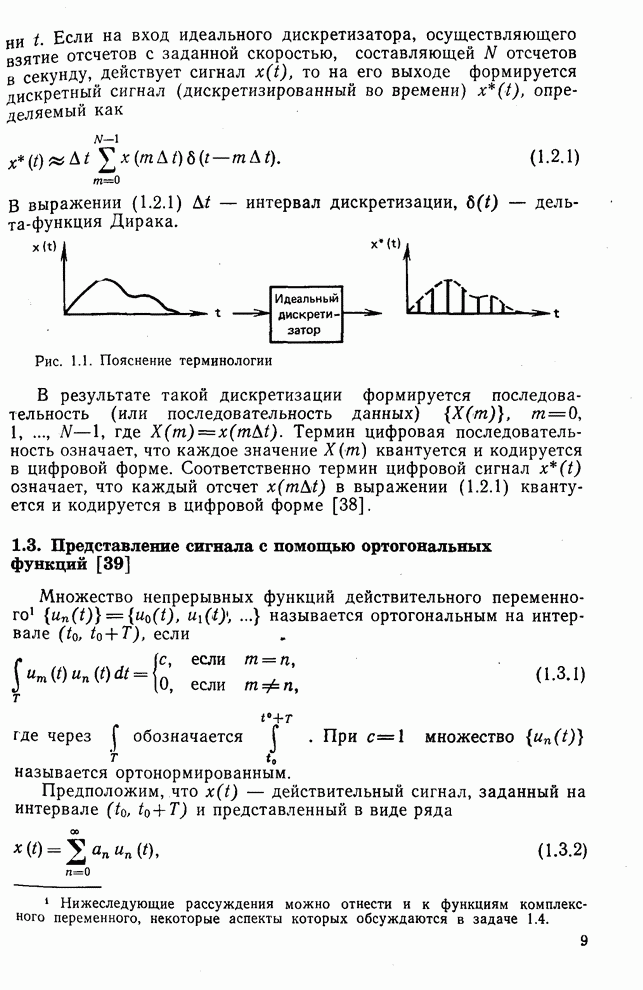
- 1.2. Терминология
- 1.3. Представление сигнала с помощью ортогональных функций [39]
- 1.4. Содержание книги
- ЗАДАЧИ
- ГЛАВА 2. Фурье-представление сигналов
- 2.1. Фурье-представление
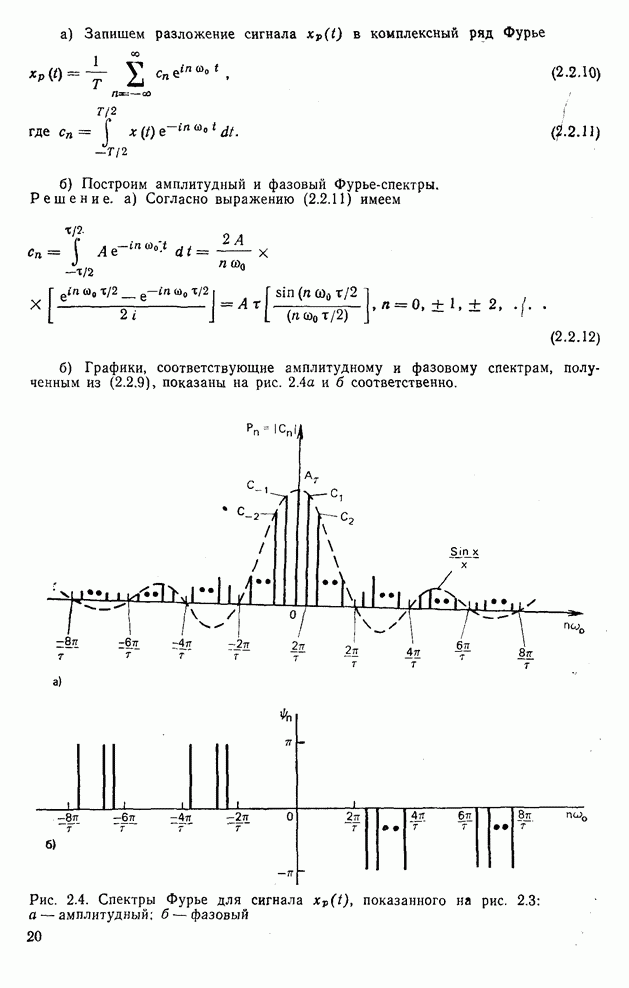
- 2.2. Спектр мощности, амплитудный и фазовый спектры
- 2.3. Преобразование Фурье
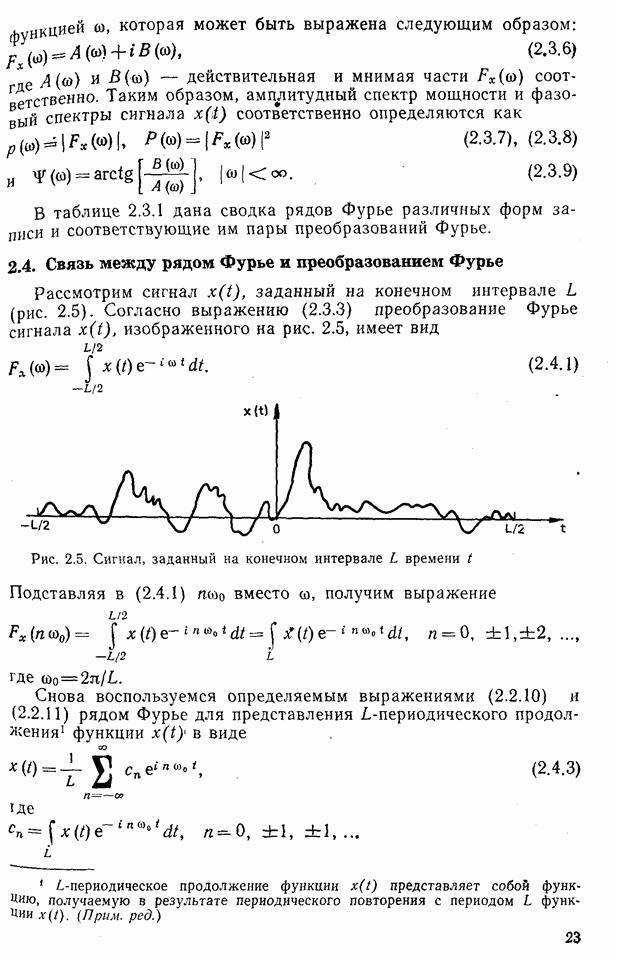
- 2.4. Связь между рядом Фурье и преобразованием Фурье
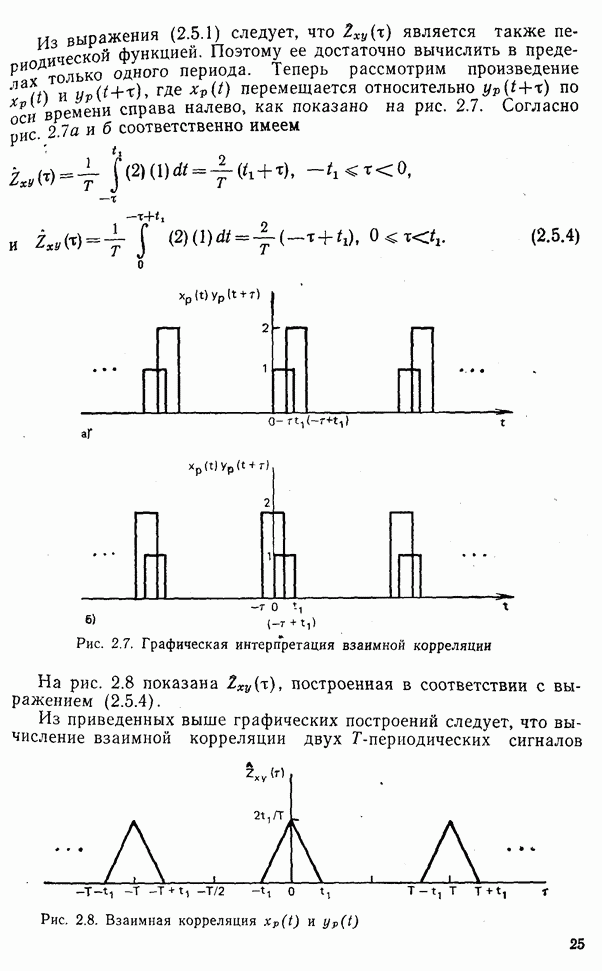
- 2.5. Взаимная корреляция, автокорреляция и свертка
- 2.6. Теорема отсчетов
- 2.7. Заключение
- ЗАДАЧИ
- ГЛАВА 3. Фурье-представление временных последовательностей
- 3.1. Определение дискретного преобразования Фурье
- 3.2. Свойства ДПФ
- 3.3. Матричное представление корреляции и свертки
- 3.4. Соотношение между ДПФ, преобразованием Фурье и рядом Фурье
- 3.5. Спектр мощности, амплитудный и фазовый спектры
- 3.6. Двумерное ДПФ
- 3.7. Мгновенный спектр Фурье
- 3.8. Заключение
- ЗАДАЧИ 3.1.
- ГЛАВА 4. Быстрое преобразование Фурье
- 4.1. Постановка задачи
- 4.2. Обоснование поиска алгоритма
- 4.3. Основа для вывода алгоритма
- 4.4. Вывод алгоритма
- 4.5. Численные примеры
- 4.6. Перестановка данных
- 4.7. Объем вычислений и памяти
- 4.8. Некоторые приложения
- 4.9. Заключение
- Приложение 4.1
- ЗАДАЧИ
- ГЛАВА 5. Класс ортогональных функций
- 5.1. Определение частости
- 5.2. Обозначение непрерывных и дискретных функций
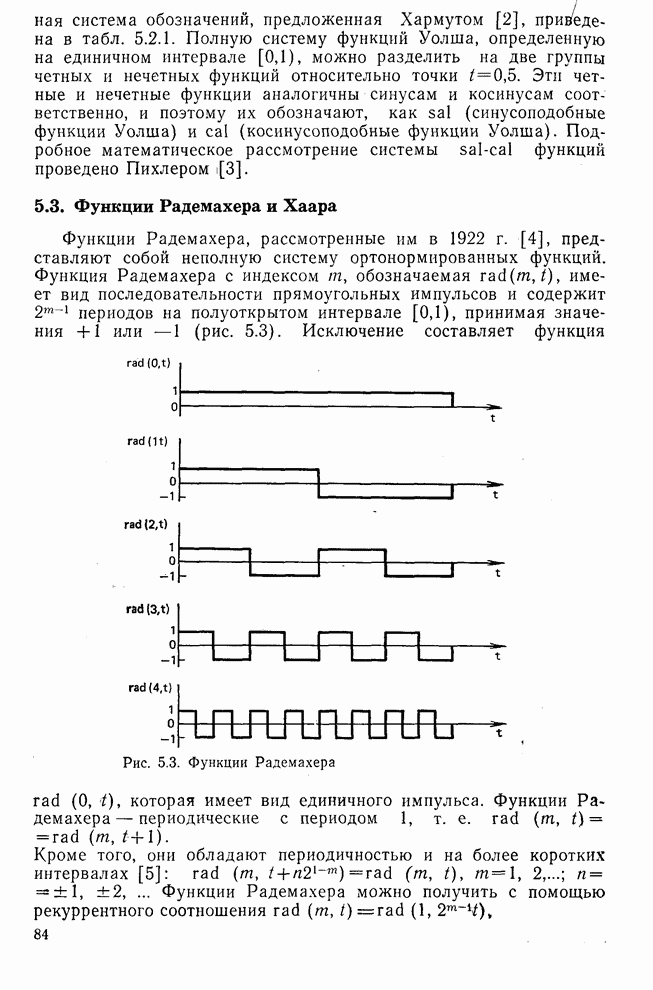
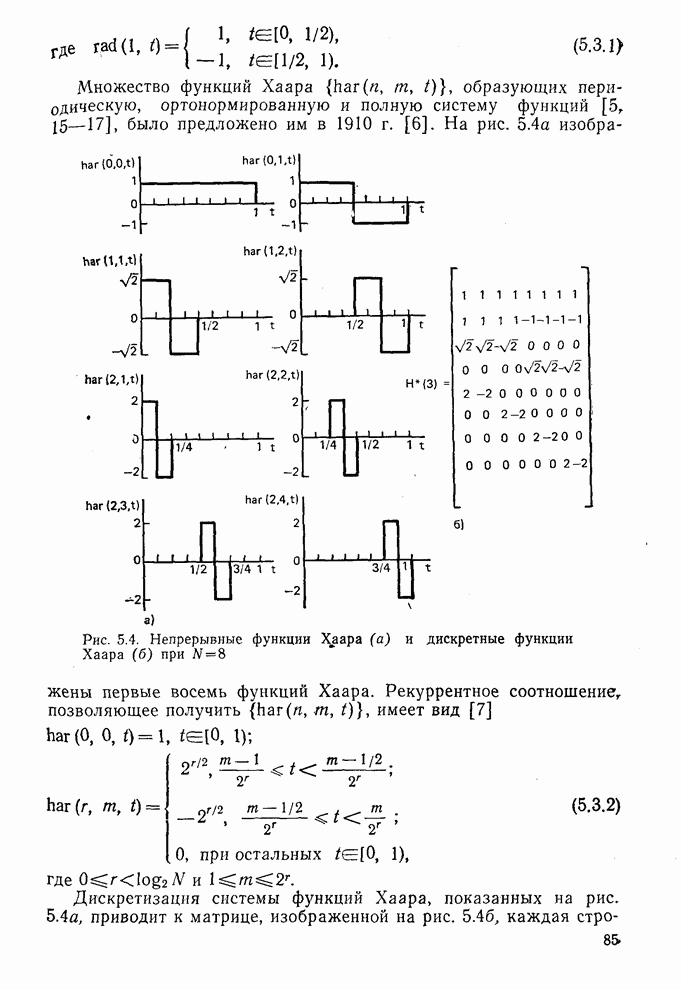
- 5.3. Функции Радемахера и Хаара
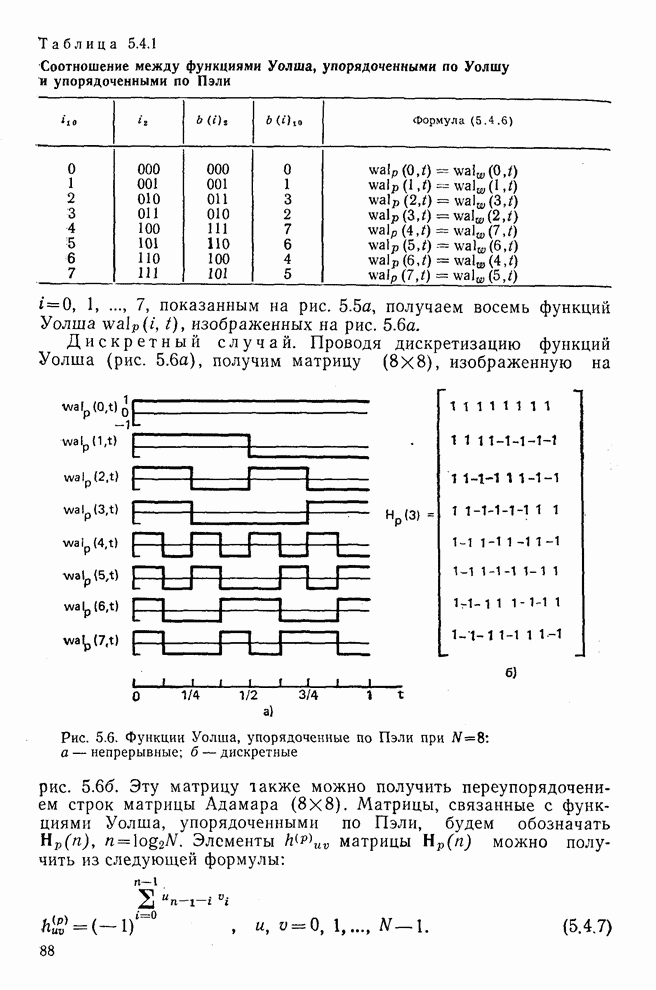
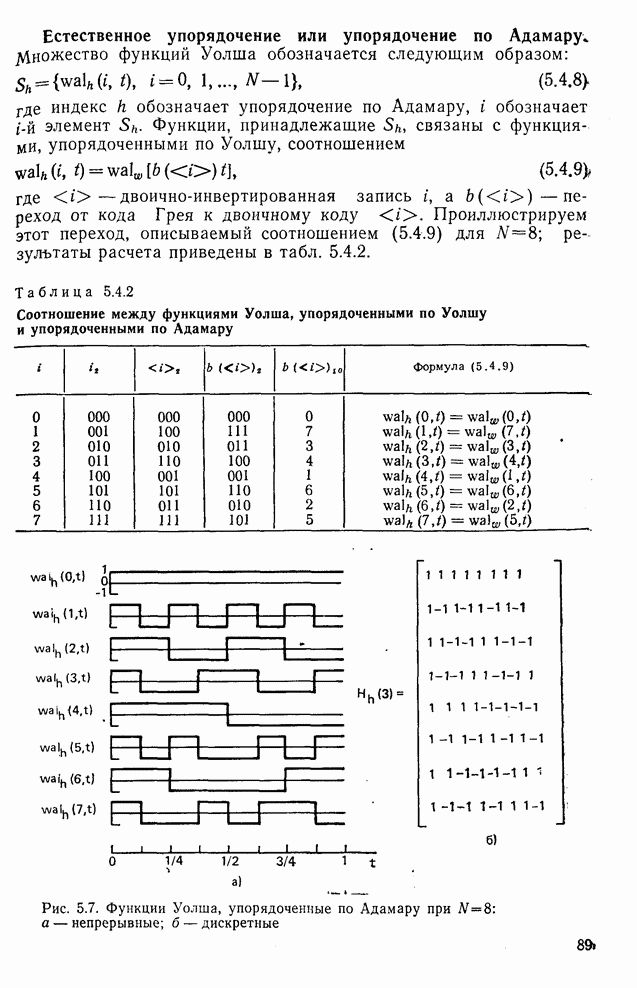
- 5.4. Функции Уолша
- 5.5. Заключение
- Приложение 5.1. Код Грея
- ЗАДАЧИ
- ГЛАВА 6. Преобразование Уолша—Адамара
- 6.1. Представление сигналов в виде ряда Уолша
- 6.2. Преобразование Уолша—Адамара, упорядоченное по Адамару
- 6.3. Быстрое преобразование Уолша-Адамара, упорядоченное по Адамару (БПУА)
- 6.4. Преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.5. Быстрое преобразование Уолша—Адамара, упорядоченное по Уолшу
- 6.6. Циклический и диадический сдвиги
- 6.7. Спектр ПУА с упорядочением по Уолшу [10—12]
- 6.8. Спектр ПУА с упорядочением по Адамару [4, 13]
- 6.9. Физическая интерпретация энергетического спектра ПУА с упорядочением по Адамару [13]
- 6.10. Модифицированное преобразование Уолша—Адамара МПУА)
- 6.11. Циклическая и диадическая корреляция (свертка)
- 6.12. Многомерные преобразования Уолша—Адамара с упорядочением по Адамару и по Уолшу
- 6.13. Заключение
- ПРИЛОЖЕНИЕ 6.1
- ЗАДАЧИ
- ГЛАВА 7. Различные ортогональные преобразования
- 7.1. Факторизация матриц
- 7.2. Обобщенное преобразование [4, 5]
- 7.3. Преобразование Хаара [ПХ]
- 7.4. Алгоритмы для вычисления преобразования Хаара (ПХ)
- 7.5. Пилообразные матрицы
- 7.6. Определение пилообразного преобразования
- 7.7. Дискретное косинусное преобразование (ДКП)
- 7.8. Двумерные преобразования
- 7.9. Заключение
- ПРИЛОЖЕНИЕ 7.1. Кронекеровское произведение матриц
- ПРИЛОЖЕНИЕ 7.2 Факторизация матриц
- ЗАДАЧИ
- ГЛАВА 8. Обобщенная винеровская фильтрация
- 8.1. Некоторые основные матричные операции
- 8.2. Математическая модель [2]
- 8.3. Расчет фильтра
- 8.4. Субоптимальная винеровская фильтрация
- 8.5. Оптимальные диагональные фильтры
- 8.6. Субоптимальные диагональные фильтры [2—4]
- 8.7. Двумерная винеровская фильтрация
- 8.8. Заключение
- ПРИЛОЖЕНИЕ 8.1. Терминология и определения
- ЗАДАЧИ
- ГЛАВА 9. Сжатие данных
- 9.1. Поиск оптимального преобразования
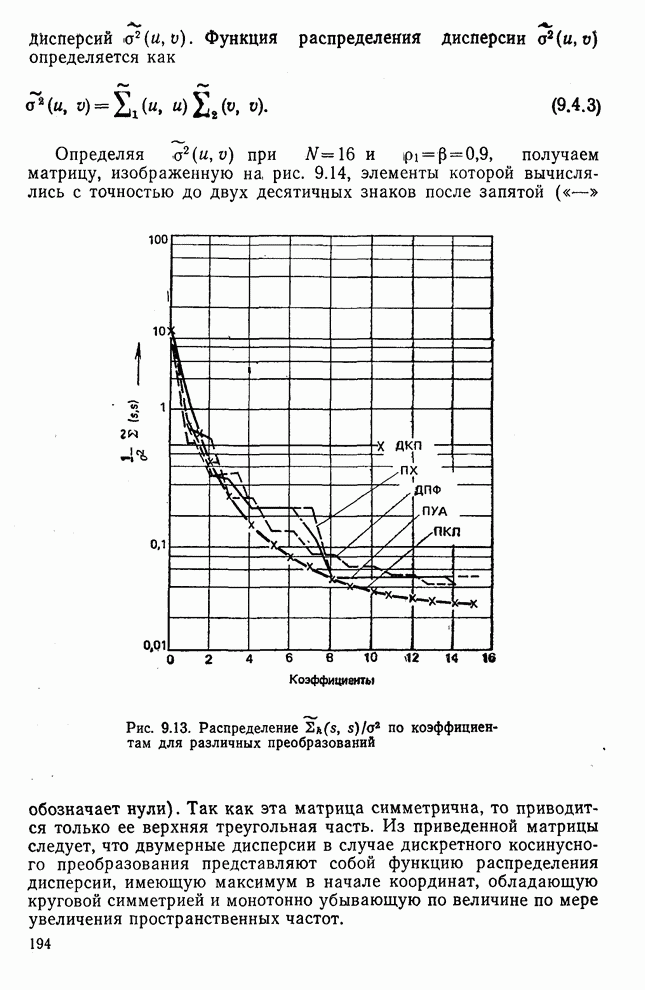
- 9.2. Дисперсионный критерий и распределение дисперсии [1]
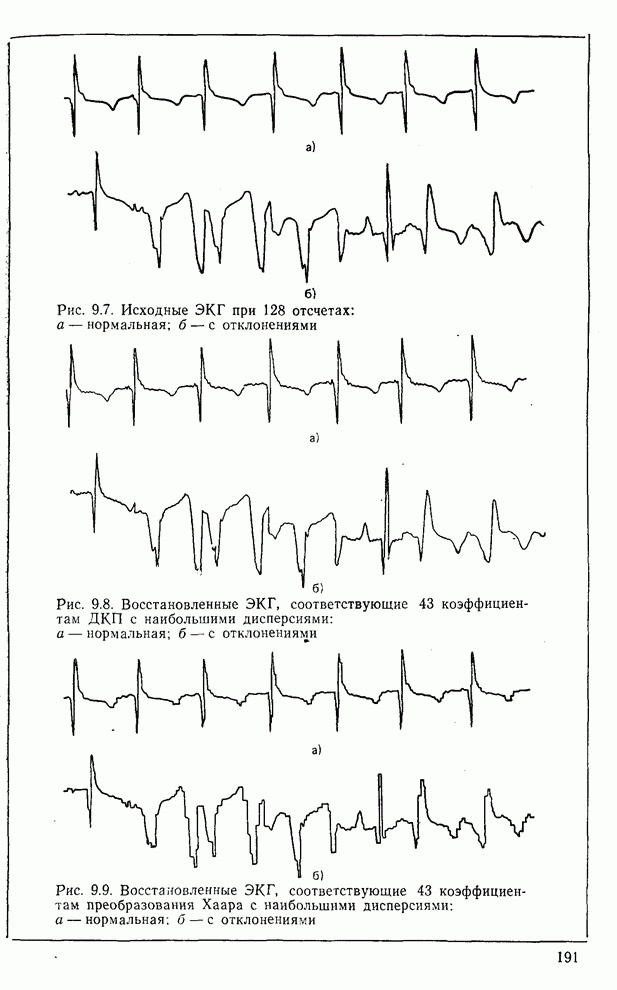
- 9.3. Сжатие электрокардиограмм [2]
- 9.4. Основные понятия сжатия изображений
- 9.5. Примеры сжатия изображений
- 9.6. Дополнительные соображения
- 9.7. Заключение
- ПРИЛОЖЕНИЕ 9.1. Множители Лагранжа [9]
- ЗАДАЧИ
- ГЛАВА 10. Выбор признаков и распознавание образов
- 10.1. Введение
- 10.2. Принцип обучения
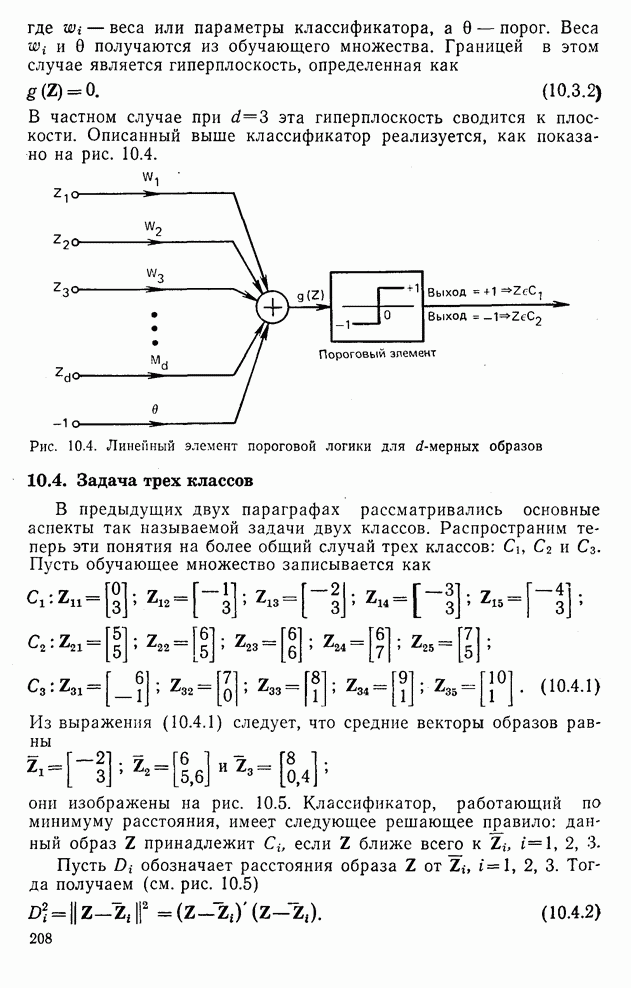
- 10.3. d-мерные образы
- 10.4. Задача трех классов
- 10.5. Эксперимент по классификации изображений
- 10.6. Метод отображения по методу наименьших квадратов
- 10.7. Расширенное пространство признаков
- 10.8. Классификатор для распознавания трех классов образов по критерию наименьшего среднеквадратичного расстояния
- 10.9. Классификатор для распознавания К классов образов по критерию наименьшего среднеквадратичного расстояния [9-11]
- 10.10. Квадратичные классификаторы [2]
- 10.11. Эксперимент по классификации ЭКГ
- 10.12. Заключение
- ЗАДАЧИ
- СПИСОК ЛИТЕРАТУРЫ