| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 12. ТОЧНО ИНТЕГРИРУЕМЫЕ ВОЛНОВЫЕ УРАВНЕНИЯ
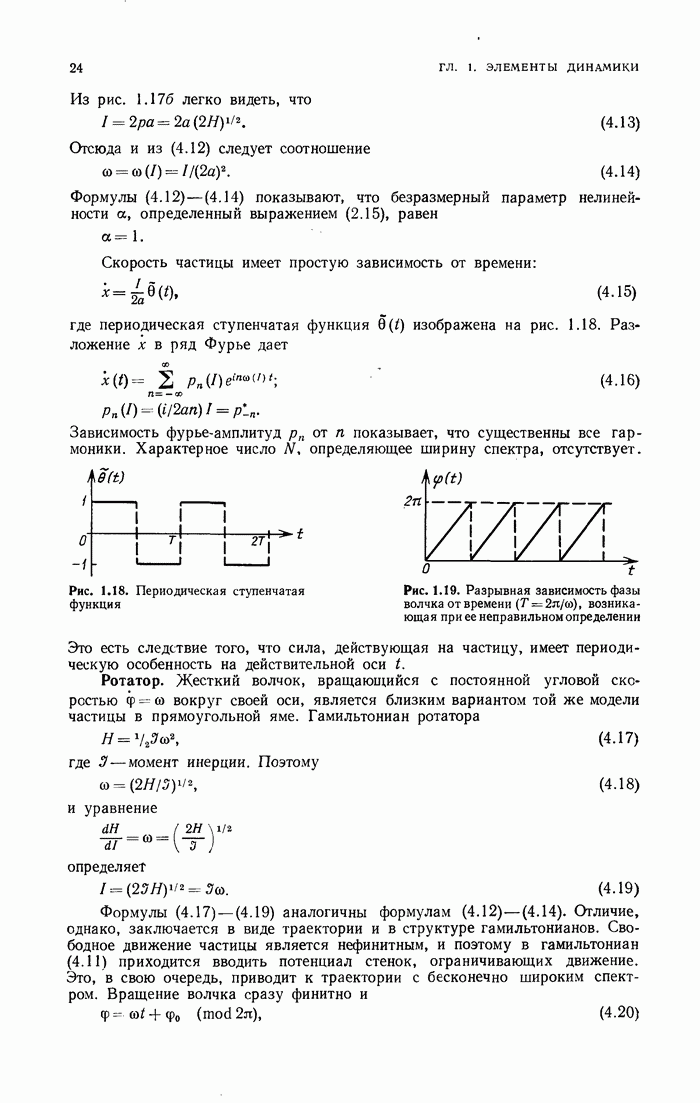
Несмотря на большую сложность нелинейных волновых уравнений, некоторые из них обладают уникальным свойством — они являются точно интегрируемыми. Мы уже познакомились с одним из таких уравнений — уравнением Бюргерса. Однако оно является простым, и способ его интегрирования не имеет обобщений. В действительности могут быть указаны некоторые формальные схемы, позволяющие «вылавливать» из множества различных уравнений те из них, которые интегрируются точно. Начало этим методам положило открытие Гарднера — Грина — Крускала-Миуры (ГГКМ) [1], которые показали, что уравнение КдВ может быть проинтегрировано точно с помощью метода обратной задачи рассеяния (ОЗР); этот результат был усилен Лаксом, сформулировавшим метод  -пары [2]. Идеи Лакса сразу получили многочисленные обобщения, после которых начался период открытия новых уравнений, допускающих точную интегрируемость. К сожалению, методы, используемые здесь, выходят за рамки книги. Поэтому мы остановимся лишь на изложении некоторых простейших их вариантов (ком. 1).
-пары [2]. Идеи Лакса сразу получили многочисленные обобщения, после которых начался период открытия новых уравнений, допускающих точную интегрируемость. К сожалению, методы, используемые здесь, выходят за рамки книги. Поэтому мы остановимся лишь на изложении некоторых простейших их вариантов (ком. 1).
§ 1. Интегрирование КдВ-уравнения
Здесь мы изложим метод точного интегрирования уравнения Кортвега — де Вриза

которое явилось первым из уравнений, решаемых методом ОЗР. При изложении его мы используем метод  Лакса, который позволяет взглянуть на результаты
Лакса, который позволяет взглянуть на результаты  с более общей точки зрения.
с более общей точки зрения.
Операторные пары Лакса. Введем специально подобранную пару линейных дифференциальных операторов  которые составляют суть замены переменных. Положим сначала
которые составляют суть замены переменных. Положим сначала

Этот оператор действует на некоторые комплексные функции  которые достаточно быстро убывают при
которые достаточно быстро убывают при  То же свойство поведения на бесконечности будем предполагать относительно и.
То же свойство поведения на бесконечности будем предполагать относительно и.
Рассмотрим задачу на собственные значения для оператора 

Уравнение (1.3) является стационарным уравнением Шредингера с потенциалом и  Однако переменная
Однако переменная  не является в нем обычным временем — это просто параметр, от которого зависит потенциал. Поэтому, вообще говоря, и собственные значения X, и собственные функции
не является в нем обычным временем — это просто параметр, от которого зависит потенциал. Поэтому, вообще говоря, и собственные значения X, и собственные функции  зависят от
зависят от 
Подберем такой унитарный оператор  что произведение
что произведение  не зависит от параметра
не зависит от параметра  Это означает, что
Это означает, что

Действуя этим выражением на функцию  где параметр
где параметр  получаем также
получаем также

Как мы сейчас увидим, найти  можно далеко не единственным образом. Если такой оператор
можно далеко не единственным образом. Если такой оператор  существует, то собственные значения X не зависят от
существует, то собственные значения X не зависят от  Это — важное место, так как собственные значения задачи (1.3) не зависят от изменения потенциала и
Это — важное место, так как собственные значения задачи (1.3) не зависят от изменения потенциала и  от
от 
Здесь и далее все время следует обращать внимание на то, что для функции  являющейся решением КдВ-уравнения, величина
являющейся решением КдВ-уравнения, величина  является временем. В то же время в операторах
является временем. В то же время в операторах  и в собственных функциях
и в собственных функциях  величина
величина  параметр, не имеющий ничего общего с временной зависимостью уравнения Шредингера.
параметр, не имеющий ничего общего с временной зависимостью уравнения Шредингера.
Удобно отыскивать оператор  в виде
в виде

где А — самосопряженный оператор. Тогда условие того, что (1.4) не зависит от  эквивалентно равенству
эквивалентно равенству

Оператор А имеет важное значение, которое легко выясняется. Для этого достаточно заметить, что согласно (1.5), (1.6),

Это выражение эквивалентно уравнению для

Таким образом, итог наших выкладок в следующем. Пусть потенциал уравнения Шредингера  зависит от
зависит от  как от параметра. Тогда однопараметрические семейства операторов Шредингера
как от параметра. Тогда однопараметрические семейства операторов Шредингера  для разных
для разных  унитарно эквивалентны. Их собственные значения X не зависят от
унитарно эквивалентны. Их собственные значения X не зависят от  а собственные функции
а собственные функции  изменяются в зависимости от
изменяются в зависимости от  согласно уравнению (1.9). В нем оператор А является дополнительным к
согласно уравнению (1.9). В нем оператор А является дополнительным к  в том смысле, что он удовлетворяет уравнению (1.7), реализующему унитарное преобразование
в том смысле, что он удовлетворяет уравнению (1.7), реализующему унитарное преобразование  при изменении
при изменении 
Теперь остается сделать последний шаг и выбрать какой-либо вид А. Из определения  имеем просто
имеем просто

Положим

Тогда равенство (1.7) эквивалентно тривиальному уравнению

Нетривиальное уравнение получим, если положить

Простые выкладки после подстановки (1.11) в (1.7) и учета (1.10) дают уравнение  . В этом интересующем нас случае собственные функции
. В этом интересующем нас случае собственные функции  удовлетворяют уравнению
удовлетворяют уравнению

Уравнение (1.12) является очень примечательным. Если рассмотреть асимптотику  где и
где и  по условию обращается достаточно быстро в нуль, то
по условию обращается достаточно быстро в нуль, то

Это выражение сразу интегрируется и дает

Таким образом, зависимость  от
от  при
при  можно определить независимо от уравнения (1.3). Достаточно лишь знать 0) при значении параметра
можно определить независимо от уравнения (1.3). Достаточно лишь знать 0) при значении параметра  Поэтому наше продвижение заключается в следующем: собственные значения к уравнения (1.1) можно определить при начальном условии
Поэтому наше продвижение заключается в следующем: собственные значения к уравнения (1.1) можно определить при начальном условии  но не только их, а также асимптотики собственных функций
но не только их, а также асимптотики собственных функций  при
при 
Если мы все это сможем сделать, то тогда по собственным значениям к (не зависящим от  и по асимптотикам собственных функций
и по асимптотикам собственных функций  следует определить потенциал уравнения Шредингера
следует определить потенциал уравнения Шредингера  для произвольного значения параметра
для произвольного значения параметра  Но им как раз и является решение уравнения КдВ в момент времени
Но им как раз и является решение уравнения КдВ в момент времени 
Метод ОЗР. Мы показали, что задача определения решения  уравнения (1.1) сводится к восстановлению потенциала уравнения Шредингера по некоторой информации о его собственных значениях и об асимптотике его собственных функций. Определим эти данные более точно.
уравнения (1.1) сводится к восстановлению потенциала уравнения Шредингера по некоторой информации о его собственных значениях и об асимптотике его собственных функций. Определим эти данные более точно.
Если  достаточно быстро убывает при
достаточно быстро убывает при  то оператор
то оператор  имеет не более, чем конечное число невырожденных собственных значений
имеет не более, чем конечное число невырожденных собственных значений

Собственные функции ведут себя при  как
как

где  имеют смысл нормировочных констант. Подставляя (1.16) в (1.14), получаем
имеют смысл нормировочных констант. Подставляя (1.16) в (1.14), получаем

Формула (1.17) — первый результат. Перейдем теперь к непрерывному спектру оператора  и обозначим
и обозначим 
Асимптотику волновой функции при  можно представить в виде
можно представить в виде

Известно, что для уравнения Шредингера (для оператора  имеют место соотношения
имеют место соотношения

Подставляя (1.18) в (1.14), получаем

Запишем теперь задачу о рассеянии на потенциале в стандартной форме. Это означает:

где введены комплексные амплитуды прохождения  и отражения
и отражения 

Соотношение (1.22) следует непосредственно из (1.21). Для того чтобы сохранить единичную амплитуду падающей волны при любых  необходимо, очевидно, положить
необходимо, очевидно, положить

Так же из формул (1.20) и (1.21) следует

Теперь мы имеем замечательные соотношения, установленные  это выражения (1.23), (1.24) и (1.17) для коэффициентов
это выражения (1.23), (1.24) и (1.17) для коэффициентов  как функций времени, выраженных через их начальные значения. Введем следующую функцию:
как функций времени, выраженных через их начальные значения. Введем следующую функцию:

где  - число собственных значений дискретного спектра. С ее помощью происходит восстановление потенциала по данным рассеяния. Для этого используется уравнение Гельфанда-Левитана-Марченко
- число собственных значений дискретного спектра. С ее помощью происходит восстановление потенциала по данным рассеяния. Для этого используется уравнение Гельфанда-Левитана-Марченко

для неизвестной функции двух переменных  . Это уравнение линейно. Потенциал определяется через его решение следующим образом:
. Это уравнение линейно. Потенциал определяется через его решение следующим образом:

Поскольку  зависят от времени, следует считать, что функция
зависят от времени, следует считать, что функция  Для ее получения необходимо выражения (1.17) и (1.23) подставить в формулу (1.25):
Для ее получения необходимо выражения (1.17) и (1.23) подставить в формулу (1.25):

Поэтому вместо (1.27) имеем

Это и есть конечный результат, решающий проблему интегрирования КдВ-уравнения.
Солитонные решения. Покажем, как реально выглядит процедура решения для некоторых частных случаев.
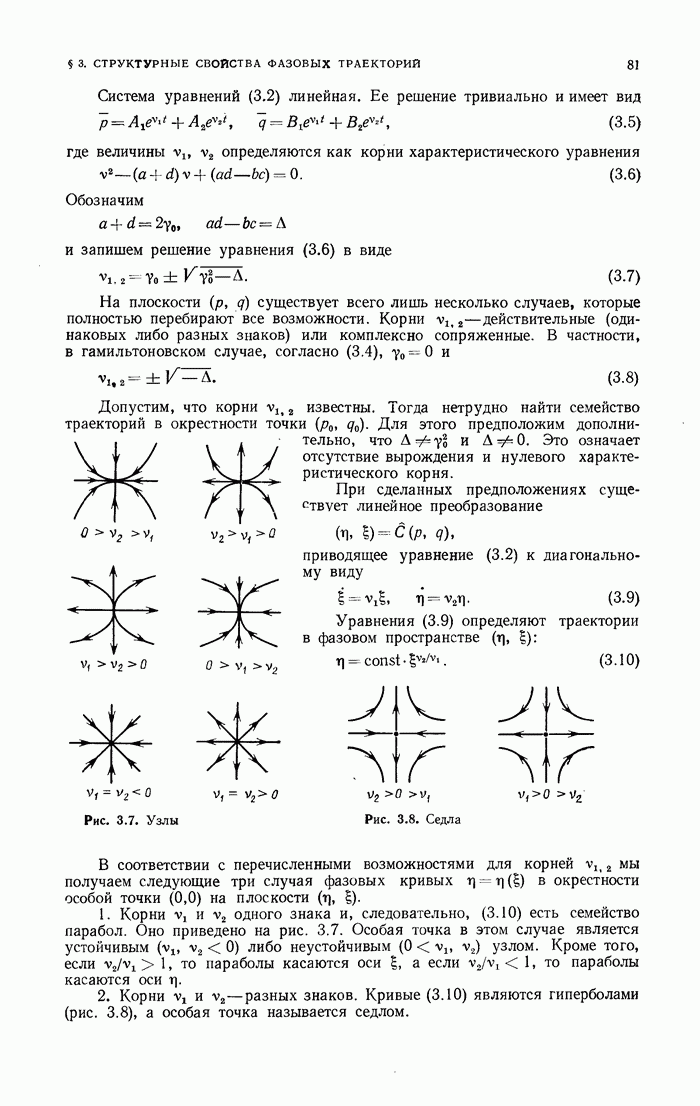
Существует некоторый специальный класс начальных условий, для которого точное решение может быть выписано в явном виде. Это так называемые  -солитонные решения.
-солитонные решения.
Решение уравнения КдВ начинается с задания начального профиля  Выберем его в виде
Выберем его в виде

Задача на собственные значения в потенциале (1.29а) решается точно [6]. Имеется только одно собственное значение в дискретном спектре:

Однако наиболее интересное свойство потенциала  - это отсутствие отраженной волны в области непрерывного спектра, т. е.
- это отсутствие отраженной волны в области непрерывного спектра, т. е.

для всех к. Частица произвольной энергии  не может «обнаружить» существование этого потенциала вследствие отсутствия рассеяния на нем. Мы еще вернемся к этому вопросу чуть ниже.
не может «обнаружить» существование этого потенциала вследствие отсутствия рассеяния на нем. Мы еще вернемся к этому вопросу чуть ниже.
Подстановка формул (1.30) и (1.31) в уравнение (1.28) дает просто

Тогда уравнение (1.26) принимает вид

Это уравнение решается разделением переменных. Полагая

получаем

Отсюда решение (1.29) дает

т. е. движущийся солитон с правильным соотношением между скоростью и амплитудой.
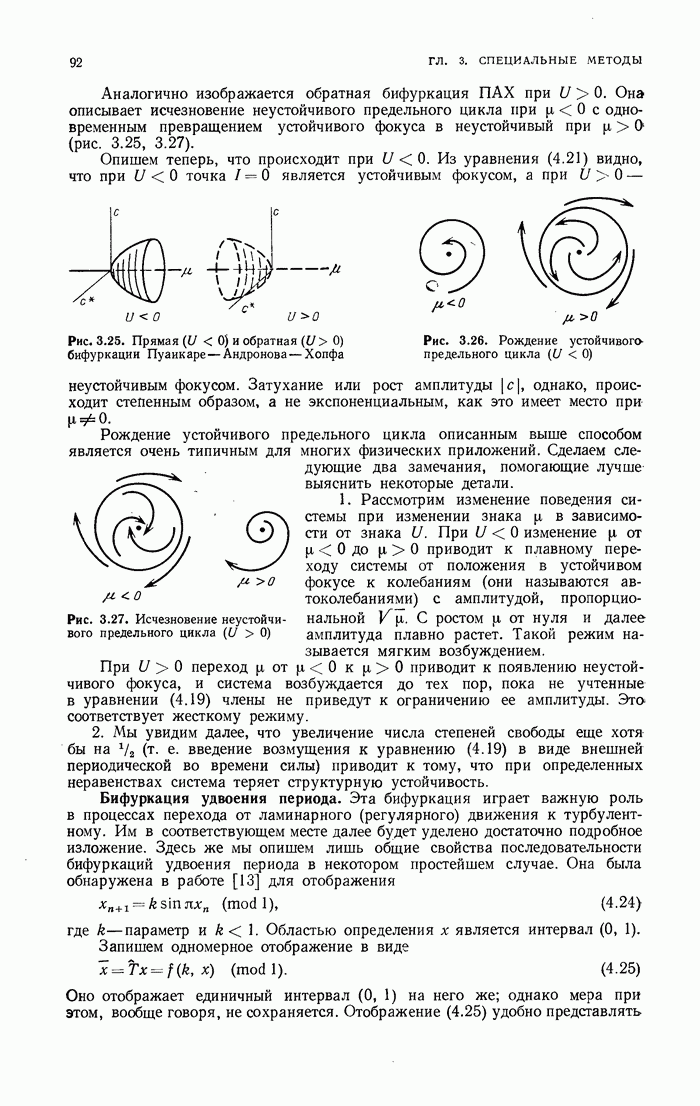
В той же работе [1] было показано, что, если  т. е. потенциал
т. е. потенциал  является безотражательным, то решение уравнения (1.26) приводит к
является безотражательным, то решение уравнения (1.26) приводит к  -солитонному решению. Это решение имеет не совсем простую структуру. Однако асимптотический ее вид при
-солитонному решению. Это решение имеет не совсем простую структуру. Однако асимптотический ее вид при  стремится к суперпозиции
стремится к суперпозиции  далеко отстоящих друг от друга солитонов. Это получается естественным образом, так как в одномерном потенциале и
далеко отстоящих друг от друга солитонов. Это получается естественным образом, так как в одномерном потенциале и  нет вырожденных уровней. Поэтому скорости всех солитонов должны быть различны. За большое время «квазисолитоны», движущиеся с различными скоростями, разойдутся достаточно сильно друг от друга и перестанут взаимодействовать.
нет вырожденных уровней. Поэтому скорости всех солитонов должны быть различны. За большое время «квазисолитоны», движущиеся с различными скоростями, разойдутся достаточно сильно друг от друга и перестанут взаимодействовать.
Мы видим, что  -солитонная задача непосредственно связана с безотражательными потенциалами для уравнения Шредингера. Решение такой задачи, которое не является единственным, было получено еще ранее в [7] в связи с задачами оптики.
-солитонная задача непосредственно связана с безотражательными потенциалами для уравнения Шредингера. Решение такой задачи, которое не является единственным, было получено еще ранее в [7] в связи с задачами оптики.
Условие безотражательности  позволяет свести проблему решения
позволяет свести проблему решения  -уравнения к чисто алгебраической задаче. Хотя она и требует некоторых выкладок, полезно привести соответствующее решение. Многие черты этого решения, как способа получения, так и его структуры, оказываются типичными для других интегрируемых уравнений.
-уравнения к чисто алгебраической задаче. Хотя она и требует некоторых выкладок, полезно привести соответствующее решение. Многие черты этого решения, как способа получения, так и его структуры, оказываются типичными для других интегрируемых уравнений.
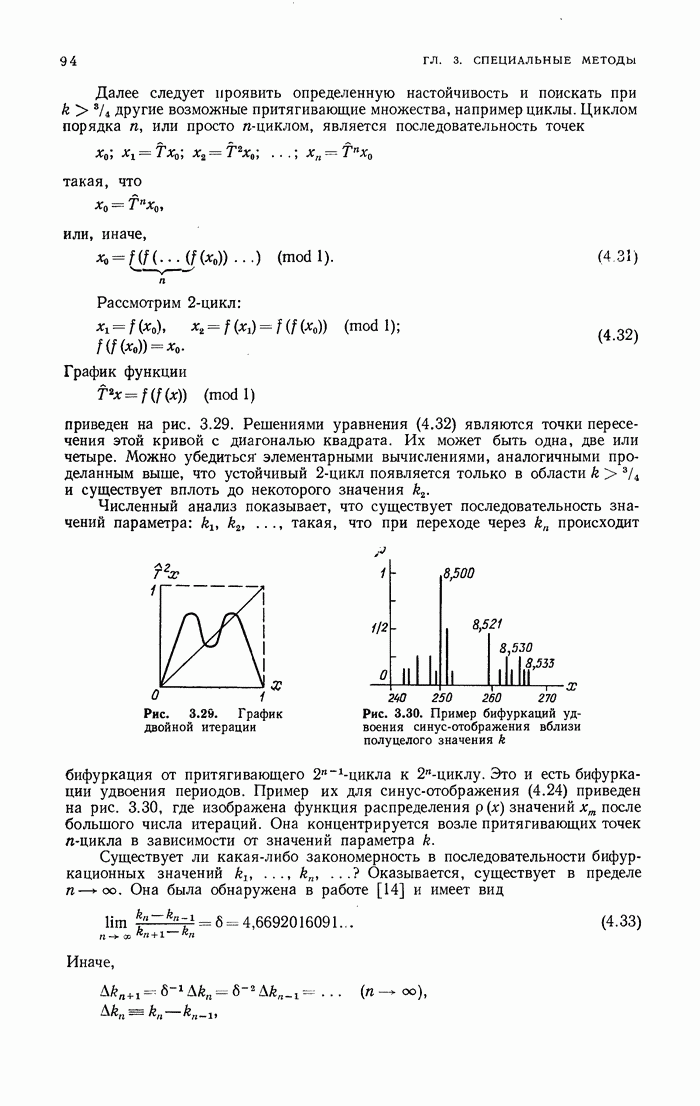
N-солитонные решения. Итак, пусть начальное условие  представляет собой безотражательный потенциал, имеющий
представляет собой безотражательный потенциал, имеющий  дискретных уровней
дискретных уровней  соответствующих нормировочных констант
соответствующих нормировочных констант  Тогда в
Тогда в
соответствии с (1.25) имеем

где

Уравнение (1.26) принимает вид

Так же, как и в случае односолитонного решения,  -солитонное решение можно получить из этого уравнения разделением переменных. Полагаем
-солитонное решение можно получить из этого уравнения разделением переменных. Полагаем

Это дает

Обозначим через  определитель системы (1.34):
определитель системы (1.34):

Решение системы (1.34) имеет вид

где  -матрица, получающаяся из
-матрица, получающаяся из  заменой
заменой  столбца на столбец, составляющий правую часть (1.34).
столбца на столбец, составляющий правую часть (1.34).
Согласно (1.33), (1.36) и известному правилу дифференцирования определителей, имеем

Отсюда следует формула

Новым, по сравнению с результатом работы [1], здесь является зависимость коэффициентов  от
от 
Решение (1.37) и представляет  -солитонное решение. Если использовать для
-солитонное решение. Если использовать для  формулу (1.32), то получается выражение, связывающее скорость распространения солитона
формулу (1.32), то получается выражение, связывающее скорость распространения солитона  с собственным значением
с собственным значением 

Мы здесь не будем исследовать асимптотические выражения формулы (1.37). Заметим лишь, что это сравнительно просто делается, поскольку компонентами детерминанта  являются «бегущие экспоненты» типа
являются «бегущие экспоненты» типа  Поэтому при больших
Поэтому при больших  решение сосредоточено вблизи точки
решение сосредоточено вблизи точки  Это и есть уединенная волна, движущаяся со скоростью
Это и есть уединенная волна, движущаяся со скоростью  и сдвинутая по фазе на
и сдвинутая по фазе на 
Сдвиг фазы обусловлен взаимодействием солитонов. Проходя друг сквозь друга, солитоны сначала деформируются, а потом полностью восстанавливают свою форму. Единственным последствием их взаимодействия является сдввдгпфазы на величину 
Интегралы движения. Уравнение КдВ имеет бесконечное число законов сохранения. Это — уравнения в форме

где  — сохраняющиеся плотности,
— сохраняющиеся плотности,  потоки. Функции
потоки. Функции  являются полиномами от
являются полиномами от  , их и т. д. Если и и все производные достаточно быстро убывают при
, их и т. д. Если и и все производные достаточно быстро убывают при  то интегрирование (1.39) дает интегралы движения
то интегрирование (1.39) дает интегралы движения

Факт существования бесконечного числа интегралов движения был установлен в [8]. Их можно представить в виде некоторой рекуррентной формулы. Воспользуемся представлением из [3]:

где плотности  удовлетворяют рекуррентным соотношениям:
удовлетворяют рекуррентным соотношениям:

Приведем явный вид нескольких первых интегралов движения:

Интеграл  выделен, так как он является гамильтонианом для КдВ-уравнения:
выделен, так как он является гамильтонианом для КдВ-уравнения:  Уравнения движения записываются в виде
Уравнения движения записываются в виде

 и приводят К (1.1).
и приводят К (1.1).
Факт существования бесконечного числа интегралов движения в данном случае однозначно связан с интегрируемостью задачи. Инварианты, не зависящие от  можно было указать еще раньше. Это — собственные значения дискретного спектра
можно было указать еще раньше. Это — собственные значения дискретного спектра  и комбинация амплитуд
и комбинация амплитуд  в непрерывном спектре (см. формулу
в непрерывном спектре (см. формулу  (ком. 2). Их представление через
(ком. 2). Их представление через  и производные от и приводят к формуле (1.41).
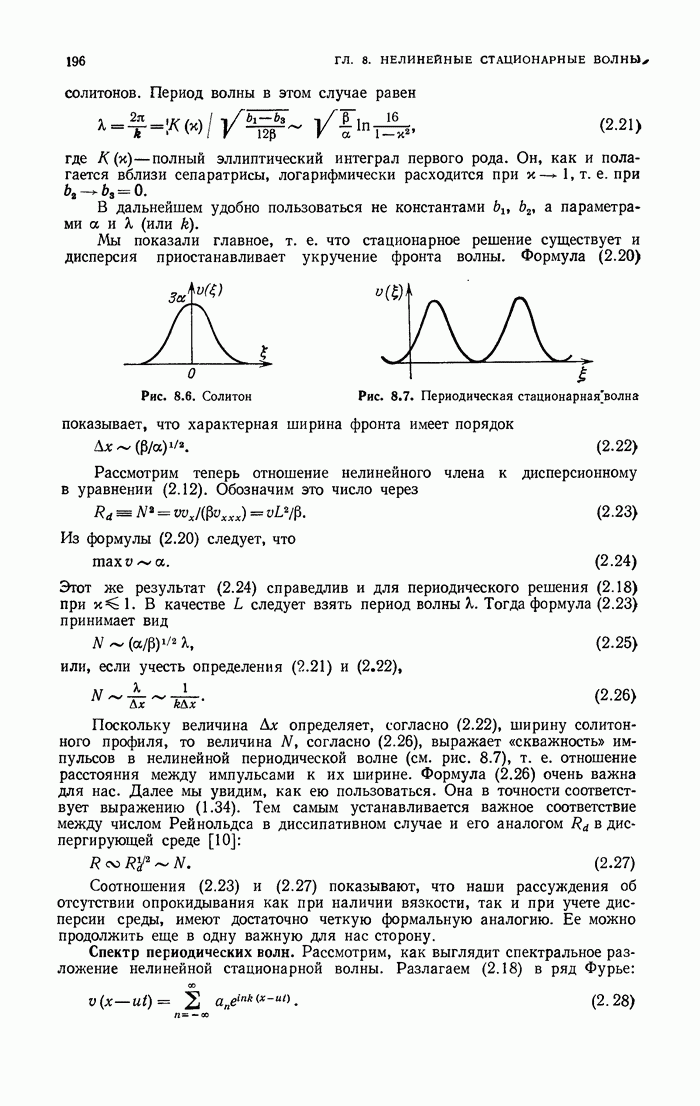
и производные от и приводят к формуле (1.41).
Еще одно важное свойство интегралов движения следует отметить. Используя уравнение (1.43), можно определить понятие скобок Пуассона для уравнения КдВ:

Все интегралы движения  попарно коммутируют друг с другом, т. е. для любой их пары скобки Пуассона (1.44) тождественно обращаются в нуль.
попарно коммутируют друг с другом, т. е. для любой их пары скобки Пуассона (1.44) тождественно обращаются в нуль.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть I. ЧАСТИЦЫ
- Глава 1. ЭЛЕМЕНТЫ ДИНАМИКИ
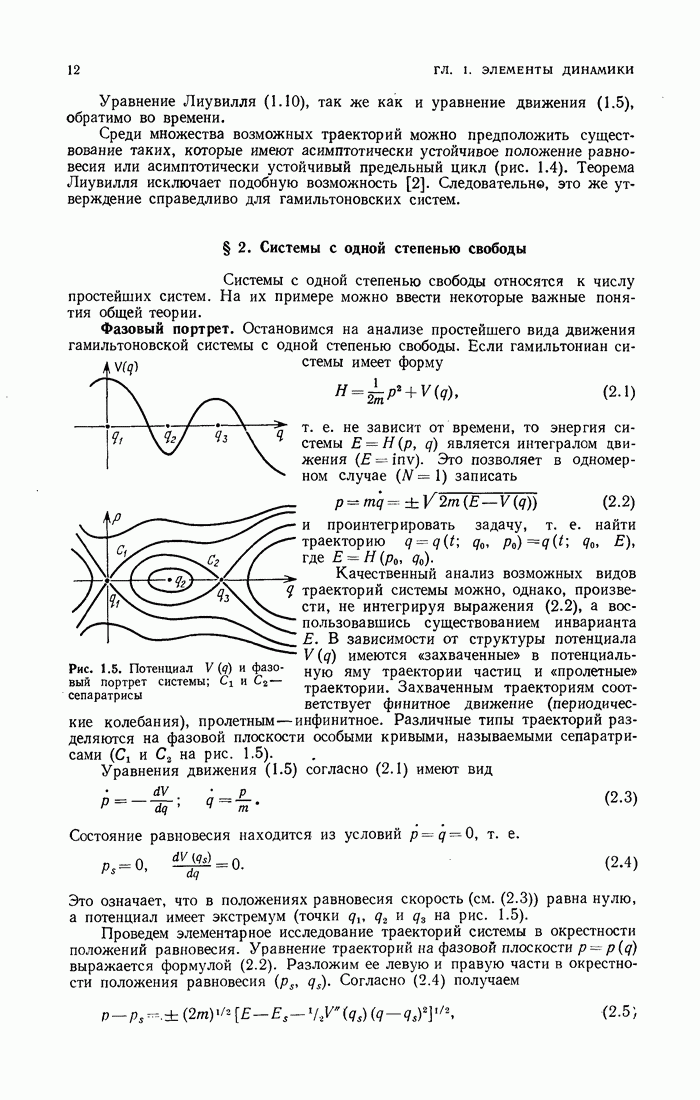
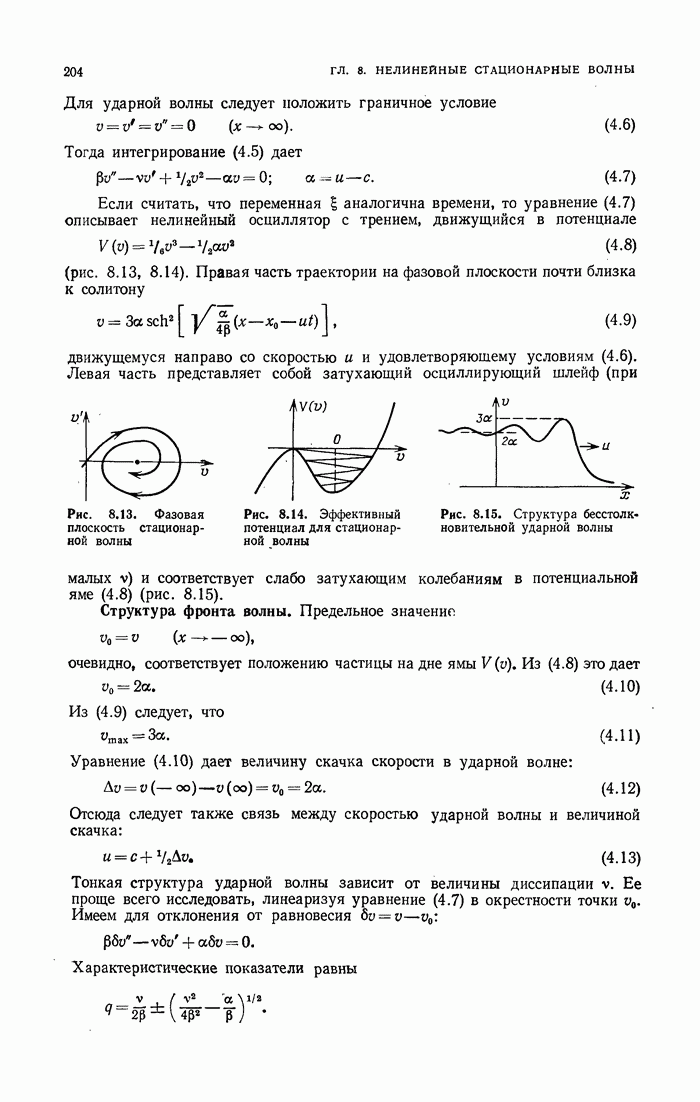
- § 2. Системы с одной степенью свободы
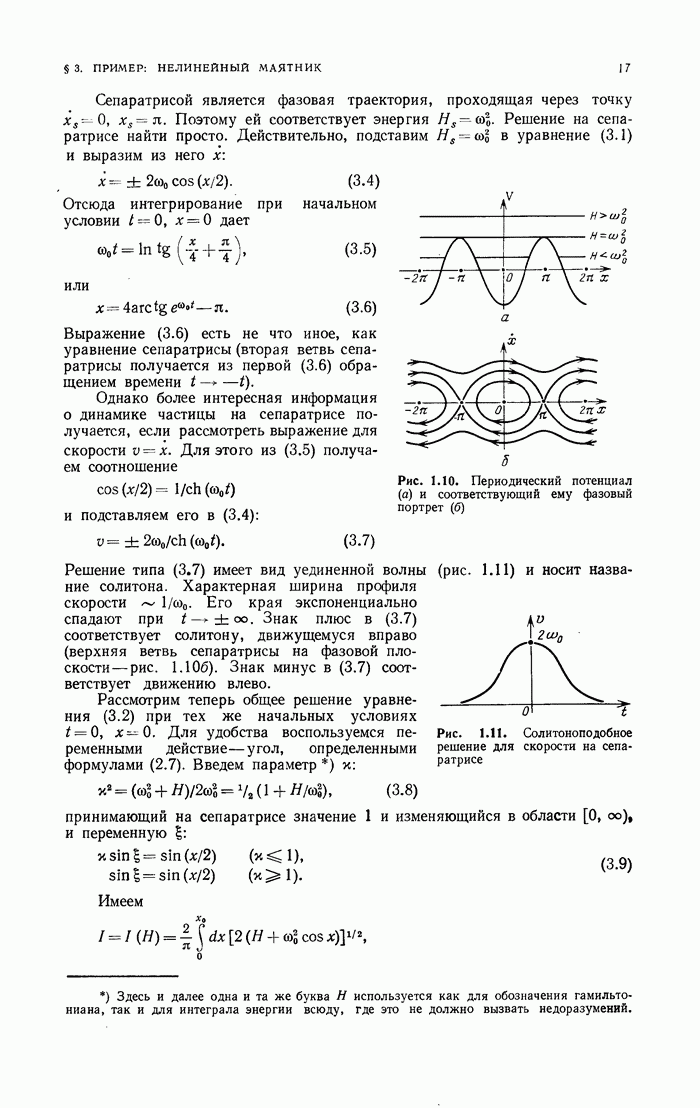
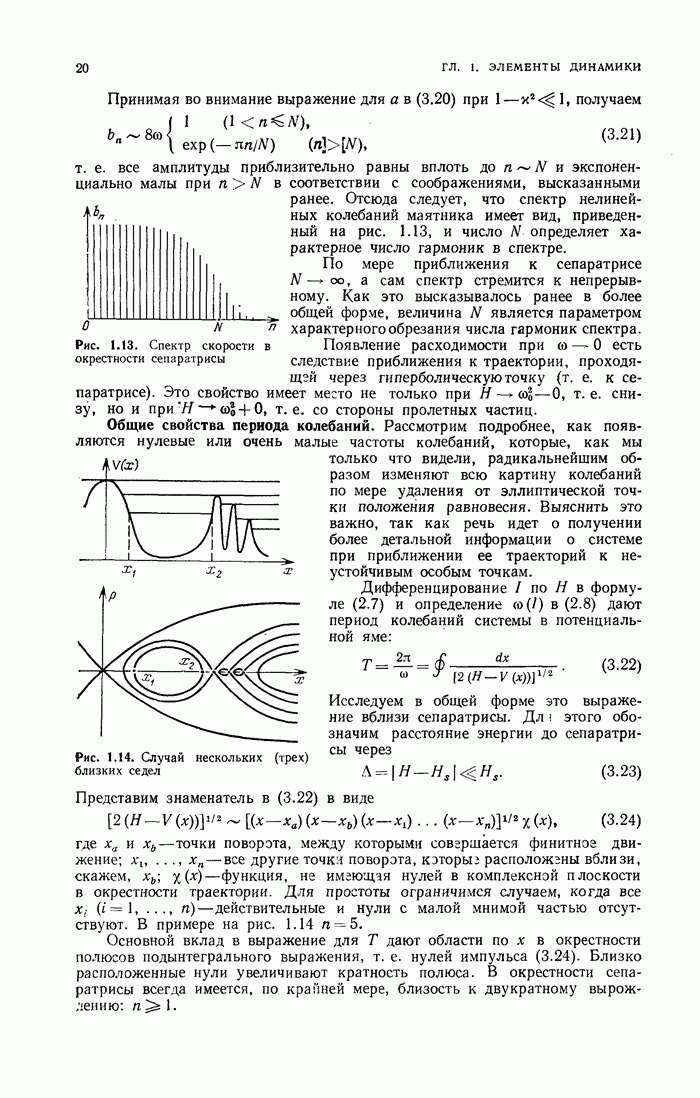
- § 3. Пример: нелинейный маятник
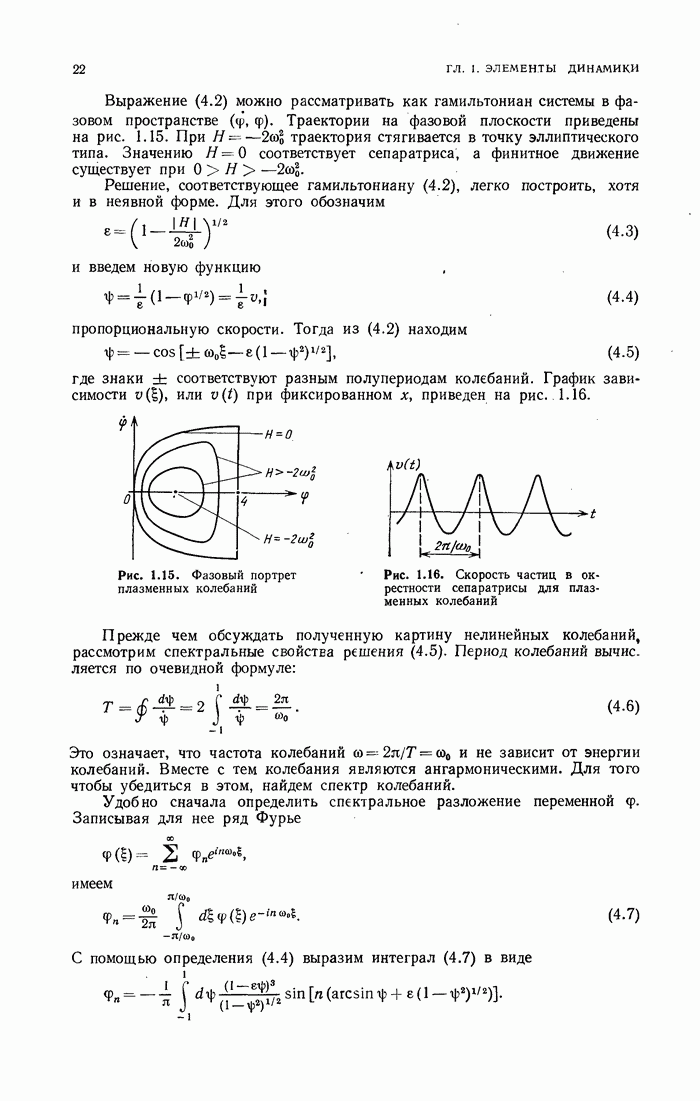
- § 4. Еще два примера нелинейных колебаний
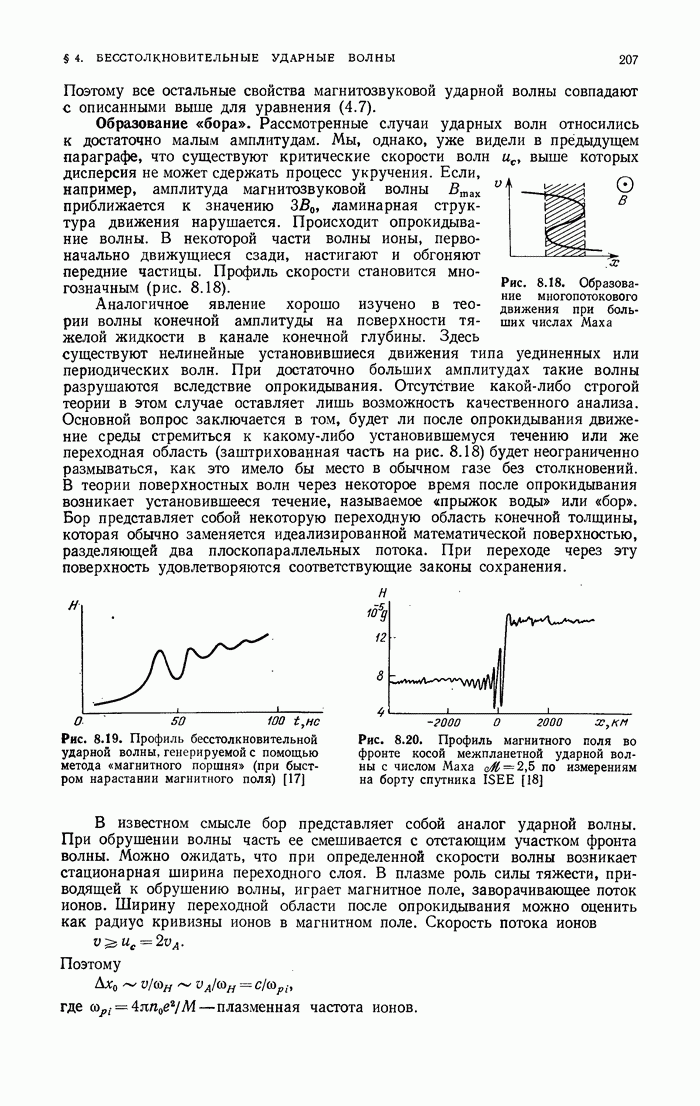
- § 5. Интегральные инварианты Пуанкаре
- § 6. Многомерные интегрируемые системы
- § 7. Отображения
- § 8. Заключительные замечания
- Глава 2. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- § 1. Теория возмущений
- § 2. Метод усреднения
- § 3. Адиабатические инварианты
- § 4. Заряженные частицы в магнитном поле
- § 5. Линейные аналогии адиабатической инвариантности
- Глава 3. СПЕЦИАЛЬНЫЕ МЕТОДЫ
- § 1. Нелинейный резонанс
- § 2. Теория Колмогорова-Арнольда — Мозера (КАМ)
- § 3. Структурные свойства фазовых траекторий
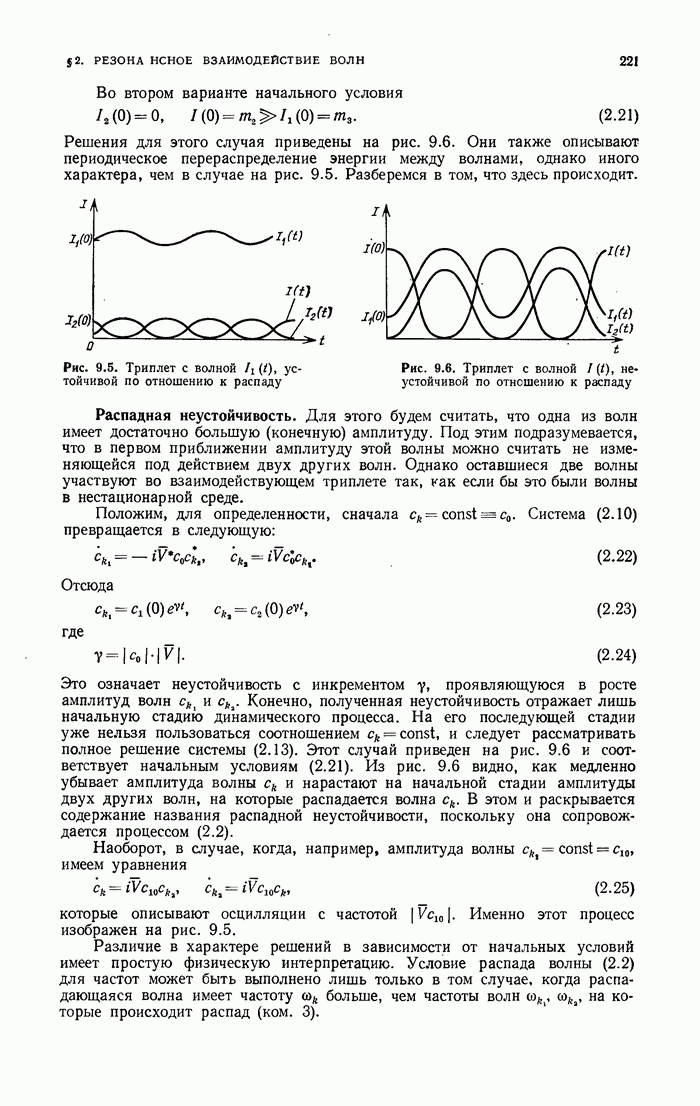
- § 4. Простейшие бифуркации
- Глава 4. ЭРГОДИЧЕСКАЯ ТЕОРИЯ И ХАОС
- § 1. Эргодичность и перемешивание
- § 2. К-системы
- 3. Примеры
- § 4. Возвраты и периодические орбиты
- Глава 5. ХАОС В ДЕТАЛЯХ
- § 1. Универсальное отображение для нелинейных колебаний
- § 2. Перекрытие резонансов
- § 3. Образование стохастического слоя
- § 4. Разрушение интегралов движения
- § 5. Стохастические аттракторы
- § 6. Примеры стохастических аттракторов
- § 7. Общие замечания о появлении хаоса
- Глава 6. ЭЛЕМЕНТЫ КИНЕТИКИ
- § 1. Уравнение Фоккера-Планка-Колмогорова
- § 2. Кинетика при диссипативных отображениях
- § 3. Стохастическое ускорение и «нагрев» частиц
- Глава 7. ФРАКТАЛЬНЫЕ СВОЙСТВА ХАОСА
- § 2. Фракталы и хаос
- Часть II. ВОЛНЫ
- Глава 8. НЕЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ ВОЛНЫ
- § 2. Стационарные волны
- § 3. Примеры стационарных волн
- § 4. Бесстолкновительные ударные волны
- Глава 9. ГАМИЛЬТОНОВСКОЕ ОПИСАНИЕ ВОЛН
- § 2. Резонансное взаимодействие волн
- § 3. Резонансы нелинейных волн
- § 4. Взаимодействие нелинейных волн
- Глава 10. ХАОС В ВОЛНОВЫХ ПОЛЯХ
- § 1. Слабонелинейные поля
- § 2. Проблема Ферми — Паста-Улама (ФПУ)
- § 3. Турбулентность слабонелинейного поля
- § 4. Стохастическая неустойчивость нелинейной волны
- Глава 11. СИЛЬНАЯ ТУРБУЛЕНТНОСТЬ
- § 1. Модель Лоренца
- § 2. Конвективные ячейки
- § 3. Особенности возникновения турбулентности
- § 4. Ленгмюровская турбулентность
- § 5. Солитонная турбулентность
- Глава 12. ТОЧНО ИНТЕГРИРУЕМЫЕ ВОЛНОВЫЕ УРАВНЕНИЯ
- § 2. Интегрируемые уравнения
- Часть III. ПРИМЕРЫ
- § 1. Регулярная и стохастическая динамика частиц в поле волнового пакета
- § 2. Движение в магнитном поле и поле волнового пакета
- § 3. Парадокс исчезновения затухания Ландау
- § 4. Стохастическая паутина
- Глава 14. БИЛЛИАРДЫ
- § 2. Нелинейная динамика лучей
- Глава 15. НЕЛИНЕЙНАЯ ОПТИКА
- § 1. Нелинейная геометрическая оптика
- § 2. Нелинейные кооперативные явления при взаимодействии поля излучения с веществом
- Глава 16. СТРУКТУРНЫЕ СВОЙСТВА ОДНОМЕРНЫХ ЦЕПОЧЕК
- § 2. Спиновые цепочки
- § 3. Возбуждение в молекулярных цепочках
- Глава 17. ВОЗМУЩЕНИЯ В ЗАДАЧЕ КЕПЛЕРА
- § 1. Нелинейная динамика в кулоновском поле
- § 2. Возбуждение и ионизация атома водорода
- § 3. Диффузия эксцентриситета орбит в гравитационном поле планет
- § 4. Диффузия комет из облака Оорта
- СПИСОК ЛИТЕРАТУРЫ