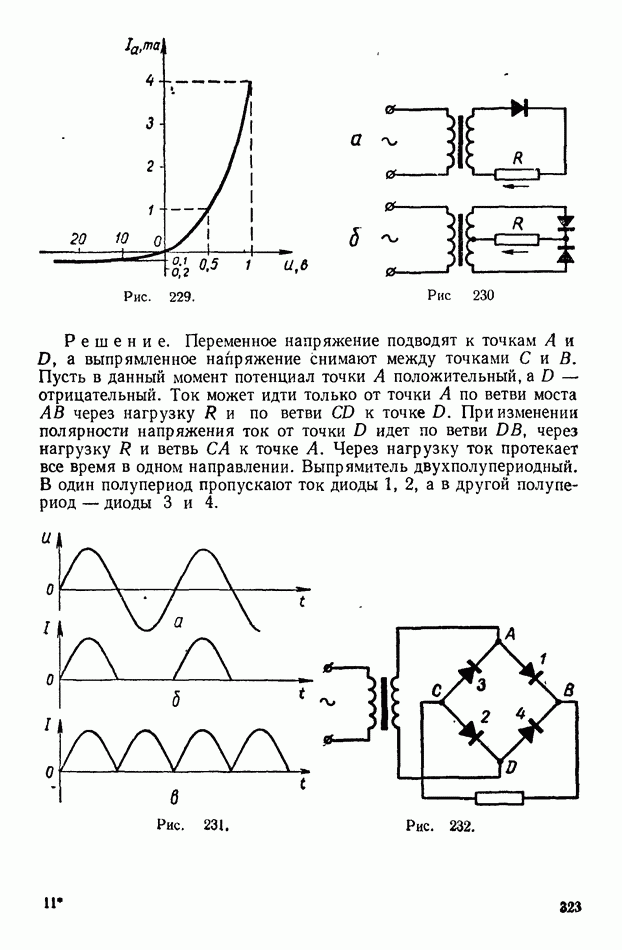
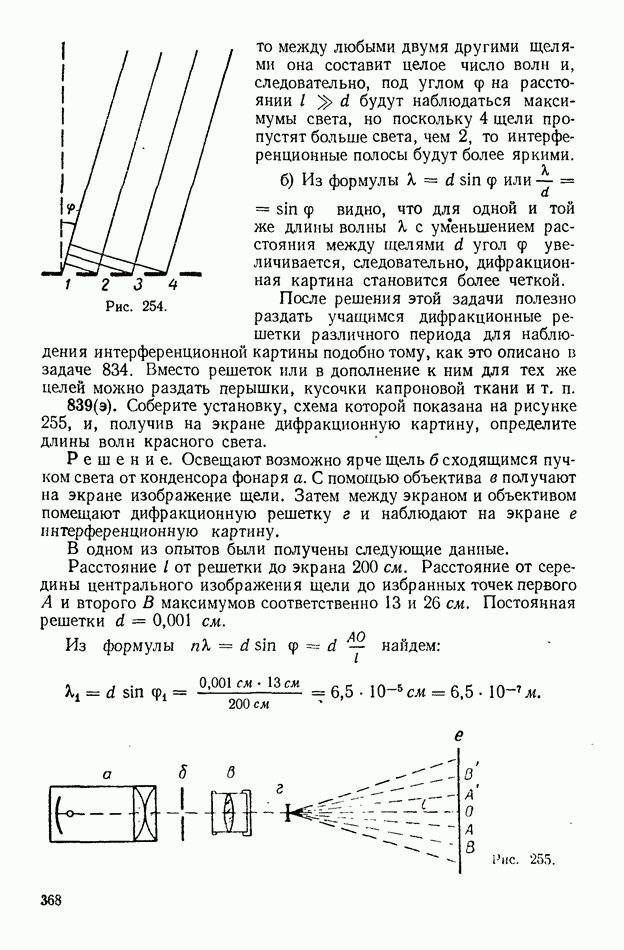
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Сдвиг фаз. Сложение колебаний
Понятие о фазе и тем более о сдвиге фаз трудно усваивается учащимися. Фаза — это физическая величина, характеризующая колебание в определенный момент времени. Состояние колебания в соответствии с формулой  можно охарактеризовать, например, отклонением точки от положения равновесия. Так как при заданных значениях
можно охарактеризовать, например, отклонением точки от положения равновесия. Так как при заданных значениях  значение
значение  однозначно определяется величиной угла
однозначно определяется величиной угла  фазой в уравнениях колебательного движения обычно называют значение угла
фазой в уравнениях колебательного движения обычно называют значение угла 
Время  может быть измерено в долях периода. Следовательно, фаза пропорциональна доле периода, прошедшего от начала колебания. Поэтому фазой колебаний называют также величину, измеряемую долей периода, прошедшей от начала колебаний.
может быть измерено в долях периода. Следовательно, фаза пропорциональна доле периода, прошедшего от начала колебания. Поэтому фазой колебаний называют также величину, измеряемую долей периода, прошедшей от начала колебаний.
Задачи на сложение гармонических колебательных движений решают преимущественно графически с постепенным усложнением условий. Сначала складывают колебания, отличающиеся только по амплитуде, затем — по амплитуде и начальной фазе, и, наконец, колебания, имеющие различные амплитуды, фазы и периоды колебаний.
Все эти задачи единообразны и не сложны по методике решения, но требуют тщательного и кропотливого выполнения чертежей. Для облегчения трудоемкой работы по составлению таблиц и вычерчиванию синусоид целесообразно заготовить их шаблоны в виде прорезей в картоне или жести. На одном трафарете может быть сделано три-четыре синусоиды. Это приспособление позволяет сосредоточить внимание учащихся именно на сложении колебаний и взаимном расположении синусоид, а не на их вычерчивании. Однако, прибегая к такому вспомогательному приему, учитель должен быть уверен в том, что учащиеся уже умеют вычерчивать графики синусоид и косинусоид. Особое внимание нужно обратить на сложение колебаний с одинаковым периодом и фазами, что подведет учащихся к понятию о резонансе.
Используя знания учащихся по математике, следует также решить ряд задач на сложение гармонических колебаний аналитическим методом. При этом представляют интерес следующие случаи:
1) Сложение двух колебаний с одинаковыми периодами и фазами:

Амплитуды колебаний могут быть как одинаковыми, так и различными.
2) Сложение двух колебаний с одинаковыми периодами, но разными амплитудами и фазами. В общем виде сложение таких колебаний дает результирующее смещение:

где

а значение  определяется из формулы
определяется из формулы

В средней школе со всеми учащимися нет необходимости решать эту задачу в таком общем виде. Вполне достаточно рассмотреть частный случай, когда  и разность фаз
и разность фаз  или
или 
Это сделает задачу (см. № 771) вполне доступной и не помешает получить из нее важные выводы о колебаниях, которые получаются при сложении двух гармонических колебаний, имеющих одинаковые периоды, но различные фазы.
766. В одинаковых или различных фазах находятся крылья летающей птицы? руки человека при ходьбе? две щепки, попавшие на гребень и впадину волны от теплохода.
Решение. Условившись о начале отсчета, а также о положительном и отрицательном (например, влево и вниз) направлении движения, заключаем, что крылья летящей птицы движутся одинаково и в одну сторону, они находятся в одной фазе; руки человека, а также щепки отклонились от положения равновесия на одинаковое расстояние, но движутся в противоположные стороны — они находятся в различных, как говорят, «противоположных», фазах.
767(э). Подвесьте два одинаковых маятника и приведите их в колебания, отклонив в разные стороны на одинаковое расстояние. Какова разность фаз данных колебаний? Уменьшается ли она со временем?
Решение. Движения маятников описываются уравнениями:

или в общем случае  где
где  целое число. Разность фаз для данных движений
целое число. Разность фаз для данных движений

со временем не изменяется.
768(э). Проделайте опыт, аналогичный предыдущему, взяв маятники разной длины. Может ли наступить момент, когда маятники

Рис. 239.
будут двигаться в одном направлении? Подсчитайте, когда это наступит для взятых вами маятников.
Решение. Движения отличаются фазой и периодом колебаний

Маятники будут двигаться в одном направлении, когда их фазы станут одинаковыми:  откуда
откуда 
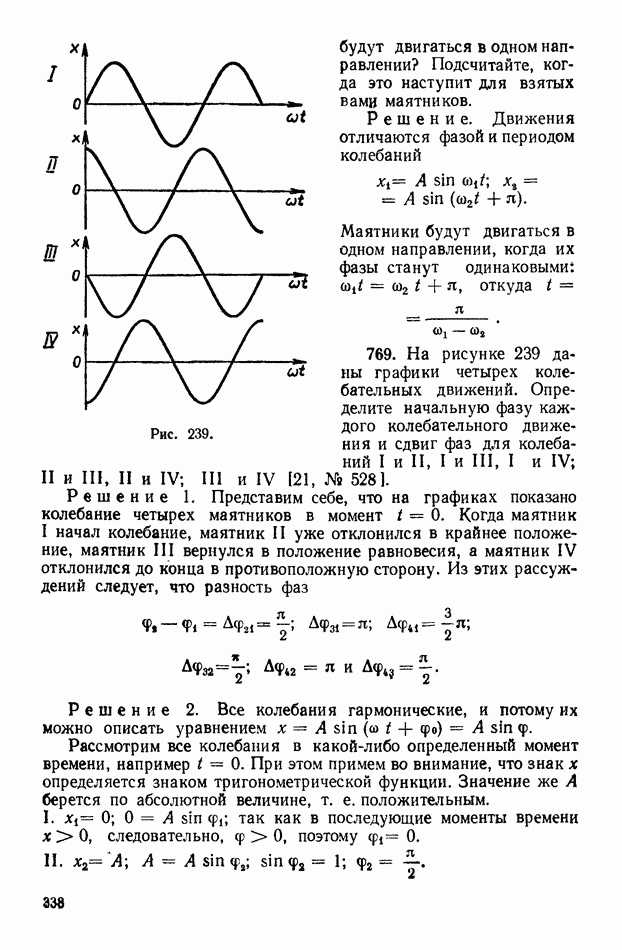
769. На рисунке 239 даны графики четырех колебательных движений. Определите начальную фазу каждого колебательного движения и сдвиг фаз для колебаний I и II, I и III, I и IV; II и III, II и IV; III и IV [21, № 528].
Решение 1. Представим себе, что на графиках показано колебание четырех маятников в момент  Когда маятник I начал колебание, маятник II уже отклонился в крайнее положение, маятник III вернулся в положение равновесия, а маятник IV отклонился до конца в противоположную сторону. Из этих рассуждений следует, что разность фаз
Когда маятник I начал колебание, маятник II уже отклонился в крайнее положение, маятник III вернулся в положение равновесия, а маятник IV отклонился до конца в противоположную сторону. Из этих рассуждений следует, что разность фаз

Решение 2. Все колебания гармонические, и потому их можно описать уравнением 
Рассмотрим все колебания в какой-либо определенный момент времени, например  При этом примем во внимание, что знак х определяется знаком тригонометрической функции. Значение же А берется по абсолютной величине, т. е. положительным.
При этом примем во внимание, что знак х определяется знаком тригонометрической функции. Значение же А берется по абсолютной величине, т. е. положительным.
I.  ; так как в последующие моменты времени
; так как в последующие моменты времени  следовательно,
следовательно,  поэтому
поэтому 


Рис. 240.
III.  ; так как в последующие моменты времени
; так как в последующие моменты времени  следовательно,
следовательно, 

Произведя соответствующие вычисления, получим тот же результат, что и при первом решении: 
Несмотря на некоторую громоздкость второго решения, им надо воспользоваться для формирования у учащихся навыков в применении уравнения гармонического колебательного движения.
770. Сложите два колебательных движения с одинаковыми периодами и фазами, если амплитуда одного колебания  см, а второго
см, а второго  см. Какую амплитуду будет иметь результирующее колебательное движение?
см. Какую амплитуду будет иметь результирующее колебательное движение?
Решение 1. Вычерчивают синусоиды колебаний I и II (рис. 240).
При построении синусоид по таблицам достаточно взять 9 характерных значений фазы: 0°, 45°, 90° и т. д. Амплитуду результирующего колебания находят для тех же фаз, как сумму амплитуд первого и второго колебаний (график III).
Решение 2.

Следовательно, амплитуда результирующего колебания  см, и колебание совершается по закону
см, и колебание совершается по закону  Пользуясь тригонометрическими таблицами, по данной формуле строят синусоиду результирующего колебания.
Пользуясь тригонометрическими таблицами, по данной формуле строят синусоиду результирующего колебания.
771. Сложите два колебания с одинаковыми периодами и амплитудами, если они: не отличаются по фазе; имеют разность фаз отличаются по фазе на 
Решение 1.
Первый случай  вполне аналогичен тому, который рассмотрен в предыдущей задаче и не требует особых пояснений.
вполне аналогичен тому, который рассмотрен в предыдущей задаче и не требует особых пояснений.
Для второго случая  сложение колебаний показано на рисунке 241, а.
сложение колебаний показано на рисунке 241, а.
Сложение колебаний, отличающихся по фазе на  показано на рисунке 241, б.
показано на рисунке 241, б.

Рис. 241.
Решение 2. Для каждого случая выведем уравнение результирующего колебания.

Результирующее колебание имеет ту же частоту и вдвое большую амплитуду.
Для второго и третьего случая можно записать следующее уравнение:

где  разность фаз между двумя колебаниями.
разность фаз между двумя колебаниями.
При  уравнение принимает вид
уравнение принимает вид

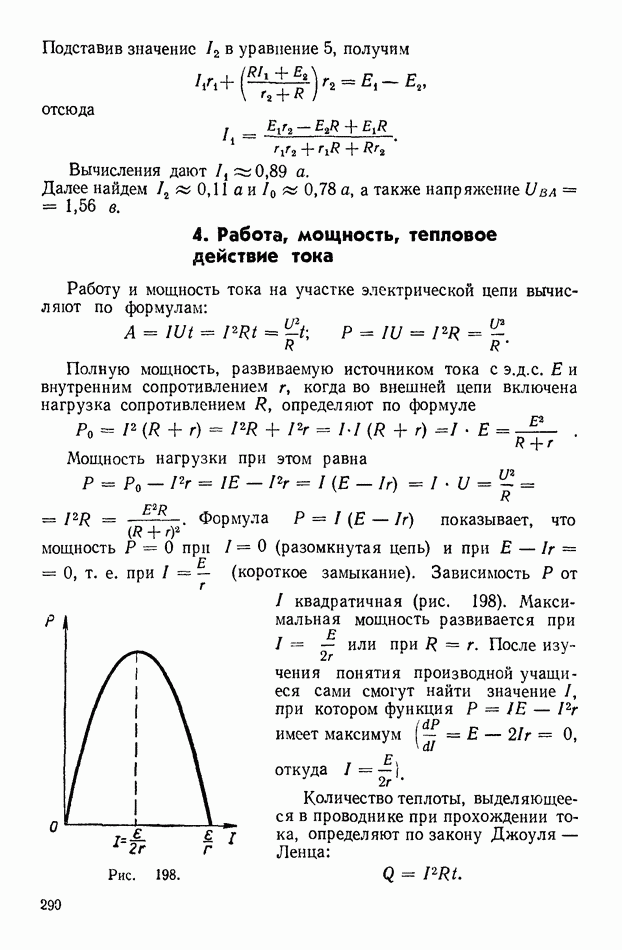
Как видно из этой формулы, при сложении двух гармонических колебаний одного периода, отличающихся по фазе, получается гармоническое колебание того же периода, но с иной, чем у слагаемых колебаний, амплитудой и начальной фазой.
При  Следовательно, результат сложения существенно вависит также от разности фаз. При разности фаз
Следовательно, результат сложения существенно вависит также от разности фаз. При разности фаз  и равенстве амплитуд одно колебание полностью «гасит» другое.
и равенстве амплитуд одно колебание полностью «гасит» другое.
Анализируя решения, следует также обратить внимание на то, что результирующее колебание будет иметь наибольшую амплитуду в том случае, когда разность фаз у складываемых колебаний равна нулю (резонанс).
772. Как зависит качка корабля от периода колебания волн?
Ответ. Качка будет наибольшей при совпадении периода колебаний волн с периодом собственных колебаний корабля.
773. Почему на дороге, по которой самосвалы возят из карьера камень, песок и т. д., с течением времени образуются периодически повторяющиеся углубления (вмятины)?
Ответ. Достаточно образоваться самой незначительной неровности, как кузов, имеющий определенный период колебаний, придет в движение, в результате чего при движении самосвала
будут создаваться, периодические повышенные и пониженные нагрузки на грунт, приводящие к образованию углублений (вмятин) на дороге.
774. Используя решение задачи 760, определите, при какой скорости движения  наступят наибольшие вертикальные колебания вагона, если длина рельса равна
наступят наибольшие вертикальные колебания вагона, если длина рельса равна 
Решение. Период колебаний вагона  сек.
сек.
Если с этой частотой колебаний будут совпадать удары колео на стыках, то наступит резонанс.

775. Правильно ли утверждение, что вынужденные колебания только тогда достигают значительных размеров, когда собственная частота колеблющегося тела равна частоте вынуждающей силы. Приведите примеры, поясняющие ваше утверждение.
Ответ. Резонанс может наступить и тогда, когда периодически, но не по гармоническому закону изменяющаяся сила имеет период, в целое число раз меньший собственного периода тела.
Примером могут быть периодические толчки, действующие на качели не при каждом их качании. В связи с этим следует уточнить ответ предыдущей задачи. Резонанс может наступить не только при скорости поезда  но и при скорости в
но и при скорости в  раз большей, где
раз большей, где  целое число.
целое число.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
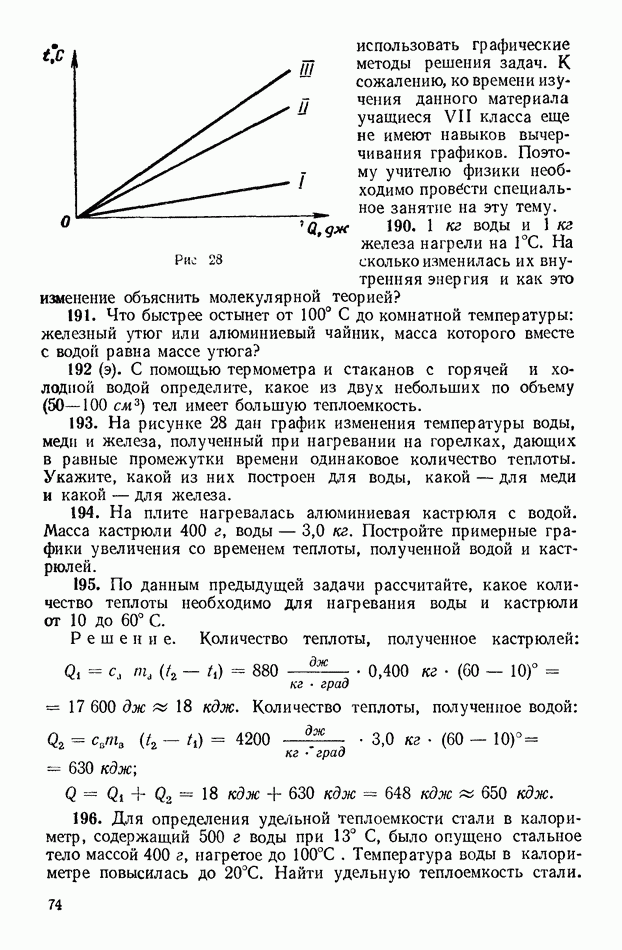
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
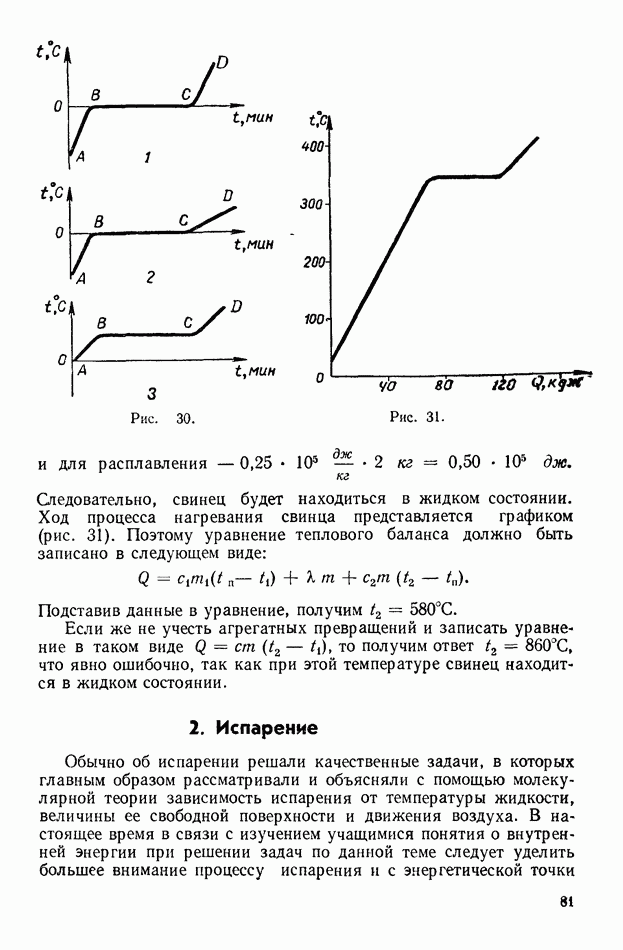
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА