2. Соединения проводников

Вначале решают тренировочные задачи по известным учащимся из VII класса формулам для общего сопротивления при последовательном и при параллельном соединениях проводников и резисторов

Далее решают более сложные задачи, в том числена смешанные соединения. При решении задач со смешанными сложными соединениями резисторов полезны следующие приемы.

Все точки соединения или разветвления в схемах следует обозначить буквами, а сопротивления участков — буквенными индексами, например и т. п.

Вместо сложных схем соединения начертить так называемые эквивалентные схемы, в которых видны все точки разветвления и характер соединения отдельных участков цепи.

Расчеты в общем виде в большинстве случаев проводить не

следует. Удобнее вначале определить сопротивление каждого участка цепи, а потом уже — сопротивление цепи в целом.

Наибольшие затруднения представляют задачи со сложными соединениями резисторов, в которых эквивалентные схемы начертить сразу не удается (рис. 184).

В общем случае сопротивления таких цепей определяют с помощью законов Кирхгофа, но эти законы полностью в средней школе не изучают. В средней школе учащиеся должны научиться вычислять сопротивление лишь симметричных контуров, в которых есть точки с равными потенциалами. Не внося никаких изменений в цепь, точки с равными потенциалами можно соединить или, наоборот, разъединить (тока между такими точками нет). После этого удается начертить эквивалентные схемы цепей и провести расчет сопротивления.

Задачи на определение сопротивлений шунтов и добавочных сопротивлений можно и следует решать вначале как обычные задачи на последовательное и параллельное соединения резисторов, После вывода формул для определения

сопротивления амперметра и вольтметра, число, показывающее, во сколько раз расширены пределы их измерения, можно пользоваться этими формулами при решении большого числа последующих задач.

В задачах с мостиком Уитстона можно применять предварительно выведенную формулу где известное сопротивление резистора, включенного в одно из плеч моста, а и 12— длины плеч реохорда.

Приводим примеры качественных задач.

659. На сколько равных частей надо разрезать проводник сопротивлением ом, чтобы при параллельном соединении этих частей получить сопротивление ом.

Решение. Проводник надо разрезать на 10 частей и соединить эти части параллельно. Действительно, сопротивление каждого отрезка ом. Соединяя все эти отрезки, получаем сопротивление ом.

660. Какие по величине сопротивления можно получить с помощью трех резисторов сопротивлением по 2 ом каждый?

Решение. Составим различные схемы соединений из трех резисторов: последовательное, параллельное и смешанное. Соединять можно не резисторы, а лишь два из них или брать даже один резистор. При последовательном соединении можно получить сопротивления 2,4 и 6 ом, при параллельном —1 ом и 2/3 ом, а при смешанном — 3 ом.

Рис. 182.

661 (э). Как изменятся показания амперметра, когда параллельно ему включить резистор?

Ответ. При любом резисторе ток в цепи амперметра уменьшится.

662 (э). Как изменятся показания вольтметра, если последовательно с ним включить резистор?

Ответ. При последовательном соединении резистора с вольтметром падение напряжения и показания вольтметра уменьшатся. Ответы задач 661 и 662 проверяют опытом. Вычислительные задачи на параллельное и смешанное соединения проводников вначале решают примерно следующей трудности.

663. Из проволоки сопротивлением 10 ом сделано кольцо (рис. 182). Где следует присоединить провода, подводящие ток, чтобы сопротивление получившейся цепи равнялось 1 ом?

Решение. Сопротивление ветви обозначим тогда сопротивление ветви будет равно Ветви соединены параллельно, и общее сопротивление составит

Подводящие ток проводники надо присоединить так, чтобы отрезки проволочного кольца имели сопротивление 8,9 и 1,1 ом.

664. Найдите распределение токов и напряжений в цепи (рис. 183), если напряжение .

Решение. Точки разветвления обозначим буквами Так как участки соединены последовательно, общее сопротивление цепи На участках и резисторы соединены параллельно. Поэтому

В итоге

Рис. 183.

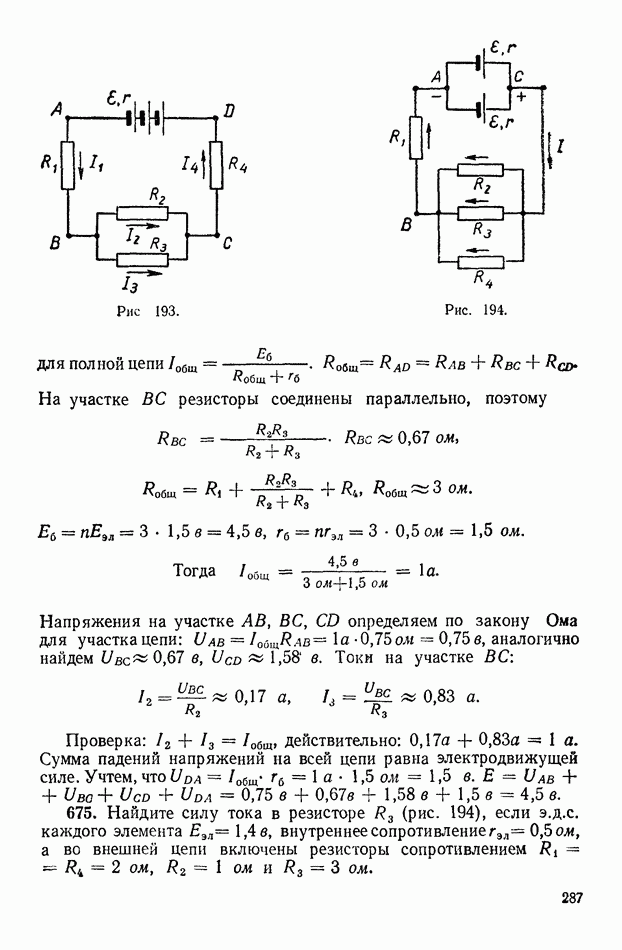
Этот ток течет через токи в других резисторах определяем по закону Ома для участка цепи, предварительно определив

(см. скан)

Расчеты дают:

Аналогично решали задачи на смешанное соединение проводников и в VII классе. Только там схемы соединения были проще. При решении задач в IX классе важно использовать дополнительные сведения, полученные в этом классе:

(для случая параллельного соединения двух проводников).

Рассмотренная выше задача является типовой. Умение решать подобные задачи — необходимое условие для положительной оценки знаний учащихся.

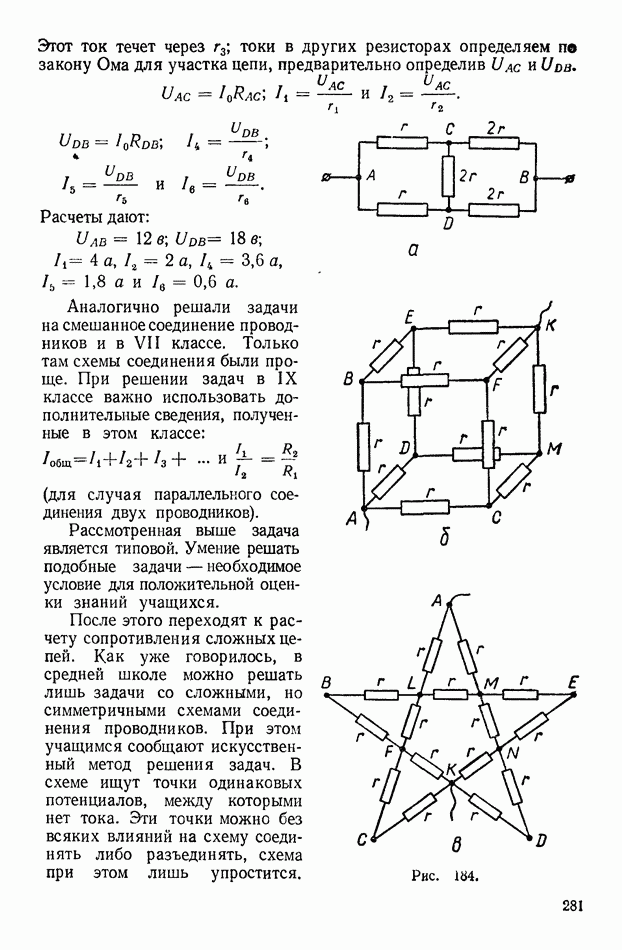
После этого переходят к расчету сопротивления сложных цепей. Как уже говорилось, в средней школе можно решать лишь задачи со сложными, но симметричными схемами соединения проводников. При этом учащимся сообщают искусственный метод решения задач. В схеме ищут точки одинаковых потенциалов, между которыми нет тока. Эти точки можно без всяких влияний на схему соединять либо разъединять, схема при этом лишь упростится.

Рис. 184. (см. скан)

Рис. 185.

665. Определите общее сопротивление показанных на рисунке 184 соединений, считая, что все участки имеют одинаковое сопротивление

Решение. Найдем точки одинаковых потенциалов: а) В цепи (рис. 184, а) точки имеют в силу симметричности ветвей схемы одинаковые потенциалы. Разъединив их, исключаем из цепи резистор сопротивлением ток через который не течет. В упрощенной схеме (рис. 185) явно видны две параллельные ветвй, в каждой из которых последовательно соединены резисторы сопротивлениями поэтому В цепи, имеющей вид куба (рис. 184, б), точки имеют одинаковые между собой потенциалы. Также одинаковы между собой потенциалы точек Соединяя точки равных потенциалов, приходим к эквивалентной схеме (рис. 186), для которой Цепь, схема которой имеет вид пятиконечной звезды (рис. 184, в), симметрична относительно оси звезды, проведенной через вершину А. Одинаковые потенциалы имеют точки Если эти точки разъединить, получим эквивалентную схему (рис. 187), для которой

Как уже говорилось, задачи на расчеты шунта и добавочного сопротивления могут быть решены по предварительно выведенным формулам.

666. Амперметр сопротивлением 3 ом имеет предел измерения тока до Какой длины манганиновую проволоку диаметром надо взять для изготовления шунта к амперметру, чтобы расширить пределы его измерения до 2,5 а? Решение.

Рис. 186.

Рис. 187.

Для манганина

Расчеты дают

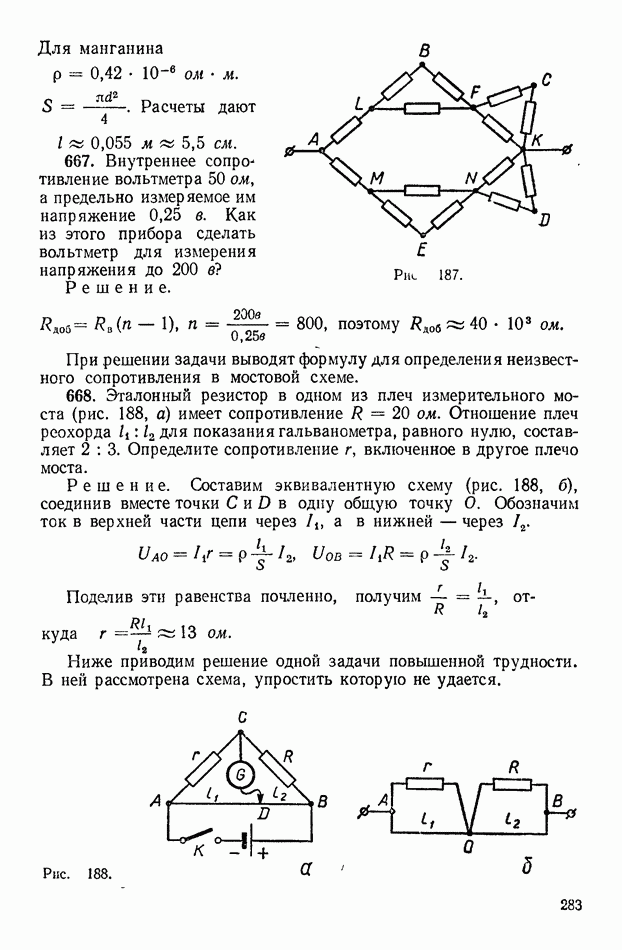
667. Внутреннее сопротивление вольтметра 50 ом, а предельно измеряемое им напряжение 0,25 в. Как из этого прибора сделать вольтметр для измерения напряжения до 200 в?

Решение.

При решении задачи выводят формулу для определения неизвестного сопротивления в мостовой схеме.

668. Эталонный резистор в одном из плеч измерительного моста (рис. 188, а) имеет сопротивление ом. Отношение плеч реохорда для показания гальванометра, равного нулю, составляет Определите сопротивление включенное в другое плечо моста.

Решение. Составим эквивалентную схему (рис. 188, б), соединив вместе точки в одну общую точку О. Обозначим ток в верхней части цепи через а в нижней — через

Поделив эти равенства почленно, получим откуда ом.

Ниже приводим решение одной задачи повышенной трудности. В ней рассмотрена схема, упростить которую не удается.

Рис. 188.

Рис. 189

669. Определите общее сопротивление цепи, схема которой изображена на рисунке 189.

Решение. Схему упростить не удается, так как нельзя найти точки с равными потенциалами. Для решения задачи записывают уравнение для токов и напряжений. Неизвестных токов шесть: кроме того, неизвестного Чтобы решить задачу, необходимо составить систему из семи уравнений.

Во-первых, воспользуемся тем, что сумма токов, «притекающих» к точке разветвления, равна току, «утекающему» из этой точки. Тогда

Во-вторых, работа по перемещению единичного заряда между точками не зависит от формы пути. Эта работа численно равна напряжению и может быть найдена как сумма падений напряжения на участках или

Может быть составлено и восьмое уравнение для контура но оно не является независимым.

Решая систему уравнений получаем искомую величину