| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Электрическая емкость
Здесь решают задачи на определение емкости уединенного тела, емкости конденсатора, а также по известному значению емкостей находят потенциалы тел, расстояния между пластинами конденсаторов и т. п.
Электрическая емкость уединенного тела  где
где  заряд,
заряд,  потенциал этого тела.
потенциал этого тела.
Емкость плоского конденсатора  площадь одной пластинки, перекрывающейся другой,
площадь одной пластинки, перекрывающейся другой,  расстояние между ними).
расстояние между ними).
Емкость уединенного шара радиусом  в среде с диэлектрической проницаемостью
в среде с диэлектрической проницаемостью  можно вычислить по формуле
можно вычислить по формуле 
Конденсатор емкости С при разности потенциалов  и заряде
и заряде  обладает энергией
обладает энергией 
При решении задач на соединения конденсаторов применяют формулы  при параллельном и
при параллельном и  при последовательном соединении.
при последовательном соединении.
Необходимо также решение задач, в которых имеет место перетекание зарядов при соединении тел.
При разборе качественных задач подчеркивают, что емкость зависит только от формы и размеров тела и не зависит от того, сплошное тело или полое, и от материала проводника. Емкость тела зависит также от наличия соседних тел и от их расположения. Приближение какого-либо тела увеличивает емкость, а при неизменном заряде тела уменьшает его потенциал. Приводим примеры таких задач.
638. Два проводника имеют одинаковую форму и размеры, но один из них сплошной, а другой полый. Какое из тел имеет большую емкость?
Ответ. Емкости тел одинаковы.
639. Можно ли изменить потенциал проводника, не касаясь его, не изменяя его заряда?
Ответ. Можно, если приближать к телу или удалять от него другое тело.
Более глубокому пониманию вопроса о емкости способствует разбор качественных задач, в которых рассматривают конденсатор, пластины которого сближают или раздвигают.
При увеличении расстояния  между пластинами совершают работу против сил электрического поля, так как пластины конденсатора имеют разноименные заряды и притягиваются друг к другу.
между пластинами совершают работу против сил электрического поля, так как пластины конденсатора имеют разноименные заряды и притягиваются друг к другу.
Емкость конденсатора  при увеличении
при увеличении  уменьшается.
уменьшается.
Изменение заряда  напряжения
напряжения  и энергии
и энергии  зависит от того, соединен ли конденсатор с источником тока.
зависит от того, соединен ли конденсатор с источником тока.
640. Конденсатор заряжен и отключен от источника тока. Как изменяются емкость С, разность потенциалов  энергия конденсатора
энергия конденсатора  при увеличении расстояния
при увеличении расстояния  между пластинами конденсатора?
между пластинами конденсатора?
Решение. С увеличением  емкость конденсатора уменьшается. Уменьшение емкости С приводит при неизменном заряде
емкость конденсатора уменьшается. Уменьшение емкости С приводит при неизменном заряде  к увеличению разности потенциалов
к увеличению разности потенциалов 
Суждение  можно сделать сразу по закону сохранения энергии. Совершая работу против сил электрического поля, мы увеличиваем энергию конденсатора
можно сделать сразу по закону сохранения энергии. Совершая работу против сил электрического поля, мы увеличиваем энергию конденсатора  Никаких других преобразований энергии в этом случае не происходит.
Никаких других преобразований энергии в этом случае не происходит.
Вывод об увеличении энергии  может быть получен и в результате анализа формул
может быть получен и в результате анализа формул  Заряд
Заряд 
С уменьшается и  увеличивается.
увеличивается.  при этом увеличивается.
при этом увеличивается.
Поставить задачу можно как экспериментальную. К пластинкам раздвижного конденсатора подключают неоновую лампу. Если зарядить конденсатор от кенотронного выпрямителя  , то неоновая лампа загорится. Раздвигая пластины, наблюдают вспыхивание (более яркое свечение) неоновой лампы. Учащимся предлагают объяснить наблюдаемое явление.
, то неоновая лампа загорится. Раздвигая пластины, наблюдают вспыхивание (более яркое свечение) неоновой лампы. Учащимся предлагают объяснить наблюдаемое явление.
641. Конденсатор подключили к источнику тока и раздвинули его пластины. Как изменятся при этом 
Решение.  Заряд
Заряд  уменьшается, так как уменьшилась емкость С. Часть заряда стекает с пластин конденсатора, образуя в цепи ток, обратный току заряда конденсатора. Энергия конденсатора уменьшается,
уменьшается, так как уменьшилась емкость С. Часть заряда стекает с пластин конденсатора, образуя в цепи ток, обратный току заряда конденсатора. Энергия конденсатора уменьшается,  так как
так как  уменьшаются,
уменьшаются, 
Закон сохранения энергии для решения этой задачи применить сложнее, так как надо учитывать преобразования энергии при иротекании тока в цепи.
В вычислительных тренировочных задачах используют формулы

642. Сообщив проводнику заряд  его потенциал увеличили на
его потенциал увеличили на  Определите электроемкость проводника.
Определите электроемкость проводника.
Решение. 
643. Определите толщину диэлектрика конденсатора, емкость которого  площадь перекрывающих друг друга пластин
площадь перекрывающих друг друга пластин  если диэлектрик — слюда
если диэлектрик — слюда 
Решение. 
644. Заряд конденсатора  разность потенциалов на его обкладках
разность потенциалов на его обкладках  Определите энергию конденсатора.
Определите энергию конденсатора.
Решение. 
Формулу  можно вывести в процессе решения данной задачи. Энергия конденсатора равна работе при его разряде, но при этом напряжение меняется от
можно вывести в процессе решения данной задачи. Энергия конденсатора равна работе при его разряде, но при этом напряжение меняется от  до нуля. Закон изменения линейный, поэтому получаем
до нуля. Закон изменения линейный, поэтому получаем  откуда
откуда 
В задачах, где рассматривают соединение заряженных тел и перетекание зарядов с одного тела на другое, необходимо применять:
а) закон сохранения заряда (общий заряд не изменяется, т. е. 
б) условие равновесия статических зарядов. После того как движение зарядов прекратилось, потенциалы всех частей соединения одинаковы 
645. Два шара, емкости которых  заряженные соответственно зарядами
заряженные соответственно зарядами  соединили. Определите заряды на шарах после их соприкосновения.
соединили. Определите заряды на шарах после их соприкосновения.
Решение. Пусть заряды на шарах после их соприкосновения  а потенциалы
а потенциалы  По закону сохранения заряда
По закону сохранения заряда  Равенство потенциалов шаров можно записать в виде
Равенство потенциалов шаров можно записать в виде  Из системы уравнений 1 и 2 определяем неизвестные
Из системы уравнений 1 и 2 определяем неизвестные  Из уравнения (1) выразим
Из уравнения (1) выразим  и подставим в уравнение (2). Получаем
и подставим в уравнение (2). Получаем

Заряд  Вычисления дают значения:
Вычисления дают значения:

В задачах такого типа могут быть даны не емкости  а радиусы шаров
а радиусы шаров  Тогда емкости их определяют по формуле
Тогда емкости их определяют по формуле  Если надо определить, с какого шара и на какой будет перетекать заряд, то вычисляют потенциалы шаров до соединения
Если надо определить, с какого шара и на какой будет перетекать заряд, то вычисляют потенциалы шаров до соединения

Задачи на расчет емкости батарей конденсаторов простые, и обычно рассматривают более сложный случай, когда соединяют  яженные конденсаторы.
яженные конденсаторы.
646. Конденсатор емкостью  заряженный до напряжения
заряженный до напряжения  в, соединили параллельно с конденсатором емкостью
в, соединили параллельно с конденсатором емкостью  заряженным до напряжения
заряженным до напряжения  в (соединяют одноименно заряженные пластины между собой). Определите емкость батареи и напряжение на ее зажимах.
в (соединяют одноименно заряженные пластины между собой). Определите емкость батареи и напряжение на ее зажимах.
Решение. Общая емкость батареи  Напряжение на ее зажимах
Напряжение на ее зажимах  заряд
заряд  где
где  заряды на первом и втором конденсаторах до их соединения. Так как
заряды на первом и втором конденсаторах до их соединения. Так как  то
то  Вычисления дают
Вычисления дают  . Подставлять числовое значение емкости надо в фарадах
. Подставлять числовое значение емкости надо в фарадах 
647. Батарея из двух конденсаторов емкостями  соединенных последовательно, заряжена до напряжения 400 в. Определите емкость батареи и напряжение на зажимах каждого конденсатора.
соединенных последовательно, заряжена до напряжения 400 в. Определите емкость батареи и напряжение на зажимах каждого конденсатора.
Решение. Емкость батареи  определяют по формуле
определяют по формуле

откуда


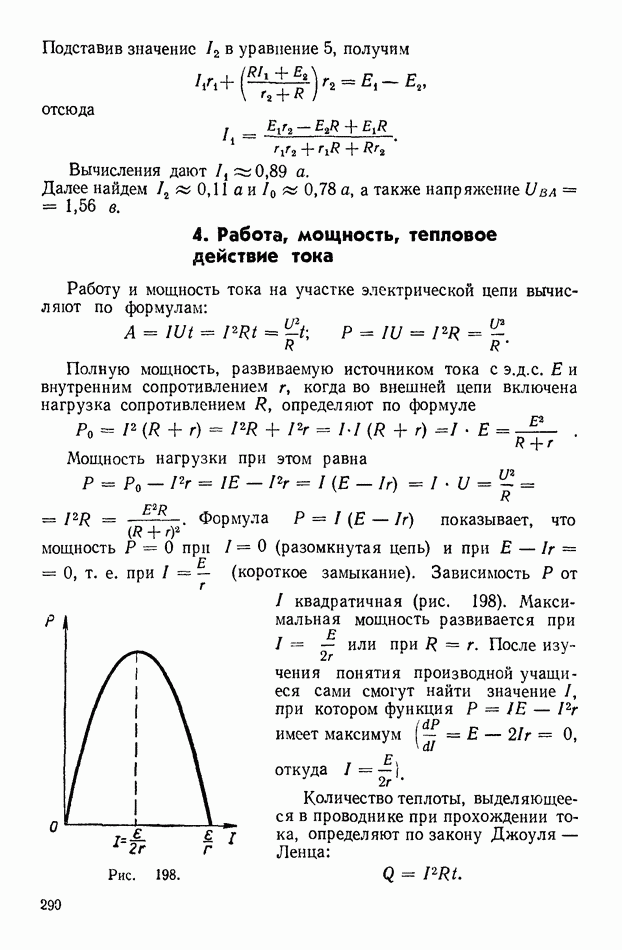
Рис. 180.
Общий заряд на батарее

При последовательном соединении конденсаторов заряд на каждом конденсаторе равен общему заряду батареи:  Это легко понять, если рассмотреть заряды на соединенных пластинах конденсаторов (рис. 180). Эти заряды равны между собой, но имеют разные знаки. Общий заряд на этих пластинах равен нулю. Оказывается, что общий заряд
Это легко понять, если рассмотреть заряды на соединенных пластинах конденсаторов (рис. 180). Эти заряды равны между собой, но имеют разные знаки. Общий заряд на этих пластинах равен нулю. Оказывается, что общий заряд  равен зарядам
равен зарядам  Напряжение на конденсаторах
Напряжение на конденсаторах

Ниже приводим задачи повышенной трудности, разбор которых дает очень много для уяснения понятия электроемкости.
648. Площадь пластин конденсатора  расстояние между ними
расстояние между ними  Частично, как показано на рисунке 181, пространство между пластинами заполнено диэлектриком с относительной диэлектрической проницаемостью
Частично, как показано на рисунке 181, пространство между пластинами заполнено диэлектриком с относительной диэлектрической проницаемостью  Определите емкости конденсаторов.
Определите емкости конденсаторов.
Решение. В первом случае (рис. 181, а) конденсатор можно представить состоящим из двух параллельно соединенных конденсаторов, один из которых — с диэлектриком, а другой — без диэлектрика.
Площадь всей пластины  а части ее с диэлектриком
а части ее с диэлектриком  без
без  диэлектрика
диэлектрика  Тогда емкости этих конденсаторов
Тогда емкости этих конденсаторов

Общая емкость 
Во втором случае (рис. 181, б) электрическое поле, а следовательно, и емкость не изменится, если верхнюю поверхность диэлектрика покрыть бесконечно тонким слоем проводника. Поэтому

Рис. 181.
общая емкость равна емкости двух последовательно соединенных конденсаторов 

649. Выразите энергию конденсатора через напряженность электрического поля.
Решение. Энергия конденсатора  Емкость конденсатора
Емкость конденсатора  а для однородного электрического поля справедливо равенство
а для однородного электрического поля справедливо равенство  Получаем
Получаем

где  объем, занимаемый электрическим полем между пластинами конденсатора. Величину называют плотностью энергии электрического поля (энергия единицы объема).
объем, занимаемый электрическим полем между пластинами конденсатора. Величину называют плотностью энергии электрического поля (энергия единицы объема).
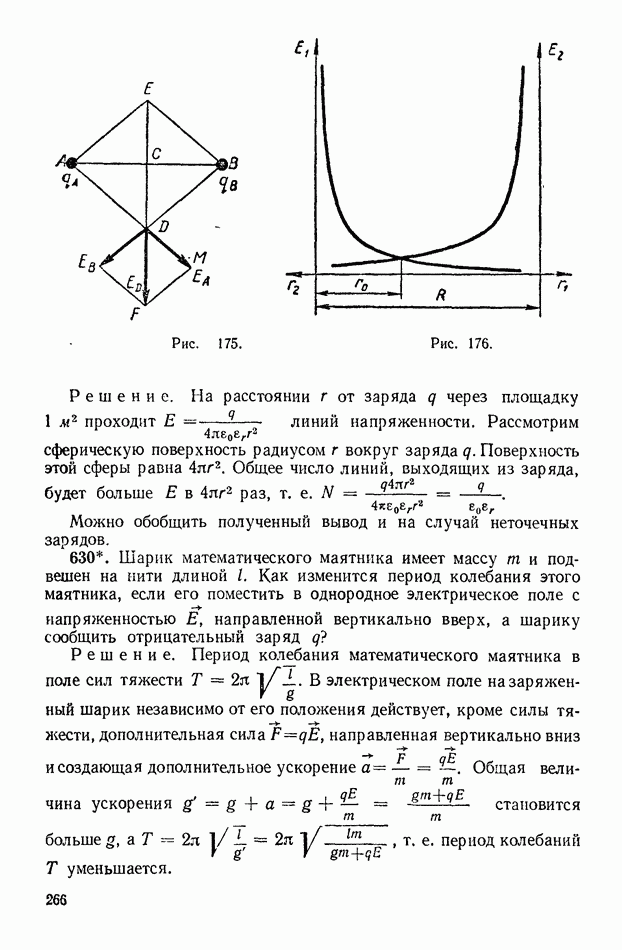
650. Выведите формулу емкости плоского конденсатора, используя данные задачи 629.
Решение. По определению  но для однородного поля
но для однородного поля  где
где  общее число линий напряженности, проходящих через площадь
общее число линий напряженности, проходящих через площадь  Число линий напряженности выражают через заряд (см. № 629):
Число линий напряженности выражают через заряд (см. № 629): 
Окончательно получаем:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
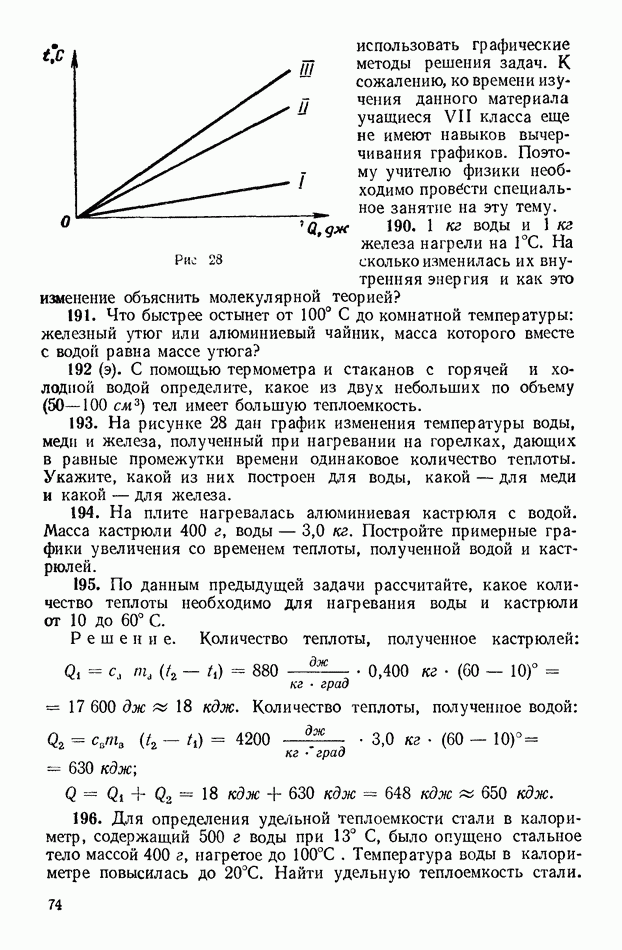
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
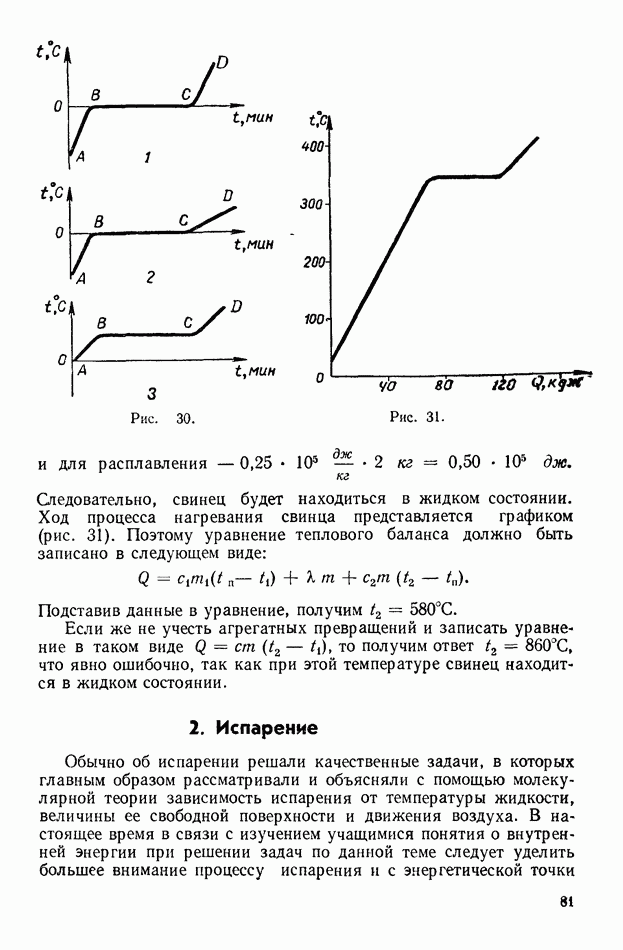
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
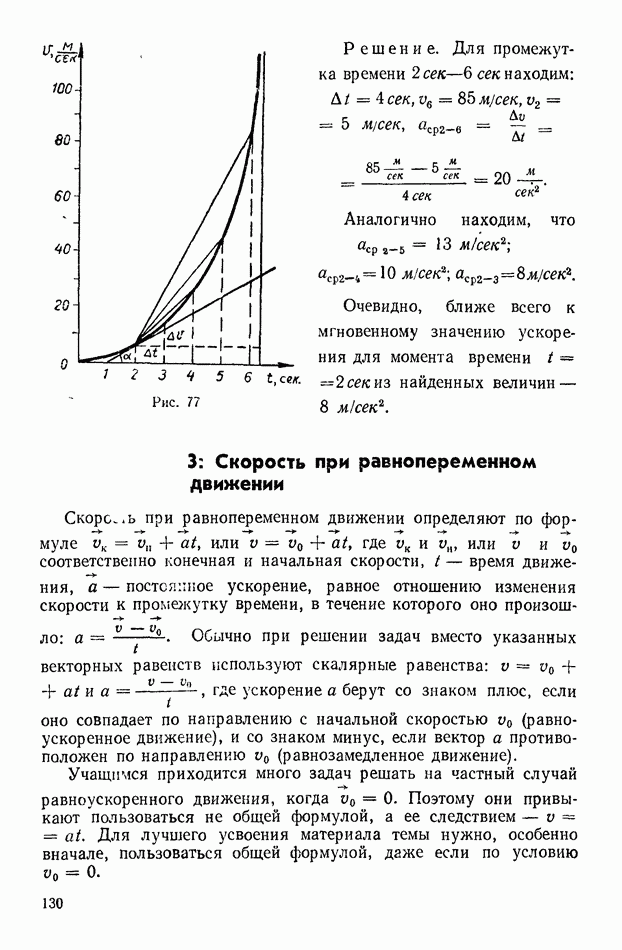
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
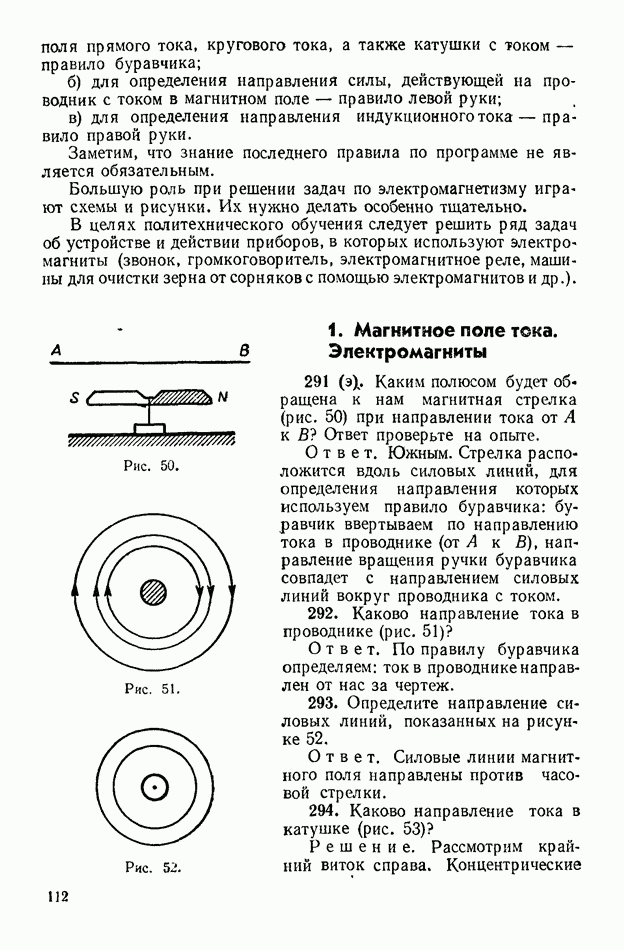
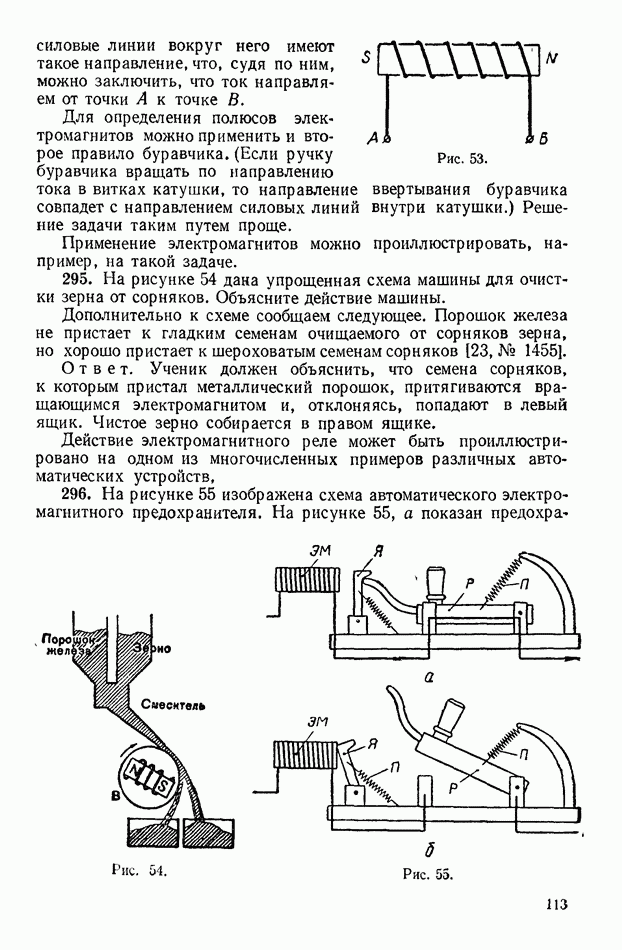
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА