| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Большинство вопросов темы «Основы теории относительности» излагают в ознакомительном плане. Исключением являются зависимость массы тела от скорости, закон взаимосвязи массы и энергии, а также вопрос о скорости света в вакууме как предельной скорости передачи сигнала.
По теме в основном решаются задачи, иллюстрирующие на числовых примерах сокращение длин, замедление хода часов, изменение массы тел и т. п.. Используя формулы специальной теории относительности, учащиеся часто затрудняются в определении, к какой системе отсчета относитсята или иная
величина. Поэтому следует весьма четко разделять величины, относящиеся к разным системам отсчета, для наглядности всегда чертить эти системы координат.
Так как большинство вопросов темы излагается в ознакомительном плане, часть задач следует решать самому учителю при объяснении материала, иллюстрируя полученные соотношения. Обязательными для учащихся являются лишь задачи по зависимости массы тела от скорости и по закону взаимосвязи массы и энергии.

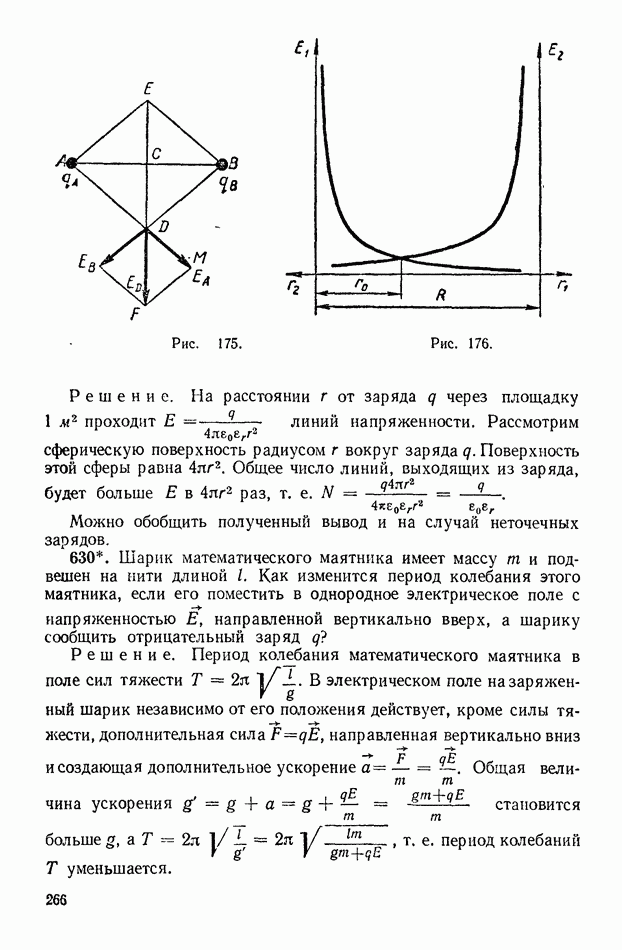
Рис. 312.
Введем обозначения и зависимости, которые используются при решении задач. На рисунке 312 изображены две системы координат  Система К характеризуется координатами
Система К характеризуется координатами  а система К, движущаяся относительно системы К с постоянной скоростью
а система К, движущаяся относительно системы К с постоянной скоростью  направленной вдоль оси
направленной вдоль оси  характеризуется координатами
характеризуется координатами 
В классической механике координаты одного и того же события в системах  связаны между собой преобразованиями Галилея
связаны между собой преобразованиями Галилея 
Если обозначить скорости тела в системе К буквой и, а в системе К — буквой и, то классический закон сложения скоростей можно записать в виде  или
или 
Согласно теории относительности, при больших значениях  необходимо применять преобразования Лоренца:
необходимо применять преобразования Лоренца:

где с — скорость света в вакууме.
В простейшем случае, когда скорость тела в системе К направлена вдоль оси  и равна и, а скорость системы
и равна и, а скорость системы  относительно К также направлена вдоль оси
относительно К также направлена вдоль оси  и равна
и равна  скорость тела в системе К определяется по формуле
скорость тела в системе К определяется по формуле

Это релятивистский закон сложения скоростей.
В специальной теории относительности учитывают сокращение длин тел и замедление хода движущихся часов. Один и тот же стержень имеет разную длину в разных системах отсчета. Его длина  максимальна в системе отсчета, в которой стержень покоится. В системе отсчета, которая движется по отношению к стержню со скоростью
максимальна в системе отсчета, в которой стержень покоится. В системе отсчета, которая движется по отношению к стержню со скоростью  длина стержня будет равна
длина стержня будет равна  Поперечные размеры стержня не меняются
Поперечные размеры стержня не меняются
Если промежуток времени между двумя событиями, происшедшими в одной и той же точке пространства, обозначить  то в любой другой системе отсчета, движущейся относительно первой со скоростью
то в любой другой системе отсчета, движущейся относительно первой со скоростью  промежуток времени
промежуток времени 
В классической физике массу тела принимают за постоянную величину. В теории относительности установлена зависимость массы  от скорости
от скорости  имеющая вид
имеющая вид

где  масса покоя.
масса покоя.
Кроме того, масса тела  является мерой запаса полной энергии тела
является мерой запаса полной энергии тела  В соответствии с формулой Эйнштейна
В соответствии с формулой Эйнштейна  Всякое изменение энергии тела на величину
Всякое изменение энергии тела на величину  влечет за собой изменение массы тела на величину
влечет за собой изменение массы тела на величину  т. е.
т. е. 
Формулы  учащиеся должны помнить и уметь их применять в простейших задачах, примеры которых будут приведены ниже. Очень важно, чтобы учащиеся усвоили, что преобразования Лоренца, релятивистский закон сложения скоростей, зависимости
учащиеся должны помнить и уметь их применять в простейших задачах, примеры которых будут приведены ниже. Очень важно, чтобы учащиеся усвоили, что преобразования Лоренца, релятивистский закон сложения скоростей, зависимости

имеет смысл применять только в случаях, когда скорость  сравнима со скоростью света в вакууме с. При
сравнима со скоростью света в вакууме с. При  возможно применение классических представлений.
возможно применение классических представлений.
949. Запишите преобразования Лоренца и покажите, какой вид они приобретут при 
Решение. Преобразования Лоренца  имеют вид:
имеют вид:

В этом случае система К. движется относительно К вдоль оси  с постоянной скоростью
с постоянной скоростью  Если
Если  то можно пренебречь величинами
то можно пренебречь величинами  и Преобразования координат примут вид:
и Преобразования координат примут вид: 

Это классические преобразования Галилея.
950. Линейка и часы находятся в кабине космического корабля. Космонавт измерил длину линейки 10 и промежуток времени  между двумя событиями. Какова длина линейки и промежуток времени между этими событиями для наблюдателя, находящегося на Земле?
между двумя событиями. Какова длина линейки и промежуток времени между этими событиями для наблюдателя, находящегося на Земле?
Решение. 
Из формул видно, что  Длина движущихся предметов для земного наблюдателя сокращается, а промежуток времени между событиями возрастает.
Длина движущихся предметов для земного наблюдателя сокращается, а промежуток времени между событиями возрастает.
951. Какую скорость должно приобрести тело, чтобы его продольные размеры уменьшились для наблюдателя в 3 раза? До этого тело покоилось относительно данного наблюдателя.
Решение. По условию  но
но  Отсюда
Отсюда  Поперечные размеры тела не меняются.
Поперечные размеры тела не меняются.
952. Частица, масса покоя которой  движется со скоростью:
движется со скоростью:  с.
с.
Определите массу движущейся частицы  (для наблюдателя, относительно которого движется частица со скоростями
(для наблюдателя, относительно которого движется частица со скоростями  Решение.
Решение.

При скорости  с масса частицы
с масса частицы  мало отличается от то.
мало отличается от то.
б)  . Таким образом, при скоростях
. Таким образом, при скоростях  сравнимых со скоростью света в вакууме, необходим учет зависимости массы от скорости.
сравнимых со скоростью света в вакууме, необходим учет зависимости массы от скорости.
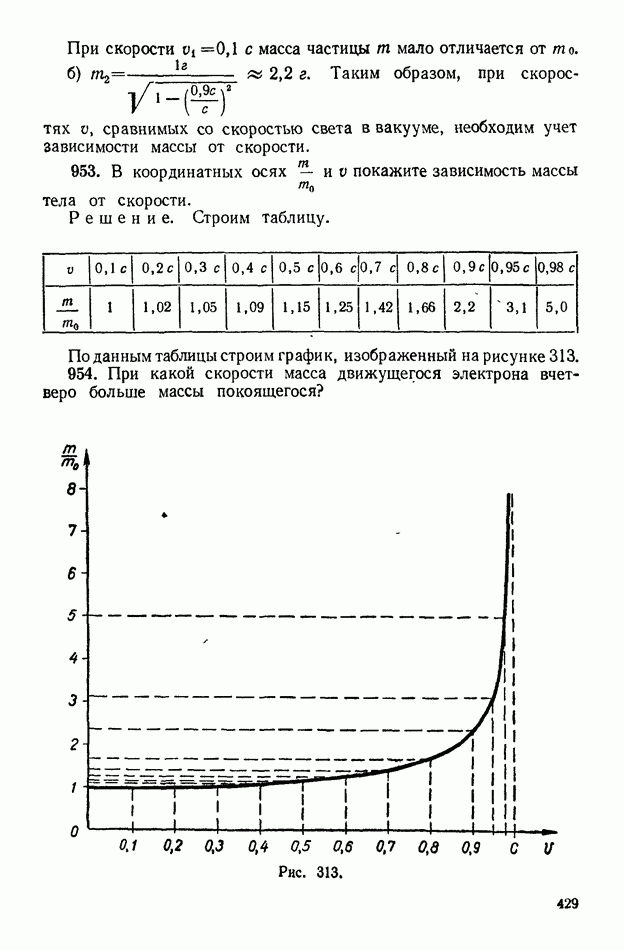
953. В координатных осях  и
и  покажите зависимость массы тела от скорости.
покажите зависимость массы тела от скорости.
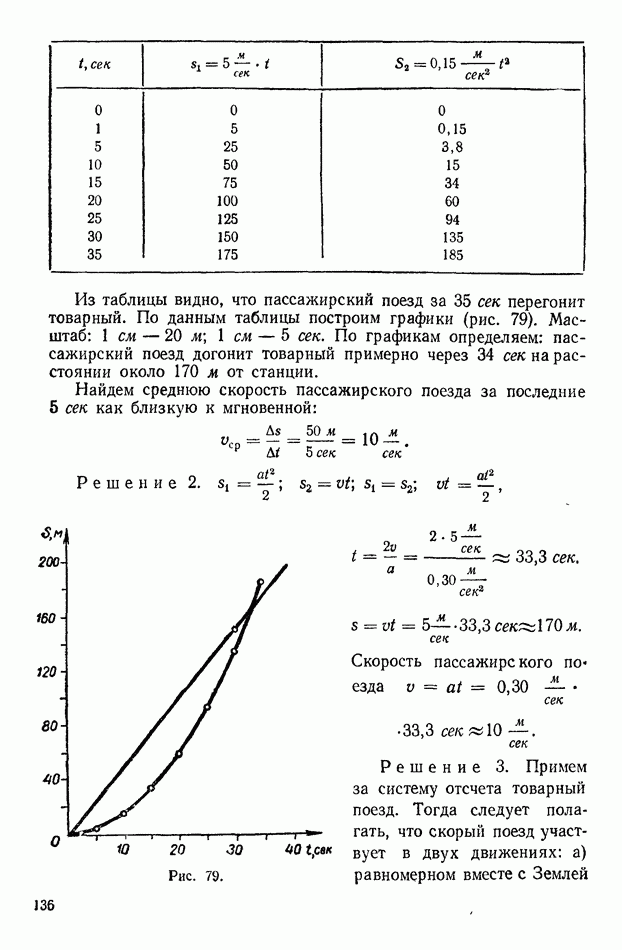
Решение. Строим таблицу.
(см. скан)
По данным таблицы строим график, изображенный на рисунке 313. 954. При какой скорости масса движущегося электрона вчетверо больше массы покоящегося?

Рис. 273.
Решение,  По условию задачи
По условию задачи

955. Определите полную энергию тела массой  Решение. Полная энергия тела
Решение. Полная энергия тела  т. е.
т. е.  Здесь
Здесь  полная релятивистская масса.
полная релятивистская масса.
Полную энергию тела, неподвижного относительно системы отсчета, называют энергией покоя тела и определяют по формуле 
956. Найдите такое изменение энергии, которое соответствует изменению массы на величину массы покоящегося электрона.
Решение.  По условию задачи
По условию задачи  равно массе электрона, т. е.
равно массе электрона, т. е.  Тогда
Тогда 
957. Система К движется относительно системы К со скоростью  Частица движется относительно системы К со скоростью
Частица движется относительно системы К со скоростью  Определите скорость частицы и в системе К.
Определите скорость частицы и в системе К.
Решение. По релятивистскому закону сложения скоростей

Анализируя полученный результат, следует также показать, что по классическому закону сложения скоростей было бы  т. е.
т. е.  т. е.
т. е.  что недопустимо, так как скорость света с в вакууме является предельной скоростью передачи сигнала.
что недопустимо, так как скорость света с в вакууме является предельной скоростью передачи сигнала.
958. Покажите, при каких условиях релятивистский закон сложения скоростей переходит в классический закон.
Решение. Релятивистский закон сложения скоростей  а классический
а классический  Сравнивая эти формулы, легко установить, что релятивистский закон перейдет в классический при
Сравнивая эти формулы, легко установить, что релятивистский закон перейдет в классический при  что будет при условии
что будет при условии 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
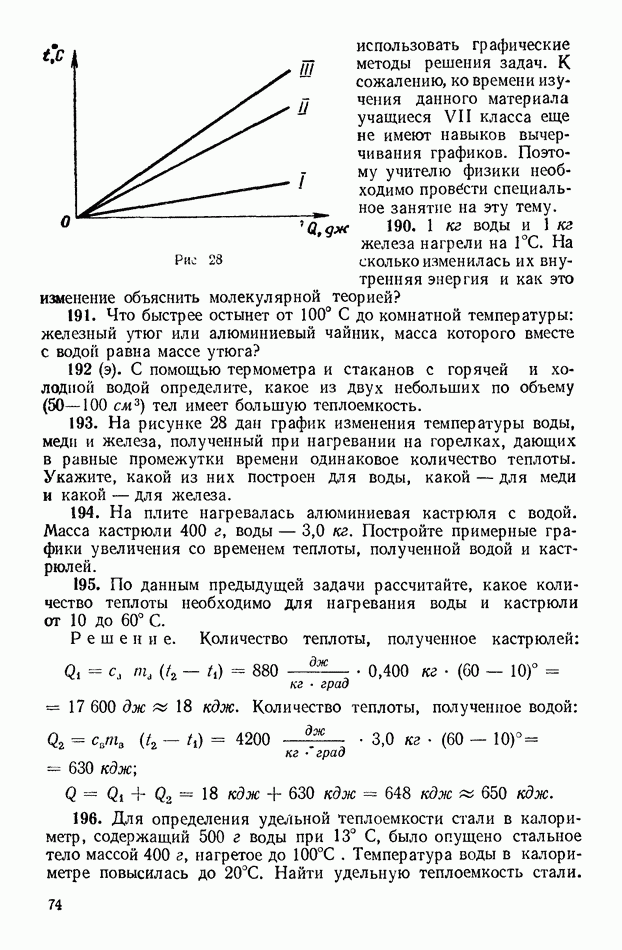
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
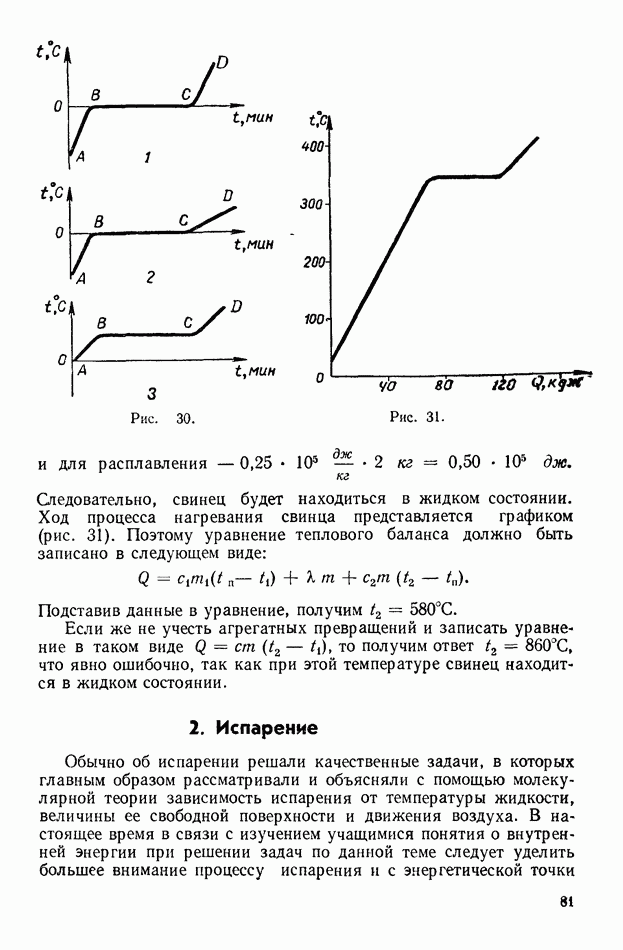
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА