| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Методика решения физической задачи
Методика решения задачи зависит от многих условий: от ее содержания, подготовки учащихся, целей, которые поставил учитель и т. д. Тем не менее существует ряд общих для большинства задач положений, которые следует иметь в виду при их решении с учащимися. Эти общие вопросы методики решения физической задачи мы рассмотрим на следующем примере, данные для которого взяты из опыта.
12. По наклонной плоскости с высоты  см соскальзывает брусок а массой
см соскальзывает брусок а массой  и попадает на брусок
и попадает на брусок  массой
массой  лежащий на горизонтальной доске. На какое расстояние переместится брусок 67 Коэффициент трения бруска
лежащий на горизонтальной доске. На какое расстояние переместится брусок 67 Коэффициент трения бруска  о доску равен 0,37. Трением бруска а о наклонную плоскость пренебречь. Удар считать неупругим.
о доску равен 0,37. Трением бруска а о наклонную плоскость пренебречь. Удар считать неупругим.
Решение задачи начинают с внимательного чтения и изучения ее условия. В классе после чтения условия полезно попросить одного из учеников повторить его своими словами. Это побуждает учащихся внимательно слушать и вдумываться в содержание задачи. При этом выясняют значение новых терминов, непонятных

Рис. 2.
выражений и т. п. Затем в столбец записывают данные задачи в том порядке, как они встречаются в условии. Ниже, «на всякий случай», оставляют несколько строк для табличных данных.
Задача 12. Решение.

Рядом справа пишут «Решение» и делают соответствующий чертеж, даже если он имеется в задачнике. Пользуясь чертежом, анализируют условие задачи, обращая особое внимание на различного рода допущения, которые неизбежны почти в каждой задаче. Одни из допущений оговорены в условии задачи, другие следует делать по ходу ее решения в зависимости от поставленной учителем цели, подготовки учащихся и т. д.
В данном случае в условии задачи говорится, что удар следует считать неупругим. Этим конкретизируется условие задачи и облегчается ее решение. Следует обратить внимание учащихся на то, что, хотя абсолютно неупругих тел нет, практически соударение тел во многих случаях можно считать неупругим.
При прочих равных условиях сила трения на наклонной плоскости меньше, чем на горизонтальной. При большом угле а сила нормального давления значительно меньше веса тела, поэтому сила трения невелика и ею можно в первом приближении пренебречь.
Это допущение значительно упрощает решение задачи.
О других допущениях скажем в процессе решения задачи.
Большинство задач решают аналитико-синтетическим методом (гл. 2,3; стр. 20—24). Но при этом все же нужно приучать учащихся начинать решение «с конца», т. е. с анализа выражений, в которые входит искомая величина. Поясним это подробнее на примере приведенного выше решения задачи 12.
Решение (1-й вариант). Бруски после соударения движутся равнозамедленно, так как на них действует постоянная по величине сила трения. При этом допускаем следующее: время
соударения брусков столь мало, что смещением соударяющихся тел за это время можно пренебречь. (В противном случае необходимо было бы рассматривать более сложное движение, при котором брусок  вначале двигался ускоренно.)
вначале двигался ускоренно.)
Для данного равнозамедленного движения справедлива формула:  откуда
откуда 
Ускорение а найдем по второму закону Ньютона:  Для нахождения скорости
Для нахождения скорости  используем закон сохранения количества движения:
используем закон сохранения количества движения:  откуда
откуда  где
где  скорость бруска а перед соударением с бруском
скорость бруска а перед соударением с бруском 
Значение  найдем по закону сохранения энергии
найдем по закону сохранения энергии  откуда
откуда  (данная формула может быть записана и сразу, если ученики знают ее).
(данная формула может быть записана и сразу, если ученики знают ее).
При этом, однако, мы должны принять, что скорость бруска а перед соударением равна его скорости в нижней точке наклонной плоскости. Это возможно только в том случае, если мы пренебрежем изменением скорости бруска а на небольшом горизонтальном участке его движения между наклонной плоскостью и бруском 
В соответствии со вторым законом Ньютона изменение скорости  невелико, если время движения и силы трения малы.
невелико, если время движения и силы трения малы.
Проводя все необходимые расчеты, оформляем запись решения так, как указано на странице 12.
Горизонтальный участок указан на рисунке не случайно. Если бы брусок а падал на брусок  под углом а, то решение задачи значительно усложнилось (см. № 369).
под углом а, то решение задачи значительно усложнилось (см. № 369).
Решение (2-й вариант). Так как работа против сил трения совершается за счет кинетической энергии движущихся брусков,  откуда
откуда 
Далее находим  аналогично тому, как это делалось в первом варианте решения.
аналогично тому, как это делалось в первом варианте решения.
Большинство задач, особенно в старших классах, нужно стараться решать в общем виде, а уже затем производить числовые расчеты. Это экономит время, так как промежуточные числовые вычисления могут оказаться лишними, а также облегчает проверку решения и его анализ.
Для числовых расчетов важнейшее значение имеет выбор единиц. Программа рекомендует пользоваться на одинаковых правах двумя системами единиц СГС и СИ. При изучении отдельных тем, например по теплоте и молекулярной физике, можно пользоваться
также внесистемными единицами. Однако применение нескольких систем единиц крайне нежелательно. Поэтому нужно стремиться к преимущественному решению задач в одной системе — СИ. Решения большинства приведенных в пособии задач даны в системе СИ.
Если величины в условии задачи даны в разных системах единиц, то обычно считается, что сначала их нужно перевести в одну систему — СГС или СИ, а уже затем приступать к решению задачи. Такой прием действительно полезен, особенно при решении первых задач по механике в VIII классе, где вводится понятие о системах единиц. Но в дальнейшем, когда учащиеся усвоят систему единиц, такое требование будет излишним педантизмом. Обоснованный выбор системы единиц легче и уместнее сделать после решения задачи в общем виде. Тогда может оказаться, что величины не нужно выражать в одной системе ввиду, например, их пропорциональности или особенности поставленного в задаче вопроса, когда требуется узнать, во сколько раз одна величина больше другой. Например, в данной задаче в конечную формулу входит отношение масс, поэтому размерность перемещения зависит только от размерности высоты h. Переводить все величины в одну систему здесь не обязательно. Однако, подчеркнем еще раз, так можно делать только в хорошо подготовленных классах и на определенном этапе обучения.
Подставлять числовые значения величин в формулы лучше с их наименованиями. Это обязывает следить за выбором единиц и позволяет провести проверку решения с помощью действий над наименованиями.
В тех случаях, когда перевод данных задачи в одну систему единиц обязателен, поступают следующим образом, В младших классах сначала такой перевод выполняют арифметическим способом, а затем постепенно приучают учащихся пользоваться общим правилом (см. решение задачи № 70).
В старших, IX—X классах, где учащиеся свободно владеют алгебраическими преобразованиями, часто нет необходимости производить до конца вычисления при переводе одних единиц в другие. Величина в новых единицах в виде дроби или произведения подставляется в конечную формулу, где возможны различные сокращения и упрощения.
Следующий этап — выполнение вычислений. На них нередко тратят много времени. Происходит это главным образом из-за известного формализма в математических знаниях учащихся, из-за неумения применять их на практике. Поэтому при решении задач на первый план нужно выдвигать физическую сторону вопроса, а затем искать пути и средства рациональных вычислений. Для этого, в частности, нужно приучать учащихся пользоваться справочными таблицами, логарифмической линейкой и неукоснительно выполнять правила действий с приближенными числами.
Логарифмическая линейка длиной 25 см позволяет с достаточной точностью производить деление, умножение, возведение в степень, извлечение квадратных и кубических корней, определение тригонометрических функций или соответствующих им углов. Можно, конечно, обойтись и более короткой линейкой — в 12,5 см.
Применение логарифмических линеек — важнейший резерв времени при решении задач.
С правилами приближенных вычислений учащиеся знакомятся на уроках математики до изучения физики. Однако применяют их главным образом на занятиях по физике, где и приходится по-настоящему формировать соответствующие вычислительные навыки. Дело это оказывается нелегким, так как учащиеся, привыкнув производить вычисления «точно», на первых порах с недоверием и неохотой пользуются этими правилами.
Достаточная для учащихся сводка правил о действиях с приближенными числами имеется в задачнике В. П. Демковича [21]. Более полные сведения учитель найдет в книге В. П. Демковича и Н. Я. Прайсмана [2].
Подставим числовые значения величин с их наименованиями в формулу (стр. 12), не переводя по указанным выше причинам их в одну систему, и выполним последовательно все арифметические действия:

В заключение проводят проверку и анализ решения
Сначала проверяют порядок полученной величины, производя более грубое, чем это положено правилами действий с приближенными числами, округление чисел и комбинируя действия с ними таким образом, чтобы облегчить выполнение математических операций в уме. Такую проверку ответов должен постоянно делать учитель, приучая к этому и учащихся, которые нередко ошибаются в «запятых», не имея навыков приближенных подсчетов. В простейших случаях подсчеты делают устно, а в более сложных, как например в этом, используют краткие вспомогательные записи, так как «держать в уме» большое количество данных нет надобности.

Далее проводят действия над наименованиями. Ответ получают в линейных единицах — сантиметрах, что также является подтверждением правильности решения задачи.
Для проверки и анализа ответа в ряде случаев полезно решить задачу несколькими способами, а также использовать эксперимент.
В данном случае идея опыта ясна из рисунка 2. Бруску  придают
придают  -образную форму, чтобы скатывающееся с наклонной плоскости тело задерживалось на нем. Для того чтобы удар был неупругим, на брусок можно положить кусок пластилина.
-образную форму, чтобы скатывающееся с наклонной плоскости тело задерживалось на нем. Для того чтобы удар был неупругим, на брусок можно положить кусок пластилина.
Скатывая брусок а с высоты  см, найдем, что он перемещается на меньшее расстояние, чем следует из расчетов.
см, найдем, что он перемещается на меньшее расстояние, чем следует из расчетов.
Различие объясняется неучтенными потерями энергии при трении бруска а о наклонную плоскость и преодолении сопротивления воздуха, а также допущением, что бруски взаимодействуют как неупругие тела.
Далее перед учащимися можно поставить задачу — снизить потери энергии на преодоление трения и тем самым уменьшить разницу теоретических расчетов и опытных данных.
Учащиеся могут предложить заменить трение скольжения трением качения, скатывая с наклонной плоскости шарик. Учителю нужно иметь в виду, что в этом случае кинетическая энергия шарика  где энергия вращения
где энергия вращения 
Поэтому скорость поступательного движения шарика оказывается в 1,18 раз меньшей, чем для соскальзывающего без трения тела. Не сообщая учащимся указанных формул, можно пояснить существо вопроса качественно.
Очевидно, в данном случае лучше всего скатывать массивную тележку на маленьких колесиках, энергией вращения которых можно пренебречь.
Помимо рассмотренных выше общих вопросов, в методике решения задач различных типов имеются и некоторые специфические особенности. Они рассмотрены ниже, в главе 2.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
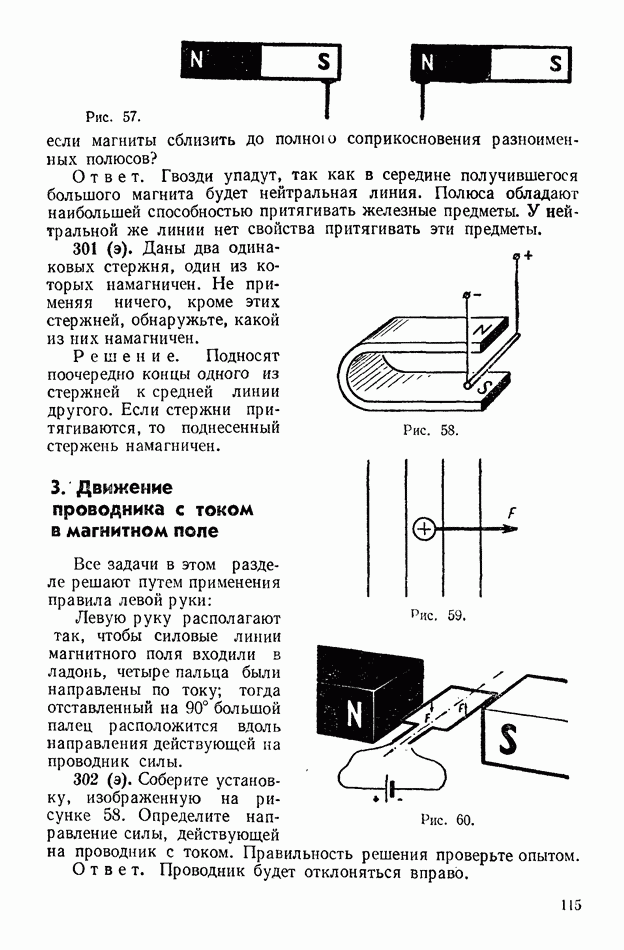
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА