| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
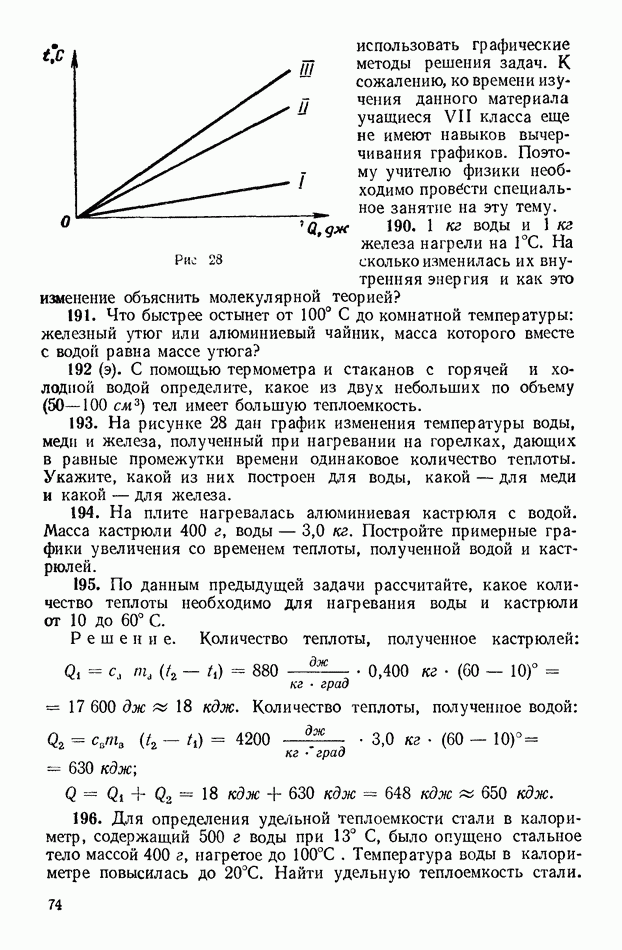
По данной теме решают задачи, в которых исследуют или находят величины, характеризующие неравномерное движение: траекторию, путь, перемещение, скорость и ускорение. Из различных видов неравномерного движения подробно рассматривают только равнопеременное движение.
Тему завершают решением задач о движении по окружности. Здесь наибольшую трудность представляют новые для учащихся понятия об угловой скорости и нормальном ускорении. Для первоначального формирования этих понятий рассматривают несложные задачи. Более сложные задачи решают в связи с изучением законов динамики 
1. Средняя и мгновенная скорость
Первое понятие о средней и мгновенной скорости учащиеся получили в VI классе. Поэтому в порядке повторения сначала полезно решить задачи, подобные тем, которые приведены в гл. 5,1. Затем главное внимание уделяют формированию умений составлять и решать уравнения движения.
При решении задач о средней скорости нужно предупредить распространенную ошибку учащихся, пытающихся найти среднюю скорость как среднее арифметическое скоростей тела на разных участках пути.
Используя понятие средней скорости, с помощью графических задач следует углубить понятие о мгновенной скорости как пределе отношения — при 
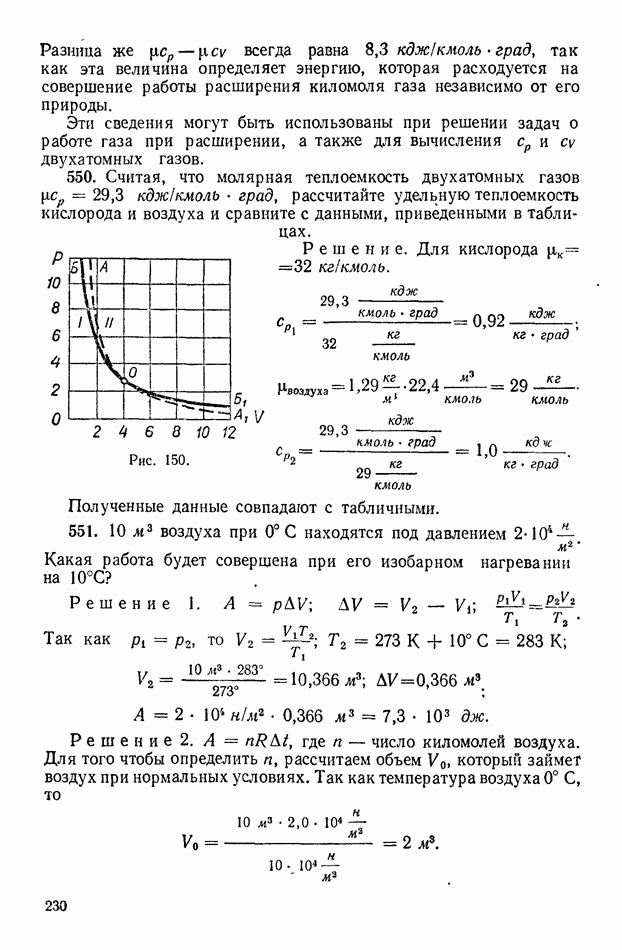
326. Автомашина ехала по ровной дороге 1 мин со скоростью 90 км/ч, затем 2 мин на подъем со скоростью 60 км/ч и 0,5 мин под уклон со скоростью 120 км/ч. Найдите среднюю скорость движения автомашины за это время.
Решение. Изобразим условно, без соблюдения масштаба отрезки пути  (рис. 73).
(рис. 73).


Рис. 73.
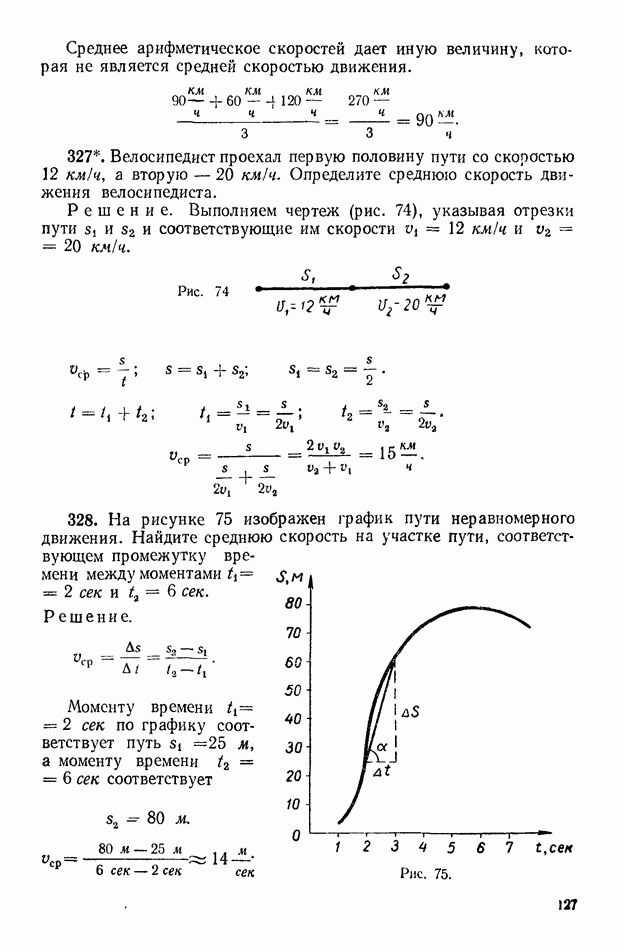
Среднее арифметическое скоростей дает иную величину, которая не является средней скоростью движения.

327. Велосипедист проехал первую половину пути со скоростью  а вторую
а вторую  Определите среднюю скорость движения велосипедиста.
Определите среднюю скорость движения велосипедиста.
Решение. Выполняем чертеж (рис. 74), указывая отрезки пути  и соответствующие им скорости
и соответствующие им скорости 

Рис. 74 1 1 ТТ?

328. На рисунке 75 изображен график пути неравномерного движения. Найдите среднюю скорость на участке пути, соответствующем промежутку времени между моментами  .
.
Решение.

Моменту времени  сек по графику соответствует путь
сек по графику соответствует путь  а моменту времени
а моменту времени  сек соответствует
сек соответствует


Рис. 75.
329. По графику, изображенному на рисунке 75, определите среднюю скорость движения тела для промежутков времени: 2 сек  сек — 2,5 сек. Какое из найденных значений скорости ближе всего к мгновенной скорости движения тела для
сек — 2,5 сек. Какое из найденных значений скорости ближе всего к мгновенной скорости движения тела для  сек? Как получить значение средней скорости, еще более близкое к мгновенной?
сек? Как получить значение средней скорости, еще более близкое к мгновенной?
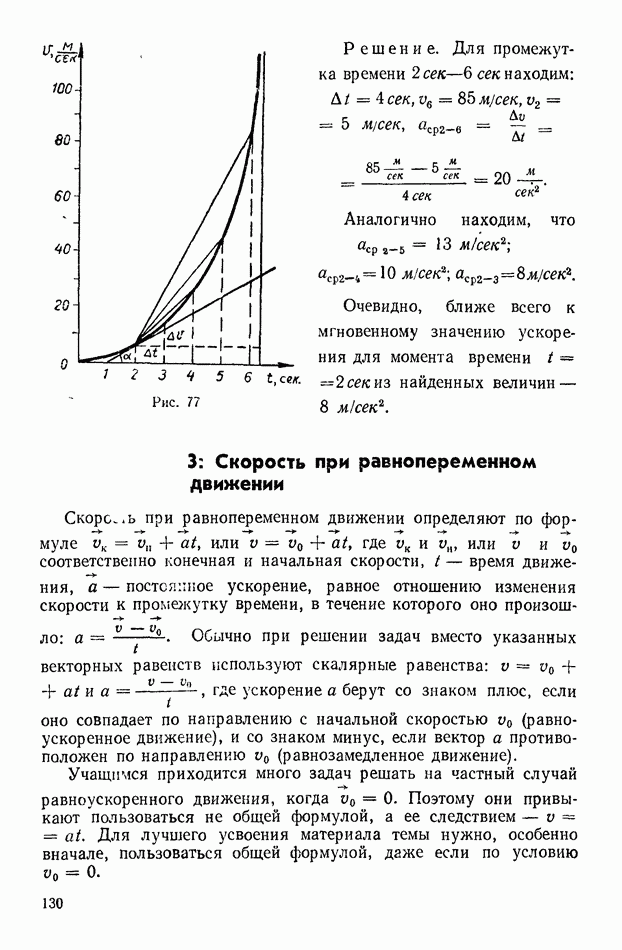
Решение. Аналогично предыдущей задаче находим: 
Скорость  наиболее близка к мгновенному значению скорости для
наиболее близка к мгновенному значению скорости для  сек. Чем меньше промежуток времени
сек. Чем меньше промежуток времени  тем значение средней скорости ближе к мгновенной.
тем значение средней скорости ближе к мгновенной.
При повторении в конце года полезно сообщить, что отношение  численно равно тангенсу угла наклона хорды, соединяющей
численно равно тангенсу угла наклона хорды, соединяющей  соответствующие точки кривой, к оси времени. Мгновенная же скорость численно равна тангенсу угла наклона касательной к кривой графика пути в заданной точке.
соответствующие точки кривой, к оси времени. Мгновенная же скорость численно равна тангенсу угла наклона касательной к кривой графика пути в заданной точке.
330. Определите, в каких случаях говорится о средней и в каких о мгновенной скорости: 1) спидометр мотоцикла показал скорость  ураган распространялся со скоростью
ураган распространялся со скоростью  скорость ветра достигала
скорость ветра достигала  скорость звука в сухом воздухе при
скорость звука в сухом воздухе при  равна
равна 
Ответ. В 1-м и 3-м случаях говорится о мгновенной, а во  о средней скорости. Скорость звука при данных условиях постоянна; движение равномерное, поэтому среднее и мгновенное значения скорости совпадают.
о средней скорости. Скорость звука при данных условиях постоянна; движение равномерное, поэтому среднее и мгновенное значения скорости совпадают.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
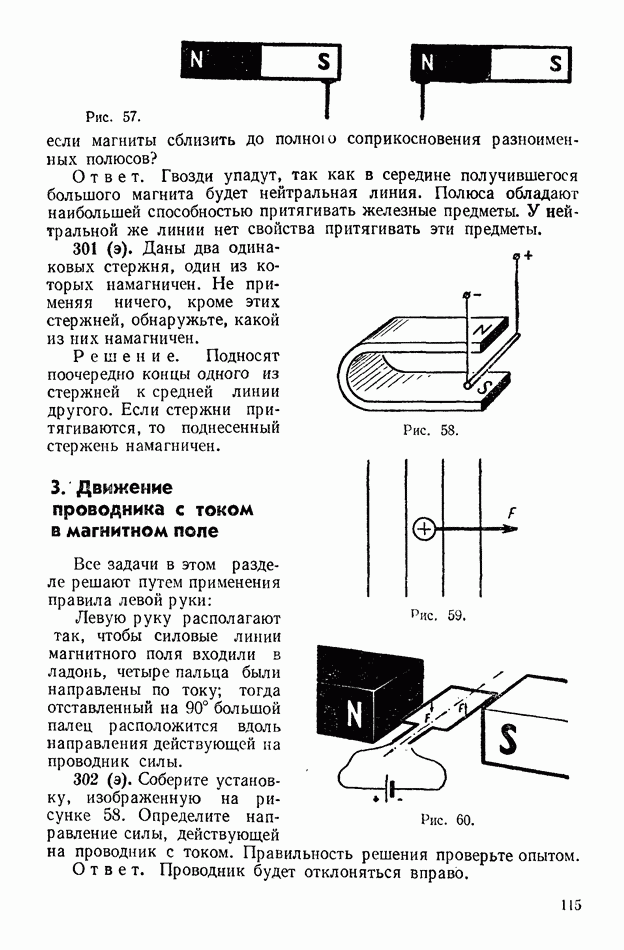
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
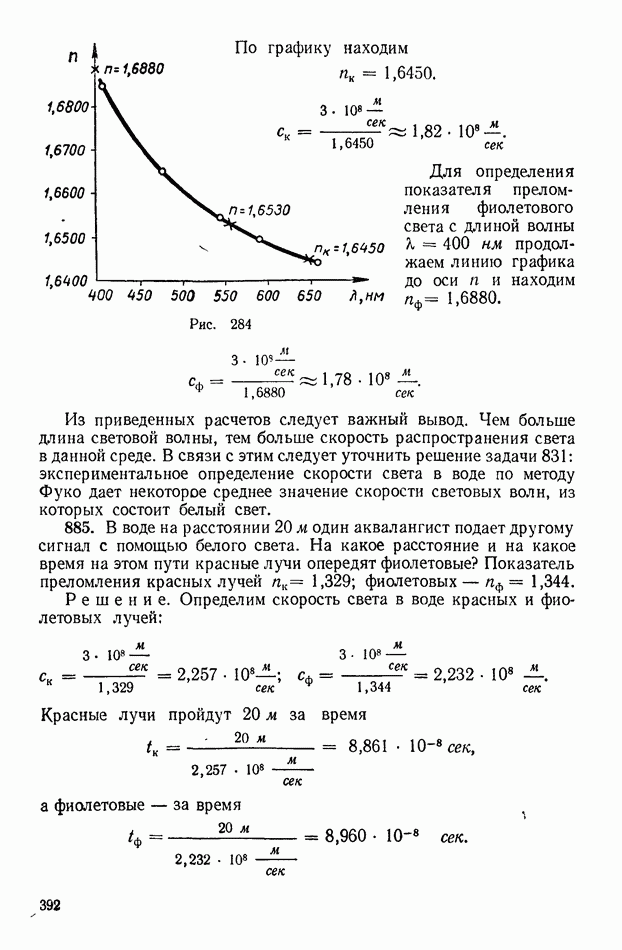
- 1. Скорость света
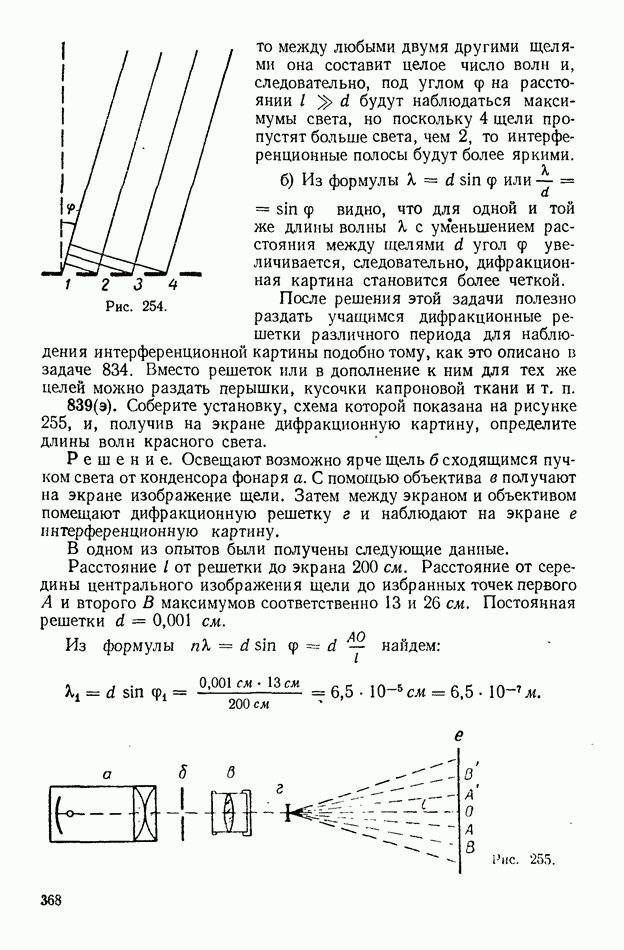
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
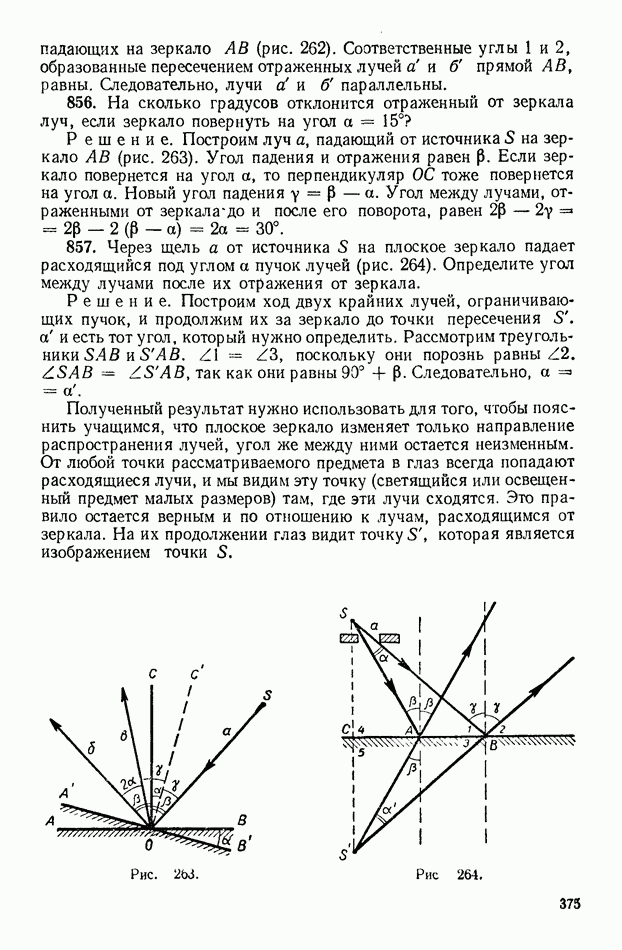
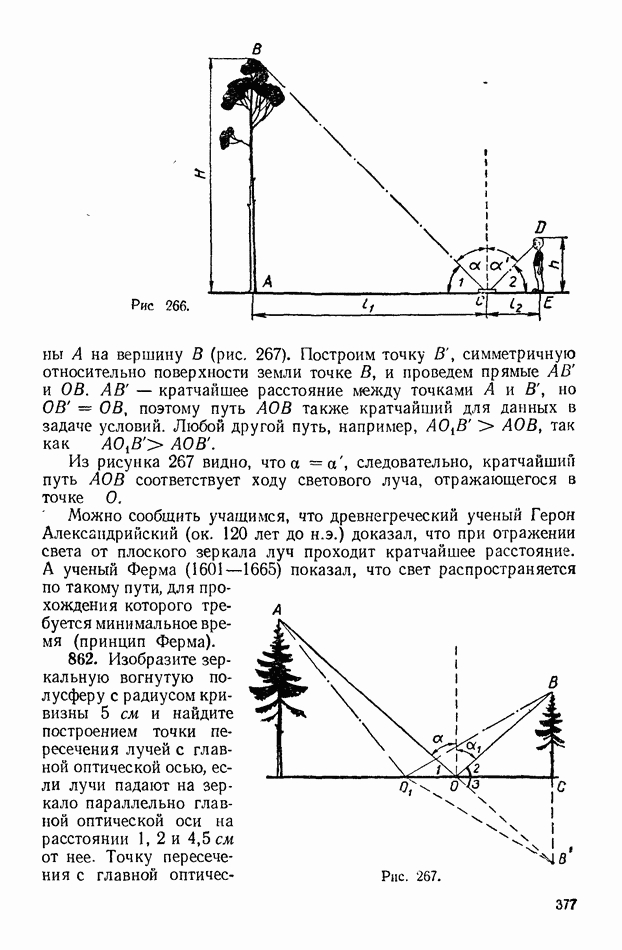
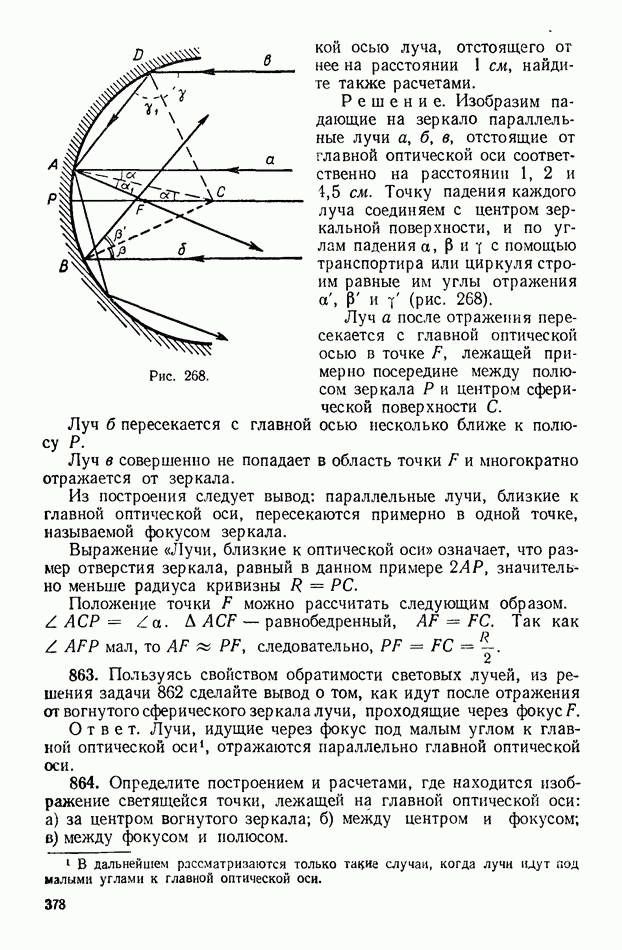
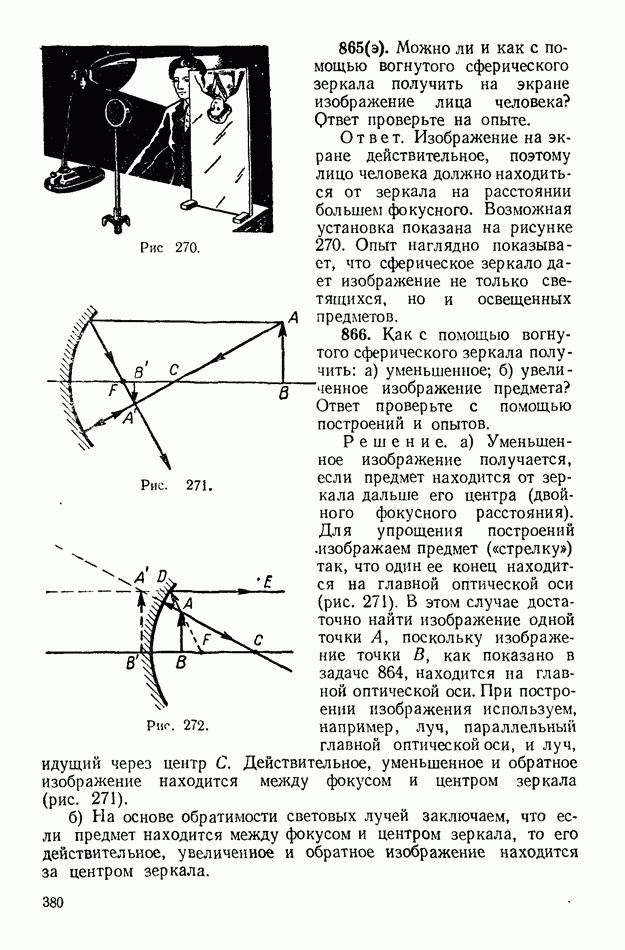
- 2. Отражение света
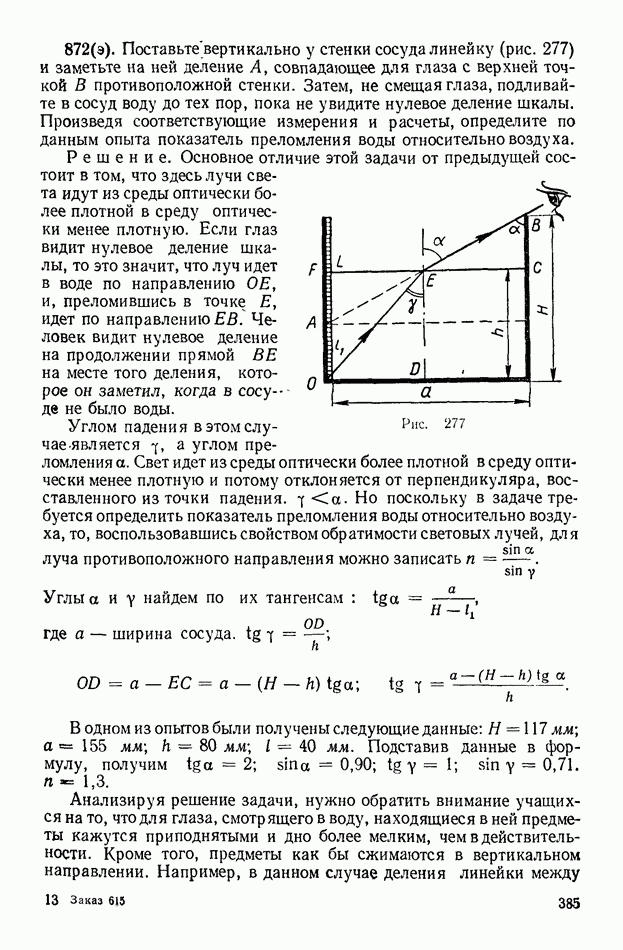
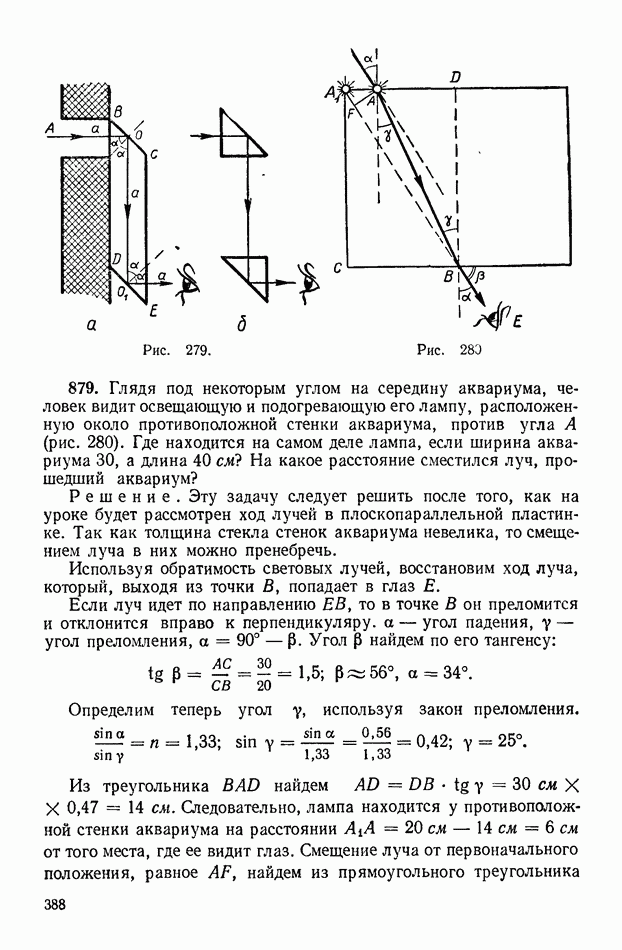
- 3. Преломление света
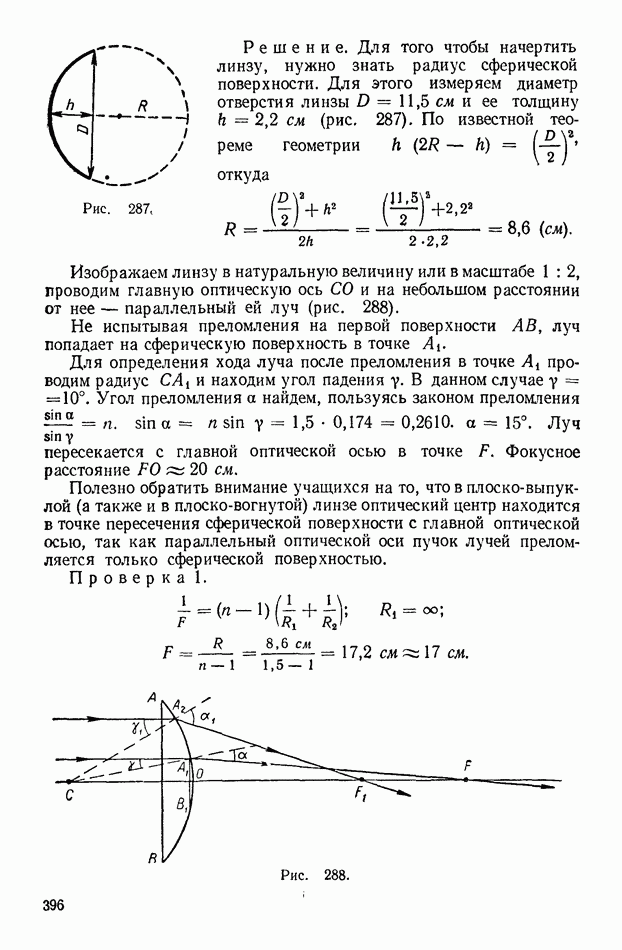
- 4. Линзы
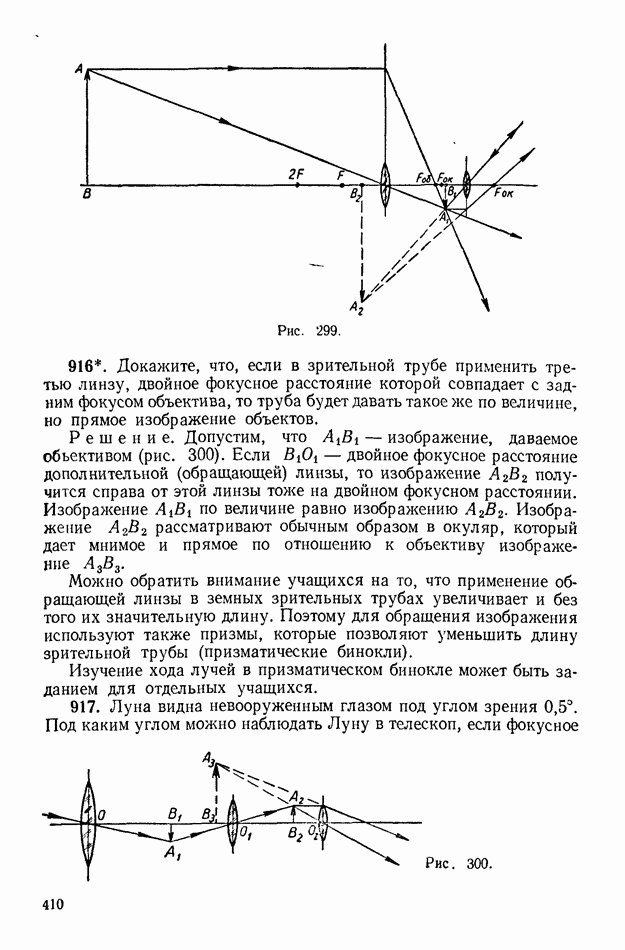
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
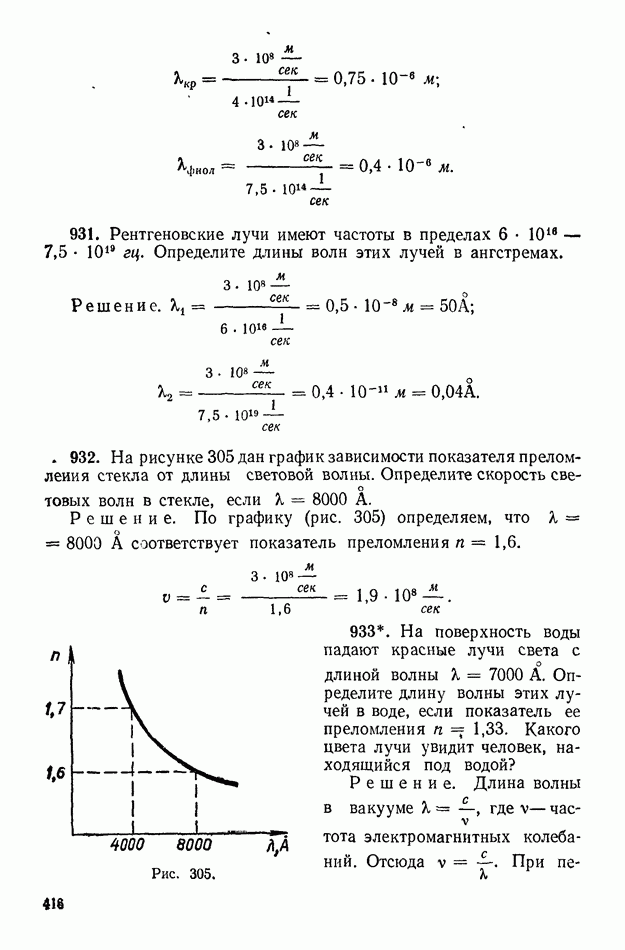
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА