| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Отражение света
По данной теме решают задачи об отражении света от оптически гладких зеркальных поверхностей, размеры шероховатостей которых сравнимы с длиной световой волны.
Закон отражения света, как известно, можно сформулировать в следующем виде: луч падающий, луч отраженный и перпендикуляр к отражающей поверхности, восставленный в точке падения луча, лежат в одной плоскости, а угол падения равен углу отражения. Нужно обратить внимание на то, что учащиеся нередко за угол падения или отражения ошибочно принимают угол между лучом и плоскостью.
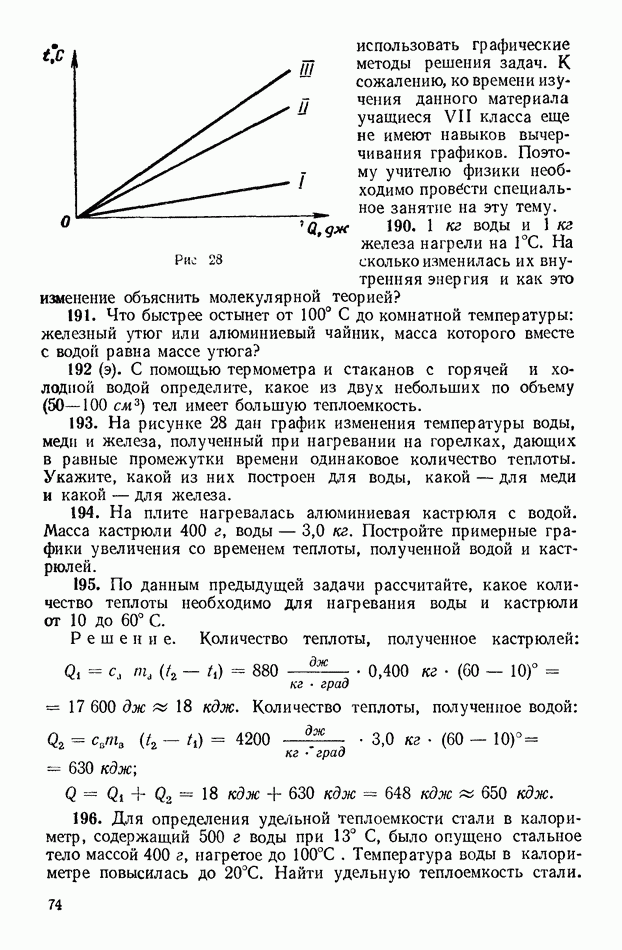
Вначале рассматривают задачи об отражении света от плоских, а затем — от сферических, главным образом вогнутых, зеркал. Эти задачи весьма разнообразны как по содержанию, так и по методам решения. При этом решение задач всех типов должно сопровождаться выполнением аккуратных построений хода лучей.
В вычислительных задачах на сферические зеркала используют две формулы: формулу линейного увеличения  где
где  соответственно линейные размеры изображения и предмета, а
соответственно линейные размеры изображения и предмета, а  расстояния от изображения и предмета до зеркала, и
расстояния от изображения и предмета до зеркала, и
формулу сферического зеркала  где
где  радиус сферической поверхности.
радиус сферической поверхности.
Расстояние от зеркала до действительных изображений или точек следует брать со знаком  а до мнимых — со знаком
а до мнимых — со знаком 
Формула зеркала приближенная и соблюдается она с тем большей точностью, чем меньше угол между лучами, идущими от предмета, и оптической осью зеркала.
Первые построения хода лучей, отраженных от сферических зеркал, нужно делать, пользуясь законом отражения, т. е. выполняя построения углов падения и отражения, а затем, когда учащиеся усвоят суть дела, прибегать к построениям с помощью лучей, ход которых известен: луча, параллельного оптической оси, после отражения проходящего через фокус; луча, идущего через фокус, отражающегося параллельно оптической оси; луча, идущего через центр зеркала, отражающегося по тому же направлению; луча, падающего на зеркало в его полюсе, отражающегося симметрично главной оптической оси. Чем больше радиус кривизны зеркала, тем точнее выполняются перечисленные правила. Следует также иметь в виду свойство обратимости световых лучей, согласно которому свет может проходить один и тот же путь и в прямом, и в обратном направлениях.
854(э). Согните под прямым углом лист картона или плотной бумаги а и сделайте в нем прорез б, как показано на рисунке 261. Поставив на пути пучка света от какого-либо источника зеркало в, убедитесь в правильности закона отражения.
Решение задачи ясно из рисунка 261.
855. Докажите, что параллельные лучи, падающие на плоское зеркало, остаются параллельными.
Решение. Рассмотрим ход двух параллельных лучей а и б,

Рис. 261.

Рис. 262.
падающих на зеркало  (рис. 262). Соответственные углы 1 и 2, образованные пересечением отраженных лучей
(рис. 262). Соответственные углы 1 и 2, образованные пересечением отраженных лучей  прямой А В, равны. Следовательно, лучи
прямой А В, равны. Следовательно, лучи  параллельны.
параллельны.
856. На сколько градусов отклонится отраженный от зеркала луч, если зеркало повернуть на угол 
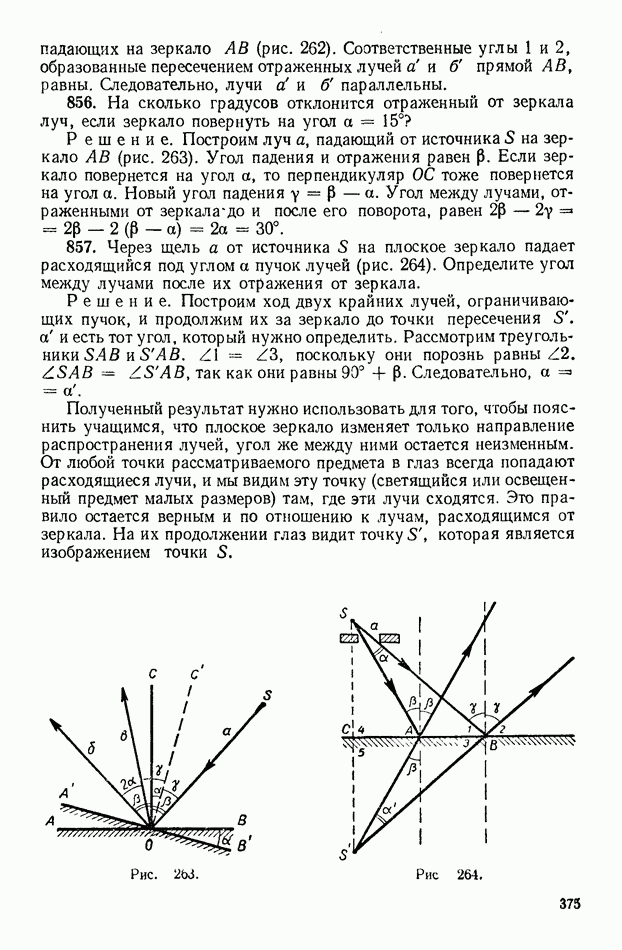
Решение. Построим луч а, падающий от источника  на зеркало
на зеркало  (рис. 263). Угол падения и отражения равен
(рис. 263). Угол падения и отражения равен  Если зеркало повернется на угол а, то перпендикуляр
Если зеркало повернется на угол а, то перпендикуляр  тоже повернется на угол а. Новый угол падения
тоже повернется на угол а. Новый угол падения  а. Угол между лучами, отраженными от зеркала до и после его поворота, равен
а. Угол между лучами, отраженными от зеркала до и после его поворота, равен 
857. Через щель а от источника  на плоское зеркало падает расходящийся под углом а пучок лучей (рис. 264). Определите угол между лучами после их отражения от зеркала.
на плоское зеркало падает расходящийся под углом а пучок лучей (рис. 264). Определите угол между лучами после их отражения от зеркала.
Решение. Построим ход двух крайних лучей, ограничивающих пучок, и продолжим их за зеркало до точки пересечения  а и есть тот угол, который нужно определить. Рассмотрим треугольники
а и есть тот угол, который нужно определить. Рассмотрим треугольники  и
и  поскольку они порознь равны
поскольку они порознь равны  так как они равны
так как они равны  Следовательно, а
Следовательно, а 
Полученный результат нужно использовать для того, чтобы пояснить учащимся, что плоское зеркало изменяет только направление распространения лучей, угол же между ними остается неизменным. От любой точки рассматриваемого предмета в глаз всегда попадают расходящиеся лучи, и мы видим эту точку (светящийся или освещенный предмет малых размеров) там, где эти лучи сходятся. Это правило остается верным и по отношению к лучам, расходящимся от зеркала. На их продолжении глаз видит точку  которая является изображением точки
которая является изображением точки 

Рис. 263.

Рис. 264.
858. Пользуясь решением предыдущей задачи, определите, где получится изображение точки 
Решение. Соединим прямой точки  и заметим, что
и заметим, что  так как они имеют равные углы 1 и 3, заключенные между равными сторонами. Поэтому
так как они имеют равные углы 1 и 3, заключенные между равными сторонами. Поэтому  Следовательно, точки
Следовательно, точки  расположены симметрично относительно поверхности зеркала.
расположены симметрично относительно поверхности зеркала.
859(э). а) Укрепите в листе картона две булавки или держите сертикально в руках на различном расстоянии от глаза два карандаша так, чтобы ближний закрывал собой дальний. Слегка смещая глаз вправо и влево, установите правило, в какую сторону при этом смещается дальний предмет относительно ближнего.
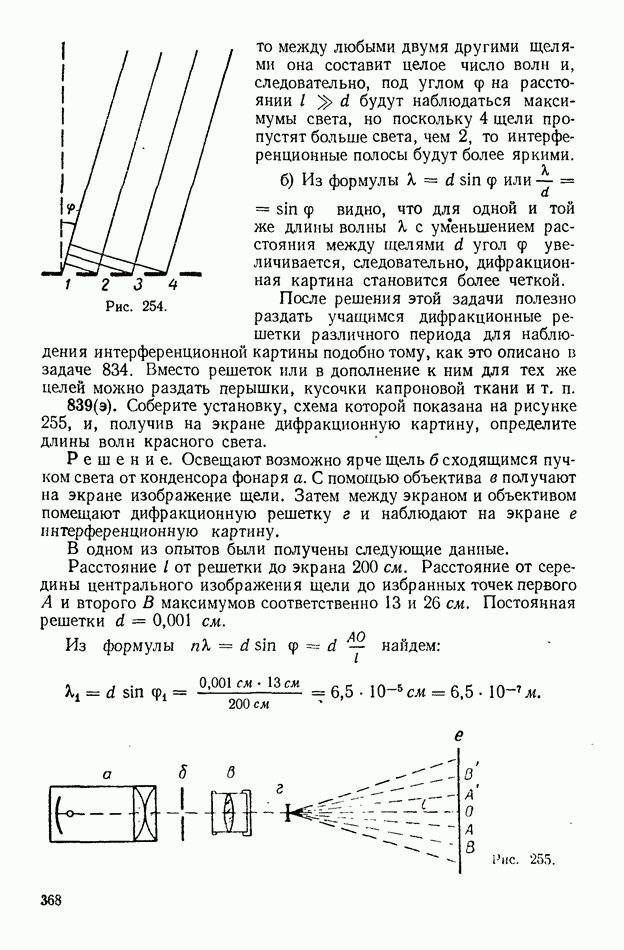
б) Установите перед зеркалом а карандаш  и определите, где за зеркалом находится его изображение в. Для этого поместите второй карандаш
и определите, где за зеркалом находится его изображение в. Для этого поместите второй карандаш  за зеркало (рис. 265) и, смещая глаз вправо и влево, как в первом задании, и двигая карандаш
за зеркало (рис. 265) и, смещая глаз вправо и влево, как в первом задании, и двигая карандаш  найдите такое положение, когда карандаш
найдите такое положение, когда карандаш  за зеркалом не будет смещаться относительно изображения в. На основе опыта сделайте вывод, где находится изображение в.
за зеркалом не будет смещаться относительно изображения в. На основе опыта сделайте вывод, где находится изображение в.
Ответ, а) Дальний предмет смещается относительно ближнего в ту же сторону, что и глаз, б) Измерением находим, что изображение карандаша находится за зеркалом на таком же расстоянии, как и сам карандаш перед зеркалом, что подтверждает выводы, полученные в задаче 858.

Рис. 265
860(a). Положив недалеко от своих ног зеркало, найдите в нем изображение верхушки дерева, столба или другого высокого предмета и, произведя соответствующие измерения и расчеты, найдите их высоту.
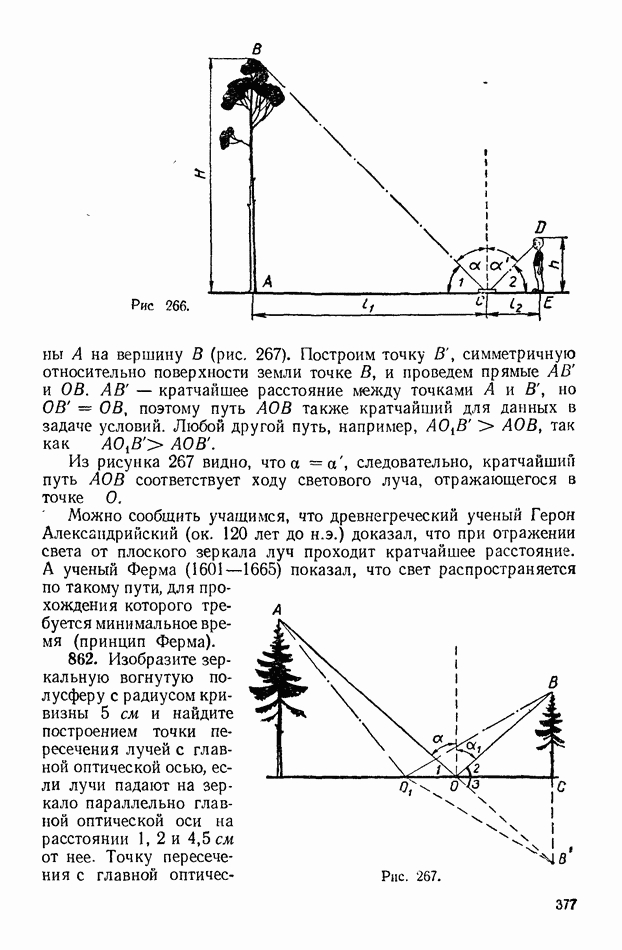
Решение. Сделаем чертеж, подобный изображенному на рисунке 266. В соответствии с законом отражения света а  Поэтому
Поэтому  Следовательно,
Следовательно,  откуда высота дерева
откуда высота дерева  где
где  расстояние от глаз человека до земли,
расстояние от глаз человека до земли,  соответственно расстояния от зеркала до дерева и ног человека.
соответственно расстояния от зеркала до дерева и ног человека.
861. На верхушке дерева у поляны сидит птица. Где на земле она должна схватить ягоду, чтобы кратчайшим путем перелететь на другое дерево на противоположной стороне поляны?
Решение. Допустим, что птица должна перелететь с

Рис. 266
вершины А на вершину В (рис. 267). Построим точку В, симметричную относительно поверхности земли точке В, и проведем прямые  и
и  кратчайшее расстояние между точками
кратчайшее расстояние между точками  но
но  поэтому путь
поэтому путь  также кратчайший для данных в задаче условий. Любой другой путь, например,
также кратчайший для данных в задаче условий. Любой другой путь, например,  так как
так как 
Из рисунка 267 видно, что а  следовательно, кратчайший путь
следовательно, кратчайший путь  соответствует ходу светового луча, отражающегося в точке О.
соответствует ходу светового луча, отражающегося в точке О.
Можно сообщить учащимся, что древнегреческий ученый Герон Александрийский (ок. 120 лет до н. э.) доказал, что при отражении света от плоского зеркала луч проходит кратчайшее расстояние. А ученый Ферма (1601—1665) показал, что свет распространяется по такому пути, для прохождения которого требуется минимальное время (принцип Ферма).
862. Изобразите зеркальную вогнутую полусферу с радиусом кривизны 5 см и найдите построением точки пересечения лучей с главной оптической осью, если лучи падают на зеркало параллельно главной оптической оси на расстоянии 1, 2 и 4,5 см от нее. Точку пересечения с главной

Рис. 267.

Рис. 268.
оптической осью луча, отстоящего от нее на расстоянии 1 см, найдите также расчетами.
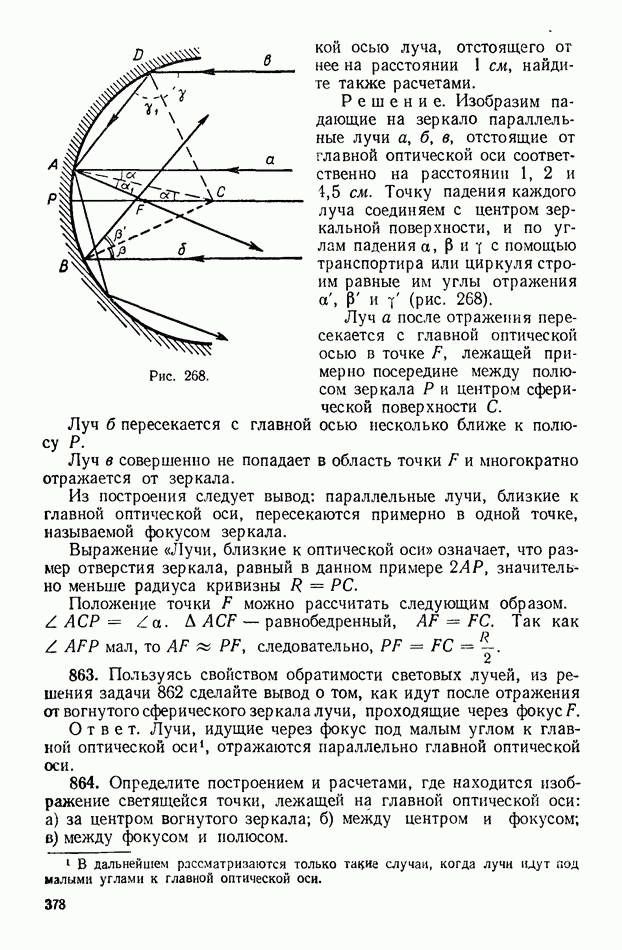
Решение. Изобразим падающие на зеркало параллельные лучи а, б, в, отстоящие от главной оптической оси соответственно на расстоянии 1, 2 и 4,5 см. Точку падения каждого луча соединяем с центром зеркальной поверхности, и по углам падения  с помощью транспортира или циркуля строим равные им углы отражения
с помощью транспортира или циркуля строим равные им углы отражения  (рис. 268).
(рис. 268).
Луч а после отражения пересекается с главной оптической осью в точке  лежащей примерно посередине между полюсом зеркала
лежащей примерно посередине между полюсом зеркала  и центром сферической поверхности С.
и центром сферической поверхности С.
Луч  пересекается с главной осью несколько ближе к полюсу
пересекается с главной осью несколько ближе к полюсу 
Луч в совершенно не попадает в область точки  и многократно отражается от зеркала.
и многократно отражается от зеркала.
Из построения следует вывод: параллельные лучи, близкие к главной оптической оси, пересекаются примерно в одной точке, называемой фокусом зеркала.
Выражение «Лучи, близкие к оптической оси» означает, что размер отверстия зеркала, равный в данном примере  значительно меньше радиуса кривизны
значительно меньше радиуса кривизны 
Положение точки  можно рассчитать следующим образом.
можно рассчитать следующим образом.  равнобедренный,
равнобедренный,  Так как
Так как  мал, то
мал, то  следовательно,
следовательно, 
863. Пользуясь свойством обратимости световых лучей, из решения задачи 862 сделайте вывод о том, как идут после отражения от вогнутого сферического зеркала лучи, проходящие через фокус 
Ответ. Лучи, идущие через фокус под малым углом к главной оптической оси, отражаются параллельно главной оптической оси.
864. Определите построением и расчетами, где находится изображение светящейся точки, лежащей на главной оптической оси: а) за центром вогнутого зеркала; б) между центром и фокусом; в) между фокусом и полюсом.

Рис. 269.
Решение 1. а) Через центр зеркала С проводим побочную ось  равноправную с осью
равноправную с осью  выделение которой, вообще говоря, условно (рис. 269, а). Затем из точки
выделение которой, вообще говоря, условно (рис. 269, а). Затем из точки  проводим луч
проводим луч  параллельный
параллельный  При отражении от зеркала он должен пройти через фокус
При отражении от зеркала он должен пройти через фокус  лежащий на середине отрезка
лежащий на середине отрезка  Точка
Точка  пересечение двух лучей
пересечение двух лучей  и является изображением точки
и является изображением точки  Расположена эта точка между фокусом и центром.
Расположена эта точка между фокусом и центром.
б) Используя свойство обратимости лучей, сразу утверждаем следующее: если светящаяся точка  расположена между фокусом и центром, то сопряженная точка, являющаяся ее изображением, расположена за центром зеркала. Это утверждение нетрудно проверить построением, аналогичным предыдущему: проводим побочную ось
расположена между фокусом и центром, то сопряженная точка, являющаяся ее изображением, расположена за центром зеркала. Это утверждение нетрудно проверить построением, аналогичным предыдущему: проводим побочную ось  и рассматриваем ход параллельного ей луча
и рассматриваем ход параллельного ей луча  После отражения от зеркала этот луч пройдет через фокус побочной оси и пересечется с главной оптической осью в точке
После отражения от зеркала этот луч пройдет через фокус побочной оси и пересечется с главной оптической осью в точке  являющейся изображением точки
являющейся изображением точки  (рис. 269, б).
(рис. 269, б).
в) Проводим побочную ось  и рассматриваем ход параллельного ей луча
и рассматриваем ход параллельного ей луча  При отражении от зеркала этот луч пройдет через фокус
При отражении от зеркала этот луч пройдет через фокус  и не пересечется с лучом, идущим по главной оптической оси. Изображения не будет. Но глаз, если в него попадут эти расходящиеся лучи, увидит мнимое изображение за зеркалом на продолжении лучей в точке
и не пересечется с лучом, идущим по главной оптической оси. Изображения не будет. Но глаз, если в него попадут эти расходящиеся лучи, увидит мнимое изображение за зеркалом на продолжении лучей в точке  (рис, 269, в).
(рис, 269, в).
Решение 2. Запишем формулу зеркала  и выразим из нее интересующую нас величину
и выразим из нее интересующую нас величину 
Если
а) При  знаменатель будет величиной большей но меньшей 1, поэтому
знаменатель будет величиной большей но меньшей 1, поэтому  .
.
б)  (из сравнения случаев
(из сравнения случаев  видно, что точки, лежащие на расстоянии
видно, что точки, лежащие на расстоянии  являются сопряженными).
являются сопряженными).
в) d < F. Знаменатель — величина отрицательная. Мнимое изображение лежит за зеркалом.

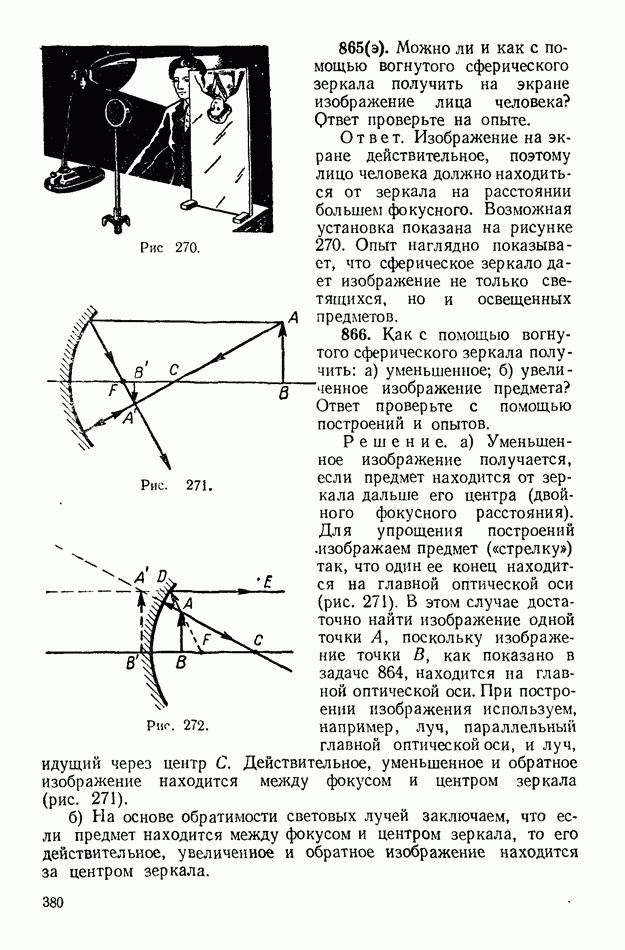
Рис. 270.

Рис. 271.

Рис. 272.
865(э). Можно ли и как с помощью вогнутого сферического зеркала получить на экране изображение лица человека? Ответ проверьте на опыте.
Ответ. Изображение на экране действительное, поэтому лицо человека должно находиться от зеркала на расстоянии большем фокусного. Возможная установка показана на рисунке 270. Опыт наглядно показывает, что сферическое зеркало дает изображение не только светящихся, но и освещенных предметов.
866. Как с помощью вогнутого сферического зеркала получить: а) уменьшенное; б) увеличенное изображение предмета? Ответ проверьте с помощью построений и опытов.
Решение, а) Уменьшенное изображение получается, если предмет находится от зеркала дальше его центра (двойного фокусного расстояния). Для упрощения построений изображаем предмет («стрелку») так, что один ее конец находится на главной оптической оси (рис. 271). В этом случае достаточно найти изображение одной точки А, поскольку изображение точки В, как показано в задаче 864, находится на главной оптической оси. При построении изображения используем, например, луч, параллельный главной оптической оси, и луч, идущий через центр С. Действительное, уменьшенное и обратное изображение находится между фокусом и центром зеркала (рис. 271).
б) На основе обратимости световых лучей заключаем, что если предмет находится между фокусом и центром зеркала, то его действительное, увеличенное и обратное изображение находится за центром зеркала.
Поскольку в условии задачи не сказано, каким должно быть увеличенное изображение, действительным или мнимым, то к данному вопросу следует привести и другой ответ. Увеличенное (мнимое) изображение получится, если предмет поместить между зеркалом и фокусом (рис. 272).
Отраженные от зеркала лучи, как видно из рисунка 272, расходятся, поэтому действительного изображения нет. Но глаз увидит мнимое изображение, например, точки А за зеркалом на продолжении лучей  и
и  Мнимое изображение предмета получается увеличенным, что, например, используется в зеркалах для бритья.
Мнимое изображение предмета получается увеличенным, что, например, используется в зеркалах для бритья.
В связи с решением этой задачи нужно обратить внимание учащихся на то, что в зеркалах прямое изображение всегда мнимое, а обратное — действительное.
867 (з). Как, не пользуясь расчетами, определить радиус кривизны вогнутого зеркала. Ответ проверьте на опыте.
Решение. Как показано в задаче 866, если предмет находится дальше центра зеркала, изображение будет уменьшенным, если ближе — увеличенным. Логично предположить, что если предмет находится на расстоянии, равном радиусу зеркала, то изображение будет по величине равно самому предмету, что и можно использовать для определения радиуса зеркала.
Данное заключение можно подтвердить с помощью формулы увеличения зеркала  При
При  Тогда из формулы зеркала
Тогда из формулы зеркала  следует, что
следует, что 
При постановке опыта укрепляют лист картона а с прорезом  и зеркало в на штативах (рис. 273). Прорез освещают параллельным пучком света (от проекционного фонаря). Сдвигая картон вдоль главной оптической оси зеркала, получают на нем обратное изображение
и зеркало в на штативах (рис. 273). Прорез освещают параллельным пучком света (от проекционного фонаря). Сдвигая картон вдоль главной оптической оси зеркала, получают на нем обратное изображение  по величине равное «прорезу». Изображение находится на двойном фокусном расстоянии, которое равно радиусу зеркала.
по величине равное «прорезу». Изображение находится на двойном фокусном расстоянии, которое равно радиусу зеркала.
868. Источник света перемещается равномерно со скоростью 2 смсек от центра зеркала, радиус кривизны которого  см, к его полюсу. Как перемещается при этом изображение источника света и как изменяется его скорость? Постройте график зависимости расстояния изображения
см, к его полюсу. Как перемещается при этом изображение источника света и как изменяется его скорость? Постройте график зависимости расстояния изображения  расстояния источника света до зеркала.
расстояния источника света до зеркала.

Рис. 377.
Решение 1. Источник света перемещается от центра зеркала к его фокусу, а его изображение перемещается в противоположную сторону сколь угодно далеко от центра. Ясно, что средняя скорость перемещения источника света меньше, чем изображения, которое за одно и то же время проходит большее расстояние  откуда
откуда 
(см. скан)
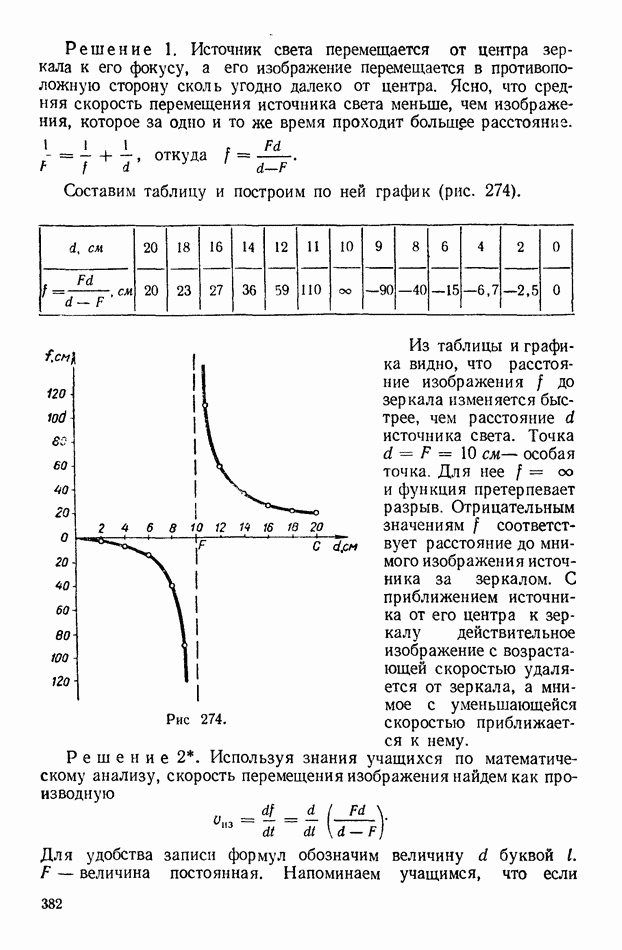
Составим таблицу и построим по ней график (рис. 274).
Из таблицы и графика видно, что расстояние изображения  до зеркала изменяется быстрее, чем расстояние
до зеркала изменяется быстрее, чем расстояние  источника света. Точка
источника света. Точка  — особая точка. Для нее
— особая точка. Для нее  и функция претерпевает разрыв. Отрицательным значениям
и функция претерпевает разрыв. Отрицательным значениям  соответствует расстояние до мнимого изображения источника за зеркалом. С приближением источника от его центра к зеркалу действительное изображение с возрастающей скоростью удаляется от зеркала, а мнимое с уменьшающейся скоростью приближается к нему.
соответствует расстояние до мнимого изображения источника за зеркалом. С приближением источника от его центра к зеркалу действительное изображение с возрастающей скоростью удаляется от зеркала, а мнимое с уменьшающейся скоростью приближается к нему.

Рис. 274.
Решение 2. Используя знания учащихся по математическому анализу, скорость перемещения изображения найдем как производную

Для удобства записи формул обозначим величину  буквой
буквой  величина постоянная. Напоминаем учащимся, что если
величина постоянная. Напоминаем учащимся, что если
 то производная
то производная

Поэтому 
По условию задачи  скорость перемещения источника — величина постоянная, равная 2 см/сек и
скорость перемещения источника — величина постоянная, равная 2 см/сек и  см. Поэтому мгновенная скорость перемещения изображения
см. Поэтому мгновенная скорость перемещения изображения

Знак минус показывает, что изображение перемещается в направлении, противоположном перемещению источника света.
Наибольшую величину скорость изображения приобретает тогда, когда движущийся источник находится вблизи фокуса  . При
. При  что качественно уже было выяснено с помощью графика (рис. 274).
что качественно уже было выяснено с помощью графика (рис. 274).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
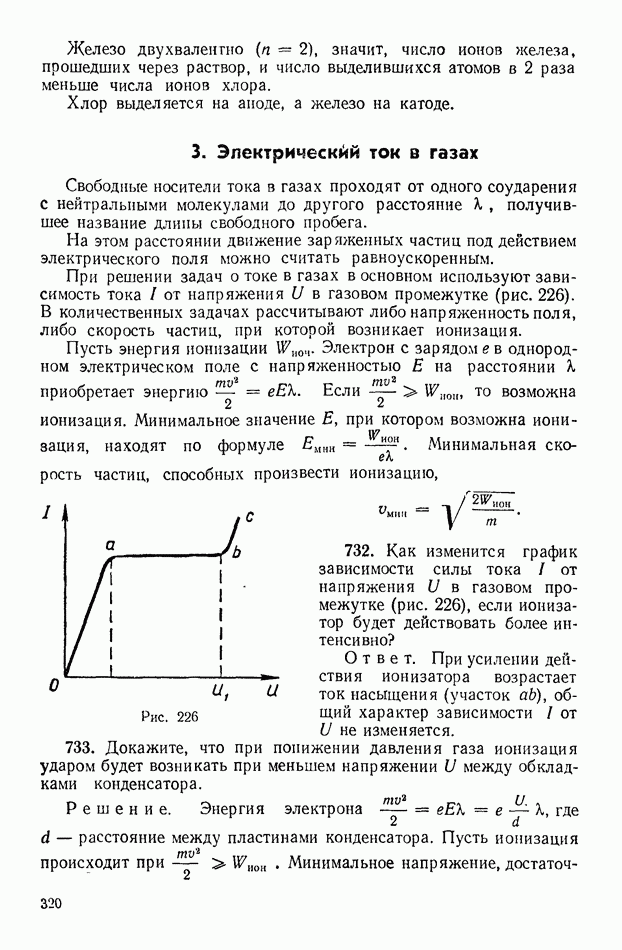
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА