| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
6. Соединения проводников
Соединение проводников изучают теперь в VII классе. Поэтому  необходимо решение большого числа задач на последовательное и параллельное соединение проводников. В старших классах эти вопросы только повторяют и решают задачи на расчеты сопротивления более сложных цепей.
необходимо решение большого числа задач на последовательное и параллельное соединение проводников. В старших классах эти вопросы только повторяют и решают задачи на расчеты сопротивления более сложных цепей.
Важно научить учащихся разбираться в схемах электрических цепей и находить точки разветвления в случае параллельных соединений. Учащиеся должны научиться составлять эквивалентные схемы, т. е. схемы, на которых яснее видны соединения проводников. Для этого надо проследить все участки цепи, начиная от одного зажима до другого, и вычерчивать схему в более простом виде.
Начинают решение задач со случая последовательного соединения, потом рассматривают параллельное и смешанное соединения проводников.
Все сопротивления в цепи можно обозначать буквой  с числовыми индексами:
с числовыми индексами:  Можно все точки соединения проводников обозначить буквами
Можно все точки соединения проводников обозначить буквами  тогда сопротивления участков цепи обозначают соответственно
тогда сопротивления участков цепи обозначают соответственно  Более удобным оказывается в большинстве случаев последний способ. Поэтому рекомендуется при решении всех задач точки соединения проводников обозначать буквами. Преимущества этого особенно заметны для случаев параллельного и смешанного соединений проводников.
Более удобным оказывается в большинстве случаев последний способ. Поэтому рекомендуется при решении всех задач точки соединения проводников обозначать буквами. Преимущества этого особенно заметны для случаев параллельного и смешанного соединений проводников.
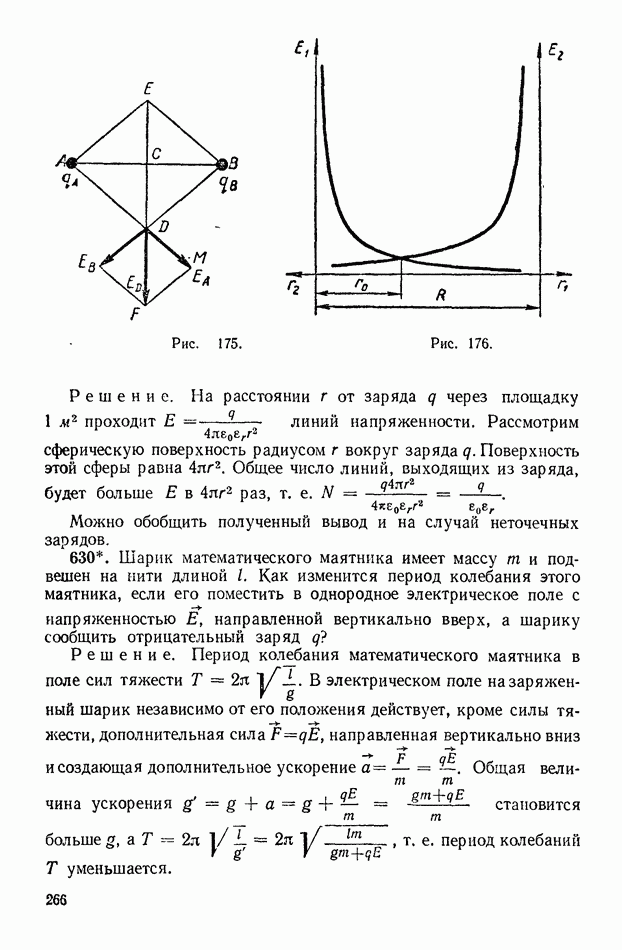
272. В электрическую цепь включены последовательно резистор сопротивлением 5 ом и две электрические лампы сопротивлением каждая 0,25 ом. Определите общее сопротивление цепи.
Решение задачи начинают с вычерчивания схемы (рис. 43). Точки соединения резистора и ламп обозначают буквами 
Общее сопротивление цепи  ом
ом  ом
ом  ом.
ом.
273. Два резистора сопротивлением  ом включены, как показано на рисунке 44, к зажимам источника тока напряжением
ом включены, как показано на рисунке 44, к зажимам источника тока напряжением  Найдите силу тока на всех участках цепи.
Найдите силу тока на всех участках цепи.
Решение. Обозначим точки разветвления тока буквами  Общий ток в цепи
Общий ток в цепи

Соединительные провода, как условлено, сопротивлением не обладают. Величину  находим по формуле для параллельного соединения проводников:
находим по формуле для параллельного соединения проводников:  В эту формулу и следует подставлять числовые значения, так как выражение из этой формулы
В эту формулу и следует подставлять числовые значения, так как выражение из этой формулы  в явном виде, особенно если число сопротивлений более двух, затруднительно для учащихся. Токи в сопротивлениях обозначим
в явном виде, особенно если число сопротивлений более двух, затруднительно для учащихся. Токи в сопротивлениях обозначим  Найдем эти токи по закону Ома для участка цепи:
Найдем эти токи по закону Ома для участка цепи:

Вычисления дают следующие значения:  ом,
ом,  а.
а.
Проверкой правильности решения может служить равенство 
В данной задаче проще было бы не искать  а определить токи
а определить токи  и сразу по формулам:
и сразу по формулам:

а затем общий ток


Рис. 43.

Рис. 44

Рис. 34.
В случае же смешанных или более сложных соединений проводников необходимо искать  Поэтому и в этой задаче имеет смысл все же идти данным, хотя и более длинным путем. В итоге вырабатывается определенный алгоритм решения задач на соединение проводников.
Поэтому и в этой задаче имеет смысл все же идти данным, хотя и более длинным путем. В итоге вырабатывается определенный алгоритм решения задач на соединение проводников.
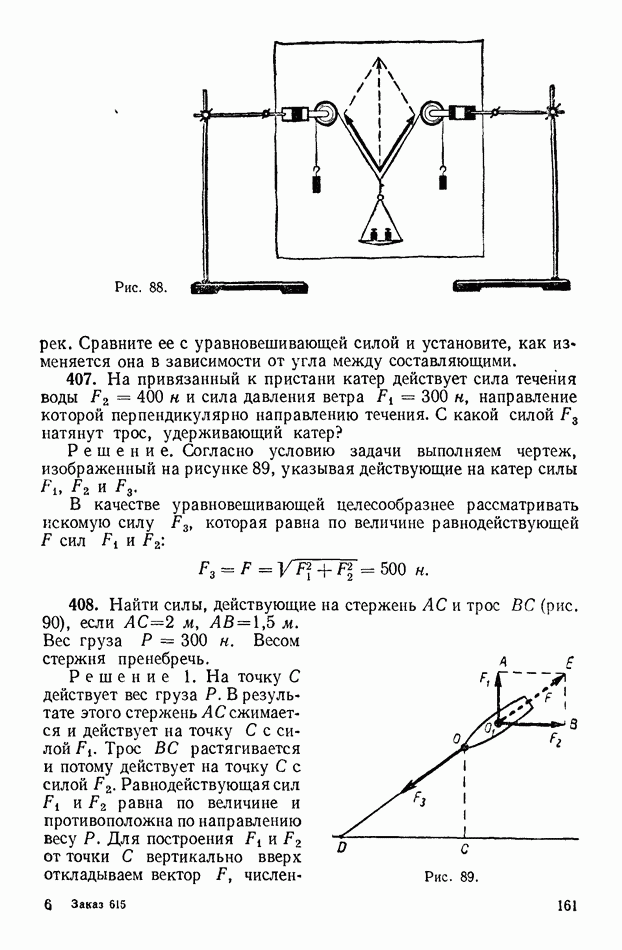
274. Определите полное сопротивление цепи и токи в каждом проводнике, если проводники соединены так, как показано на рисунке 45, 
Решение. В цепи на участке  параллельно соединены два проводника с сопротивлениями
параллельно соединены два проводника с сопротивлениями  Полное сопротивление цепи
Полное сопротивление цепи

Сила тока в цепи

Этот ток течет через проводник с сопротивлением  Чтобы найти силу тока в ветвях параллельного соединения
Чтобы найти силу тока в ветвях параллельного соединения  надо вначале вычислить напряжение
надо вначале вычислить напряжение  а потом и токи
а потом и токи

Вычисления дают значения:  ом,
ом,  ом,
ом, 
Заметим, что в VII классе решение этой задачи основывается только на законе Ома для участка цепи. В IX классе можно было бы  находить из следующих уравнений:
находить из следующих уравнений: 

Напряжение  можно было бы не определять.
можно было бы не определять.
После рассмотрения смешанного соединения проводников переходят к анализу и расчету реальных цепей, схемы которых не всегда имеют такой вид, где явно выражен характер соединения проводников. В этих случаях чертят так называемые эквивалентные схемы.

Рис. 46.

Рис. 47.
275. Составьте дома схему квартирной проводки. Разберитесь, как включены потребители, и начертите эквивалентную схему данной цепи.
Решение. Допустим, ученик начертил схему, показанную на рисунке 46. Обозначим точки соединения проводов буквами  Считая, что соединительные провода имеют незначительное сопротивление, которым можно пренебречь, установим характер соединения потребителей. Все потребители соединены параллельно. Начертим эквивалентную схему цепи. Для этого проследим путь тока от точки а до точки
Считая, что соединительные провода имеют незначительное сопротивление, которым можно пренебречь, установим характер соединения потребителей. Все потребители соединены параллельно. Начертим эквивалентную схему цепи. Для этого проследим путь тока от точки а до точки  Оказывается, точки
Оказывается, точки  можно заменить одной точкой разветвления, а точки
можно заменить одной точкой разветвления, а точки  другой. Параллельных ветвей в цепи четыре. Эквивалентную схему чертим в привычном для нас виде, располагая все потребители в явно выраженных параллельных ветвях (рис. 47).
другой. Параллельных ветвей в цепи четыре. Эквивалентную схему чертим в привычном для нас виде, располагая все потребители в явно выраженных параллельных ветвях (рис. 47).
276. Определите ток, текущий через каждый резистор в цепи, схема которой изображена на рисунке 48, если напряжение на зажимах 6 в, а сопротивление резисторов  ом.
ом.
Решение. Сразу нельзя сказать, как соединены резисторы. Но если составить эквивалентную схему (рис. 49), то видно, что все резисторы соединены параллельно. Решение теперь не сложно

Рис. 48.

Рис. 49.

Общий ток в цепи

Этот общий ток можно определить по закону Ома и через  Тогда
Тогда 

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
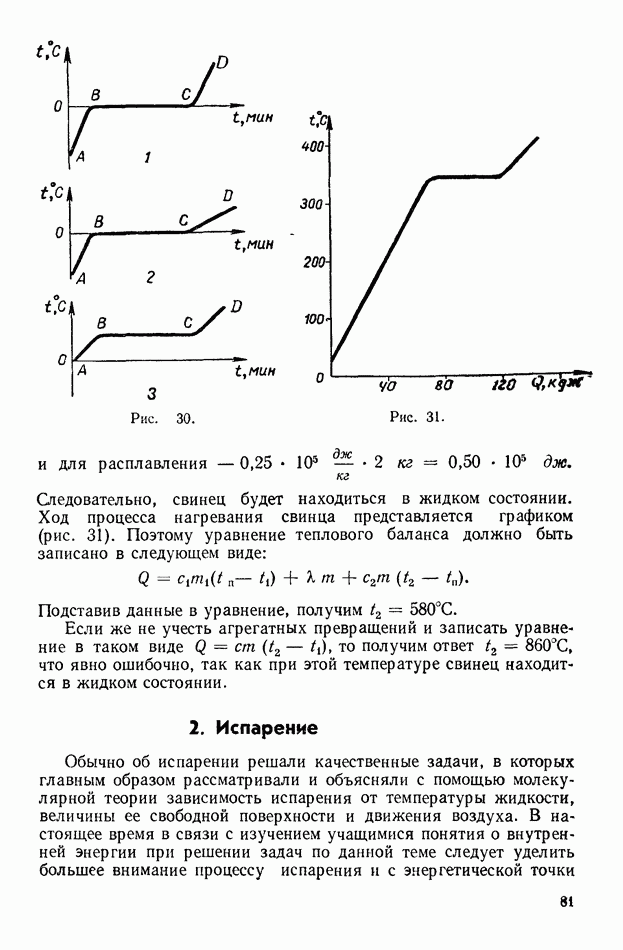
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
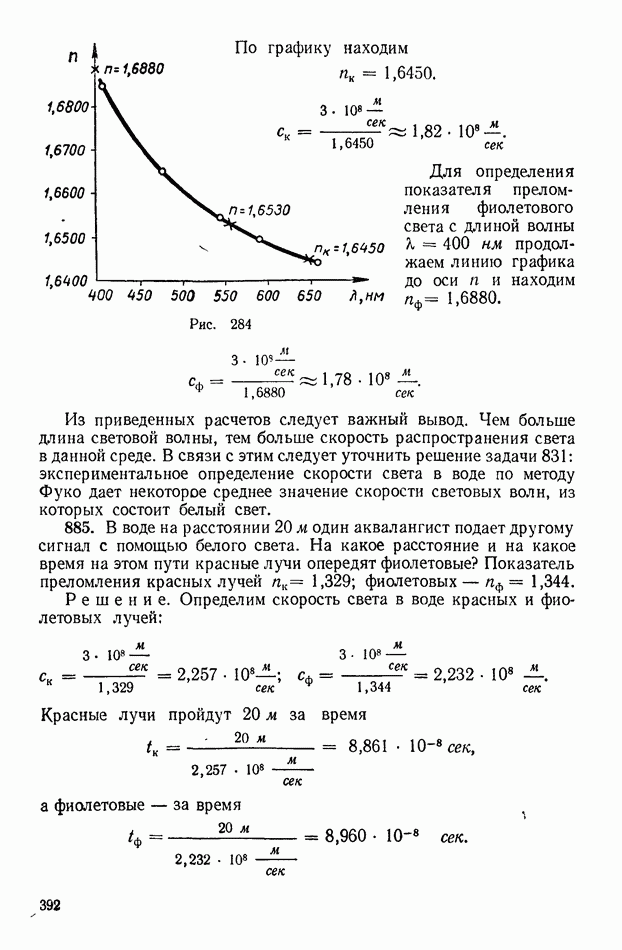
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
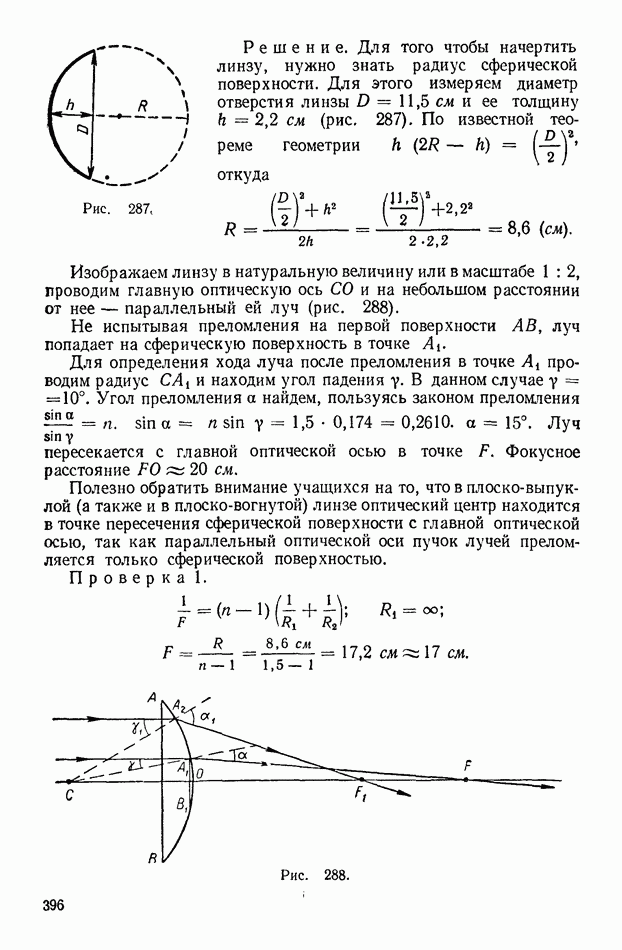
- 4. Линзы
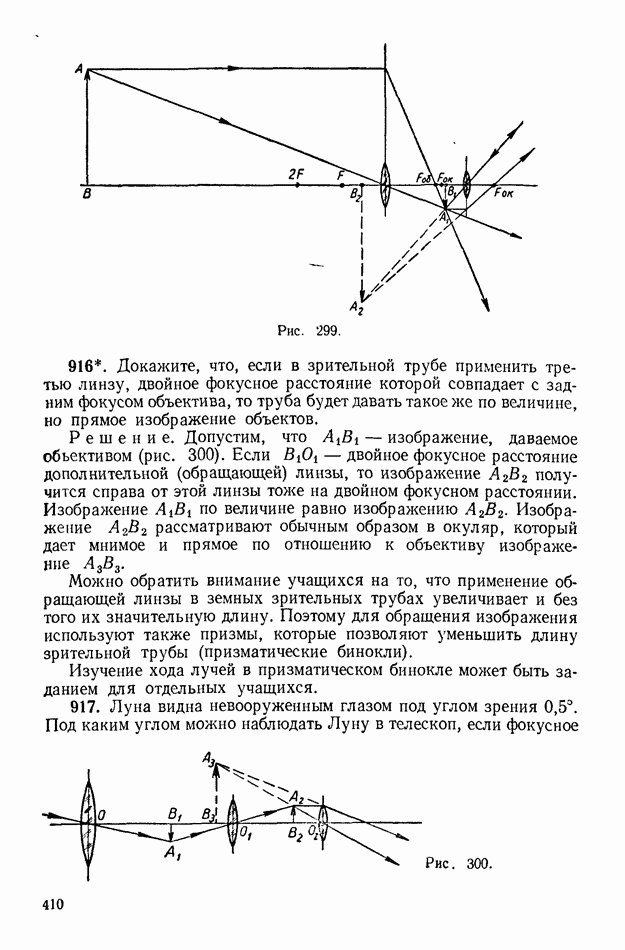
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
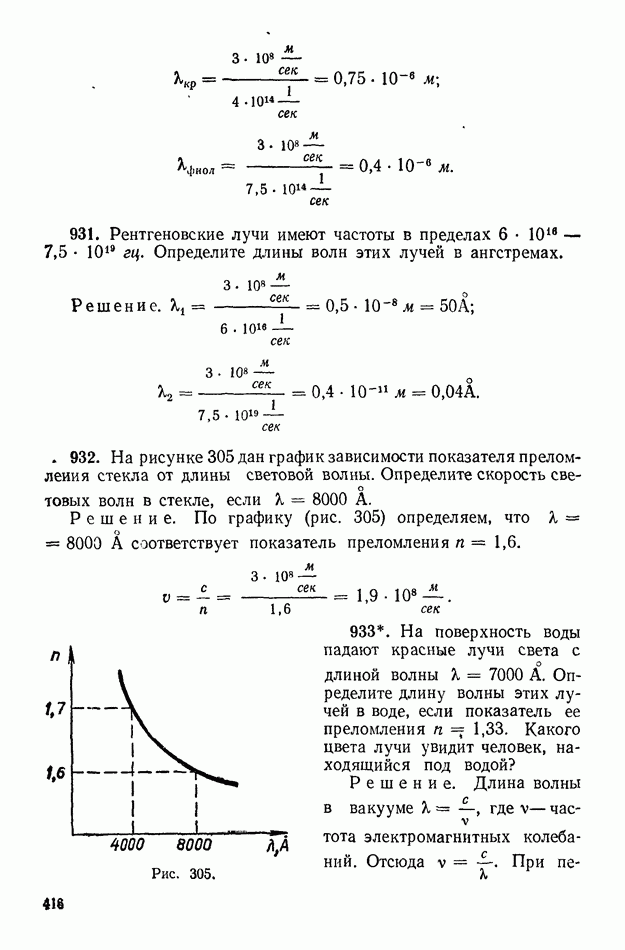
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА