| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Потенциал электрического поля
Потенциал электрического поля в некоторой точке  где
где  потенциальная энергия, которой обладает заряд
потенциальная энергия, которой обладает заряд  в данной точке поля.
в данной точке поля.
В случае электрического поля, созданного точечным зарядом, потенциал 
Работа А по перемещению заряда  из точки поля с потенциалом
из точки поля с потенциалом  в точку с потенциалом
в точку с потенциалом  не зависит от формы пути и определяется по формуле
не зависит от формы пути и определяется по формуле 
Для однородного электрического поля справедливо соотношение  где
где  расстояние вдоль линии напряженности между точками с потенциалами
расстояние вдоль линии напряженности между точками с потенциалами  Отсюда единица напряженности
Отсюда единица напряженности 
Важно учитывать, что потенциал электрического поля, созданного в данной точке несколькими точечными зарядами, равен алгебраической (а не геометрической, как напряженность) сумме потенциалов полей, создаваемых в этой точке каждым зарядом отдельно.
Качественные задачи дают возможность обсудить все эти основные положения о потенциале.
631. Поле создано двумя одинаковыми положительными зарядами  находящимися на расстоянии
находящимися на расстоянии  друг от друга. Чему равен потенциал в средней точке прямой, соединяющей эти заряды?
друг от друга. Чему равен потенциал в средней точке прямой, соединяющей эти заряды?
Решение. В средней точке напряженность  А потенциал
А потенциал  так как общий потенциал
так как общий потенциал  равен не геометрической, а алгебраической сумме потенциалов
равен не геометрической, а алгебраической сумме потенциалов  созданных зарядами
созданных зарядами  в этой точке (считаем
в этой точке (считаем  где
где 
632. Сравните работу по перемещению заряда  в электрическом поде заряда
в электрическом поде заряда  между точками
между точками  и
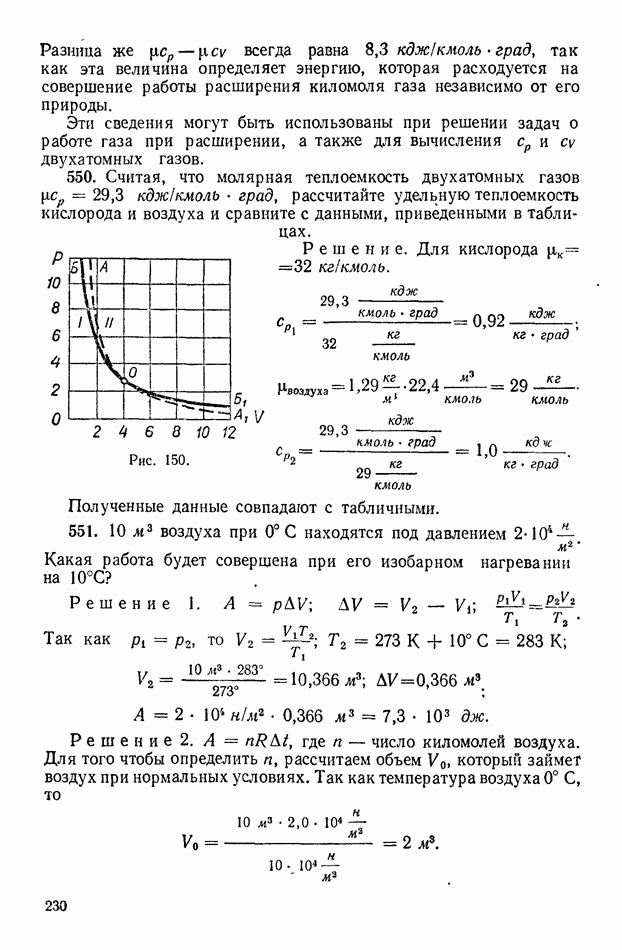
и  происходящему по двум путям (I и II), указанным на рисунке 177, если
происходящему по двум путям (I и II), указанным на рисунке 177, если  помещен в точку О.
помещен в точку О.
Решение. Работы, совершаемые электрическими зарядами по указанным путям, одинаковы, так как работа не зависит от

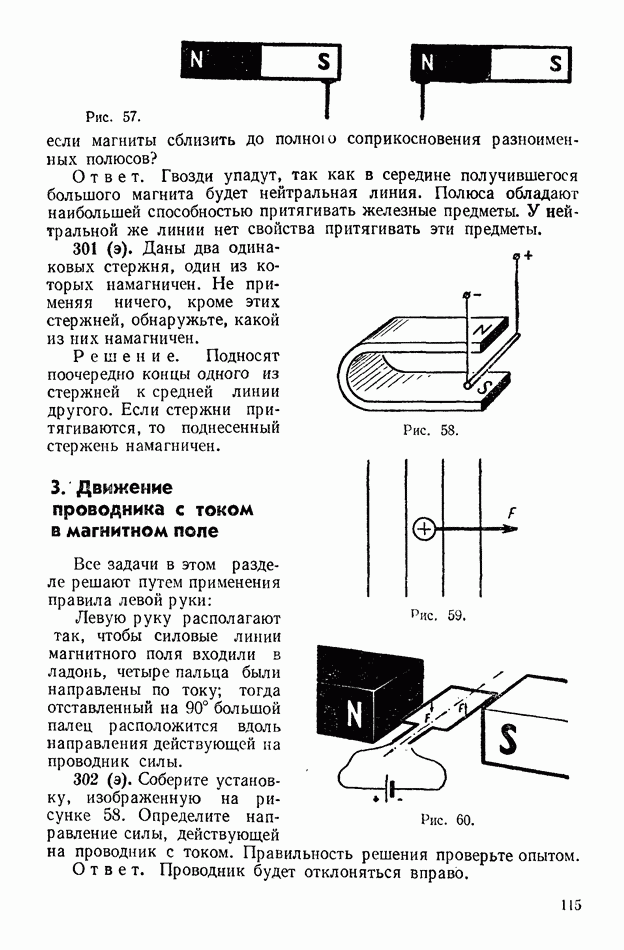
Рис. 177.
формы пути, а определяется лишь разностью потенциалов точек поля, соответствующих началу и концу пути:  но
но 
Вычислительные задачи здесь довольно простые. В них используют зависимости 
Энергию в  измеряют в джоулях. Иногда при решении задач энергию выражают и в других единицах: эргах и электронвольтах. 633. Работа А при переносе заряда
измеряют в джоулях. Иногда при решении задач энергию выражают и в других единицах: эргах и электронвольтах. 633. Работа А при переносе заряда  к из бесконечности в некоторую точку электрического поля равна
к из бесконечности в некоторую точку электрического поля равна  Найдите потенциал этой точки поля.
Найдите потенциал этой точки поля.
Решение. Работа по переносу заряда из бесконечности в данную точку поля равна потенциальной энергии заряда в этой точке, а по определению  в.
в.
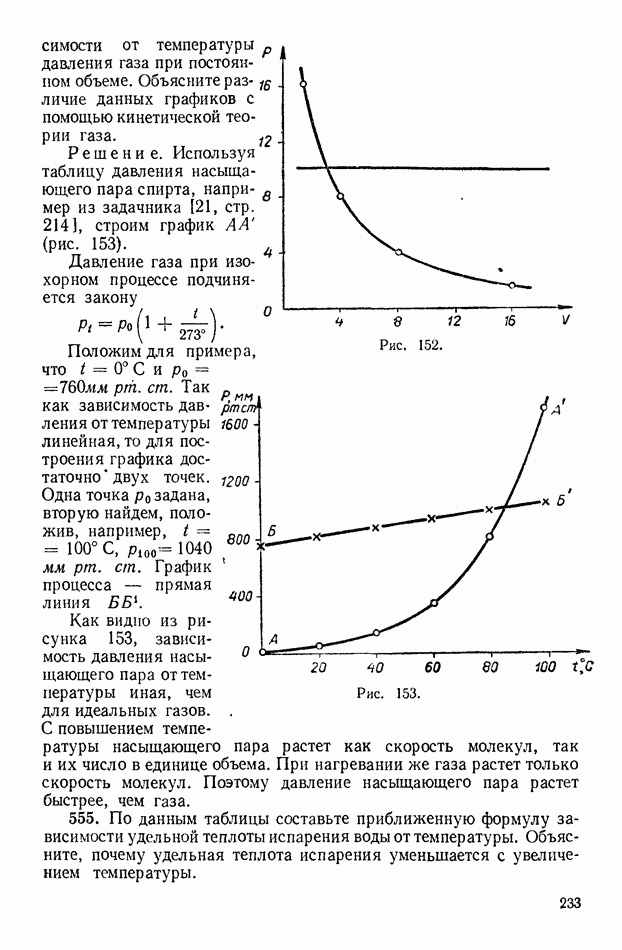
634. Поле образовано точечным зарядом  Какую работу надо совершить, чтобы одноименный заряд
Какую работу надо совершить, чтобы одноименный заряд  к перенести из точки А, удаленной от
к перенести из точки А, удаленной от  на
на  в точку В, удаленную от
в точку В, удаленную от  на
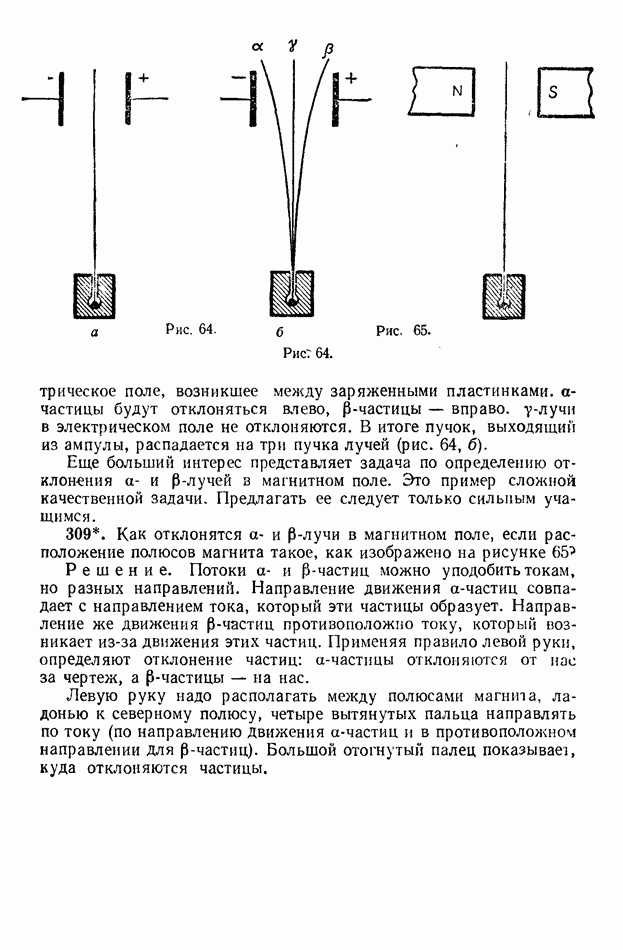
на  (рис. 178).
(рис. 178).
Решение.  по любому пути. Для точечного заряда в воздухе при
по любому пути. Для точечного заряда в воздухе при 
Вычисления дают значение 
635. Определите энергию и скорость, которые приобретает электрон, пролетевший в электрическом поле ускорителя от точки с потенциалом  до точки с потенциалом
до точки с потенциалом  если
если  Решение. Кинетическая энергия
Решение. Кинетическая энергия  где
где  Отсюда
Отсюда  Энергия электрона
Энергия электрона  легко выражается в электронвольтах
легко выражается в электронвольтах  Если же заряд электрона
Если же заряд электрона  взять в кулонах, а разность потенциалов
взять в кулонах, а разность потенциалов  в вольтах, то энергия будет выражена в джоулях.
в вольтах, то энергия будет выражена в джоулях.

Рис. 178.

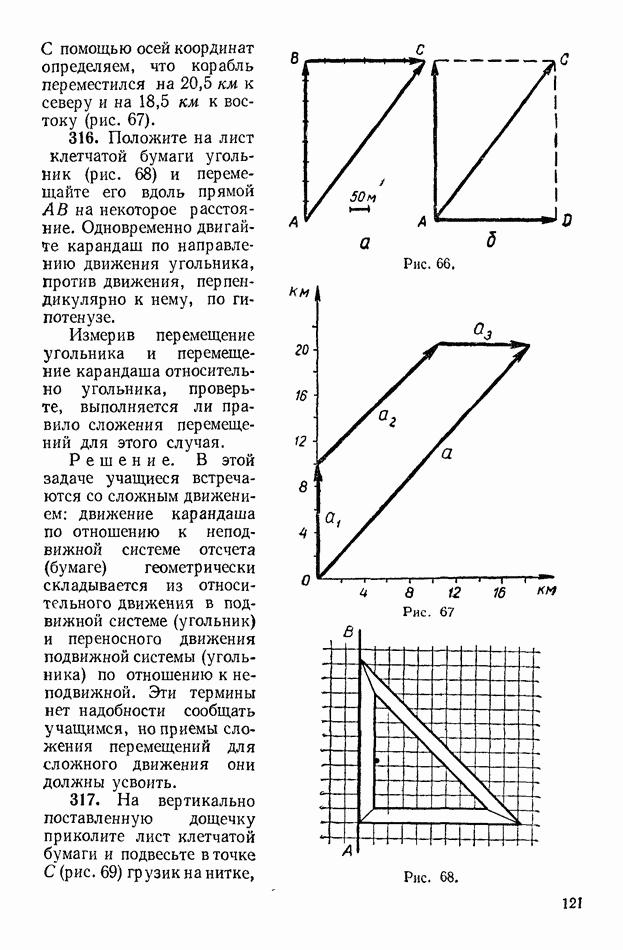
Рис. 179.
Получают: 
Большой интерес представляют задачи, в которых рассматривается однородное электрическое поле, образовавшееся между пластинами конденсатора.
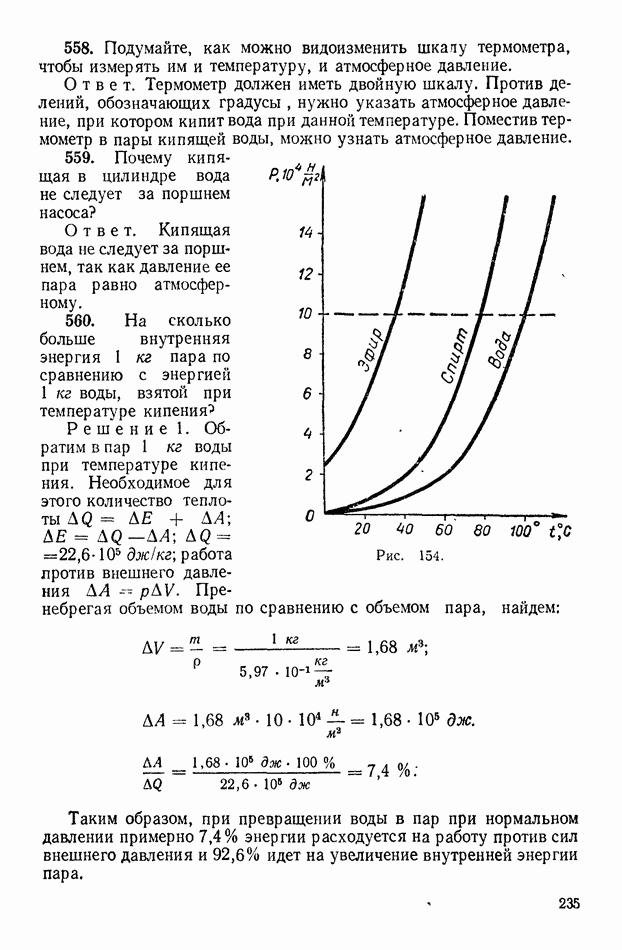
636. В опыте Иоффе в однородном электрическом поле между параллельными разноименно заряженными пластинами (рис. 179) находится пылинка массой  Разность потенциалов между пластинами
Разность потенциалов между пластинами  в, а расстояние
в, а расстояние  см. Определите заряд пылинки
см. Определите заряд пылинки  если она находится в равновесии в электрическом поле.
если она находится в равновесии в электрическом поле.
Решение. На рисунке 179 обозначены силы  действующие на пылинку. Поле сил тяжести действует с силой
действующие на пылинку. Поле сил тяжести действует с силой  а электрическое поле — с силой
а электрическое поле — с силой  Чтобы уравновесить силу
Чтобы уравновесить силу  сила
сила  должна быть направлена вверх, т. е. заряд пылинки должен быть отрицательным. Для однородного поля величина
должна быть направлена вверх, т. е. заряд пылинки должен быть отрицательным. Для однородного поля величина  а величина силы
а величина силы  т. е.
т. е.  Условие равновесия
Условие равновесия  (силы равны по величине и противоположно направлены) или-
(силы равны по величине и противоположно направлены) или-  откуда
откуда  Вычисления дают
Вычисления дают 
В заключение решают задачи повышенной трудности. Ниже приведен пример такой задачи.
637. N одинаковых шарообразных капелек ртути заряжены до одного и того же потенциала  Каков будет потенциал
Каков будет потенциал  большой капли ртути, получившейся в результате слияния этих капель?
большой капли ртути, получившейся в результате слияния этих капель?
Решение. Пусть радиус каждой малой капли  а ее заряд
а ее заряд  Так как электрическое поле равномерно заряженного шара совпадает вне шара с электрическим полем точечного заряда той же величины, помещенного в центре шара, потенциал в воздухе
Так как электрическое поле равномерно заряженного шара совпадает вне шара с электрическим полем точечного заряда той же величины, помещенного в центре шара, потенциал в воздухе  на поверхности шарообразной капли будет
на поверхности шарообразной капли будет  а заряд
а заряд 
Заряд большой капли  а радиус ее
а радиус ее  Потенциал на поверхности большой капли
Потенциал на поверхности большой капли 
Объем малой капли  а большой —
а большой —  Но объем большой капли равен
Но объем большой капли равен  объемам малых капель, т. е.
объемам малых капель, т. е.  .
.
Радиусы капель связаны соотношением  Окончательно
Окончательно

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
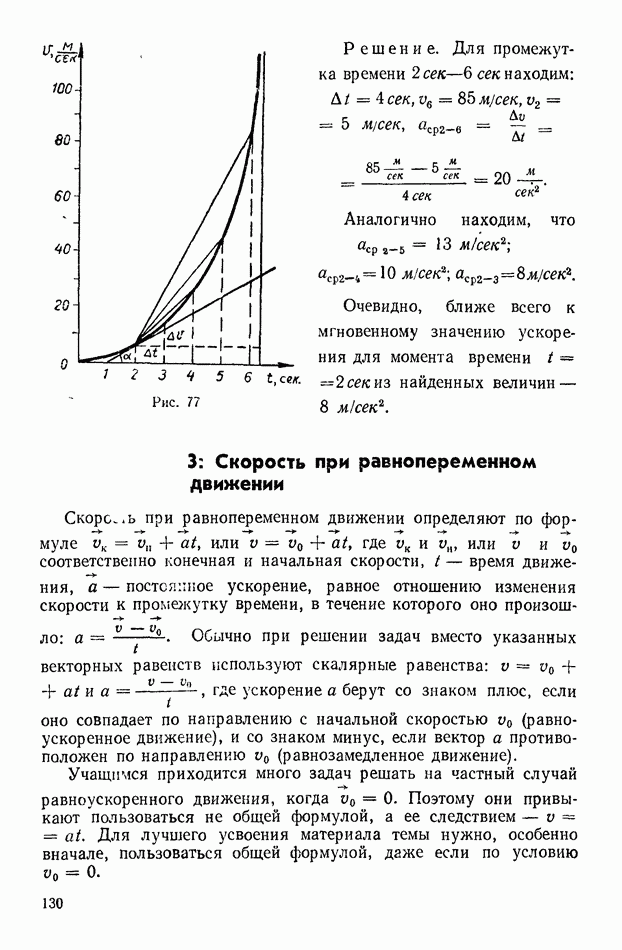
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА