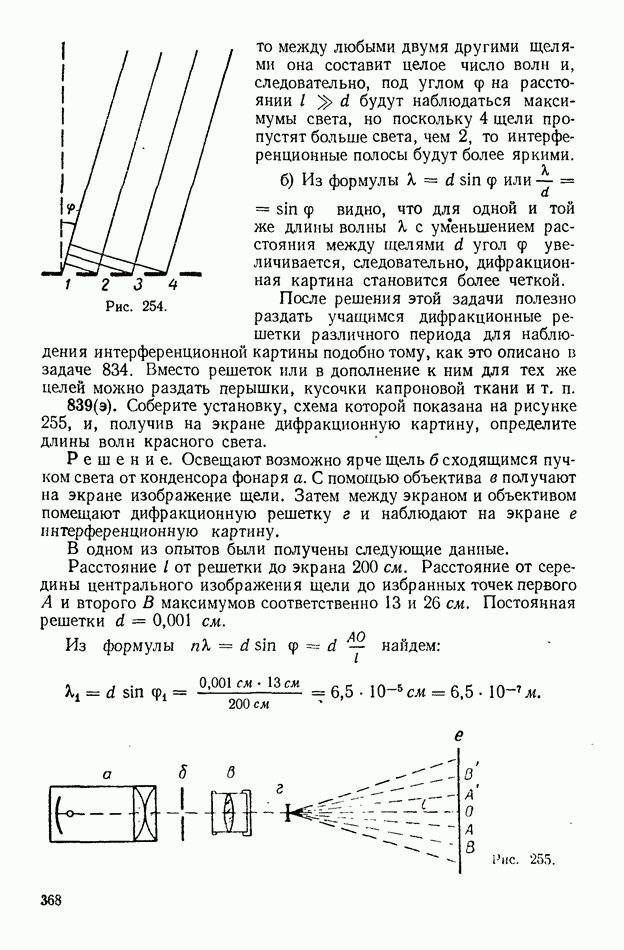
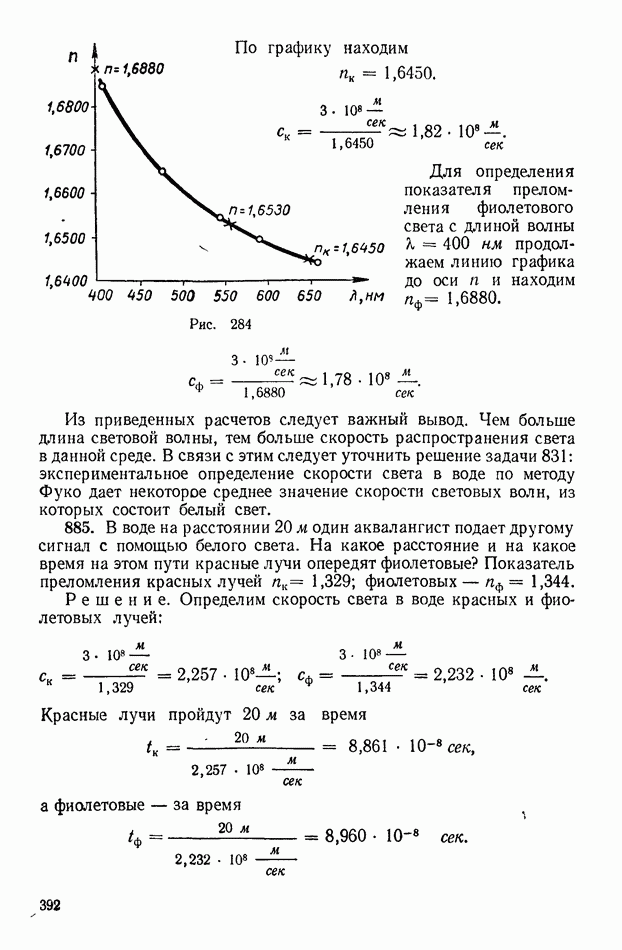
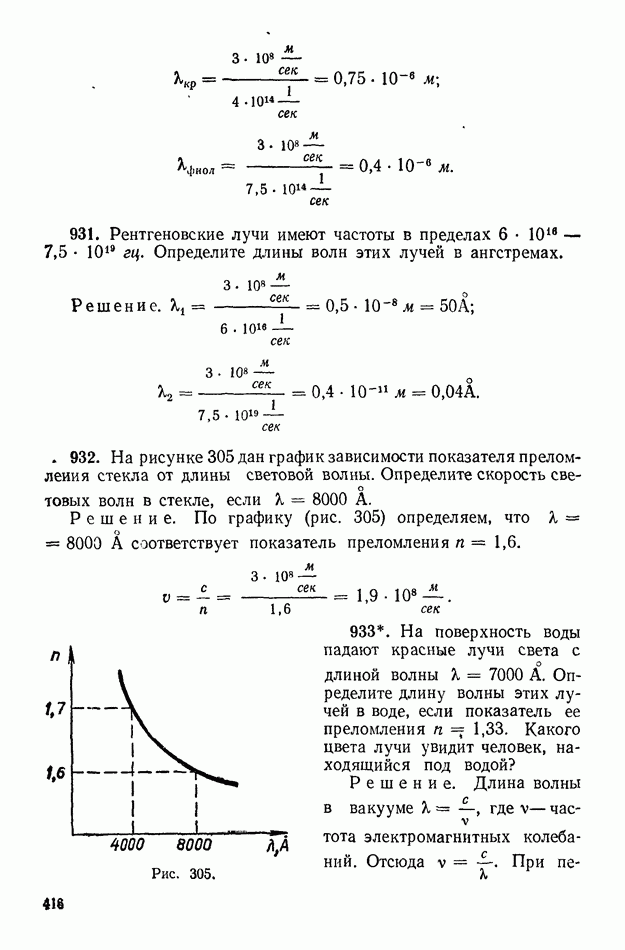
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Линзы
В средней школе по данной теме решают задачи только о тонких сферических линзах, толщина которых мала по сравнению с радиусами их сферических поверхностей.
В первых задачах, используя сведения о преломлении лучей трехгранной призмой, нужно рассмотреть принцип действия линз, обратив особое внимание на преломление лучей на обеих

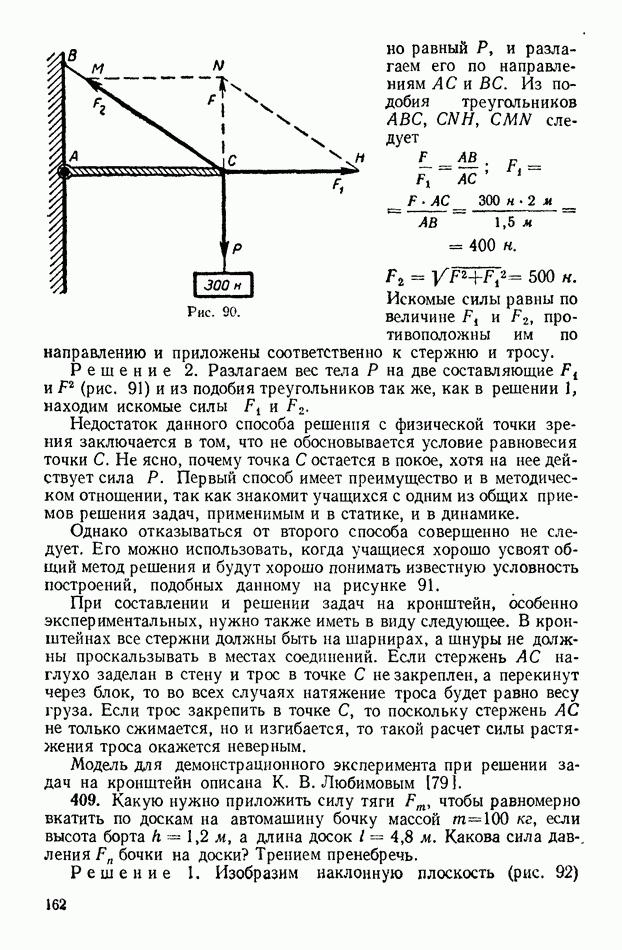
Рис. 286.
сферических поверхностях. Без этого соответствующие правила построения хода лучей могут быть усвоены учащимися формально.
В первых задачах следует также обратить внимание на закрепление следующих понятий (рис. 286).
Главная оптическая ось  или, как мы будем далее говорить для краткости, главная ось — прямая, проходящая через центры обеих преломляющих поверхностей. Оптический центр
или, как мы будем далее говорить для краткости, главная ось — прямая, проходящая через центры обеих преломляющих поверхностей. Оптический центр  точка, при прохождении через которую лучи не преломляются; фокус — точка, в которой пересекаются лучи, падающие на линзу параллельно главной оптической оси. Фокусное расстояние
точка, при прохождении через которую лучи не преломляются; фокус — точка, в которой пересекаются лучи, падающие на линзу параллельно главной оптической оси. Фокусное расстояние  Побочная ось — любая прямая, проходящая через оптический центр. Побочный фокус
Побочная ось — любая прямая, проходящая через оптический центр. Побочный фокус 
Фокус  находящийся с той стороны, откуда падают на линзу лучи, называют передним. Фокус
находящийся с той стороны, откуда падают на линзу лучи, называют передним. Фокус  называют задним. Поскольку преломляющее действие половины линзы, находящейся, например, выше оптической оси, подобно действию трехгранной призмы, то ясно, что угол отклонения луча и, следовательно, положение точки зависят от вещества линзы и от ее формы. Значение
называют задним. Поскольку преломляющее действие половины линзы, находящейся, например, выше оптической оси, подобно действию трехгранной призмы, то ясно, что угол отклонения луча и, следовательно, положение точки зависят от вещества линзы и от ее формы. Значение  может быть определено из формулы:
может быть определено из формулы:  где
где  соответственно абсолютные показатели преломления вещества линзы и среды;
соответственно абсолютные показатели преломления вещества линзы и среды;  радиусы сферических поверхностей.
радиусы сферических поверхностей.
В средней школе рассматривают главным образом линзы, ограниченные сферическими поверхностями равной кривизны, находящиеся в воздухе. Для этого случая формула имеет вид 
Главное внимание при решении задач уделяют построению изображений, даваемых линзой, и расчетам по формуле тонкой линзы

Для собирательной линзы  величина положительная, а для рассеивающей — отрицательная. Величина
величина положительная, а для рассеивающей — отрицательная. Величина  всегда положительная. Отсюда следует правило. Для рассеивающей линзы величина
всегда положительная. Отсюда следует правило. Для рассеивающей линзы величина  должна быть всегда отрицательной. Для собирательной линзы
должна быть всегда отрицательной. Для собирательной линзы  может быть как отрицательной, так и положительной величиной. Если изображение действительное, то
может быть как отрицательной, так и положительной величиной. Если изображение действительное, то  положительно, если мнимое, то оно отрицательно.
положительно, если мнимое, то оно отрицательно.
Формула тонкой линзы приближенная. Как и для зеркала, она позволяет тем точнее рассчитать ход лучей, чем уже световые пучки и чем меньший угол они составляют с оптической осью.
При утолщении линзы, расширении световых пучков и увеличении их угла с оптической осью начинают появляться погрешности изображения, или, как их называют, аберрации: сферическая, хроматическая и др. В ознакомительном плане о них можно сказать учащимся, тем более, что они нередко сами задают вопросы или высказывают предположения о том, почему, например, на экране при употреблении проекционного фонаря получается радужная каемка или изображение становится нечетким.
При выполнении построений и решении расчетных задач в средней школе указанные ограничения в применении формулы тонкой линзы и возможные погрешности обычно не учитывают, но о них все же нужно помнить и знать.
При выполнении построений в целях наглядности предметы («стрелки») рисуют значительных размеров, в том числе и больших самой линзы (см. № 891).
В заключение по данной теме решают задачи о линейном и угловом увеличении.
Как и для сферических зеркал, линейное увеличение определяют по формуле 
Желательно также решить две-три задачи о системах линз и зеркал. Новым для учащихся здесь явится только одно хорошо запоминающееся правило. Оптическая сила  системы из нескольких сложенных вплотную тонких линз равна алгебраической сумме оптических сил всех линз
системы из нескольких сложенных вплотную тонких линз равна алгебраической сумме оптических сил всех линз  или
или

887(э). Как отличить собирательную линзу от рассеивающей, не определяя их толщину в разных местах на ощупь? Ответ проверьте на опыте.
Решение, а) Собирательная линза дает на экране действительное изображение, например, солнца или лампочки. От рассеивающей линзы на экране можно получить круглую тень, окаймленную светлым кольцом.
б) Через собирательную линзу можно увидеть прямое увеличенное изображение предметов, например букв в книге (лупа), а через рассеивающую — уменьшенное изображение.
888(з). Дана плоско-выпуклая линза от конденсора проекционного фонаря. Найдите построением ее фокусное расстояние, приняв коэффициент преломления стекла  Ответ проверьте по известным вам формулам и на опыте.
Ответ проверьте по известным вам формулам и на опыте.

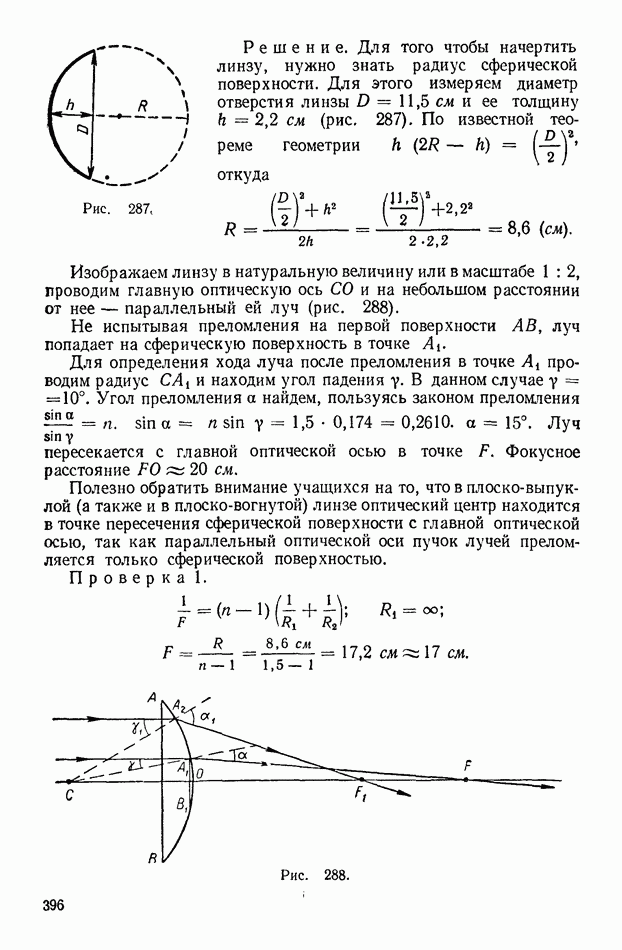
Рис. 287,
Решение. Для того чтобы начертить линзу, нужно знать радиус сферической поверхности. Для этого измеряем диаметр отверстия линзы  см и ее толщину
см и ее толщину  см (рис. 287). По известной теореме геометрии
см (рис. 287). По известной теореме геометрии  откуда
откуда

Изображаем линзу в натуральную величину или в масштабе  проводим главную оптическую ось
проводим главную оптическую ось  и на небольшом расстоянии от нее — параллельный ей луч (рис. 288).
и на небольшом расстоянии от нее — параллельный ей луч (рис. 288).
Не испытывая преломления на первой поверхности  луч попадает на сферическую поверхность в точке
луч попадает на сферическую поверхность в точке 
Для определения хода луча после преломления в точке  проводим радиус
проводим радиус  и находим угол падения у. В данном случае
и находим угол падения у. В данном случае  Угол преломления а найдем, пользуясь законом преломления
Угол преломления а найдем, пользуясь законом преломления  Луч пересекается с главной оптической осью в точке
Луч пересекается с главной оптической осью в точке  Фокусное расстояние
Фокусное расстояние  см.
см.
Полезно обратить внимание учащихся на то, что в плоско-выпуклой (а также и в плоско-вогнутой) линзе оптический центр находится в точке пересечения сферической поверхности с главной оптической осью, так как параллельный оптической оси пучок лучей преломляется только сферической поверхностью. Проверка 1.


Рис. 288.
Проверка 2 (э). Получаем на экране с помощью линзы изображение удаленной на несколько метров лампочки. Опыт дает значение 
Все три ответа согласуются между собой.
Отличие первого ответа от остальных объясняется главным образом неточностью построений, которые обусловлены прежде всего большими погрешностями при измерении углов с помощью транспортира. Ошибку вносит также и незнание точного значения показателя преломления стекла.
Анализируя условие задачи, следует сказать учащимся, что совпадение результата, полученного по формуле тонкой линзы, с результатами, полученными другими способами, объясняется тем, что рассматривался луч, близкий к оптической оси, а поэтому можно было считать, что изображение создавалось тонкой линзой 
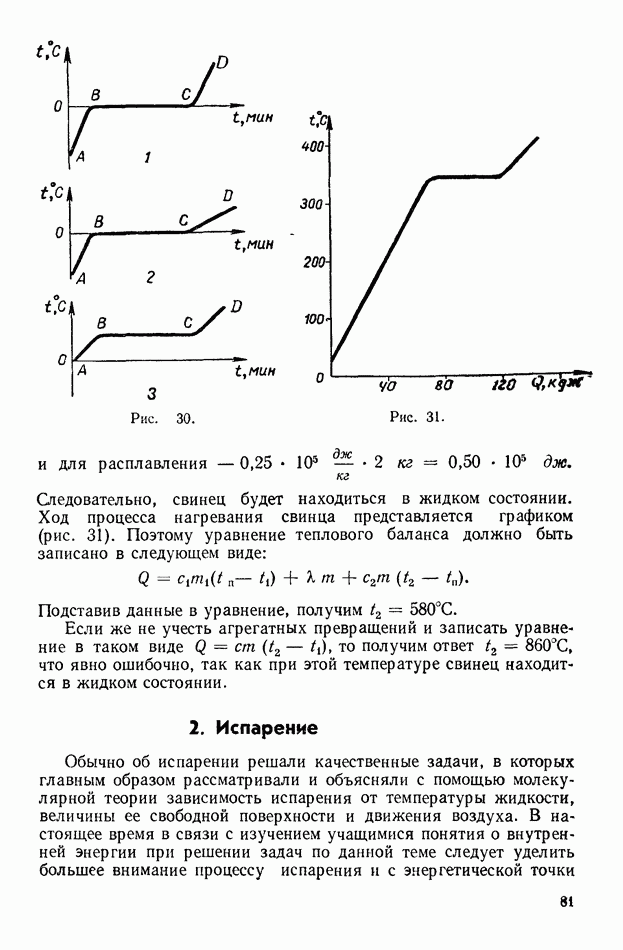
Желательно построить также ход луча, далеко отстоящего от оси. Он пересечется с осью в другой точке  расположенной значительно ближе к линзе. Лучи далекие от оси создают на экране вокруг изображения светлый ореол.
расположенной значительно ближе к линзе. Лучи далекие от оси создают на экране вокруг изображения светлый ореол.
Отдельным учащимся можно дать задание изготовить из картона экран с отверстием (диафрагмой), диаметр которого равен примерно  и круг, немного меньший по диаметру отверстия линзы
и круг, немного меньший по диаметру отверстия линзы 
Используя экран с отверстием, получим более четкое, чем без него, изображение нити лампочки на расстоянии  Светлого ореола вокруг изображения не будет. Закрыв же середину линзы кружком, получим изображение нити лампочки на расстоянии, которое меньше, чем
Светлого ореола вокруг изображения не будет. Закрыв же середину линзы кружком, получим изображение нити лампочки на расстоянии, которое меньше, чем  на 3—4 см (сферическая аберрация). При этом изображение имеет яркую, на большем расстоянии от линзы преимущественно красную, а на меньшем — синюю окраску (хроматическая аберрация).
на 3—4 см (сферическая аберрация). При этом изображение имеет яркую, на большем расстоянии от линзы преимущественно красную, а на меньшем — синюю окраску (хроматическая аберрация).
Явление можно продемонстрировать всему классу, получив увеличенное изображение нити лампочки на стене или потолке. Результаты опыта можно затем использовать при изучении фотоаппарата.
889. Всегда ли выпуклая линза является собирательной?
Ответ. Используя решение задачи о воздушной призме, помещенной в воду (№ 882), заключают, что, если выпуклая линза находится в среде оптически более плотной, чем материал самой линзы, то она является рассеивающей. Этот вывод полезно пояснить чертежом, рассмотрев качественно преломление луча на каждой сферической поверхности и экспериментально с помощью выпуклой линзы, склеенной из двух часовых стекол и помещенной в воду.
890. Постройте изображение точки  лежащей на оптической оси.
лежащей на оптической оси.
Решение. Изображаем линзу, проводим оптическую ось и указываем положение фокусов (рис. 289). Проводим из точки  изображение которой надо построить, какой-либо луч под углом к оси до середины линзы в точке А.
изображение которой надо построить, какой-либо луч под углом к оси до середины линзы в точке А.

Рис. 289,
Этим приемом мы будем пользоваться при построениях и в дальнейшем: преломление луча будем показывать только один раз, на средней линии линзы, а не на каждой ее поверхности. Через задний фокус  проводим прямую
проводим прямую  перпендикулярную оси, которая изображает заднюю фокальную плоскость. Затем через оптический центр О проводим побочную ось, параллельную лучу
перпендикулярную оси, которая изображает заднюю фокальную плоскость. Затем через оптический центр О проводим побочную ось, параллельную лучу  Она пересечется с фокальной плоскостью вточке В. Так как в этой точке должны собраться все лучи, параллельные побочной оси, то луч
Она пересечется с фокальной плоскостью вточке В. Так как в этой точке должны собраться все лучи, параллельные побочной оси, то луч  после преломления в линзе также пройдет через точку В и пересечет ось в точке 5, которая и является изображением точки
после преломления в линзе также пройдет через точку В и пересечет ось в точке 5, которая и является изображением точки  поскольку она лежит на пересечении двух лучей, идущих из точки 5 (луча
поскольку она лежит на пересечении двух лучей, идущих из точки 5 (луча  и луча
и луча 
891. Постройте изображение предмета, находящегося за двойным фокусным расстоянием, если его размеры больше отверстия линзы.
Решение. Изобразим предмет в виде стрелки, один конец которой находится на оптической оси (рис. 290). Это облегчит построение, поскольку изображение точки В, как показано в задаче 890, лежит на оси. (Этим приемом мы будем пользоваться и в дальнейшем). Если вместо маленькой линзы поставить большую по размерам, но с таким же фокусным расстоянием, то положение изображения не изменится. Рисовать большую линзу нет надобности. Достаточно увеличить размеры средней плоскости  и преломить на ней лучи по общим правилам: луч, параллельный оптической оси, пройдет через задний фокус, а луч, идущий через оптический центр, пройдет не преломляясь. Точка пересечения лучей
и преломить на ней лучи по общим правилам: луч, параллельный оптической оси, пройдет через задний фокус, а луч, идущий через оптический центр, пройдет не преломляясь. Точка пересечения лучей  и является
и является

Рис. 396.
изображением точки А. Опустив на ось перпендикуляр, найдем положение точки
В нескольких первых задачах полезно провести и третий луч. Луч, прошедший через передний фокус после преломления, идет параллельно оси и также попадает в точку А.
Следует подчеркнуть, что и любой другой луч, падающий на линзу из точки А, попадет в точку  что нередко упускается учащимися из виду.
что нередко упускается учащимися из виду.
Практическим примером рассмотренного случая получения изображения является фотоаппарат.
892(э). С помощью линзы на стене получили увеличенное изображение пламени свечи. Пропадет ли часть изображения, если закрыть нижнюю половину линзы? Ответ проверьте на опыте.
Ответ. Никакая часть изображения не исчезнет, оно станет только менее ярким.
Опыт должен еще раз подтвердить, что все лучи, падающие на линзу от какой-либо точки, пересекаются в одной точке изображения, которую можно получить, пользуясь любым участком линзы.
893. Составьте и решите с помощью построений и расчетов задачи на формулу собирательной линзы. Решение проверьте с помощью опытов, если у вас имеются, например, очковые стекла, лупа и т. п.
Эту задачу можно дать на дом. При проверке ее в классе нужно отобрать и проанализировать примеры,  которых рассматривают наиболее характерные случаи построения действительных изображений:
которых рассматривают наиболее характерные случаи построения действительных изображений:

Если позволяет время, обобщая эти случаи, можно также решить задачу, подобную 868, рассмотрев, как изменяется величина  в зависимости от
в зависимости от  При этом построить график в координатных осях
При этом построить график в координатных осях 
При выполнении построений, методика которых ясна из рисунков 289—290, полезно прибегать к аналогиям с построением изображений в вогнутом зеркале.
894. Какая из двух линз с оптической силой  дптр даст большего размера изображение и во сколько раз, если расстояние предмета до экрана
дптр даст большего размера изображение и во сколько раз, если расстояние предмета до экрана  Ответ проверьте на опыте.
Ответ проверьте на опыте.
Решение. Линейное увеличение  Из формулы линзы
Из формулы линзы  найдем
найдем 

Из формулы видно, что, чем меньше фокусное расстояние линзы  тем больше увеличение, которое она дает при одном и том же
тем больше увеличение, которое она дает при одном и том же  и называют оптической силой линзы.)
и называют оптической силой линзы.)
Результаты легко проверить, получив на экране одновременно изображения волоска лампочки с помощью двух линз различной оптической силы.
895. Поместив на расстоянии 20 см от линзы свечу, получили на экране ее изображение. Увеличение  Какое получится увеличение, если вплотную к данной линзе приложить линзу с оптической силой
Какое получится увеличение, если вплотную к данной линзе приложить линзу с оптической силой  ?
?
Решение. Если приложить положительную (собирательную) линзу, то оптическая сила системы линз станет больше и увеличение возрастет. Если же приложить отрицательную (рассеивающую) линзу, то увеличение уменьшится.
Для количественных расчетов найдем оптическую силу данной линзы, используя уравнения:

Найдем расстояние до экрана.  Найдем оптическую силу сложенных вместе линз.
Найдем оптическую силу сложенных вместе линз. 
896. Какое изображение и где даст очковое стекло с оптической силой  , если предмет высотой 10 см расположен от него на расстоянии 50 см? Задачу решите с помощью построений и расчетов.
, если предмет высотой 10 см расположен от него на расстоянии 50 см? Задачу решите с помощью построений и расчетов.
Решение. 1. Найдем расстояние  до изображения, пользуясь формулой тонкой линзы
до изображения, пользуясь формулой тонкой линзы  Применяя эту формулу в таком виде, нужно подставлять в нее числовые значения
Применяя эту формулу в таком виде, нужно подставлять в нее числовые значения  со знаком минус. Если же формула будет записана в виде
со знаком минус. Если же формула будет записана в виде  то в нее следует все числа подставлять со знаком плюс.
то в нее следует все числа подставлять со знаком плюс.
Предпочтительнее все же пользоваться первой, общей для всех тонких линз записью данной формулы, 
Увеличение  Изображение
Изображение

Рис. 291.
меньше предмета в 2,5 раза. Знак минус показывает, что изображение мнимое.
Решение. 2. Определим для построения изображения значение  см и выберем масштаб:
см и выберем масштаб:  см.
см.
Взаимное положение линзы, предмета и фокуса показано на рисунке 291. Построение изображения точек выполняем по общему правилу с помощью двух лучей, ход которых известен.
Луч, параллельный оптической оси, преломившись в линзе, пойдет так, что его продолжение пересечется с осью в фокусе  Луч, идущий через центр О, не преломляется. Глаз, расположенный справа от линзы, увидит изображение точки А в точке пересечения лучей А у. Величины, найденные по чертежу, совпадают с вычисленными по формулам. Ответ желательно проверить также с помощью опыта. Для этого смотрят одним глазом на предмет, например линейку, а вторым — на его изображение в линзе. При этом сразу видно, что изображение уменьшенное и прямое (значит, оно и мнимое). При некотором навыке не трудно оценить на глаз и примерное уменьшение размеров изображения.
Луч, идущий через центр О, не преломляется. Глаз, расположенный справа от линзы, увидит изображение точки А в точке пересечения лучей А у. Величины, найденные по чертежу, совпадают с вычисленными по формулам. Ответ желательно проверить также с помощью опыта. Для этого смотрят одним глазом на предмет, например линейку, а вторым — на его изображение в линзе. При этом сразу видно, что изображение уменьшенное и прямое (значит, оно и мнимое). При некотором навыке не трудно оценить на глаз и примерное уменьшение размеров изображения.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
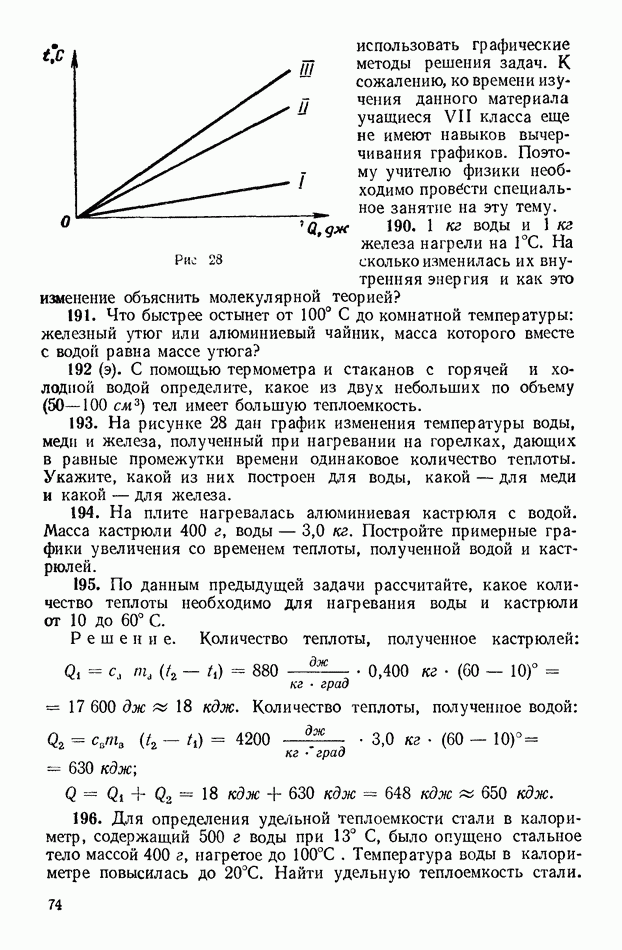
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
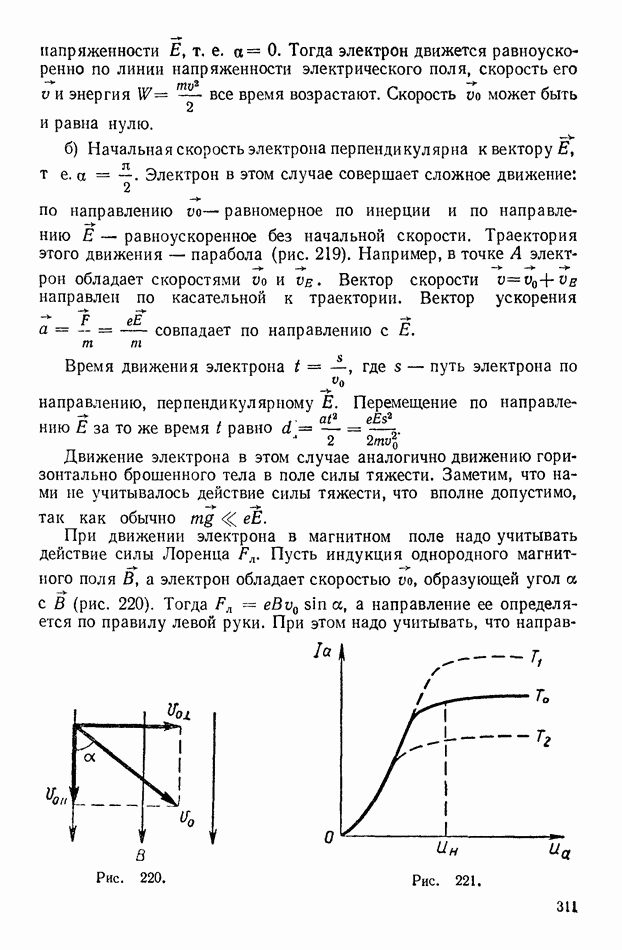
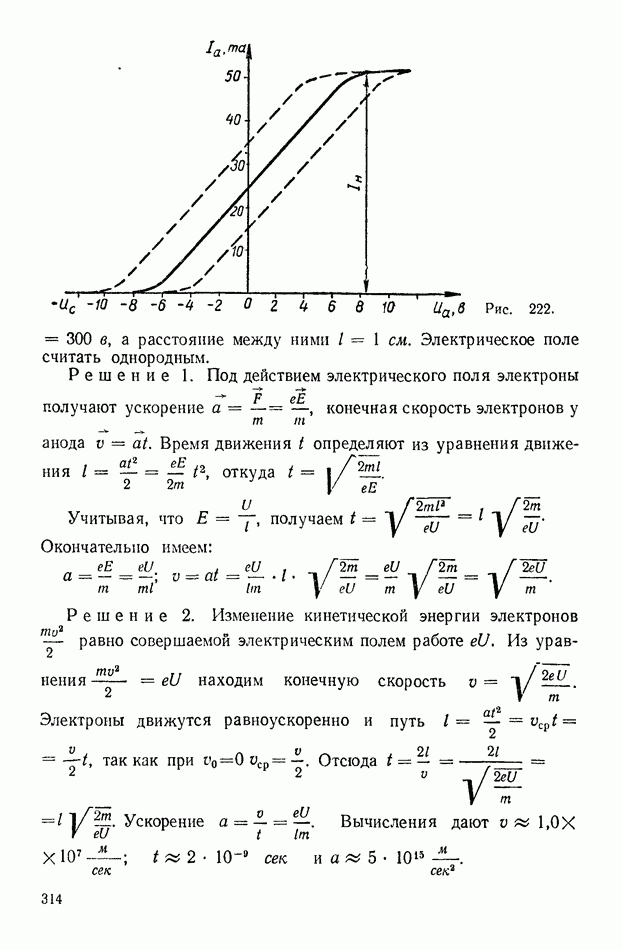
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА