| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
10 КЛАСС
ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
Колебательные и волновые процессы изучают в одном разделе. Этим подчеркивается огромная роль учения о колебаниях в современной науке и технике и то общее, что присуще этим движениям независимо от их природы.
Вначале изучают механические колебания, на примере которых вводят основные понятия и рассматривают важнейшие закономерности колебательных движений. При этом подробно рассматривают только наиболее простые, гармонические колебания, которые, однако, имеют очень большое значение, поскольку согласно теореме Фурье всякое периодическое колебание может быть представлено в виде суммы гармонических колебаний. В процессе решения задач учащиеся должны научиться пользоваться соответствующими формулами, осознать те специфические отличия, которые имеет колебательное движение по сравнению с равномерным и равномерно переменным. В этих целях сначала решают задачи по кинематике колебательного движения материальной точки. Как частный, но важный случай этого движения рассматривают движение математического маятника.
Вопросы динамики колебательного движения и превращения энергии углубляют с помощью задач об упругих колебаниях и задач о «тяжелом» маятнике. После этого решают задачи о сложении колебаний.
Распространение колебаний в упругой среде рассматривают главным образом на примере звуковых волн, в том числе полезно решить ряд задач об ультразвуке.
1. Гармонические колебания
При решении задач по этой теме нужно учитывать знания учащихся по математике. По новой программе будут изучаться производные тригонометрических функций и их свойства. Учащиеся должны хорошо запомнить прежде всего зависимость смещения
точки от времени

Поскольку скорость колебательного движения  и ускорение а являются, соответственно первой и второй производными этой функции:
и ускорение а являются, соответственно первой и второй производными этой функции:

Для того чтобы избежать формально математического решения задач, нужно широко использовать эксперимент и графики.
Полезно также с помощью задач показать, как можно получить указанные зависимости без дифференцирования, используя законы кинематики и динамики (12, гл. V).
В тех случаях, когда начальная фаза  не является предметом изучения и не влияет на конечный результат, для простоты записей и экономии времени ее лучше полагать в условии задачи равной нулю. Однако учащиеся должны во всех случаях сначала записывать формулу в общем виде, а уже затем, в зависимости от конкретных данных упрощать ее.
не является предметом изучения и не влияет на конечный результат, для простоты записей и экономии времени ее лучше полагать в условии задачи равной нулю. Однако учащиеся должны во всех случаях сначала записывать формулу в общем виде, а уже затем, в зависимости от конкретных данных упрощать ее.
Как показывает опыт, учащиеся не легко усваивают понятие о круговой частоте  На это надо обратить внимание, подчеркивая, что под знаком тригонометрической функции стоит всегда величина угла
На это надо обратить внимание, подчеркивая, что под знаком тригонометрической функции стоит всегда величина угла  Если под знаком тригонометрической функции и принимают равным 180°, то значение угла получают в градусах. Если же принять, что
Если под знаком тригонометрической функции и принимают равным 180°, то значение угла получают в градусах. Если же принять, что  то угол получится в радианах. Для закрепления этих сведений полезно проверить решение ряда задач с помощью действий над размерностями величин, входящих в формулы гармонических колебаний. Смещение
то угол получится в радианах. Для закрепления этих сведений полезно проверить решение ряда задач с помощью действий над размерностями величин, входящих в формулы гармонических колебаний. Смещение  скорость
скорость  и ускорение а могут иметь одно и то же значение при различных углах или времени
и ускорение а могут иметь одно и то же значение при различных углах или времени  так как они выражаются циклическими функциями. При решении задач, если в том нет специальной необходимости, за величину угла
так как они выражаются циклическими функциями. При решении задач, если в том нет специальной необходимости, за величину угла  можно принимать его наименьшее значение.
можно принимать его наименьшее значение.
741. При колебательном движении пружинного маятника в соответствий с законом Гука на него действует сила  Принимая во внимание эту формулу, ответьте на следующие вопросы:
Принимая во внимание эту формулу, ответьте на следующие вопросы:
а) В чем отличие движения маятника от равномерного движения?
б) В чем отличие его от движения равномерно переменного? в) В каком положении маятник имеет наибольшие и в каком наименьшие значения ускорения а и скорости 
Ответ, а) В отличие от равномерного движения скорость тела меняется. Это следует из того, что на тело действует неуравновешенная сила; следовательно, тело движется с ускорением.
б) В отличие от равномерно переменного движения ускорение колеблющегося тела не постоянно. Это следует из формулы  Ускорение а изменяется, так как изменяется сила
Ускорение а изменяется, так как изменяется сила  Наибольшее по величине ускорение тело имеет в крайних (правом и левом) положениях при максимальном смещении
Наибольшее по величине ускорение тело имеет в крайних (правом и левом) положениях при максимальном смещении  а наименьшее, равное нулю, — при
а наименьшее, равное нулю, — при  в положении равновесия. В крайнем положении скорость тела
в положении равновесия. В крайнем положении скорость тела  Затем скорость возрастает, поскольку есть ускорение, достигая максимального значения в положении равновесия.
Затем скорость возрастает, поскольку есть ускорение, достигая максимального значения в положении равновесия.
742. Можно ли сказать, что смещение х пропорционально времени  или
или
Ответ. Нельзя. Зависимость  применима только для равномерного, а
применима только для равномерного, а  для равномерно переменного движения.
для равномерно переменного движения.
743. Напишите уравнение гармонического колебания, амплитуда которого  см, период колебания
см, период колебания  Ответ. В общем случае —
Ответ. В общем случае —  Для данных условий
Для данных условий

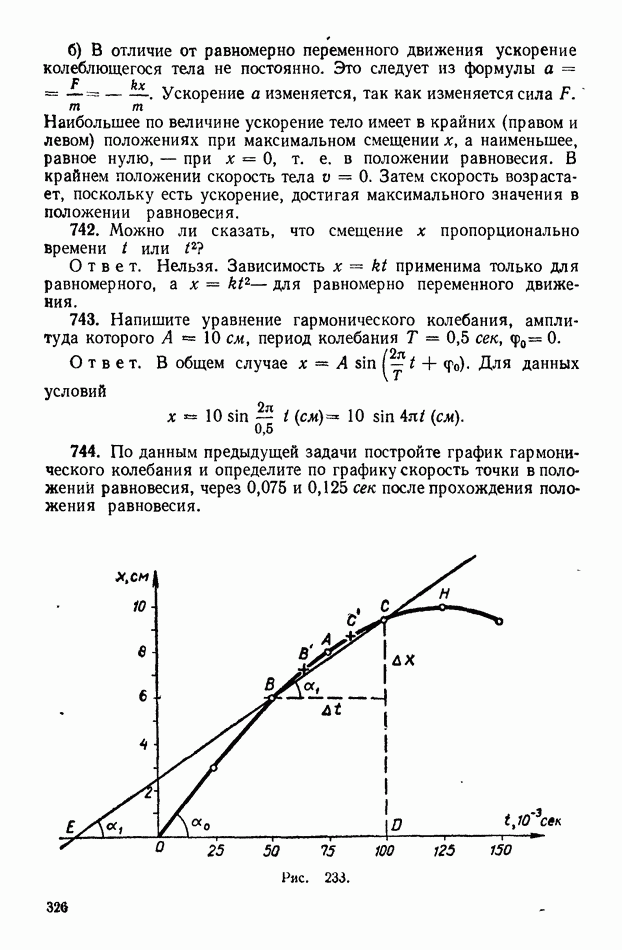
744. По данным предыдущей задачи постройте график гармонического колебания и определите по графику скорость точки в положений равновесия, через 0,075 и 0,125 сек после прохождения положения равновесия.

Рис. 233.
Указание. Масштаб выбрать для времени 1 см  для смещения
для смещения  . График построить по семи точкам для промежутка времени
. График построить по семи точкам для промежутка времени  .
.
Решение. Составим таблицу и построим график (рис. 233).
(см. скан)
Скорость  тела, соответствующая точке А графика, численно равна тангенсу угла наклона касательной в точке А к оси времени. Касательную в точке А синусоиды можно провести на глаз, но лучше найти некоторое среднее значение скорости
тела, соответствующая точке А графика, численно равна тангенсу угла наклона касательной в точке А к оси времени. Касательную в точке А синусоиды можно провести на глаз, но лучше найти некоторое среднее значение скорости  для небольшого интервала времени
для небольшого интервала времени 

Для точки О

Для точки 
745. Проверьте решение предыдущей задачи по формуле скорости гармонического колебательного движения.
Решение, 

Как видим, расчеты хорошо согласуются с данными графического решения. При этом следует сказать учащимся, что если взять на графике точки  более близкие к точке А, то точность определения
более близкие к точке А, то точность определения  повысится.
повысится.
Не злоупотребляя подобными графическими задачами ввиду их трудоемкости, все же следует настоятельно рекомендовать их решение, без чего ученики «не прочувствуют» особенности гармонических колебаний и останутся беспомощными в построении графиков.
Одну задачу такого типа необходимо обстоятельно разобрать в классе и одну-две задать на дом, требуя самых тщательных построений в достаточно крупном масштабе.
746. Постройте от руки график гармонического колебания и, пользуясь им, покажите, как изменяется при движении ускорение.
Решение. Ускорение  численно равно тангенсу
численно равно тангенсу

Рис. 234.
угла наклона касательной к кривой графика скорости в заданной точке (рис. 234). Так как график скорости представляет собой косинусоиду, он сдвинут по сравнению с графиком перемещений на четверть периода. Когда скорость точки наибольшая, ускорение равно О (касательная параллельна оси времени), и, наоборот, при скорости, равной нулю, ускорение колеблющейся точки максимально. 747. Колебания материальной точки совершаются по закону  см. Найти амплитуду, период, начальную фазу, максимальную скорость и максимальное ускорение колеблющейся точки.
см. Найти амплитуду, период, начальную фазу, максимальную скорость и максимальное ускорение колеблющейся точки.
Решение. Приведем уравнение к виду  см и сравним его с данным в задаче уравнением
см и сравним его с данным в задаче уравнением

Знак минус означает, что график данной синусоиды симметричен относительно оси времени синусоиде

Но колебания (1) опережают по фазе колебания (2) на  . Следовательно, можно записать
. Следовательно, можно записать  см.
см.
Амплитуда  сек;
сек;

На этом конкретном примере поясняют, что движение, происходящее по закону  отличается от гармонического колебательного движения, описываемого уравнением
отличается от гармонического колебательного движения, описываемого уравнением  только тем, что опережает его по фазе на
только тем, что опережает его по фазе на 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
- 2. Постоянные магниты
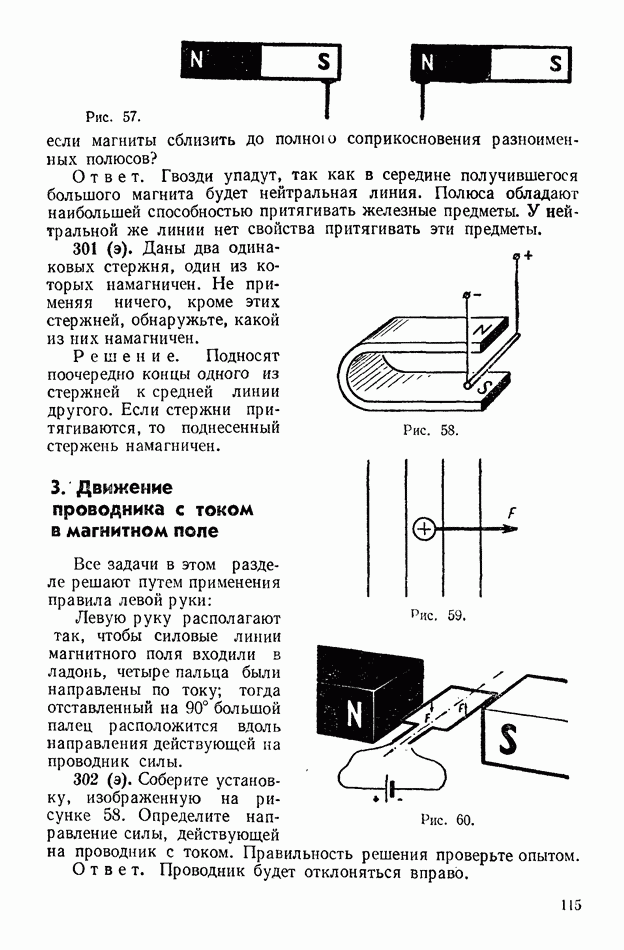
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
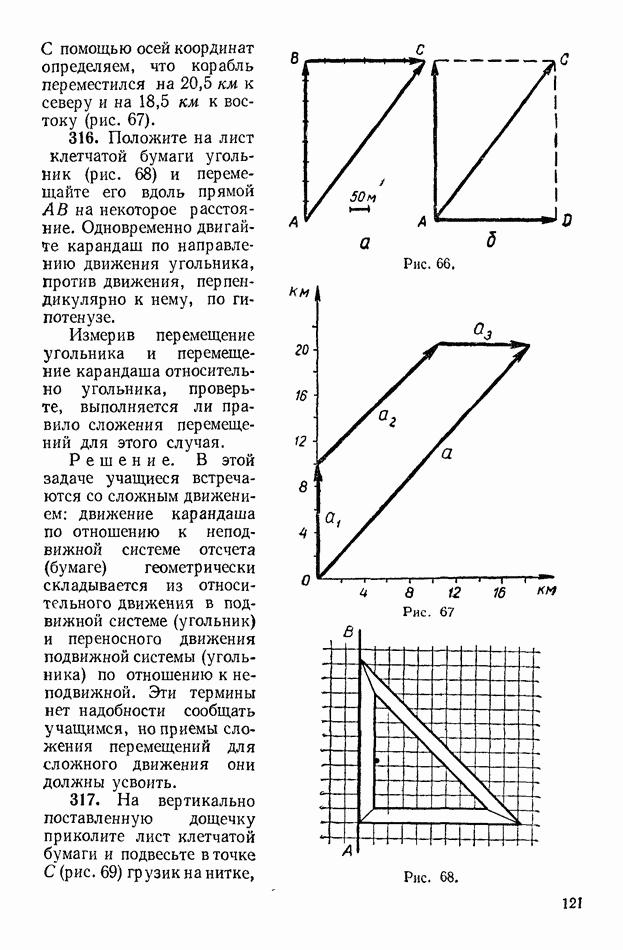
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
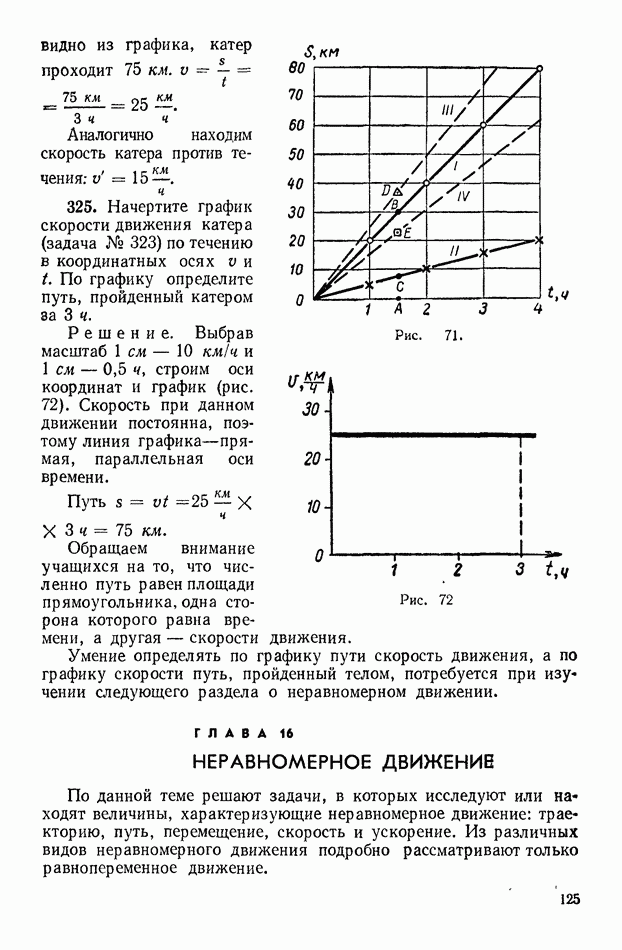
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА