| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Механическая энергия
Вначале решают задачи о потенциальной энергии тел, учитывая сведения, полученные учащимися в VI классе (гл. 7, 6), а затем — задачи об энергии кинетической. Эти задачи требуют к себе большего внимания, поскольку формулу  дают учащимся впервые.
дают учащимся впервые.
После этого главное внимание уделяют задачам на закон сохранения энергии в механических процессах, в том числе при работе простых механизмов. Комбинированные задачи с использованием закона сохранения энергии представляют собой прекрасное средство повторения многих разделов кинематики и динамики.
Для уяснения физической сущности закона сохранения энергии в механических процессах сначала на примере энергии падающего тела решают задачи для идеальных условий, без учета сил
сопротивления, пользуясь формулой  Величины
Величины  характеризуют равнопеременное движение тел под действием силы тяжести. Далее решают задачи, в которых необходимо учитывать работу, совершаемую телом за счет кинетической или потенциальной энергии. Для упрощения расчетов берут среднее значение силы сопротивления среды
характеризуют равнопеременное движение тел под действием силы тяжести. Далее решают задачи, в которых необходимо учитывать работу, совершаемую телом за счет кинетической или потенциальной энергии. Для упрощения расчетов берут среднее значение силы сопротивления среды  Задачи решают по формуле
Задачи решают по формуле  где
где  изменение кинетической или потенциальной энергии тела. Поскольку в формулу входит значение силы, задачи этого типа часто допускают решение с использованием второго закона Ньютона (№ 481).
изменение кинетической или потенциальной энергии тела. Поскольку в формулу входит значение силы, задачи этого типа часто допускают решение с использованием второго закона Ньютона (№ 481).
При решении задач о потенциальной энергии нужно обратить внимание на то, что величину потенциальной энергии определяют относительно уровня, условно принимаемого за нулевой. Обычно это уровень поверхности Земли.
Учащиеся должны также помнить, что формула  приближенная, так как
приближенная, так как  изменяется с высотой. Только для небольших по сравнению с радиусом Земли значений
изменяется с высотой. Только для небольших по сравнению с радиусом Земли значений  можно считать
можно считать  постоянной величиной.
постоянной величиной.
Кинетическая энергия, определяемая по формуле  также зависит от системы отсчета, в которой измеряют скорость. Чаще всего систему отсчета связывают с Землей.
также зависит от системы отсчета, в которой измеряют скорость. Чаще всего систему отсчета связывают с Землей.
482. На сколько увеличится потенциальная энергия вашего тела, когда вы подниметесь с первого этажа на второй?
483. Сравните, в каких случаях тела обладают большей потенциальной энергией: а) молот на наковальне и на высоте  от нее; б) воздушный шар у поверхности Земли и на высоте
от нее; б) воздушный шар у поверхности Земли и на высоте  спасательный круг на поверхности воды и на глубине
спасательный круг на поверхности воды и на глубине  недеформированная, растянутая и сжатая (на ту же величину) пружина.
недеформированная, растянутая и сжатая (на ту же величину) пружина.
Ответ, а) Поднятый молот в соответствии с формулой  обладает большей потенциальной энергией, б) На воздушный шар действует подъемная сила, за счет которой он может совершить работу, поднимаясь вверх, следовательно, шар у Земли обладает большей потенциальной энергией, чем на высоте
обладает большей потенциальной энергией, б) На воздушный шар действует подъемная сила, за счет которой он может совершить работу, поднимаясь вверх, следовательно, шар у Земли обладает большей потенциальной энергией, чем на высоте  Подобно шару, погруженный в воду круг обладает большей потенциальной энергией, чем на ее поверхности, г) Растянутая и сжатая пружины обладают одинаковой энергией
Подобно шару, погруженный в воду круг обладает большей потенциальной энергией, чем на ее поверхности, г) Растянутая и сжатая пружины обладают одинаковой энергией  равной работе по их деформации. Недеформированная пружина такой энергией не обладает.
равной работе по их деформации. Недеформированная пружина такой энергией не обладает.
484. В классе решали задачу: «Два груза массой по  каждый подняли один с земли на третий этаж, а второй с третьего этажа на четвертый. Какая работа по поднятию грузов затрачена? Чему равна потенциальная энергия грузов, если высота этажа
каждый подняли один с земли на третий этаж, а второй с третьего этажа на четвертый. Какая работа по поднятию грузов затрачена? Чему равна потенциальная энергия грузов, если высота этажа 
Один ученик решил задачу следующим образом.

Правильно ли это решение?
Ответ. В решении допущена ошибка:  По смыслу задачи под потенциальной энергией груза понимают его энергию относительно уровня Земли.
По смыслу задачи под потенциальной энергией груза понимают его энергию относительно уровня Земли. 
485. Какую нужно совершить работу, чтобы поднять из воды глыбу льда в форме куба объемом 
Решение 1. Работа равна увеличению потенциальной энергии поднятого льда по сравнению с потенциальной энергией льда в воде. 
Определим объем льда, находящегося над водой. Архимедова сила уравновешивает силу тяжести  где
где  и V соответственно плотность воды и объем погруженной части льда, отсюда
и V соответственно плотность воды и объем погруженной части льда, отсюда

Над водой находится  льда массой
льда массой  Толщина этой части льда
Толщина этой части льда  Следовательно, лед нужно поднимать на
Следовательно, лед нужно поднимать на  Поскольку сила тяжести уравновешивается архимедовой силой, в первый момент необходимая для подъема сила
Поскольку сила тяжести уравновешивается архимедовой силой, в первый момент необходимая для подъема сила  Затем эта сила по мере подъема льда будет возрастать, так как будет уменьшаться выталкивающая сила. В последний момент
Затем эта сила по мере подъема льда будет возрастать, так как будет уменьшаться выталкивающая сила. В последний момент 
Строго говоря, для того, чтобы пользоваться при расчетах средней силой  нужно было предварительно доказать линейную зависимость силы от высоты подъема льда. Такое задание в качестве дополнительного можно дать отдельным учащимся.
нужно было предварительно доказать линейную зависимость силы от высоты подъема льда. Такое задание в качестве дополнительного можно дать отдельным учащимся.
486. Сравните кинетическую энергию пули массой  летящей со скоростью
летящей со скоростью  и человека массой
и человека массой  бегущего со скоростью
бегущего со скоростью 
Решение. 

В данном случае летящая пуля имеет большую кинетическую энергию, чем бегущий человек.
487. Стрелок бомбардировщика стреляет из пушки в летящий навстречу истребитель. Какова кинетическая энергия снаряда массой  относительно Земли и истребителя? Скорость истребителя
относительно Земли и истребителя? Скорость истребителя  бомбардировщика
бомбардировщика  и снаряда пушки
и снаряда пушки 
Решение. Скорость снаряда относительно Земли 

Примем за тело отсчета истребитель. Как говорилось в главе 15,2, для нахождения относительной скорости тела в новой системе координат  нужно к абсолютной скорости в первой системе
нужно к абсолютной скорости в первой системе  прибавить с обратным знаком переносную скорость, т. е. скорость второй системы отсчета относительно первой
прибавить с обратным знаком переносную скорость, т. е. скорость второй системы отсчета относительно первой  Так как направление
Так как направление  противоположно
противоположно  то
то 
То есть величина кинетической энергии зависит от того, в какой системе отсчета измеряется скорость тела.
488. Мяч массой  свободно падает с высоты
свободно падает с высоты  Определите потенциальную и кинетическую энергию мяча в начале и конце падения и на расстоянии
Определите потенциальную и кинетическую энергию мяча в начале и конце падения и на расстоянии  от Земли. Принять
от Земли. Принять  Сопротивлением воздуха пренебречь.
Сопротивлением воздуха пренебречь.
Решение. На высоте  мяч обладает потенциальной энергией
мяч обладает потенциальной энергией  На высоте
На высоте  мяч обладает потенциальной и кинетической энергией.
мяч обладает потенциальной и кинетической энергией.  По закону сохранения энергии
По закону сохранения энергии 
Проверка.  закону свободного падения
закону свободного падения

В нижней точке вся энергия мяча будет кинетической: 
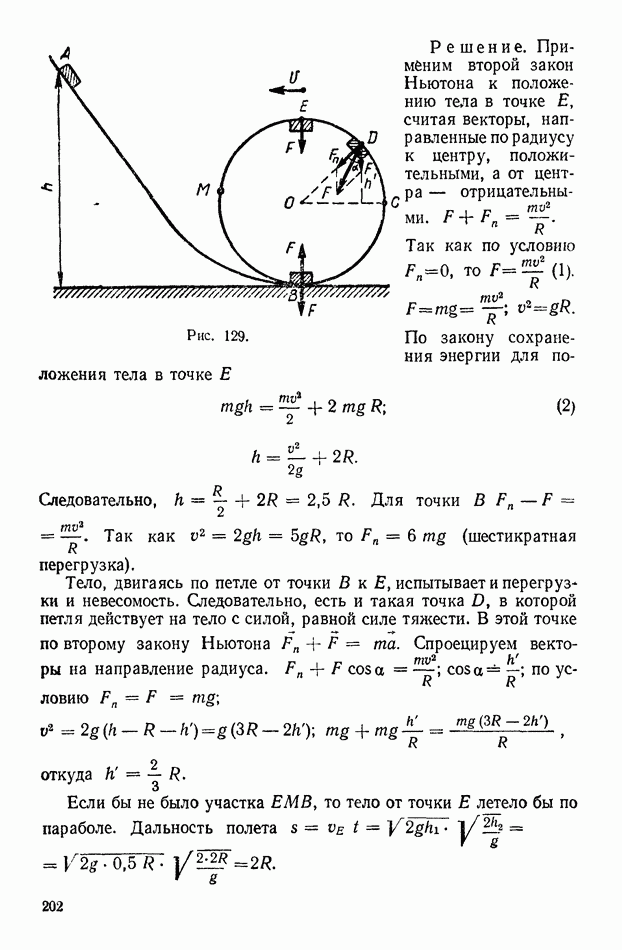
489. С какой минимальной высоты должен скользить без трения брусок, чтобы описать «мертвую петлю» (рис. 129), не оказывая на нее давления в верхней точке? Рассчитайте силу давления бруска на петлю в точках  Найдите точку
Найдите точку  в которой тело прижимается к «петле» с силой, равной силе тяжести. Как двигался бы дальше брусок, пройдя точку
в которой тело прижимается к «петле» с силой, равной силе тяжести. Как двигался бы дальше брусок, пройдя точку  если бы не было участка петли
если бы не было участка петли 

Рис. 129.
Решение. Применим второй закон Ньютона к положению тела в точке  считая векторы, направленные по радиусу к центру, положительными, а от центра — отрицательными.
считая векторы, направленные по радиусу к центру, положительными, а от центра — отрицательными.  Так как по условию
Так как по условию  , то
, то 
По закону сохранения энергии для положения тела в точке 

Следовательно,  Для точки
Для точки  Так как
Так как  (шестикратная перегрузка).
(шестикратная перегрузка).
Тело, двигаясь по петле от точки В к  испытывает и перегрузки и невесомость. Следовательно, есть и такая точка
испытывает и перегрузки и невесомость. Следовательно, есть и такая точка  в которой петля действует на тело с силой, равной силе тяжести. В этой точке по второму закону Ньютона
в которой петля действует на тело с силой, равной силе тяжести. В этой точке по второму закону Ньютона  . Спроецируем векторы на направление радиуса.
. Спроецируем векторы на направление радиуса.  по условию
по условию 

откуда 
Если бы не было участка  то тело от точки
то тело от точки  летело бы по параболе. Дальность полета
летело бы по параболе. Дальность полета 
490. Цирковой артист массой  прыгает с высоты
прыгает с высоты  на растянутую сетку. С какой средней силой он давит на сетку, если она прогибается на
на растянутую сетку. С какой средней силой он давит на сетку, если она прогибается на  Какова была бы средняя сила давления на сетку, если бы прогиб был только
Какова была бы средняя сила давления на сетку, если бы прогиб был только 
Решение. Поскольку в задаче не учитываются потери энергии, можно считать, что потенциальная энергия поднятого тела превратилась в потенциальную энергию упруго деформированной сетки.

Примем 

При 
На примере этой задачи видно значение «мягких» амортизаторов для уменьшения силы удара, что полезно пояснить также формулой  Так как
Так как  то
то  Чем больше величина прогиба
Чем больше величина прогиба  тем больше время
тем больше время  и меньше сила
и меньше сила 
491. По условию задачи № 488 найдите работу по преодолению сопротивления воздуха, если скорость мяча в конце падения была 
Решение. Вся энергия мяча в нижней точке кинетическая.

492. При испытаниях обнаружили, что тормозной путь «Москвича» массой  по сухому асфальту при начальной скорости
по сухому асфальту при начальной скорости  оказался равным
оказался равным  а при скорости
а при скорости  Определите по этим данным среднюю силу сопротивления при
Определите по этим данным среднюю силу сопротивления при  можении для каждой скорости.
можении для каждой скорости.
Решение. Работа против сил сопротивления совершается за счет кинетическоп энергии, поэтому 

Аналогично находим 
На примере этой задачи следует пояснить, что сопротивление (трение) зависит от скорости движения тел. В газах и жидкостях сопротивление возрастает с увеличением скорости (№ 513). В
дан ном случае сила сопротивления зависела не только от трения шин о дорогу, но и от сопротивления воздуха.
493. Трубка с каплей эфира подвешена на легком стержне длиной  (рис. 130). С какой скоростью должна вылетать пробка после подогревания эфира, чтобы трубка сделала полный оборот в вертикальной плоскости? Масса пробки
(рис. 130). С какой скоростью должна вылетать пробка после подогревания эфира, чтобы трубка сделала полный оборот в вертикальной плоскости? Масса пробки  масса трубки
масса трубки  [21, № 442].
[21, № 442].

Рис. 130.
Решение. Трубка и пробка будут двигаться в противоположные стороны (реактивное движение). По закону сохранения количества движения, пренебрегая массой эфира и стержня, можно записать

так как 
Знак минус показывает, что тела движутся в противоположных направлениях. В данном уравнении две неизвестные величины и  Поэтому составим еще одно уравнение, используя закон сохранения энергии. В нижнем положении пробирка обладает кинетической энергией
Поэтому составим еще одно уравнение, используя закон сохранения энергии. В нижнем положении пробирка обладает кинетической энергией  а в верхнем — потенциальной
а в верхнем — потенциальной  где I — длина подвеса.
где I — длина подвеса.  Из уравнения (1) найдем
Из уравнения (1) найдем  и подставим в уравнение (2). Получим
и подставим в уравнение (2). Получим 

494. Два упругих шара массой  подвесили к одной точке опоры на нитях длиной
подвесили к одной точке опоры на нитях длиной  см, а затем развели в разные стороны до горизонтального положения нитей и отпустили. На какую высоту поднимется каждый шар после соударения в нижней точке?
см, а затем развели в разные стороны до горизонтального положения нитей и отпустили. На какую высоту поднимется каждый шар после соударения в нижней точке?
Решение. Для решения задачи нужно знать скорости шаров в нижней точке после соударения. Тогда высоту можно найти из формулы  Скорости шаров найдем по закону сохранения импульса:
Скорости шаров найдем по закону сохранения импульса:

Шары падают с одинаковой высоты, следовательно, 

Примем направление движения шара массой  за положительное и учтем, что
за положительное и учтем, что  Тогда в левой части скалярного уравнения будет стоять положительная величина
Тогда в левой части скалярного уравнения будет стоять положительная величина  Импульс
Импульс  также должен быть положительной величиной, в противном случае шар двигался бы в прежнем направлении вместе с шаром массой
также должен быть положительной величиной, в противном случае шар двигался бы в прежнем направлении вместе с шаром массой  т. е. обе величины и
т. е. обе величины и  были бы отрицательными, что невозможно.
были бы отрицательными, что невозможно.
Направление вектора  нам неизвестно. Допустим, что оно положительное: Тогда уравнение (1) в скалярной форме примет вид
нам неизвестно. Допустим, что оно положительное: Тогда уравнение (1) в скалярной форме примет вид

Так как уравнение содержит две неизвестные величины  используем также закон сохранения энергии, приравняв кинетические энергии шаров до и после соударения:
используем также закон сохранения энергии, приравняв кинетические энергии шаров до и после соударения:

Подставим в уравнение (3) значение  из уравнения (2):
из уравнения (2):

Первый корень не отвечает условию задачи, так как скорость шара массой  не может остаться без изменения. Следовательно,
не может остаться без изменения. Следовательно,

Знак минус означает, что шар массой  движется после соударения в противоположном направлении.
движется после соударения в противоположном направлении.
 Высоту шаров найдем из формулы
Высоту шаров найдем из формулы  Значит, шар массой
Значит, шар массой  поднимется на высоту, которую позволяет ему нить, и будет далее двигаться с некоторой скоростью.
поднимется на высоту, которую позволяет ему нить, и будет далее двигаться с некоторой скоростью.
Проверка решения. Потенциальная энергия шаров до падения  После падения
После падения 
495. По условию задачи 494 определите скорость и шаров при их совместном движении и потенциальную энергию  упругого взаимодействия для этого момента времени.
упругого взаимодействия для этого момента времени.
Решение. В момент наибольшей деформации шары движутся как тело массой  с некоторой скоростью и. По закону сохранения импульса
с некоторой скоростью и. По закону сохранения импульса  откуда
откуда 
Интересно, что шары движутся в том же направлении, в котором двигался шар массой  Но затем в результате упругого взаимодействия шар массой
Но затем в результате упругого взаимодействия шар массой  стал двигаться в обратном направлении. По закону сохранения энергии, считая, что шары находятся в нижней точке,
стал двигаться в обратном направлении. По закону сохранения энергии, считая, что шары находятся в нижней точке,

496. Как можно определить выигрыш в силе, который дает простой механизм (лебедка, полиспаст, домкрат и т. п.), не рассматривая его устройства? Трение не учитывать.
Ответ. Нужно найти отношение путей, которые проходят точки приложения сил на концах механизма.
497(э). Определите, пользуясь решением предыдущей задачи, какой выигрыш в силе дает школьный гидравлический пресс, учитывая и действие его рукоятки как рычага. Трение не учитывать.
498. С помощью блоков на высоту  поднимают груз массой
поднимают груз массой  Конец веревки, за который тянут с силой 300 н, перемещается на расстояние
Конец веревки, за который тянут с силой 300 н, перемещается на расстояние  Начертите возможную схему блоков и определите их к.п.д.
Начертите возможную схему блоков и определите их к.п.д.
Решение. При использовании данных блоков проигрывают в два раза в расстоянии  следовательно, применяют один подвижный блок.
следовательно, применяют один подвижный блок.

Какую силу развивает домкрат, имеющий рукоятку длиной  и шаг винта
и шаг винта  , если на рукоятку действует сила
, если на рукоятку действует сила  домкрата
домкрата 
Решение: Для одного оборота рукоятки

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ВИДЫ ЗАДАЧ И ОБЩИЕ ВОПРОСЫ МЕТОДИКИ ИХ РЕШЕНИЯ
- 1. Задачи как средство обучения и воспитания учащихся на занятиях по физике
- 2. Классификация задач
- 3. Методика решения физической задачи
- ГЛАВА 2. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ РАЗНЫХ ТИПОВ
- 2. Экспериментальные задачи
- 3. Вычислительные задачи
- 4. Графические задачи
- ГЛАВА 3. МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЙ ПО РЕШЕНИЮ ЗАДАЧ
- 2. Решение задач на уроках
- 3. Решение задач на внеклассных занятиях
- 4. О некоторых особенностях решения задач в различных классах
- 6 Класс
- 1. Существование молекул. Размеры молекул
- 2. Движение молекул
- 3. Молекулярные силы
- 4. Особенности строения газов, жидкостей и твердых тел
- ГЛАВА 5. ДВИЖЕНИЕ И СИЛЫ
- 1. Механическое движение. Скорость
- 2. Масса. Плотность вещества
- 3. Инерция
- 4. Сила тяжести. Вес тел
- 5. Графическое изображение и сложение сил
- 6. Сила давления. Давление
- 7. Сила трения. Силы взаимодействия молекул
- ГЛАВА 6. ДАВЛЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ (ГИДРО- И АЭРОСТАТИКА)
- 2. Весовое давление жидкости
- 3. Атмосферное давление
- 4. Архимедова сила
- ГЛАВА 7. РАБОТА И МОЩНОСТЬ. ПОНЯТИЕ ОБ ЭНЕРГИИ
- 1. Механическая работа
- 2. Мощность
- 3. Рычаги. Блоки
- 4. Механическая энергия
- 7 КЛАСС
- ГЛАВА 8. ТЕПЛОПЕРЕДАЧА И РАБОТА
- 2. Способы передачи теплоты
- 3. Количество теплоты. Удельная теплоемкость
- 4. Теплота сгорания топлива. Тепловая отдача
- ГЛАВА 9. ИЗМЕНЕНИЕ АГРЕГАТНЫХ СОСТОЯНИЙ ВЕЩЕСТВА
- 1. Плавление и отвердевание
- 2. Испарение
- 3. Кипение и конденсация
- ГЛАВА 10. ТЕПЛОВЫЕ МАШИНЫ
- ГЛАВА 11. СТРОЕНИЕ АТОМА
- ГЛАВА 12. СИЛА ТОКА, НАПРЯЖЕНИЕ, СОПРОТИВЛЕНИЕ
- 1. Электрический ток. Электрическая цепь
- 2. Сила тока
- 3. Напряжение
- 4. Сопротивление проводников
- 5. Закон Ома для участка цепи
- 6. Соединения проводников
- ГЛАВА 13. РАБОТА И МОЩНОСТЬ ТОКА
- 1. Работа и мощность тока
- 2. Тепловое действие тока
- ГЛАВА 14. ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ
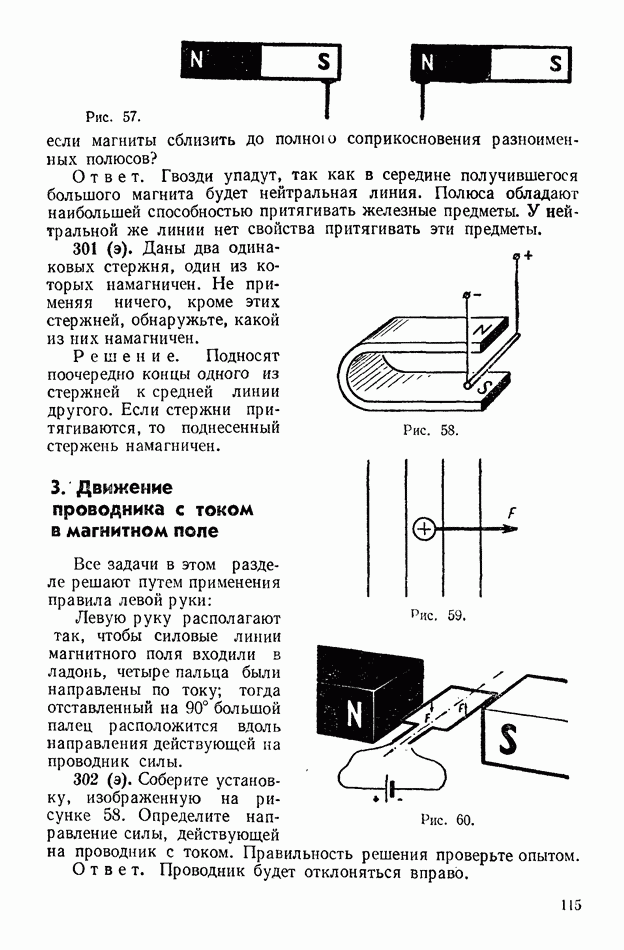
- 2. Постоянные магниты
- 3. Движение проводника с током в магнитном поле
- 8 КЛАСС
- 1. Система отсчета. Относительность механического движения. Сложение перемещений
- 2. Скорость. Сложение скоростей
- ГЛАВА 16. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ
- 2. Ускорение
- 3: Скорость при равнопеременном движении
- 4. Перемещение и путь в равнопеременном движении
- 5. Движение по окружности
- ГЛАВА 17. ЗАКОНЫ ДВИЖЕНИЯ
- 1. Первый закон Ньютона (закон инерции)
- 2. Закон сохранения импульса (количества движения)
- 3. Второй закон Ньютона
- 4. Третий закон Ньютона
- ГЛАВА 18. СИЛЫ В ПРИРОДЕ
- 1. Гравитационные силы
- 2. Силы упругости
- 3. Силы трения
- ГЛАВА 19. РАВНОВЕСИЕ ТЕЛ (СТАТИКА)
- 1. Сложение и разложение сил
- 2. Момент силы. Равновесие тел, имеющих ось вращения
- 3. Центр тяжести. Виды равновесия. Устойчивость тел
- ГЛАВА 20. ПРИМЕНЕНИЕ ЗАКОНОВ ДВИЖЕНИЯ НЬЮТОНА
- 1. Прямолинейное движение под действием постоянной силы
- 2. Движение тела, брошенного горизонтально и под углом к горизонту
- 3. Движение по окружности
- 4. Движение планет и искусственных спутников
- ГЛАВА 21. РАБОТА И ЭНЕРГИЯ
- 1. Работа и мощность
- 2. Механическая энергия
- 3. Движение жидкостей и газов
- 9 КЛАСС
- 1. Основы молекулярно — кинетической теории
- 2. Свойства газов
- ГЛАВА 23. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
- 2. Работа при расширении газа
- ГЛАВА 24. СВОЙСТВА ПАРОВ
- 2. Кипение
- 3. Сжижение газов. Критическое состояние вещества
- 4. Влажность
- ГЛАВА 25. СВОЙСТВА ЖИДКОСТЕЙ И ТВЕРДЫХ ТЕЛ
- 2. Смачивание и несмачивание. Давление под кривой поверхностью, капиллярные явления
- 3. Свойства твердых тел
- 4. Тепловое расширение жидкостей и твердых тел
- ГЛАВА 26. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
- 2. Напряженность электрического поля
- 3. Потенциал электрического поля
- 4. Электрическая емкость
- ГЛАВА 27. ЭЛЕКТРИЧЕСКИЙ ТОК В МЕТАЛЛАХ. ЗАКОНЫ ПОСТОЯННОГО ТОКА
- 2. Соединения проводников
- 3. Закон Ома для полной цепи
- 4. Работа, мощность, тепловое действие тока
- 5. Термоток
- ГЛАВА 28. ЭЛЕКТРОМАГНЕТИЗМ
- 1. Магнитное поле тока
- 2. Электромагнитная индукция
- ГЛАВА 29. ОСНОВЫ ЭЛЕКТРОНИКИ
- 2. Электрический ток в электролитах
- 3. Электрический ток в газах
- 4. Электрические свойства полупроводников
- 10 КЛАСС
- ГЛАВА 30. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ. ЗВУК
- 2. Колебания математического маятника
- 3. Упругие колебания. Превращение энергии при колебательном движении
- 4. Сдвиг фаз. Сложение колебаний
- 5. Распространение колебаний в упругой среде. Волны
- 6. Интерференция и дифракция волн
- 7. Инфразвук и ультразвук
- ГЛАВА 31. ПЕРЕМЕННЫЙ ТОК
- ГЛАВА 32. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ГЛАВА 33. ВОЛНОВЫЕ СВОЙСТВА СВЕТА
- 1. Скорость света
- 2. Интерференция и дифракция света
- ГЛАВА 34. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2. Отражение света
- 3. Преломление света
- 4. Линзы
- 5. Оптические приборы
- ГЛАВА 35. ИЗЛУЧЕНИЕ И СПЕКТРЫ
- 1. Явление дисперсии и спектры
- 2. Фотометрия и законы освещенности
- ГЛАВА 36. ДЕЙСТВИЕ СВЕТА. КВАНТЫ СВЕТА
- 1. Кванты света
- 2. Фотоэффект
- ГЛАВА 37. ОСНОВЫ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- ГЛАВА 38. ФИЗИКА АТОМНОГО ЯДРА