| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
Метод разделения переменных, известный в математической физике, используется и для исследования разностных задач. Применение этого метода
позволяет расчленить исходную задачу, зависящую от нескольких независимых переменных, на более простые задачи, зависящие от меньшего числа переменных. При этом, как правило, по отдельным координатным направлениям возникают задачи на собственные значения. Такая же ситуация имеет место и в разностном случае.
В этом пункте мы рассмотрим задачу на отыскание собственных значений для простейшего разностного оператора.
Сведения, полученные здесь, потребуются нам в дальнейшем, так как использование метода разделения переменных приводит к задачам именно такого типа.
В последующих главах будут приведены примеры использования этого метода для анализа устойчивости и сходимости конкретных разностных схем.
Предварительно напомним основные факты (см., например, А. Н. Тихонов и А. А. Самарский [6]), связанные с простейшей задачей на отыскание собственных функций и собственных значений для дифференциального уравнения

Нетривиальные решения этой задачи — собственные функции  и отвечающие им собственные значения
и отвечающие им собственные значения  выражаются следующим образом:
выражаются следующим образом: 

2. Собственные функции  образуют ортонормированную систему
образуют ортонормированную систему

где

3. Для производной от собственной функции имеет место равенство

откуда следует, что система  также ортонормирована, т. е.
также ортонормирована, т. е.

4. Если  дважды дифференцируема и удовлетворяет однородным краевым условиям, т. е.
дважды дифференцируема и удовлетворяет однородным краевым условиям, т. е.  , то она представима в виде равномерно сходящегося ряда
, то она представима в виде равномерно сходящегося ряда

где

причем

Поставим в соответствие дифференциальной задаче (13) разностную задачу

об отыскании нетривиальных решений — собственных функций задачи (14) и соответствующих собственных значений. Перейдем в (14) к индексной форме

Решение задачи (14) будем искать в виде

где а подлежит определению. Тогда

Подставляя полученное выражение в (15), получим

Так как мы ищем нетривиальные решения, т. е.  то из последнего равенства следует:
то из последнего равенства следует:

и далее

Значение параметра а выберем так, чтобы функция  удовлетворяла граничным условиям задачи (14)
удовлетворяла граничным условиям задачи (14)

Заметим, что при  граничное условие выполняется автоматически при любых а. При
граничное условие выполняется автоматически при любых а. При  имеем:
имеем:

откуда

Итак, мы получили собственные функции и собственные значения задачи (14). Перечислим их свойства.

2. Собственные значения  перенумерованы в порядке возрастания и для всей совокупности
перенумерованы в порядке возрастания и для всей совокупности  справедливы следующие оценки:
справедливы следующие оценки:

Из (17), в частности, следует, что все собственные значения задачи (14) положительны.
3. Собственные функции задачи  отвечающие различным собственным значениям, ортогональны в смысле скалярного произведения, определяемого соотношением (5):
отвечающие различным собственным значениям, ортогональны в смысле скалярного произведения, определяемого соотношением (5):

Для доказательства этого факта воспользуемся второй разностной формулой Грина, записанной для однородных краевых условий (10),

Так как по предположению  и — собственные функции, соответствующие различным собственным значениям, т. е.
и — собственные функции, соответствующие различным собственным значениям, т. е.  то из последнего равенства следует ортогональность
то из последнего равенства следует ортогональность 

4. Норма собственной функции  есть
есть

Норма понимается в смысле скалярного произведения (5), определенного выше,

Проведем несложные преобразования

Для того, чтобы просуммировать в (19) ряд из косинусов, построим вспомогательную функцию, разностная производная от которой равна 
Используя очевидное равенство

имеем

Теперь сумму ряда косинусов определить несложно:

Учитывая полученные результаты, находим из (19) требуемое соотношение  Таким образом, набор сеточных функций
Таким образом, набор сеточных функций

образует ортогональную и нормированную в смысле скалярного произведения  систему:
систему: 
5. Первые разностные производные от собственных функций, имеющие вид

ортогональны в смысле скалярного произведения  определенного формулой (5) и, кроме того,
определенного формулой (5) и, кроме того,

В том, что разностные производные от собственных функций имеют вид (21), можно убедиться, проводя простые вычисления:

Далее вычислим произведение

где  при
при  Здесь мы воспользовались разностной формулой Грина, а также тем обстоятельством, что функция является решением уравнения
Здесь мы воспользовались разностной формулой Грина, а также тем обстоятельством, что функция является решением уравнения  Итак, свойство 5 доказано.
Итак, свойство 5 доказано.
6. Пусть на сетке сол задана функция  причем
причем  Тогда, очевидно, она представим а в виде суммы по собственным функциям задачи (14)
Тогда, очевидно, она представим а в виде суммы по собственным функциям задачи (14)

где коэффициенты определяются соотношениями

При этом оказывается справедливым равенство

Докажем (22). В самом деле,

так как 
В дальнейшем изложении мы будем часто пользоваться неравенством

которое будем называть иногда  -неравенством. Из него, в частности, следует:
-неравенством. Из него, в частности, следует:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
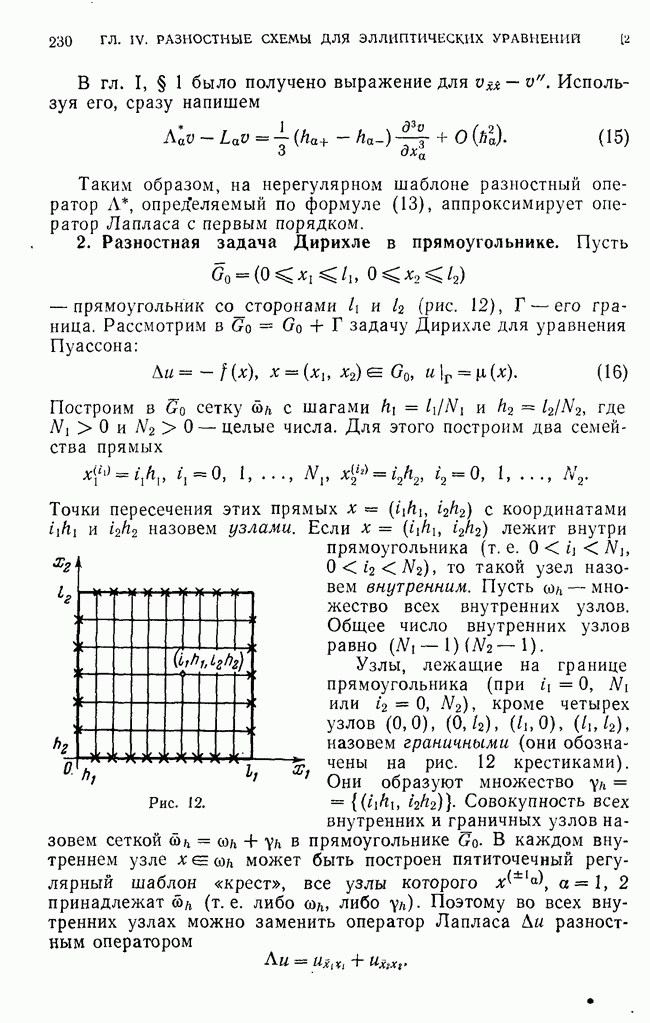
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка