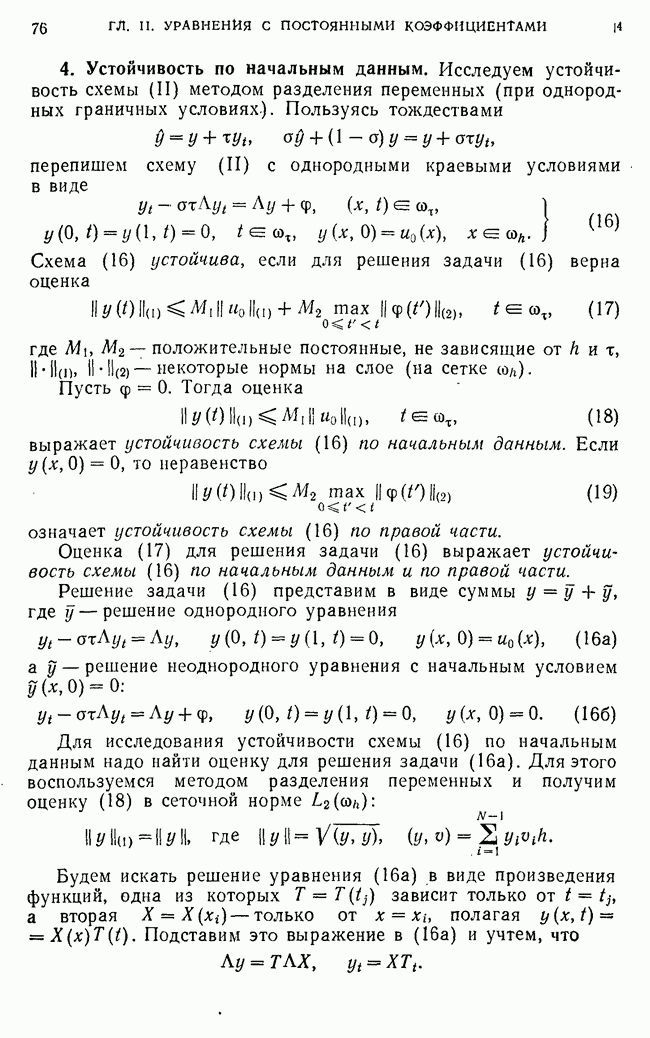| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
7. Примеры устойчивых и неустойчивых разностных схем.
Использование разностных схем позволяет свести решение задачи для дифференциального уравнения к решению системы линейных алгебраических уравнений. При этом правые части уравнений, краевые и начальные данные, которые мы будем в дальнейшем называть одним общим термином — входные данные — задаются с определенной погрешностью. В процессе самого численного решения системы также неизбежны ошибки, связанные с округлением. Естественно потребовать от разностной схемы, чтобы малые ошибки, допущенные во входных данных, не нарастали в процессе вычислений и не приводили к искажению решения.
Схемы, которые в процессе счета усиливают начальные погрешности, именуются неустойчивыми и не могут быть использованы на практике.
Прежде чем дать определение устойчивости разностной схемы по входным данным, к понятию которого мы интуитивно подошли, приведем несколько примеров. Пример 1.

Точным решением задачи (44), как нетрудно видеть, является функция  Задачу (44) на равномерной
Задачу (44) на равномерной
сетке  аппроксимирует разностная задача
аппроксимирует разностная задача

Задачу (45) можно переписать в виде

Отсюда следует

Рассмотрим фиксированную точку х и выберем такую последовательность шагов  чтобы х все время оставалось узловой точкой,
чтобы х все время оставалось узловой точкой,  Тогда при измельчении сетки,
Тогда при измельчении сетки,  номер
номер  соответствующий выбранной нами точке х, неограниченно возрастает.
соответствующий выбранной нами точке х, неограниченно возрастает.
Вычислим значение у в этой точке

В силу разложения

имеем

Из последнего равенства видно, что решение разностной задачи (45) непрерывно зависит от начальных данных. В таких случаях будем говорить, что разностная схема устойчива по начальным Данным.
Пример 2. Неустойчивая схема. Для задачи (44) рассмотрим схему

где  числовой параметр. Так как схема трехточечная (разностное уравнение имеет второй порядок), то помимо
числовой параметр. Так как схема трехточечная (разностное уравнение имеет второй порядок), то помимо  следует задать
следует задать  При любом а схема (46) имеет, по крайней мере, первый порядок аппроксимации. Если положить
При любом а схема (46) имеет, по крайней мере, первый порядок аппроксимации. Если положить  то
то  Частные решения разностного уравнения (46) ищем в виде
Частные решения разностного уравнения (46) ищем в виде  Подставляя
Подставляя  в (46), получим для
в (46), получим для  квадратное уравнение
квадратное уравнение

которое имеет два различных корня

Общее решение уравнения (46) имеет вид

Полагая  и учитывая, что
и учитывая, что  найдем постоянные А и В:
найдем постоянные А и В:

Предположим, что  Тогда получим
Тогда получим

Как и в рассмотренном выше примере, зафиксируем точку х и выберем последовательность сеток  таких, чтобы
таких, чтобы  Нетрудно видеть, что
Нетрудно видеть, что

т. е.

Так как  то при
то при  первое слагаемое неограниченно возрастает. Не спасает положение и выбор
первое слагаемое неограниченно возрастает. Не спасает положение и выбор  при котором
при котором  поскольку функция
поскольку функция  при любом конечном показателе
при любом конечном показателе  Можно, наконец, выбрать
Можно, наконец, выбрать  так, что
так, что  Для этого достаточно положить
Для этого достаточно положить  Однако в процессе вычислений из-за ошибок округления, решение
Однако в процессе вычислений из-за ошибок округления, решение  неизбежно появляется, что приводит к неустойчивости указанного типа. При фиксированном
неизбежно появляется, что приводит к неустойчивости указанного типа. При фиксированном  эта схема приводит к нарастанию решения с ростом
эта схема приводит к нарастанию решения с ростом  Сгущение сетки (уменьшение
Сгущение сетки (уменьшение  приводит к нарастанию ошибок. Малое изменение начальных данных приводит при
приводит к нарастанию ошибок. Малое изменение начальных данных приводит при  к неограниченному возрастанию решения задачи в любой фиксированной точке х.
к неограниченному возрастанию решения задачи в любой фиксированной точке х.
Разобранные примеры позволяют сделать вывод, что понятие устойчивости по входным данным совпадает с понятием непрерывной зависимости решения разностной задачи от входных данных при 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
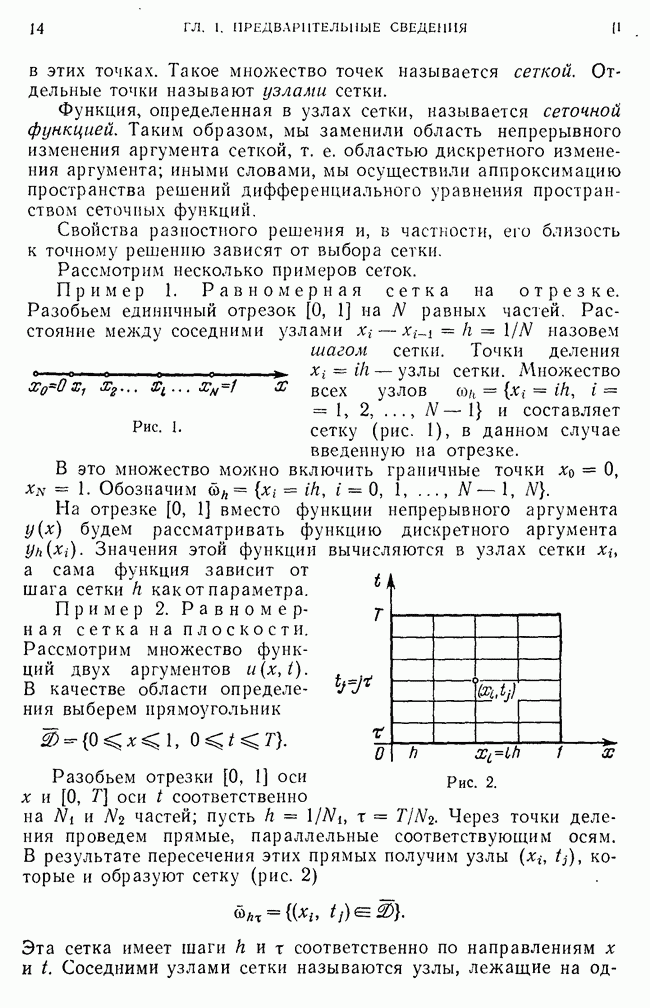
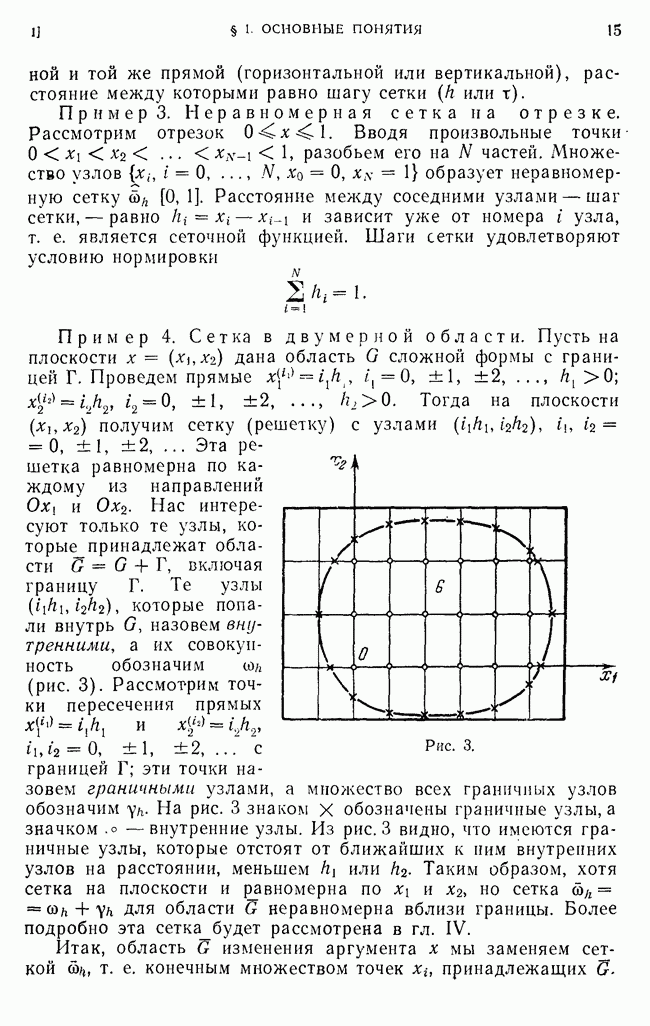
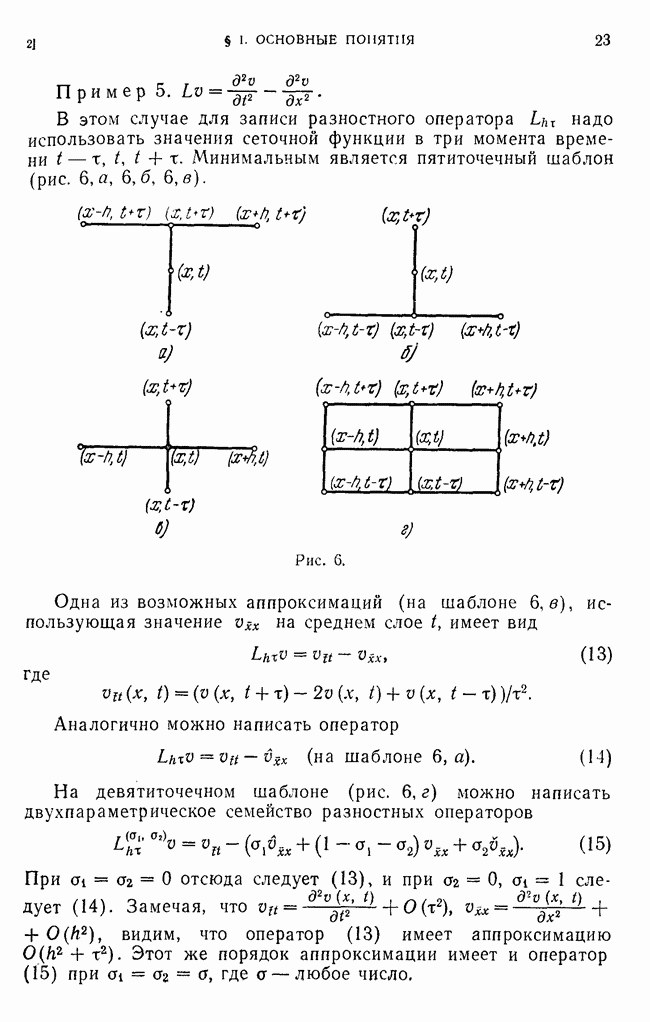
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
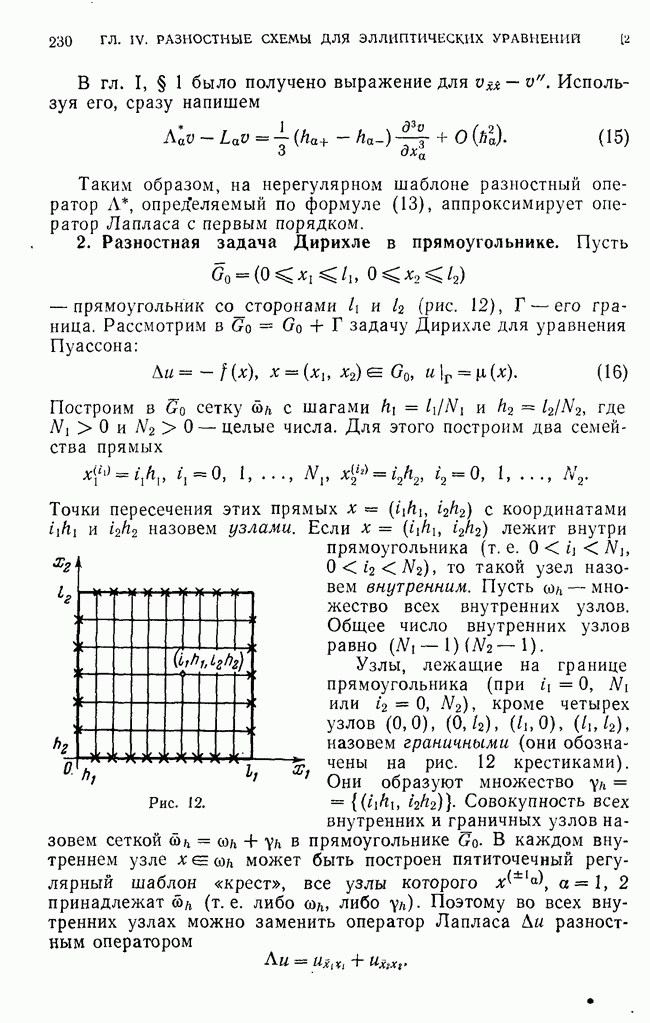
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
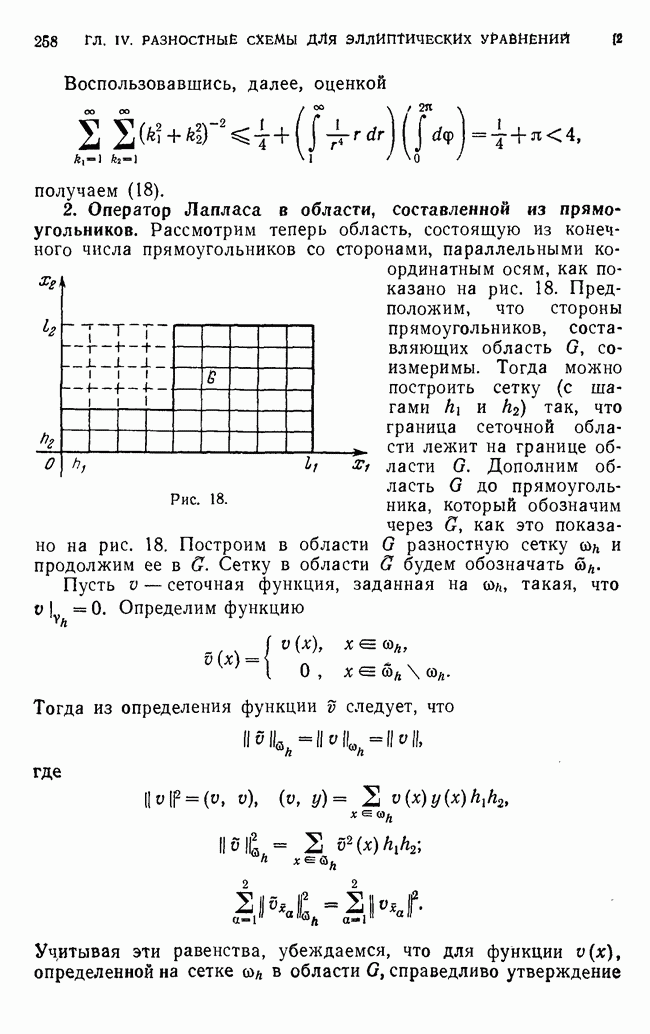
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка