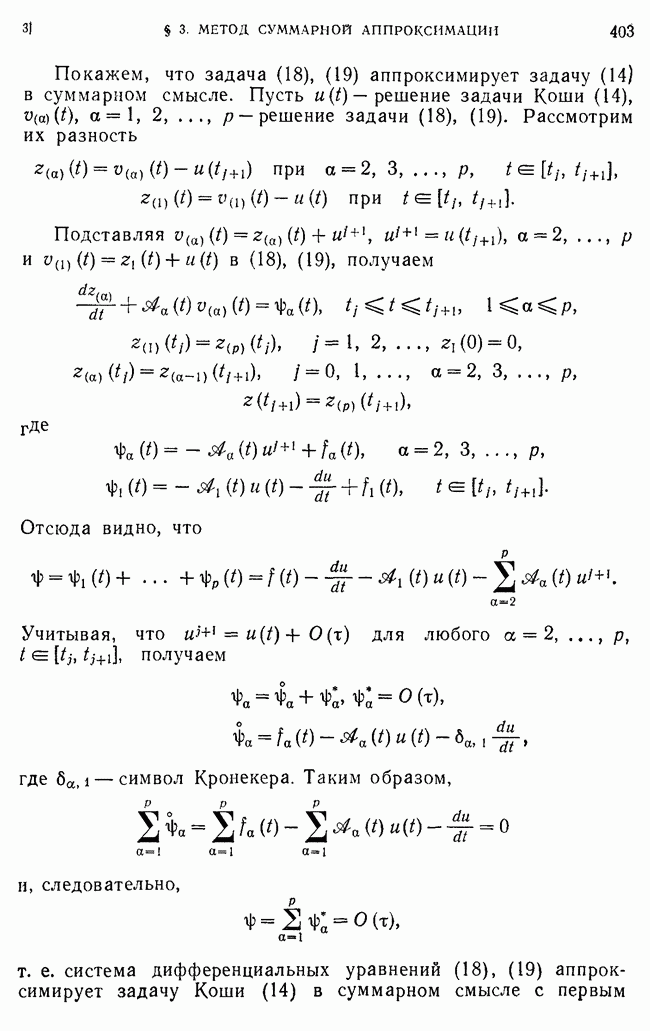| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
Обратимся к задаче (7). Пусть на  заданы однородные граничные условия. Будем
заданы однородные граничные условия. Будем
рассматривать функцию  как функцию х в качестве элемента некоторого линейного нормированного пространства
как функцию х в качестве элемента некоторого линейного нормированного пространства  Тогда
Тогда  будет линейным оператором в этом пространстве,
будет линейным оператором в этом пространстве,  абстрактной функцией
абстрактной функцией  со значениями в
со значениями в  для всех
для всех  Вместо частной производной в (7) можно писать обыкновенную производную по
Вместо частной производной в (7) можно писать обыкновенную производную по 
В результате мы приходим к абстрактной задаче Коши:

где  линейный оператор в банаховом пространстве
линейный оператор в банаховом пространстве  Область определения
Область определения  оператора
оператора  является всюду плотной в
является всюду плотной в  и состоит из функций, удовлетворяющих однородным граничным условиям на
и состоит из функций, удовлетворяющих однородным граничным условиям на  Область значений
Область значений  оператора
оператора  принадлежит
принадлежит 
Пусть  представлен в виде суммы
представлен в виде суммы

линейных операторов пересечение областей определения которых есть 
В этом случае решение задачи Коши (14) можно свести к последовательному решению задач Коши того же типа, по с операторами  вместо
вместо 
Остановимся на двух способах такого сведения. Пусть на отрезке  введена сетка
введена сетка

с шагом  По аналогии с п. 2, представим
По аналогии с п. 2, представим  в виде суммы
в виде суммы  и перепишем (14) в виде
и перепишем (14) в виде

На отрезке  введем промежуточные значения
введем промежуточные значения  рассмотрим систему задач Коши
рассмотрим систему задач Коши

с начальными условиями

полагая  Будем называть решением этой задачи при
Будем называть решением этой задачи при  функцию
функцию 
Эта конструкция (совпадающая с конструкцией из п. 2) была использована (см. А. А. Самарский [4]-[16], [19]) при построении экономичных аддитивных схем для многих многомерных задач математической физики и, в частности, для параболического уравнения (см. п. 5). Исследование связи задач (14) и (16), (17) показало, что решение задачи (16),  сходится при
сходится при  к решению задачи (14), причем
к решению задачи (14), причем  точнее
точнее  где
где  не зависит от
не зависит от  норма в
норма в  (см. Н. Н. Яненко [5], Н. Н. Яненко, Г. В. Демидов [1]).
(см. Н. Н. Яненко [5], Н. Н. Яненко, Г. В. Демидов [1]).
Если оператор  зависит от
зависит от  (является переменным), то более точным оказывается второй способ аппроксимации задачи (14) системой задач Коши (А. А. Самарский [15]).
(является переменным), то более точным оказывается второй способ аппроксимации задачи (14) системой задач Коши (А. А. Самарский [15]).
На всем промежутке  последовательно решаются
последовательно решаются  задач Коши
задач Коши 

с начальными данными

Решением задачи (18) при  является, по определению, элемент
является, по определению, элемент

При  полагаем
полагаем

Пусть известно  Из первого уравнения при
Из первого уравнения при  определяем
определяем  которое затем используем в качестве начального значения при
которое затем используем в качестве начального значения при  для
для  решаем второе уравнение (при
решаем второе уравнение (при  ) и т. д. После решения всех
) и т. д. После решения всех  задач найдем
задач найдем  Это и есть решение системы уравнений (18) -(20) при
Это и есть решение системы уравнений (18) -(20) при  .
.
Если не зависят от  то обе задачи (16), (17) и (18)-(20) эквивалентны.
то обе задачи (16), (17) и (18)-(20) эквивалентны.
Покажем, что задача (18), (19) аппроксимирует задачу (14) в суммарном смысле. Пусть  решение задачи Коши
решение задачи Коши  решение задачи (18), (19). Рассмотрим их разность
решение задачи (18), (19). Рассмотрим их разность

Подставляя  в (18), (19), получаем
в (18), (19), получаем

где

Отсюда видно, что

Учитывая, что  для любого
для любого  получаем
получаем

где  символ Кроиекера. Таким образом,
символ Кроиекера. Таким образом,

и, следовательно,

т. е. система дифференциальных уравнений (18), (19) аппроксимирует задачу Коши (14) в суммарном смысле с первым
порядком при этом требуется существование и ограниченность (в некоторой норме) 
Представляет интерес сравнение решения  задачи (18) — (20) с решением
задачи (18) — (20) с решением  исходной задачи.
исходной задачи.
Приведем без доказательства некоторые результаты.
А. Пусть  и все
и все 
Если постоянные операторы  попарно перестановочны,
попарно перестановочны,  то при любых
то при любых  имеет место равенство
имеет место равенство

где  решение задачи
решение задачи  — решение задачи (14).
— решение задачи (14).
Если же  зависят от
зависят от  то (21) имеет место при перестановочности операторов
то (21) имеет место при перестановочности операторов  взятых в разные моменты времени,
взятых в разные моменты времени,  так что
так что

для любых 
Приведем несколько примеров. Пример 1. Рассмотрим задачу Коши

где  число. Очевидно, что
число. Очевидно, что 
Представим а в виде суммы  и напишем задачу
и напишем задачу 

где  любое число. Решая эти уравнения, находим
любое число. Решая эти уравнения, находим  Отсюда видно, что
Отсюда видно, что

Пример  Гольдин,
Гольдин,  Данилова,
Данилова,  . Калиткин [1]). Рассмотрим задачу Коши для уравнения переноса
. Калиткин [1]). Рассмотрим задачу Коши для уравнения переноса

Решение этой задачи есть бегущая волна

если  дважды дифференцируемая функция.
дважды дифференцируемая функция.
Так как операторы  перестановочны, то
перестановочны, то

где  решение системы уравнений
решение системы уравнений

В самом деле, решение первого из этих уравнений имеет вид

Из второго уравнения находим

Пример 3. Рассмотрим задачу Коши для уравнения теплопроводности

Ее решение дается формулой

где  функция источника, равная
функция источника, равная 

Напишем систему уравнений, соответствующую (18) -(20). Нетрудно заметить, что

Подставляя  из (22) в (23), получим
из (22) в (23), получим

при любом 
Б. Пусть операторы  и неперестановочны. Тогда справедлива оценка
и неперестановочны. Тогда справедлива оценка

при дополнительном условии «гладкости»

Возникает вопрос, нельзя ли повысить точность по  без существенного усложнения составной задачи Коши?
без существенного усложнения составной задачи Коши?
Составную задачу Коши (18) схематически запишем следующим образом

Рассмотрим симметризованную составную задачу Коши, представляющую собой цепочку  задач Коши
задач Коши

что соответствует представлению оператора  в виде суммы
в виде суммы

Эта задача имеет второй порядок точности по 

при некотором дополнительном требовании гладкости начального вектора  вида
вида  и условиях гладкости
и условиях гладкости  по
по 
Идея симметризации была развита И. В. Фрязиновым  [6], который построил и исследовал ряд аддитивных схем повышенного порядка точности для уравнений параболического типа в ступенчатых областях, составленных из
[6], который построил и исследовал ряд аддитивных схем повышенного порядка точности для уравнений параболического типа в ступенчатых областях, составленных из  -мерных параллелепипедов. При этом оказалось, что для выполнения требования суммарной аппроксимации
-мерных параллелепипедов. При этом оказалось, что для выполнения требования суммарной аппроксимации  требуется вводить поправки к естественным краевым значениям.
требуется вводить поправки к естественным краевым значениям.
Итак, решение задачи (14) сводится к решению последовательности более простых задач  Для их решения
Для их решения
можно использовать как аналитические, так и приближенные методы, в частности, метод конечных разностей.
В случае, когда  попарно перестановочны, точность приближенного метода решения задачи (14) целиком зависит от того, с какой точностью мы решаем каждую из промежуточных задач (18) номера а. Следует подчеркнуть, что проведенное выше изложение справедливо для случая однородных краевых условий. Если краевые условия неоднородны, то точность составной задачи Коши (18) — (20) существенно зависит от способа задания краевых условий для
попарно перестановочны, точность приближенного метода решения задачи (14) целиком зависит от того, с какой точностью мы решаем каждую из промежуточных задач (18) номера а. Следует подчеркнуть, что проведенное выше изложение справедливо для случая однородных краевых условий. Если краевые условия неоднородны, то точность составной задачи Коши (18) — (20) существенно зависит от способа задания краевых условий для  Это же замечание относится и к разностным аналогам задачи (18)-(20).
Это же замечание относится и к разностным аналогам задачи (18)-(20).
Разностная аппроксимация каждой из задач (18), например, простейшей двухслойной схемой с весами приводит к аддитивной разностной схеме. Она является экономичной, если экономична каждая из промежуточных схем номера а. Таким способом можно, в частности, получить схему, формально совпадающую при  со схемой расщепления Н. Н. Яненко [1] (схема (34) из § 2), но трактуемую как аддитивная схема. При этом не возникает никаких трудностей ни с постановкой краевых условий для
со схемой расщепления Н. Н. Яненко [1] (схема (34) из § 2), но трактуемую как аддитивная схема. При этом не возникает никаких трудностей ни с постановкой краевых условий для  ни с заданием правых частей
ни с заданием правых частей

Если  одномерные дифференциальные операторы, то соответствующую аддитивную схему мы называем локально-одномерной схемой. Локально-одномерная схема для уравнения теплопроводности исследуется ниже.
одномерные дифференциальные операторы, то соответствующую аддитивную схему мы называем локально-одномерной схемой. Локально-одномерная схема для уравнения теплопроводности исследуется ниже.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка