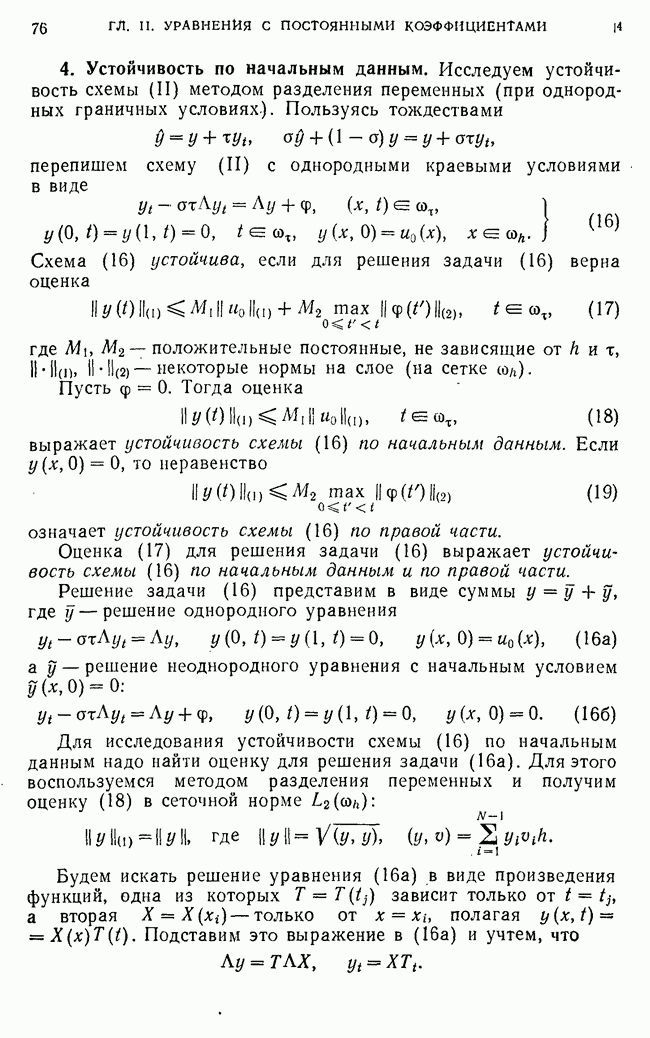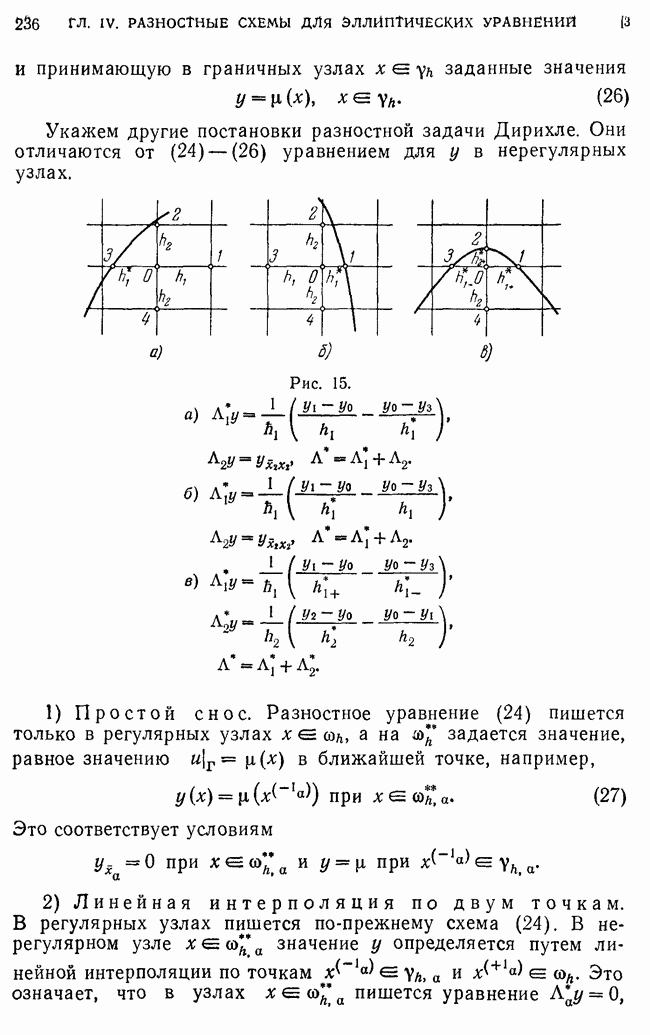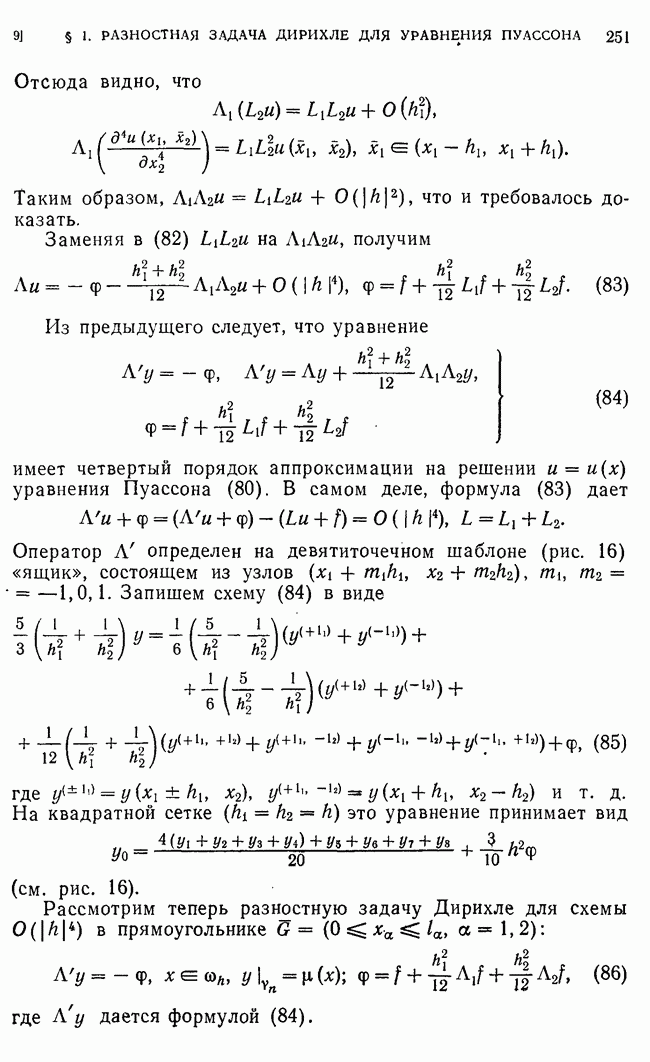| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
В § 1 настоящей главы изучается разностная задача Дирихле для уравнения Пуассона. Излагаются способы аппроксимации оператора Лапласа и постановка разностных граничных условий на регулярных и нерегулярных сетках. Установлен принцип максимума и на его основе доказана равномерная сходимость со скоростью  построенных разностных схем в случае произвольной области.
построенных разностных схем в случае произвольной области.
В § 2 получены некоторые оценки для разностных операторов, аппроксимирующих оператор Лапласа и эллиптический оператор со смешанными производными.
Изучению разностных аппроксимаций для эллиптических уравнений, и особенно для уравнения Лапласа, посвящена обширная литература. Укажем лишь некоторые литературные источники: В. Б. Андреев [1], [2], [5], [7], В. В. Бадагадзе [1], Н. С. Бахвалов [1]-[3], И. С. Березин и Н. П. Жидков [2], В. Вазов и Д. Форсайт [1], Р. Варга [1], Е. А. Волков [1]-[3], Л. В. Канторович и В. И. Крылов [1], Коллатц [2], В. И. Лебедев [2], [3], Л. А. Люстерник [1], Г. И. Марчук [1], Ш. Е. Микеладзе [1], С. Г. Михлин и X. Л. Смолицкий [1], А. А. Самарский и И. В. Фрязинов [2], В. К. Саульев [1].
§ 1. Разностная задача Дирихле для уравнения Пуассона
Перейдем к изучению разностных схем для решения задачи Дирихле

где  есть
есть  -мерная конечная область с границей
-мерная конечная область с границей 
1. Разностная аппроксимация оператора Лапласа.
Начнем с построения разностного аналога оператора Лапласа

на плоскости 
В точке  каждый из операторов
каждый из операторов  или
или  аппроксимируем трехточечным оператором
аппроксимируем трехточечным оператором  или
или 

где  знак аппроксимации,
знак аппроксимации,  заданные числа (шаги поосям
заданные числа (шаги поосям 
Оператор  определен на регулярном трехточечном шаблоне
определен на регулярном трехточечном шаблоне

оператор  на регулярном трехточечном шаблоне
на регулярном трехточечном шаблоне


Рис. 8. Регулярный шаблон «крест».
Используя (3) и (4), заменим оператор Лапласа (2) разностным оператором

который определен на пятиточечном шаблоне «крест», состоящем из узлов

Этот регулярный шаблон изображен на рис. 8. Здесь  точка
точка  — точка
— точка  Из (3) — (5) и рис. 8 следует, что
Из (3) — (5) и рис. 8 следует, что

В частности, при  (на квадратном шаблоне) имеем
(на квадратном шаблоне) имеем

Вычислим погрешность аппроксимации оператора Лапласа (2) разностным оператором (5). Так как (см. гл. I, § 1) при 

то

Отсюда следует, что

если  — любая функция, имеющая не менее четырех ограниченных (хотя бы в прямоугольнике
— любая функция, имеющая не менее четырех ограниченных (хотя бы в прямоугольнике  при
при  производных по
производных по  Таким образом, разностный оператор (5) аппроксимирует оператор Лапласа (2) со вторым порядком на регулярном шаблоне «крест».
Таким образом, разностный оператор (5) аппроксимирует оператор Лапласа (2) со вторым порядком на регулярном шаблоне «крест».
Аналогично строится разностная аппроксимация  -мерного
-мерного  оператора Лапласа
оператора Лапласа

Заменяя  трехточечным разностным оператором
трехточечным разностным оператором  получаем
получаем

так что

где  Здесь (или
Здесь (или  точка, в которую переходит точка
точка, в которую переходит точка  при сдвиге по направлению
при сдвиге по направлению  направо (или налево) на отрезок длины
направо (или налево) на отрезок длины  (рис. 9).
(рис. 9).

Рис. 9.
Шаблон для оператора (10) состоит, очевидно, из  точек
точек  (из 7 точек при
(из 7 точек при  а погрешность аппроксимации имеет второй порядок.
а погрешность аппроксимации имеет второй порядок.
Рассмотрим теперь разностную аппроксимацию оператора Лапласа на нерегулярном шаблоне «крест». В случае двух измерений  этот шаблон состоит из пяти точек
этот шаблон состоит из пяти точек

где  причем
причем  по крайней мере, для одного а (рис. 10).
по крайней мере, для одного а (рис. 10).
Каждый из операторов  аппроксимируем по трем точкам
аппроксимируем по трем точкам

и

соответственно. Для этого воспользуемся выражениями (см. гл.  :
:

где
Разностный оператор Лапласа на нерегулярном шаблоне будет иметь вид

Если, например,  и т.д. Чтобы не выписывать аргументов (это слишком громоздко при
и т.д. Чтобы не выписывать аргументов (это слишком громоздко при  введем обозначения
введем обозначения


Рис. 10. Нерегулярный шаблон «крест».

Рис. 11.
На рис. 11 показано расположение точек  Выражение для
Выражение для  можно записать в виде
можно записать в виде

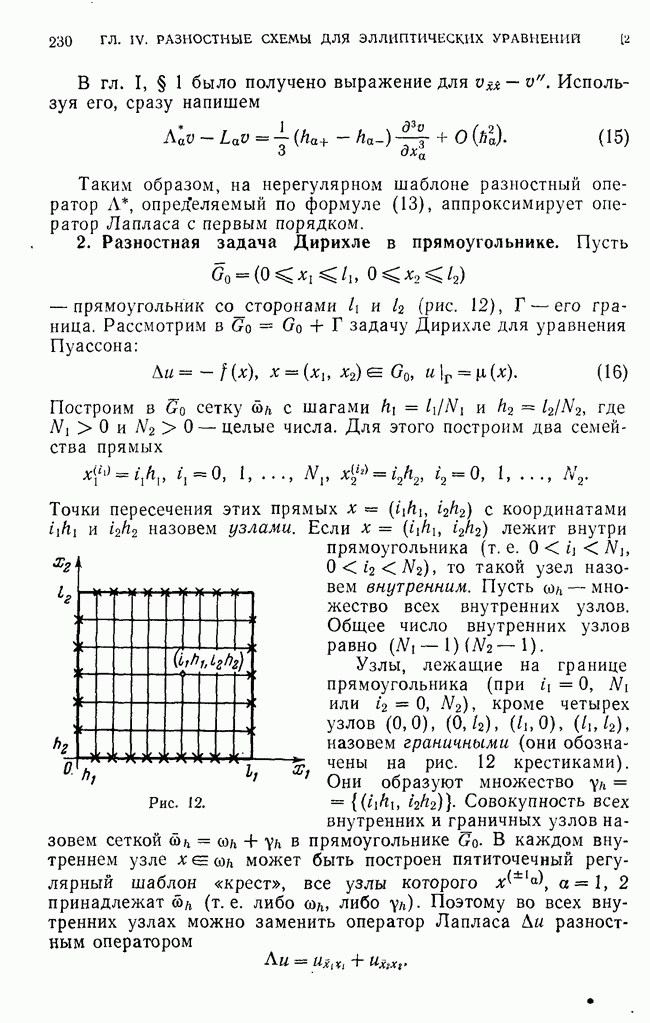
В гл. I, § 1 было получено выражение для  Используя его, сразу напишем
Используя его, сразу напишем

Таким образом, на нерегулярном шаблоне разностный оператор  определяемый по формуле (13), аппроксимирует оператор Лапласа с первым порядком.
определяемый по формуле (13), аппроксимирует оператор Лапласа с первым порядком.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
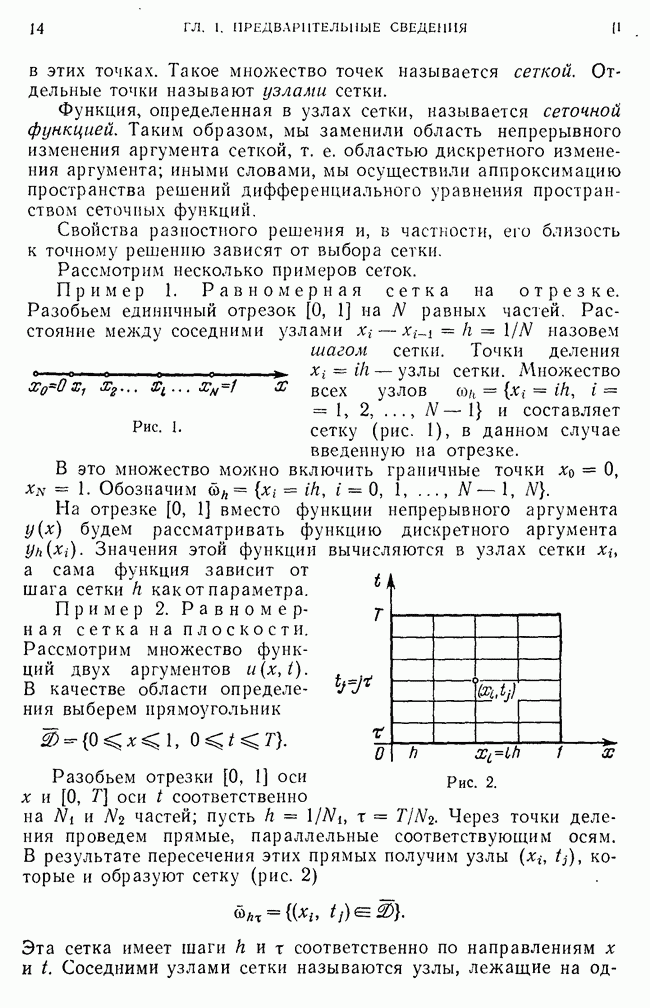
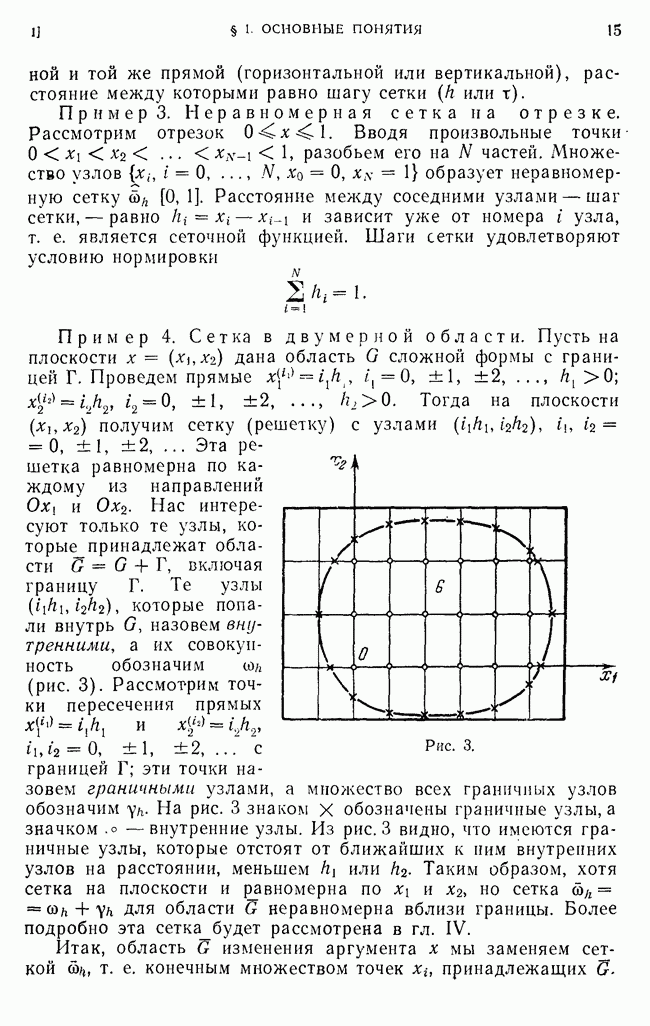
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
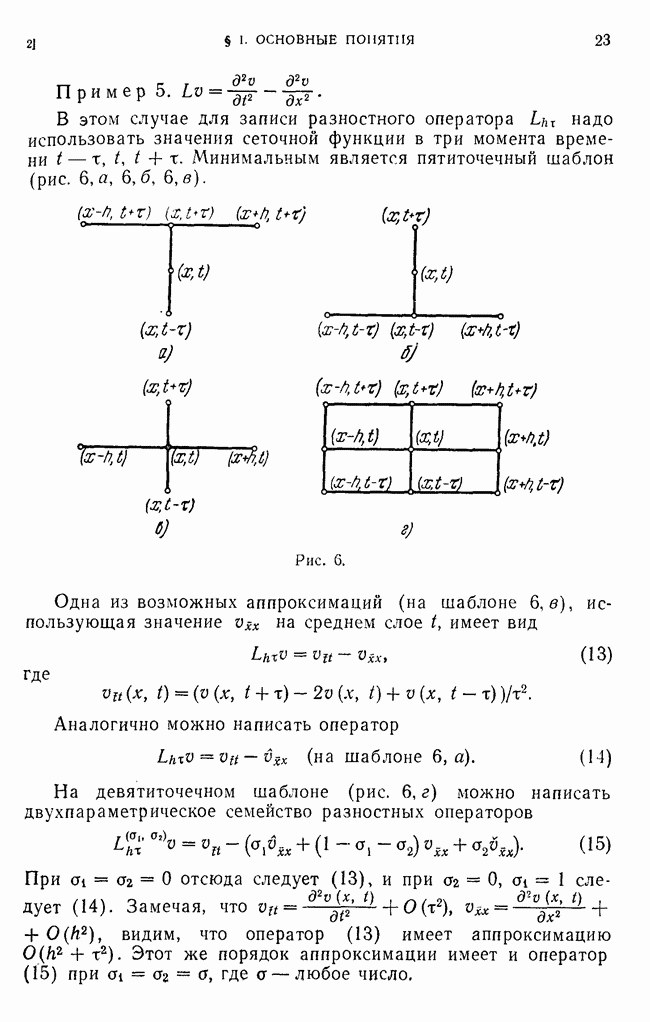
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
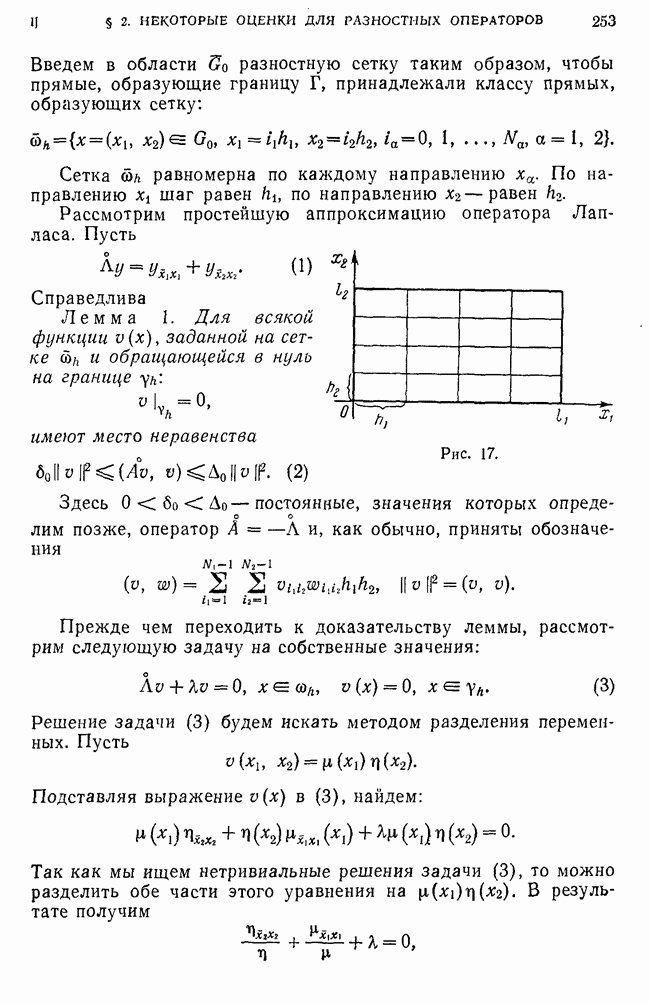
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
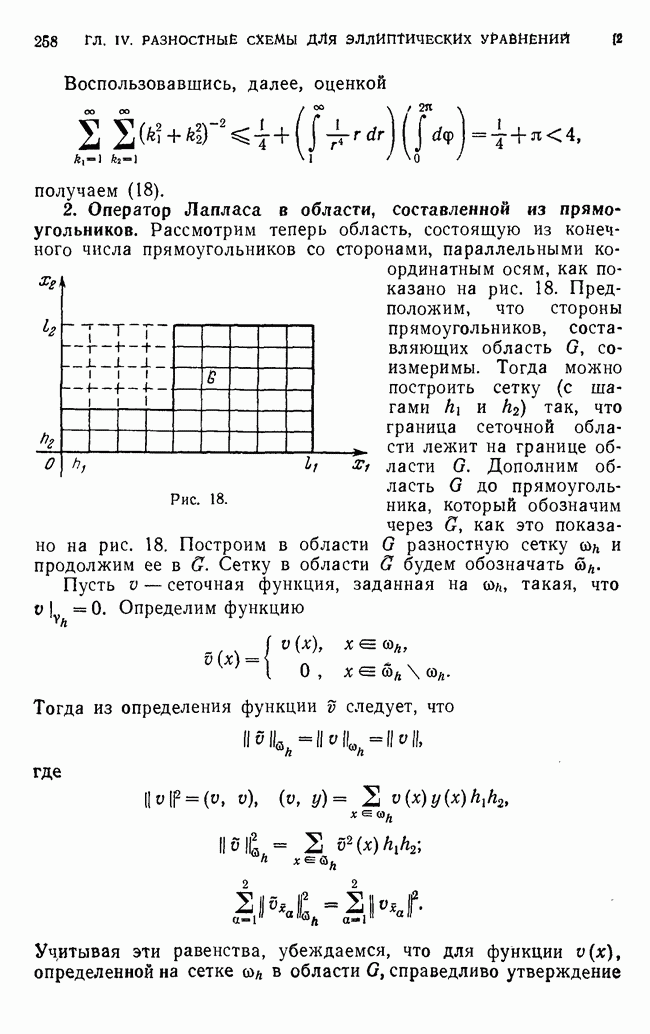
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка