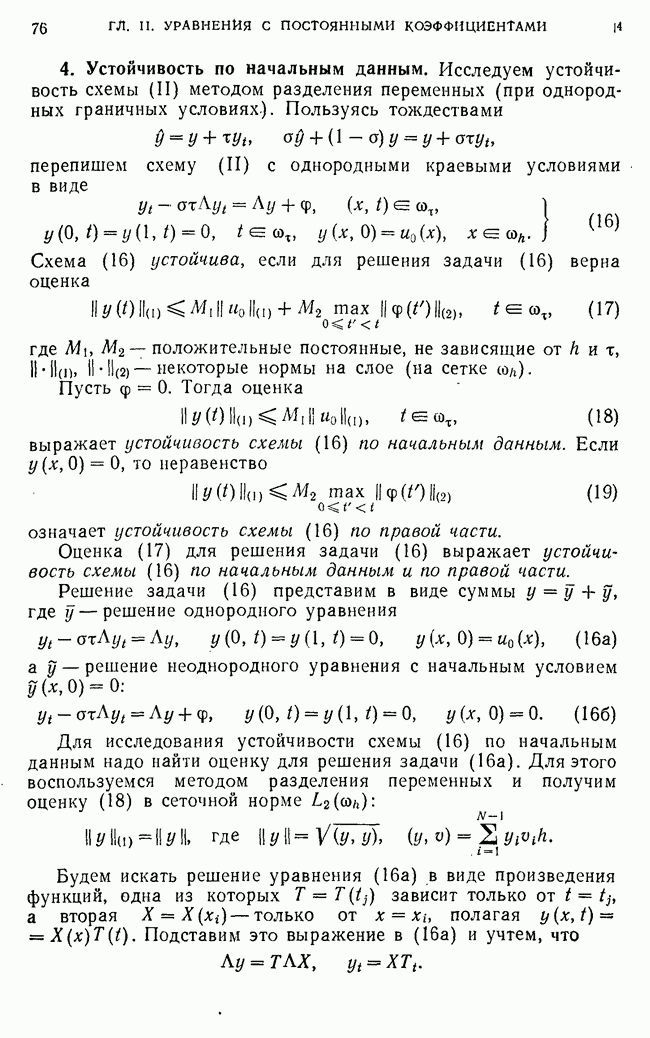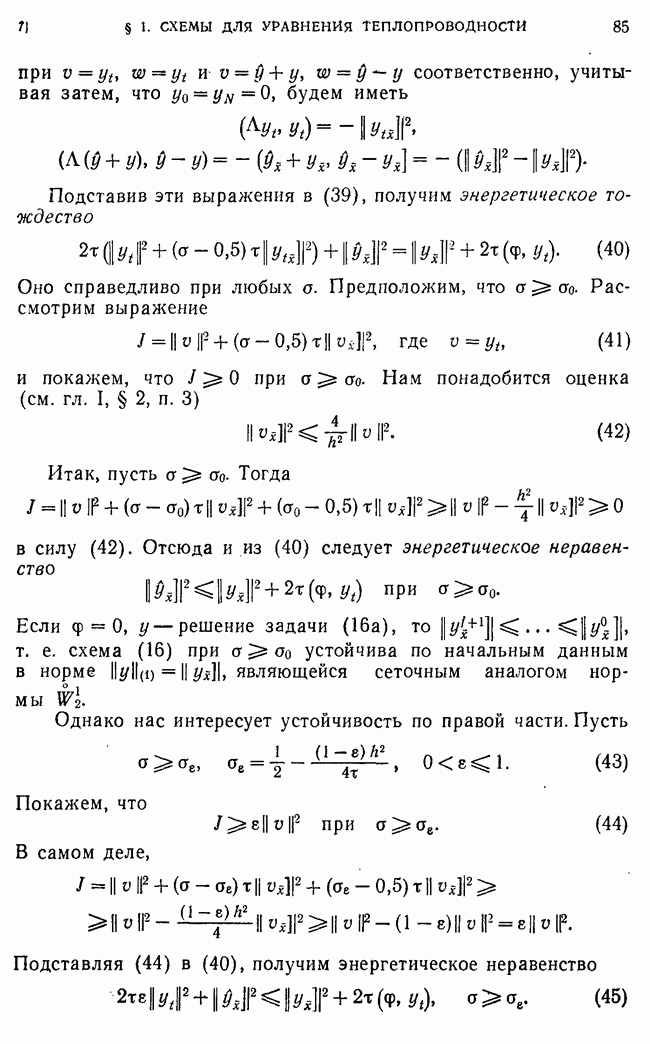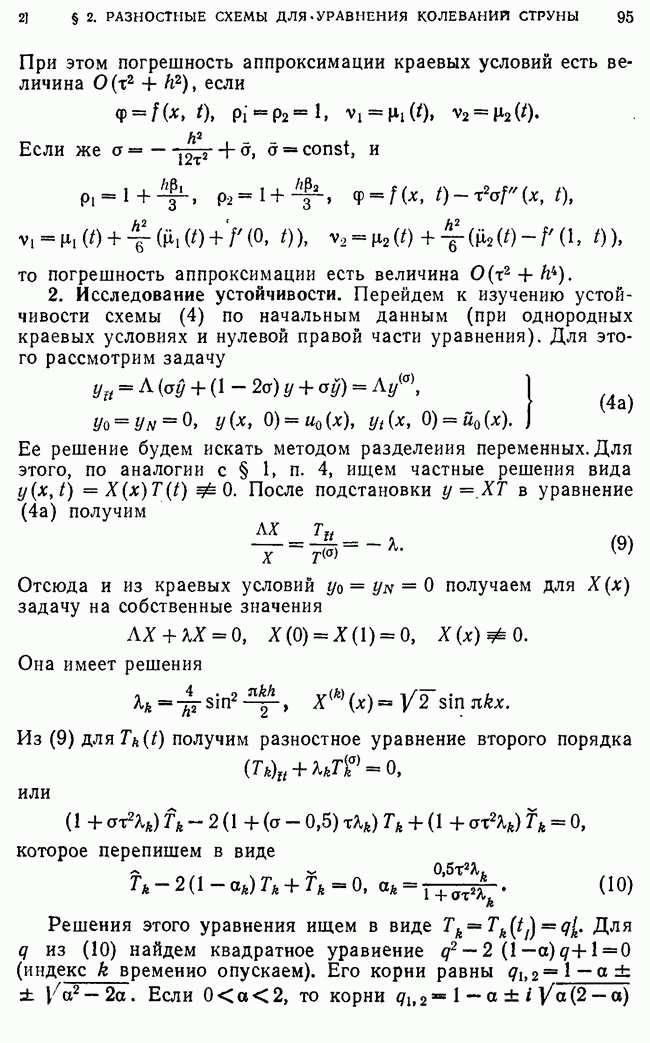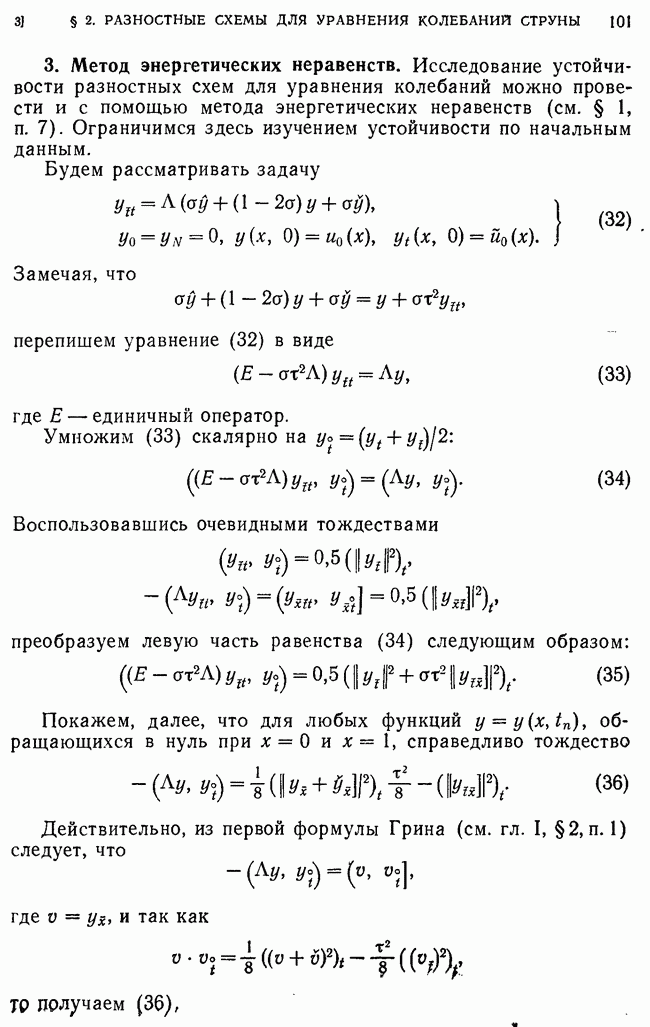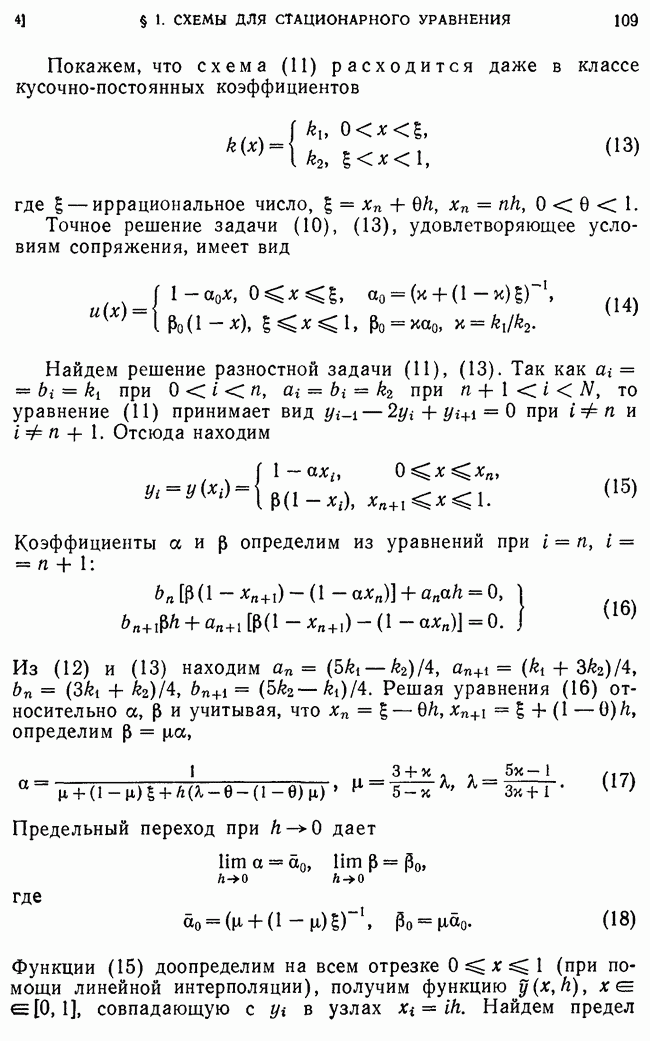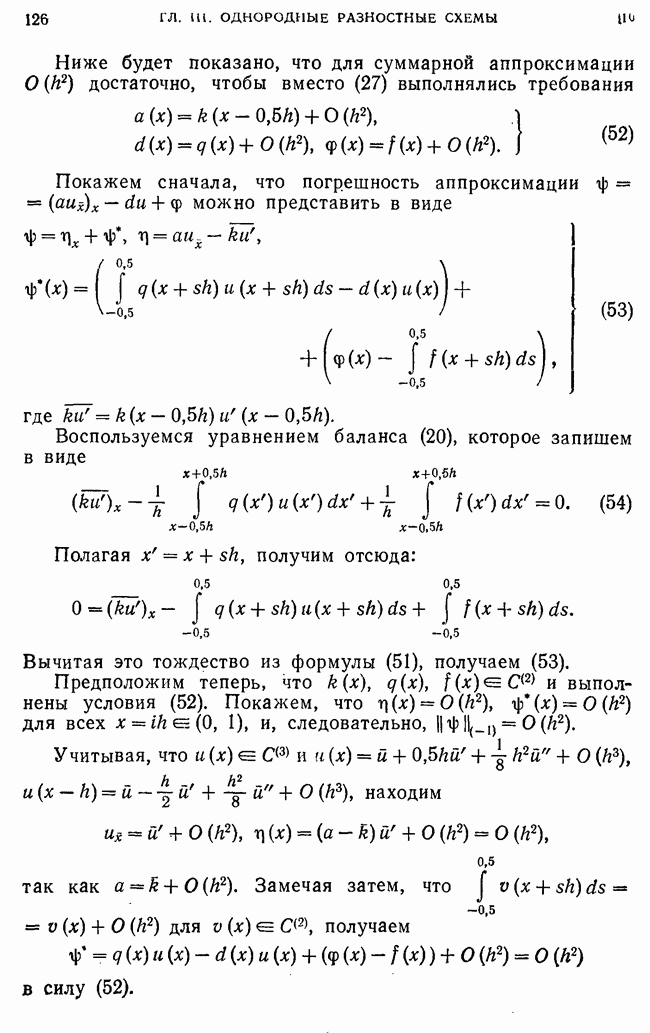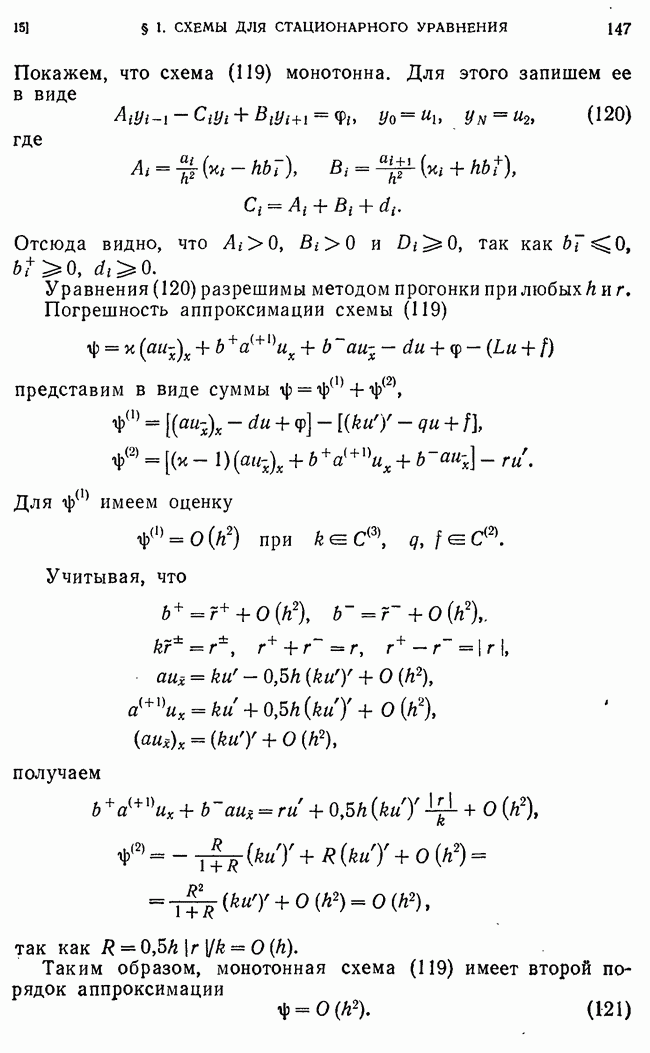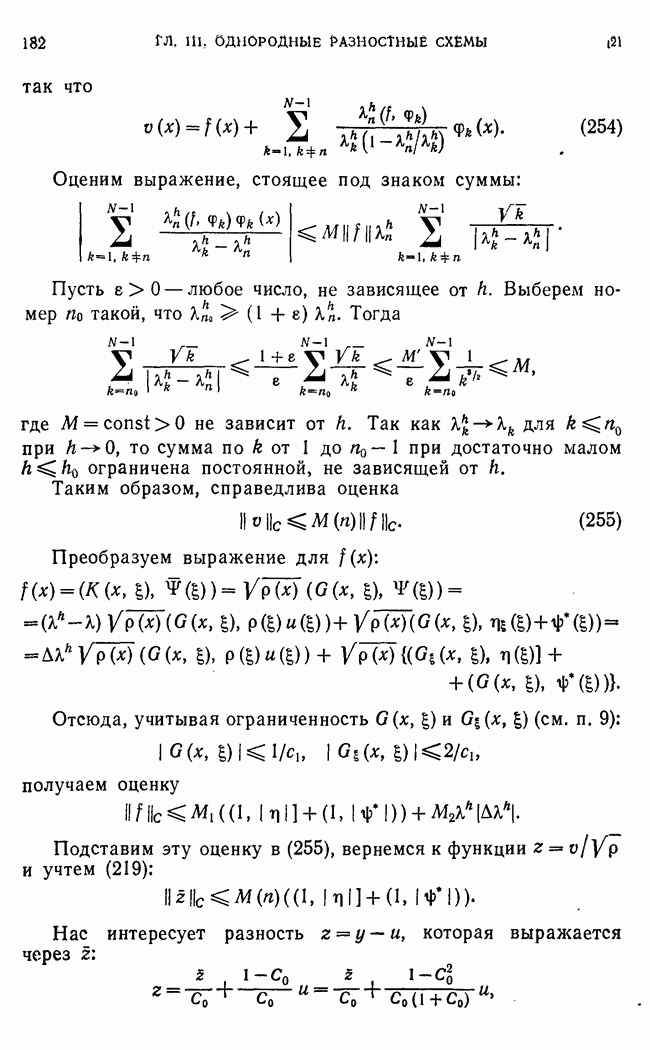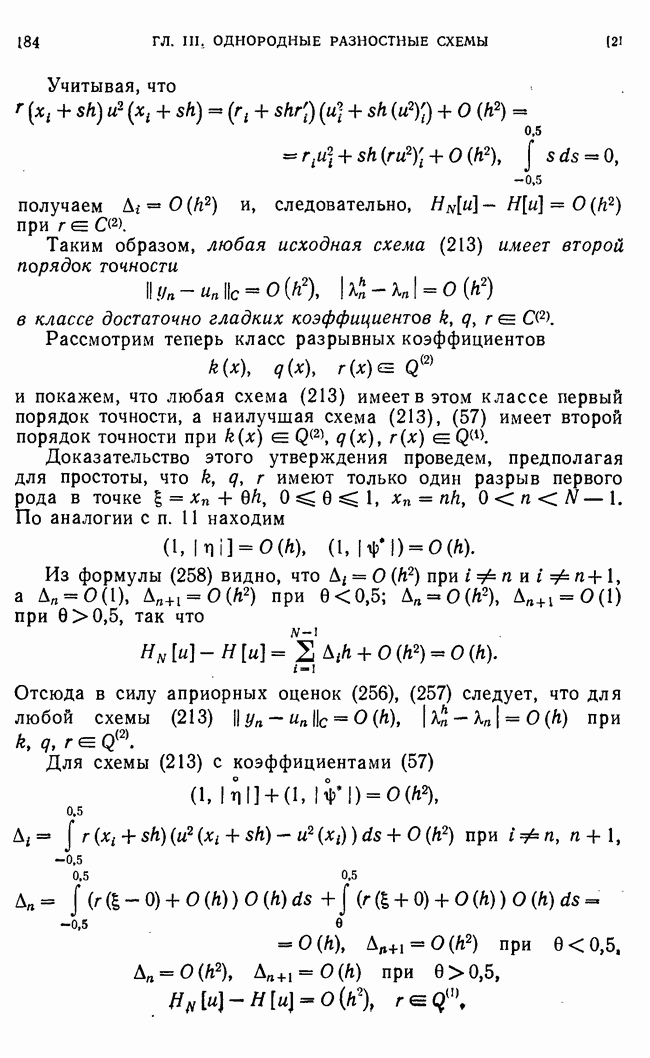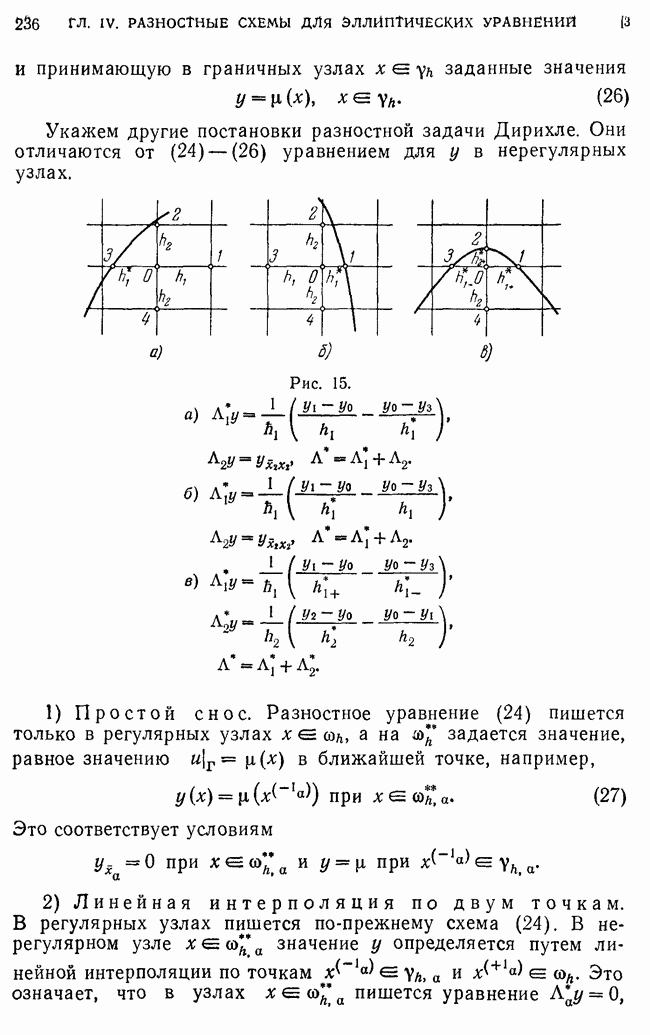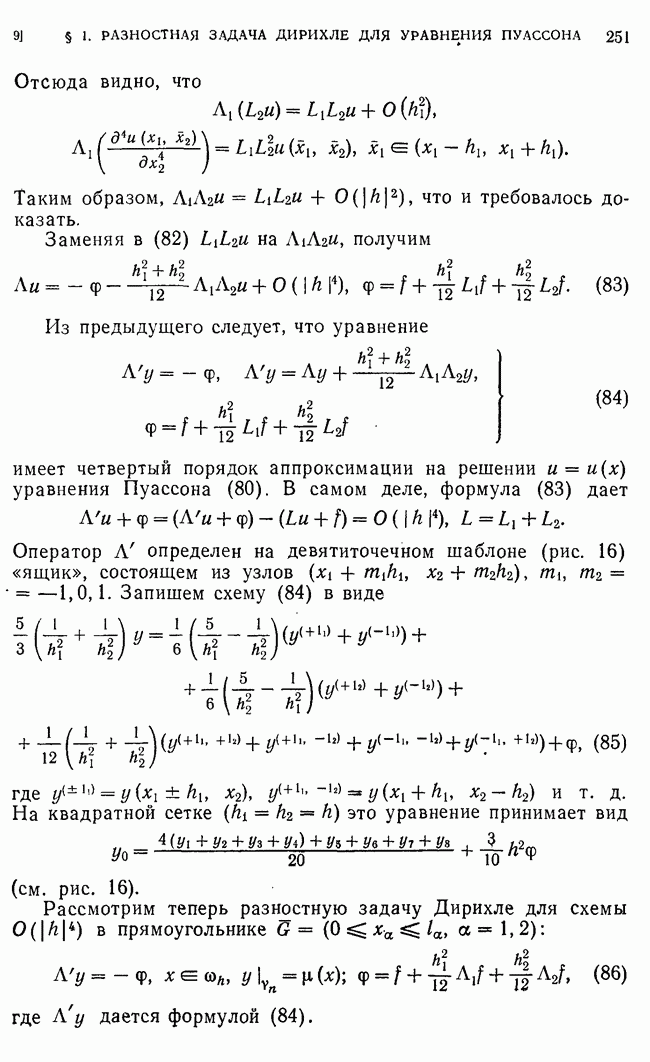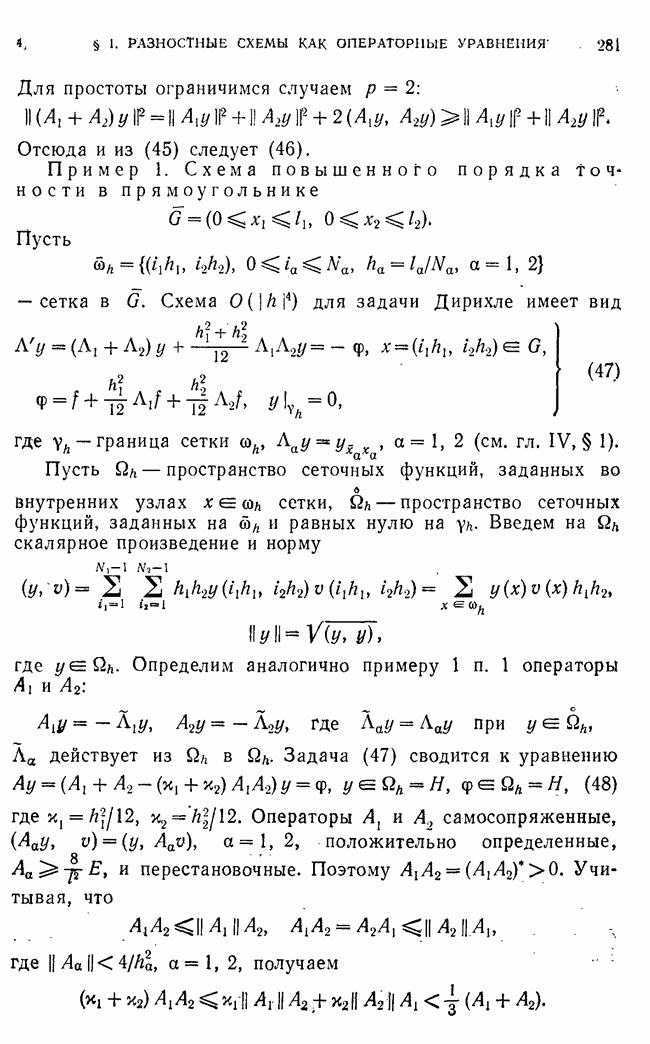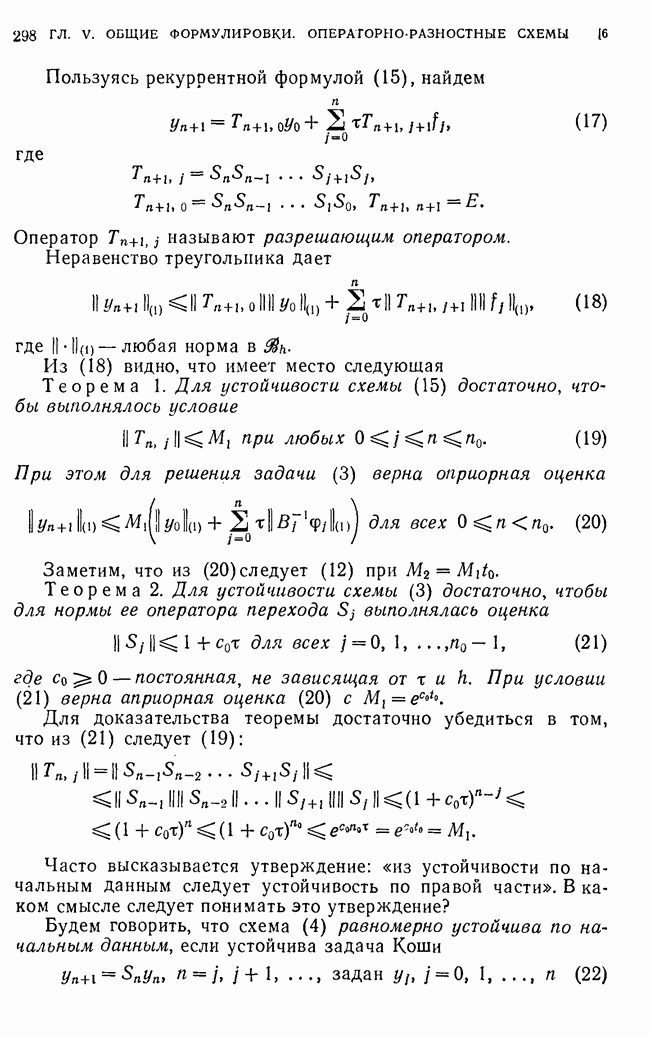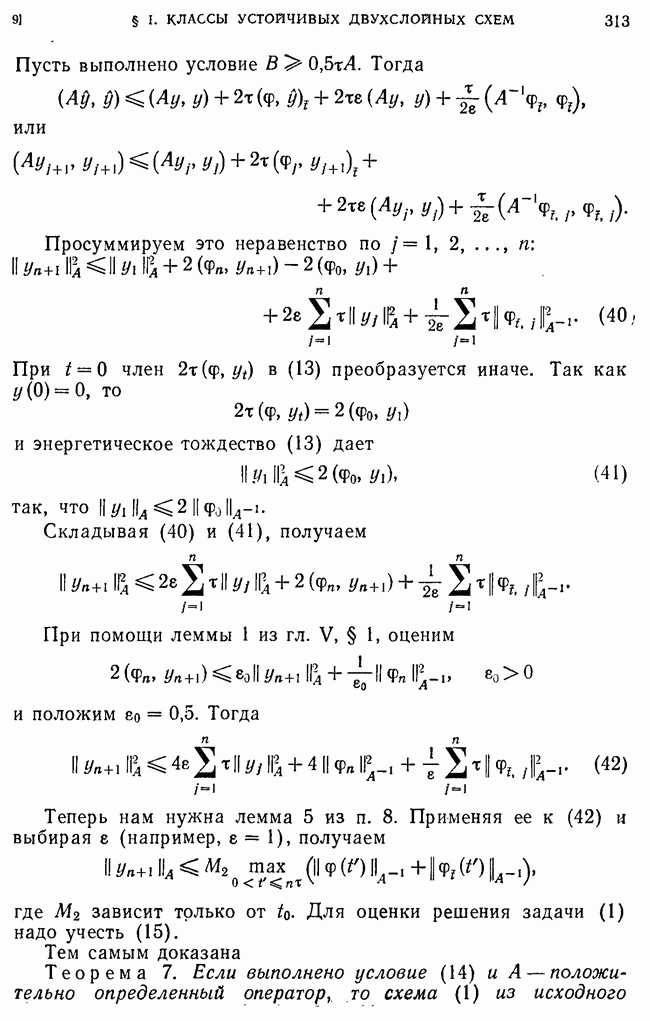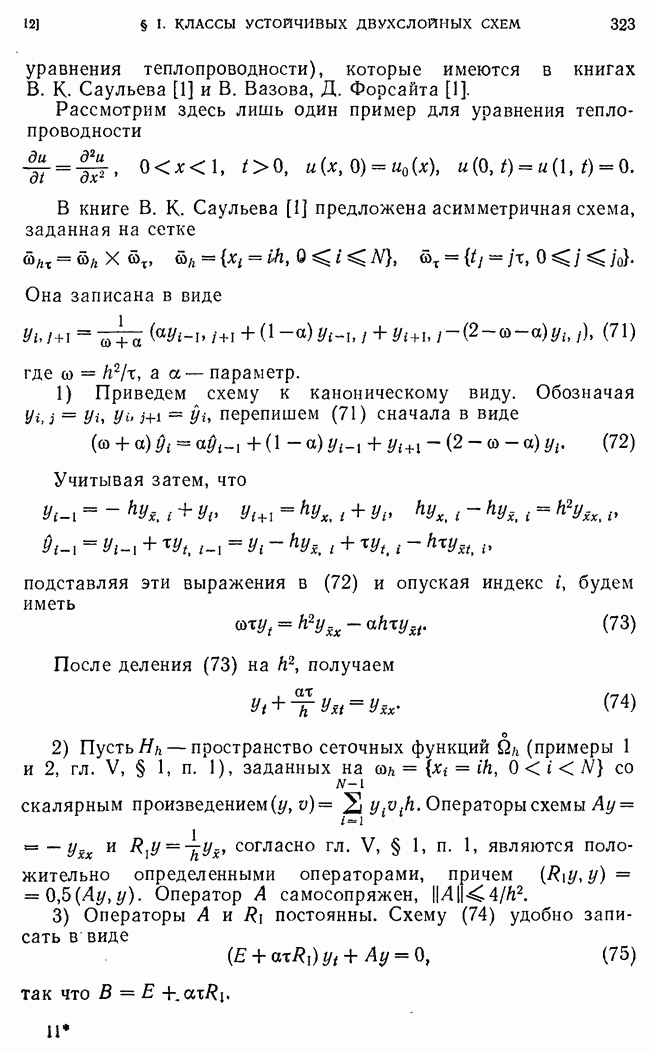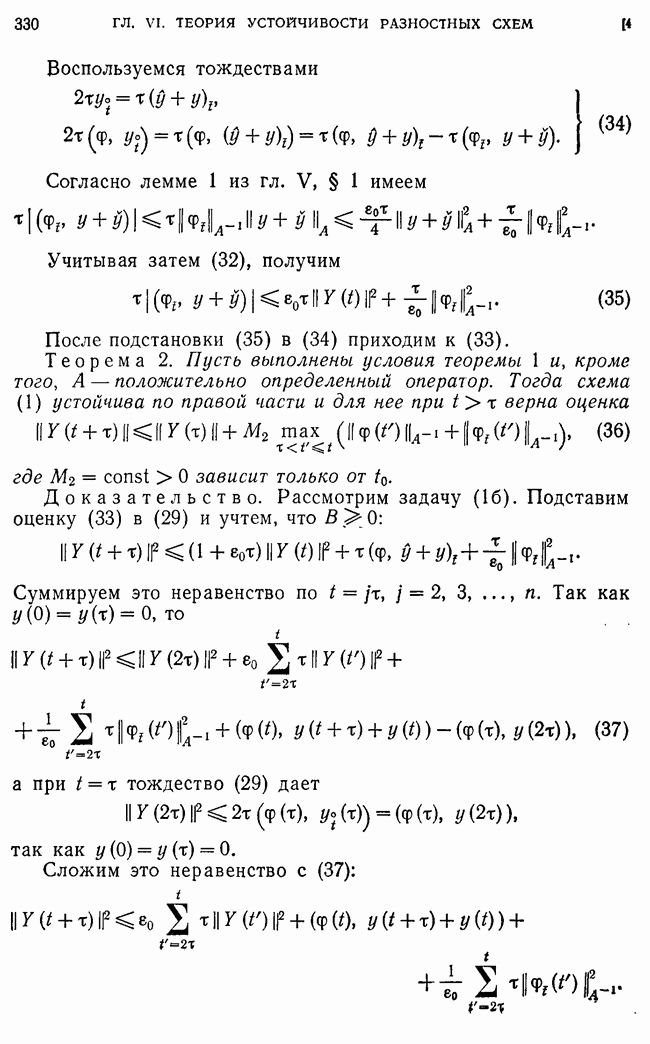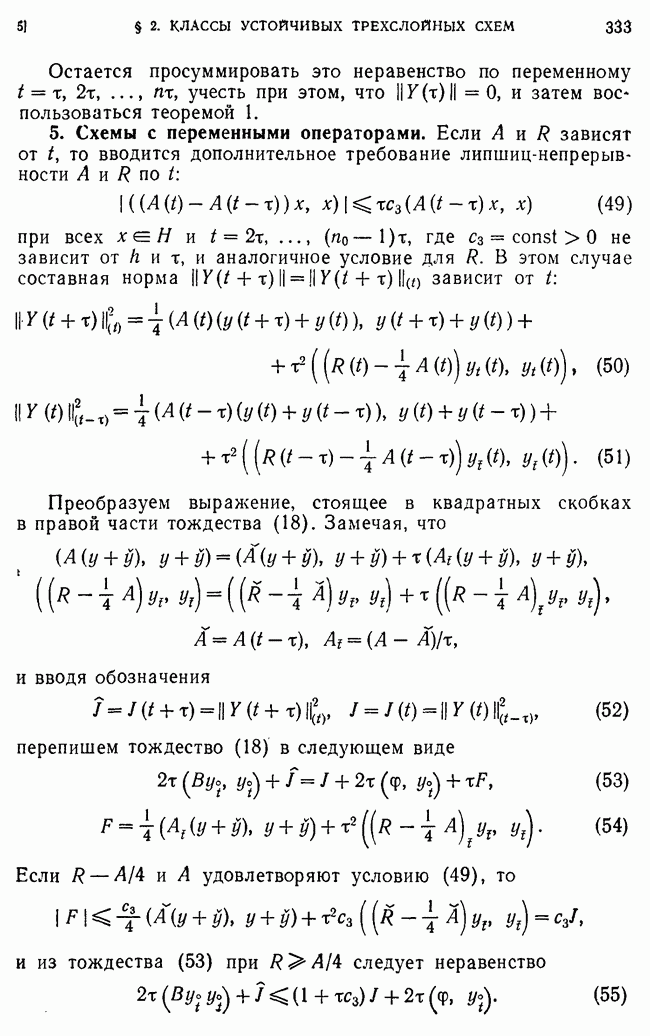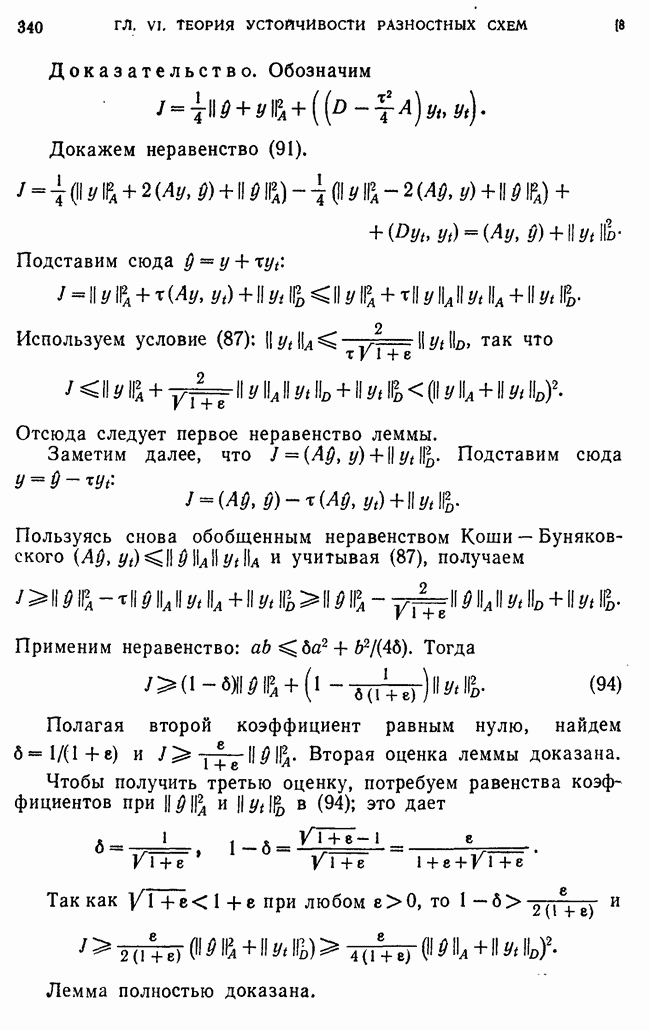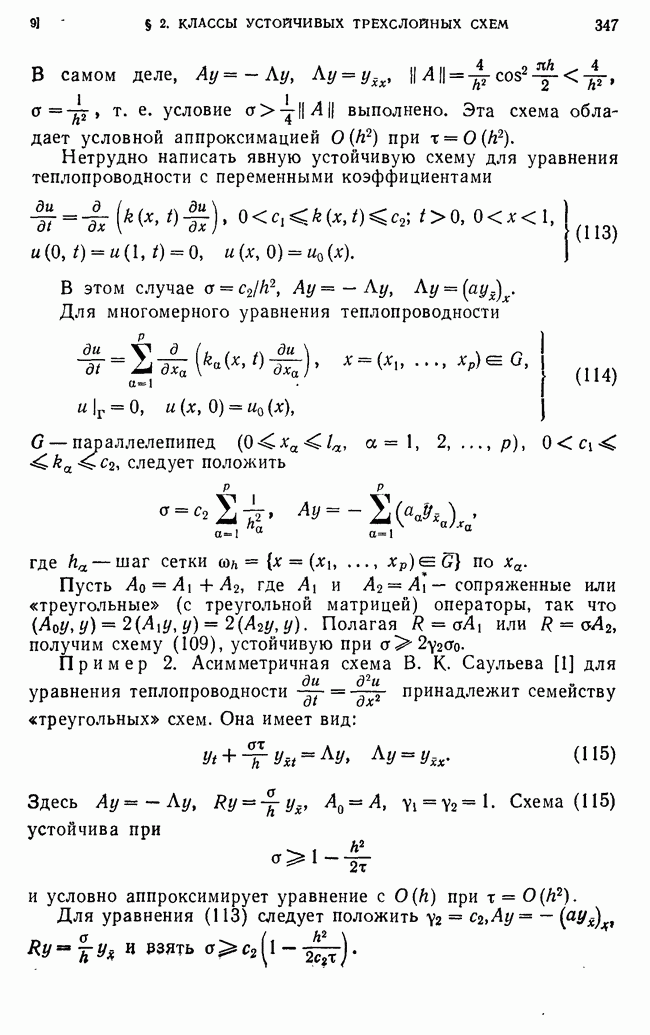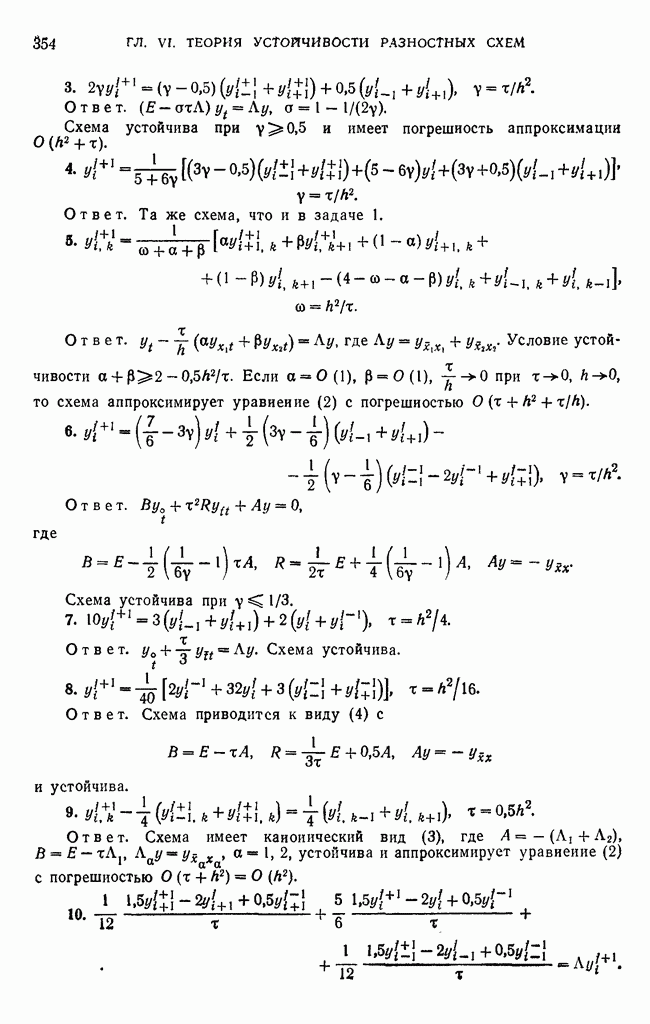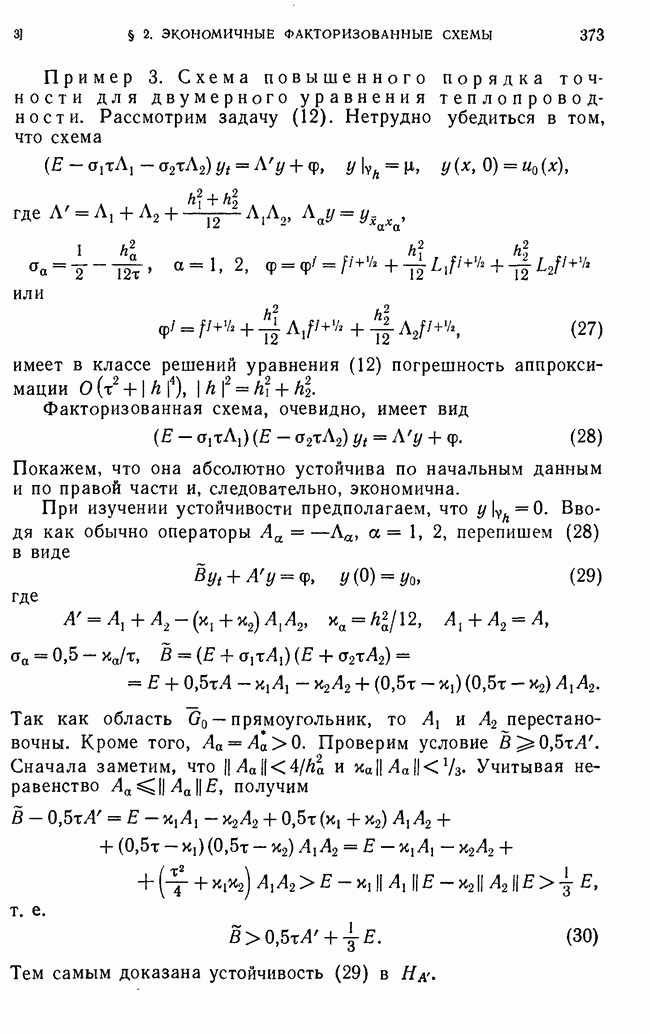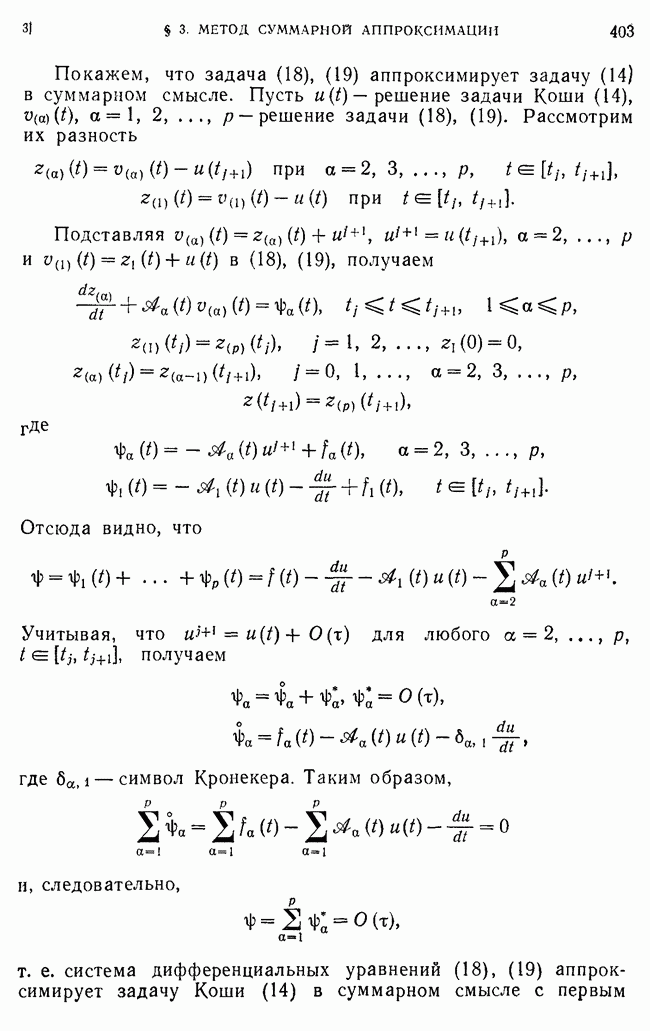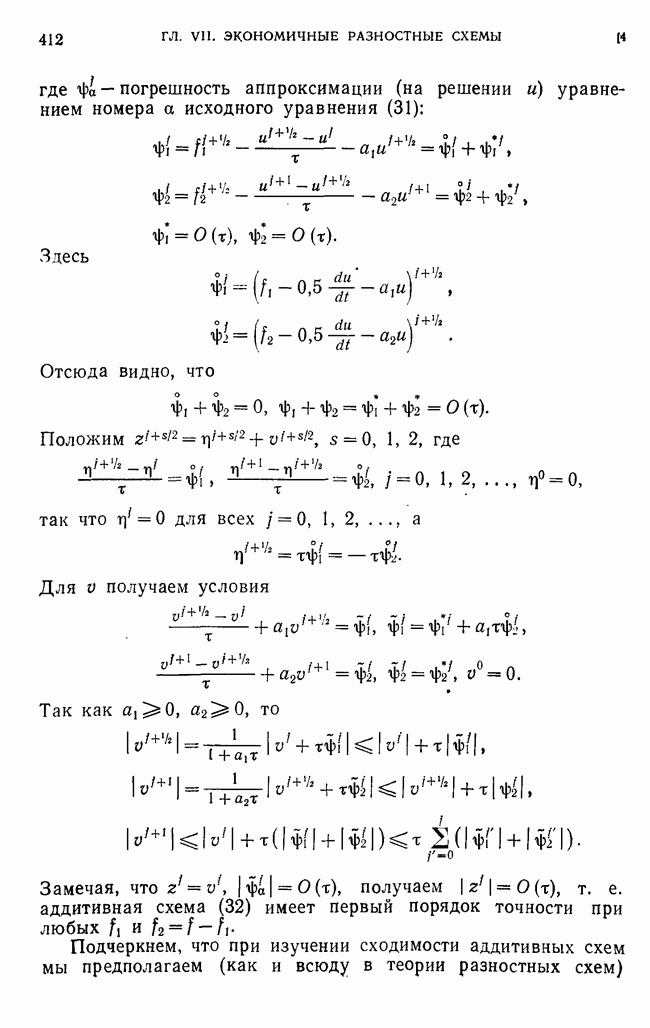| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
В гл. VI изучается устойчивость по начальным данным и по правой части двухслойных и трехслойных разностных схем с операторами, действующими в гильбертовом пространстве. Методом энергетических неравенств получены эффективные достаточные условия устойчивости и построены соответствующие априорные оценки. Установлена также необходимость некоторых условий устойчивости.
§ 1. Классы устойчивых двухслойных схем
1. Постановка задачи.
При изучении устойчивости двухслойных схем будем пользоваться их канонической формой

Пусть  - вещественное пространство,
- вещественное пространство,  скалярное произведение,
скалярное произведение,  норма в
норма в  Операторы схемы
Операторы схемы  в общем случае зависят от
в общем случае зависят от  Условимся зависимость от
Условимся зависимость от  явно не указывать.
явно не указывать.
Наша ближайшая задача — найти достаточные условия устойчивости схемы (1) и получить априорные оценки решения задачи (1), выражающие устойчивость схемы по правой части и начальным данным.
Решение задачи (1) можно представить в виде суммы  — решение однородного уравнения с начальным условием
— решение однородного уравнения с начальным условием 

а у — решение неоднородного уравнения с нулевым начальным условием:

Оценка решения задачи (1а)

означает, что схема (1) устойчива по начальным данным, а оценка решения задачи (16)

выражает устойчивость схемы (1) по правой части.
Мы будем также пользоваться и другим определением устойчивости схемы по правой части

где  Из (2) и (3) или (4), в силу неравенства треугольника
Из (2) и (3) или (4), в силу неравенства треугольника  следует априорная оценка
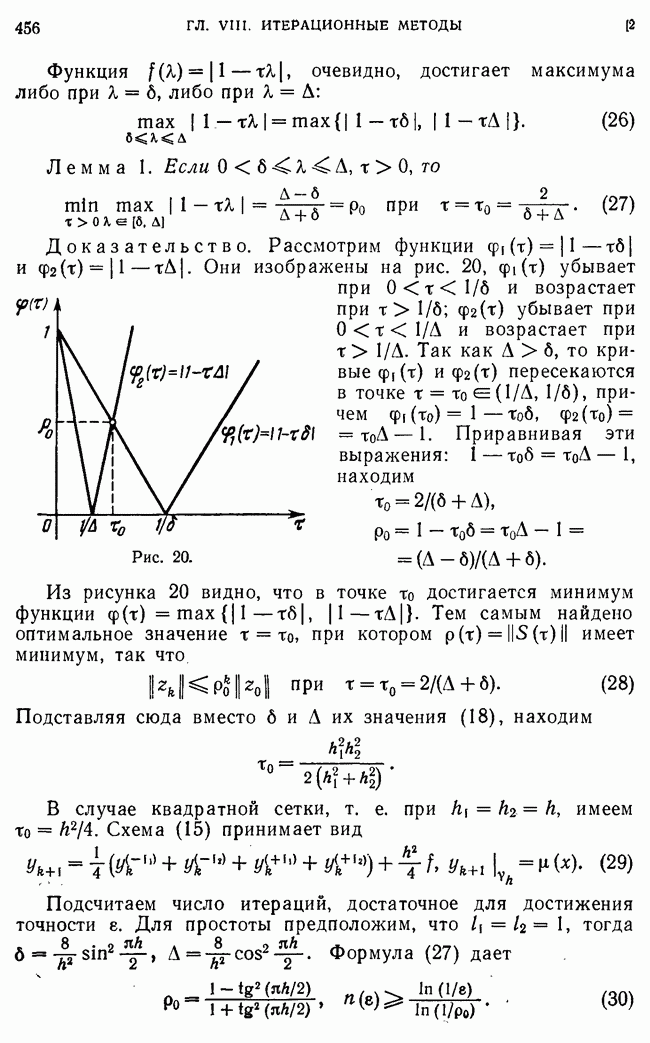
следует априорная оценка

или

В качестве нормы  будем пользоваться энергетическими нормами
будем пользоваться энергетическими нормами 

Будем говорить, что схема (1) устойчива в  (или
(или  если выполнено (5) с
если выполнено (5) с 
2. Исходное семейство схем.
Исследование устойчивости будем проводить в некотором исходном семействе разностных схем.
Операторы  считаем ограниченными линейными операторами, заданными на всем пространстве
считаем ограниченными линейными операторами, заданными на всем пространстве  Всюду будем предполагать, что разностная задача (1) разрешима при любых входных данных
Всюду будем предполагать, что разностная задача (1) разрешима при любых входных данных  т. е. что существует ограниченный оператор
т. е. что существует ограниченный оператор  с областью определения
с областью определения 
Для упрощения выкладок детальное изложение проведем в предположении, что
1) операторы  не зависят от
не зависят от  (постоянные операторы),
(постоянные операторы),
2) оператор В — положительный,  ,
,
3) А — самосопряженный и положительный оператор, 
Условия  и требование разрешимости выделяют из множества всех возможных схем (1) семейство допустимых схем (исходное семейство).
и требование разрешимости выделяют из множества всех возможных схем (1) семейство допустимых схем (исходное семейство).
Условие 1) может быть ослаблено, т. е. будем иногда рассматривать операторы  зависящие от
зависящие от 
3. Энергетическое тождество.
Исследование устойчивости схемы (1) проведем методом энергетических неравенств. Умножим уравнение (1) скалярно на 

Пользуясь формулой

перепишем (9) в виде

Лемма 1. Пусть А — самосопряженный оператор. Тогда

В самом деле

так как  в силу самосопряженности А.
в силу самосопряженности А.
Подставляя (12) в  получим энергетическое тождество для схемы (1):
получим энергетическое тождество для схемы (1):

4. Устойчивость по начальным данным в ...
Теорема 1. Если для некоторой схемы (1) из исходного семейства выполнено условие

то эта схема устойчива в  по начальным данным с постоянной
по начальным данным с постоянной  так что для решения задачи (1а) имеет место оценка
так что для решения задачи (1а) имеет место оценка

Доказательство. При  тождество (13) (для
тождество (13) (для  принимает вид
принимает вид

В силу (14) первое слагаемое в левой части этого тождества неотрицательно. Отбрасывая указанное слагаемое, получим
неравенство

или

где
Условие (14) выделяет из исходного семейства класс устойчивых в  схем.
схем.
Покажем, что условие (14) и необходимо для устойчивости схемы (1) в  по начальным данным. Для этого нам понадобится следующая лемма.
по начальным данным. Для этого нам понадобится следующая лемма.
Лемма 2. Пусть  оператор в
оператор в  имеющий ограниченный обратный. Тогда эквивалентны следующие условия:
имеющий ограниченный обратный. Тогда эквивалентны следующие условия:

В самом деле, пусть выполнено (16), т. е.  или
или

Тогда  Полагая
Полагая  получим
получим

или  Обратный ход рассуждений очевиден.
Обратный ход рассуждений очевиден.
Теорема 2. Пусть схема (1) принадлежит исходному семейству схем и, кроме того, оператор А — положительно определенный. Тогда условие (14) необходимо для устойчивости схемы (1) по начальным данным в На с постоянной 
Доказательство. Сведем сначала схему (1а) к явной схеме

где  .
.
Перепишем (1а) в виде  Так как
Так как  самосопряженный положительно определенный оператор, то существуют операторы
самосопряженный положительно определенный оператор, то существуют операторы  (см. теоремы 3 и 4 из гл. I, § 3), которые также являются самосопряженными положительными операторами. Поэтому уравнение (1а) эквивалентно уравнению
(см. теоремы 3 и 4 из гл. I, § 3), которые также являются самосопряженными положительными операторами. Поэтому уравнение (1а) эквивалентно уравнению

которое совпадает с (18).
Устойчивость схемы (18) в  эквивалентна устойчивости в
эквивалентна устойчивости в  схемы (1а), так как
схемы (1а), так как 
Пусть схема  устойчива в
устойчива в  выполнено (15). Тогда для схемы (18) выполнено неравенство
выполнено (15). Тогда для схемы (18) выполнено неравенство  в частности, при
в частности, при  имеем
имеем

Применяя лемму 2, получим неравенство (17) с  Покажем теперь, что неравенство (17), где
Покажем теперь, что неравенство (17), где  эквивалентно неравенству (14). Так как
эквивалентно неравенству (14). Так как  то
то

где 
Это и завершает доказательство теоремы. Объединяя теоремы 1 и 2, видим, что верна Теорема 3. Пусть схема (1), где А — положительно определенный оператор, принадлежит исходному семейству схем. Тогда условие (14) необходимо и достаточно для ее устойчивости по начальным данным в  с постоянной
с постоянной 
Напомним, что оператор В является, вообще говоря, несамосопряженным.
5. Устойчивость по начальным данным в ...
Напишем второе энергетическое тождество для схемы (1а), предполагая, что и В — самосопряженный оператор,  Умножим скалярно (1а) на
Умножим скалярно (1а) на 

Учитывая формулы

и пользуясь леммой 1, найдем

После подстановки этих выражений в (19) получим

Теорема 4. Пусть в схеме (1) операторы  не зависят от
не зависят от  Тогда условие (14) достаточно для устойчивости схемы (1) по начальным данным в
Тогда условие (14) достаточно для устойчивости схемы (1) по начальным данным в 
В самом деле, пусть  Тогда
Тогда

6. Необходимые и достаточные условия устойчивости по начальным данным.
При изучении вопроса о необходимых и достаточных условиях устойчивости двухслойной схемы эффективным оказался метод сведения неявной схемы к явной схеме с последующей оценкой нормы оператора перехода явной схемы. Простейший пример применения этого метода с постоянной  был рассмотрен в п. 4.
был рассмотрен в п. 4.
Нам теперь понадобится несколько отличное от прежнего определение устойчивости двухслойной схемы по начальным данным. Везде в этом пункте будем предполагать, что операторы  существуют, ограничены и
существуют, ограничены и  (о достаточных условиях существования обратного оператора см. в гл. I, § 3, п. 2).
(о достаточных условиях существования обратного оператора см. в гл. I, § 3, п. 2).
Пусть  постоянный оператор. Будем говорить, что схема (1)
постоянный оператор. Будем говорить, что схема (1)  -устойчива в
-устойчива в  по начальным данным, если для решения задачи (1а) при любых
по начальным данным, если для решения задачи (1а) при любых  выполнено неравенство
выполнено неравенство

где  постоянная, не зависящая от
постоянная, не зависящая от  и от выбора
и от выбора  Если схема (1а)
Если схема (1а)  -устойчива в
-устойчива в  то она устойчива в
то она устойчива в 

с постоянной  при
при  при
при 
Двухслойную неявную схему (1) с постоянными операторами  можно при помощи простых преобразований свести к явной схеме, которую запишем в форме
можно при помощи простых преобразований свести к явной схеме, которую запишем в форме

где 5 — оператор перехода  слоя на слой). Возможны три варианта преобразования:
слоя на слой). Возможны три варианта преобразования:
1) Если  то полагаем
то полагаем

2) Если  , то
, то

3) Если  перестановочны, то
перестановочны, то

В самом деле, запишем схему (1) в виде

Если  то существует корень
то существует корень  из оператора А. Действуя на уравнение (24) оператором
из оператора А. Действуя на уравнение (24) оператором  и полагая
и полагая  получаем схему (21) с условиями (22). Аналогично, в случае
получаем схему (21) с условиями (22). Аналогично, в случае  действуем на (24) оператором
действуем на (24) оператором  и вводим обозначения (23).
и вводим обозначения (23).
Если операторы  перестановочны, то
перестановочны, то

Таким образом, мы убедились, что в ряде случаев неявная схема (1) сводится к явной схеме. Из (22) видно, что  а из (23) следует
а из (23) следует  Поэтому исследование устойчивости в
Поэтому исследование устойчивости в  или
или  неявной схемы сводится к исследованию устойчивости явной схемы в
неявной схемы сводится к исследованию устойчивости явной схемы в  При изучении устойчивости по начальным данным рассматриваем задачу:
При изучении устойчивости по начальным данным рассматриваем задачу:

Отсюда непосредственно следует

Это неравенство соответствует оценке

где  один из операторов
один из операторов  или
или 
Вопрос ставится так: какими свойствами должен обладать оператор С, чтобы выполнялось условие

(условие  -устойчивости схемы
-устойчивости схемы 
Рассмотрим здесь случай самосопряженного оператора С. Случай  при
при  был рассмотрен в п. 4.
был рассмотрен в п. 4.
Будем пользоваться следующим определением нормы оператора 

В силу леммы 3 из гл. I, § 3  и из условия
и из условия  следует
следует  Определение (26) дает:
Определение (26) дает:

и следовательно, —  (так как
(так как  или
или

Лемма 3. Если  то условия (27) и
то условия (27) и

эквивалентны.
Мы убедились в том, что из (28) следует (27). Обратный ход рассуждений очевиден.
Обратимся к неявной схеме (1а).
Лемма 4. Если  то условия (27) и
то условия (27) и

равносильны при  Если же, кроме того, А — положительно определенный оператор, то (27) и (29) равносильны при
Если же, кроме того, А — положительно определенный оператор, то (27) и (29) равносильны при 
Доказательство. Первое утверждение леммы следует из тождеств

где  Для доказательства второго утверждения заметим, что если С — самосопряженный неотрицательный оператор и
Для доказательства второго утверждения заметим, что если С — самосопряженный неотрицательный оператор и  существует, то неравенства
существует, то неравенства  и эквивалентны. Действительно, обозначив
и эквивалентны. Действительно, обозначив  запишем неравенство
запишем неравенство  в виде
в виде

т. е.
Таким образом, если  существует, то условия (27) эквивалентны следующим:
существует, то условия (27) эквивалентны следующим:

Положив здесь  имеем
имеем

Обозначив  получим отсюда
получим отсюда

что и требовалось.
Теорема 5. Пусть  постоянные операторы и
постоянные операторы и

Тогда условия

необходимы и достаточны для  -устойчивости в
-устойчивости в  схемы (1а):
схемы (1а):

а если, кроме того, А — положительно определенный оператор, то и для  -устойчивости в
-устойчивости в 

Для доказательства теоремы достаточно свести схему (1а) к явной схеме (25) (случай  или
или  и затем воспользоваться леммами 3 и 4.
и затем воспользоваться леммами 3 и 4.
Отметим, что необходимые и достаточные условия устойчивости в данном случае совпадают. Энергетический метод не позволяет получить такой результат. Более того, энергетическим методом удается доказать устойчивость (25) или (1а) при  только при достаточно малом
только при достаточно малом 
7. Метод разделения переменных.
Пусть  — конечномерное (скажем,
— конечномерное (скажем,  -мерное) пространство. Если
-мерное) пространство. Если  постоянные и самосопряженные операторы,
постоянные и самосопряженные операторы,

то исследование устойчивости может быть проведено методом разделения переменных по аналогии с гл. II, § 1.
Пусть  собственные значения,
собственные значения,  собственные функции следующей задачи (см., например, Ф. Р. Гантмахер [1]):
собственные функции следующей задачи (см., например, Ф. Р. Гантмахер [1]):

причем 
Решение задачи (1а) будем искать в виде суммы

Подставляя это выражение в  и учитывая (31), получаем
и учитывая (31), получаем

Замечая, что  будем иметь
будем иметь 

или

Требование устойчивости с постоянной  будет выполнено, если
будет выполнено, если  или
или

Условия (32) эквивалентны энергетическому неравенству  или
или

В самом деле,

Отсюда и следует эквивалентность неравенства В  условиям (32).
условиям (32).
Таким образом, мы показали, что при условиях (30) неравенство

достаточно для устойчивости в  схемы (1а):
схемы (1а):

Следует подчеркнуть, что требование самосопряженности оператора В является здесь обязательным, в то время как для применения энергетического метода достаточно лишь положительности оператора В.
Аналогично доказывается устойчивость схемы (1а) в  если выполнены условия (30), (33). Нетрудно показать, что условия
если выполнены условия (30), (33). Нетрудно показать, что условия

обеспечивают  -устойчивость схемы (1а):
-устойчивость схемы (1а):

Для этого достаточно потребовать

Прежде чем применять метод разделения переменных, можно свести схему (1а) к явной схеме  или
или  Тогда получим обычную задачу на собственные значения
Тогда получим обычную задачу на собственные значения

8. Некоторые вспомогательные неравенства.
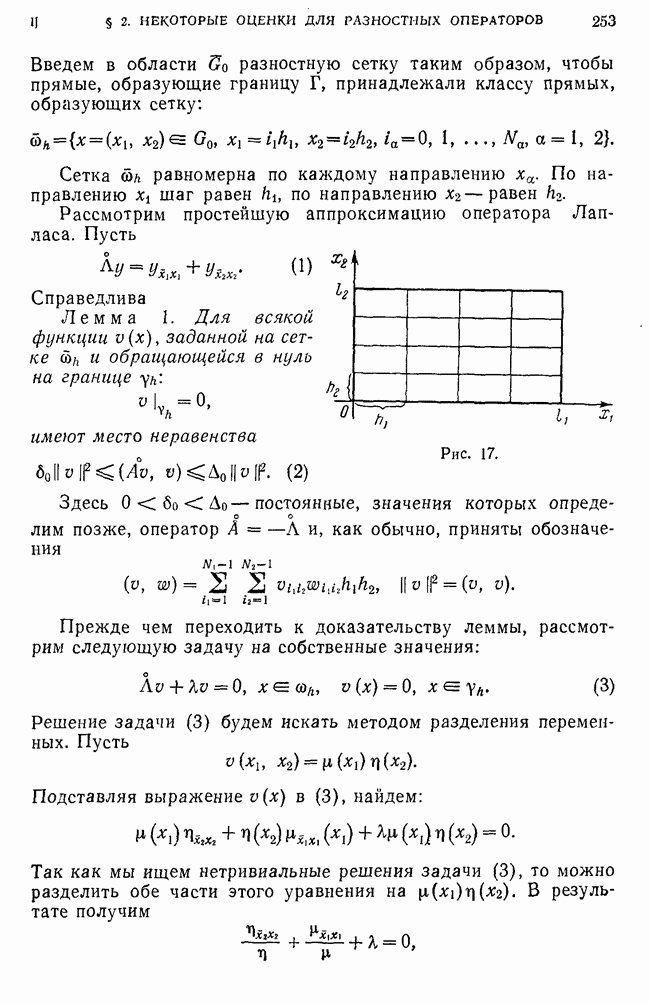
Пусть  сеточные функции, заданные при
сеточные функции, заданные при 
Лемма 5. Пусть  неотрицательные функции. Если
неотрицательные функции. Если  неубывающая функция
неубывающая функция  то из неравенства 1
то из неравенства 1

следует оценка

Доказательство. Пусть  решение системы уравнений
решение системы уравнений

Нетрудно заметить, что  для всех
для всех  . В самом деле,
. В самом деле,

Из (34) и (36) видно, что из неравенств  при следует Заменим в
при следует Заменим в  на
на  и вычтем из (36) полученное уравнение. Тогда для
и вычтем из (36) полученное уравнение. Тогда для  получим разностное уравнение
получим разностное уравнение

Отсюда находим

Так как  и, следовательно,
и, следовательно, 
Лемма доказана.
Замечание. Лемма 5 верна, если вместо (34) дано неравенство

так что 
Лемма  то из (34) следует
то из (34) следует

Положим  Тогда из (34) получим
Тогда из (34) получим  неубывающая функция. Для
неубывающая функция. Для  оценки
оценки  пользуемся леммой 5.
пользуемся леммой 5.
Леммы 5 и 6 будут использованы при доказательстве устойчивости схемы (1) по правой части.
9. Устойчивость по правой части.
В гл. V, § 2 была доказана теорема о том, что из устойчивости по начальным данным в норме  следует устойчивость по правой части, взятой в норме
следует устойчивость по правой части, взятой в норме  Отсюда следует
Отсюда следует
Теорема 6. Если выполнено условие (14), то схема (1) из исходного семейства схем устойчива по правой части и для решения задачи (1) справедлива априорная оценка

Если, кроме того, оператор В самосопряжен, то

Покажем, что, кроме того, имеют место априорные оценки (3), (4), где

Воспользуемся энергетическим тождеством (13) для схемы (16).
Лемма 7. Если А — постоянный, самосопряженный и положительно определенный оператор, то для любых  из
из  имеет место оценка:
имеет место оценка:

где  число.
число.
Представим  в виде
в виде

и воспользуемся леммой 1 из гл. V, § 1 для оценки второго слагаемого. Тогда получим (39). Подставим (39) в (13):

Пусть выполнено условие  Тогда
Тогда

или

Просуммируем это неравенство по 

При  член
член  в (13) преобразуется иначе. Так как
в (13) преобразуется иначе. Так как  то
то

и энергетическое тождество (13) дает

так, что 
Складывая (40) и (41), получаем

При помощи леммы 1 из гл. V, § 1, оценим

и положим  Тогда
Тогда

Теперь нам нужна лемма 5 из п. 8. Применяя ее к (42) и выбирая  (например,
(например,  ), получаем
), получаем

где  зависит только от
зависит только от  Для оценки решения задачи (1) надо учесть (15).
Для оценки решения задачи (1) надо учесть (15).
Тем самым доказана
Теорема 7. Если выполнено условие (14) и А — положительно определенный оператор, то схема (1) из исходного
семейства схем устойчива по правой части и для решения задачи (1) при  верна априорная оценка
верна априорная оценка

При каких условиях имеет место устойчивость в норме  Ответ на этот вопрос дает Теорема 8. Пусть выполнено условие
Ответ на этот вопрос дает Теорема 8. Пусть выполнено условие

где  любое положительное число и схема (1) принадлежит исходному семейству схем. Тогда для задачи (1) верна априорная оценка
любое положительное число и схема (1) принадлежит исходному семейству схем. Тогда для задачи (1) верна априорная оценка

Доказательство. Обратимся к тождеству (13). Неравенство Коши — Буняковского и  -неравенство дают:
-неравенство дают:

Подставим эту оценку в (13) и спользуем условие (44):

Суммируя затем по  ли учитывая, что
ли учитывая, что  получаем
получаем

Отсюда и из (15) следует (45). Теорема 8 доказана.
Замечание. Теоремы 7 и 8 сохраняют силу и в случае переменного оператора  а теорема 4 справедлива для переменного оператора
а теорема 4 справедлива для переменного оператора  Это видно из доказательств указанных теорем.
Это видно из доказательств указанных теорем.
10. Устойчивость схемы с весами.
Покажем, как надо пользоваться доказанными выше теоремами на примере схемы с весами:

В гл. V, § 2, п. 3 схема (46) была приведена к каноническому виду

Сравнивая (46) с (1), видим, что

Пусть существует оператор  Действуя
Действуя  на (47), получим вторую каноническую форму для схемы с весами:
на (47), получим вторую каноническую форму для схемы с весами:

Записью в виде (47) будем пользоваться в случае самосопряженного оператора А, (48) — в случае несамосопряженного положительно определенного оператора 
Пусть  Покажем, что
Покажем, что  если
если

В самом деле, так как  или
или  то
то

Таким образом, при  схема (46) устойчива в
схема (46) устойчива в  по начальным данным. В частности, для явной схемы (при
по начальным данным. В частности, для явной схемы (при  из условия
из условия  следует
следует  т. е. явная схема устойчива в
т. е. явная схема устойчива в  при
при  В силу теоремы 2 это условие не только достаточно, но и необходимо для устойчивости с постоянной
В силу теоремы 2 это условие не только достаточно, но и необходимо для устойчивости с постоянной  если
если  положительно определенный оператор.
положительно определенный оператор.
Пример 1. Рассмотрим схему с весами для одномерного уравнения теплопроводности

с краевыми условиями первого рода. В этом случае  Оператор
Оператор  (см. гл. V, § 1, п. 1), его норма
(см. гл. V, § 1, п. 1), его норма  Условие (49) принимает вид
Условие (49) принимает вид

и совпадает с условием, полученным в гл. II методом разделения переменных. Явная схема  устойчива при
устойчива при  Если
Если

то

Теорема 9. Пусть  постоянный положительно определенный оператор. Тогда для схемы (46) при условии (49) верна априорная оценка (43). Если
постоянный положительно определенный оператор. Тогда для схемы (46) при условии (49) верна априорная оценка (43). Если  и
и

где  постоянная, не зависящая от
постоянная, не зависящая от  то для схемы (46) верна оценка (45).
то для схемы (46) верна оценка (45).
Первое утверждение следует из теоремы 7 для схемы (47), так как  при
при  второе утверждение — из теоремы 8, так как неравенство (44) выполняется при
второе утверждение — из теоремы 8, так как неравенство (44) выполняется при  В самом деле,
В самом деле,

Теорема 10. Пусть  положительно определенный оператор и выполнено условие (49). Тогда для схемы (46) верна оценка
положительно определенный оператор и выполнено условие (49). Тогда для схемы (46) верна оценка

Если же выполнено условие (50), то

Доказательство, а) Возьмем схему с весами в форме (48) и напишем для нее априорную оценку (43), учитывая при этом, что  постоянный оператор:
постоянный оператор:

Подставляя сюда  получаем (51).
получаем (51).
б) Получим неравенство (51а). По аналогии с (13) напишем для (48) энергетическое тождество (учитывая, что 

Обобщенное неравенство Коши — Буняковского и  -неравенство дают:
-неравенство дают:

Из условия (50) следует, что

В самом деле,

при а  При этом мы учли оценку
При этом мы учли оценку

 следует из неравенства
следует из неравенства  (см. гл. I, § 3), если положить
(см. гл. I, § 3), если положить 
Если учесть (54), то из (52) получим

Подставляя сюда (53), будем иметь

или  Суммирование по
Суммирование по  приводит к оценке (51) с
приводит к оценке (51) с 
Рассмотрим теперь случай, когда  -положительно определенный несамосопряженный оператор. Покажем, что для схемы (48)
-положительно определенный несамосопряженный оператор. Покажем, что для схемы (48)

если выполнено условие

Заметим, что для самосопряженного оператора А

Итак, пусть а 0,5. Тогда

Для доказательства неравенства (55) потребуется
Лемма 8. Пусть А — положительно определенный оператор, для которого выполнено (56). Тогда

Доказательство. 1) Положим  Тогда (56) дает
Тогда (56) дает  т. е.
т. е. 
2) Из неравенств  и (56) следует, что
и (56) следует, что

Лемма 9. Пусть А — положительно определенный оператор и выполнено (56). Тогда

Доказательство. 1) Так как  при а
при а  то, применяя к схеме (48) теорему 1, получим, что для решения задачи (48) при любых
то, применяя к схеме (48) теорему 1, получим, что для решения задачи (48) при любых  справедлива оценка
справедлива оценка

Заметим теперь, что схему (48) при  можно записать в виде
можно записать в виде

Отсюда и из (60) получаем оценку (57).
2) Для оценки  где
где  достаточно получить неравенство вида
достаточно получить неравенство вида  Тогда
Тогда

и, следовательно,  Если
Если  то
то  и
и  Если
Если  то
то

Так как, согласно лемме  то
то

и, следовательно,  Отметим, что оценка (58) верна для любого несамосопряженного оператора
Отметим, что оценка (58) верна для любого несамосопряженного оператора  Лемма доказана. Из (60) и леммы 9 следует
Лемма доказана. Из (60) и леммы 9 следует
Теорема 11. Пусть  положительно определенный оператор и выполнено условие (56). Тогда для схемы (46) при
положительно определенный оператор и выполнено условие (56). Тогда для схемы (46) при  верна априорная оценка
верна априорная оценка

Если одновременно выполнены два условия

то оценка (61) выполняется при 
Для доказательства запишем схему (46) в виде

где 
Используя неравенство треугольника и оценки  получаем
получаем

откуда и следует (61).
Замечание. Мы всюду предполагали, что оператор А положительно определен или, по меньшей мере, положителен. Однако можно получить некоторые априорные оценки для схемы (1) при условии, что А — полуограниченный оператор:

Введем оператор

Он положительно определен:

Перепишем схему (1) в виде

Пусть выполнены условия теоремы 8, так что

Тогда верна априорная оценка

где

Подставляя это неравенство в предыдущую оценку, получим

или

Так как  монотонно неубывающая функция, то в силу, леммы 5 имеем
монотонно неубывающая функция, то в силу, леммы 5 имеем  или
или

Постоянную с выберем так, чтобы постоянная со была минимальна. Из условия минимума функции  с следует, что
с следует, что  при этом
при этом 
Тем самым доказана устойчивость схемы (1) в случае  При этом важно отметить, что 1) достаточное условие устойчивости имеет вид
При этом важно отметить, что 1) достаточное условие устойчивости имеет вид  схема устойчива при любых
схема устойчива при любых 
Рассмотрим, например, схему с весами. Тогда  и условие
и условие  выполнено при
выполнено при

11. Априорные оценки в случае переменного оператора А.
До сих пор мы предполагали при изучении устойчивости в  что оператор А постоянный, т. е. не зависит от
что оператор А постоянный, т. е. не зависит от  Если
Если  зависит от
зависит от  то будем требовать, чтобы выполнялось следующее условие липшиц-непрерывности
то будем требовать, чтобы выполнялось следующее условие липшиц-непрерывности  по
по 

для всех  где
где  положительная постоянная, не зависящая от
положительная постоянная, не зависящая от 
Исходное семейство схем определим требованиями

Как и ранее, предполагаем существование оператора  что означает разрешимость задачи (1) при любых входных данных
что означает разрешимость задачи (1) при любых входных данных 
Это семейство, очевидно, содержит исходное семейство, введенное в п. 2.
Исследования, проведенные методом энергетических неравенств, показывают, что условия

оказываются достаточными для устойчивости схемы (1) с переменными операторами  При этом сами нормы
При этом сами нормы  оказываются зависящими от
оказываются зависящими от 

Поэтому надо говорить об устойчивости в  (вместо
(вместо  и
и 
Исходным для исследования является энергетическое тождество (13), где  Чтобы получить рекуррентное неравенство, преобразуем выражение
Чтобы получить рекуррентное неравенство, преобразуем выражение

и оценим второе слагаемое в правой части при помощи (62):

Подставив эту оценку в (13), получим энергетическое неравенство:

где

Если выполнено условие (64), то из (66) при  следует:
следует:

Энергетическое тождество при  записывается в виде
записывается в виде

Отсюда при условии (64) и  получим
получим

В результате (67) и (68) дают для задачи (1) при 

Проведенные выше рассуждения показывают по существу единственное принципиальное отличие случая переменных операторов от случая постоянных операторов.
Суммируем результаты в виде двух теорем — аналогов теорем 7 и 8.
Теорема 12. Пусть выполнены условия (63), (64) и А — положительно определенный оператор. Тогда для решения задачи (1) верна оценка

где  зависят только от
зависят только от 
Теорема 13. Пусть выполнены условия (63) и (65). Тогда для схемы (1) верна априорная оценка

Сравнивая (69) и (70) с (43) и (45), видим, что оценки (43) и (45) для случая постоянного А получаются из (69) и (70) пои 
Если вместо (64) ставится условие

где  не зависит от
не зависит от  то оценки (69) и (70) сохраняют силу при достаточно малом
то оценки (69) и (70) сохраняют силу при достаточно малом  а постоянные
а постоянные  зависят только от
зависят только от  На доказательстве этого факта останавливаться не будем.
На доказательстве этого факта останавливаться не будем.
12. Пример.
Для того, чтобы пользоваться изложенной выше общей теорией устойчивости для конкретных разностных схем, необходимо:
1) привести двухслойную схему к каноническому виду (1), т. е. выделить операторы А и  ввести пространство сеточных функций
ввести пространство сеточных функций  и исследовать свойства
и исследовать свойства  (положительность, самосопряженность и др.) как операторов, заданных на
(положительность, самосопряженность и др.) как операторов, заданных на  проверить принадлежность схемы к исходному семейству схем, а также проверить выполнение достаточных условий устойчивости (64) или (65); 4) если эти условия выполнены, то данная схема устойчива и для нее справедливы априорные оценки, например, (69) и (70).
проверить принадлежность схемы к исходному семейству схем, а также проверить выполнение достаточных условий устойчивости (64) или (65); 4) если эти условия выполнены, то данная схема устойчива и для нее справедливы априорные оценки, например, (69) и (70).
Первый шаг состоит в приведении схемы к каноническому виду. Заметим, что полученные выше достаточные условия открывают возможность написания устойчивых разностных схем сразу в каноническом виде.
В качестве упражнений на приведение схем к каноническому виду можно рекомендовать различные схемы (например, для
уравнения теплопроводности), которые имеются в книгах В. К. Саульева [1] и В. Вазова, Д. Форсайта [1].
Рассмотрим здесь лишь один пример для уравнения теплопроводности

В книге В. К. Саульева [1] предложена асимметричная схема, заданная на сетке

Она записана в виде

где  — параметр.
— параметр.
1) Приведем схему к каноническому виду. Обозначая  перепишем (71) сначала в виде
перепишем (71) сначала в виде

Учитывая затем, что

подставляя эти выражения в (72) и опуская индекс  будем иметь
будем иметь

После деления (73) на  получаем
получаем

2) Пусть  — пространство сеточных функций
— пространство сеточных функций  (примеры 1 и 2, гл. V, § 1, п. 1), заданных на
(примеры 1 и 2, гл. V, § 1, п. 1), заданных на  со скалярным произведением
со скалярным произведением  Операторы схемы
Операторы схемы  согласно гл. V, § 1, п. 1, являются положительно определенными операторами, причем
согласно гл. V, § 1, п. 1, являются положительно определенными операторами, причем  Оператор А самосопряжен,
Оператор А самосопряжен, 
3) Операторы  постоянны. Схему (74) удобно записать в виде
постоянны. Схему (74) удобно записать в виде

так что 
Условие  выполнено при
выполнено при  Действительно, для любого
Действительно, для любого 

т. е.

4) Так как  то схема (71) устойчива в
то схема (71) устойчива в  (в сеточной норме
(в сеточной норме  при
при

Наряду со схемой (71) В. К. Саульев [1] предложил другую асимметричную схему, которая после приведения ее к канонической форме запишется так:

Так как  то эта схема устойчива при том же условии (76). Из (76) видно, что асимметричные схемы безусловно устойчивы при
то эта схема устойчива при том же условии (76). Из (76) видно, что асимметричные схемы безусловно устойчивы при 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
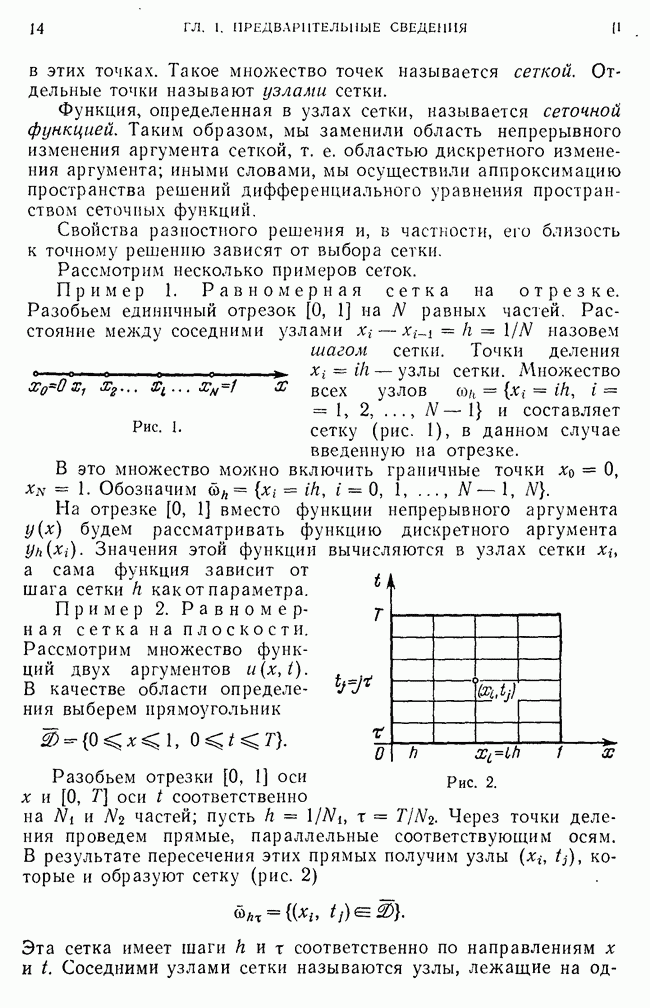
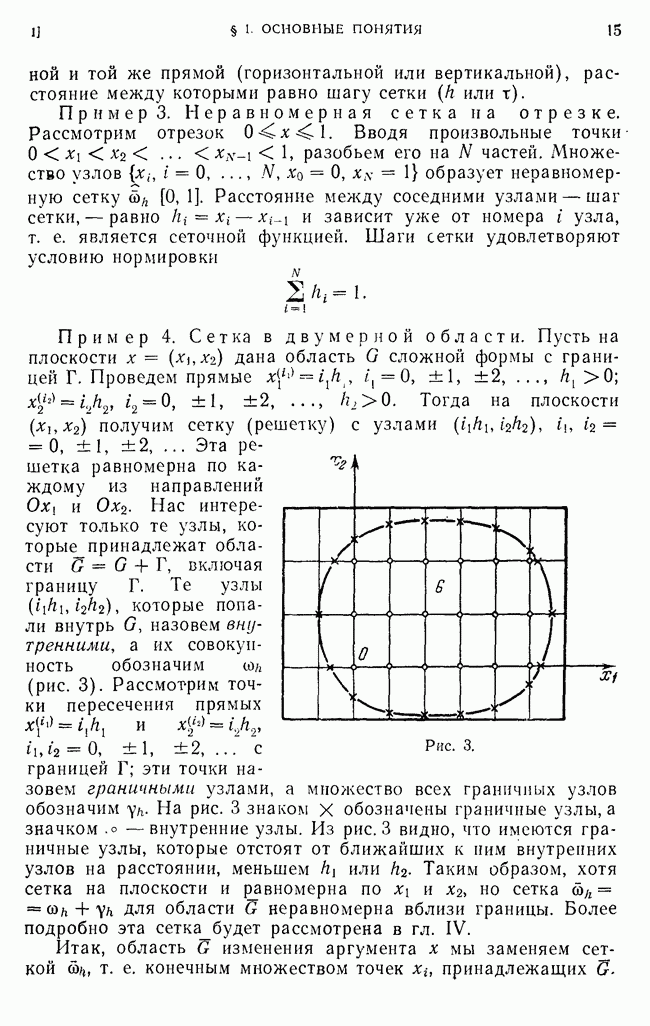
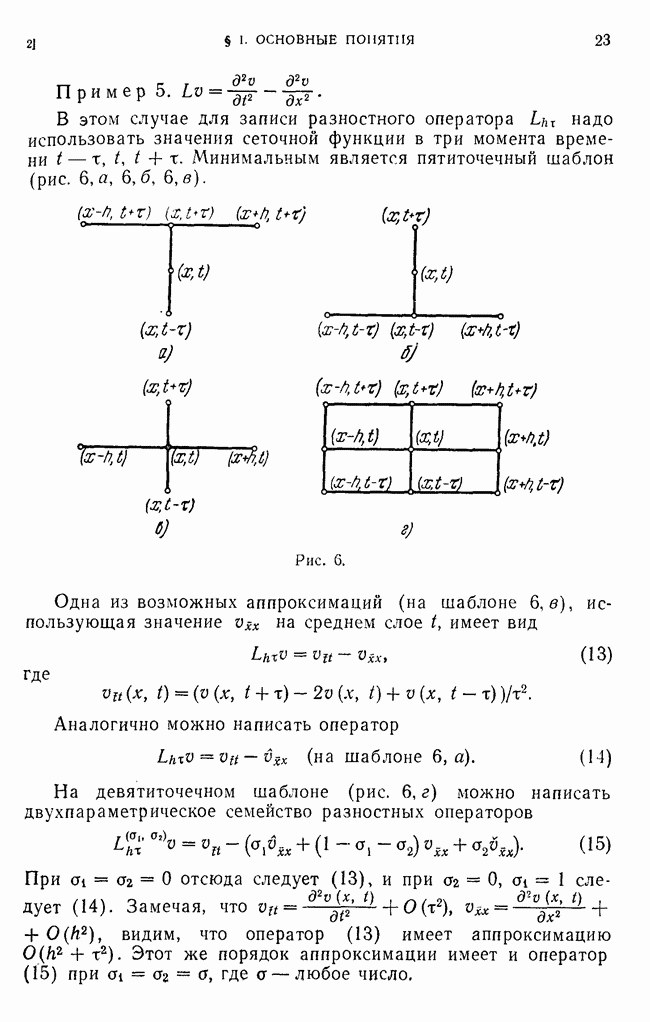
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
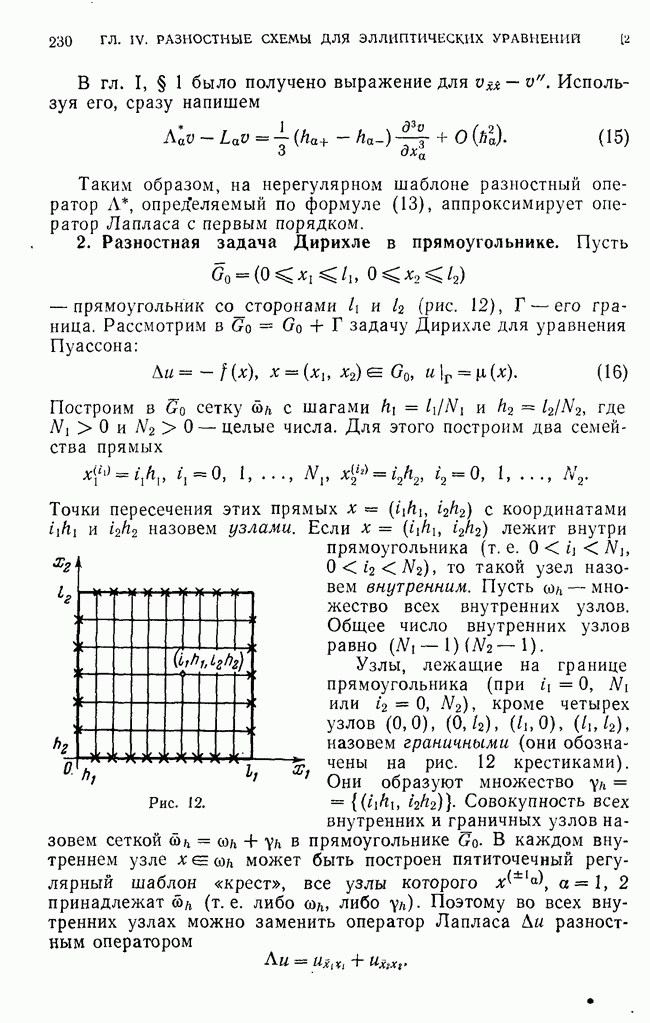
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
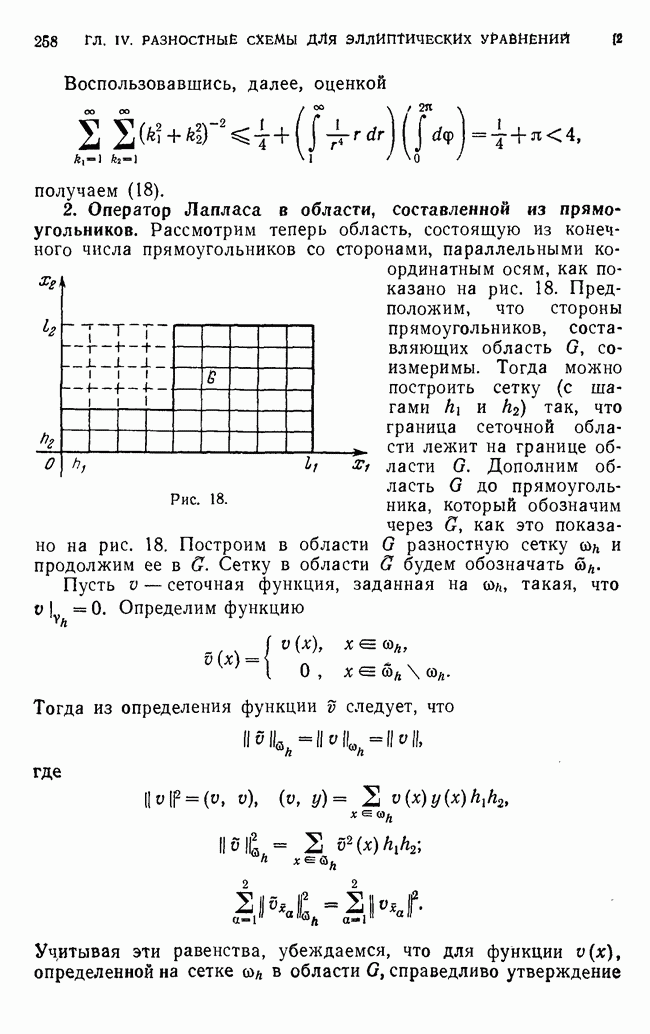
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка