| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
Рассмотрим уравнение более общего вида, чем (1):

К такому уравнению приводятся стационарные задачи диффузии с осевой симметрией  и с центральной симметрией
и с центральной симметрией 
При  ставится условие ограниченности
ставится условие ограниченности  (см. Добавление II в книге А. Н. Тихонова и А. А. Самарского [6]), которое эквивалентно условию
(см. Добавление II в книге А. Н. Тихонова и А. А. Самарского [6]), которое эквивалентно условию

При  ставится обычное краевое условие, например,
ставится обычное краевое условие, например,

Пусть  линейно независимые решения уравнения (139) при и
линейно независимые решения уравнения (139) при и  ограничено при
ограничено при  Тогда справедливы свойства:
Тогда справедливы свойства:
1) Если  конечны, то
конечны, то

2) Если  то производные
то производные  ограничены при
ограничены при
3) Второе, линейно независимое с  решение
решение  уравнения (139) имеет при
уравнения (139) имеет при  логарифмическую особенность.
логарифмическую особенность.
Условия (140) и (141) выделяют единственное решение уравнения (139). В силу свойства 1) условие (140) можно заменить требованием

Разностную схему для уравнения (139) напишем так, чтобы при  она формально переходила в схему (25):
она формально переходила в схему (25):

где 

 шаблонные функционалы, рассмотренные в п. 7.
шаблонные функционалы, рассмотренные в п. 7.
Краевое условие при  имеет вид
имеет вид

Покажем, что разностное краевое условие

аппроксимирует условие (140) с порядком  на решении уравнения (139), удовлетворяющем условию (140). В самом деле, погрешность аппроксимации условия (146), очевидно, равна
на решении уравнения (139), удовлетворяющем условию (140). В самом деле, погрешность аппроксимации условия (146), очевидно, равна

Подставляя сюда 

получаем

Из уравнения (139) имеем:

Так как  при
при  то
то  и
и

Отсюда и из формулы (147) следует, что

Разностное краевое условие (146) будем записывать в виде

Напишем условие для разности  где
где  решение задачи
решение задачи  решение задачи
решение задачи  Подставляя
Подставляя  получаем
получаем

где

погрешность аппроксимации схемы в классе решений  исходной задачи.
исходной задачи.
Напишем уравнение баланса для (139):

Вычитая это тождество из (150), будем иметь:

По условию, при  схема (143) принадлежит исходному семейству схем из п. 7, удовлетворяющих условиям второго порядка аппроксимации:
схема (143) принадлежит исходному семейству схем из п. 7, удовлетворяющих условиям второго порядка аппроксимации:

Найдем разложения  по степеням
по степеням  . Подставляя выражение
. Подставляя выражение

где  значение производной
значение производной  в некоторой средней точке интервала
в некоторой средней точке интервала  в формулу для
в формулу для  получаем
получаем

Вычислим коэффициенты при  При
При  имеем
имеем

При  имеем
имеем

Так как  неотрицательный функционал,
неотрицательный функционал,  при то
при то

Отсюда и из (155) следует, что для  справедливы формулы
справедливы формулы

Для наилучшей схемы

и, следовательно

Аналогичные формулы получаются для  Напишем теперь выражение для
Напишем теперь выражение для 

Из формулы (159) видно, что при 

Простейшие формулы для  очевидно, имеют вид
очевидно, имеют вид

В этом случае 
В дальнейшем будем предполагать, что  в нашей схеме определяются либо по этим формулам, либо по формулам (156) и (157) при условии, что
в нашей схеме определяются либо по этим формулам, либо по формулам (156) и (157) при условии, что  Тогда погрешность аппроксимации в классе
Тогда погрешность аппроксимации в классе  равна
равна

так как

В результате для  получаем формулу
получаем формулу

причем

Перейдем теперь к выводу априорной оценки для решения задачи (149) с правой частью (163).
Нам понадобится разностная функция Грина  которую определим как решение задачи (ср. с п. 8)
которую определим как решение задачи (ср. с п. 8)

Функция Грина  выражается формулой
выражается формулой

где  решения задач Коши:
решения задач Коши:

Отсюда видно, что  монотонно возрастает, а
монотонно возрастает, а  монотонно убывает.
монотонно убывает.
Изучение свойств функции  проводится по аналогии с
проводится по аналогии с  сначала устанавливаются оценки для функции
сначала устанавливаются оценки для функции  соответствующей случаю
соответствующей случаю  а затем применяется аналог леммы 1, в силу которого
а затем применяется аналог леммы 1, в силу которого

Если  то
то  находятся в явном виде
находятся в явном виде

Отсюда следует, что

Покажем, что справедливы следующие оценки

где  положительные постоянные, зависящие только от
положительные постоянные, зависящие только от 
Из сказанного выше следует, что достаточно установить эти оценки для функции  Рассмотрим сначала функцию
Рассмотрим сначала функцию

Пользуясь известным неравенством 

где  положительная убывающая функция, a и b — целые числа, суммирование ведется по целым
положительная убывающая функция, a и b — целые числа, суммирование ведется по целым  получаем
получаем

так как 

Рассмотрим теперь выражение
Так как  монотонно убывающая функция, то
монотонно убывающая функция, то  при
при  в силу (168), получим
в силу (168), получим

Далее, из определения  следует, что
следует, что

т. е.

Из формулы для  находим
находим  т. е.
т. е. 
Оценим скалярное произведение  следующим образом:
следующим образом:

Подставляя сюда оценки для  пользуясь неравенством (168), получаем
пользуясь неравенством (168), получаем

В самом деле,

Функция  принимает при
принимает при  наибольшее значение, равное
наибольшее значение, равное  а сумма оценивается так
а сумма оценивается так

так как  В результате получаем
В результате получаем

Решение задачи (149) при помощи функции Грина  выражается формулой
выражается формулой

В этом можно убедиться непосредственно путем подстановки выражения (170) в уравнение (149).
Подставим в (170) выражение (163) для  и воспользуемся формулой суммирования по частям:
и воспользуемся формулой суммирования по частям:

Учитывая  получим:
получим:

Выберем наибольшую из постоянных  и обозначим ее
и обозначим ее  Тогда обе оценки можно объединить:
Тогда обе оценки можно объединить:

Так как  при
при  то схема
то схема  сходится со скоростью
сходится со скоростью  при
при 
Пусть теперь  и
и  -разрывные функции. Выберем неравномерную сетку
-разрывные функции. Выберем неравномерную сетку  так, чтобы точки разрыва функций
так, чтобы точки разрыва функций  были узловыми точками сетки. Разностная схема для задачи (139) — (141) будет иметь вид
были узловыми точками сетки. Разностная схема для задачи (139) — (141) будет иметь вид

Коэффициент  определяются по формуле
определяются по формуле

где 
При  отсюда следует известная формула (см. п. 13)
отсюда следует известная формула (см. п. 13)

Изложенным выше методом можно получить априорную оценку для  и через погрешность аппроксимации
и через погрешность аппроксимации  из этой оценки следует, чтосхема (172) — (173) имеет второй порядок точности на сетке
из этой оценки следует, чтосхема (172) — (173) имеет второй порядок точности на сетке  в классе разрывных коэффициентов
в классе разрывных коэффициентов 
Рассмотрим схему второго типа — «схему на потоковой сетке». Разобьем отрезок [0, 1] на  частей, введя узлы (потоковые точки):
частей, введя узлы (потоковые точки):

Пусть  значения искомой сеточной функции в этих узлах.
значения искомой сеточной функции в этих узлах.
Для получения разностной схемы воспользуемся уравнением баланса для (139). Рассматривая уравнение баланса для интервала  получаем
получаем

где

Из уравнения баланса для интервала 

и условия  следует разностное уравнение при
следует разностное уравнение при 

где  определяются по формулам (175.
определяются по формулам (175.
При  ставится обычное условие
ставится обычное условие

В результате получаем разностное уравнение (174) с краевыми условиями (176) и (177).
Пусть  решение этой задачи. Для погрешности
решение этой задачи. Для погрешности  и получим следующую задачу:
и получим следующую задачу:

где  погрешность аппроксимации, равная
погрешность аппроксимации, равная

Отсюда и из уравнения баланса для интервала  следует, что
следует, что

где

Полагая  при
при  при
при  получаем для
получаем для  следующую формулу:
следующую формулу:

где

Вводя разностную функцию Грина при помощи условий

получим для  и следующее выражение:
и следующее выражение:

где

Подставляя сюда выражение для  находим:
находим:

В силу ограниченности  получаем
получаем

Отсюда и из оценок (179) следует, что схема  имеет второй порядок точности, если
имеет второй порядок точности, если 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
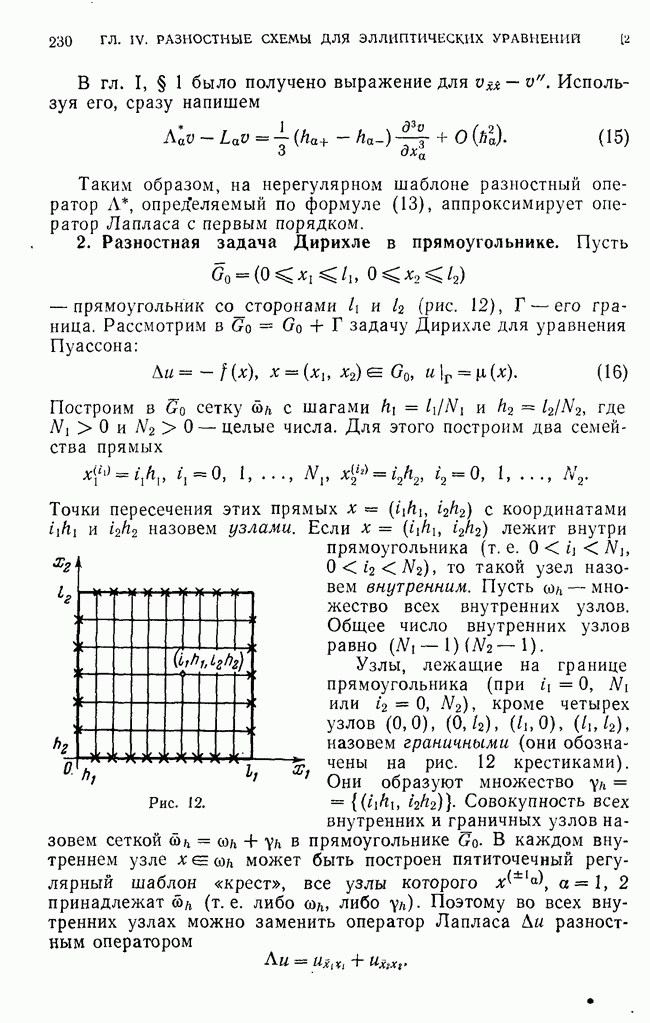
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка