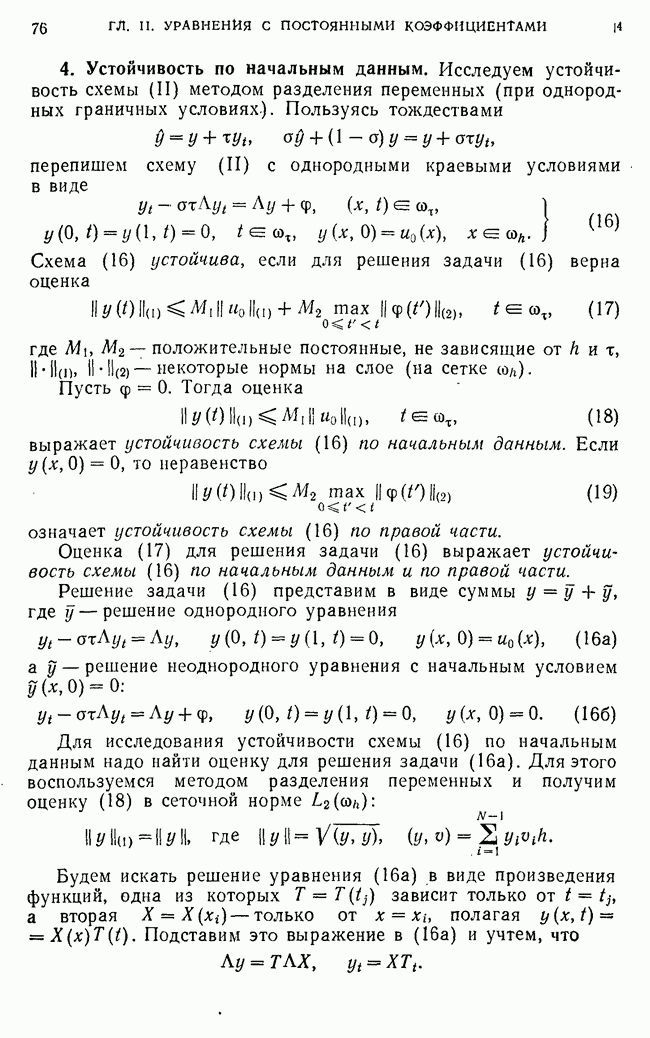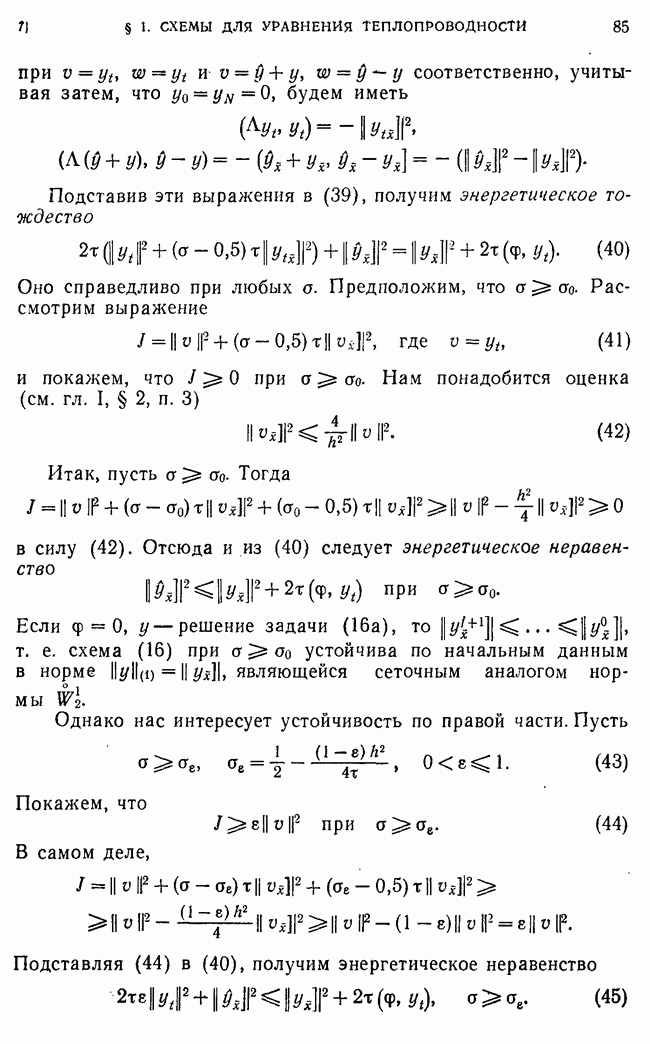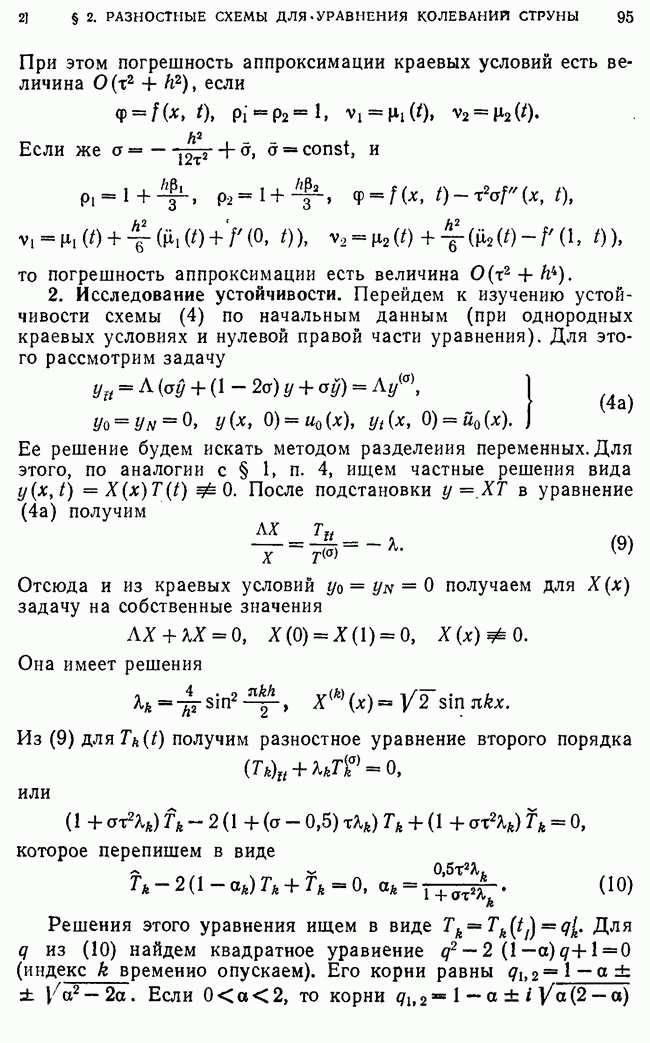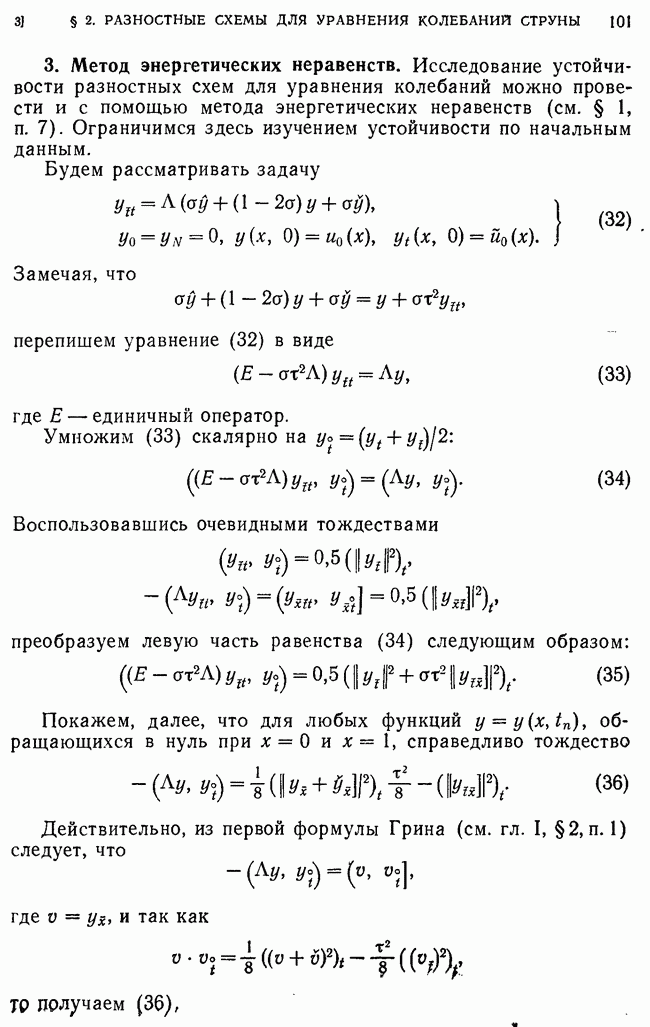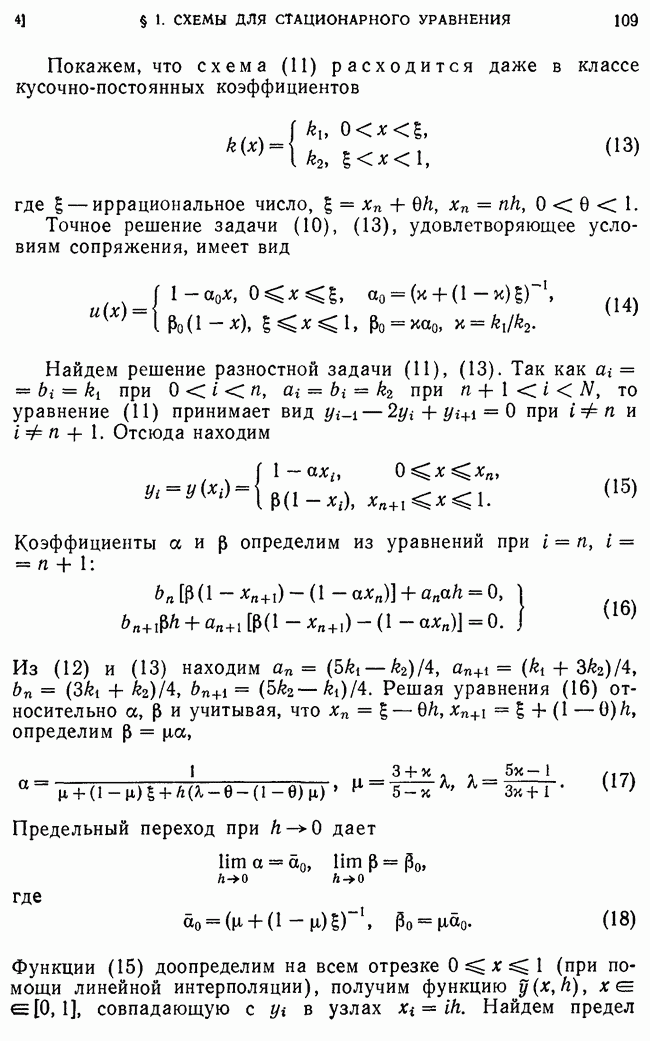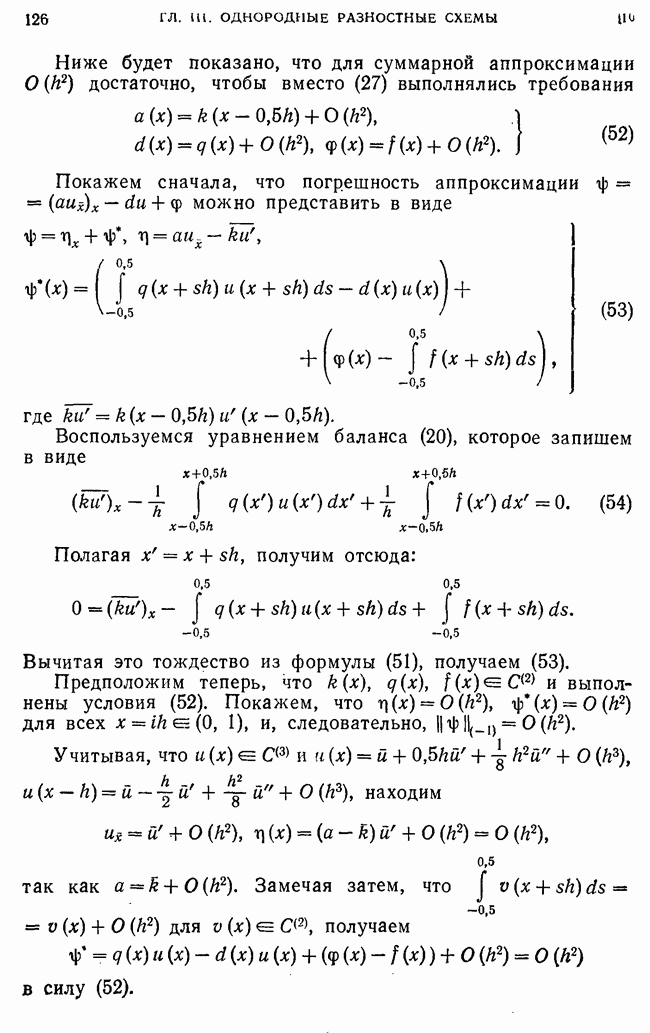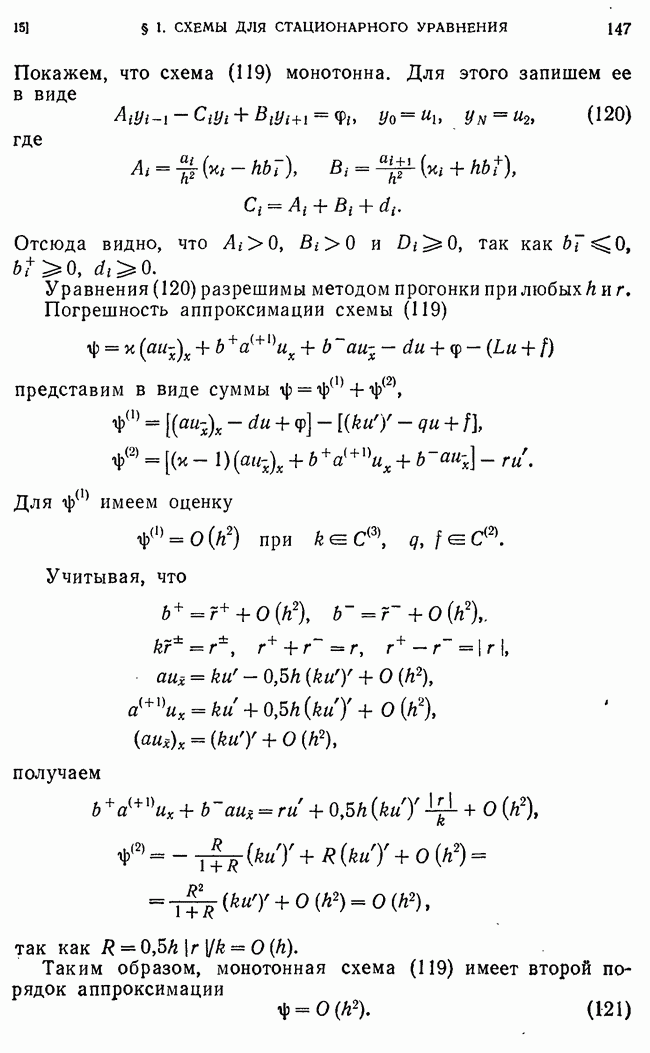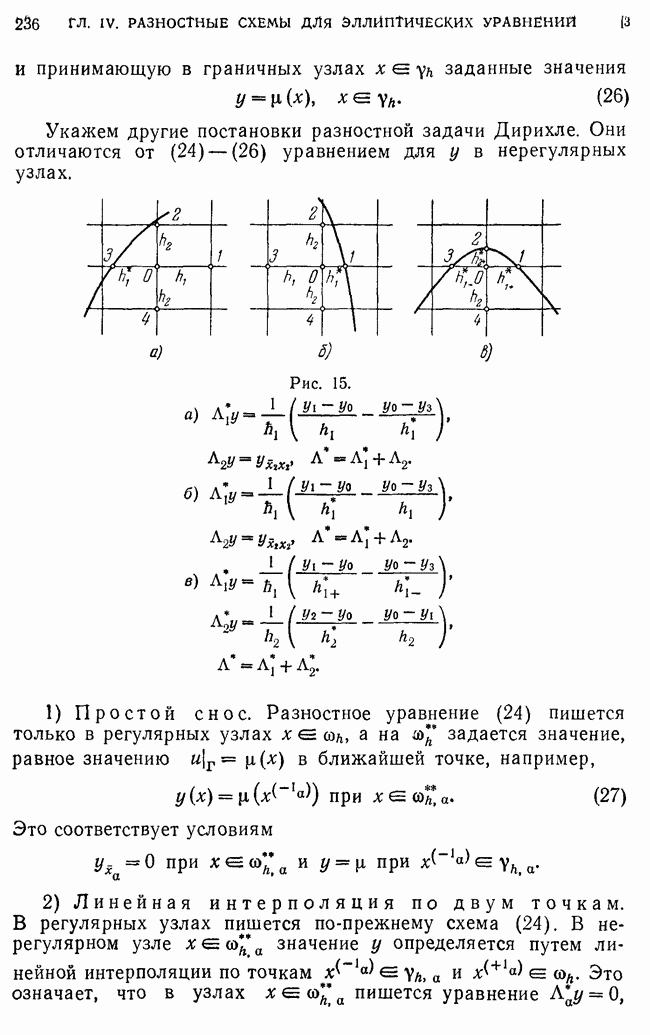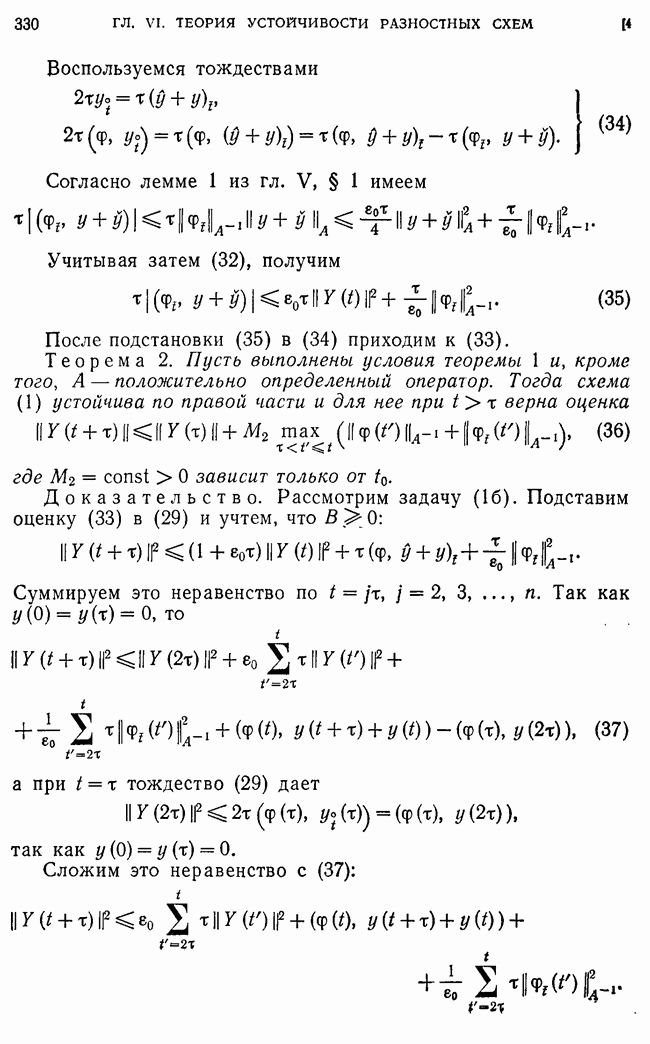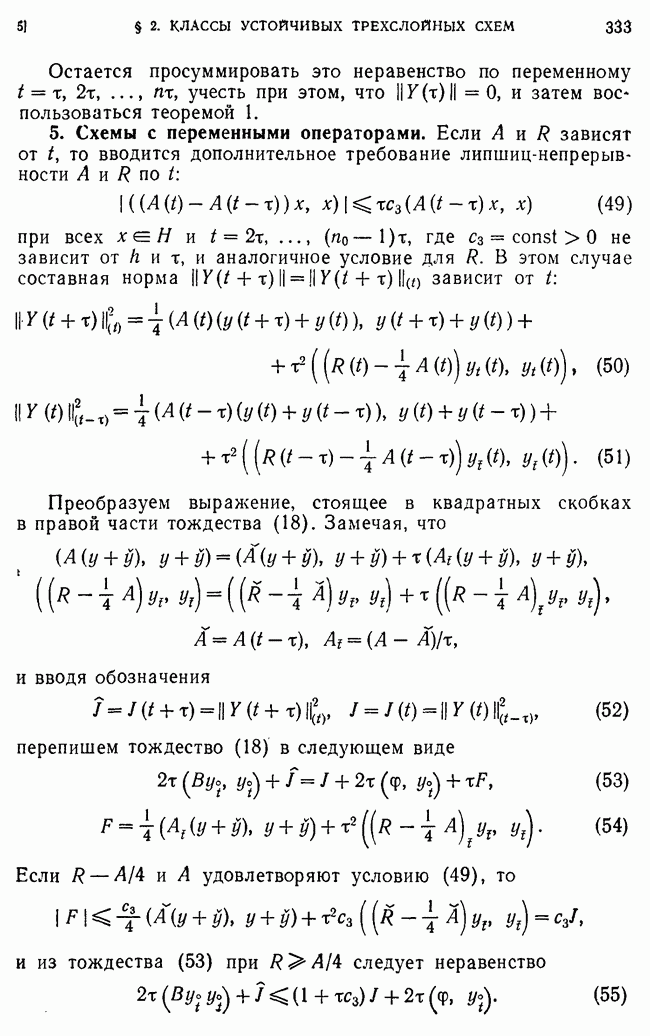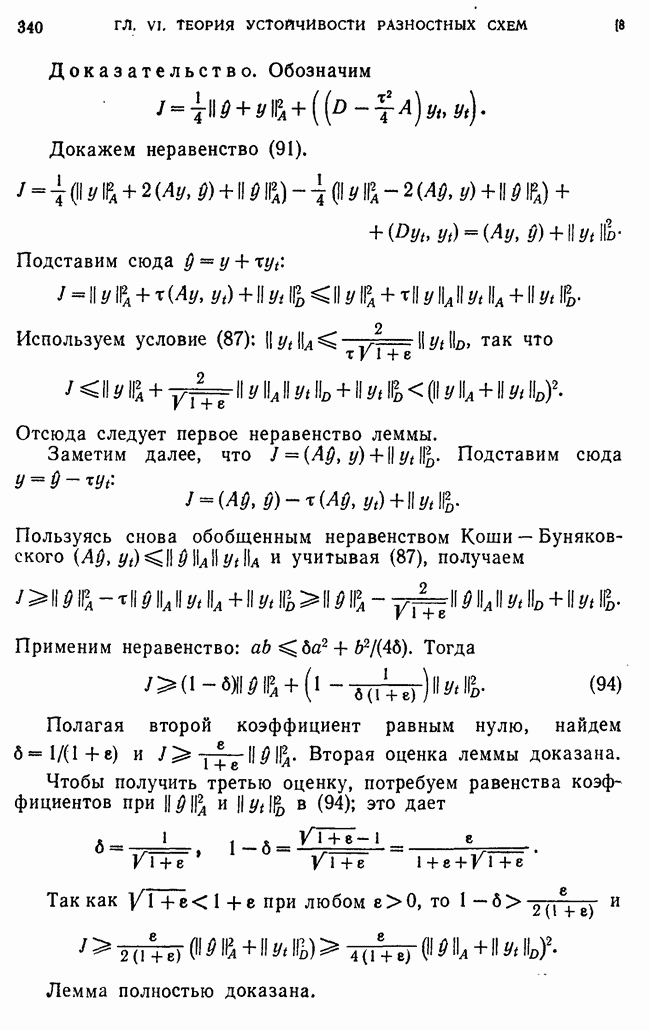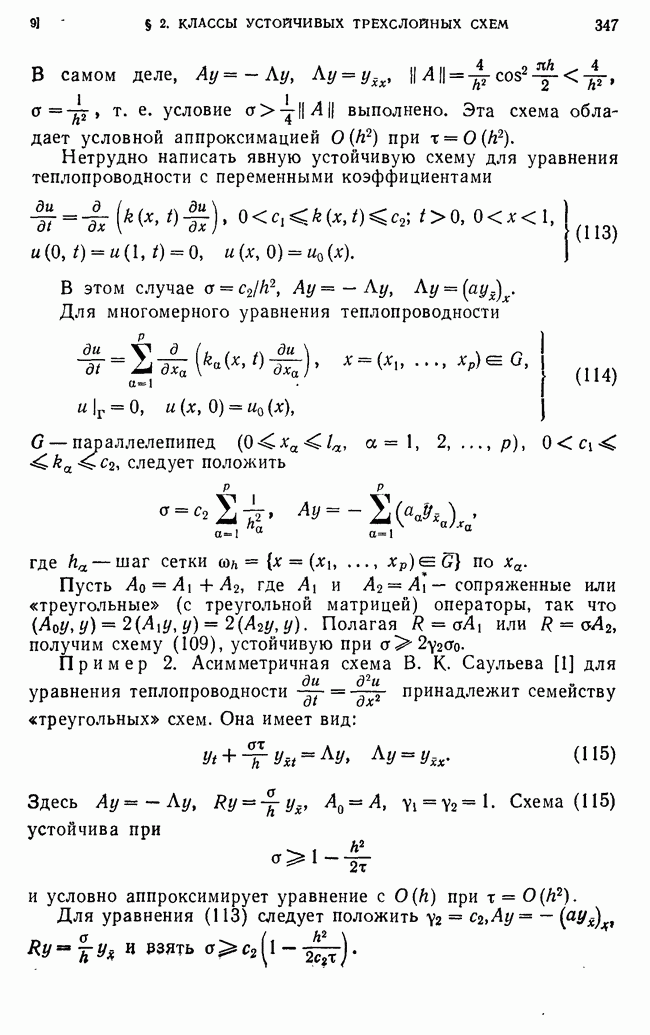| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8. Равномерная сходимость локально-одномерной схемы.
Докажем следующую теорему.
Теорема 3. Пусть задача (33) имеет единственное непрерывное в  решение
решение  и существуют непрерывные в
и существуют непрерывные в  производные
производные

Тогда схема (37), (38) равномерно сходится со скоростью  (имеет первый порядок точности по х и второй порядок точности по
(имеет первый порядок точности по х и второй порядок точности по  так что
так что

где  не зависит от
не зависит от 
Доказательство. Представим решение  задачи (39) в виде суммы
задачи (39) в виде суммы  где
где  определяется условиями
определяется условиями

Отсюда находим  для всех
для всех  так как
так как  Для
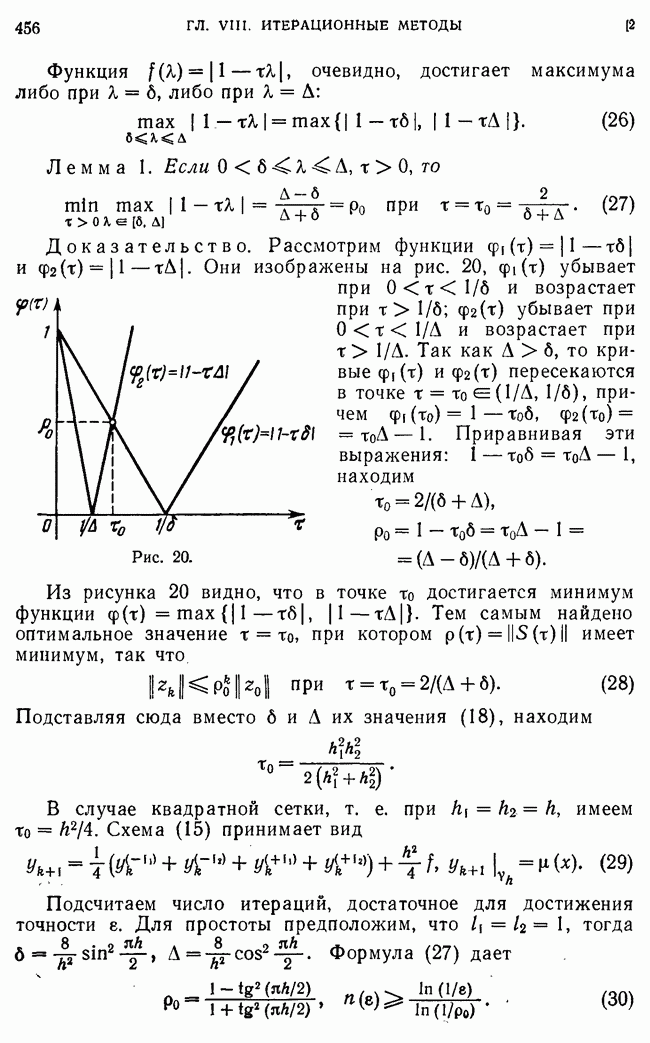
Для  получаем
получаем

Для  получаем задачу
получаем задачу

где 
Воспользуемся теперь теоремой 2 для оценки решения задачи (60). Так как  при
при  и при то
и при то

Рассмотрим  В строго внутренних узлах
В строго внутренних узлах 

если существуют непрерывные производные 

В приграничных узлах лгеюа имеем (для определенности считаем, что  :
:

В п. 7 было показано, что в таком узле  следовательно,
следовательно,

Учитывая затем, что

и  получаем
получаем  что и требовалось доказать. Из устойчивости по краевым данным и по правой части следует произвол в выборе
что и требовалось доказать. Из устойчивости по краевым данным и по правой части следует произвол в выборе  (см. стр. 416).
(см. стр. 416).
Таким образом, мы провели исчерпывающее исследование локально-одномерной схемы.
Замечание. Схема (37), (38) была исследована в работе автора [7]. В приграничных узлах  а значение
а значение  можно определять при помощи интерполяции по направлению
можно определять при помощи интерполяции по направлению  (ср. А. А. Самарский [4]), что соответствует требованию
(ср. А. А. Самарский [4]), что соответствует требованию

Принцип максимума верен и в этом случае; имеет место теорема 2.
При оценке скорости сходимости локально-одномерной схемы функцию  определяем так же, как и выше, полагая
определяем так же, как и выше, полагая  во всех внутренних узлах
во всех внутренних узлах  где
где

Тогда для  получаем задачу
получаем задачу

где

Дальнейшие рассуждения практически совпадают с рассуждениями, проведенными выше. В результате убеждаемся, что и в этом случае верна теорема 3, т. е. локально-одномерная схема равномерно сходится со скоростью  где
где 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
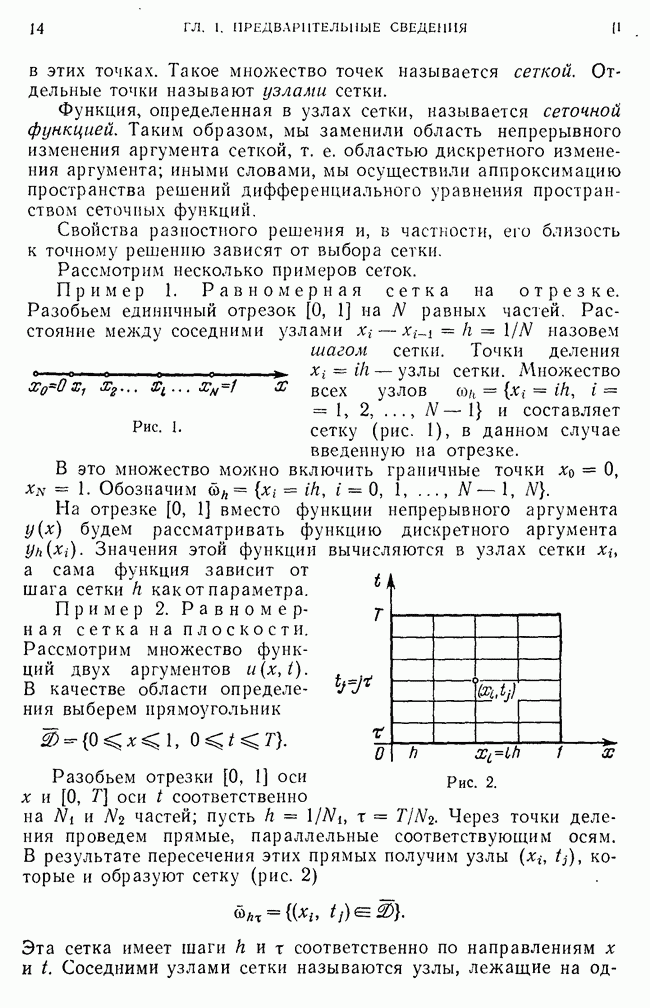
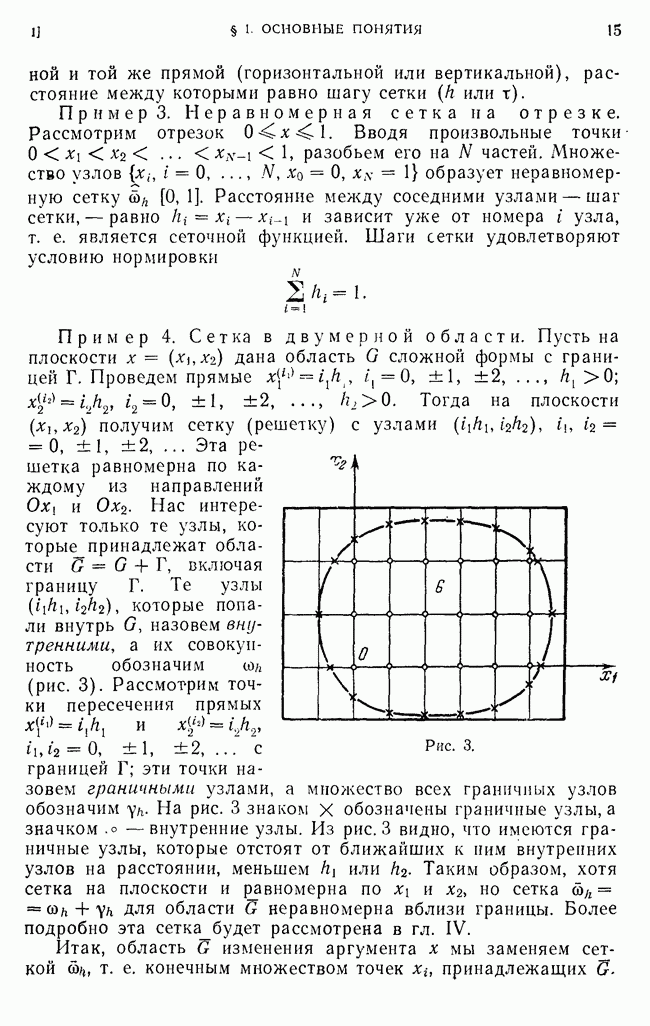
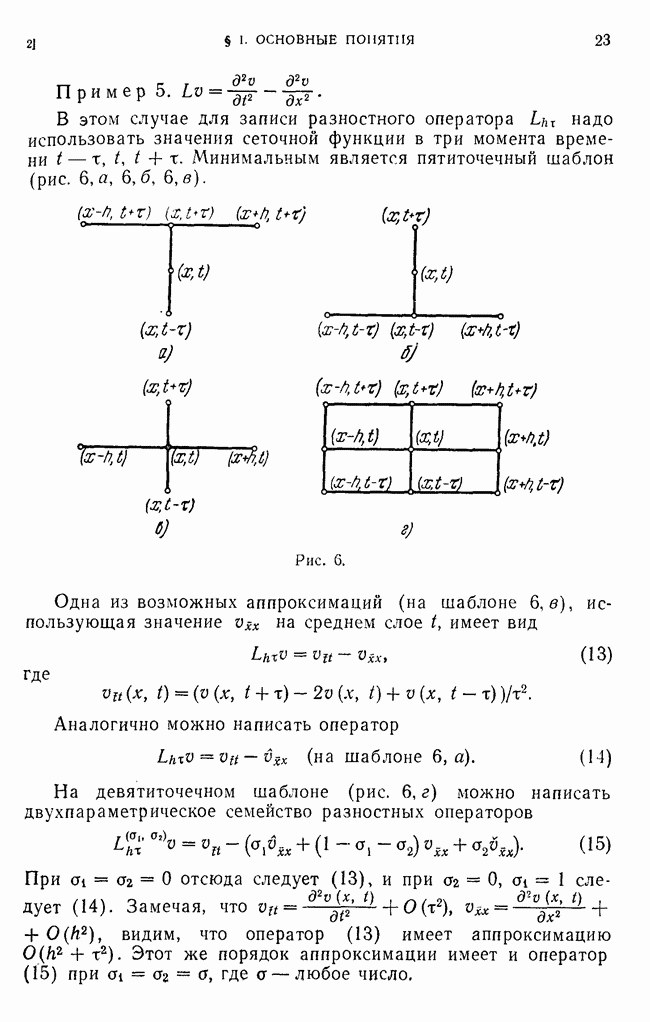
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
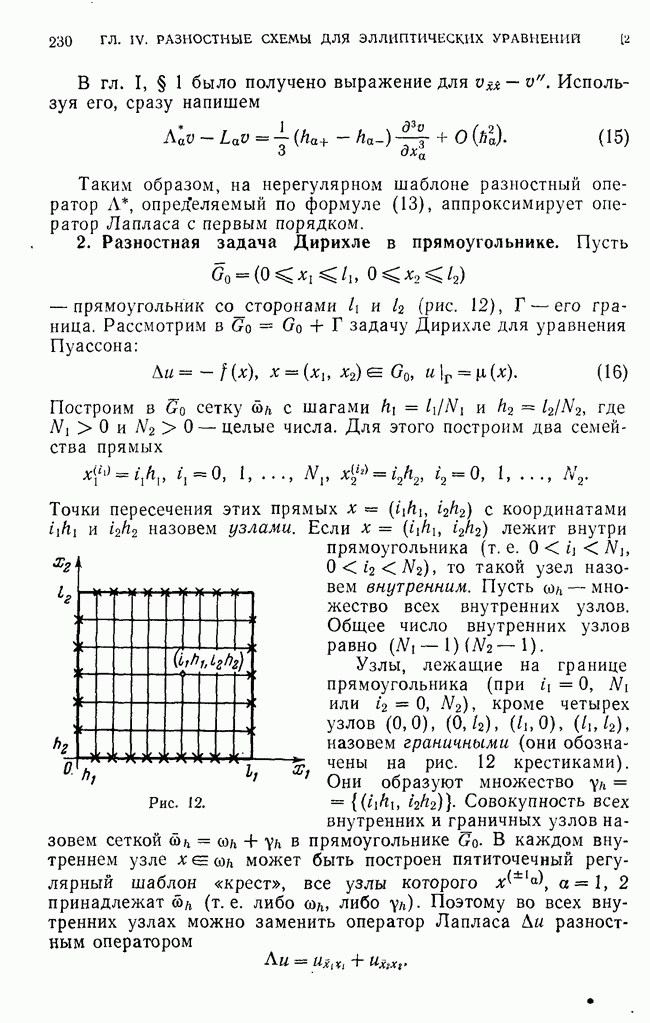
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
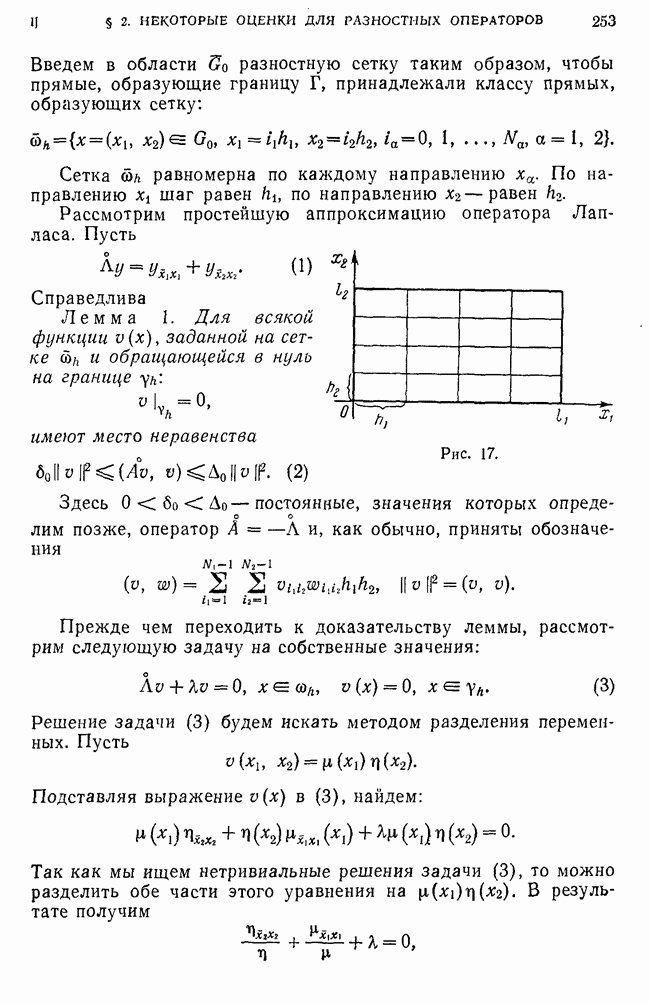
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
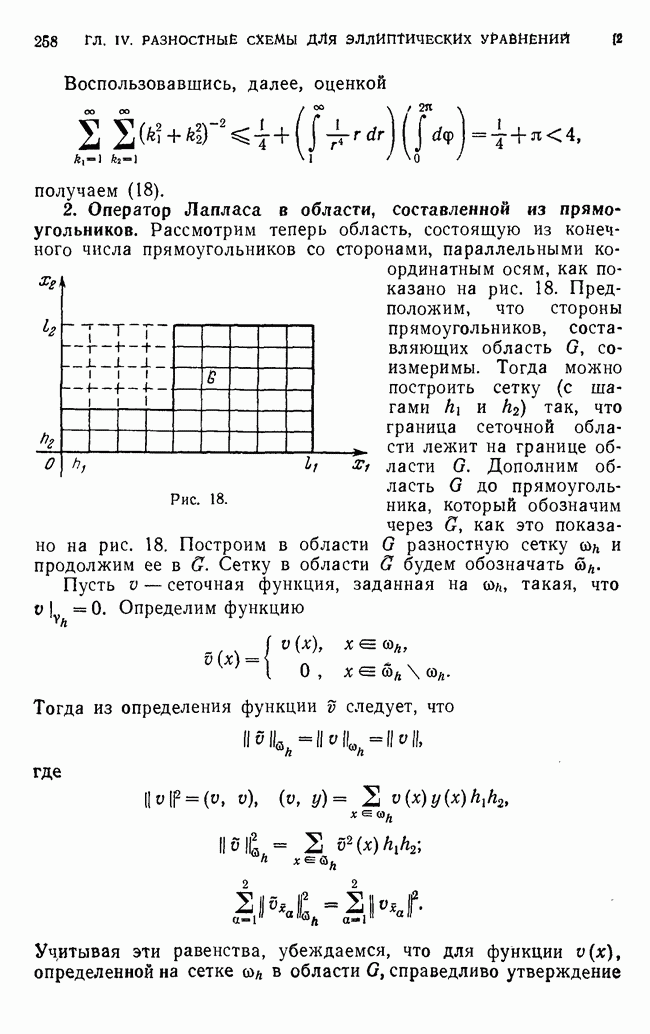
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка