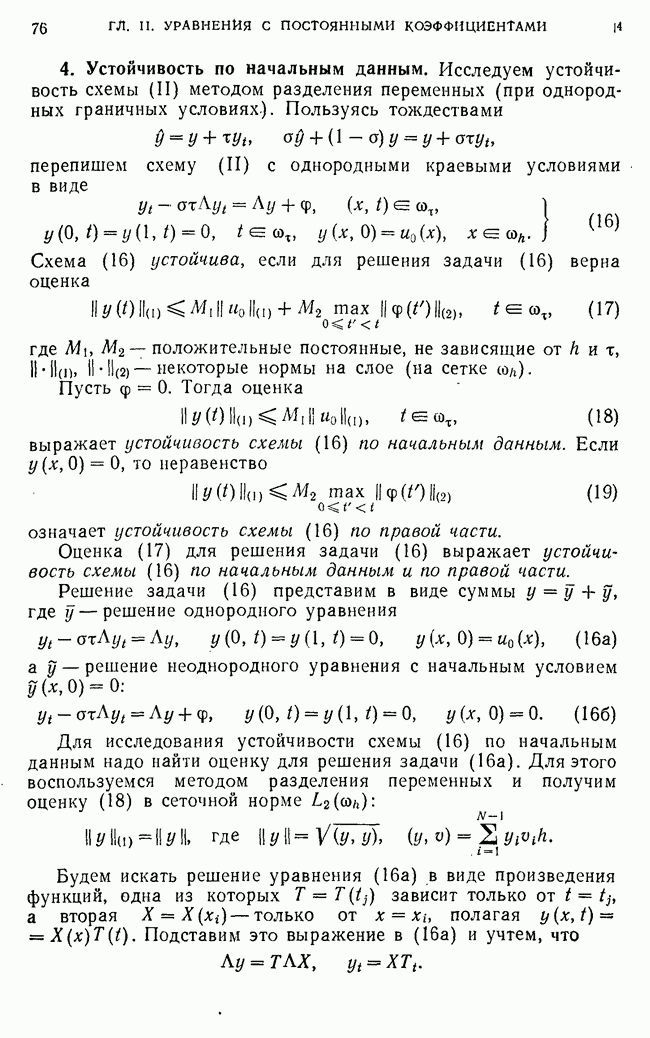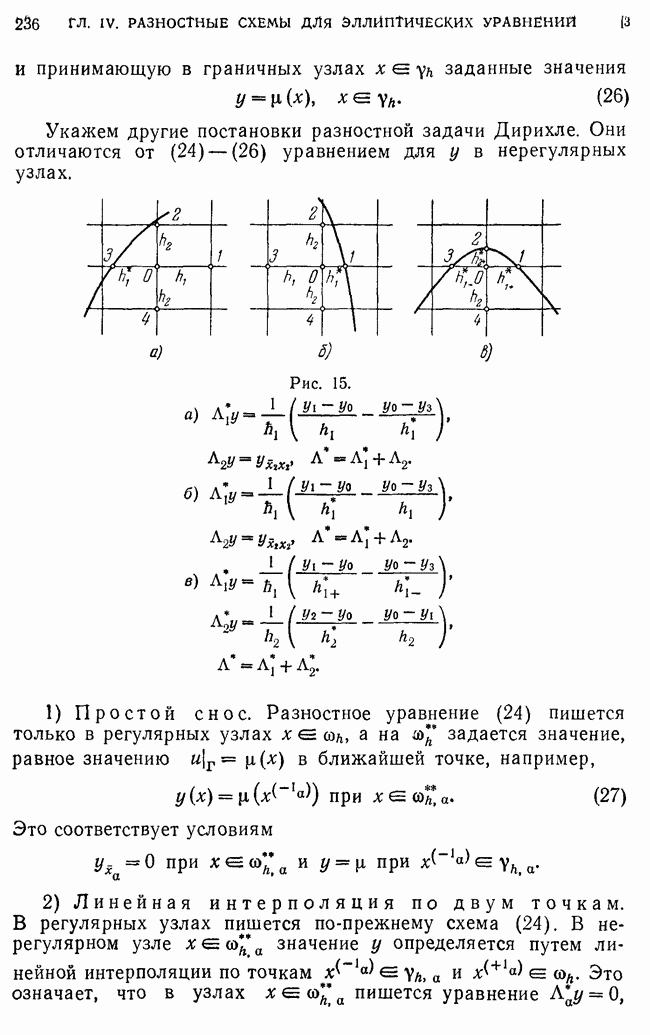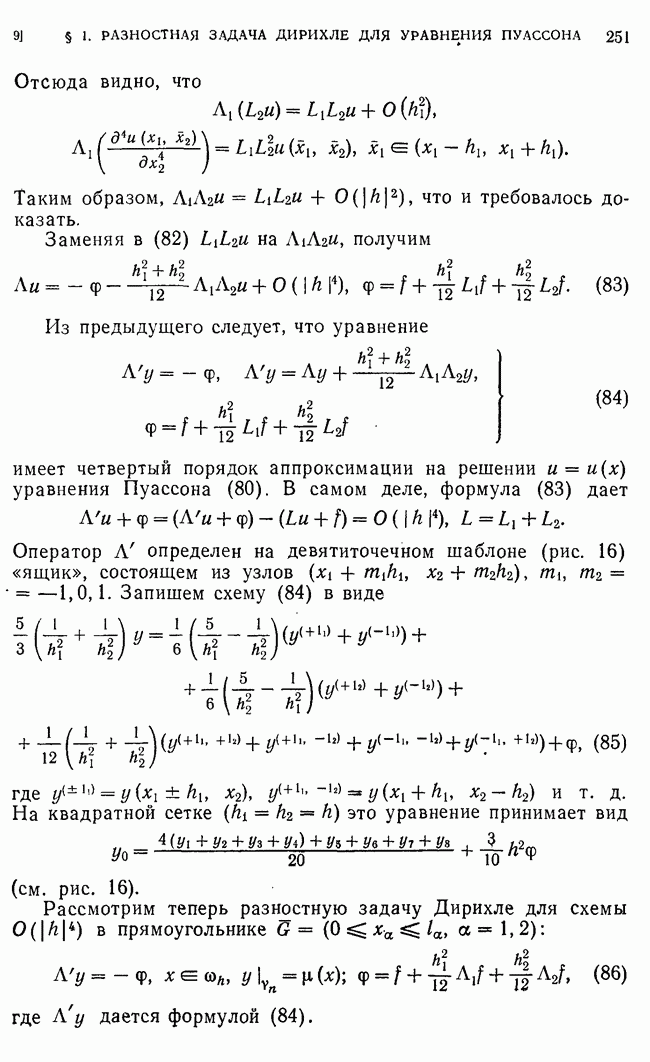| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Метод суммарной аппроксимации
1. Составные схемы. Суммарная аппроксимация.
Экономичные методы, рассмотренные в § 1 и § 2, характеризуются тем, что исходное многомерное дифференциальное уравнение аппроксимируется факторизованной разностной схемой. Решение разностной задачи для факторизованной схемы сводится к последовательному решению разностных задач более простой структуры. Так, в случае двух переменных применяются экономичные схемы вида

где и  экономичные операторы (обычно это — одномерные операторы). Для продольно-поперечной схемы
экономичные операторы (обычно это — одномерные операторы). Для продольно-поперечной схемы

для схемы расщепления

Принципиальным является требование эквивалентности задачи (1) факторизованной схеме

Эта эквивалентность имеет место не всегда, а лишь при согласованном задании правых частей и краевых значений для  Кроме того, иногда требуется попарная перестановочность
Кроме того, иногда требуется попарная перестановочность  (см. § 2). Устойчивость факторизованной схемы имеет место, если
(см. § 2). Устойчивость факторизованной схемы имеет место, если  перестановочны. Это выполняется только для областей специального типа.
перестановочны. Это выполняется только для областей специального типа.
Схемы, рассматриваемые в § 1 и § 2, применялись только для прямоугольных областей.
Между тем, очевидно, что схема расщепления и продольно-поперечная схема могут быть формально написаны для непрямоугольных областей сложной формы. Однако при этом возникают трудности с определением аппроксимации, заданием краевых условий и доказательством устойчивости. Чтобы преодолеть эти трудности (они, впрочем, как мы видели в § 2, имеются даже в случае прямоугольной области), оказалось необходимым провести пересмотр понятия разностной схемы и, прежде всего, отказаться от сведения системы уравнений (1) к факторизованной схеме (2) и от требования их эквивалентности. Это привело к новому понятию разностной схемы, к понятию аддитивной схемы (см. А. А. Самарский [4], [5], [7], [12], [19]).
Систему двух разностных уравнений (1), осуществляющих переход со слоя  к слою
к слою  будем называть составной схемой. Для составной схемы следует прежде всего дать определение аппроксимации, выяснить, в каком смысле она аппроксимирует исходное дифференциальное уравнение.
будем называть составной схемой. Для составной схемы следует прежде всего дать определение аппроксимации, выяснить, в каком смысле она аппроксимирует исходное дифференциальное уравнение.
Пусть  — решение многомерного дифференциального уравнения. Вычислим погрешность аппроксимации
— решение многомерного дифференциального уравнения. Вычислим погрешность аппроксимации  на решении и для каждой из схем (1) соответственно. Назовем погрешностью аппроксимации составной схемы (1) сумму
на решении и для каждой из схем (1) соответственно. Назовем погрешностью аппроксимации составной схемы (1) сумму  Требование аппроксимации для составной схемы (1) означает, что
Требование аппроксимации для составной схемы (1) означает, что  при
при  где
где  некоторая норма. При этом может оказаться, что
некоторая норма. При этом может оказаться, что 
Составные схемы, погрешность аппроксимации для которых понимается как сумма погрешностей аппроксимации для промежуточных схем, будем называть аддитивными схемами.
Дадим общее определение аддитивной схемы  Самарский [19], И. В. Фрязинов [4]).
Самарский [19], И. В. Фрязинов [4]).
В гл. V было введено понятие  -слойной разностной схемы как разностного (по переменному
-слойной разностной схемы как разностного (по переменному  уравнения
уравнения 
порядка с операторными коэффициентами:

где  — линейные операторы, заданные на линейном нормированном пространстве Ни. Для определения решения надо задать
— линейные операторы, заданные на линейном нормированном пространстве Ни. Для определения решения надо задать  начальных векторов
начальных векторов 
Назовем  -слойной составной схемой с периодом от (порядка
-слойной составной схемой с периодом от (порядка  систему разностных уравнений с операторными коэффициентами
систему разностных уравнений с операторными коэффициентами

где  с заданными начальными значениями
с заданными начальными значениями  (число слоев определяется числом начальных условий), причем
(число слоев определяется числом начальных условий), причем  принимает значения, равные
принимает значения, равные

Чтобы найти  по известным
по известным  где
где  надо решить систему уравнений с операторной матрицей
надо решить систему уравнений с операторной матрицей  размером
размером 
При  составная схема
составная схема  переходит в написанную выше обычную
переходит в написанную выше обычную  -слойную схему. При
-слойную схему. При  получаем двухслойную составную схему с периодом
получаем двухслойную составную схему с периодом 

Если для составной схемы  погрешность аппроксимации определяется как сумма погрешностей аппроксимации отдельных уравнений,
погрешность аппроксимации определяется как сумма погрешностей аппроксимации отдельных уравнений,  то составная схема
то составная схема  называется аддитивной схемой.
называется аддитивной схемой.
Двухслойная аддитивная схема может быть записана в каноническом виде:

где  некоторые линейные операторы.
некоторые линейные операторы.
Экономичные аддитивные схемы характеризуются тем, что для них операторная матрица перехода  является треугольной, так что систему уравнений (3) можно записать в виде:
является треугольной, так что систему уравнений (3) можно записать в виде:

Схема (1) соответствует частному случаю, когда  матрица.
матрица.
Пусть  погрешность аппроксимации на решении и исходного уравнения для одного уравнения (3) номера а. Погрешность аппроксимации для аддитивной схемы (3) определяется как сумма
погрешность аппроксимации на решении и исходного уравнения для одного уравнения (3) номера а. Погрешность аппроксимации для аддитивной схемы (3) определяется как сумма

Нетрудно убедиться в том, что все экономичные методы, записанные в виде (3) и трактуемые как аддитивные схемы, обладают суммарной аппроксимацией.
Мы рассмотрим лишь простейшие примеры аддитивных схем вида

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
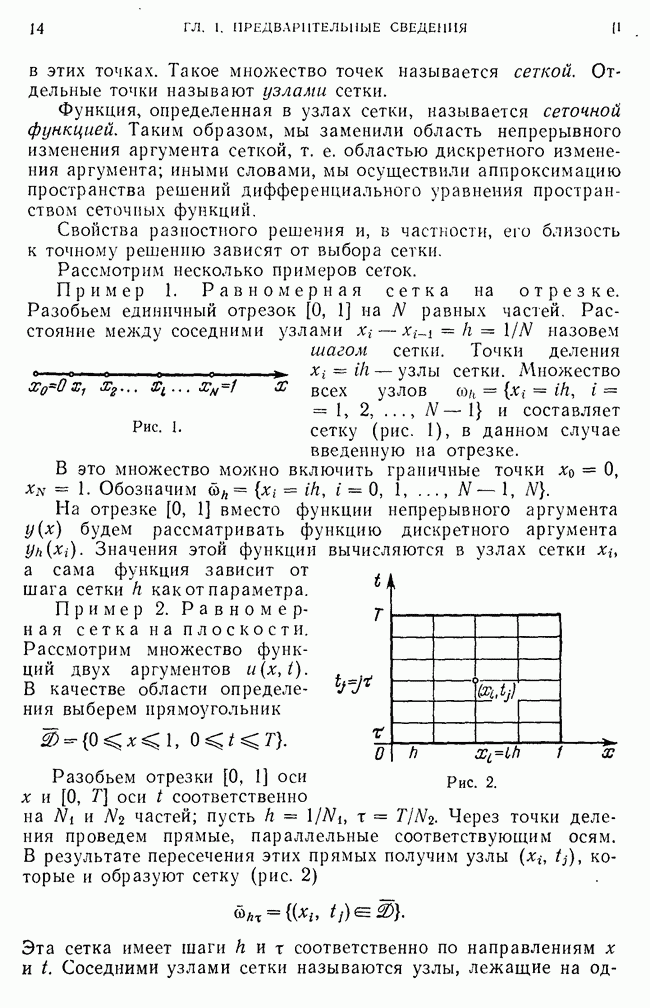
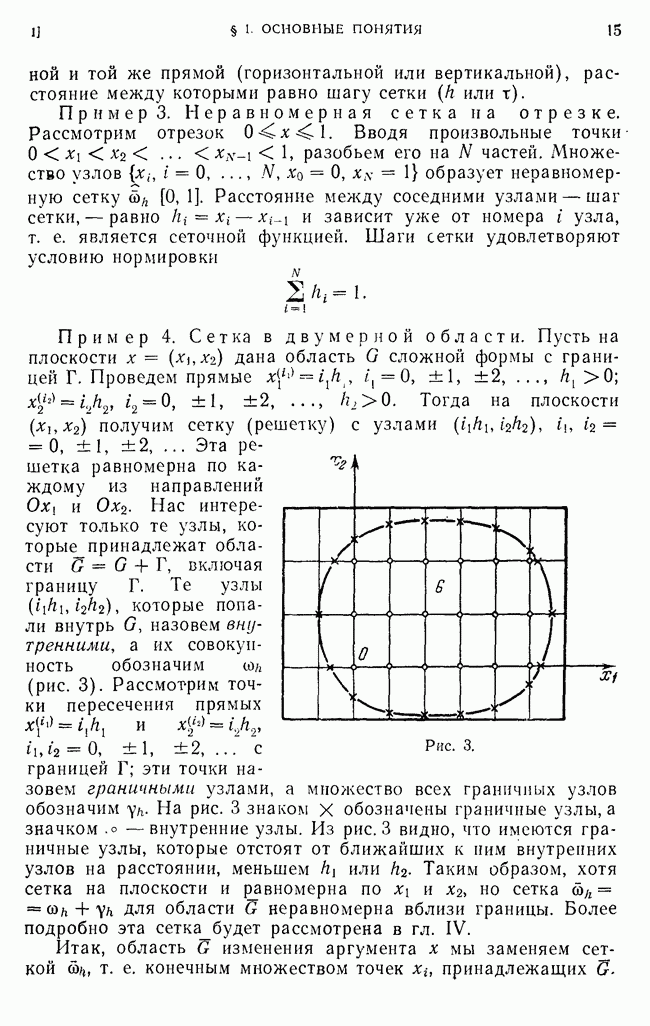
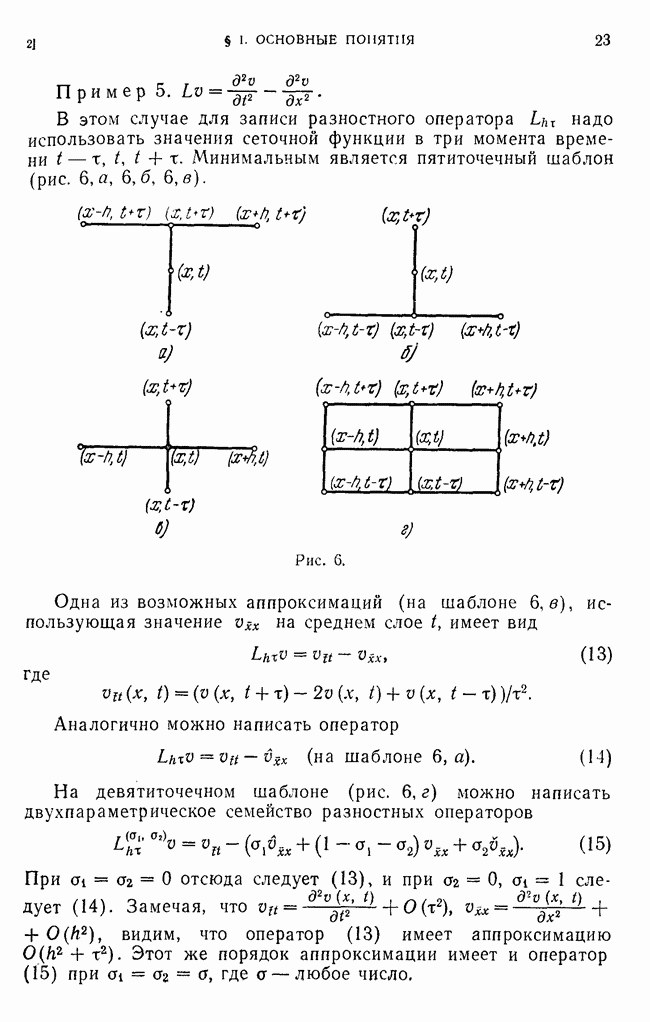
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
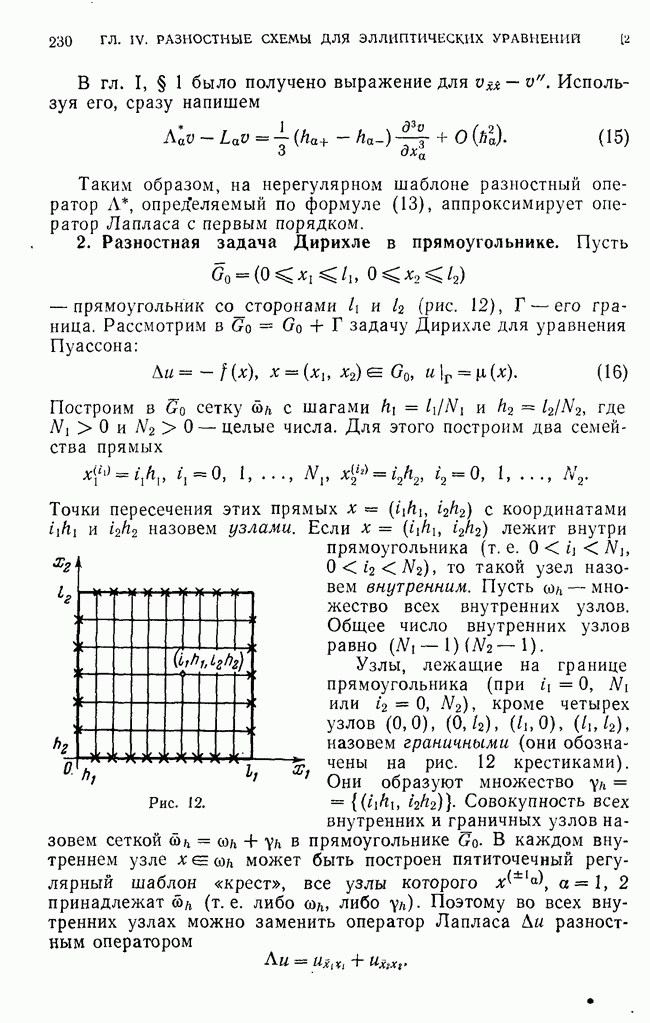
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
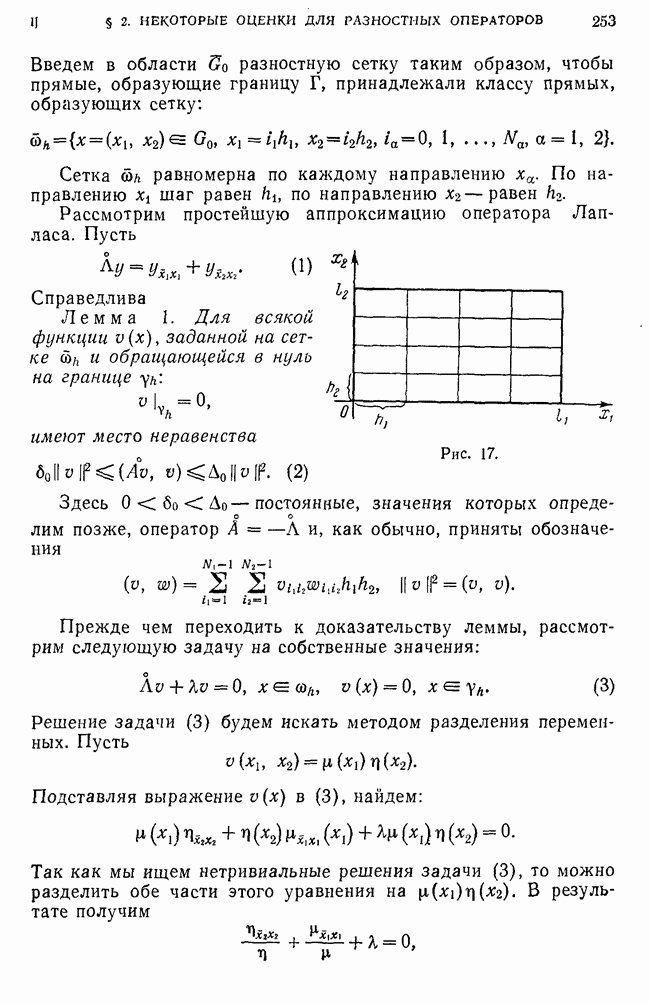
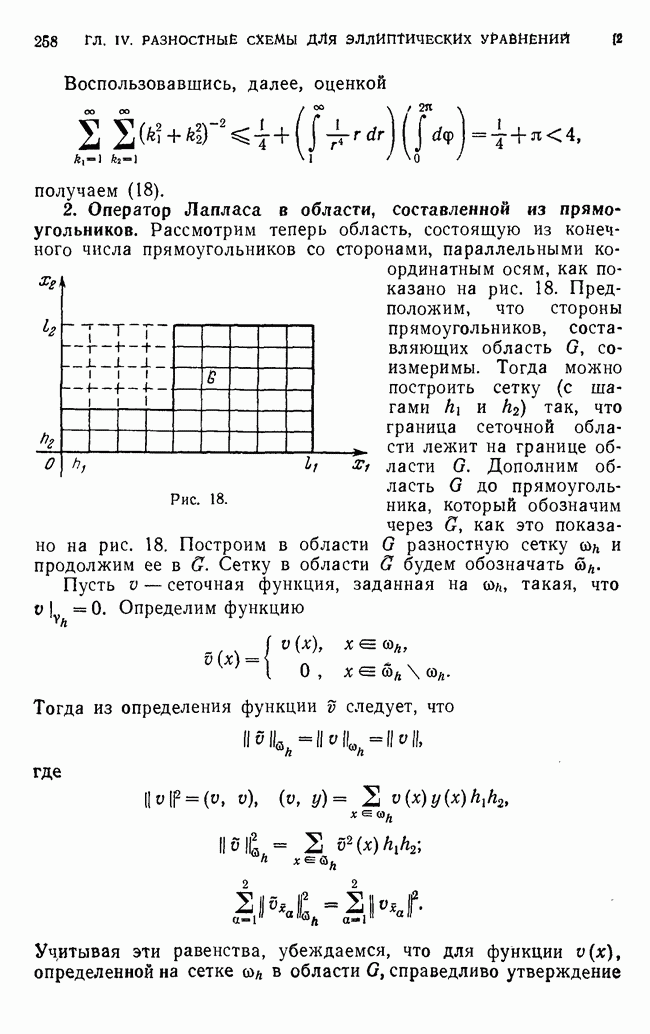
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка