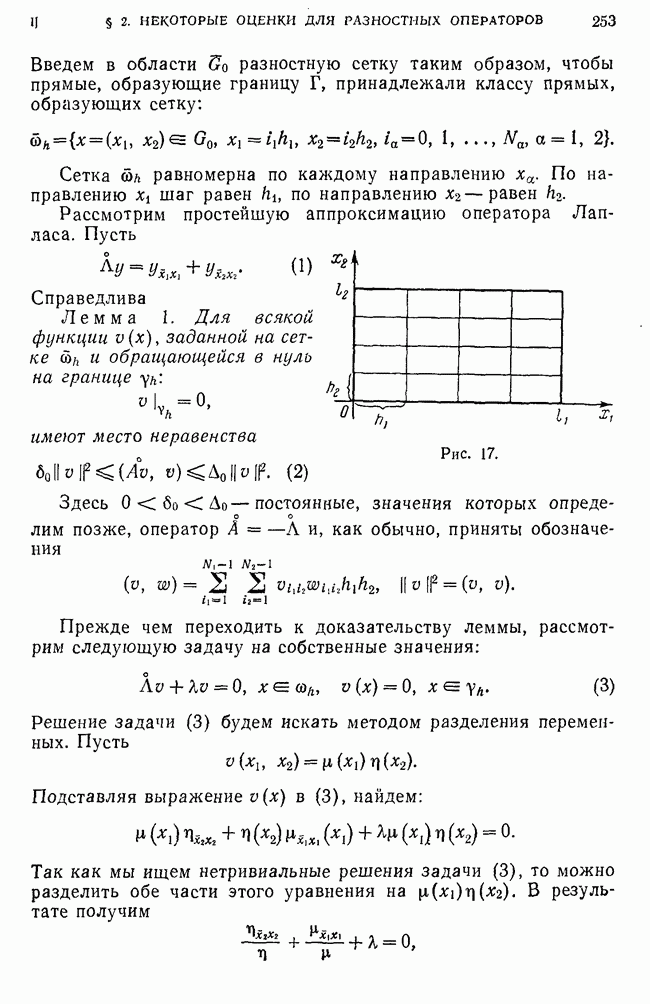
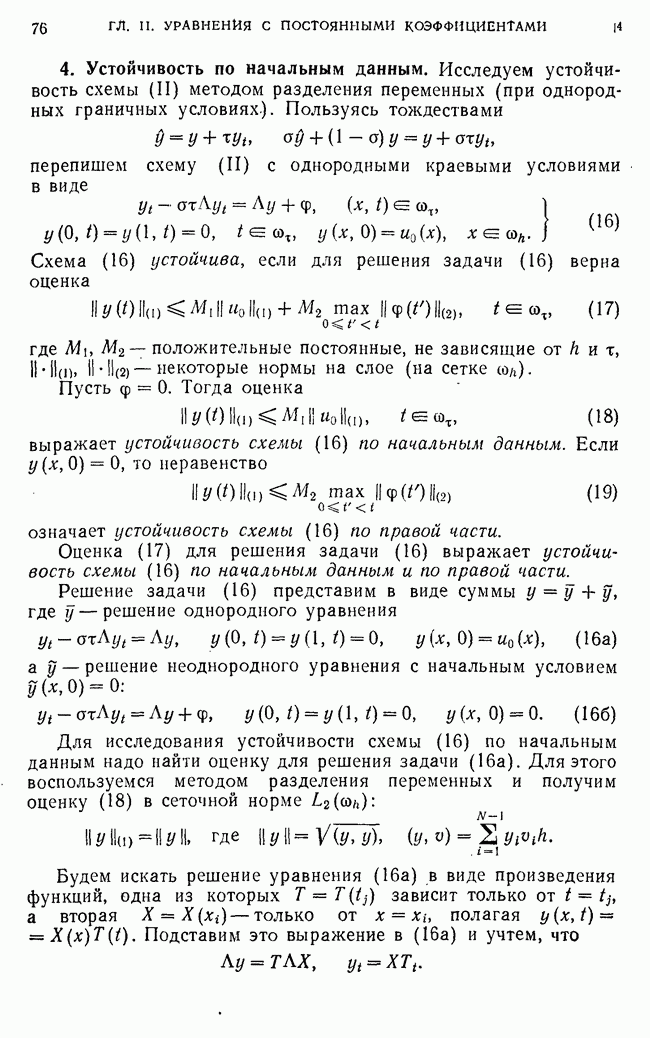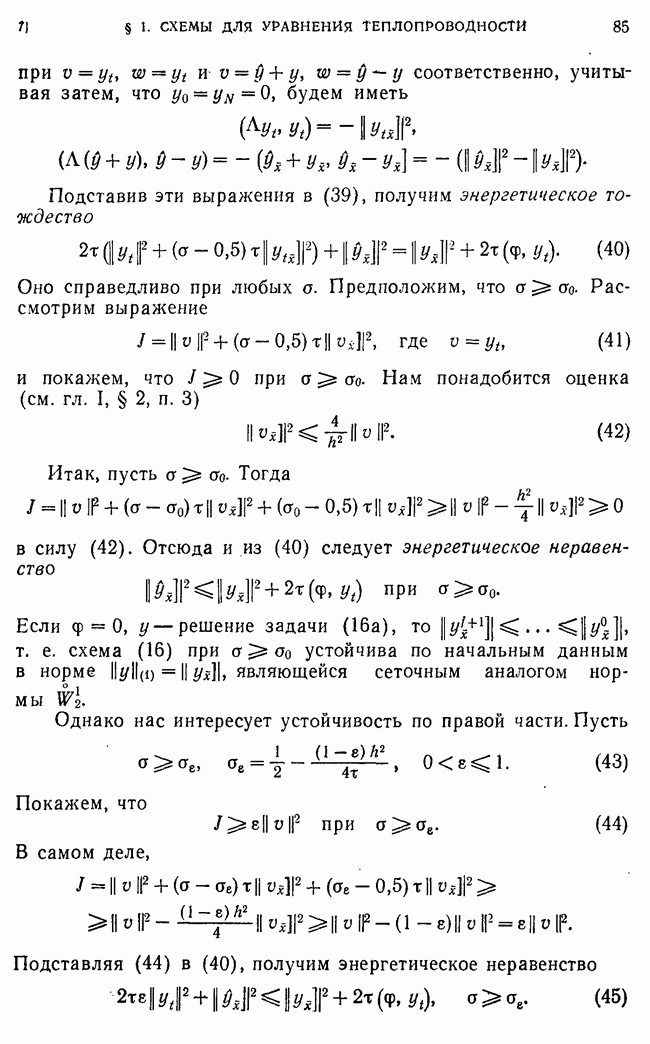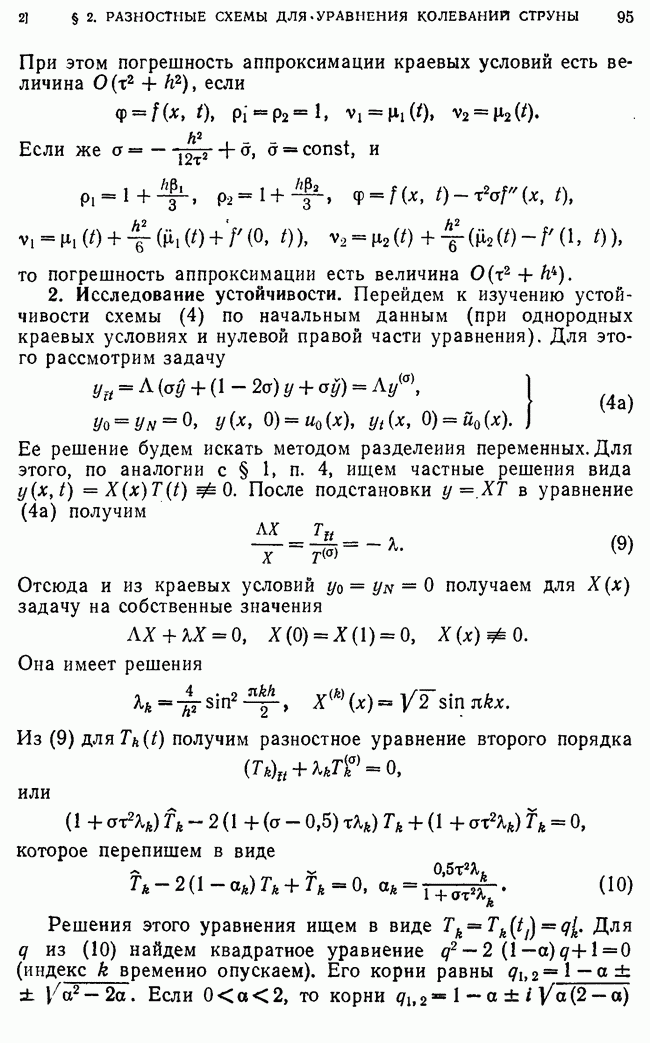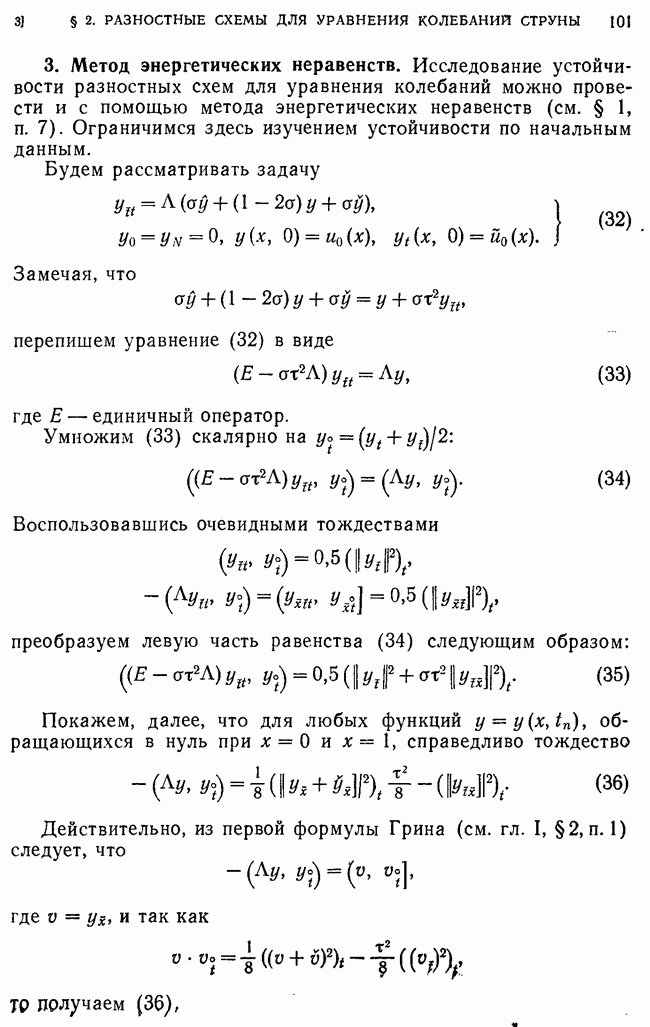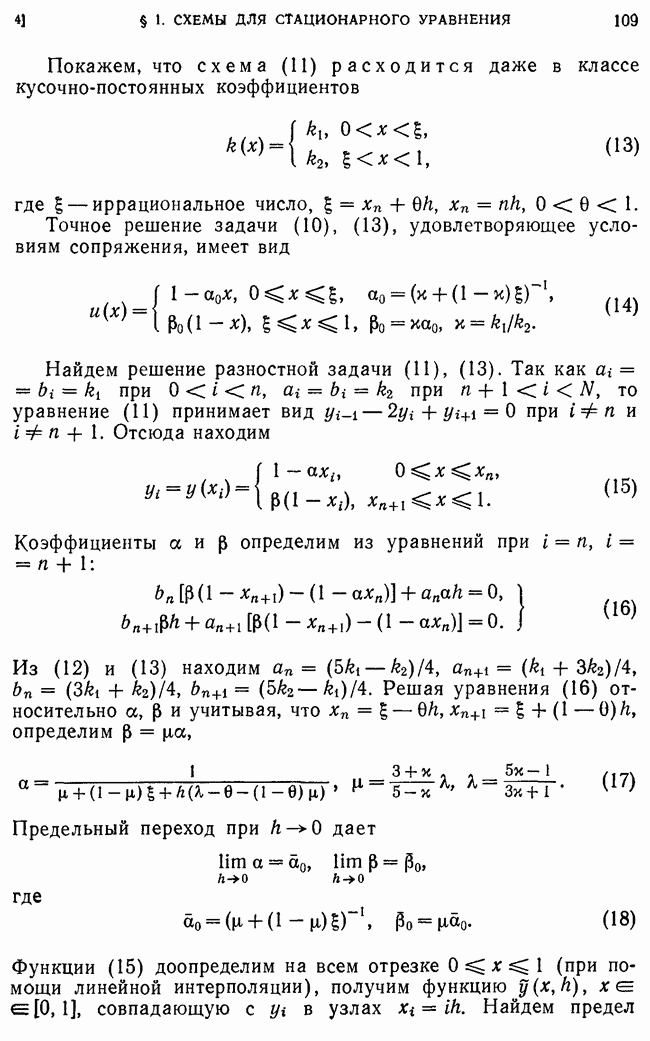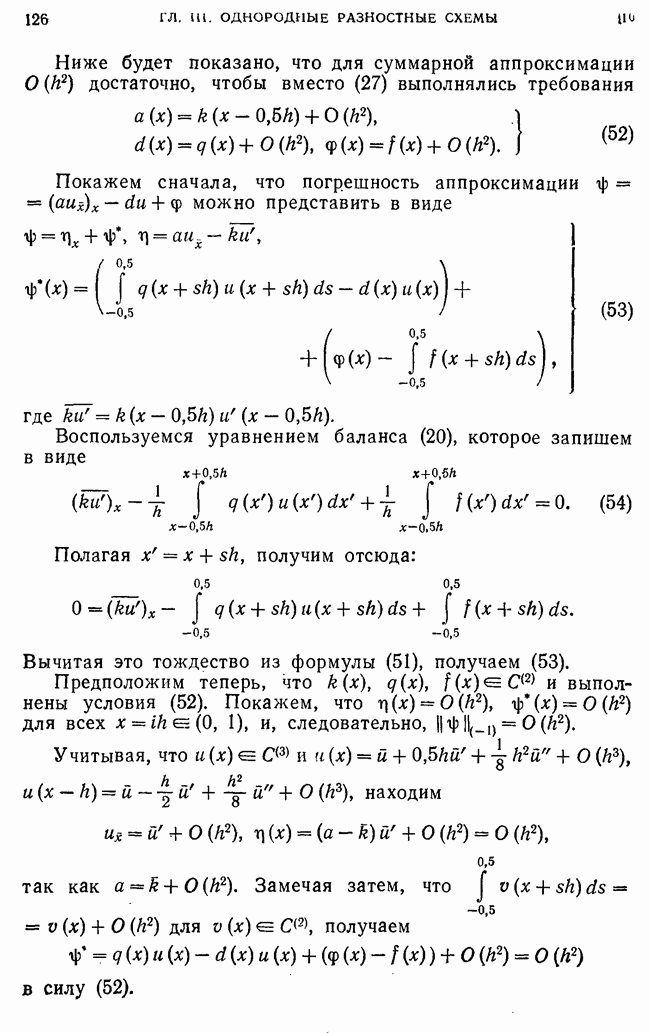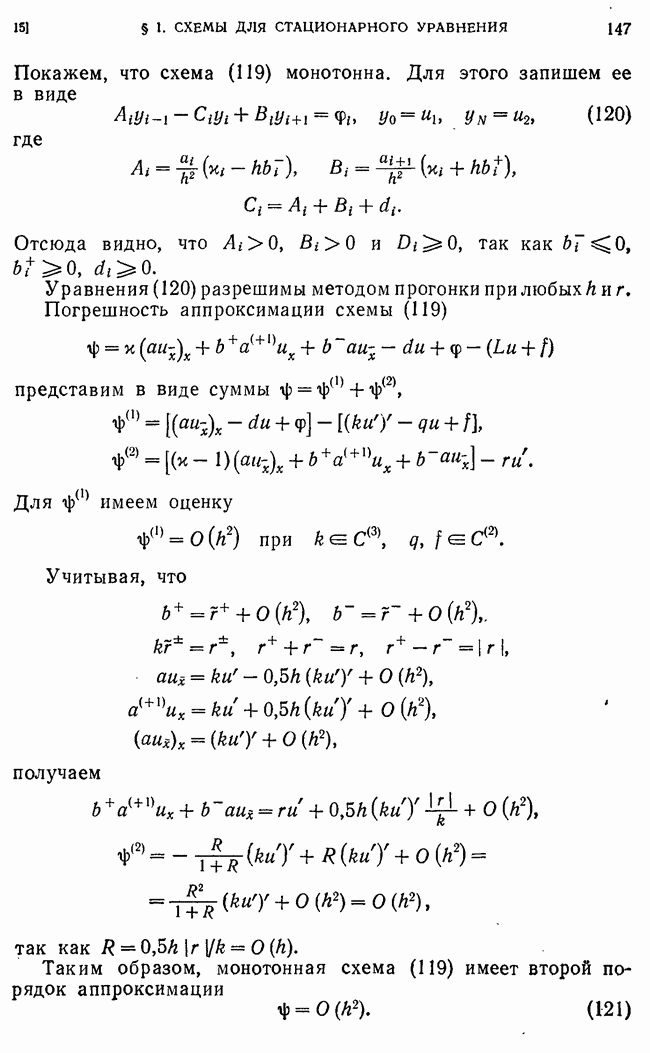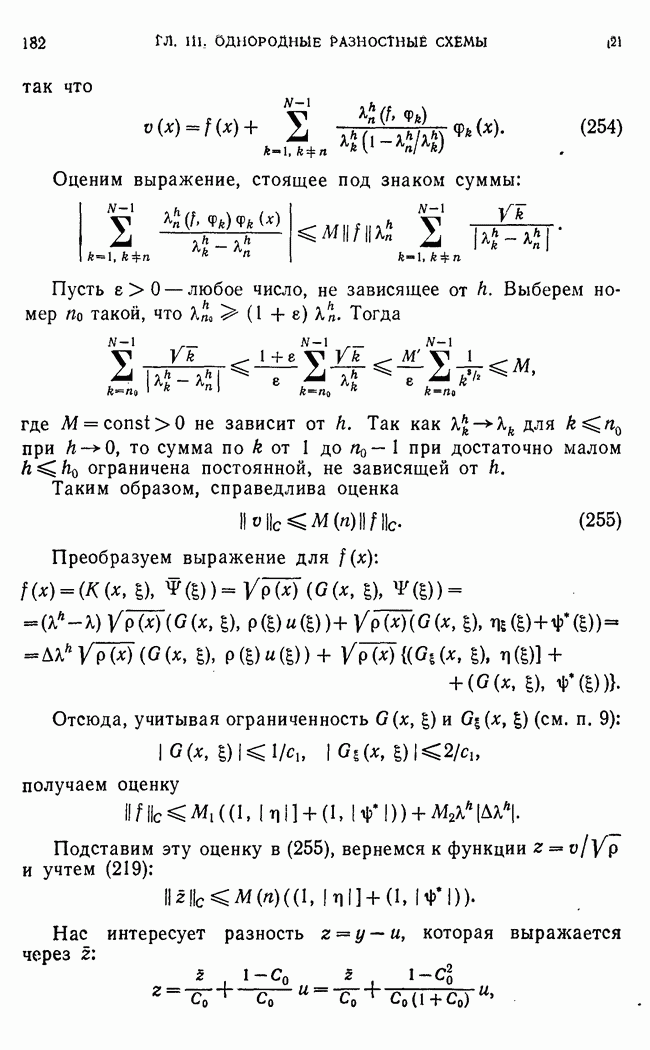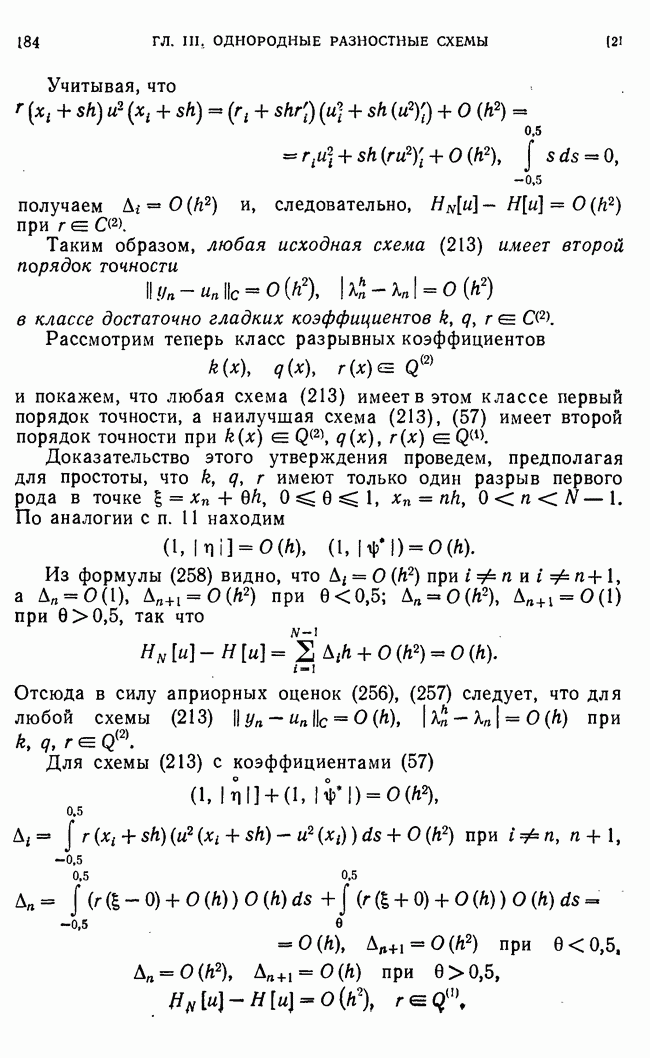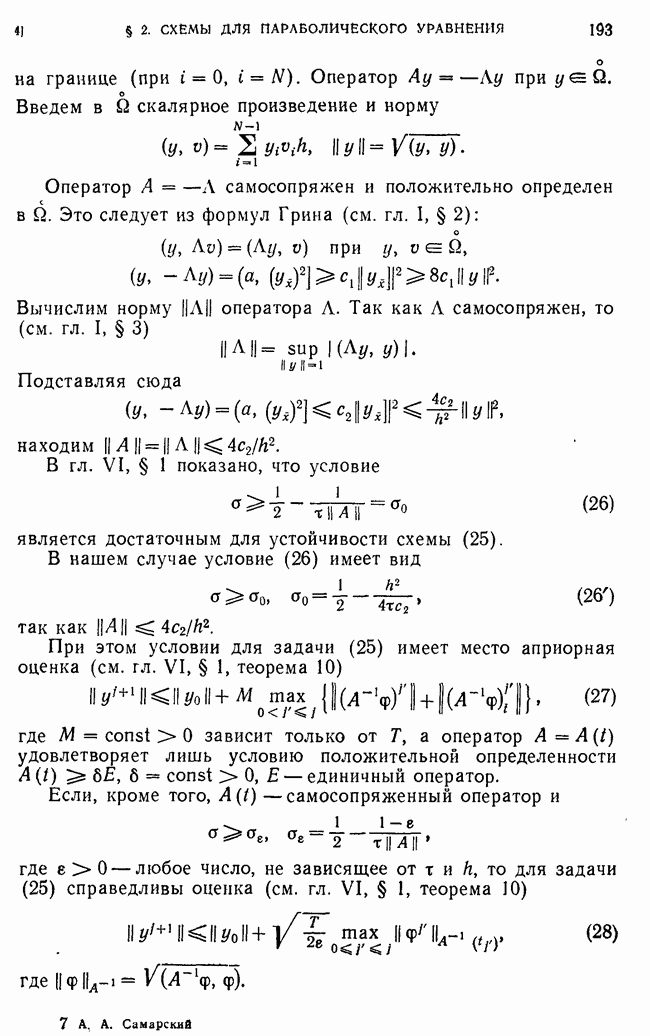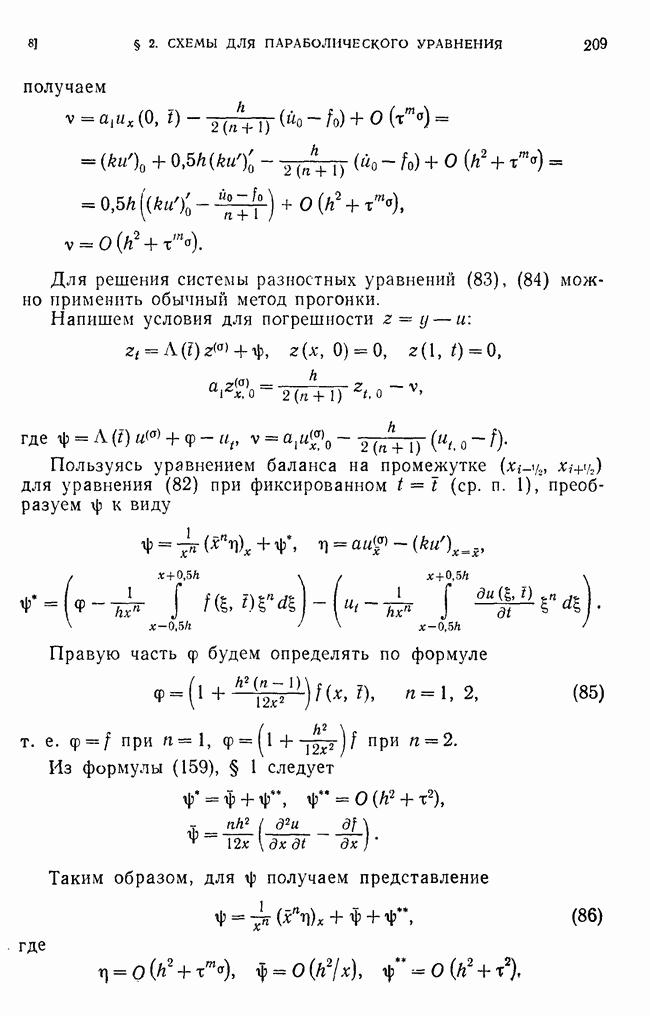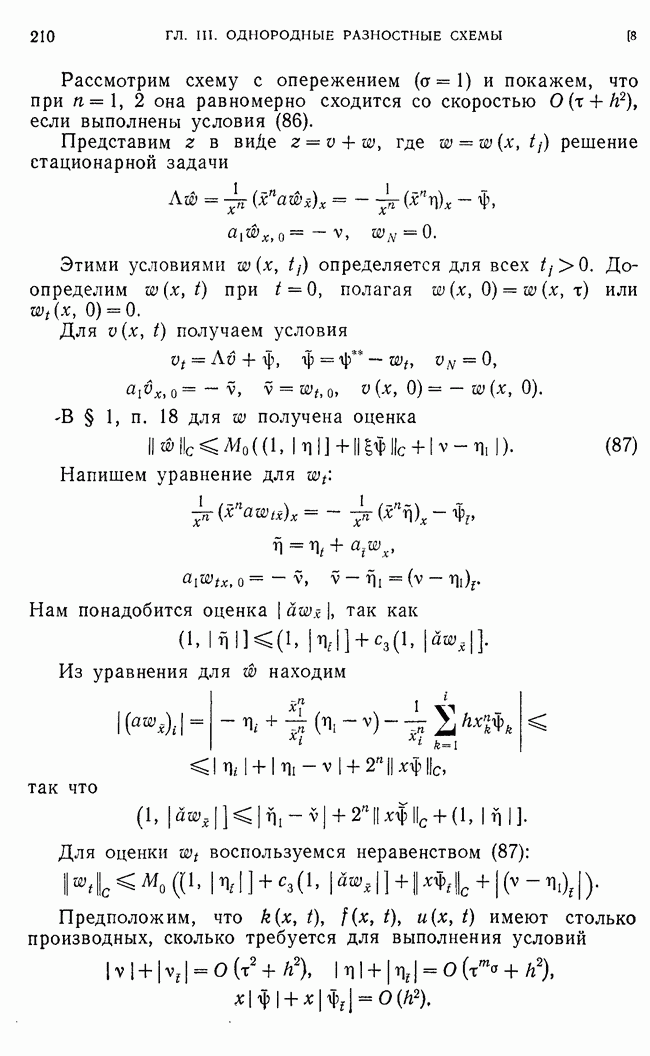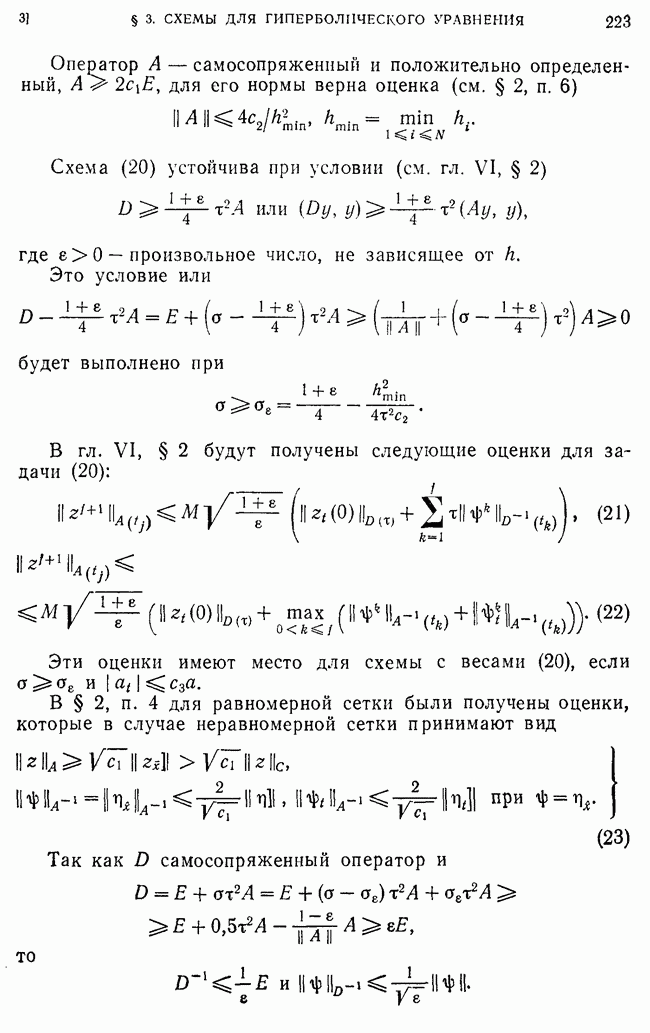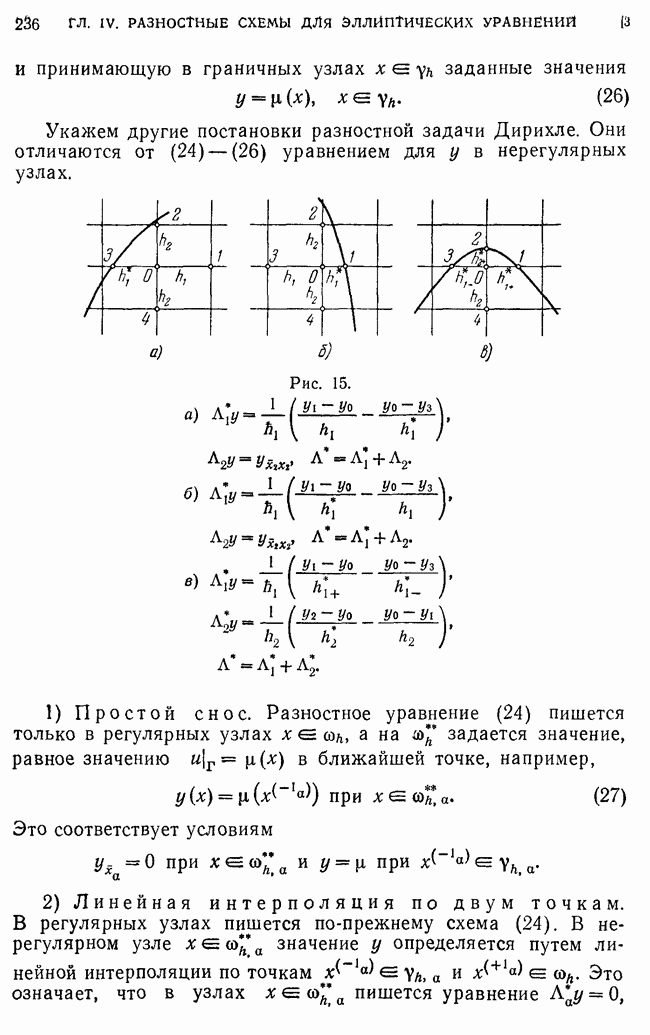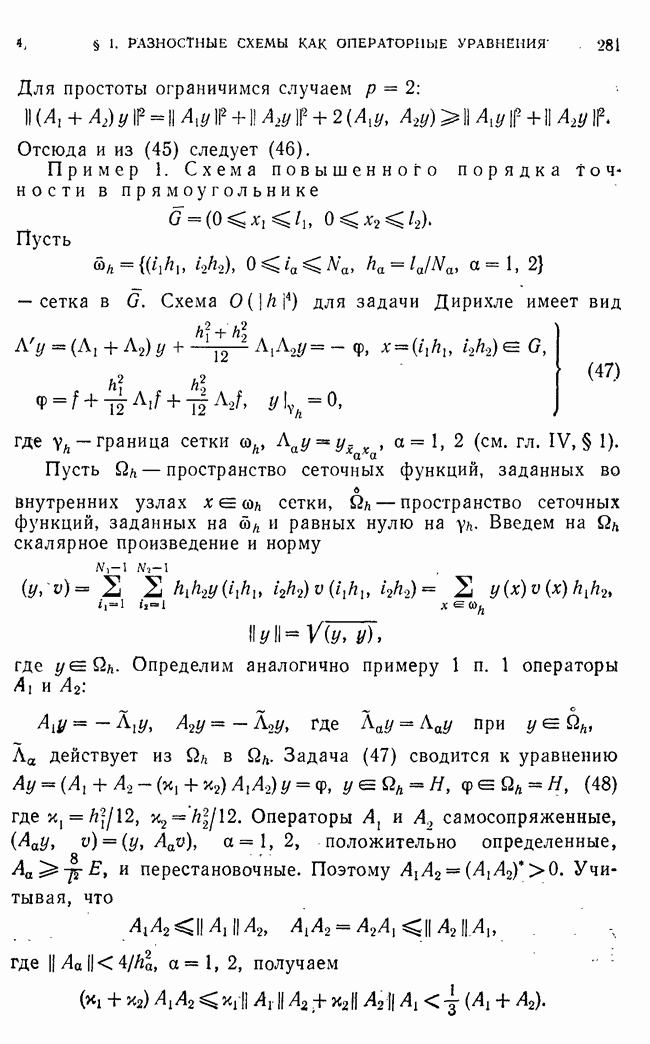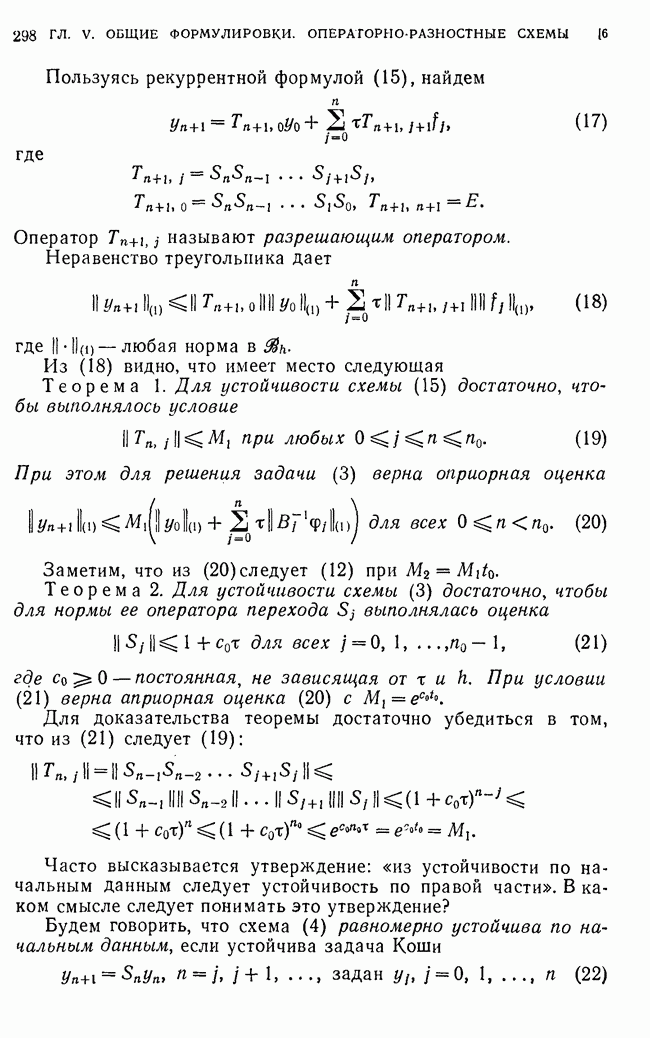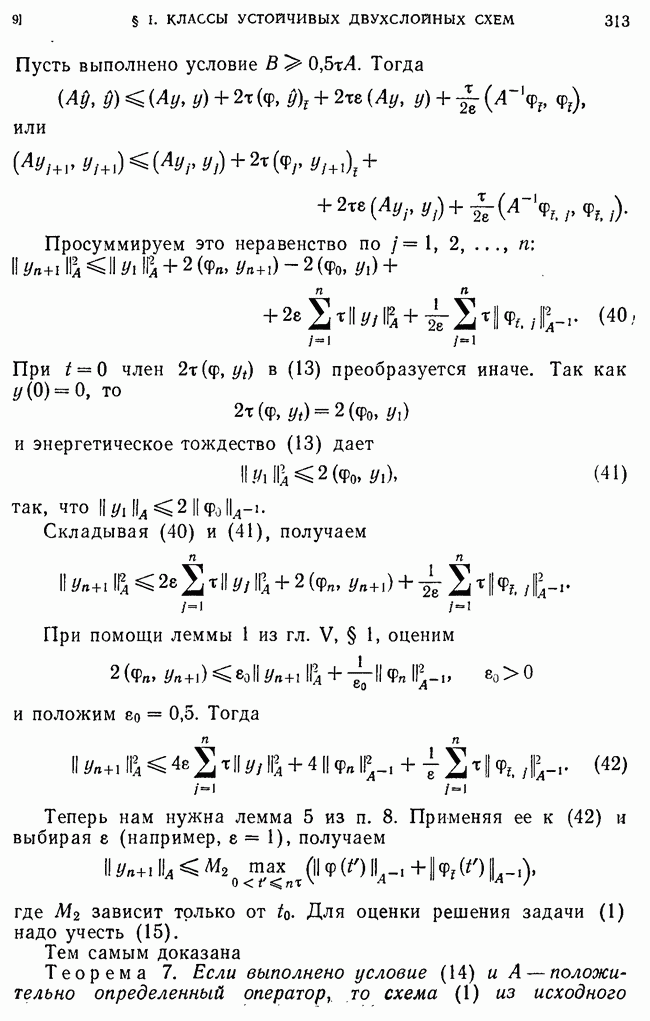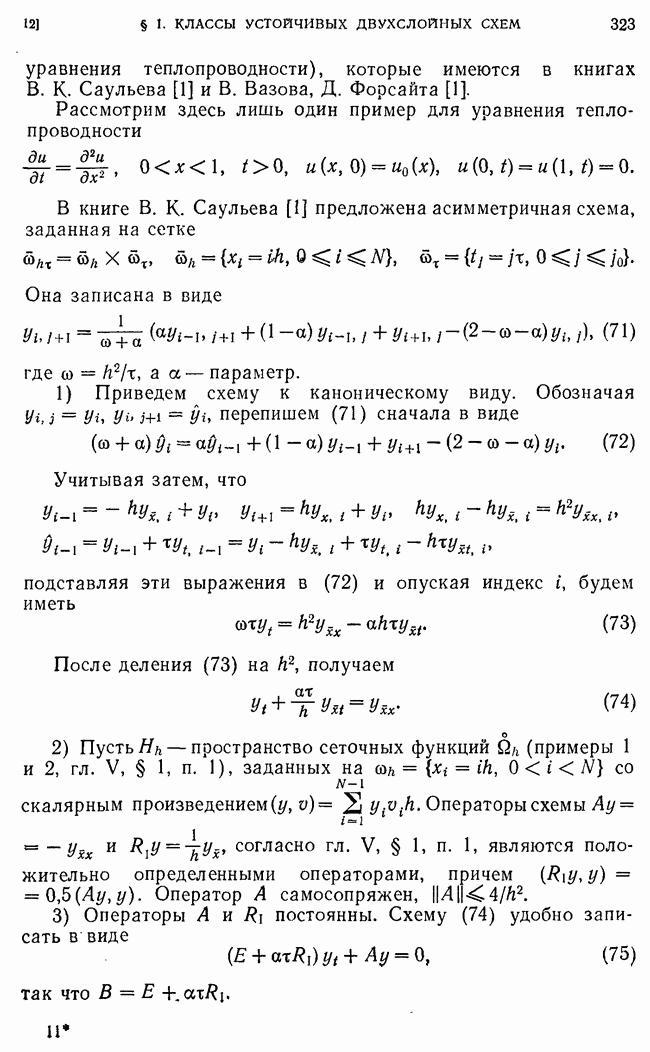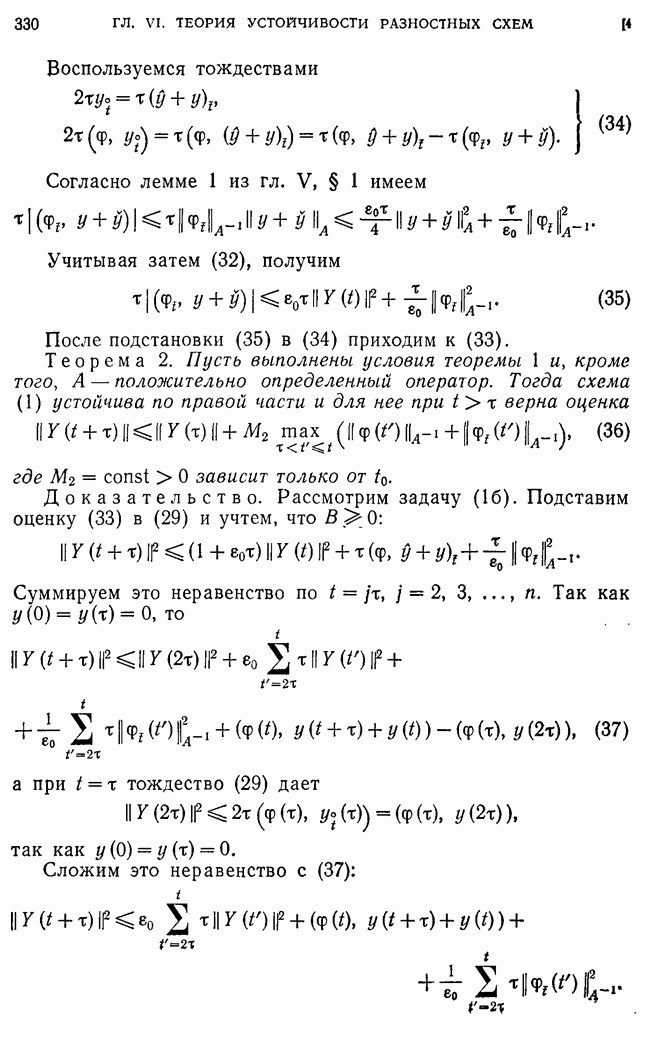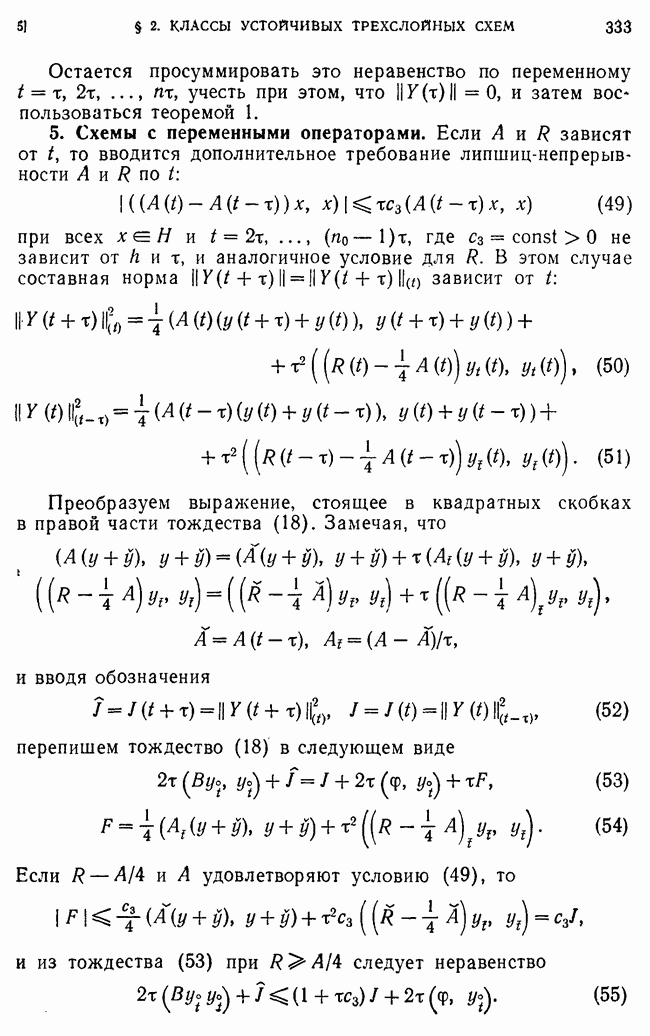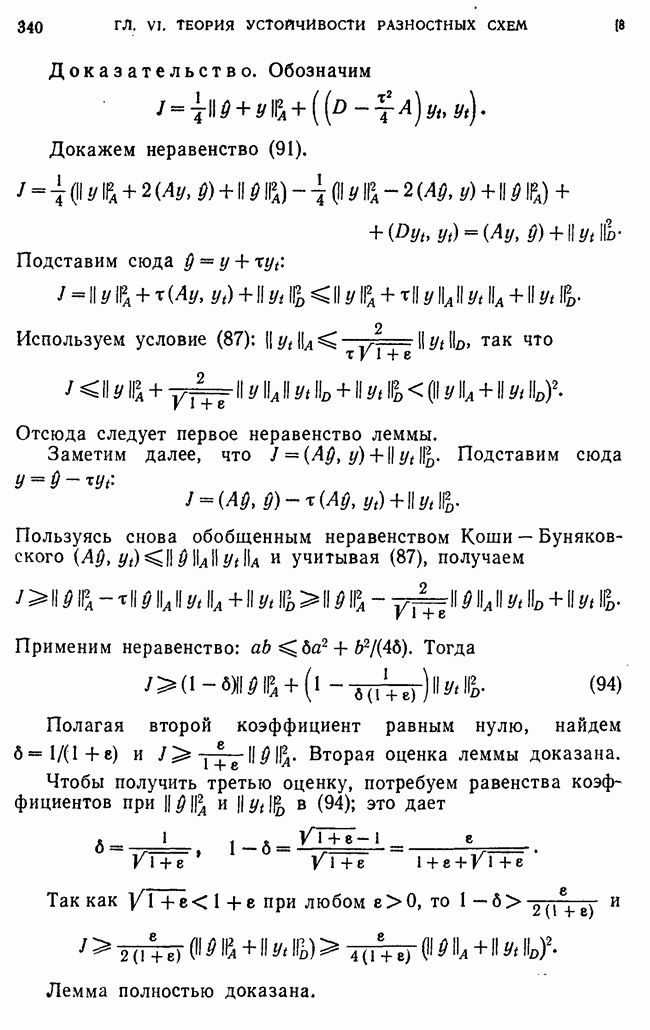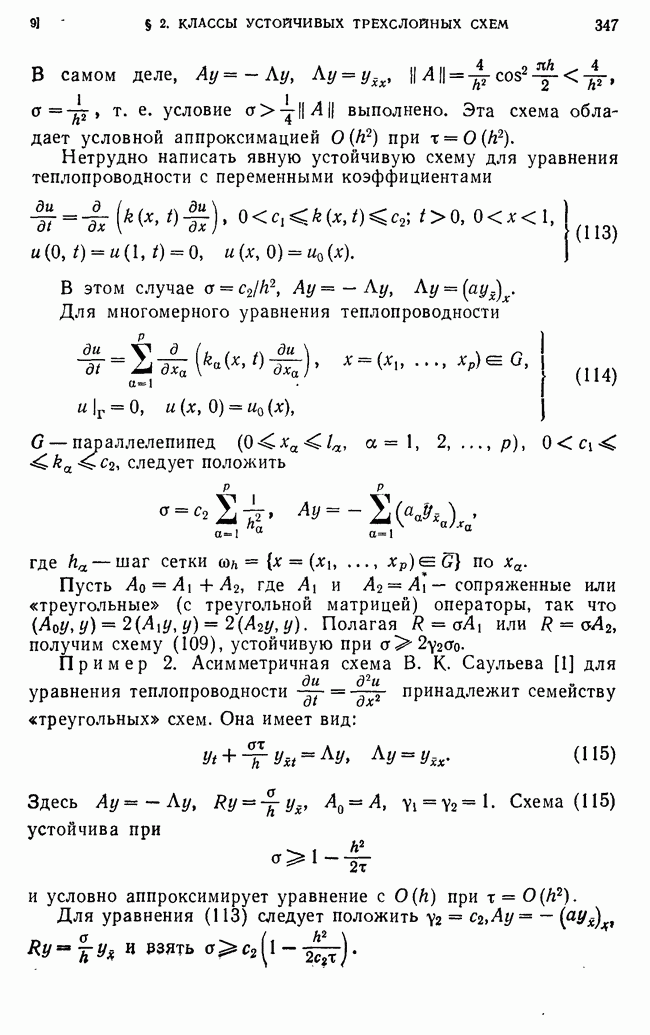| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
Пусть  — решение разностной задачи (213), а
— решение разностной задачи (213), а  соответствующее решение исходной задачи (204). Выясним вопрос об асимптотическом (при
соответствующее решение исходной задачи (204). Выясним вопрос об асимптотическом (при  ) порядке погрешностей
) порядке погрешностей  в равномерной метрике.
в равномерной метрике.
Для погрешности  и получаем разностную краевую задачу
и получаем разностную краевую задачу

где

— погрешность аппроксимации для схемы (213) на решении уравнения (204).
Преобразуем выражение для  Для этого проинтегрируем уравнение (204) по х в пределах от
Для этого проинтегрируем уравнение (204) по х в пределах от 

Вычитая это тождество из (234), получим

где

В частности, для схемы (213) с коэффициентами (57) имеем

Для выяснения точности схемы (213) надо оценить решение задачи (233).
Параметр  является собственным значением. Поэтому неоднородное уравнение (233) разрешимо только в том случае, когда собственная функция у задачи (213) ортогональна к правой части уравнения (233), или, точнее, должно быть выполнено тождество
является собственным значением. Поэтому неоднородное уравнение (233) разрешимо только в том случае, когда собственная функция у задачи (213) ортогональна к правой части уравнения (233), или, точнее, должно быть выполнено тождество

Пусть  и
и  — нормированные собственные функции:
— нормированные собственные функции:

Выше было доказано, что  при
при  Поэтому при достаточно малом
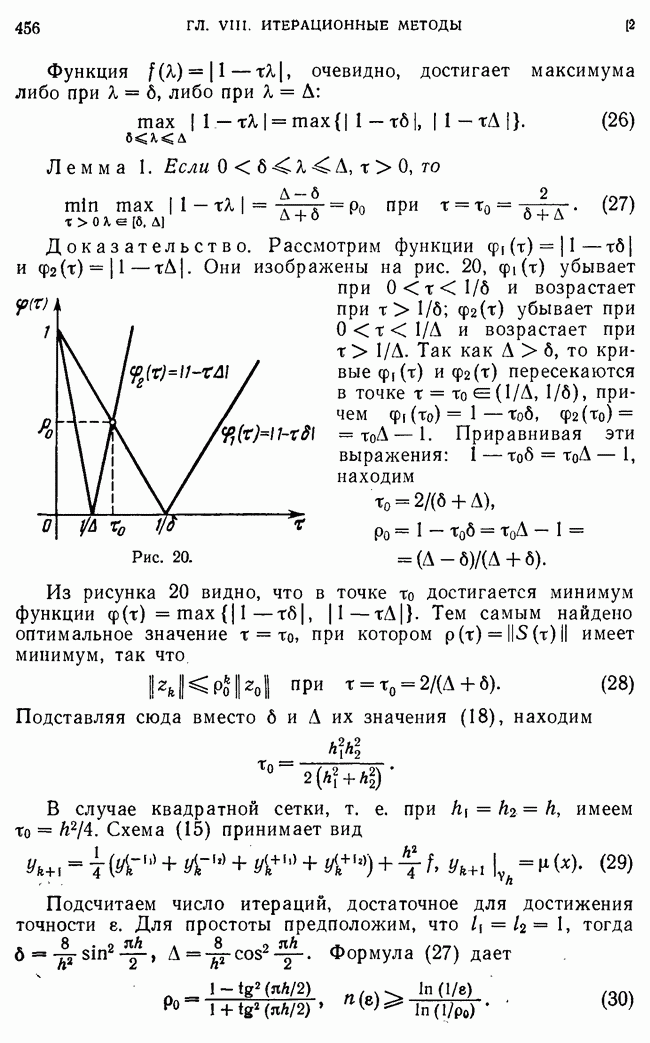
Поэтому при достаточно малом  можно утверждать, что
можно утверждать, что  Собственному значению
Собственному значению  соответствует только одна собственная функция, определяемая с точностью до произвольного множителя
соответствует только одна собственная функция, определяемая с точностью до произвольного множителя  . Выберем множитель
. Выберем множитель  таким образом, чтобы функция
таким образом, чтобы функция  был ортогональна разности
был ортогональна разности 

Отсюда получаем

В предыдущем пункте было показано, что  при 0. Поэтому
при 0. Поэтому  при
при  Будем считать, что
Будем считать, что  Далее,
Далее,

так, что

Условие (240) используем для определения 

Преобразуем теперь правую часть этого тождества, учитывая, что 

Отсюда и из оценок (220) для  следует
следует
Лемма 7. Пусть  кусочно-дифференцируемые функции,
кусочно-дифференцируемые функции,  собственные значения задач (204) и (213), соответственно. Тогда справедлива оценка
собственные значения задач (204) и (213), соответственно. Тогда справедлива оценка

где  не зависит от
не зависит от 
Перейдем к оценке  Так как
Так как  то у удовлетворяет уравнению
то у удовлетворяет уравнению  а для
а для  и получаем задачу (233).
и получаем задачу (233).
Сведем задачу (233) к дискретному аналогу интегрального уравнения

где  -разностная функция Грина оператора
-разностная функция Грина оператора  с краевыми условиями
с краевыми условиями 
Собственная функция у задачи (213) удовлетворяет уравнению

Пусть  собственное значение номера
собственное значение номера  нормированная собственная функция,
нормированная собственная функция, 
Чтобы получить вместо (245) и (246) уравнения с симметричным ядром, сделаем замену

Тогда уравнения (245) и (246) примут вид

Условие ортогональности  к функции
к функции  выполняется в силу условия (240):
выполняется в силу условия (240):

Условие (241) запишется в виде

Будем искать решение  уравнения (249) в виде
уравнения (249) в виде

при дополнительном условии (251).
Подставим это выражение в уравнение (249):

Разлагая  по собственным функциям
по собственным функциям 

получим

и

так что

Оценим выражение, стоящее под знаком суммы:

Пусть  любое число, не зависящее от
любое число, не зависящее от  Выберем номер По такой, что
Выберем номер По такой, что  Тогда
Тогда

где  не зависит от
не зависит от  Так как для
Так как для  при
при  то сумма по
то сумма по  от 1 до
от 1 до  при достаточно малом ограничена постоянной, не зависящей от
при достаточно малом ограничена постоянной, не зависящей от  Таким образом, справедлива оценка
Таким образом, справедлива оценка

Преобразуем выражение для 

Отсюда, учитывая ограниченность  (см. п. 9):
(см. п. 9):

получаем оценку

Подставим эту оценку в (255), вернемся к функции  и учтем (219):
и учтем (219):

Нас интересует разность  и, которая выражается через
и, которая выражается через 

где  постоянная, введенная ранее. Отсюда следует:
постоянная, введенная ранее. Отсюда следует:

при достаточно малом  так как
так как  при 0, а величина
при 0, а величина  ограничена. Из формулы (242) видно, что
ограничена. Из формулы (242) видно, что

и следовательно,

Подставляя сюда оценку для  , убеждаемся в том, что верна Теорема 8. Для погрешности схемы (213) при
, убеждаемся в том, что верна Теорема 8. Для погрешности схемы (213) при  и при достаточно малом имеют место оценки
и при достаточно малом имеют место оценки

где  не зависит от
не зависит от  постоянные, не зависящие от
постоянные, не зависящие от 
Перейдем теперь к оценке порядка точности разностной задачи Штурма — Лиувилля (213). Для этого нужно оценить величины 
Если  и
и  - достаточно гладкие функции, точнее,
- достаточно гладкие функции, точнее,  то так же, как и в п. 10, можно показать, что (
то так же, как и в п. 10, можно показать, что ( для любой исходной схемы. Далее, имеем
для любой исходной схемы. Далее, имеем

где

Интегралы от 0 до 0,5 и от  до 1 есть величины
до 1 есть величины  так как
так как  в силу краевых условий,
в силу краевых условий,
Учитывая, что 

получаем  следовательно,
следовательно,  при
при 
Таким образом, любая исходная схема (213) имеет второй порядок точности

в классе достаточно гладких коэффициентов  Рассмотрим теперь класс разрывных коэффициентов
Рассмотрим теперь класс разрывных коэффициентов

и покажем, что любая схема (213) имеет в этом классе первый порядок точности, а наилучшая схема (213), (57) имеет второй порядок точности при 
Доказательство этого утверждения проведем, предполагая для простоты, что  имеют только один разрыв первого рода в точке
имеют только один разрыв первого рода в точке  По аналогии с п. 11 находим
По аналогии с п. 11 находим

Из формулы (258) видно, что  при
при  так что
так что

Отсюда в силу априорных оценок (256), (257) следует, что для любой схемы  при
при 
Для схемы (213) с коэффициентами (57)

Отсюда, в силу априорных оценок (256), (257), заключаем, что для наилучшей схемы

Все результаты, полученные для однородных схем, соответствующих краевой задаче, сохраняют силу и для разностной задачи на собственные значения (213).
Так, любая исходная схема на неравномерной сетке

коэффициенты которой  определяются по формулам (83) и (85), имеет второй порядок точности в классе разрывных коэффициентов
определяются по формулам (83) и (85), имеет второй порядок точности в классе разрывных коэффициентов  на специальных последовательностях неравномерных сеток
на специальных последовательностях неравномерных сеток  (таких, что точки разрыва функций
(таких, что точки разрыва функций  являются узлами сетки).
являются узлами сетки).
По аналогии с п. 14 можно написать точную схему и усеченные схемы любого порядка точности. Такие схемы были исследованы В.  Приказчиковым [2].
Приказчиковым [2].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
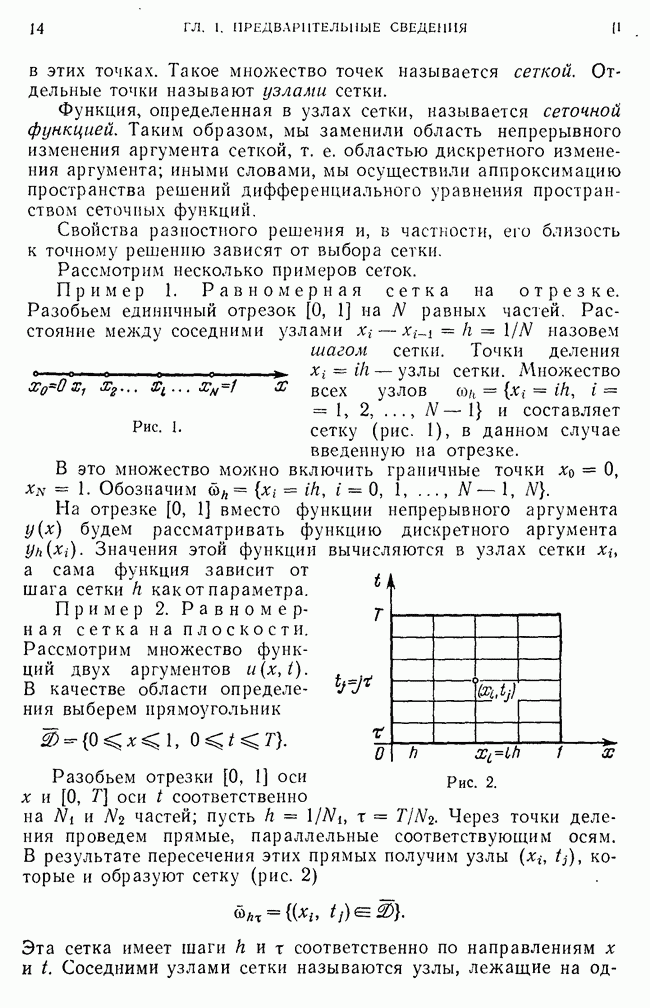
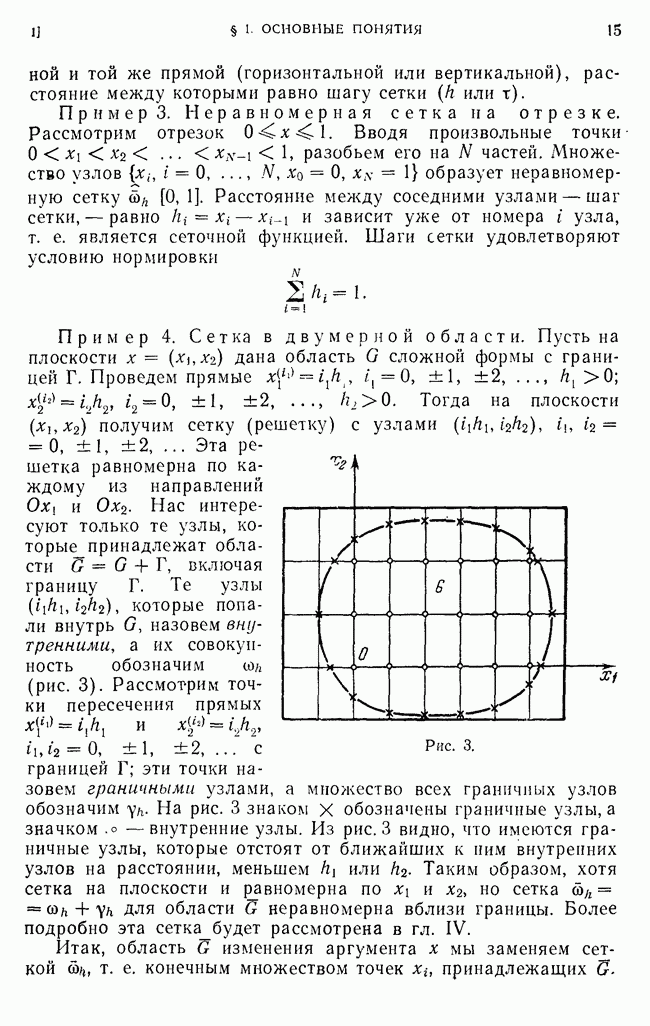
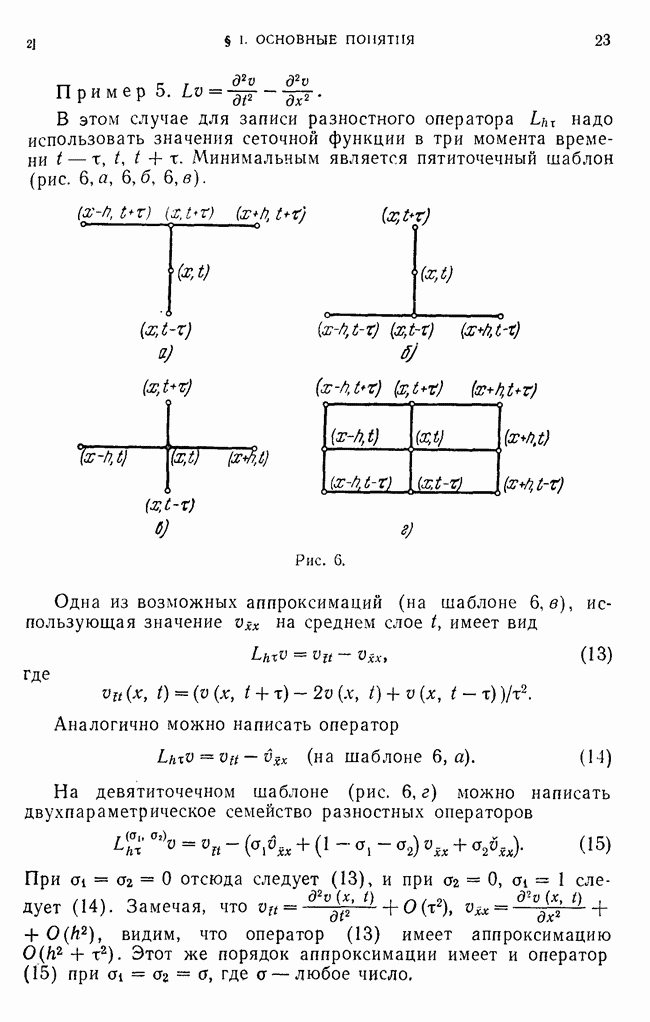
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
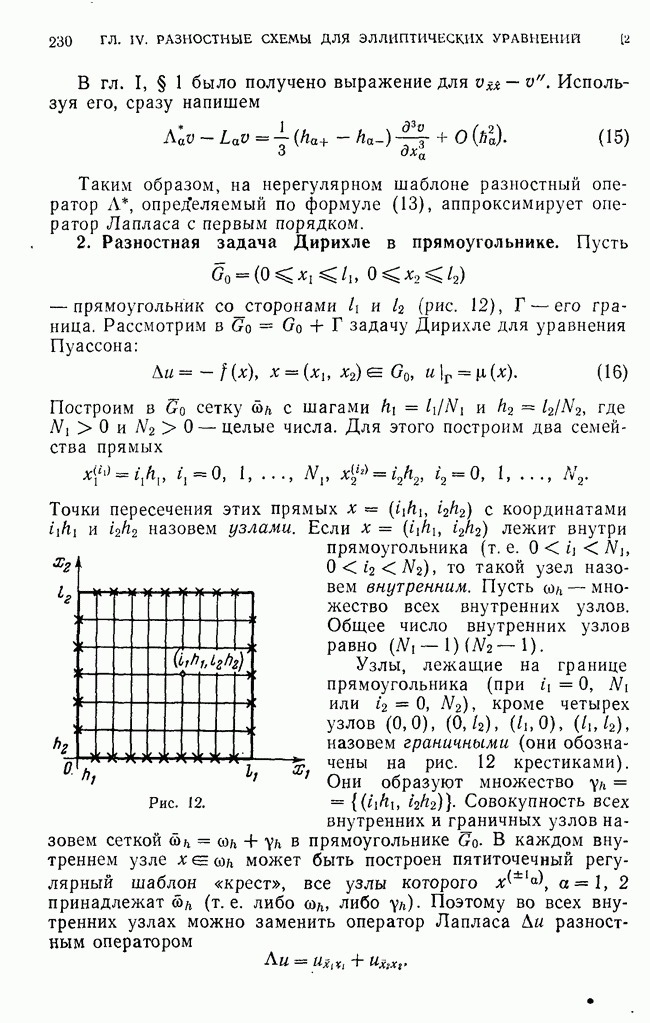
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
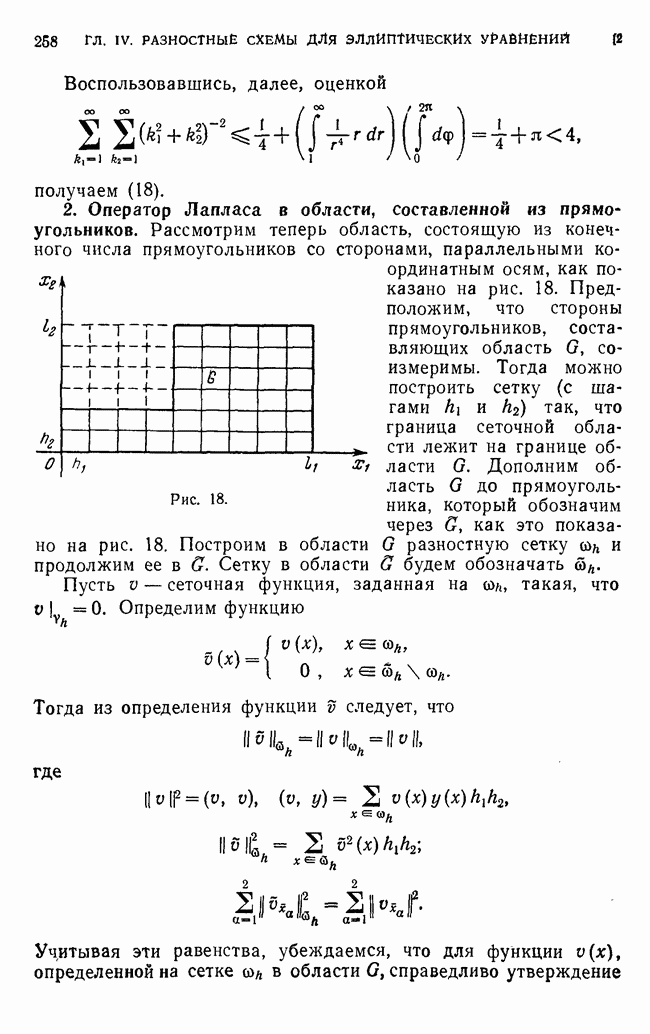
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка