| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Трехслойные итерационные схемы
В этом параграфе мы рассмотрим трехслойные итерационные схемы для уравнения

где А — линейный положительно определенный оператор,
действующий в гильбертовом пространстве  . В литературе такие схемы известны как двухшаговые, трехчленные или как итерационные схемы (методы) второго порядка (см., например, Д. К. Фаддеев и В. Н. Фаддеева [1]).
. В литературе такие схемы известны как двухшаговые, трехчленные или как итерационные схемы (методы) второго порядка (см., например, Д. К. Фаддеев и В. Н. Фаддеева [1]).
1. Постановка задачи.
Трехслойная итерационная схема для уравнения (1) связывает три итерации  так что
так что  определяется через
определяется через  Любая трехслойная итерационная схема для (1) с постоянными операторами и параметрами может быть записана в виде (ср. гл. V, § 2):
Любая трехслойная итерационная схема для (1) с постоянными операторами и параметрами может быть записана в виде (ср. гл. V, § 2):

Мы ограничимся изучением стандартных схем с регуляризатором

предполагая, что  линейные операторы, заданные на
линейные операторы, заданные на 

 энергетически эквивалентны с постоянными
энергетически эквивалентны с постоянными  Стандартная итерационная трехслойная схема имеет вид:
Стандартная итерационная трехслойная схема имеет вид:

Заданы произвольные 
Наряду с (5) будем рассматривать задачи

Пусть  решение задачи (5),
решение задачи (5),  решение уравнения (1). Для погрешности
решение уравнения (1). Для погрешности  получаем задачу
получаем задачу

Перейдем к оценке решения задачи (6). Для этого нам понадобится обобщение составной нормы, введенной в гл. VI, § 2.
Пусть  упорядоченная пара элементов пространства
упорядоченная пара элементов пространства  линейные операторы из
линейные операторы из  Обозначим
Обозначим

где  произвольное число. Отсюда видно, что
произвольное число. Отсюда видно, что  и является нормой при
и является нормой при  Если же
Если же  то
то  полунорма.
полунорма.
В дальнейшем будем пользоваться обозначениями

Нашей целью является получение для решения задачи (6) априорной оценки вида

из которой при  следует сходимость итераций по схеме (5). Оператор В и параметры
следует сходимость итераций по схеме (5). Оператор В и параметры  к должны быть выбраны из условия минимума
к должны быть выбраны из условия минимума  Сначала из этого условия выбираем тих при фиксированном В.
Сначала из этого условия выбираем тих при фиксированном В.
2. Выбор итерационных параметров.
Теорема 1. Пусть выполнены условия (3), (4). Тогда для решения задачи (6) при

имеет место априорная оценка

где  определяется по формуле (7) при
определяется по формуле (7) при  даются формулами (9).
даются формулами (9).
Доказательство. Положим в  где
где  произвольное число. Для
произвольное число. Для  после очевидных преобразований получаем задачу
после очевидных преобразований получаем задачу

с операторами

Согласно гл. VI, § 2 схема (13) устойчива в полунорме  где
где  упорядоченная пара элементов,
упорядоченная пара элементов,  если выполнены условия
если выполнены условия

Приравнивая В нулю, находим

После подстановки этого выражения в формулы для  получим
получим

Требования  будут выполнены, если
будут выполнены, если

Сравнивая эти неравенства с (4), видим, что параметры  можно найти из условий
можно найти из условий

Отсюда получим

После подстановки этих выражений в (15) определим  Из предыдущего ясно, что минимум
Из предыдущего ясно, что минимум  (максимум
(максимум  достигается лишь при условиях (16). Для
достигается лишь при условиях (16). Для  мы получили задачу
мы получили задачу

где 
Так как  то имеет место оценка (14). Подставляя в
то имеет место оценка (14). Подставляя в  получим
получим

где норма  определена тождеством (7). Так как
определена тождеством (7). Так как  то
то  полунорма. Границы
полунорма. Границы  на практике определяются неточно. Пусть
на практике определяются неточно. Пусть  и
и  - вычисленные значения
- вычисленные значения  так что
так что  Тогда
Тогда  выражаются через
выражаются через  по (9), (10) и
по (9), (10) и  - норма
- норма
Имея априорную оценку для однородного уравнения (6), нетрудно оценить решение неоднородного уравнения (5а).
Мы рассматривали схему (5) с произвольными начальными данными  Значение
Значение  можно определять по произвольному
можно определять по произвольному  пользуясь двухслойной итерационной схемой
пользуясь двухслойной итерационной схемой

Теорема 1 при этом сохраняет силу.
3. Явная схема.
Хорошо известна явная  единичный оператор) трехслойная схема с произвольным нулевым приближением
единичный оператор) трехслойная схема с произвольным нулевым приближением  и первым приближением
и первым приближением  определяемым по двухслойной схеме (18) с оптимальным значением
определяемым по двухслойной схеме (18) с оптимальным значением  (см. Д. К. Фаддеев и В. Н. Фаддеева [1]).
(см. Д. К. Фаддеев и В. Н. Фаддеева [1]).
Рассмотрим эту явную схему для уравнения

где С — самосопряженный оператор с границами у. и 

Явная схема имеет вид

Выразим  через
через 

Подставляя сюда выражения (9) для  получим
получим

где  оператор перехода двухслойной схемы с
оператор перехода двухслойной схемы с 

т. е.

Схему (23) обычно получают так. Записывают сначала уравнение (19) в так называемом подготовленном виде, т. е. в виде уравнения

и выбирают  так, чтобы
так, чтобы  была минимальна. Для этого, как было показано в § 1, надо положить
была минимальна. Для этого, как было показано в § 1, надо положить 

К этому уравнению и применяют явную схему (23).
В силу теоремы 1 для схемы (23) верна оценка (17) при 
Рассмотрим теперь схему

Она отличается от (23) только произволом в выборе  Скорость сходимости схем (23) и (26) в составной
Скорость сходимости схем (23) и (26) в составной  одна и та же:
одна и та же:

4. Оценка скорости сходимости явной схемы.
Теорема 2, Пусть выполнены условия (20). Тогда при  для задачи
для задачи

где  верна априорная оценка
верна априорная оценка

Доказательство. Последовательно применяя уравнение (27), получим

где  операторные полиномы степени
операторные полиномы степени  соответственно. Подставляя (29) в уравнение (27), получим,
соответственно. Подставляя (29) в уравнение (27), получим,
в силу произвольности  что
что  и
и  удовлетворяют рекуррентным соотношениям
удовлетворяют рекуррентным соотношениям

Из уравнений (27) и (29) при  следует:
следует:

Чтобы формула (30) была верна и для  определим
определим  из соотношения
из соотношения

Таким образом для и выполняются одни и те же соотношения (30) с начальными условиями

Отсюда следует, что

и формула (29) принимает вид

Положим

Подставляем это выражение в (30):

Разделим обе части на  и учтем, что
и учтем, что

В результате получим для  рекуррентную формулу
рекуррентную формулу

с дополнительным условием

где

Отсюда видно, что  есть полином П. Л. Чебышева второго рода (см. В. Л. Гончаров [1]),
есть полином П. Л. Чебышева второго рода (см. В. Л. Гончаров [1]),

где

Многочлены  удовлетворяют рекуррентным соотношениям
удовлетворяют рекуррентным соотношениям

где  полином П. Л. Чебышева первого рода.
полином П. Л. Чебышева первого рода.
Для многочленов  верна оценка
верна оценка

Перепишем теперь формулу (33):

Учитывая рекуррентные соотношения (35), получим

где  полином
полином  Чебышева первого рода. Используем тождество
Чебышева первого рода. Используем тождество

Нам понадобятся следующие неравенства (см. (12) из § 2 и (36)):

Подставляя (39) в (38) и учитывая (40), (41), будем иметь

Если  то отсюда следует (28). Теорема 8 доказана. Если
то отсюда следует (28). Теорема 8 доказана. Если  любой вектор, то из (37) и (36) получаем
любой вектор, то из (37) и (36) получаем

Решение уравнения  следуя гл. VI, § 3, ищется в виде
следуя гл. VI, § 3, ищется в виде  где
где  при
при  Отсюда
Отсюда  где
где  Оценка
Оценка

вместе с (43) выражает вычислительную устойчивость схемы (23). Полагая  получаем для (23) при
получаем для (23) при  оценку
оценку 
5. Априорные оценки для неявной схемы в энергетических пространствах ...
Рассмотрим теперь неявную схему (5) с  и начальными условиями
и начальными условиями

Нетрудно убедиться в том, что неявная схема (5), (45) и явная схема (23) эквивалентны при

или при

В самом деле, применяя к (5), (45) оператор и обозначая  получим схему (23) с
получим схему (23) с  Обратно, заменяя в
Обратно, заменяя в  и действуя затем оператором
и действуя затем оператором  получаем неявную схему (5), (45).
получаем неявную схему (5), (45).
Условия (20) равносильны условиям

Из (46) и (47) видно, что

Неявную схему можно трактовать, как явную схему для уравнения

эквивалентного уравнению  при
при

или при 
Теорема 3. Пусть выполнены условия (48). Тогда для неявной схемы (5), (45) при  верна оценка
верна оценка

Замечание. Можно показать, что при тех же условиях (48) и дополнительном требовании перестановочности операторов  выполняется оценка
выполняется оценка

6. Факторизованные схемы.
Оператор В выбирается из тех же соображений, что и в случае двухслойной схемы (см. §§ 2, 3). Одними и теми же операторами можно пользоваться как для двухслойных, так и для трехслойных схем. В частности, можно взять факторизованный оператор

с треугольными операторами  Операторы
Операторы  эквивалентны с постоянными
эквивалентны с постоянными 

 эквивалентны с постоянными
эквивалентны с постоянными 

так что условия (48) выполнены с постоянными

Постоянные  были определены в § 2. Если выполнены условия
были определены в § 2. Если выполнены условия  для всех
для всех  то постоянные
то постоянные  Для факторизованного оператора (51) при
Для факторизованного оператора (51) при  равны
равны

Если 

При  коэффициент
коэффициент  имеет следующую асимптотику
имеет следующую асимптотику

а скорость сходимости итераций

Это значит, что число итераций пропорционально  Напомним, что для двухслойной схемы с оператором (51) и постоянным
Напомним, что для двухслойной схемы с оператором (51) и постоянным  скорость сходимости итераций равна
скорость сходимости итераций равна

В случае разностной задачи Дирихле для уравнения Лапласа в  -мерной ступенчатой области и кубической сетки с шагом
-мерной ступенчатой области и кубической сетки с шагом  имеем
имеем  таким образом, число итераций для трехслойной схемы с факторизованным оператором (51) есть величина
таким образом, число итераций для трехслойной схемы с факторизованным оператором (51) есть величина  Решение задачи Дирихле в
Решение задачи Дирихле в  -мерной ступенчатой области для уравнения
-мерной ступенчатой области для уравнения

требует  итераций с общим объемом работы
итераций с общим объемом работы 
7. Двухступенчатый метод.
Трехслойную итерационную схему (5), (45) можно трактовать как метод поправок:

где  поправка,
поправка,  невязка. Определяя
невязка. Определяя  как решение уравнения
как решение уравнения

каким-либо итерационным методом с нулевым начальным приближением  мы получим двухступенчатый трехслойный
мы получим двухступенчатый трехслойный
метод. Зададимся числом  и сделаем
и сделаем  итераций, где
итераций, где  такое, что выполняется условие
такое, что выполняется условие

Тогда, как было показано в § 3, п. 5, для поправки  получаем уравнение
получаем уравнение

где  разрешающий оператор схемы внутренних итераций, так что
разрешающий оператор схемы внутренних итераций, так что

Скорость сходимости двухступенчатого трехслойного метода следует из теоремы 3, где

В работе Гана [1] двухступенчатый трехслойный метод применялся для решения разностной задачи Дирихле для уравнения

с переменными коэффициентами. Внутренние итерации для решения уравнения (1) проводились по методу переменных направлений с оптимальным набором параметров. Для случая малых  было отмечено существенное ускорение итераций по сравнению с двухступенчатой двухслойной схемой. В работе Вашпреса [3] внешние итерации проводились по методу Ланцоша, а внутренние — по методу переменных направлений.
было отмечено существенное ускорение итераций по сравнению с двухступенчатой двухслойной схемой. В работе Вашпреса [3] внешние итерации проводились по методу Ланцоша, а внутренние — по методу переменных направлений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
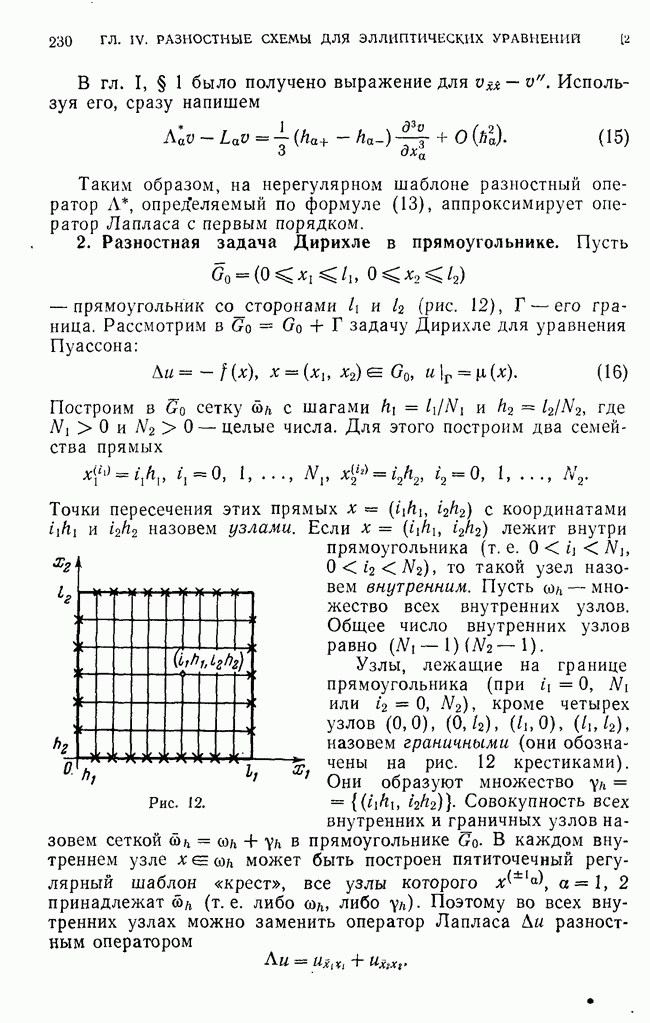
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка