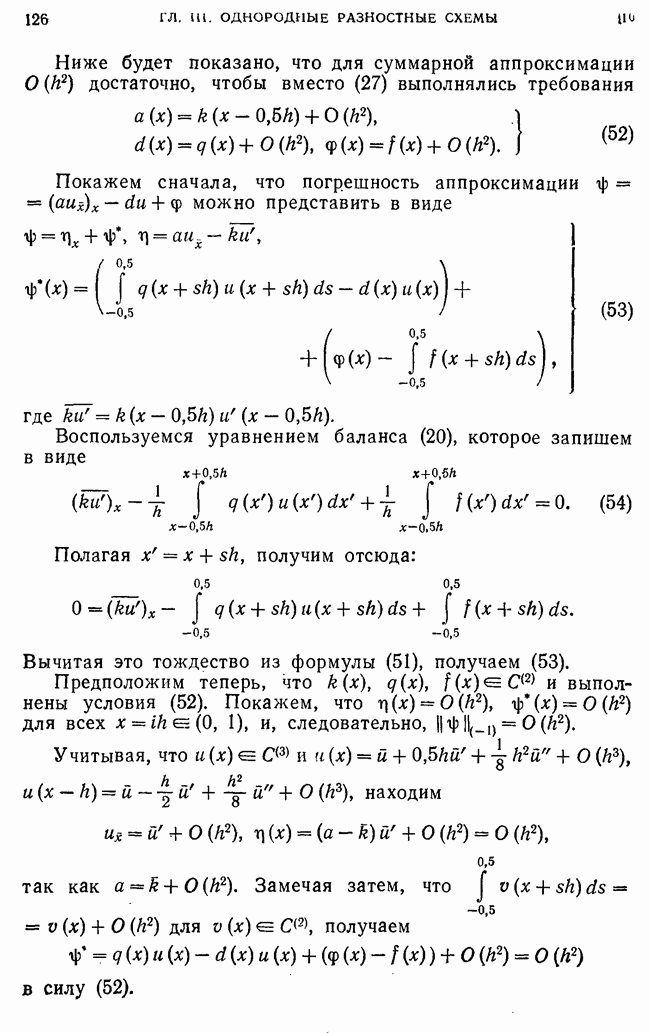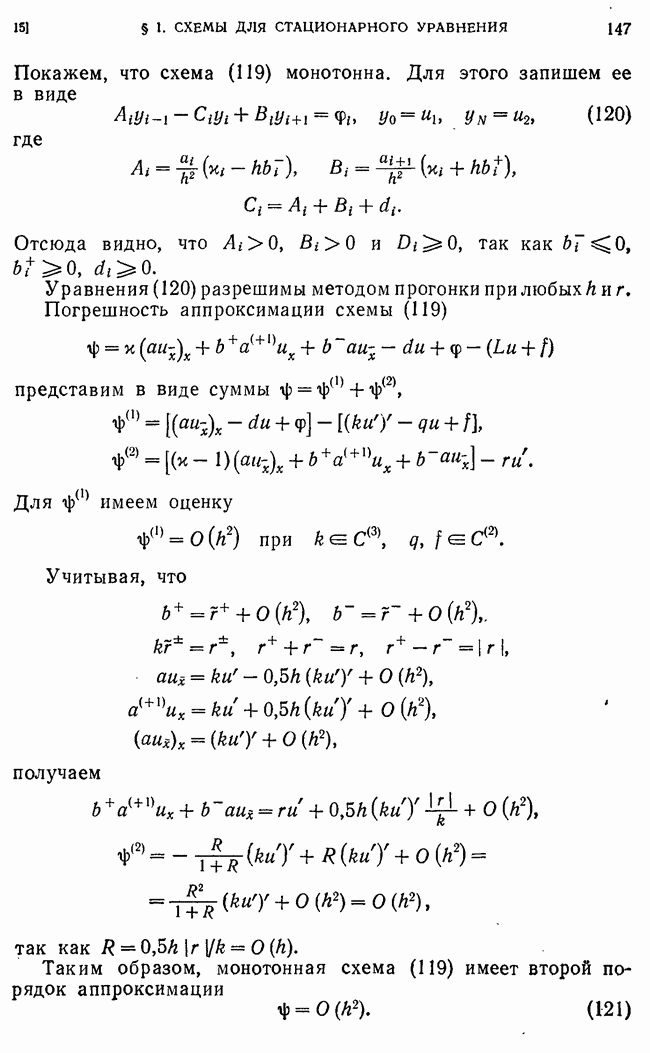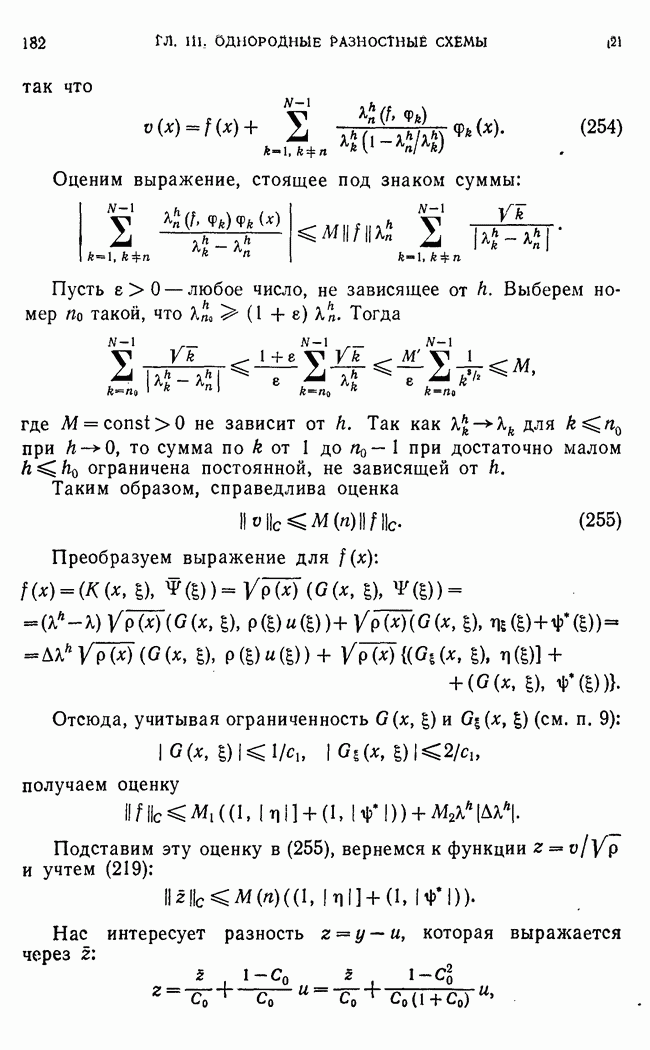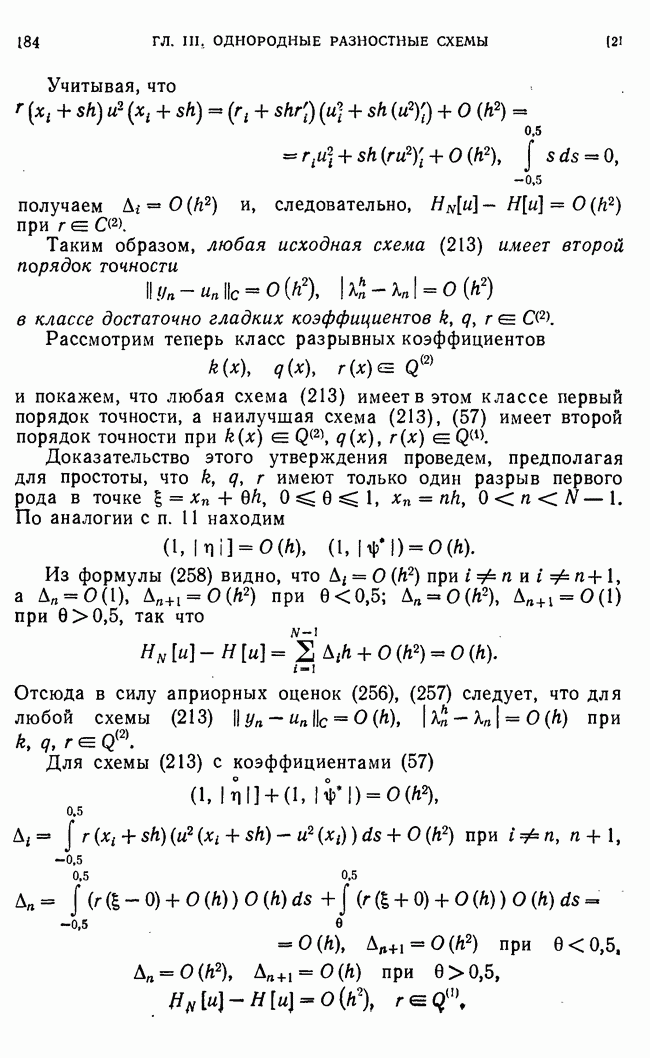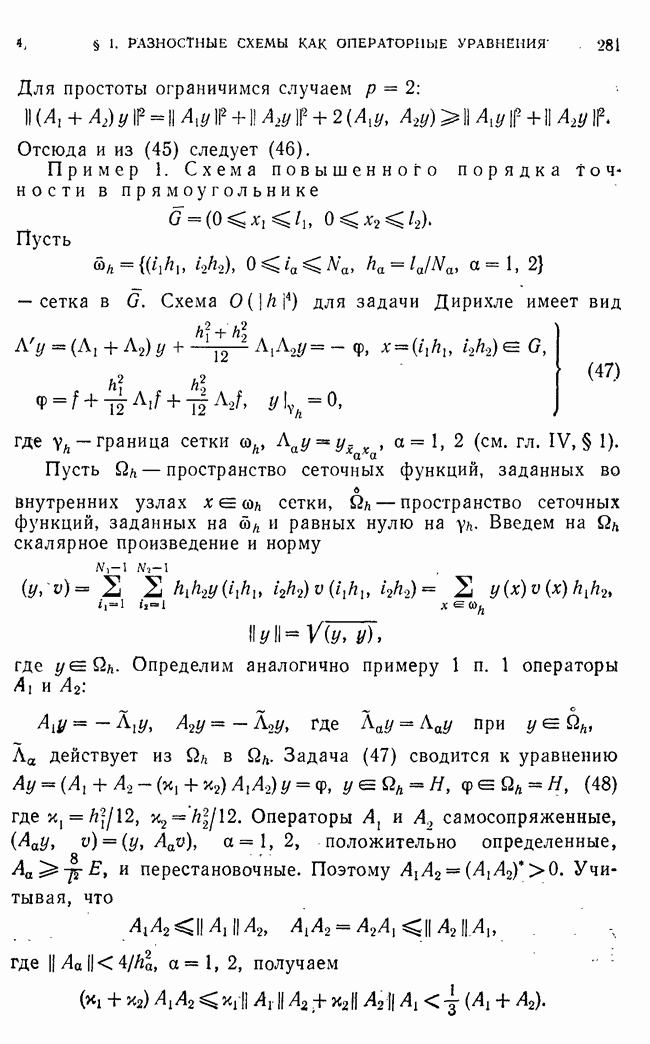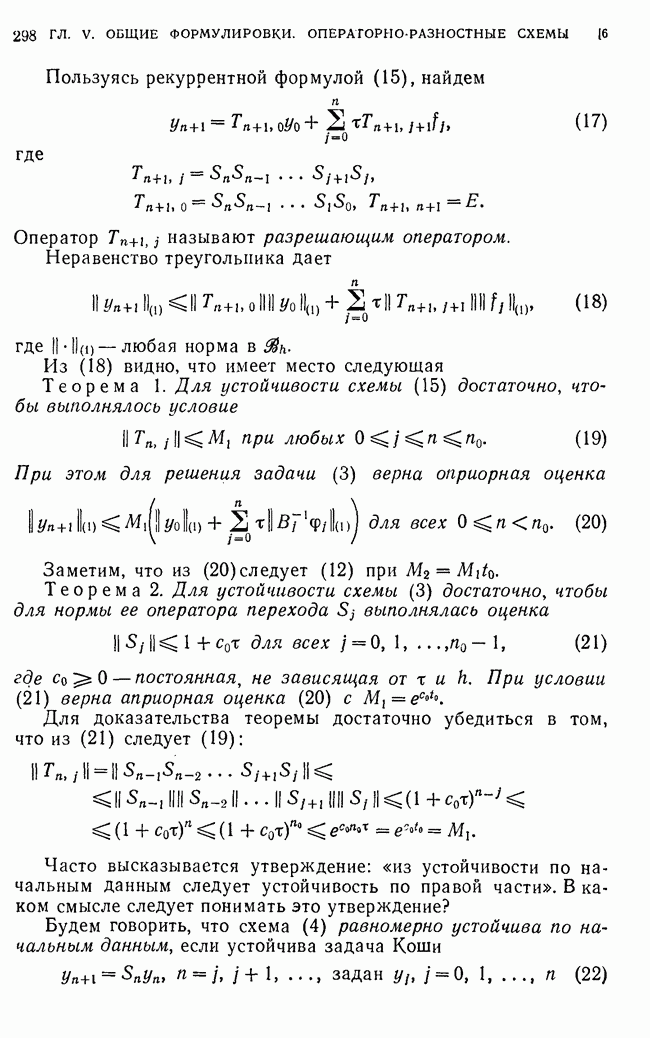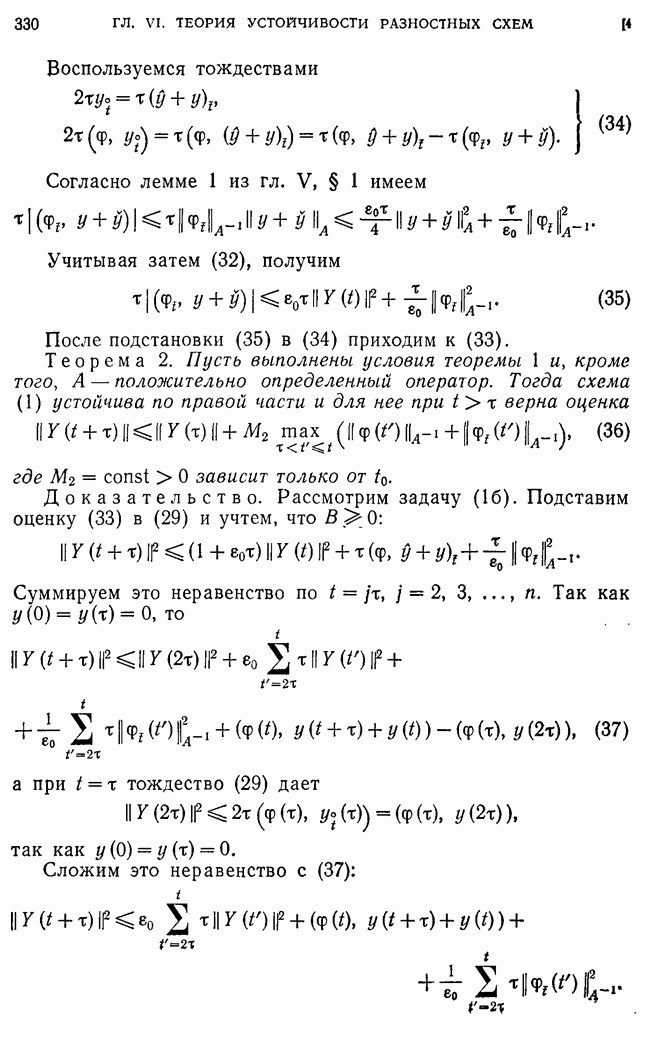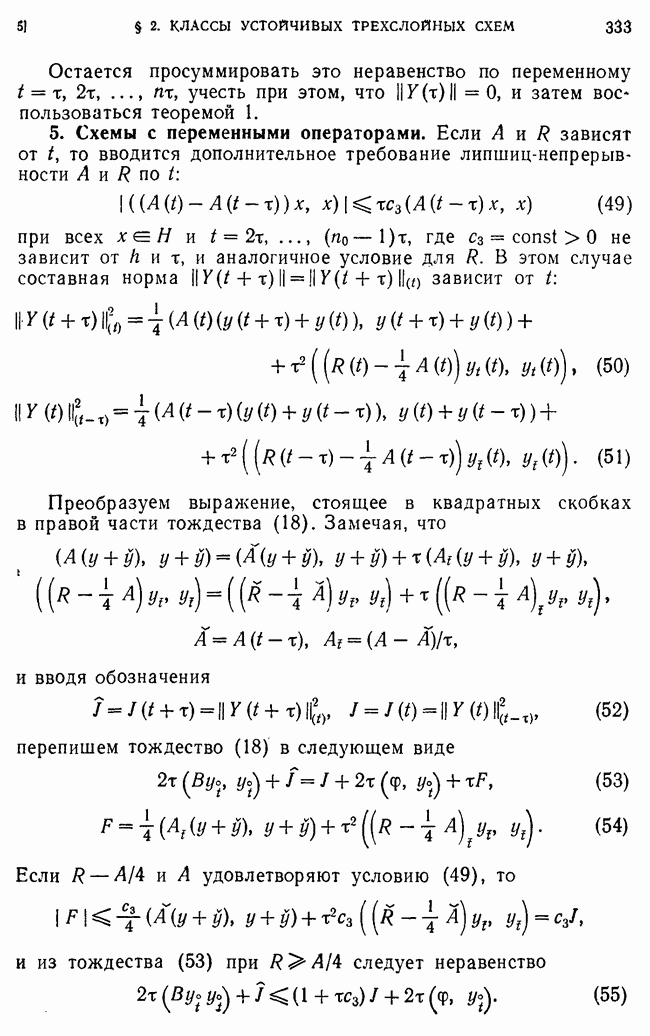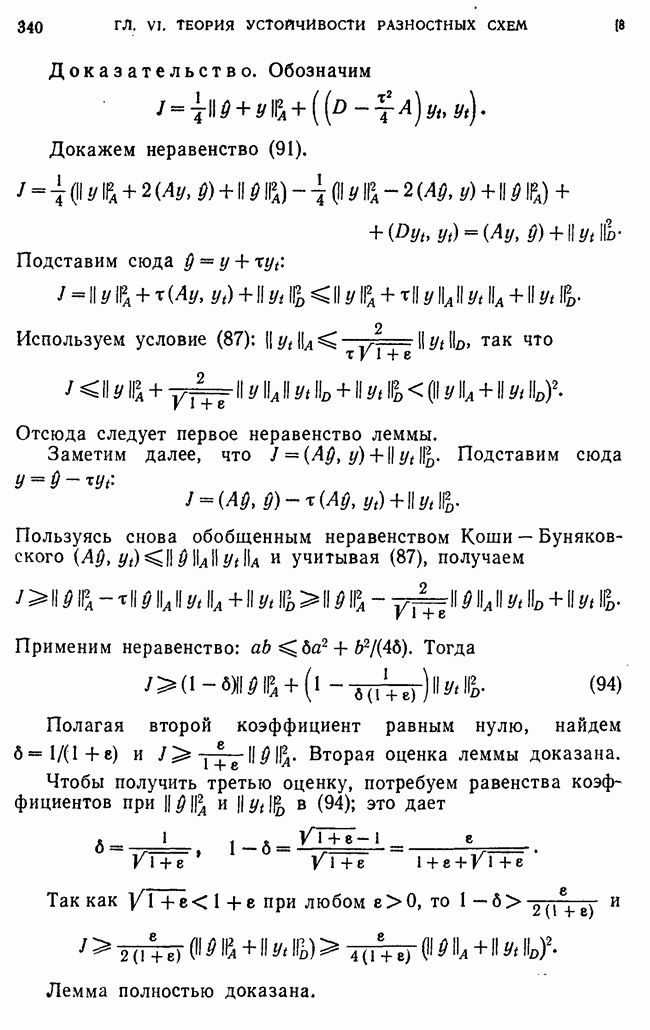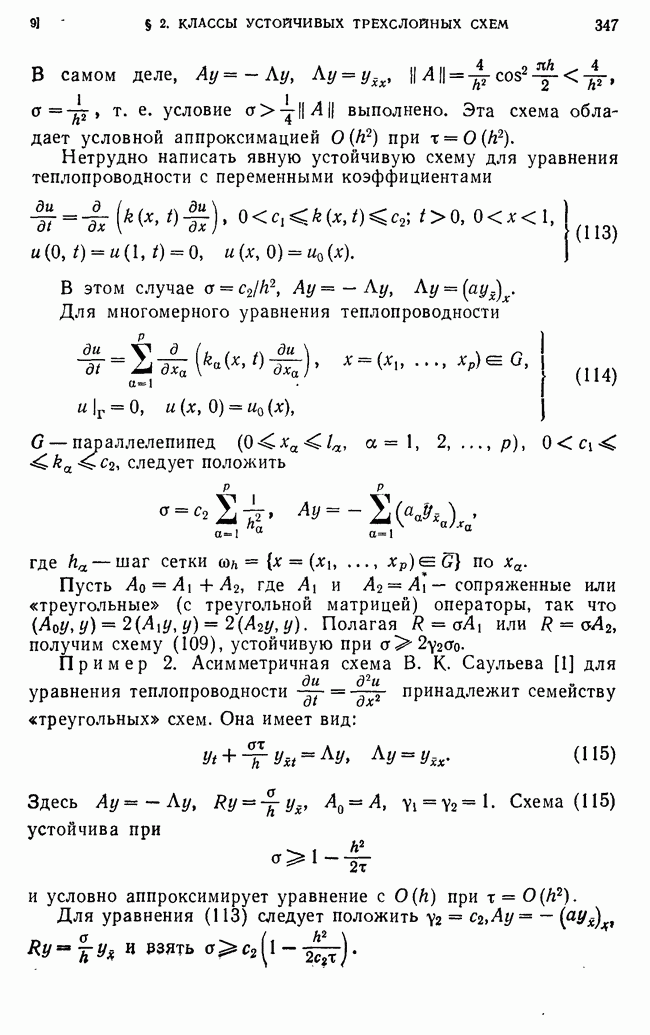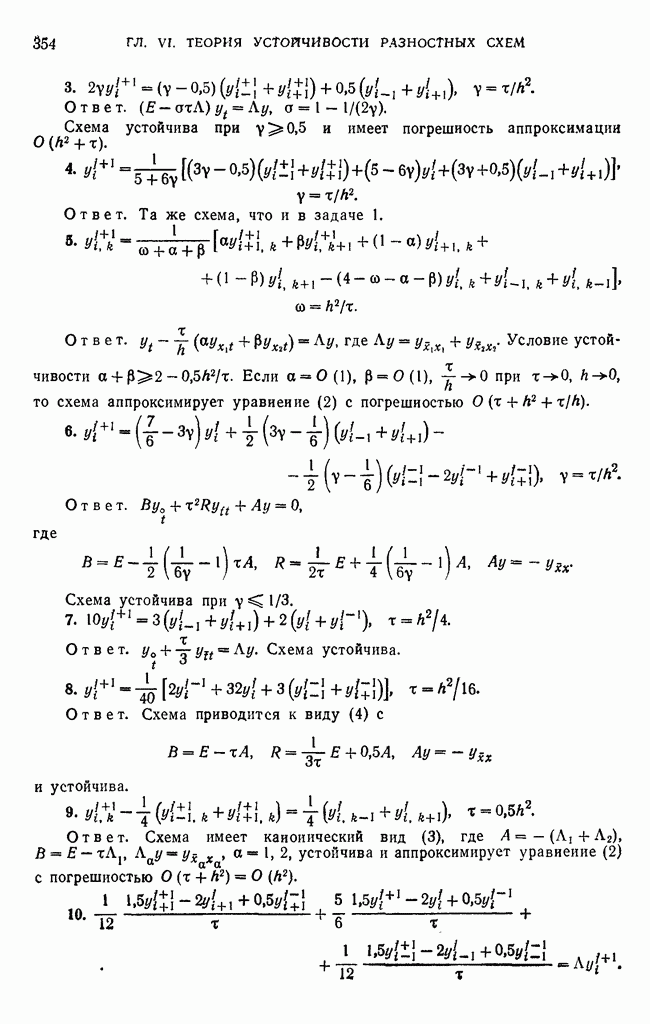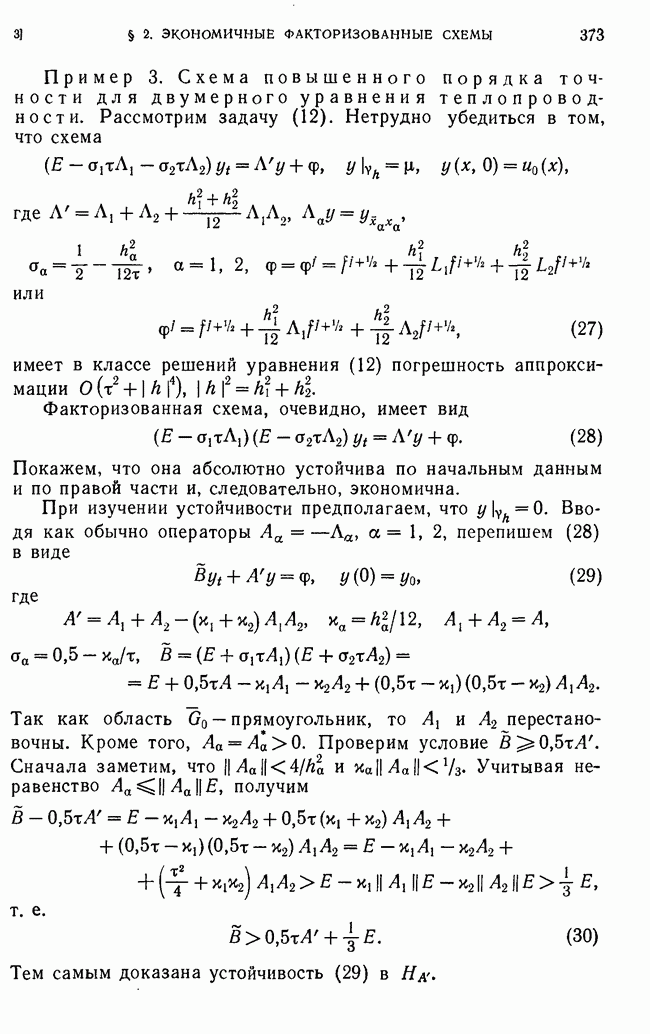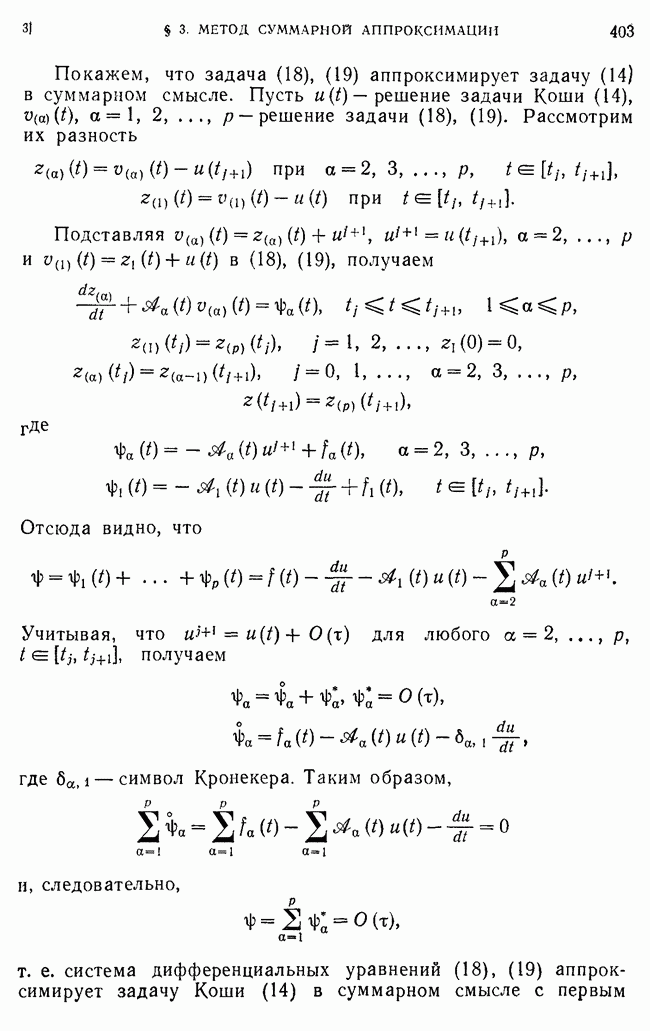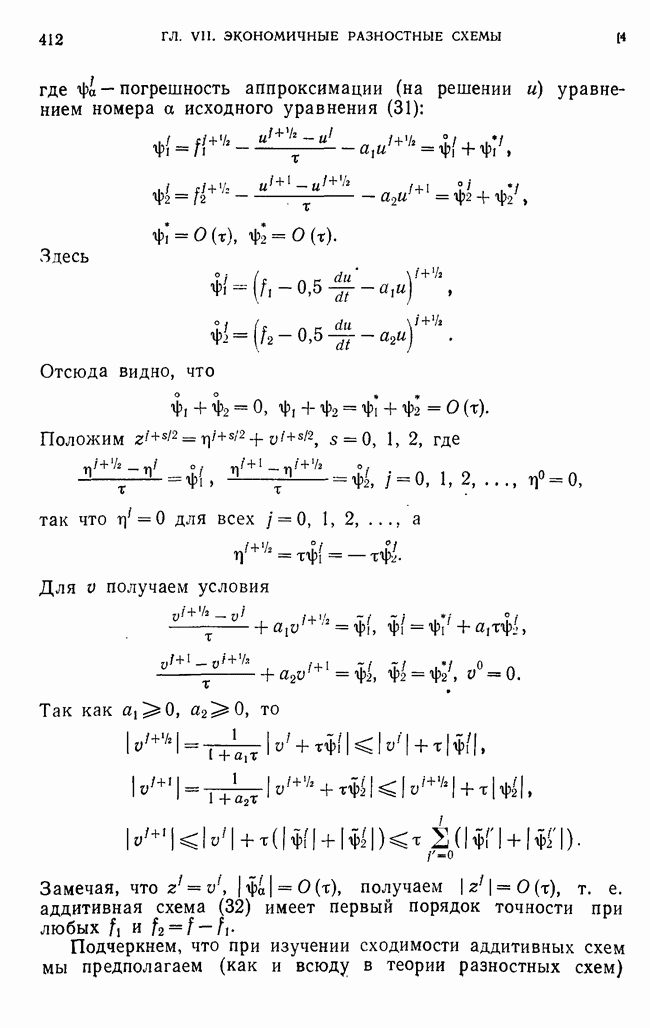| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
Ранее были рассмотрены разностные схемы для простейших дифференциальных уравнений, введены для них основные понятия теории разностных схем и продемонстрированы некоторые приемы исследования устойчивости и сходимости схем. При этом обнаружилась возможность формулировать общие определения и методы на языке функционального анализа, отвлекаясь от конкретного вида разностных схем.
В этой главе проводится систематическая трактовка разностных уравнений как операторных уравнений в абстрактном пространстве и даются соответствующие определения аппроксимации, устойчивости и еходимости.
§ 1. Разностные схемы как операторные уравнения в абстрактных пространствах
1. Разностные схемы как операторные уравнения.
После замены дифференциальных уравнений разностными уравнениями на некоторой сетке  мы получаем систему линейных алгебраических уравнений, которую можно записать в матричной форме
мы получаем систему линейных алгебраических уравнений, которую можно записать в матричной форме

где  — квадратная матрица,
— квадратная матрица,  искомый вектор,
искомый вектор,  -известная правая часть, включающая и правые части краевых условий.
-известная правая часть, включающая и правые части краевых условий.
Каждой матрице  можно поставить в соответствие некоторый линейный оператор А, отображающий пространство
можно поставить в соответствие некоторый линейный оператор А, отображающий пространство  Тогда уравнение (1) примет вид
Тогда уравнение (1) примет вид

где у — искомый,  известный векторы пространства
известный векторы пространства  Оператор А отображает в себя пространство сеточных функций,
Оператор А отображает в себя пространство сеточных функций,
заданных на  и удовлетворяющих однородным граничным условиям.
и удовлетворяющих однородным граничным условиям.
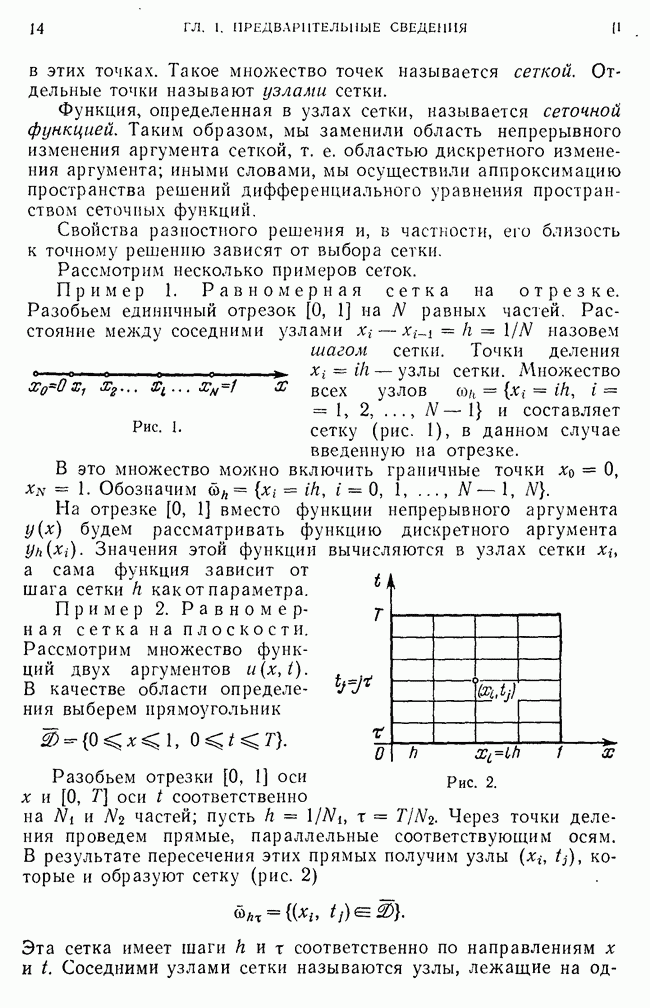
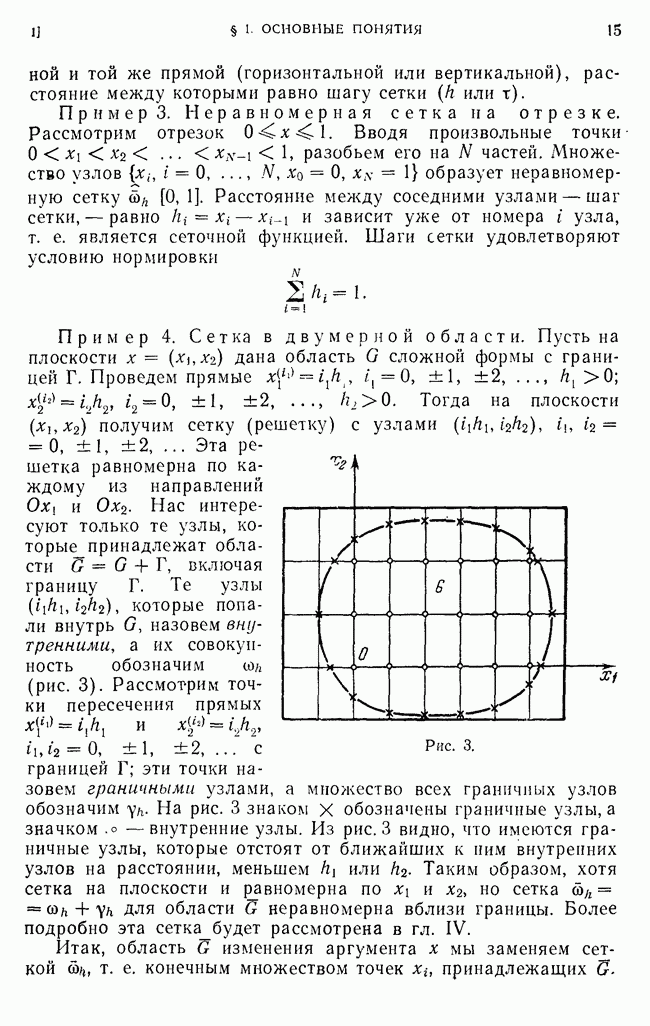
Пример 1. Первая краевая задача. Пусть на отрезке [0, 1] введена равномерная сетка

Ищется решение первой краевой задачи

Вводя вектор  перепишем уравнение (3) в виде (1), где
перепишем уравнение (3) в виде (1), где

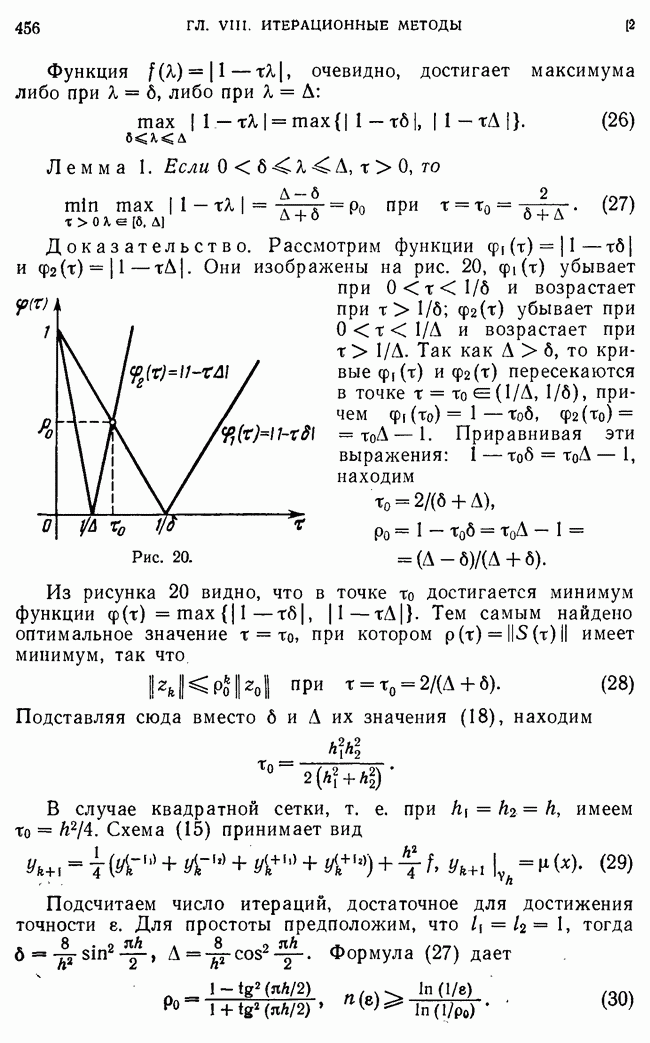
— матрица размера  Вектор правой части
Вектор правой части  учитывает правые части краевых условий (3):
учитывает правые части краевых условий (3):

так что  отличается от только в приграничных узлах
отличается от только в приграничных узлах 
Матрица  определяет оператор
определяет оператор  который преобразует сеточную функцию
который преобразует сеточную функцию  т. е. вектор
т. е. вектор  -мерного пространства в вектор того же пространства (в сеточную функцию
-мерного пространства в вектор того же пространства (в сеточную функцию  Оператор
Оператор  совпадает с оператором
совпадает с оператором  на сеточных функциях, обращающихся в нуль на границе (при
на сеточных функциях, обращающихся в нуль на границе (при  так что
так что  при
при 

Пусть  множество сеточных функций, заданных во внутренних узлах сетки со и, это множество линейно. Вводя на
множество сеточных функций, заданных во внутренних узлах сетки со и, это множество линейно. Вводя на  скалярное произведение
скалярное произведение  и норму
и норму  получим линейное нормированное пространство
получим линейное нормированное пространство 
Определенный выше оператор А линеен и отображает  на
на  (его область определения и область значений совпадают со всем пространством
(его область определения и область значений совпадают со всем пространством 
Оператор А самосопряжен, т. е.

В самом деле,  Пользуясь второй формулой Грина (гл. I, § 2) и учитывая, что
Пользуясь второй формулой Грина (гл. I, § 2) и учитывая, что  совпадает с
совпадает с  на множестве сеточных функций, обращающихся в нуль на границе сетки, получаем
на множестве сеточных функций, обращающихся в нуль на границе сетки, получаем  Оператор А положительно определен, т. е.
Оператор А положительно определен, т. е.

Это следует из леммы 3 (гл. I, § 2, п. 3). Норма оператора А равна

В самом деле, норма самосопряженного положительного оператора в конечномерном пространстве  равна его наибольшему собственному значению,
равна его наибольшему собственному значению,  Так как в данном случае, согласно гл. I, § 2, п. 2
Так как в данном случае, согласно гл. I, § 2, п. 2  то имеет место формула (5). При этом справедливо неравенство
то имеет место формула (5). При этом справедливо неравенство

Рассмотрим оператор

Он самосопряжен в силу второй формулы Грина. Первая формула Грина дает

где  Отсюда следует, что
Отсюда следует, что

т. е. А положительно определен. Его норма, как видно из формул (7) и (5), оценивается так:

Пример 2. Третья краевая задача. Пусть дана та же сетка  что и в примере 1. Рассмотрим разностную краевую задачу третьего рода
что и в примере 1. Рассмотрим разностную краевую задачу третьего рода

Пусть  множество функций, заданных на сетке
множество функций, заданных на сетке

Определим оператор  так:
так:

Полагая  перепишем задачу (9) в виде
перепишем задачу (9) в виде

где

Линейный оператор А отображает  на
на  Введем скалярное произведение
Введем скалярное произведение

и норму 
Оператор А самосопряжен, т. е.  где
где

Пользуясь формулой Грина (гл. I, § 2) и подставляя выражения для  получим
получим

Так как

то

что и требовалось доказать.
Покажем, что если  то оператор А положительно определен:
то оператор А положительно определен:

Для этого воспользуемся тем же приемом, что и при доказательстве леммы 1 из гл. I, § 2. Именно, представив функцию  в виде
в виде

и воспользовавшись  -неравенством, получим
-неравенством, получим

Так как, согласно неравенству Коши — Буняковского,

то из предыдущего неравенства получаем

Аналогично доказывается неравенство

Из последних двух неравенств следует, что

Отсюда и из тождества

положив  получаем (11).
получаем (11).
Для нормы оператора А справедлива оценка

В самом деле, так как 

где 
Учитывая затем, что  и
и

из формулы (12) получим искомую оценку (13).
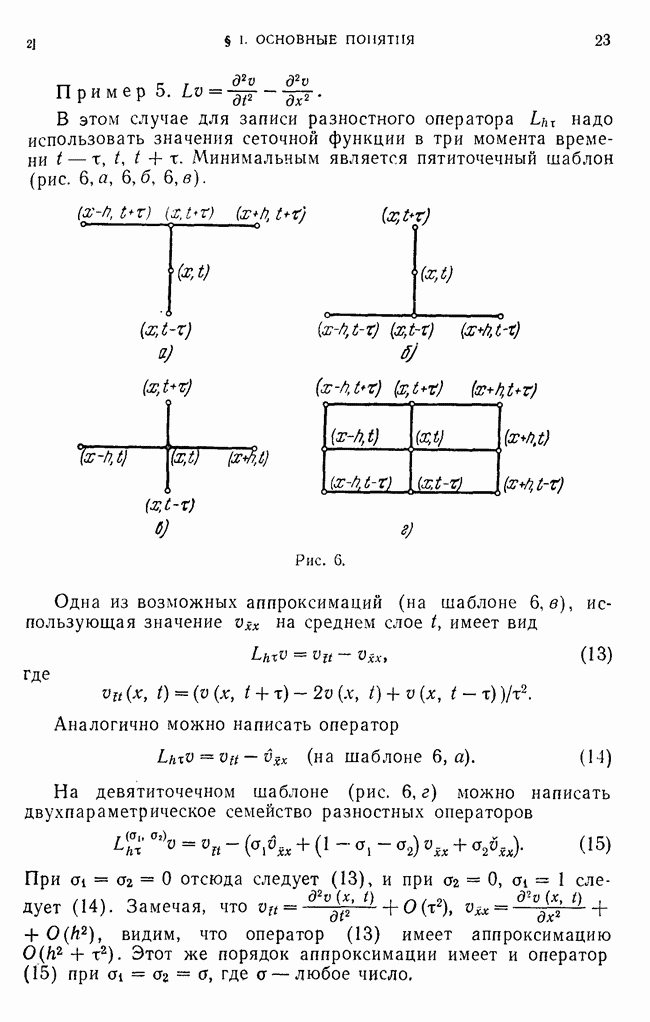
Пример 3. Несамосопряженные операторы. Пусть

сетка на отрезке Рассмотрим разностные операторы

отображающие множество сеточных функций, заданных  и равных нулю при
и равных нулю при  на
на  так что
так что

Из этих формул видно, что  можно рассматривать как операторы из
можно рассматривать как операторы из  на
на 
Пусть  скалярное произведение на
скалярное произведение на  Покажем, что операторы Л- и
Покажем, что операторы Л- и  сопряжены друг другу:
сопряжены друг другу:

В силу формулы суммирования по частям  если
если  при
при  Отсюда и следует сопряженность
Отсюда и следует сопряженность  и
и 
Нетрудно заметить, что  где
где  т. е.
т. е.  Поэтому операторы
Поэтому операторы  положительно определенные:
положительно определенные:

Последнее неравенство справедливо в силу леммы 3 из гл. I, § 2, п. 3.
Обычно рассматриваются операторы из  на
на  вида
вида

Они сопряжены друг другу

и

Из формулы

следует, что

Так как 

т. е.

Несамосопряженные разностные операторы появляются, например, при аппроксимации эллиптических операторов второго порядка, содержащих первые производные. Так, оператор

аппроксимируем разностными операторами  при
при  или
или  при
при  где
где 
Пусть  оператор из
оператор из  на
на  совпадающий с
совпадающий с  при
при  Операторы
Операторы  действующие из
действующие из  на
на  положительно определены при любом
положительно определены при любом  В самом деле,
В самом деле,

Отсюда находим

Так как  то, в силу неравенства треугольника для норм, получаем
то, в силу неравенства треугольника для норм, получаем

Заметим, что если оператор  аппроксимировать выражением
аппроксимировать выражением  при
при  то вместо
то вместо  в (19) получим
в (19) получим  и оператор
и оператор  будет положительно определенным только при
будет положительно определенным только при 
Мы ограничились здесь простейшими примерами.
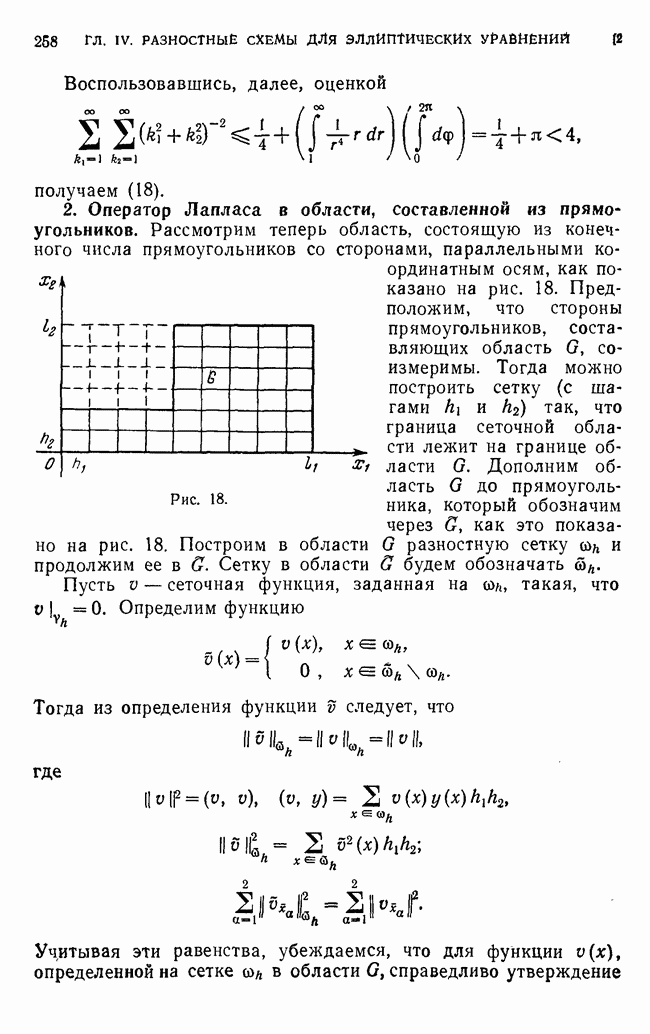
В гл. IV аналогичными методами изучались разностные операторы, аппроксимирующие эллиптические операторы (в частности, оператор Лапласа) в прямоугольных областях.
Если исходный дифференциальный оператор самосопряжен и положительно определен, то и разностный оператор надо строить так, чтобы он обладал указанными свойствами в сеточном пространстве. Этого можно добиться, используя, например, метод баланса (интегро-интерполяционный метод, см. гл. III) или вариационный метод для построения разностных схем (см., например, Ю. А. Гусман, А. А. Оганесян [1]).
Из предыдущих примеров видно, что разностные уравнения можно трактовать как операторные уравнения с операторами в линейном нормированном конечномерном пространстве. Для этих операторов характерно то, что они отображают все пространство в себя.
Перейдем к изложению теории разностных схем как операторных уравнений.
2. Устойчивость разностной схемы.
Пусть даны два линейных нормированных пространства и зависящих от параметра  являющегося вектором некоторого нормированного пространства,
являющегося вектором некоторого нормированного пространства,  норма вектора
норма вектора  Рассмотрим линейный оператор
Рассмотрим линейный оператор  с областью определения
с областью определения  множеством значений
множеством значений  Пусть
Пусть  -нормы в и
-нормы в и
Рассмотрим уравнение

где  заданный вектор.
заданный вектор.
Меняя параметр  мы получим множество решений
мы получим множество решений  уравнения (21). Операторное уравнение (21), зависящее от параметра
уравнения (21). Операторное уравнение (21), зависящее от параметра  будем называть разностной схемой.
будем называть разностной схемой.
Будем говорить, что схема (21) корректна (задача (21) корректно поставлена) у если при всех достаточно малых
1) решение  уравнения (21) существует и единственно при любых
уравнения (21) существует и единственно при любых  (схема (21) однозначно разрешима),
(схема (21) однозначно разрешима),
2) решение  уравнения (21) непрерывно зависит от
уравнения (21) непрерывно зависит от  причем эта зависимость равномерна по h {схема (21) устойчива), иными словами, существует такая положительная постоянная
причем эта зависимость равномерна по h {схема (21) устойчива), иными словами, существует такая положительная постоянная  не зависящая от
не зависящая от  что для решения уравнения (21) имеет место оценка (при любых
что для решения уравнения (21) имеет место оценка (при любых 

Разрешимость схемы (21) означает, что существует обратный оператор  т. е.
т. е.

Устойчивость схемы означает, что обратный оператор  из в равномерно по
из в равномерно по  ограничен:
ограничен:

Из (23) и (24) следует оценка (22):

В случае, когда  гильбертово пространство и
гильбертово пространство и  ограниченный оператор с областью определения
ограниченный оператор с областью определения  для корректности схемы достаточно требовать, чтобы оператор
для корректности схемы достаточно требовать, чтобы оператор  был положительно определен:
был положительно определен:

где  и
и  постоянная, не зависящая от
постоянная, не зависящая от 
В самом деле, из теоремы 4 гл. I, § 3 следует существование оператора  определенного на всем пространстве
определенного на всем пространстве  и ограниченного:
и ограниченного:

Поэтому для решения уравнения (21) верна априорная оценка

Заметим, что самосопряженность оператора  в случае вещественного пространства
в случае вещественного пространства  не предполагается.
не предполагается.
Если  комплексное гильбертово пространство, то самосопряженность
комплексное гильбертово пространство, то самосопряженность  является следствием его положительности.
является следствием его положительности.
Для доказательства устойчивости схемы (21) требуется получить априорную оценку вида (22). Вывод некоторых априорных оценок для операторного уравнения (21) будет дан в п. 4.
3. Сходимость и аппроксимация.
Пусть  — линейные нормированные пространства с нормами
— линейные нормированные пространства с нормами  Предположим, что
Предположим, что
1) существуют линейные операторы  из в и из
из в и из  в так что
в так что

2) выполнены условия согласования норм

Пусть  вектор из Нас будет интересовать сходимость
вектор из Нас будет интересовать сходимость  при
при  к некоторому фиксированному элементу и из
к некоторому фиксированному элементу и из 
Будем говорить, что
1)  , где сходится к элементу
, где сходится к элементу  если
если

2)  сходится к пер со скоростью
сходится к пер со скоростью  (или аппроксимирует и с точностью
(или аппроксимирует и с точностью  если при всех достаточно малых
если при всех достаточно малых  имеет место оценка
имеет место оценка

где  постоянная, не зависящая от А.
постоянная, не зависящая от А.
Пусть  решение задачи (21). Будем говорить, что
решение задачи (21). Будем говорить, что
1) схема (21) сходится, если существует элемент и  такой, что выполнено (28),
такой, что выполнено (28),
2) схема имеет точность  если выполнено (29). Введем понятие погрешности аппроксимации на элементе
если выполнено (29). Введем понятие погрешности аппроксимации на элементе  Для этого напишем уравнение для разности
Для этого напишем уравнение для разности  Подставляя
Подставляя  в (21), получим
в (21), получим

Правую часть  зависящую от выбора элемента и из назовем погрешностью аппроксимации на элементе
зависящую от выбора элемента и из назовем погрешностью аппроксимации на элементе  для схемы (21). Очевидно, что
для схемы (21). Очевидно, что  есть невязка, возникающая при замене в уравнении
есть невязка, возникающая при замене в уравнении  элементом
элементом  Будем говорить, что
Будем говорить, что
1) схема (21) обладает аппроксимацией на элементе  если
если

2) схема (21) имеет  порядок аппроксимации на элементе если при всех достаточно малых
порядок аппроксимации на элементе если при всех достаточно малых 

где  Положительная постоянная, не зависящая от
Положительная постоянная, не зависящая от 
Установим теперь связь между устойчивостью, аппроксимацией на элементе  и сходимостью к этому элементу для схемы (21).
и сходимостью к этому элементу для схемы (21).
Если схема (21) корректна, то и задача (30) для 2д также корректна. Поэтому для ее решения верна оценка

Отсюда следует
Теорема 1. Если схема (21) корректна и обладает аппроксимацией на некотором элементе и  то она сходится, точнее, решение
то она сходится, точнее, решение  задачи (21) при
задачи (21) при  сходится к этому элементу
сходится к этому элементу  причем порядок точности схемы (21) совпадает с порядком аппроксимации.
причем порядок точности схемы (21) совпадает с порядком аппроксимации.
До сих пор мы говорили о сходимости схемы и погрешности аппроксимации на некотором фиксированном элементе и  Однако, если и принадлежит области определения некоторого линейного оператора
Однако, если и принадлежит области определения некоторого линейного оператора  действующего из в то
действующего из в то  Поэтому можно считать, что и есть решение уравнения
Поэтому можно считать, что и есть решение уравнения

и, следовательно, говорить об аппроксимации этого уравнения разностной схемой. Мы не вводили уравнение (34) лишь потому, что нигде в определениях не используются никакие предположения относительно оператора  Всюду мы имели дело лишь с элементом и
Всюду мы имели дело лишь с элементом и 
Однако, если и есть решение некоторого уравнения (34), то можно говорить, как это обычно делается, об аппроксимации уравнения (34) схемой (21) на решении уравнения (34), о сходимости к решению уравнения (34) и т. д.
Поскольку имеется понятие аппроксимации элемента  из множеством
из множеством  из
из  то можно говорить об аппроксимации
то можно говорить об аппроксимации  элементами
элементами  оператора оператором А.
оператора оператором А.
1)  аппроксимирует
аппроксимирует  с порядком
с порядком  если
если

2) оператор  аппроксимирует оператор
аппроксимирует оператор  с порядком
с порядком  если для любого
если для любого  справедлива оценка
справедлива оценка

Очевидно, что если выполнены условия (35) и (36), то схема (21) имеет  порядок аппроксимации на решении
порядок аппроксимации на решении  уравнения (34).
уравнения (34).
В самом деле, так как  то
то

и

если выполнены условия (35) и (36).
Еще раз подчеркнем, что для оценки порядка точности схемы надо оценить ее порядок аппроксимации лишь на решении исходной задачи.
4. Некоторые априорные оценки.
Рассмотрим ряд простейших априорных оценок решения уравнения (21), вид которых зависит от информации об операторе схемы. Эти оценки типичны для разностных эллиптических задач.
Для упрощения записи будем в тех случаях, когда это не вызовет недоразумений, опускать индекс  Итак, пусть дано уравнение
Итак, пусть дано уравнение

где  - линейный ограниченный оператор, заданный на вещественном гильбертовом пространстве
- линейный ограниченный оператор, заданный на вещественном гильбертовом пространстве  известный, у — искомый элементы из
известный, у — искомый элементы из 
Будем предполагать, что задача (37) разрешима при любых правых частях  (т. е., что существует оператор
(т. е., что существует оператор  с областью определения
с областью определения 
Все постоянные, встречающиеся ниже, предполагаются не зависящими от 
Пусть  -скалярное произведение,
-скалярное произведение,  норма в
норма в  Запись
Запись  будет означать, что А — самосопряженный и положительный оператор. Введем обозначения
будет означать, что А — самосопряженный и положительный оператор. Введем обозначения

Лемма 1. Пусть оператор А имеет ограниченный обратный оператор  с областью определения
с областью определения  Тогда, если
Тогда, если  то верны оценки (для любых
то верны оценки (для любых  из
из  :
:

Доказательство. Так как  где
где  единичный оператор, то
единичный оператор, то  Применяя затем обобщенное неравенство Коши — Буняковского, получим
Применяя затем обобщенное неравенство Коши — Буняковского, получим

Неравенство (39) следует из (38) и  -неравенства.
-неравенства.
Приведем ряд априорных оценок для решения уравнения (37).
1) Имеют место точные оценки

Действительно, из уравнения (37) имеем

так как  Формула (41) очевидна.
Формула (41) очевидна.
2) Если  то
то

Это следует из (40), так как  дает
дает  и
и

3) Пусть в уравнении  где
где  самосопряженный положительный оператор, имеющий обратный оператор
самосопряженный положительный оператор, имеющий обратный оператор  Тогда
Тогда

Умножая (37) скалярно на у, получим энергетическое тождество

Так как

и, согласно лемме 1,

то из (44) получаем  т. е.
т. е. 
4) Пусть в уравнении  перестановочны. Тогда справедлива оценка
перестановочны. Тогда справедлива оценка

Достаточно показать, что  и воспользоваться (41). Из условия
и воспользоваться (41). Из условия  получаем
получаем

Учитывая перестановочность операторов  имеем отсюда
имеем отсюда

что и требовалось,
5) Пусть  где
где

 попарно перестановочны. Тогда для решения уравнения (37) справедлива оценка
попарно перестановочны. Тогда для решения уравнения (37) справедлива оценка

Для простоты ограничимся случаем 

Отсюда и из (45) следует (46).
Пример 1. Схема повышенного порядка точности в прямоугольнике

Пусть

— сетка в  Схема
Схема  для задачи Дирихле имеет вид
для задачи Дирихле имеет вид

где  граница сетки
граница сетки  (см. гл. IV, § 1).
(см. гл. IV, § 1).
Пусть  пространство сеточных функций, заданных во внутренних узлах
пространство сеточных функций, заданных во внутренних узлах  сетки,
сетки,  пространство сеточных функций, заданных на
пространство сеточных функций, заданных на  и равных нулю на
и равных нулю на  Введем на скалярное произведение и норму
Введем на скалярное произведение и норму

где  Определим аналогично примеру 1 п. 1 операторы
Определим аналогично примеру 1 п. 1 операторы 

где  . Операторы
. Операторы  , самосопряженные,
, самосопряженные,  , при
, при  действует из
действует из  Задача (47) сводится к уравнению
Задача (47) сводится к уравнению

где  Операторы
Операторы  самосопряженные,
самосопряженные,  положительно определенные,
положительно определенные,  перестановочные. Поэтому
перестановочные. Поэтому  Учитывая, что
Учитывая, что

где  получаем
получаем

Отсюда следует, что

Операторы  перестановочны,
перестановочны,  Поэтому для уравнения (48) справедливы оценки (45) и (46):
Поэтому для уравнения (48) справедливы оценки (45) и (46):

где

Пользуясь теоремой вложения (гл. IV, § 2), получаем

Из этой оценки следует равномерная сходимость со скоростью  схемы (47) к решению задачи Дирихле для уравнения Пуассона.
схемы (47) к решению задачи Дирихле для уравнения Пуассона.
Аналогично убеждаемся в справедливости оценки (50) для схемы  в параллелепипеде. В этом случае
в параллелепипеде. В этом случае

имеют место оценки  где
где  так что
так что  Оценка (50) получена В. Б. Андреевым [2].
Оценка (50) получена В. Б. Андреевым [2].
Покажем как вычисляются негативные нормы вида  для некоторых разностных операторов.
для некоторых разностных операторов.
При вычислении таких норм будем использовать тождество

где у есть решение операторного уравнения (37). Рассмотрим первую краевую задачу

Введем пространство функций  определенных на сетке
определенных на сетке  и равных нулю при
и равных нулю при  Как обычно,
Как обычно,

Задачу (52) можно записать в виде операторного уравнения (37), где 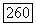 оператор
оператор 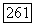 определен тождествами
определен тождествами

и правая часть 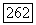 есть вектор
есть вектор

Ранее было показано, что если 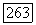 то оператор (53) — самосопряженный и положительно определенный, так что оператор
то оператор (53) — самосопряженный и положительно определенный, так что оператор 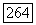 существует.
существует.
Лемма 2. Норму 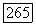 для оператора (53) можно представить в виде
для оператора (53) можно представить в виде

где

В частности, для оператора (53) с 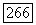 имеем
имеем

Доказательство. Представим правую часть уравнения (52) в виде 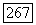 где задано соотношениями (55). Из уравнения
где задано соотношениями (55). Из уравнения

получим тогда, что

Для нахождения постоянной С поделим (57) на 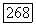 и просуммируем по
и просуммируем по 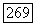 от 1 до
от 1 до 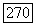

т. е.

Далее, согласно (51), имеем

Учитывая уравнение (57), получаем отсюда

что и требовалось.
Заметим, что тождество (54) справедливо и в случае, когда функция 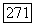 определена следующим образом:
определена следующим образом:

Следствие. 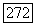 для оператора (53) имеет место оценка
для оператора (53) имеет место оценка

где

либо

Рассмотрим теперь третью краевую задачу (9). Введем также, как и в примере 2 п. 1, пространство 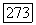 состоящее из функций, заданных на сетке
состоящее из функций, заданных на сетке

со скалярным произведением

Задачу (9) запишем в виде (37), где

Лемма 3. Норму 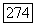 для оператора (59) можно представить в виде
для оператора (59) можно представить в виде

где

Доказательство. Введем точки 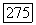 и положим
и положим 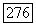 Тогда левое граничное условие в (9) можно записать в виде
Тогда левое граничное условие в (9) можно записать в виде

где 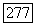
Точно так же правое граничное условие в (9) принимает вид

где
Таким образом, задача (9) эквивалентна первой краевой задаче

где 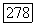
Заметим теперь, что если 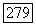 решение задачи (9), то
решение задачи (9), то

Поэтому применяя к (61) лемму 2, получаем (60).
Следствие. Если 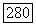 оператора (59) справедлива оценка
оператора (59) справедлива оценка

Пример 2. Пусть 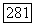 где
где 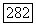 Тогда
Тогда 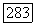 и
и

т. е.  Поэтому, в силу (43), для задачи
Поэтому, в силу (43), для задачи

верна оценка

или, учитывая следствие из леммы 2,

Применяя теорему вложения (см. лемму 1, гл. I, § 2), имеем оценку

Эта оценка была получена в гл. I, § 2 методом энергетических неравенств.
Оценкой (43) можно пользоваться, если А — разностная аппроксимация оператора

область 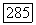 параллелепипед,
параллелепипед, 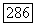 граница
граница 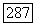 сетка
сетка  равномерна по каждому
равномерна по каждому 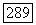 В этом случае, согласно гл. IV, § 1,
В этом случае, согласно гл. IV, § 1,

Рассмотрим теперь операторы специального вида (дивергентные или консервативные)

где 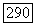 линейные операторы:
линейные операторы:  действует из
действует из 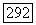 в пространство
в пространство 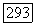 со скалярным произведением
со скалярным произведением 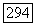 и нормой
и нормой 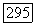 действует из
действует из 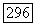 в
в 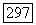 .
.
Операторы 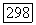 сопряжены в следующем смысле
сопряжены в следующем смысле

Пусть 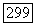 тогда
тогда

т. е. 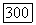 где
где  Оператор А о самосопряжен,
Оператор А о самосопряжен,

Поэтому имеет место оценка (43), которая, если существуют  принимает вид
принимает вид

В самом деле,

Оценка (64) упрощается в том случае, когда правая часть  уравнения (37) имеет специальный вид,
уравнения (37) имеет специальный вид,  Умножая (37) скалярно на у, получим
Умножая (37) скалярно на у, получим

Отсюда и из неравенств

следует оценка

Отметим, что в этом случае не требуется существования оператора 
Приведем пример построения разложения (63). Пример 3. Третья краевая задача:

В данном случае оператор А имеет вид (см. пример 2 п. 1):

Чтобы представить оператор (66) в виде (63), удобно ввести дополнительную сетку

И рассматривать пространство функций  определенных на
определенных на  со скалярным произведением
со скалярным произведением

Как и ранее,  — пространство функций, определенных на
— пространство функций, определенных на  со скалярным произведением
со скалярным произведением

Определим операторы  следующим образом:
следующим образом:

Нетрудно видеть, что  где оператор
где оператор  определен формулами
определен формулами

Очевидно, что  — самосопряженный в
— самосопряженный в  , оператор и
, оператор и

Покажем теперь, что операторы  являются взаимно сопряженными в следующем смысле:
являются взаимно сопряженными в следующем смысле:

Действительно,

Аналогично строится разложение (63) и в случае краевых условий первого рода  Единственное отличие
Единственное отличие
состоит в том, что  определяется как пространство функций, заданных на
определяется как пространство функций, заданных на  и обращающихся в нуль при
и обращающихся в нуль при  со скалярным произведением
со скалярным произведением 
Оператор вида  очевидно, соответствует разностному оператору
очевидно, соответствует разностному оператору  Для него также нетрудно получить оценки, аналогичные (64).
Для него также нетрудно получить оценки, аналогичные (64).
Мы ограничились простейшими примерами, показывающими, как надо использовать для конкретных задач априорные оценки, полученные для операторного уравнения 
5. Коэффициентная устойчивость уравнений первого рода.
Пусть А — линейный оператор, действующий из гильбертова пространства Рассмотрим операторное уравнение первого рода:
Рассмотрим операторное уравнение первого рода:

Задача (67) называется корректно поставленной, если существует единственное решение уравнения (67) для любых  и это решение непрерывно зависит от правой части
и это решение непрерывно зависит от правой части  так что
так что

где  решение уравнения (67) с возмущенной правой частью
решение уравнения (67) с возмущенной правой частью 

 - некоторые нормы на множестве
- некоторые нормы на множестве  .
.
При постановке задачи (67) задается не только правая часть, но и оператор А. Если, например, А — дифференциальный или разностный оператор, то должны быть заданы коэффициенты уравнения.
Естественно требовать, чтобы решение задачи (67) непрерывно зависело не только от возмущения правой части, но и от возмущения оператора А задачи (например, от коэффициентов разностного оператора). Это требование, возникшее при изучении разностных схем, было названо в работе А. Н. Тихонова и А. А. Самарского [1] свойством коэффициентной устойчивости или ко-устойчивости.
Устойчивость решения уравнения (67) относительно возмущения правой части  и возмущения оператора А будем называть сильной устойчивостью.
и возмущения оператора А будем называть сильной устойчивостью.
Вопрос ставится так: даны две задачи

где  линейные операторы, область определения которых совпадает с
линейные операторы, область определения которых совпадает с  произвольные векторы из
произвольные векторы из  . Требуется найти оценку для величины возмущения решения
. Требуется найти оценку для величины возмущения решения

через величины возмущений 
Предположим, что операторы  существуют. Будем считать, кроме того, что
существуют. Будем считать, кроме того, что  самосопряженные положительные операторы. Подставим
самосопряженные положительные операторы. Подставим  в (71):
в (71):

Применим  к обеим частям равенства (72):
к обеим частям равенства (72):

Вектор  будем оценивать в норме
будем оценивать в норме  пространства
пространства  в негативной норме
в негативной норме  энергетического пространства 1. Преобразуем выражение
энергетического пространства 1. Преобразуем выражение

и оценим его по норме

В качестве меры возмущения оператора  возьмем относительное изменение энергии
возьмем относительное изменение энергии  оператора
оператора  т. е. будем предполагать, что
т. е. будем предполагать, что

Отсюда следуют неравенства

Покажем, что из (76) следует (77).
Рассмотрим разность  и положим
и положим 

где  Положим
Положим 

Так как  то
то  Тем самым доказано, что из неравенства
Тем самым доказано, что из неравенства  следует неравенство
следует неравенство  для любых
для любых  Неравенства (77) эквивалентны неравенствам
Неравенства (77) эквивалентны неравенствам

В самом деле,

Итак, из (74) следует

По определению нормы самосопряженного оператора

Подставляя эту оценку в (74), получаем из (72):

или

Пусть известен некоторый оператор  имеющий более простую структуру, чем А, и удовлетворяющий условию
имеющий более простую структуру, чем А, и удовлетворяющий условию

Тогда, если оператор  осуществует, то
осуществует, то

Таким образом доказана следующая теорема сравнения: Теорема 2. Пусть и — решение уравнения (67),  — решение уравнения (70),
— решение уравнения (70),  самосопряженные положительные операторы, имеющие обратные. Тогда, если выполнены условие (75) и неравенство
самосопряженные положительные операторы, имеющие обратные. Тогда, если выполнены условие (75) и неравенство  то справедливы оценки
то справедливы оценки

Первое слагаемое в правой части (78) есть величина возмущения правой части  второе слагаемое содержит коэффициент а — величину относительного возмущения оператора.
второе слагаемое содержит коэффициент а — величину относительного возмущения оператора.
Пример. Пусть  множество сеточных функций, заданных на
множество сеточных функций, заданных на  и обращающихся в нуль при
и обращающихся в нуль при  Рассмотрим разностные операторы
Рассмотрим разностные операторы

Вводя обычным образом скалярное произведение и используя разностные формулы Грина, получим неравенства

Согласно лемме 2, имеем

Таким образом, оценка (79) принимает вид

или, в силу неравенства 

Выясним, что означает условие (75). Его можно записать в виде

откуда следует, что (75) будет выполнено, если потребовать

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка