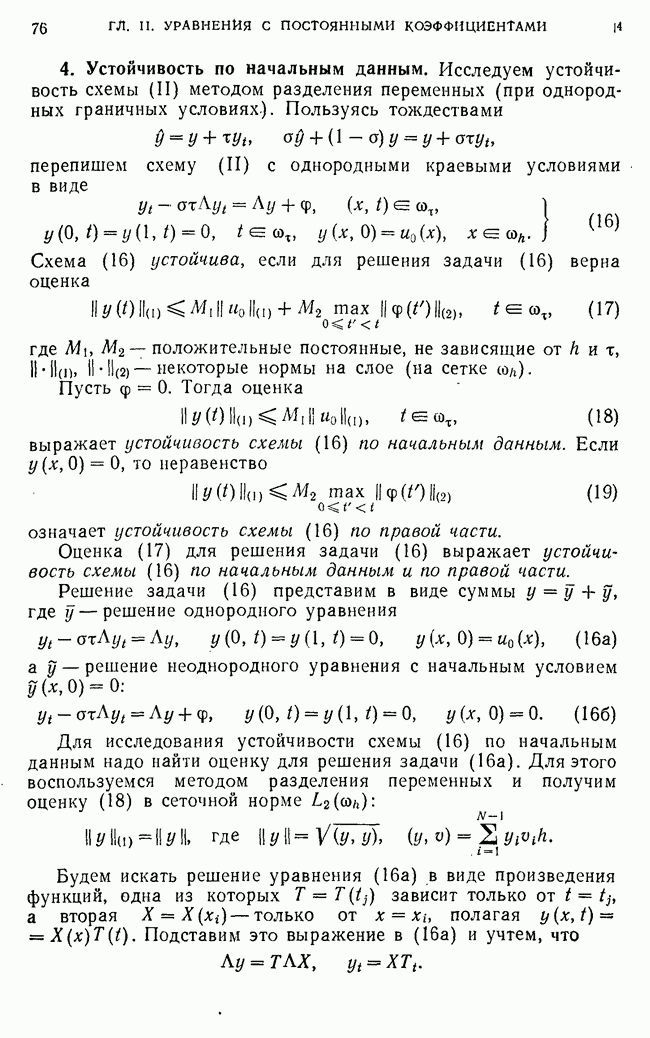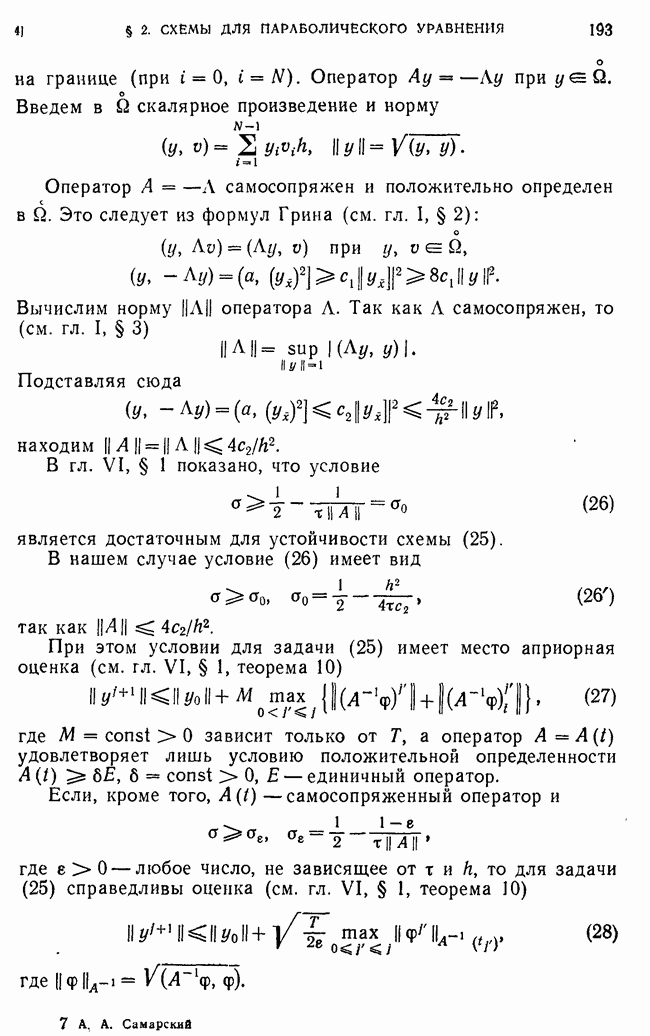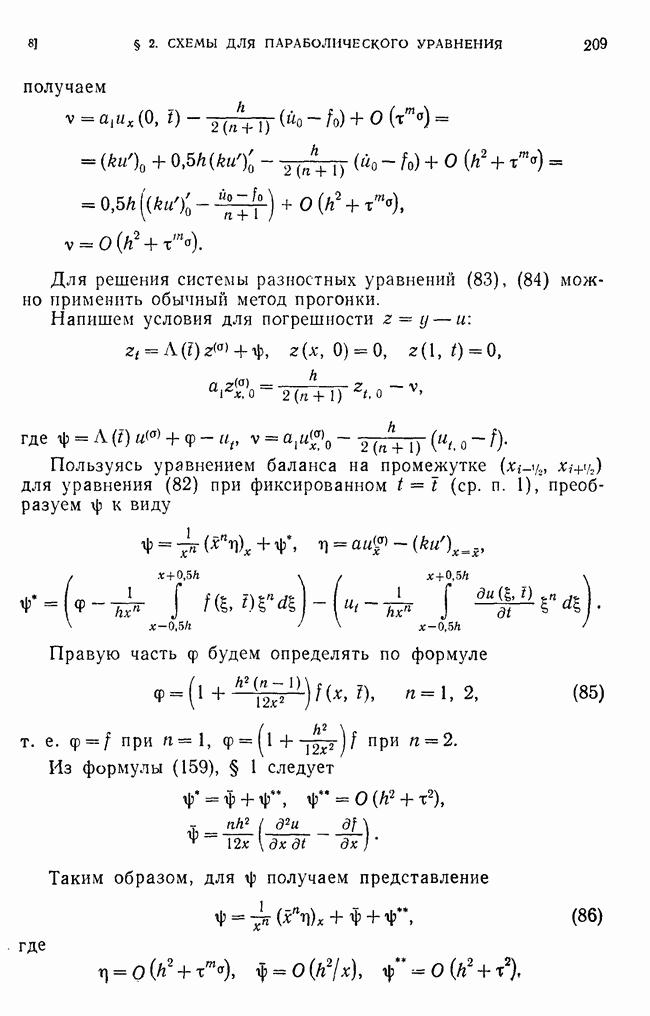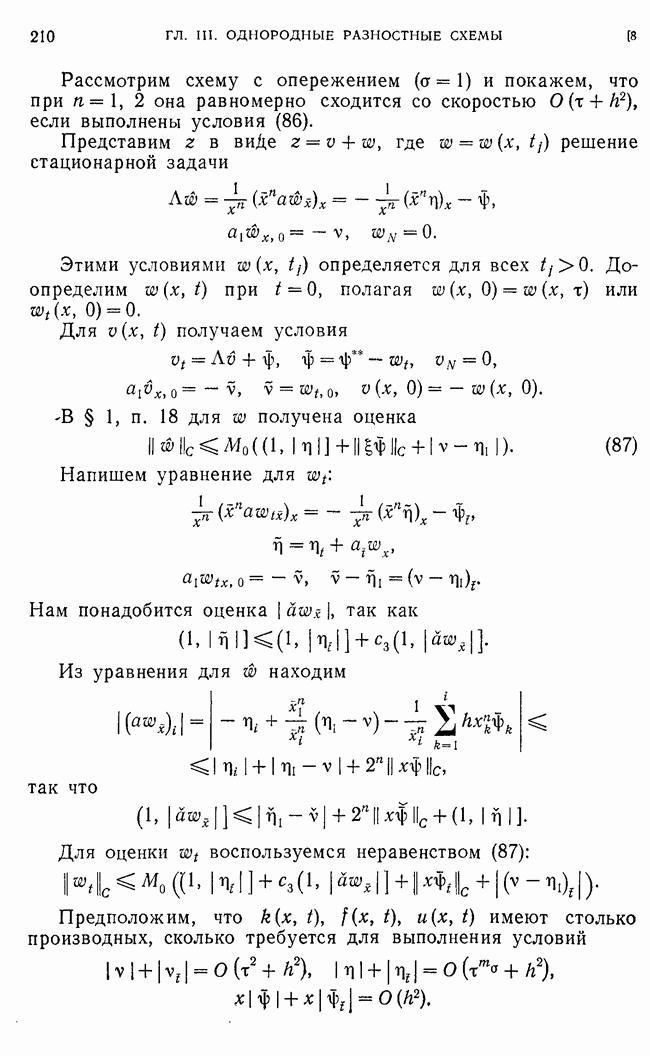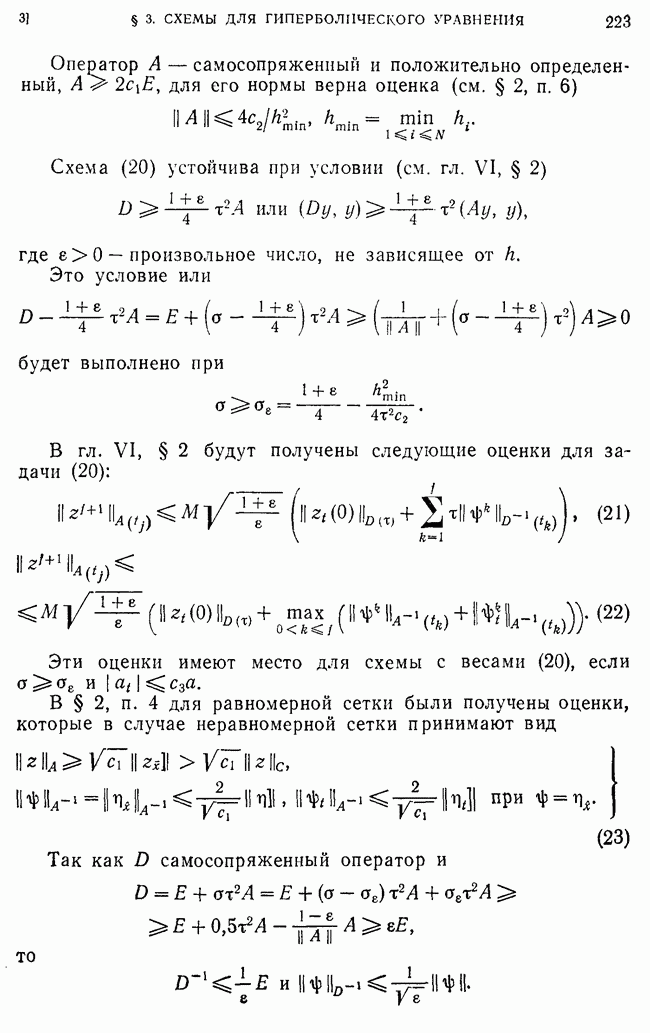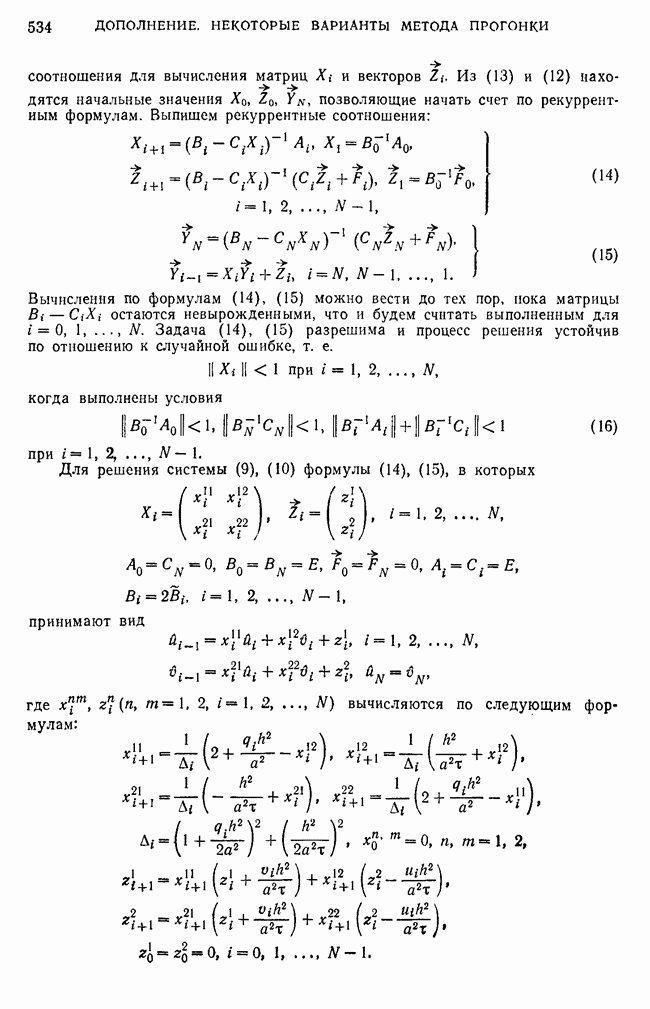| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2. Матричная прогонка
Для решения систем разностных уравнений часто используют метод матричной прогошси, который поясняется ниже на частном примере.
Рассмотрим уравнение Шредингера, в случае когда потенциал  обладает следующими свойствами:
обладает следующими свойствами:  непрерывен при
непрерывен при  при
при  и при
и при  Это соответствует краевой задаче
Это соответствует краевой задаче

где I — мнимая единица,  постоянная Планка,
постоянная Планка,  масса частицы. Без ограничения общности будем считать, что
масса частицы. Без ограничения общности будем считать, что

Введем обозначения

и представим  в виде
в виде

где  - действительная и мнимая части функции
- действительная и мнимая части функции  Из (1), (2) для определения
Из (1), (2) для определения  получаем задачу
получаем задачу

Введем сетки

и аппроксимируем задачу (6), (7) системой разностных уравнений

Запишем систему (8) в векторной форме

где

Задача (9) является частным случаем следующей задачи: найти векторы  удовлетворяющие уравнению
удовлетворяющие уравнению

и краевым условиям

где  - квадратные матрицы. Предположим существование матриц
- квадратные матрицы. Предположим существование матриц 
Решение задачи (11), (12) будем искать в виде

где  неопределенные пока матрицы и векторы. Из формулы (13) и уравнения (11) находятся (как и в случае обычной прогонки) рекуррентные
неопределенные пока матрицы и векторы. Из формулы (13) и уравнения (11) находятся (как и в случае обычной прогонки) рекуррентные
соотношения для вычисления матриц  и векторов
и векторов  Из (13) и (12) находятся начальные значения
Из (13) и (12) находятся начальные значения  позволяющие начать счет по рекуррентным формулам. Выпишем рекуррентные соотношения:
позволяющие начать счет по рекуррентным формулам. Выпишем рекуррентные соотношения:

Вычисления по формулам (14), (15) можно вести до тех пор, пока матрицы  остаются невырожденными, что и будем считать выполненным для
остаются невырожденными, что и будем считать выполненным для  Задача (14), (15) разрешима и процесс решения устойчив по отношению к случайной ошибке, т. е.
Задача (14), (15) разрешима и процесс решения устойчив по отношению к случайной ошибке, т. е.

когда выполнены условия

при 
Для решения системы (9), (10) формулы (14), (15), в которых

 принимают вид
принимают вид

где  вычисляются по следующим формулам:
вычисляются по следующим формулам:

Условие устойчивости (16) приводит к требованию  Вычислив норму
Вычислив норму  приходим к условию
приходим к условию

которое очевидно выполнено.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
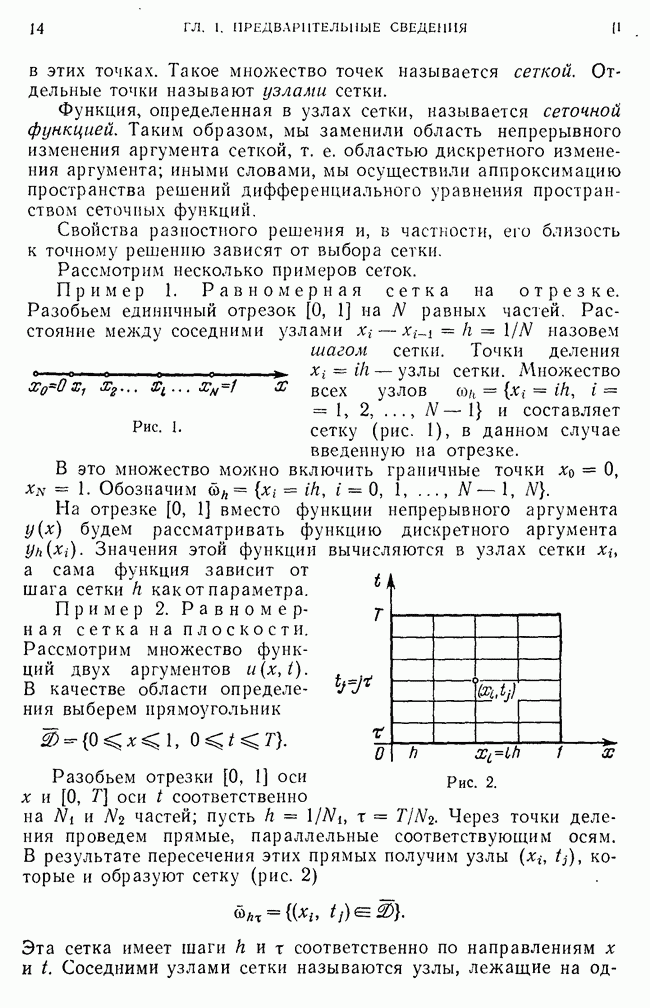
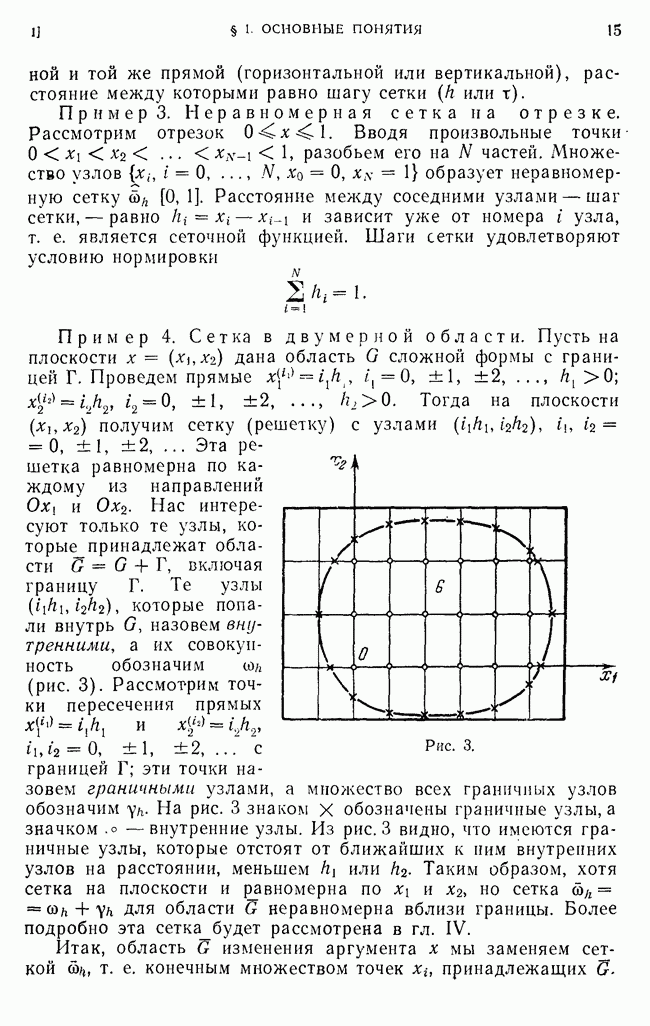
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
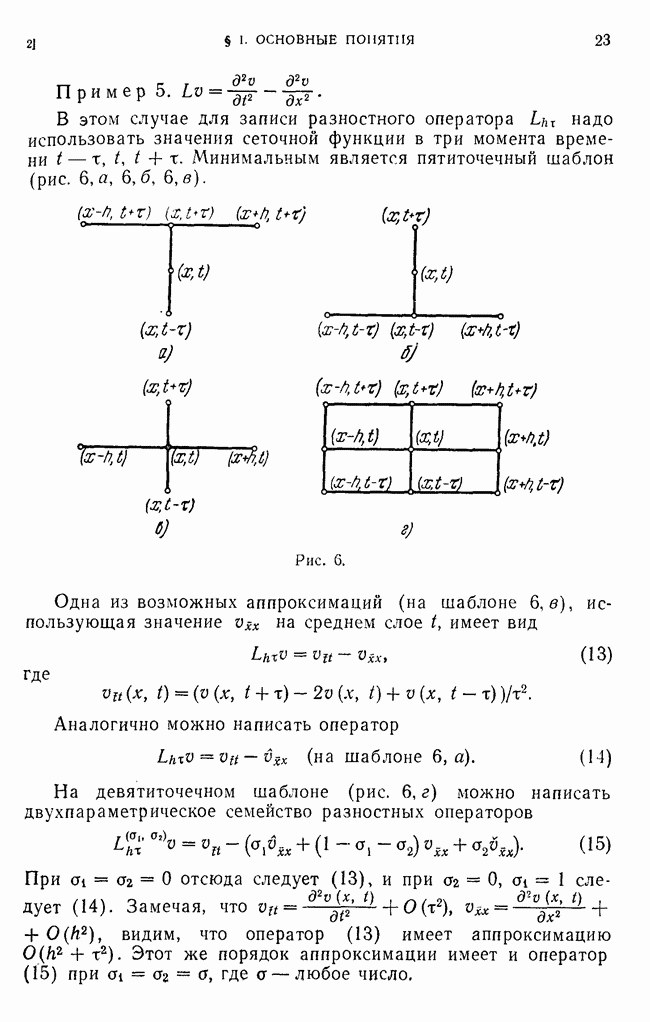
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
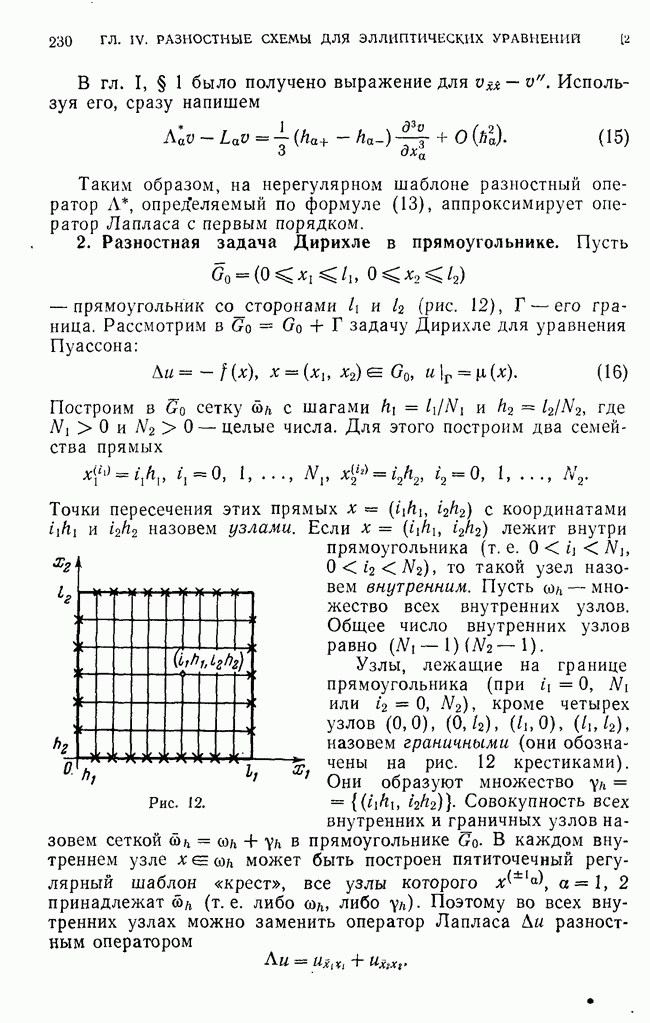
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
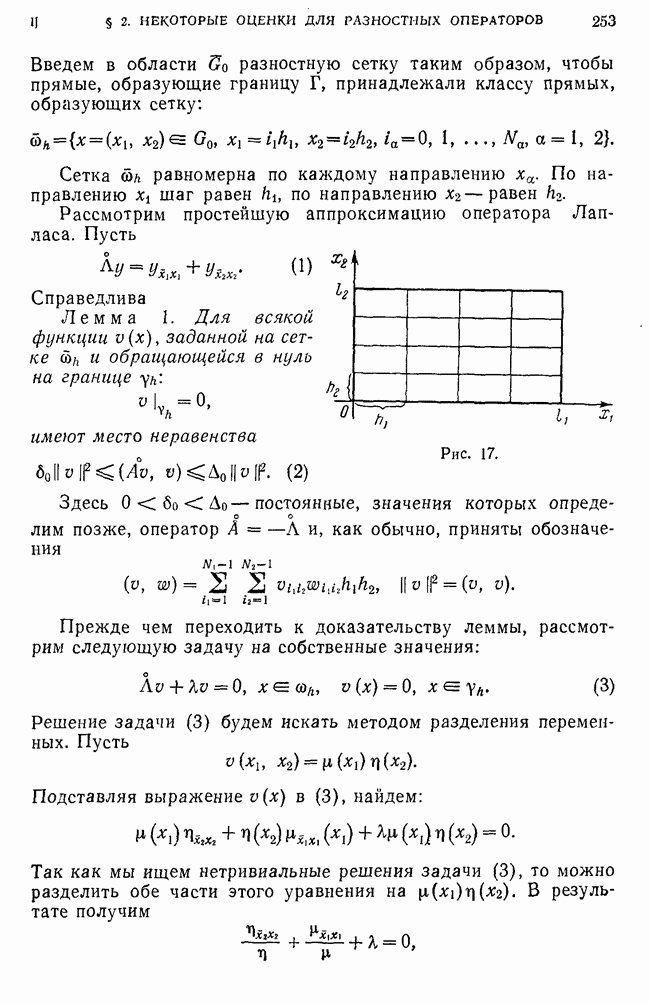
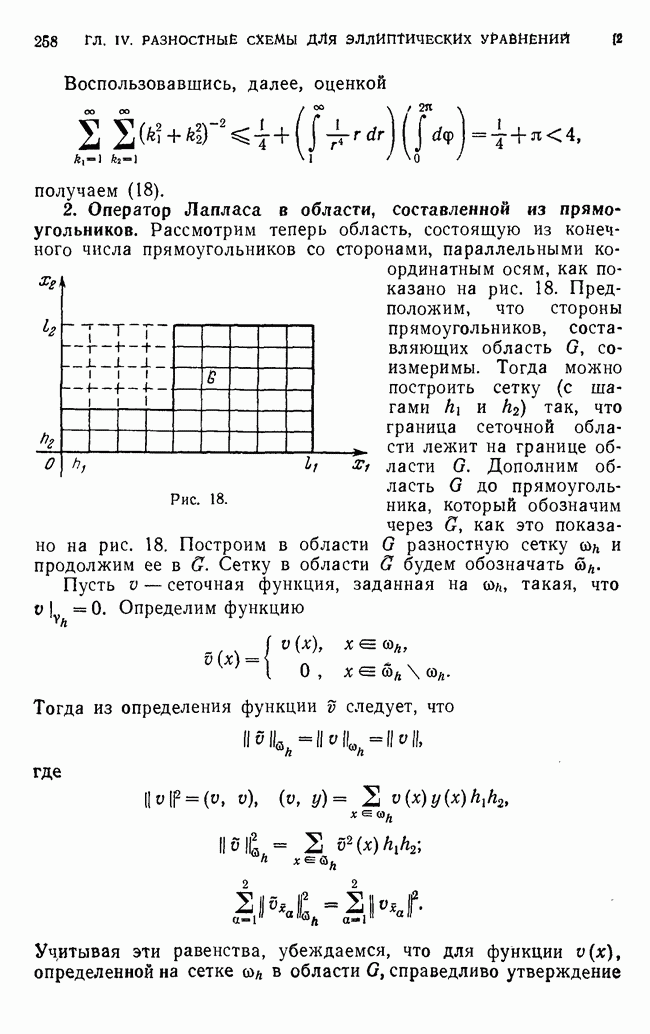
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка