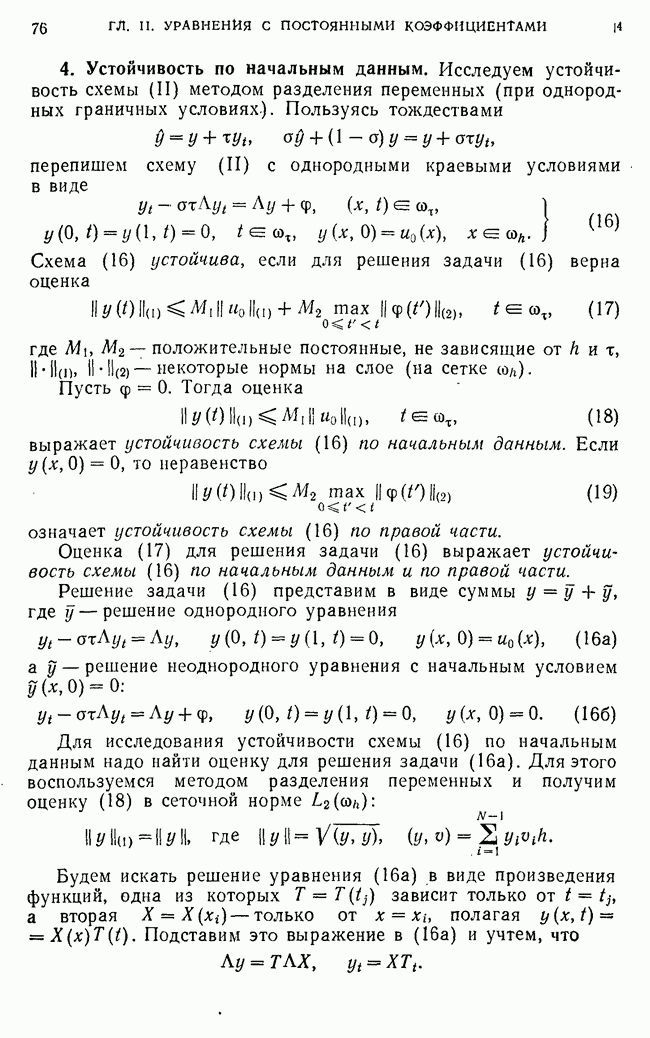| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
Этот параграф посвящен получению некоторых неравенств для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа. Эти неравенства в дальнейшем будут использованы при получении априорных оценок для разностных задач, которые в свою очередь послужат основой для доказательства устойчивости и сходимости разностных схем.
1. Разностный оператор Лапласа в прямоугольной области.
Пусть на плоскости  задана прямоугольная область
задана прямоугольная область

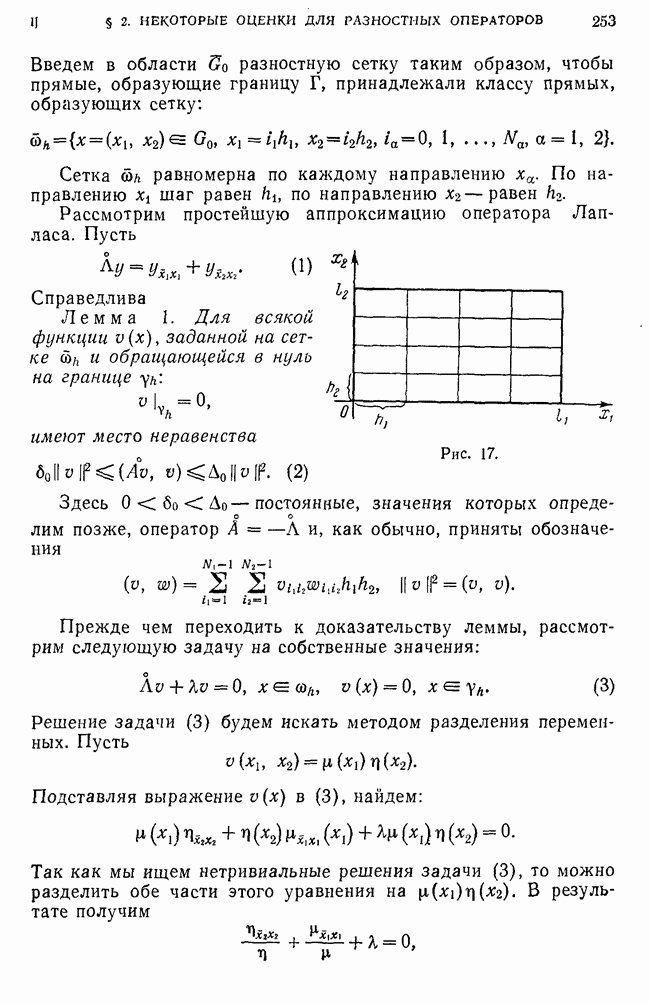
с границей  (рис. 17) и оператор Лапласа
(рис. 17) и оператор Лапласа

Введем в области  разностную сетку таким образом, чтобы прямые, образующие границу
разностную сетку таким образом, чтобы прямые, образующие границу  принадлежали классу прямых, образующих сетку:
принадлежали классу прямых, образующих сетку:

Сетка  равномерна по каждому направлению
равномерна по каждому направлению  По направлению
По направлению  шаг равен
шаг равен  по направлению
по направлению  равен
равен 
Рассмотрим простейшую аппроксимацию оператора Лапласа. Пусть

Справедлива

Рис. 17.
Лемма 1. Для всякой функции  заданной на сетке
заданной на сетке  и обращающейся в нуль на границе
и обращающейся в нуль на границе 

имеют место неравенства

Здесь  постоянные, значения которых определим позже, оператор
постоянные, значения которых определим позже, оператор  как обычно, приняты обозначения
как обычно, приняты обозначения

Прежде чем переходить к доказательству леммы, рассмотрим следующую задачу на собственные значения:

Решение задачи (3) будем искать методом разделения переменных. Пусть

Подставляя выражение  в (3), найдем:
в (3), найдем:

Так как мы ищем нетривиальные решения задачи (3), то можно разделить обе части этого уравнения на  В результате получим
В результате получим

или

причем  не зависит ни от
не зависит ни от  ни от
ни от  Тем самым для
Тем самым для  получаем задачу:
получаем задачу:

Это есть именно та задача на собственные значения, которую мы уже рассматривали в гл. I, § 2. Решением этой задачи является

и

Аналогичную задачу получаем для

где  и ее решением является
и ее решением является

Теперь можно найти функцию  являющуюся решением задачи (3)
являющуюся решением задачи (3)

Мы обозначили

поэтому

или

где

Собственные функции  ортонормированы в смысле определенного выше скалярного произведения
ортонормированы в смысле определенного выше скалярного произведения  так как они ортонормированы на каждом отрезке по направлениям
так как они ортонормированы на каждом отрезке по направлениям  Следовательно, по системе функций
Следовательно, по системе функций  можно разлагать
можно разлагать
любые функции, заданные на и обращающиеся в нуль на границе 
Приступим теперь к доказательству леммы 1. Для одномерных сеток были введены формулы суммирования по частям и формулы Грина. Они полностью переносятся на двумерный случай. Первая формула Грина для двумерной сетки в прямоугольнике принимает вид

Преобразуем с помощью первой разностной формулы Грина скалярное произведение  Получим
Получим

так как по определению  Разложим теперь функцию
Разложим теперь функцию  по системе функций
по системе функций 

и, взяв от нее левую разность по  получим
получим

где

и функции  ортонормированы в смысле скалярного произведения
ортонормированы в смысле скалярного произведения  На основании этого из (12) находим
На основании этого из (12) находим

Аналогичное выражение нормы получаем для 

После подстановки выражений норм для  в формулу (11) получаем
в формулу (11) получаем

Нам осталось оценить сумму, стоящую в правой части. Для этой цели из-под знака суммы вынесем максимальное и минимальное собственные значения

Значения наименьшего и наибольшего собственных чисел известны:

Таким образом, получение неравенств (2) закончено, причем

Эти постоянные точны в том смысле, что в соотношении (2) левое неравенство переходит в равенство при  где
где  есть собственная функция задачи (3), отвечающая первому собственному значению. Аналогично правое неравенство в (2) переходит в равенство при
есть собственная функция задачи (3), отвечающая первому собственному значению. Аналогично правое неравенство в (2) переходит в равенство при  Из неравенств (14) видно, что формулы для
Из неравенств (14) видно, что формулы для  и
и  не очень удобны, поэтому мы оценим
не очень удобны, поэтому мы оценим  снизу,
снизу,  сверху. Мы не очень сильно загрубим оценку для максимального собственного значения
сверху. Мы не очень сильно загрубим оценку для максимального собственного значения  если в его выражении заменим
если в его выражении заменим  на 1, так как
на 1, так как  Поэтому будем писать
Поэтому будем писать

Для наименьшего собственного числа ранее (см. гл. I, § 2) была доказана следующая оценка снизу:

Будем считать поэтому что

Из равенства (16) видно, что  есть абсолютная постоянная, не зависящая от сетки
есть абсолютная постоянная, не зависящая от сетки  Величина
Величина  от сетки
от сетки  зависит и стремится к бесконечности, когда шаги сетки стремятся к нулю.
зависит и стремится к бесконечности, когда шаги сетки стремятся к нулю.
Лемма 2. Для всякой функции  заданной на сетке
заданной на сетке  и обращающейся в нуль на границе
и обращающейся в нуль на границе  имеет место разностный аналог теоремы вложения:
имеет место разностный аналог теоремы вложения:

Доказательство. Разложим функцию  по системе собственных функций
по системе собственных функций 

Отсюда получаем

и, следовательно,

Оценим теперь функцию  следующим образом:
следующим образом:

Из (8) получаем

так что

Для завершения доказательства нам осталось получить оценку

Обращаясь к формуле (9) и учитывая, что  при
при  имеем
имеем

Следовательно,

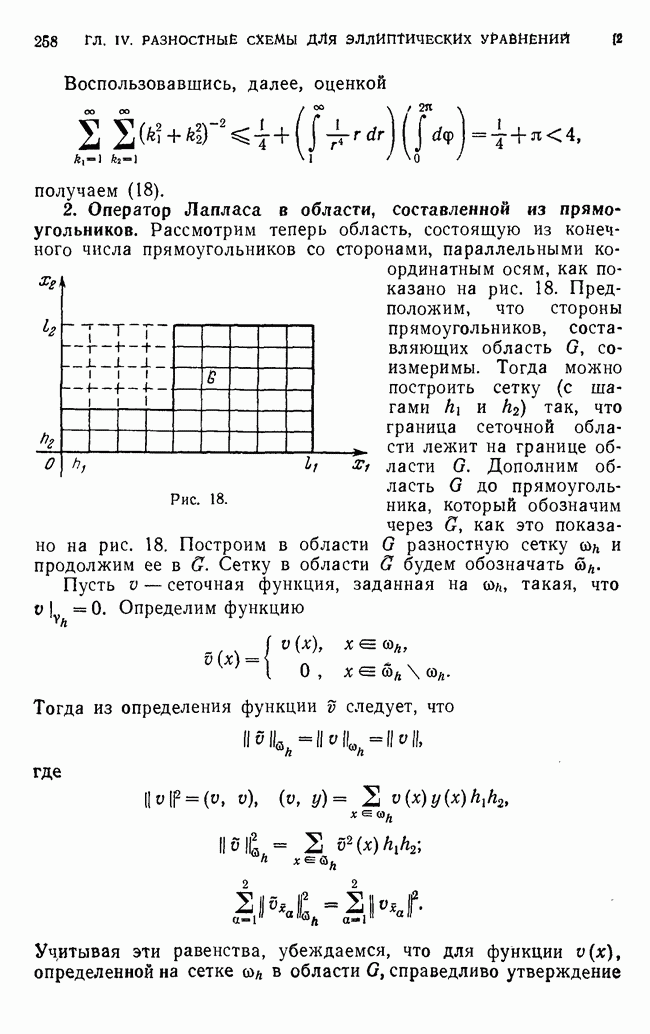
Воспользовавшись, далее, оценкой

получаем (18).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
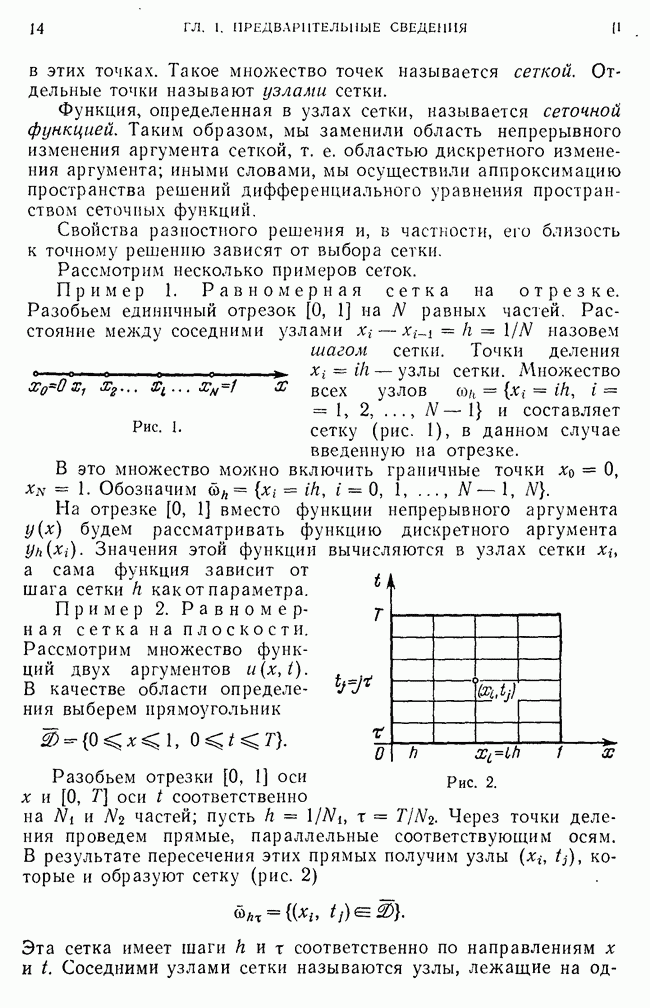
- 1. Сетки и сеточные функции.
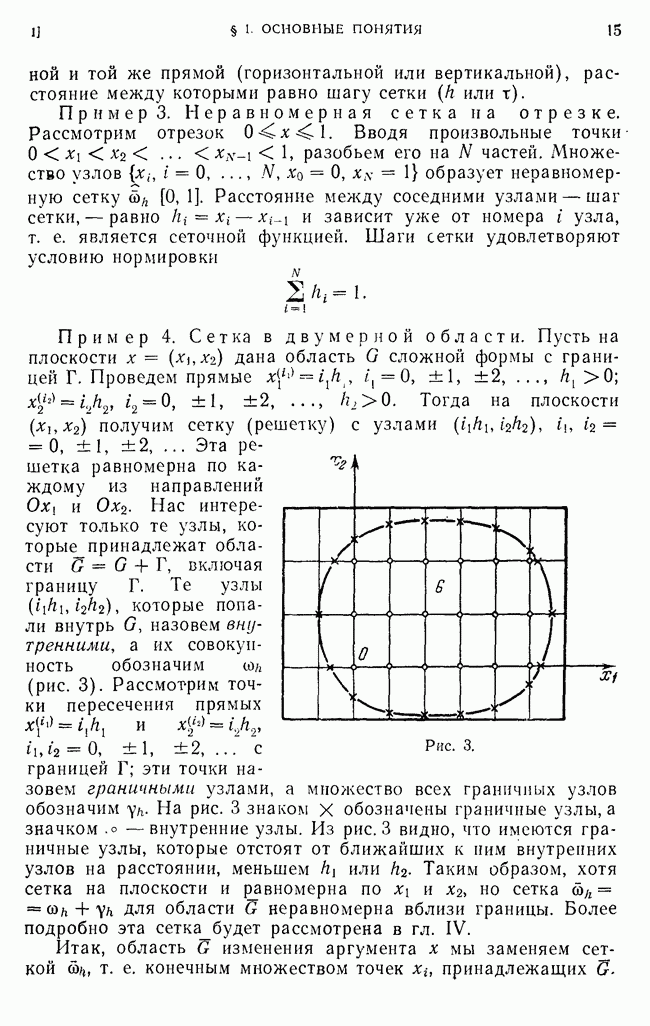
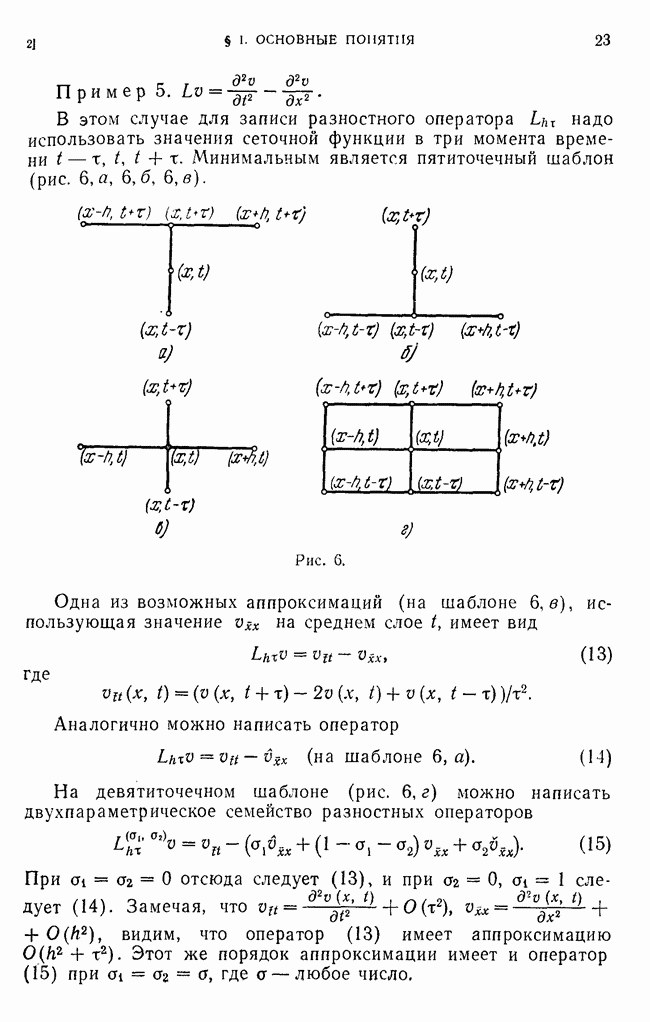
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
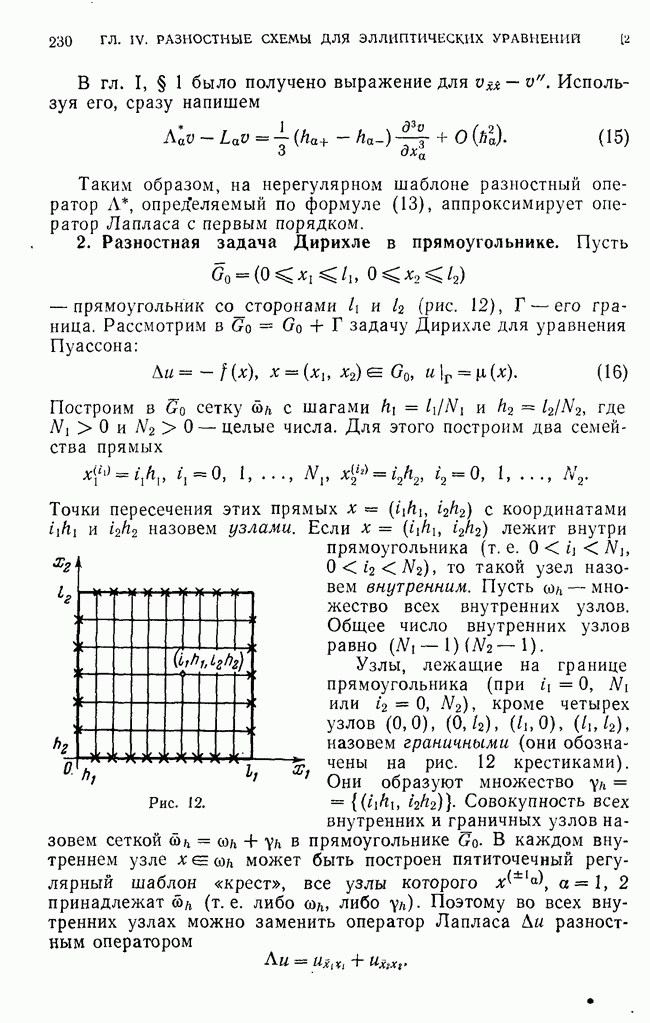
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка