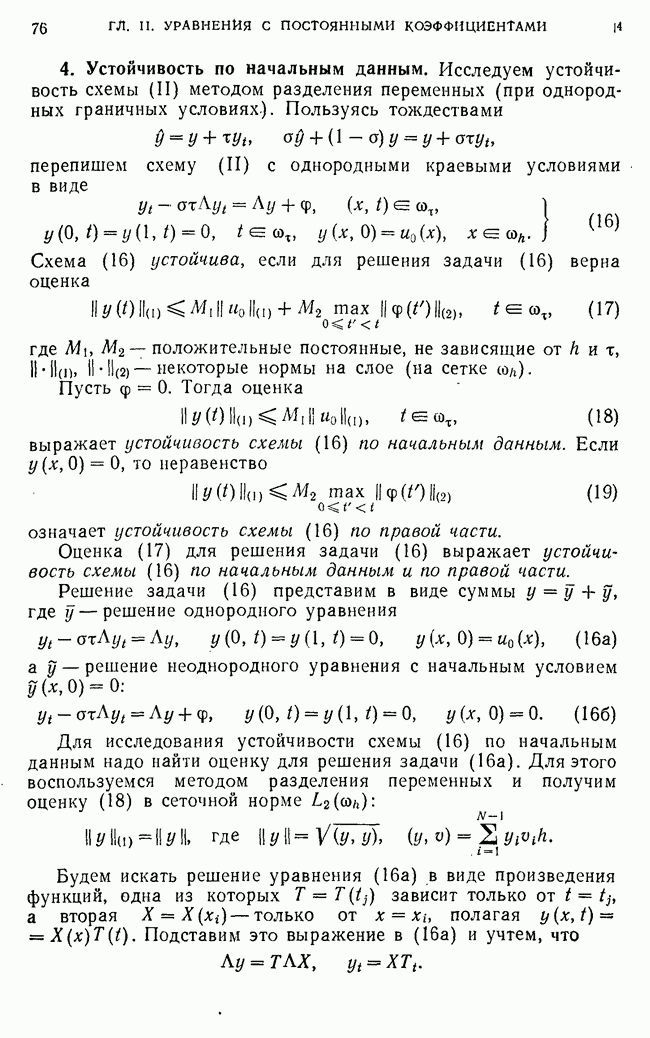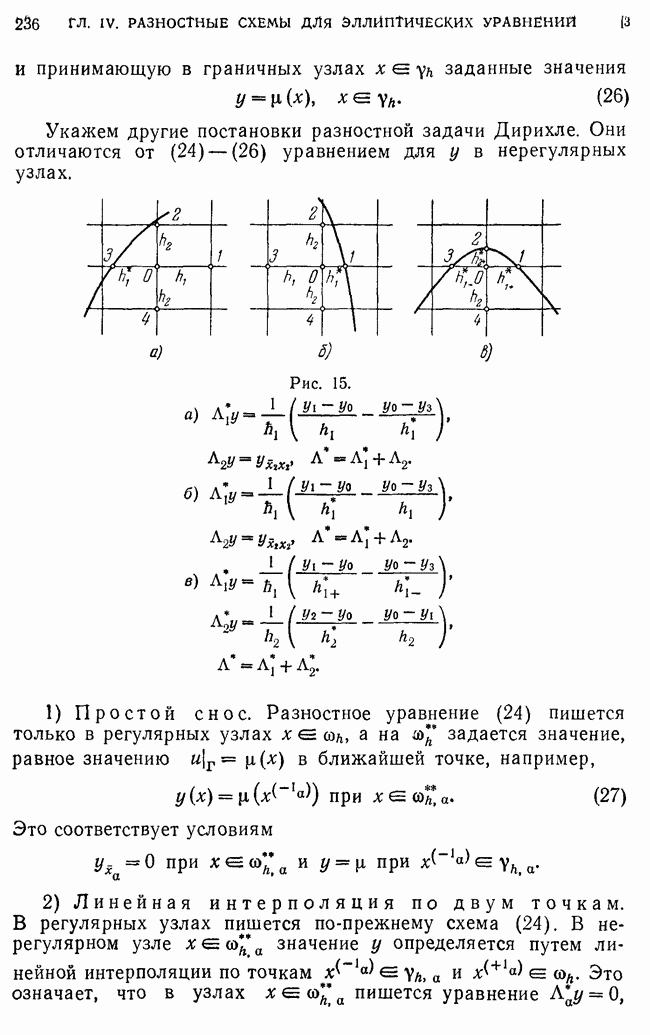| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Настоящая глава носит вводный характер. В §§ 1, 2 на простейших примерах поясняются основные понятия теории разностных схем: аппроксимация, устойчивость, сходимость и дается представление о некоторых методах исследования устойчивости и сходимости, таких как метод разделения переменных, принцип максимума, метод энергетических неравенств. В § 3 изложены необходимые для дальнейшего вспомогательные сведения из функционального анализа.
§ 1. Основные понятия
1. Сетки и сеточные функции.
Для того, чтобы написать разностную схему, приближенно описывающую данное дифференциальное уравнение, нужно совершить следующие два шага.
1. Необходимо заменить область непрерывного изменения аргумента областью дискретного его изменения.
2. Необходимо заменить дифференциальный оператор некоторым разностным оператором, а также сформулировать разностный аналог для краевых условий и для начальных данных.
После осуществления такой процедуры мы приходим к алгебраической системе уравнений. Таким образом, задача о численном решении исходного (линейного) дифференциального уравнения сводится к вопросу о нахождении решения полученной алгебраической системы.
Остановимся на этих вопросах несколько подробнее.
При численном решении той или иной математической задачи мы, очевидно, не можем воспроизвести разностное решение для всех значений аргумента, изменяющегося внутри некоторой области евклидова пространства.
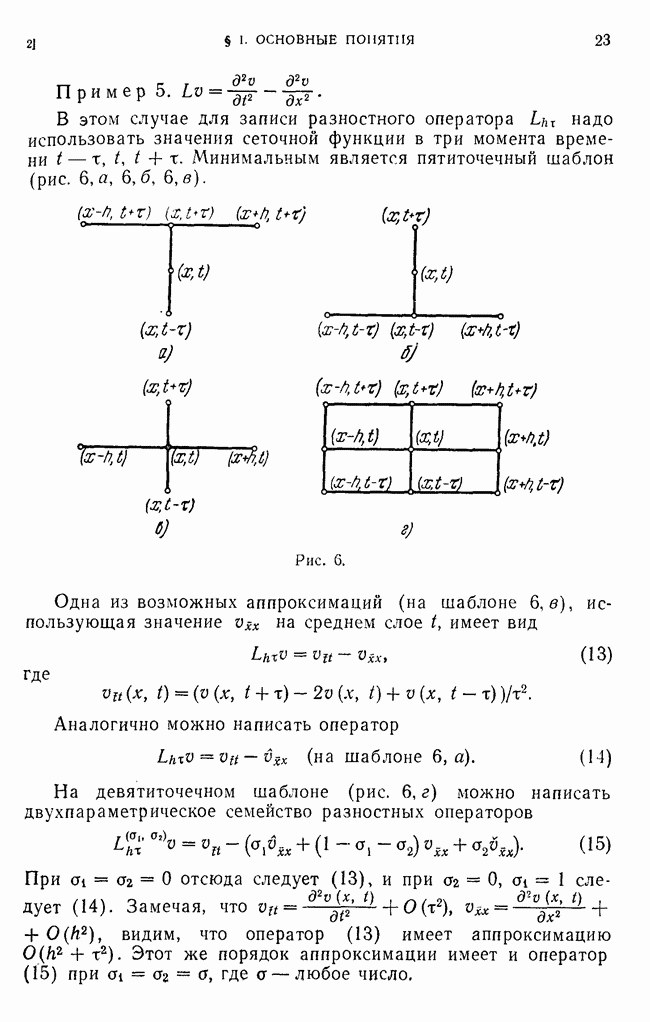
Естественно поэтому выбрать в этой области некоторое конечное множество точек и приближенное решение искать только
в этих точках. Такое множество точек называется сеткой. Отдельные точки называют узлами сетки.
Функция, определенная в узлах сетки, называется сеточной функцией. Таким образом, мы заменили область непрерывного изменения аргумента сеткой, т. е. областью дискретного изменения аргумента; иными словами, мы осуществили аппроксимацию пространства решений дифференциального уравнения пространством сеточных функций.
Свойства разностного решения и, в частности, его близость к точному решению зависят от выбора сетки.
Рассмотрим несколько примеров сеток.
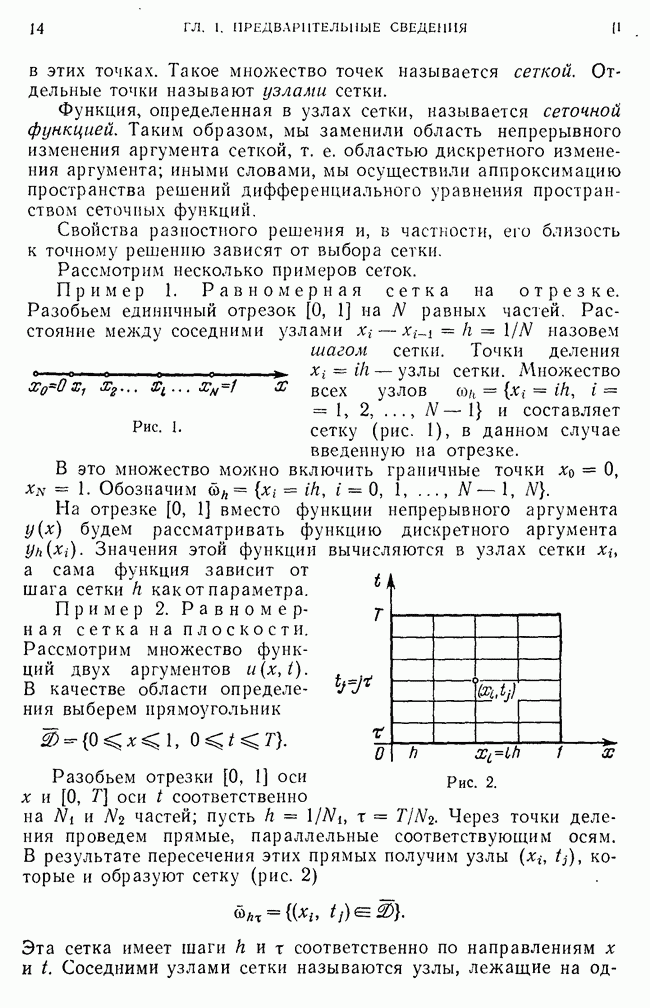
Пример 1. Равномерная сетка на отрезке. Разобьем единичный отрезок [0, 1] на  равных частей. Расстояние между соседними узлами
равных частей. Расстояние между соседними узлами  назовем шагом сетки. Точки деления
назовем шагом сетки. Точки деления  узлы сетки. Множество всех узлов
узлы сетки. Множество всех узлов  и составляет сетку (рис. 1), в данном случае введенную на отрезке.
и составляет сетку (рис. 1), в данном случае введенную на отрезке.

Рис. 1.
В это множество можно включить граничные точки  Обозначим
Обозначим 
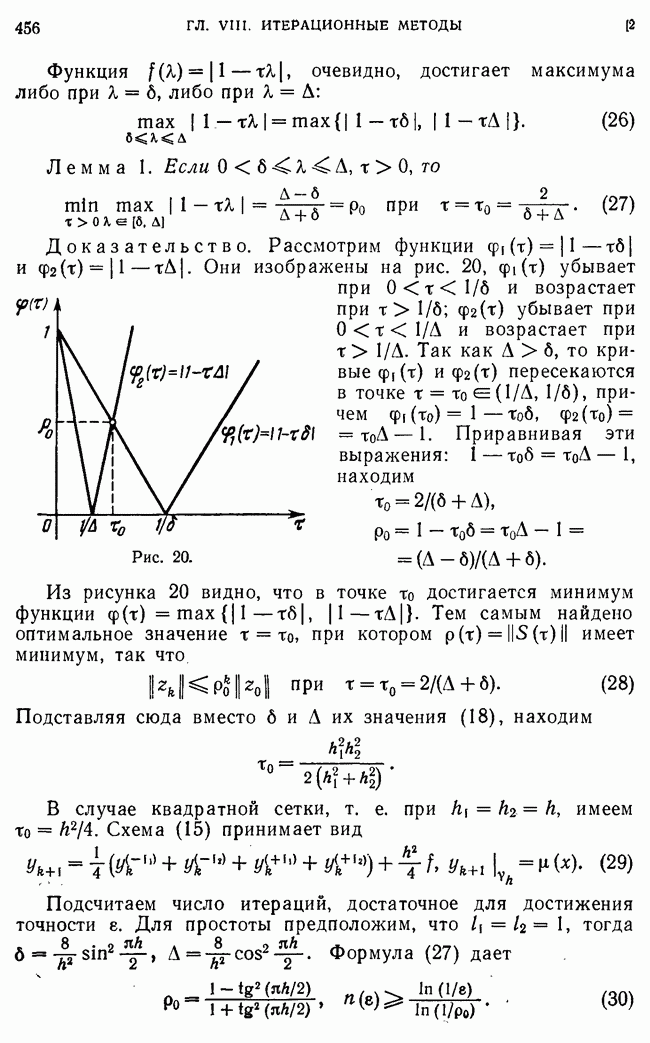
На отрезке [0, 1] вместо функции непрерывного аргумента  будем рассматривать функцию дискретного аргумента
будем рассматривать функцию дискретного аргумента  Значения этой функции вычисляются в узлах сетки
Значения этой функции вычисляются в узлах сетки  а сама функция зависит от шага сетки
а сама функция зависит от шага сетки  как от параметра.
как от параметра.

Рис. 2.
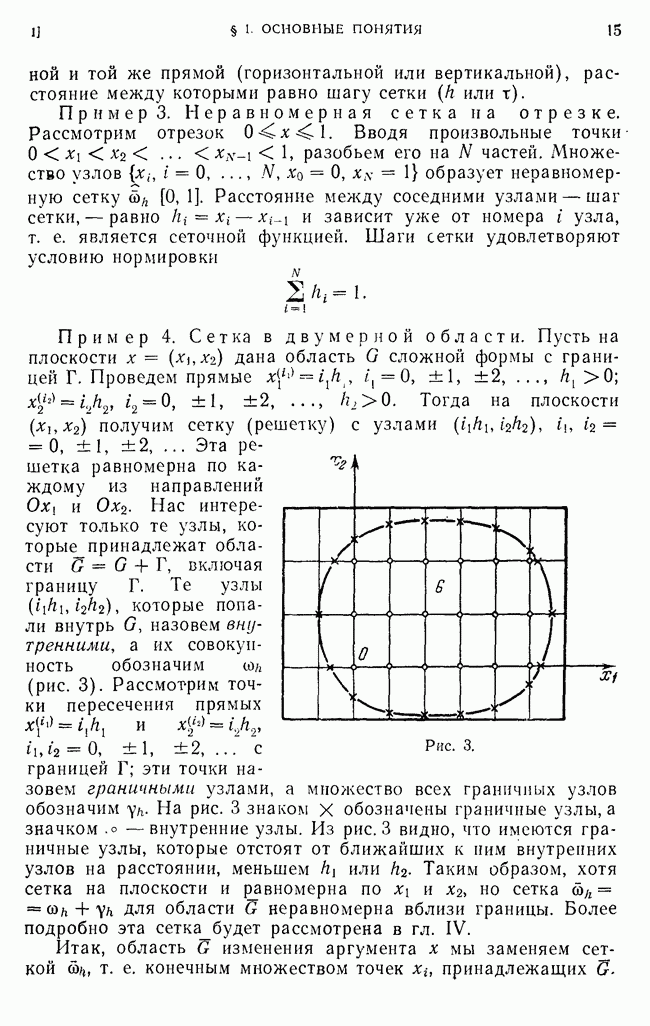
Пример 2. Равномерная сетка на плоскости. Рассмотрим множество функций двух аргументов  В качестве области определения выберем прямоугольник
В качестве области определения выберем прямоугольник

Разобьем отрезки [0, 1] оси  оси
оси  соответственно на
соответственно на  частей; пусть
частей; пусть  Через точки деления проведем прямые, параллельные соответствующим осям. В результате пересечения этих прямых получим узлы
Через точки деления проведем прямые, параллельные соответствующим осям. В результате пересечения этих прямых получим узлы  которые и образуют сетку (рис. 2)
которые и образуют сетку (рис. 2)

Эта сетка имеет шаги  соответственно по направлениям
соответственно по направлениям  Соседними узлами сетки называются узлы, лежащие на одной
Соседними узлами сетки называются узлы, лежащие на одной
и той же прямой (горизонтальной или вертикальной), расстояние между которыми равно шагу сетки  или
или  .
.
Пример 3.
Неравномерная сетка на отрезке. Рассмотрим отрезок Вводя произвольные точки  разобьем его на
разобьем его на  частей. Множество узлов
частей. Множество узлов  образует неравномерную сетку
образует неравномерную сетку  . Расстояние между соседними узлами — шаг сетки, — равно
. Расстояние между соседними узлами — шаг сетки, — равно  и зависит уже от номера
и зависит уже от номера  узла, т. е. является сеточной функцией. Шаги сетки удовлетворяют условию нормировки
узла, т. е. является сеточной функцией. Шаги сетки удовлетворяют условию нормировки

Пример 4. Сетка в двумерной области. Пусть на плоскости  дана область
дана область  сложной формы с границей
сложной формы с границей  Проведем прямые
Проведем прямые  Тогда на плоскости
Тогда на плоскости  получим сетку (решетку) с узлами
получим сетку (решетку) с узлами  Эта решетка равномерна по каждому из направлений
Эта решетка равномерна по каждому из направлений  Нас интересуют только те узлы, которые принадлежат области
Нас интересуют только те узлы, которые принадлежат области  включая границу
включая границу  Те узлы
Те узлы  которые попали внутрь
которые попали внутрь  назовем внутренними, а их совокупность обозначим сол (рис. 3). Рассмотрим точки пересечения прямых
назовем внутренними, а их совокупность обозначим сол (рис. 3). Рассмотрим точки пересечения прямых  с границей
с границей  эти точки назовем граничными узлами, а множество всех граничных узлов обозначим
эти точки назовем граничными узлами, а множество всех граничных узлов обозначим  На рис. 3 знаком X обозначены граничные узлы, а значком
На рис. 3 знаком X обозначены граничные узлы, а значком  — внутренние узлы. Из рис. 3 видно, что имеются граничные узлы, которые отстоят от ближайших к ним внутренних узлов на расстоянии, меньшем или Таким образом, хотя сетка на плоскости и равномерна по
— внутренние узлы. Из рис. 3 видно, что имеются граничные узлы, которые отстоят от ближайших к ним внутренних узлов на расстоянии, меньшем или Таким образом, хотя сетка на плоскости и равномерна по  но сетка
но сетка  Для области
Для области  неравномерна вблизи границы. Более подробно эта сетка будет рассмотрена в гл. IV.
неравномерна вблизи границы. Более подробно эта сетка будет рассмотрена в гл. IV.

Рис. 3.
Итак, область  изменения аргумента х мы заменяем сеткой
изменения аргумента х мы заменяем сеткой  т. е. конечным множеством точек
т. е. конечным множеством точек  принадлежащих
принадлежащих 
Вместо функций  непрерывного аргумента
непрерывного аргумента  будем рассматривать сеточные функции
будем рассматривать сеточные функции  функции точки
функции точки  являющейся узлом сетки
являющейся узлом сетки  Сеточную функцию
Сеточную функцию  можно представить в виде вектора. Если перенумеровать все узлы в некотором порядке
можно представить в виде вектора. Если перенумеровать все узлы в некотором порядке  то значения сеточной функции в этих узлах можно рассматривать как компоненты вектора
то значения сеточной функции в этих узлах можно рассматривать как компоненты вектора

Если область  в которой построена сетка, конечна, то размерность
в которой построена сетка, конечна, то размерность  вектора У конечна. В случае неограниченной области
вектора У конечна. В случае неограниченной области  сетка состоит из бесконечного числа узлов и размерность вектора У также бесконечна.
сетка состоит из бесконечного числа узлов и размерность вектора У также бесконечна.
Обычно рассматриваются множества сеток  зависящих от шага.
зависящих от шага.  как от параметра. Поэтому и сеточные функции
как от параметра. Поэтому и сеточные функции  зависят от параметра
зависят от параметра  (или от числа узлов
(или от числа узлов  в случае равномерной сетки). Если сетка
в случае равномерной сетки). Если сетка  неравномерна, то под
неравномерна, то под  следует понимать вектор
следует понимать вектор  с компонентами
с компонентами  Это же замечание относится и к случаю, когда область
Это же замечание относится и к случаю, когда область  многомерна,
многомерна,  тогда
тогда  если сетка
если сетка  равномерна по каждому из аргументов
равномерна по каждому из аргументов 
Функции  непрерывного аргумента
непрерывного аргумента  являются элементами некоторого функционального пространства
являются элементами некоторого функционального пространства  Множество сеточных функций
Множество сеточных функций  образует пространство
образует пространство  Таким образом, используя метод конечных разностей, мы заменяем пространство
Таким образом, используя метод конечных разностей, мы заменяем пространство  пространством
пространством  сеточных функций
сеточных функций 
Рассматривая множество сеток  получаем множество
получаем множество  пространств сеточных функций, зависящих от параметра
пространств сеточных функций, зависящих от параметра  На линейном пространстве
На линейном пространстве  вводится норма
вводится норма  являющаяся сеточным аналогом нормы
являющаяся сеточным аналогом нормы  Но в исходном пространстве
Но в исходном пространстве 
Укажем простейшие типы норм в Ни для случая сеток  на отрезке
на отрезке  (индекс
(индекс  опускаем).
опускаем).
1) Сеточный аналог нормы в С:

2) Сеточные аналоги нормы в 

В дальнейшем будем, как правило, пользоваться нормами, индуцированными скалярными произведениями на  (сеточными аналогами норм в
(сеточными аналогами норм в  и др.),
и др.),
Пусть  решение исходной непрерывной задачи, и
решение исходной непрерывной задачи, и  решение приближенной (разностной) задачи,
решение приближенной (разностной) задачи,  Основной интерес для теории приближенных методов представляет оценка близости
Основной интерес для теории приближенных методов представляет оценка близости  к и. Однако
к и. Однако  являются векторами из разных пространств. Имеются две возможности:
являются векторами из разных пространств. Имеются две возможности:
1. Сеточная функция  заданная в узлах
заданная в узлах  доопределяется (например, при помощи линейной интерполяции) во всех остальных точках х области
доопределяется (например, при помощи линейной интерполяции) во всех остальных точках х области  В результате получаем функцию
В результате получаем функцию  непрерывного аргумента
непрерывного аргумента  Разность
Разность  принадлежит
принадлежит  Близость
Близость  к и характеризуется числом
к и характеризуется числом  и
и  Но, где
Но, где  норма на
норма на 
2. Пространство  отображается на пространство
отображается на пространство  Каждой функции
Каждой функции  ставится в соответствие сеточная функция
ставится в соответствие сеточная функция  так что
так что  где — линейный оператор из
где — линейный оператор из  Это соответствие можно осуществить различными способами (выбирая разные операторы Если
Это соответствие можно осуществить различными способами (выбирая разные операторы Если  -непрерывная функция, то полагаем
-непрерывная функция, то полагаем  где
где  Иногда определяют
Иногда определяют  в узле
в узле  как интегральное среднее значение
как интегральное среднее значение  по некоторой окрестности (например, диаметра
по некоторой окрестности (например, диаметра  данного узла
данного узла  В дальнейшем всюду будем предполагать, что
В дальнейшем всюду будем предполагать, что  непрерывная функция и
непрерывная функция и  для всех
для всех 
Имея сеточную функцию  образуем разность
образуем разность  являющуюся вектором пространства
являющуюся вектором пространства  Близость
Близость  к и характеризуется числом
к и характеризуется числом  где
где  норма на
норма на  При этом естественно требовать, чтобы норма
При этом естественно требовать, чтобы норма  аппроксимировала норму
аппроксимировала норму  Но в следующем смысле:
Но в следующем смысле:

для любого вектора и из  Это условие будем называть условием согласования норм в
Это условие будем называть условием согласования норм в  .
.
Мы всюду используем второй путь, исследуем погрешность разностных методов в пространстве сеточных функций. В большинстве случаев эти пространства являются конечномерными.
Как будет показано в дальнейшем, оказывается возможным провести изложение основных вопросов теории разностных схем, трактуя  как абстрактные линейные пространства любой размерности.
как абстрактные линейные пространства любой размерности.
После того, как мы познакомились на простейших примерах со способами построения сеток и тем самым пространств Ни сеточных функций, перейдем к вопросу о разностной аппроксимации дифференциальных операторов.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
- 1. Сетки и сеточные функции.
- 2. Разностная аппроксимация простейших дифференциальных операторов.
- 3. Погрешность аппроксимации на сетке.
- 4. Постановка разностной задачи.
- 5. О сходимости и точности схем.
- 6. Метод аппроксимации краевых и начальных условий.
- 7. Примеры устойчивых и неустойчивых разностных схем.
- 8. О понятии корректности разностной задачи.
- 9. Решение разностных уравнений методом прогонки.
- § 2. Некоторые сведения о математическом аппарате теории разностных схем
- 2. Отыскание собственных функций и собственных значений на примере простейшей разностной задачи.
- 3. Разностные аналоги теорем вложения.
- 4. Метод энергетических неравенств.
- 5. Принцип максимума.
- § 3. Некоторые сведения из функционального анализа
- 2. Линейные ограниченные операторы в вещественном гильбертовом пространстве.
- 3. Линейные операторы в пространстве конечного числа измерений.
- Глава II. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- § 1. Уравнение теплопроводности с постоянными коэффициентами
- § 2. Разностные схемы для уравнения колебаний струны
- Глава III. ОДНОРОДНЫЕ РАЗНОСТНЫЕ СХЕМЫ
- § 1. Однородные схемы для стационарного уравнения с переменными коэффициентами
- 4. Пример схемы, расходящейся в случае разрывных коэффициентов.
- 5. Интегро-интерполяционный метод (метод баланса) построения однородных разностных схем.
- 6. Однородные консервативные схемы.
- 7. Исходный класс консервативных схем. Шаблонные функционалы.
- 8. Разностная функция Грина.
- 9. Априорные оценки.
- 10. Погрешность аппроксимации в классе непрерывных коэффициентов.
- 11. Погрешность аппроксимации в классе разрывных коэффициентов.
- 12. О сходимости и точности.
- 13. Однородные разностные схемы на неравномерных сетках.
- 14. Точная схема. Схема любого порядка точности.
- 15. Монотонные схемы для уравнения общего вида.
- 16. Третья краевая задача.
- 17. Коэффициентная устойчивость разностных схем.
- 18. Однородные схемы для уравнения в цилиндрической и сферической системах координат.
- 19. Задача с условиями периодичности.
- 20. Разностная задача Штурма — Лиувилля. Постановка задачи и основные свойства.
- 21. Разностная задача Штурма — Лиувилля. Оценка скорости сходимости.
- § 2. Однородные разностные схемы для уравнения теплопроводности с переменными коэффициентами
- § 3. Однородные разностные схемы для уравнений гиперболического типа
- Глава IV. РАЗНОСТНЫЕ СХЕМЫ ДЛЯ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА
- § 1. Разностная задача Дирихле для уравнения Пуассона
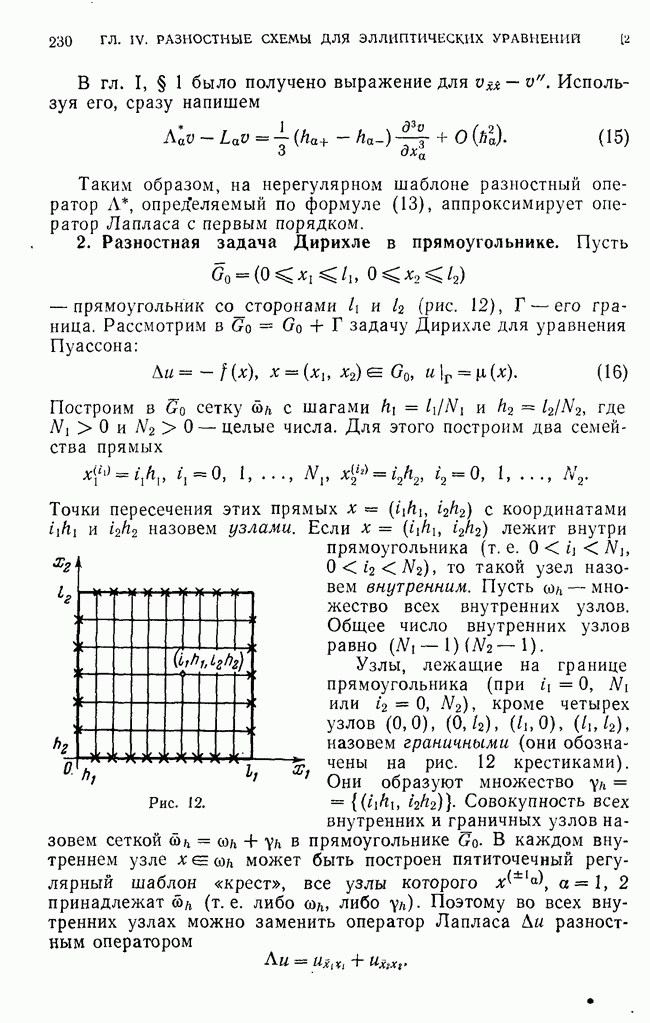
- 2. Разностная задача Дирихле в прямоугольнике.
- 3. Разностная задача Дирихле в области сложной формы.
- 4. Запись разностного уравнения в канонической форме.
- 5. Принцип максимума.
- 6. Оценка решения неоднородного уравнения.
- 7. Оценка решения разностной задачи Дирихле.
- 8. Равномерная сходимость и порядок точности разностной задачи Дирихле.
- 9. Схема повышенного порядка точности для уравнения Пуассона.
- § 2. Некоторые оценки для разностных операторов, аппроксимирующих дифференциальные операторы эллиптического типа
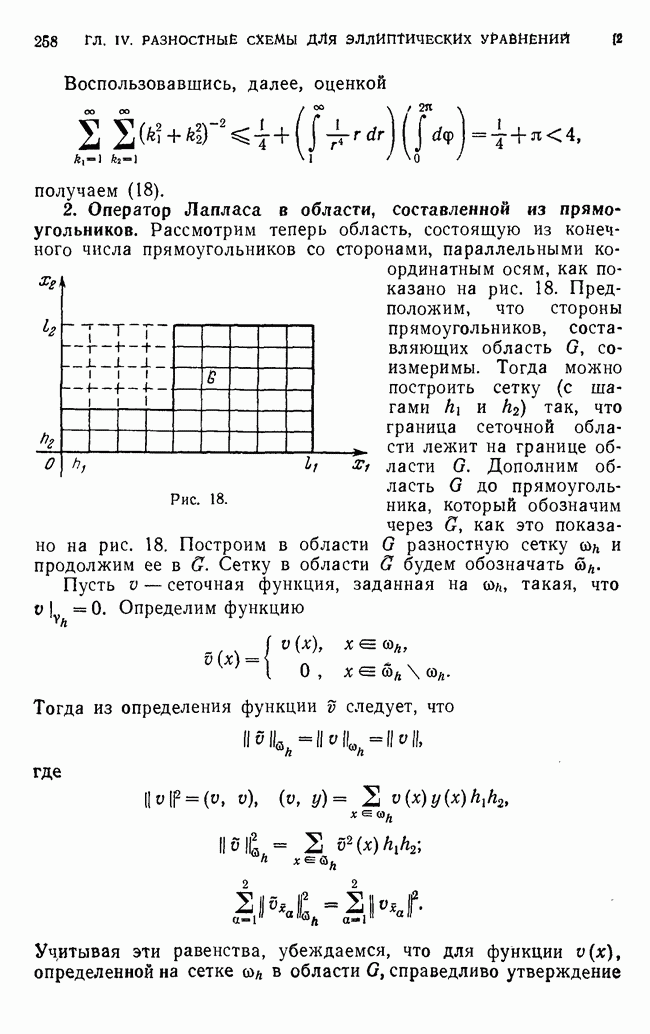
- 2. Оператор Лапласа в области, составленной из прямоугольников.
- 3. Операторы с переменными коэффициентами.
- 4. Оператор со смешанной производной.
- 5. Схема повышенного порядка точности для эллиптического уравнения со смешанными производными.
- Глава V. ОБЩИЕ ФОРМУЛИРОВКИ. ОПЕРАТОРНО-РАЗНОСТНЫЕ СХЕМЫ
- § 1. Разностные схемы как операторные уравнения в абстрактных пространствах
- § 2. Операторно-разностные схемы
- 3. Каноническая форма двухслойных схем.
- 4. Канонические формы трехслойных схем.
- 5. Понятие устойчивости.
- 6. Достаточные условия устойчивости двухслойных схем в линейных нормированных пространствах.
- Глава VI. ТЕОРИЯ УСТОЙЧИВОСТИ РАЗНОСТНЫХ СХЕМ
- § 1. Классы устойчивых двухслойных схем
- § 2. Классы устойчивых трехслойных схем
- Глава VII. ЭКОНОМИЧНЫЕ РАЗНОСТНЫЕ СХЕМЫ ДЛЯ МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- § 1. Метод переменных направлений (продольно-поперечная схема) для уравнения теплопроводности
- § 2. Экономичные факторизованные схемы
- 3. Построение экономичных факторизованных схем.
- 4. Схемы расщепления как факторизованные схемы.
- 5. Трехслойные факторизованные схемы.
- 6. Схема повышенного порядка точности для уравнения параболического типа с эллиптическим оператором, содержащим смешанные производные.
- 7. Экономичные схемы для систем уравнений параболического и гиперболического типов.
- § 3. Метод суммарной аппроксимации
- 2. Методы построения аддитивных схем.
- 3. Аппроксимация «многомерной» задачи Коши системой «одномерных» задач Коши.
- 4. Методы оценки сходимости аддитивной схемы.
- 5. Локально-одномерная схема для уравнения теплопроводности в произвольной области.
- 6. Погрешность аппроксимации локально-одномерной схемы.
- 7. Устойчивость локально-одномерной схемы.
- 8. Равномерная сходимость локально-одномерной схемы.
- 9. Локально-одномерная схема для уравнений с переменными коэффициентами.
- 10. Продольно-поперечная схема как аддитивная схема.
- 11. Локально-одномерные схемы для многомерного гиперболического уравнения второго порядка.
- 12. Аддитивные схемы для систем уравнений.
- Глава VIII. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ РАЗНОСТНЫХ ЭЛЛИПТИЧЕСКИХ УРАВНЕНИЙ
- § 1. Двухслойные итерационные схемы для разностной задачи Дирихле
- 5. Итерационная схема для разностной задачи Дирихле повышенного порядка точности.
- 6. Метод переменных направлений для трехмерной задачи Дирихле.
- § 2. Теория итерационных двухслойных схем общего вида
- § 3. Итерационные двухслойные схемы для несамосопряженных уравнений
- § 4. Трехслойные итерационные схемы
- Дополнение
- § 1. Потоковый вариант метода прогонки для разностных задач с сильно меняющимися коэффициентами
- § 2. Матричная прогонка
- § 3. Циклическая прогонка