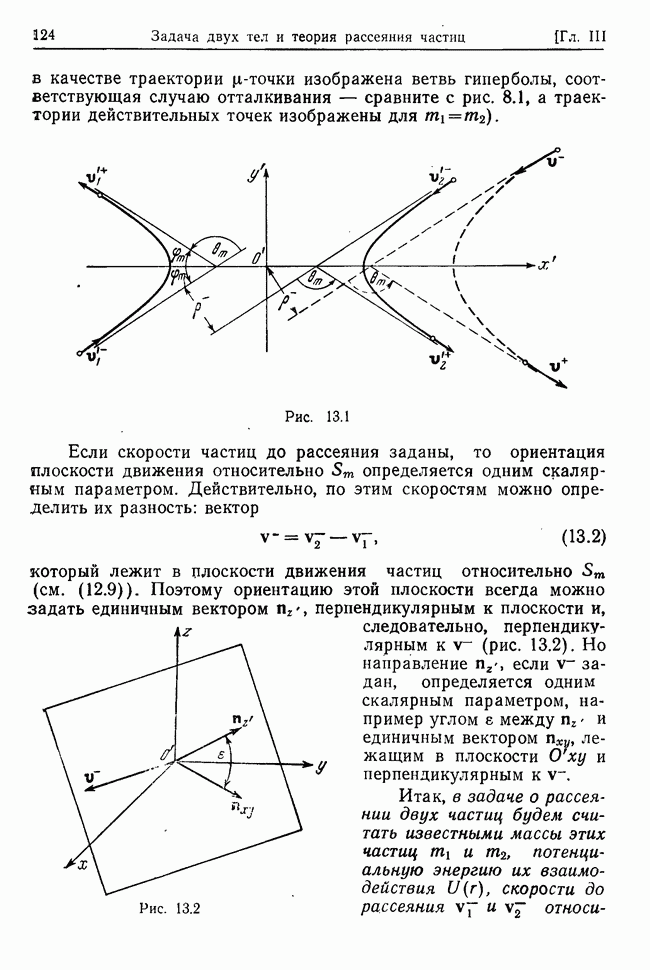
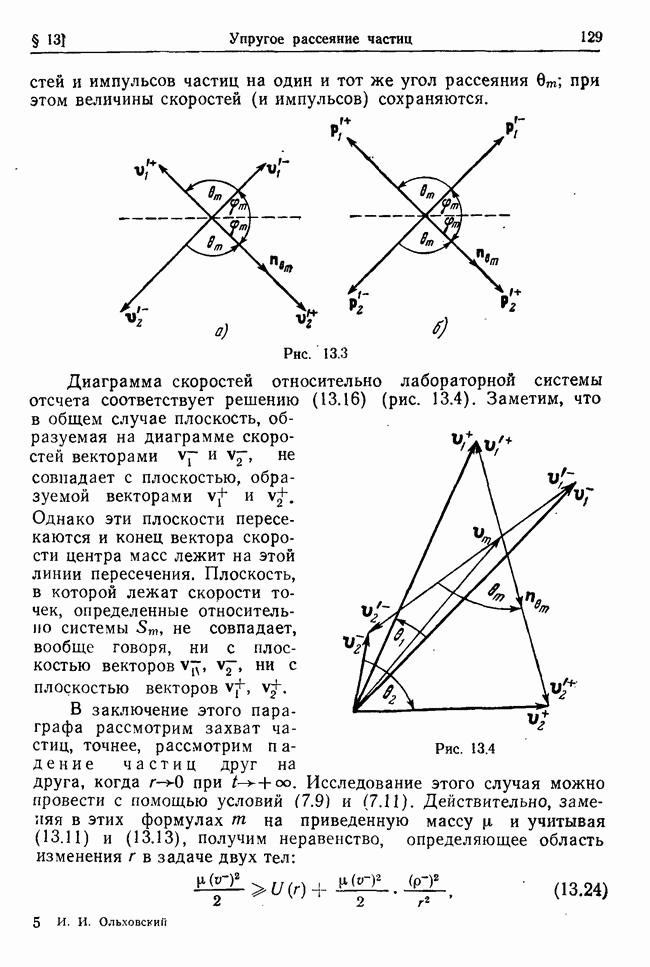
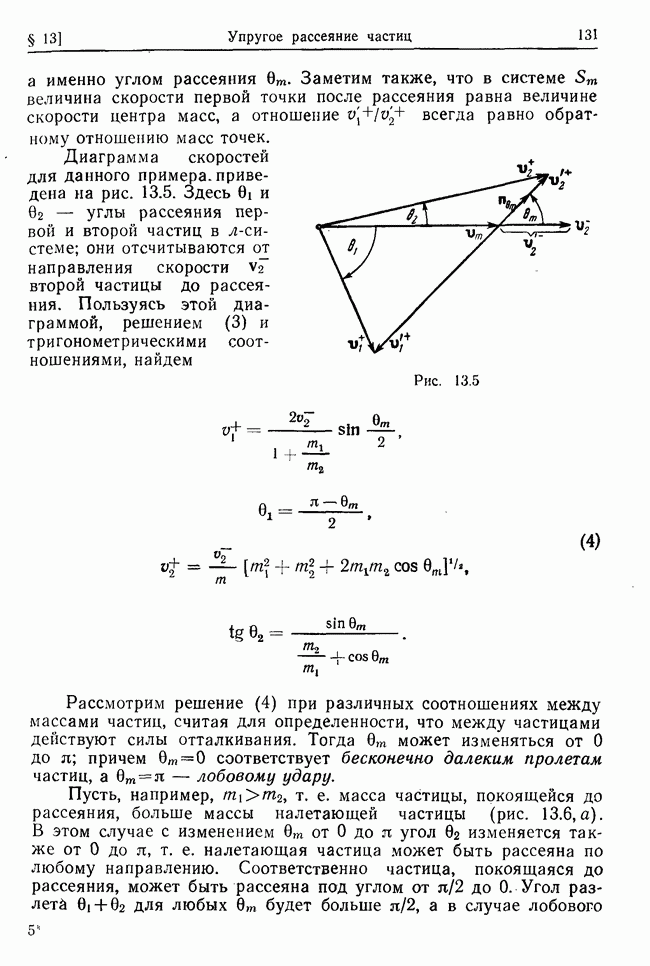
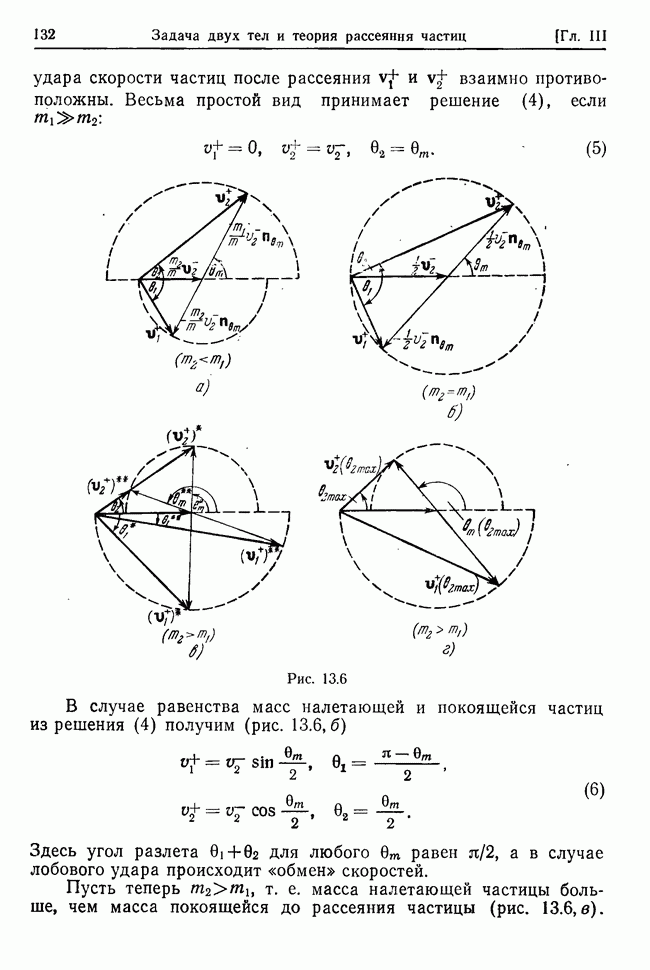
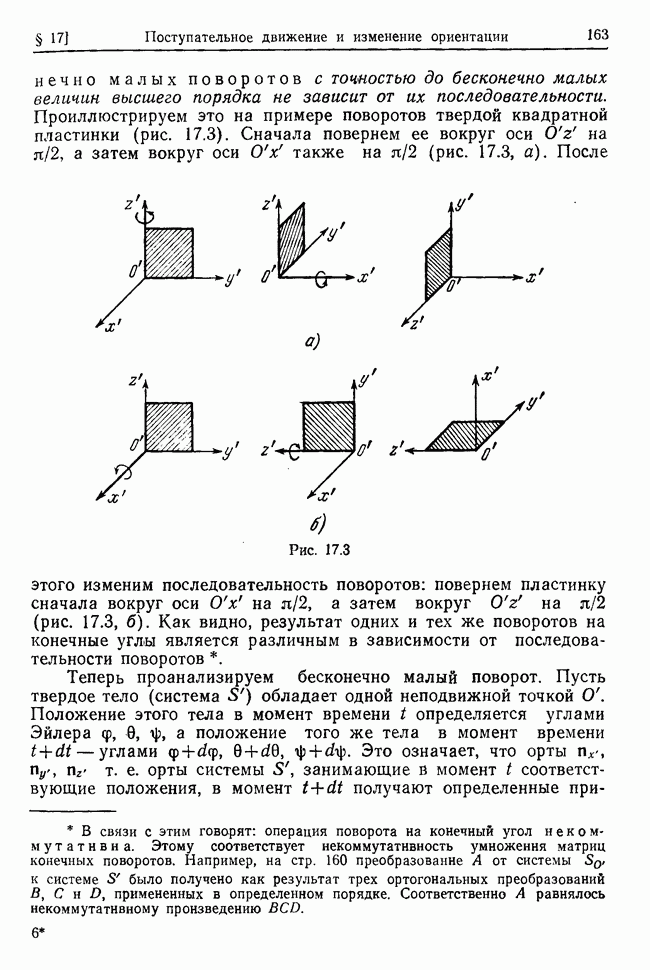
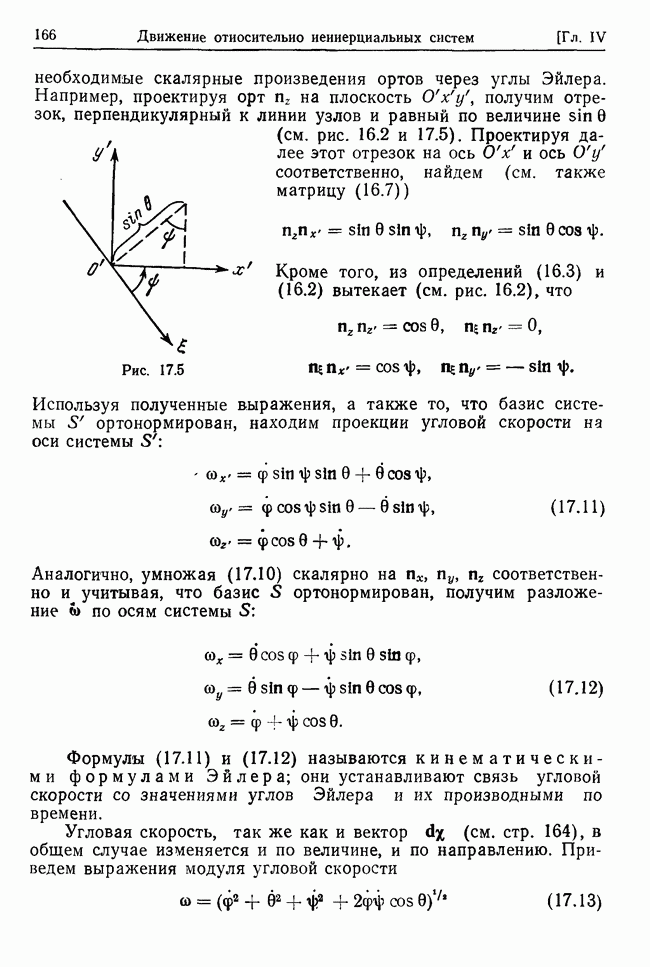
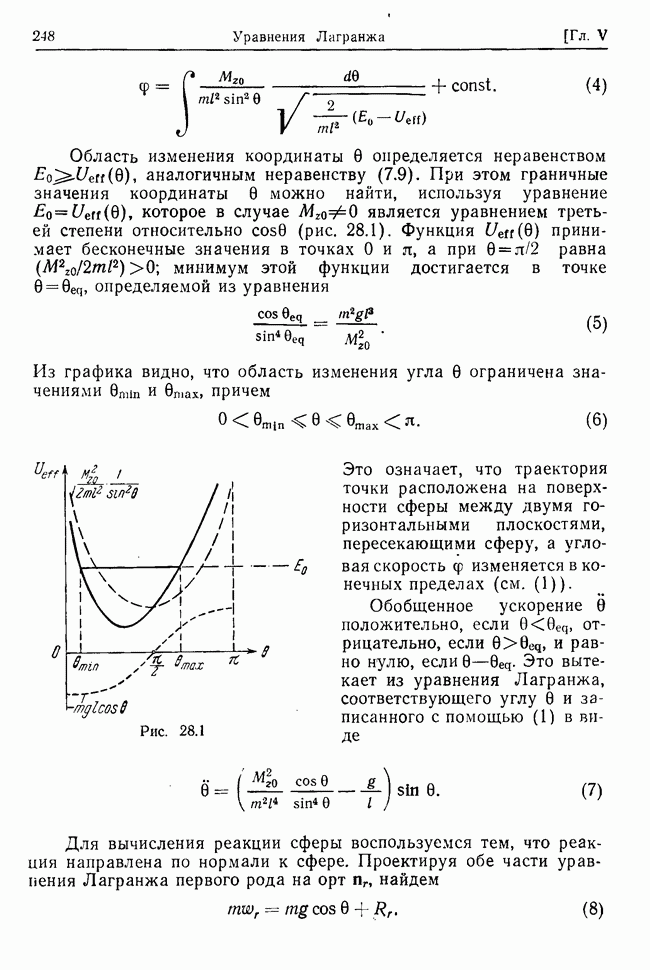
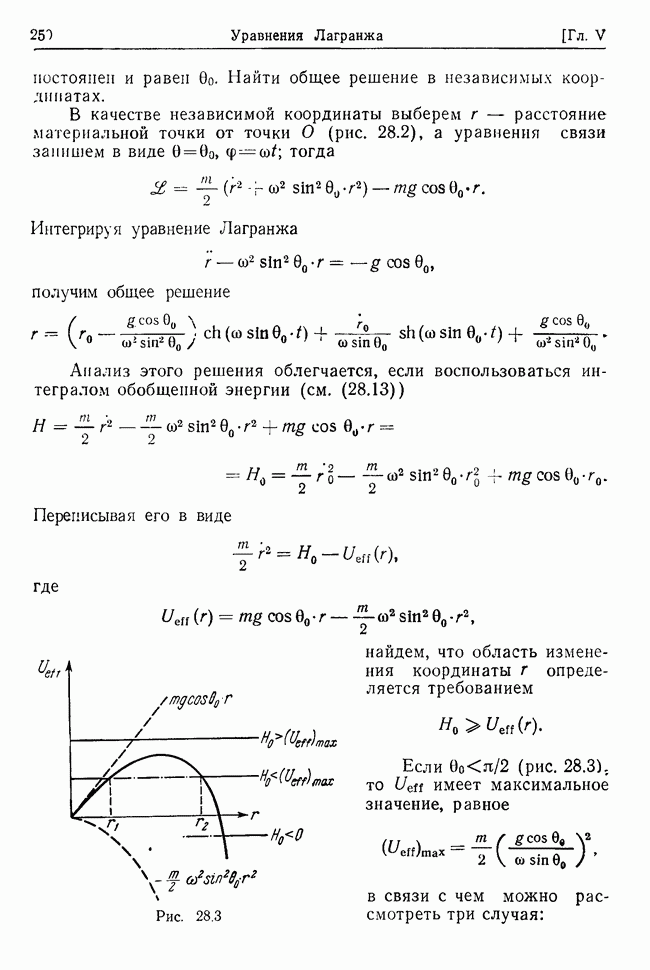
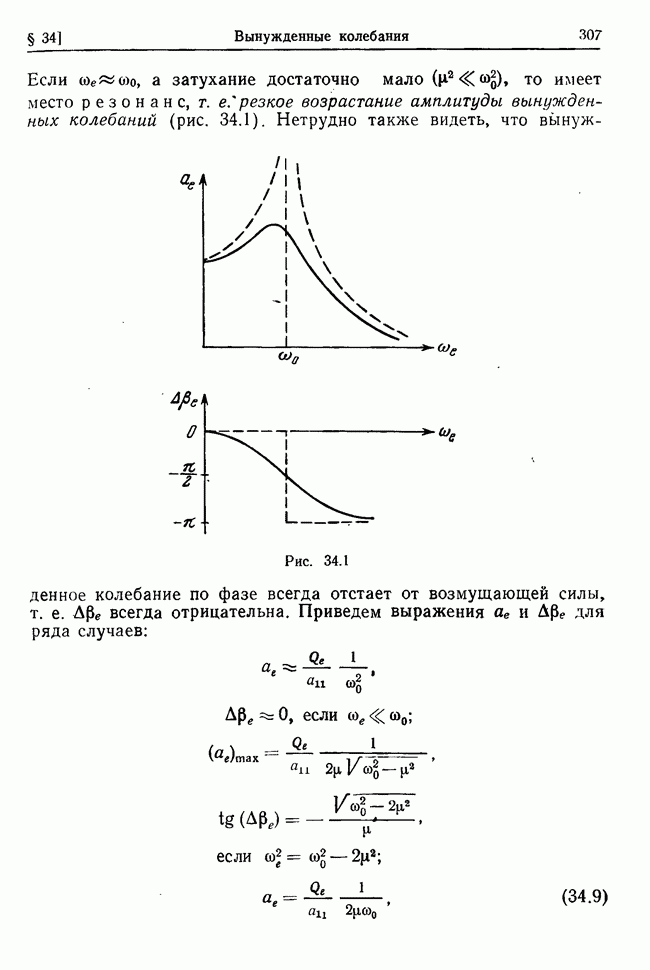
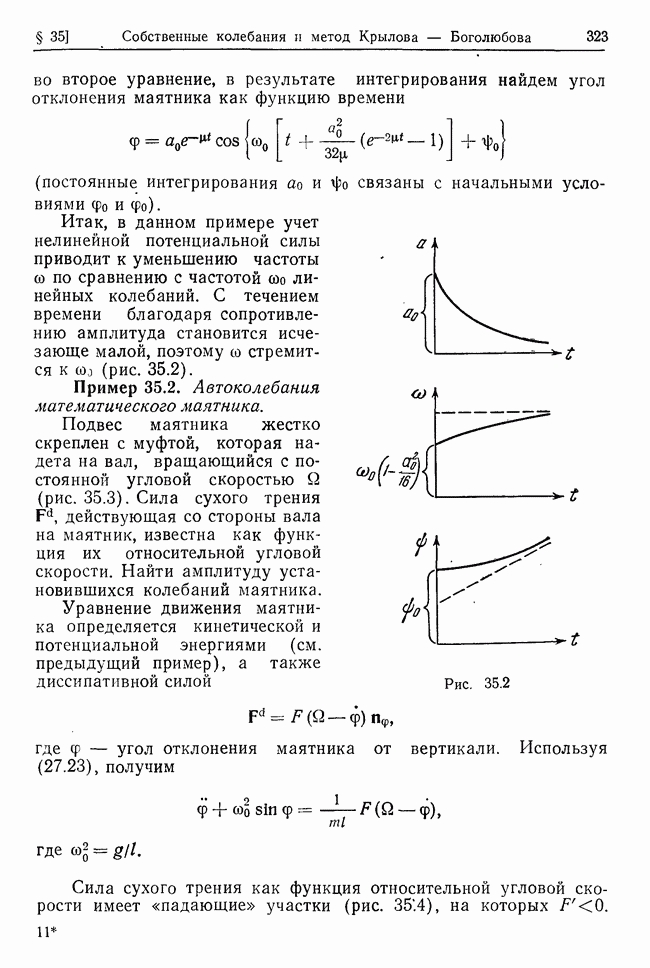
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 32. Собственные и главные колебания системы под действием потенциальных сил
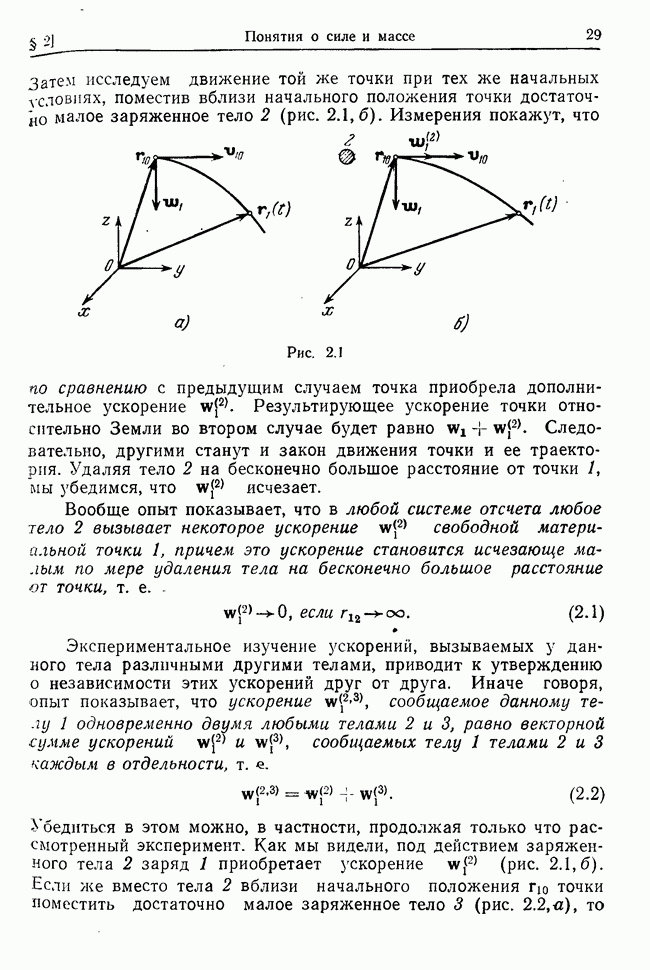
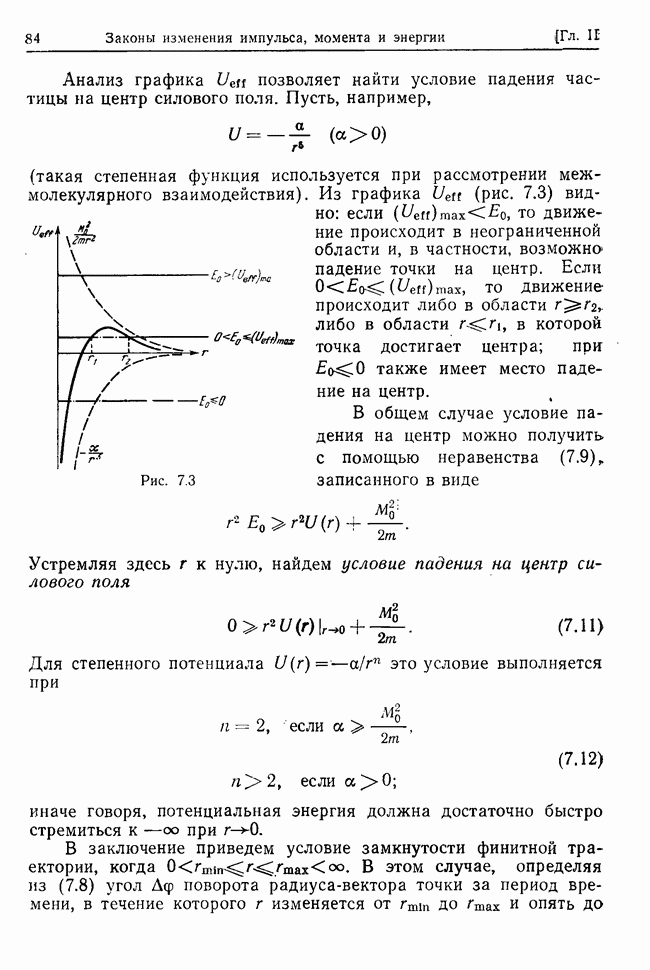
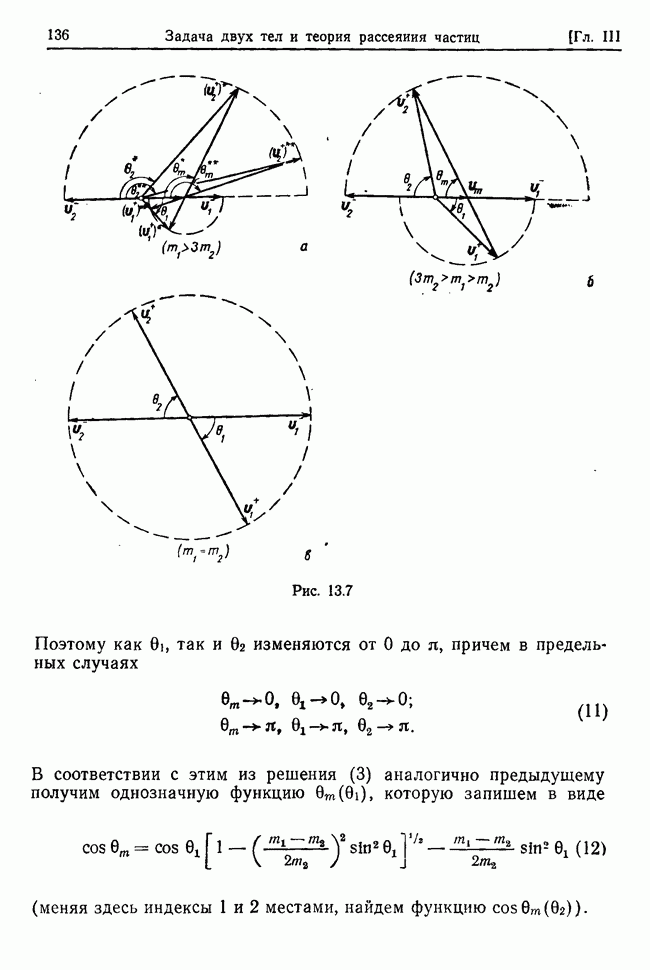
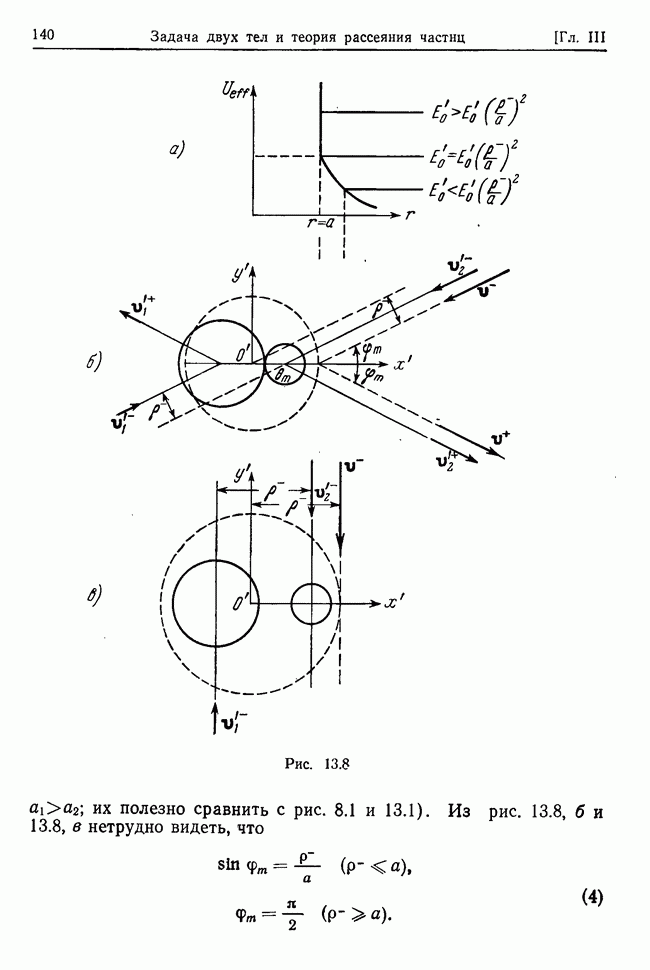
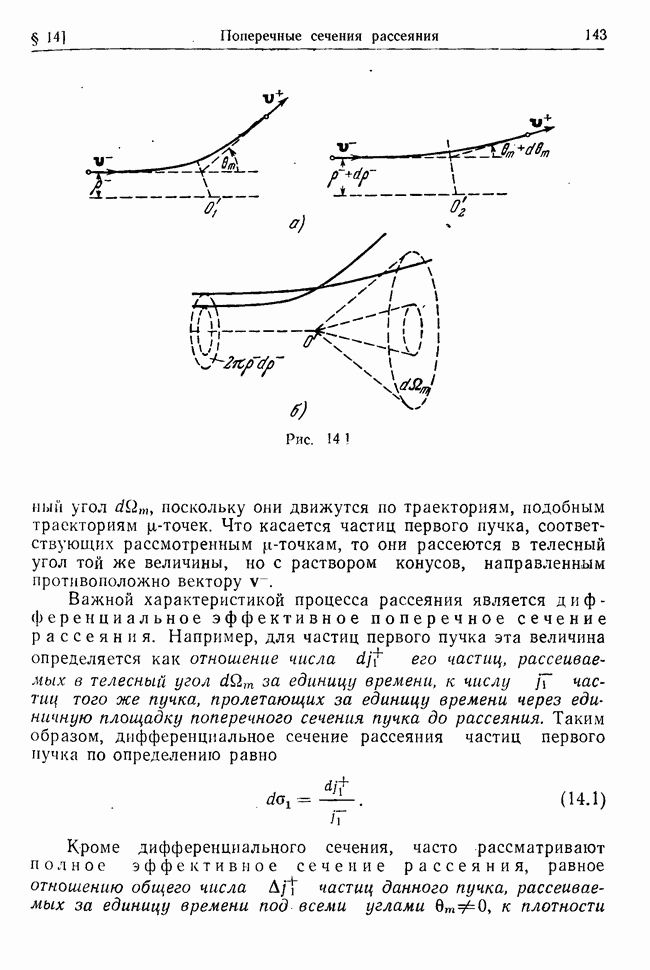
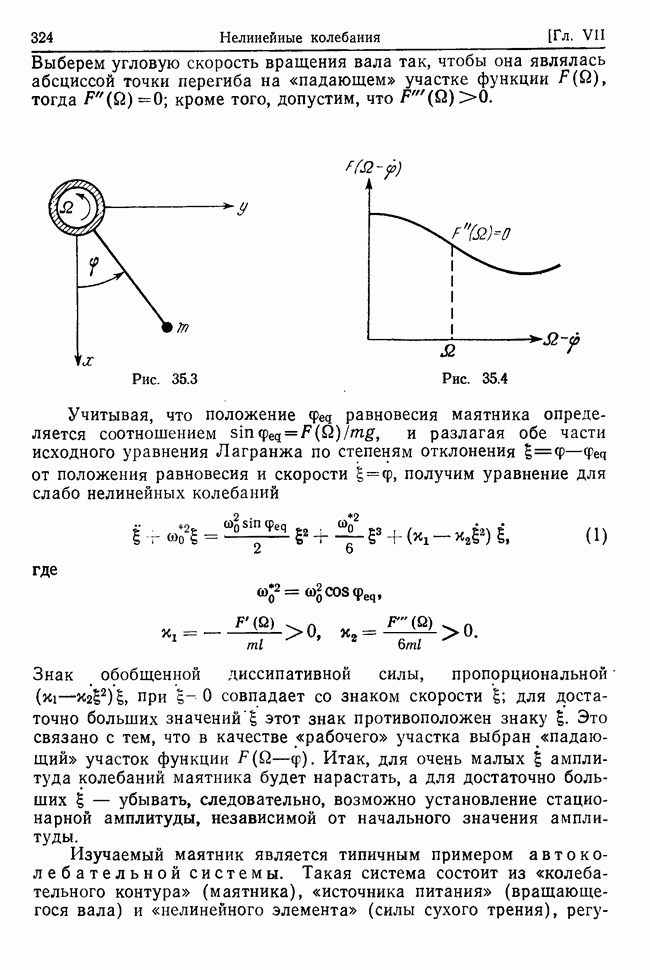
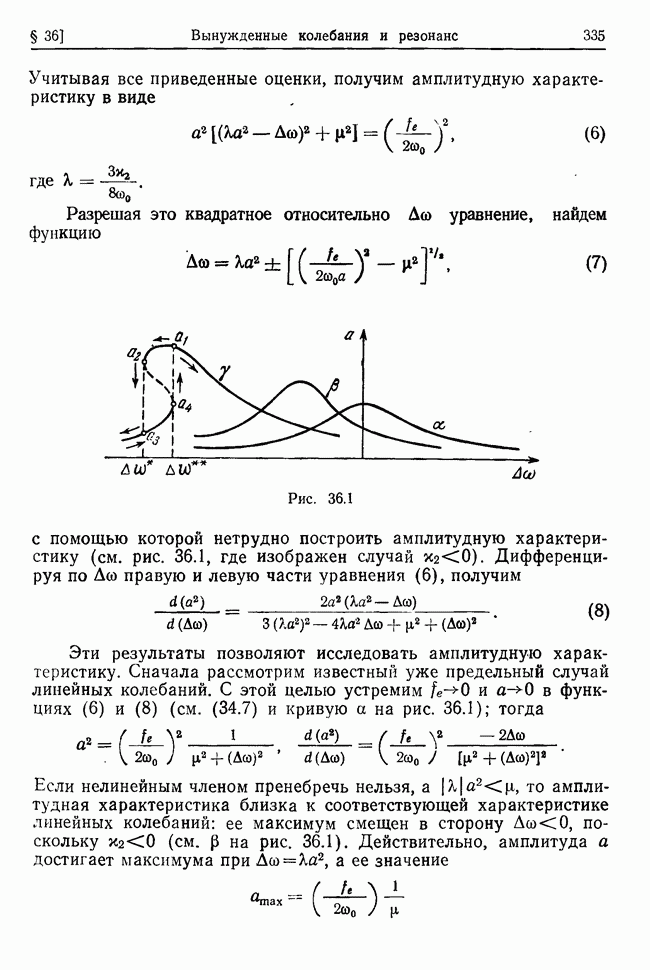
Рассмотрим несвободную систему с идеальными голономными стационарными связями и  степенями свободы, предполагая, что заданные силы, действующие на точки системы, потенциальны
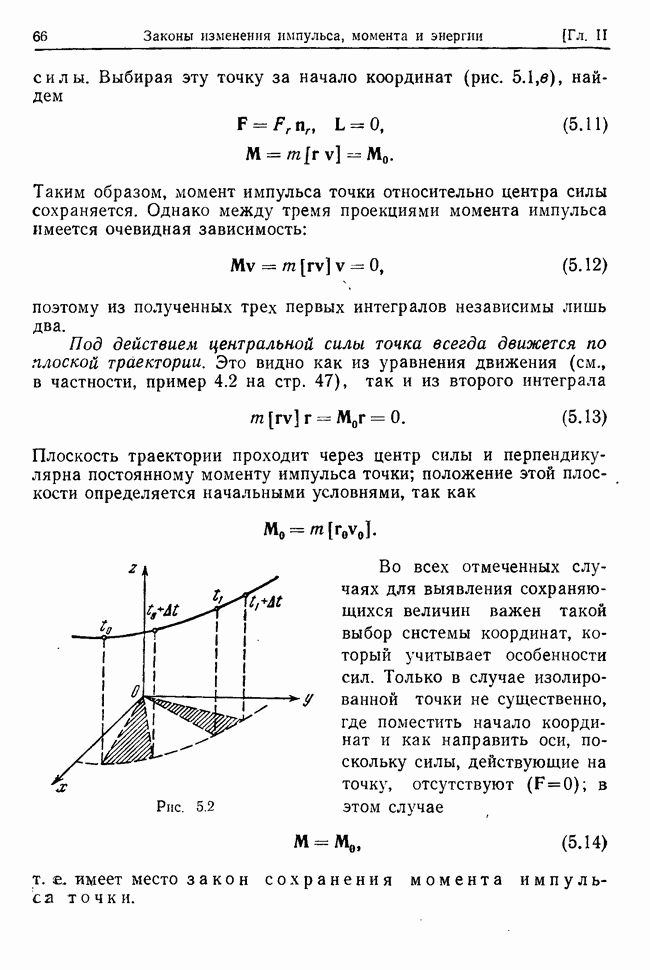
степенями свободы, предполагая, что заданные силы, действующие на точки системы, потенциальны
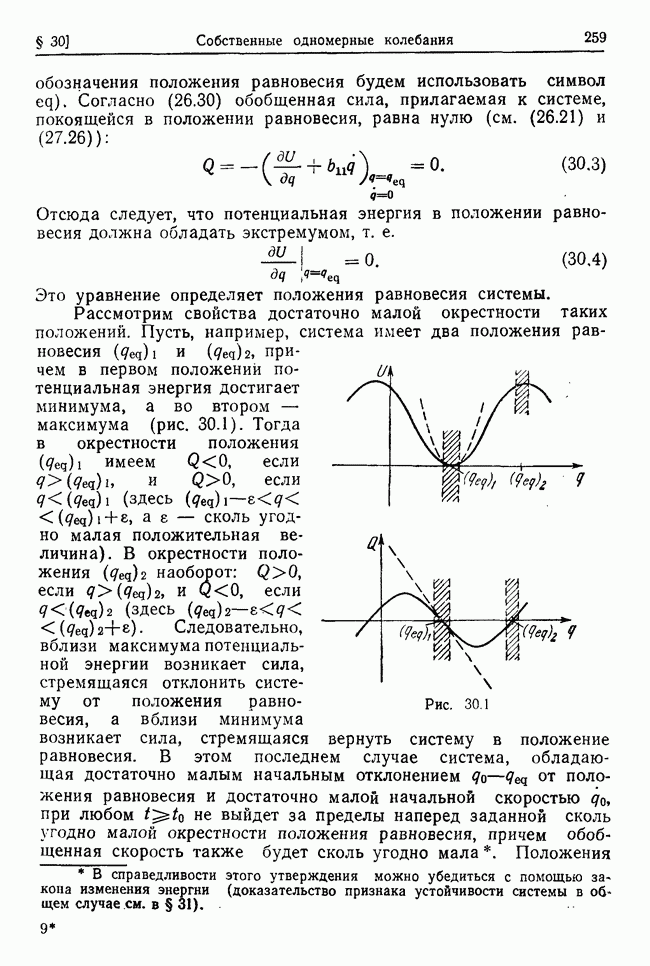
и стационарны, а у системы есть хотя бы одно положение устойчивого равновесия. Покажем, что в достаточно малой окрестности такого положения каждая независимая координата системы как функция времени может быть представлена в виде суммы гармонических функций, изменяющихся во времени с частотами, которые определяются свойствами системы, связей и заданных сил.
В силу стационарности связей

где  (см. (27.1) - (27.3)), а в силу стационарности заданных сил потенциальная энергия системы будет функцией лишь независимых координат.
(см. (27.1) - (27.3)), а в силу стационарности заданных сил потенциальная энергия системы будет функцией лишь независимых координат.
Разложим кинетическую энергию в положении устойчивого равновесия в ряд по степеням координат  и степеням обобщенных скоростей
и степеням обобщенных скоростей  . Тогда с точностью до членов второго порядка малости включительно из (32.1) получим
. Тогда с точностью до членов второго порядка малости включительно из (32.1) получим

где 
Предполагая, что в положении устойчивого равновесия потенциальная энергия  обладает изолированным минимумом и разлагая ее в том же положении по степеням отклонений найдем
обладает изолированным минимумом и разлагая ее в том же положении по степеням отклонений найдем

где  (здесь опущена несущественная постоянная). Разложение потенциальной энергии может начаться с членов третьего или более высокого порядка малости, что приведет к нелинейным уравнениям. В связи с этим допустим, что не все коэффициенты
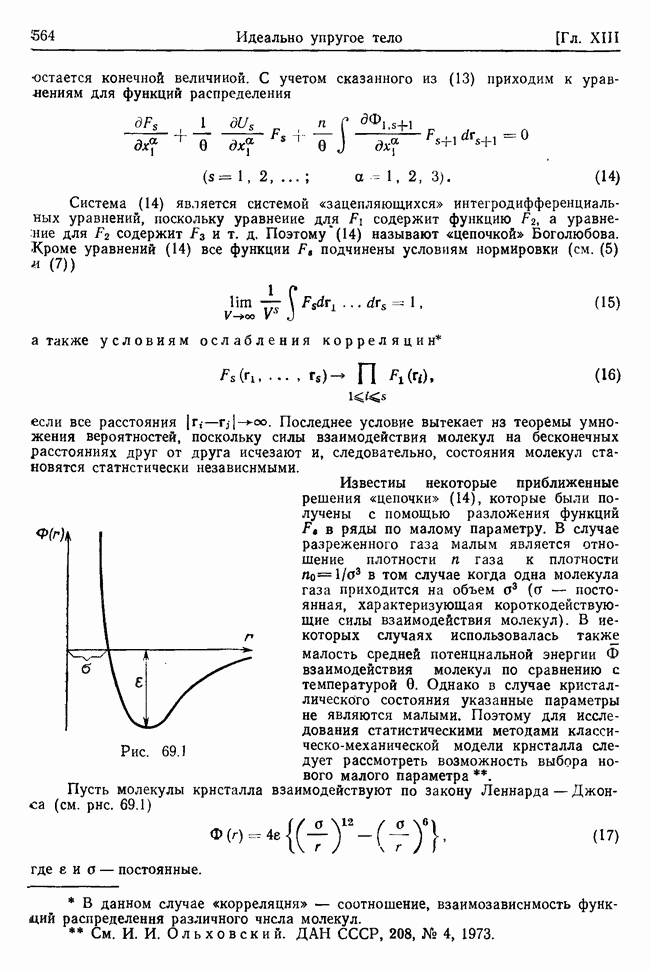
(здесь опущена несущественная постоянная). Разложение потенциальной энергии может начаться с членов третьего или более высокого порядка малости, что приведет к нелинейным уравнениям. В связи с этим допустим, что не все коэффициенты  в разложении (32.3) равны нулю.
в разложении (32.3) равны нулю.
Подставляя (32.2) и (32.3) в (27.23), придем к уравнениям

(здесь знак равновесия при коэффициентах опущен для
сокращения записи, однако всегда следует помнить, что коэффициенты в (32.4) берутся в положении равновесия, т. е. являются постоянными величинами). Итак, закон движения системы с  степенями свободы около положения устойчивого равновесия определяется линейными однородными уравнениями с постоянными действительными и симметричными коэффициентами.
степенями свободы около положения устойчивого равновесия определяется линейными однородными уравнениями с постоянными действительными и симметричными коэффициентами.
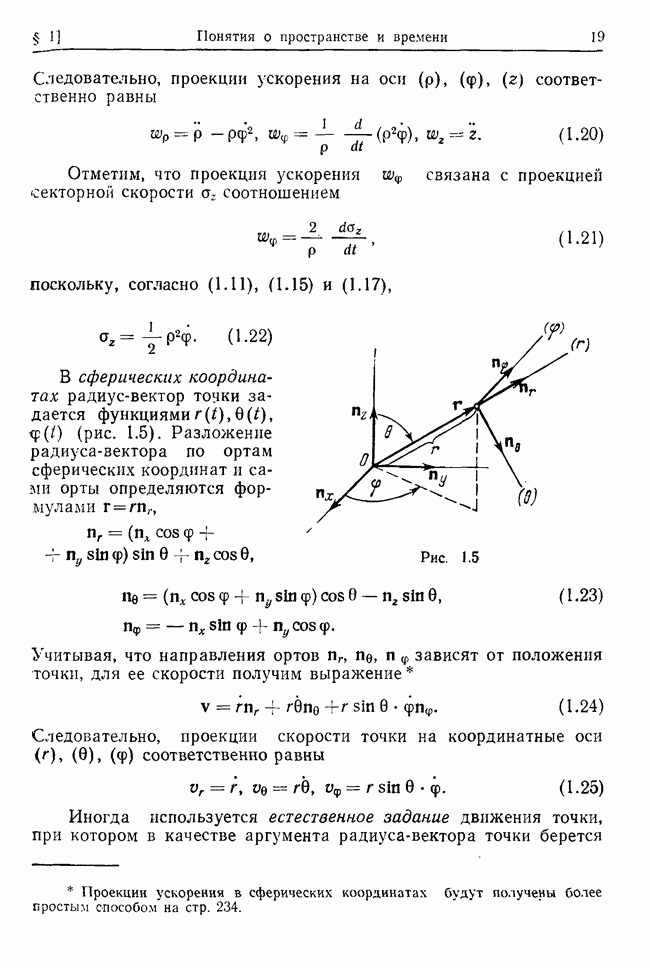
Решение этих уравнений ищем в виде

Подставляя (32.5) в (32.4), получим уравнения для «амплитуд»  .
.

Эта система однородных уравнений имеет нетривиальное решение, если ее детерминант равняется нулю:

(для краткости детерминант системы (32.6) будем обозначать символом  — см. (30.9)).
— см. (30.9)).
Характеристическое уравнение (32.7) представляет собой алгебраическое уравнение  степени относительно К и, следовательно, имеет
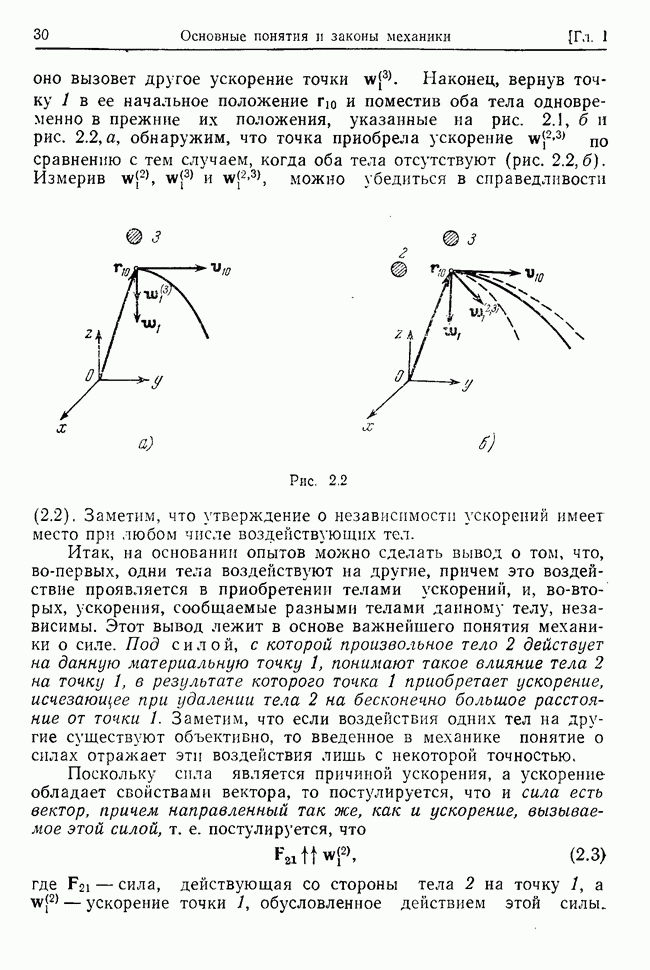
степени относительно К и, следовательно, имеет  корней
корней  (эти корни называются собственными значениями характеристического уравнения). Система (32.6) после подстановки в нее данного корня
(эти корни называются собственными значениями характеристического уравнения). Система (32.6) после подстановки в нее данного корня  определяет соотношение между «амплитудами» С:
определяет соотношение между «амплитудами» С:

Полученные отсюда амплитуды будем обозначать  и называть «амплитудами, принадлежащими собственному значению
и называть «амплитудами, принадлежащими собственному значению 
Общее решение системы дифференциальных уравнений (32.4) можно записать в виде действительной (или мнимой) части суммы частных решений, т. е. в виде

где амплитуды  (а точнее, их отношения) определяются системой (32.8), а корни
(а точнее, их отношения) определяются системой (32.8), а корни  — уравнением (32.7).
— уравнением (32.7).
Из (32.9) видно, что существенным шагом в решении уравнений (32.4) является определение собственных значений  . Поэтому большое значение имеют общие заключения о корнях характеристического уравнения. Например, можно утверждать, что в рассматриваемом случае консервативных систем действительные части всех К должны равняться нулю, так как иначе
. Поэтому большое значение имеют общие заключения о корнях характеристического уравнения. Например, можно утверждать, что в рассматриваемом случае консервативных систем действительные части всех К должны равняться нулю, так как иначе  и
и  имели бы экспоненциальные возрастающие и убывающие со временем множители, которые при произвольных условиях привели бы к нарушению закона сохранения энергии. Таким образом, если на систему действуют только потенциальные стационарные силы, то все собственные значения
имели бы экспоненциальные возрастающие и убывающие со временем множители, которые при произвольных условиях привели бы к нарушению закона сохранения энергии. Таким образом, если на систему действуют только потенциальные стационарные силы, то все собственные значения  будут чисто мнимыми:
будут чисто мнимыми:

здесь  — действительные величины, называемые собственными частотами системы, а собственные значения к перенумерованы не от 1 до
— действительные величины, называемые собственными частотами системы, а собственные значения к перенумерованы не от 1 до  , а от
, а от  поскольку каждому номеру соответствует одна пара комплексно сопряженных значений корня. Тогда (32.9) можно записать в виде
поскольку каждому номеру соответствует одна пара комплексно сопряженных значений корня. Тогда (32.9) можно записать в виде

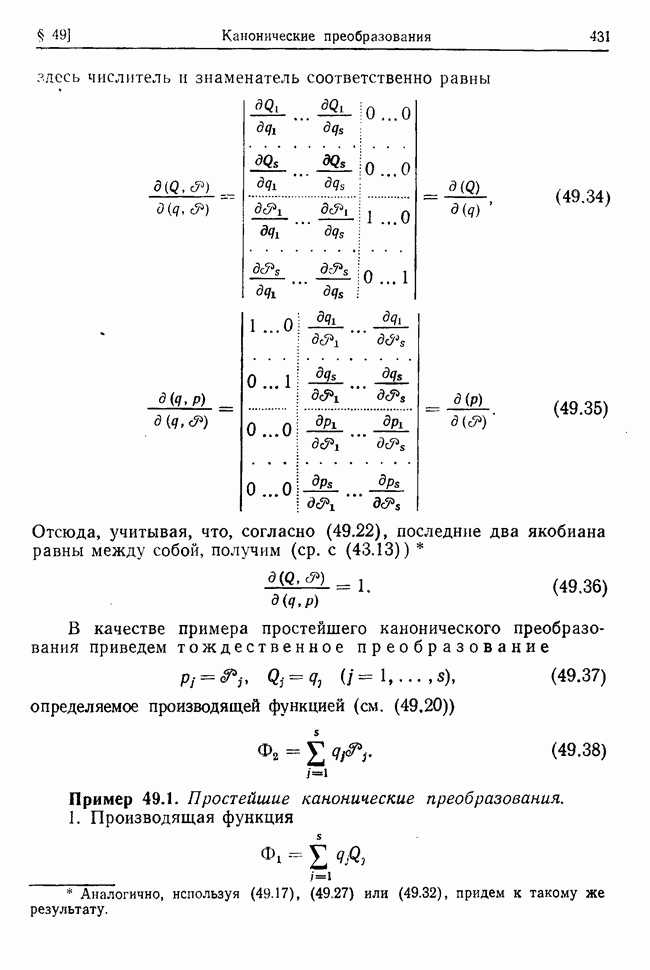
Значения амплитуд  соответствующих
соответствующих  определяются с помощью однородной системы (32.8). Поскольку интересующее нас решение нетривиально, среди амплитуд
определяются с помощью однородной системы (32.8). Поскольку интересующее нас решение нетривиально, среди амплитуд  должна существовать хотя бы одна амплитуда, отличная от нуля. Пусть от нуля отлична амплитуда
должна существовать хотя бы одна амплитуда, отличная от нуля. Пусть от нуля отлична амплитуда  (обобщенные координаты всегда можно перенумеровать так, чтобы от нуля отличалась амплитуда, соответствующая координате
(обобщенные координаты всегда можно перенумеровать так, чтобы от нуля отличалась амплитуда, соответствующая координате  . Тогда перенося в правую часть системы (32.8) слагаемые
. Тогда перенося в правую часть системы (32.8) слагаемые  согласно правилу решения линейных уравнений получим
согласно правилу решения линейных уравнений получим

где  — алгебраическое дополнение к элементу
— алгебраическое дополнение к элементу  -того столбца любой строки характеристического детерминанта, взятого при значении
-того столбца любой строки характеристического детерминанта, взятого при значении  Так как амплитуда
Так как амплитуда  не определена, то вводя обозначение
не определена, то вводя обозначение  все амплитуды можно представить в виде
все амплитуды можно представить в виде

где Со, — произвольная постоянная. Подставляя (32.13) в (32.11), получим

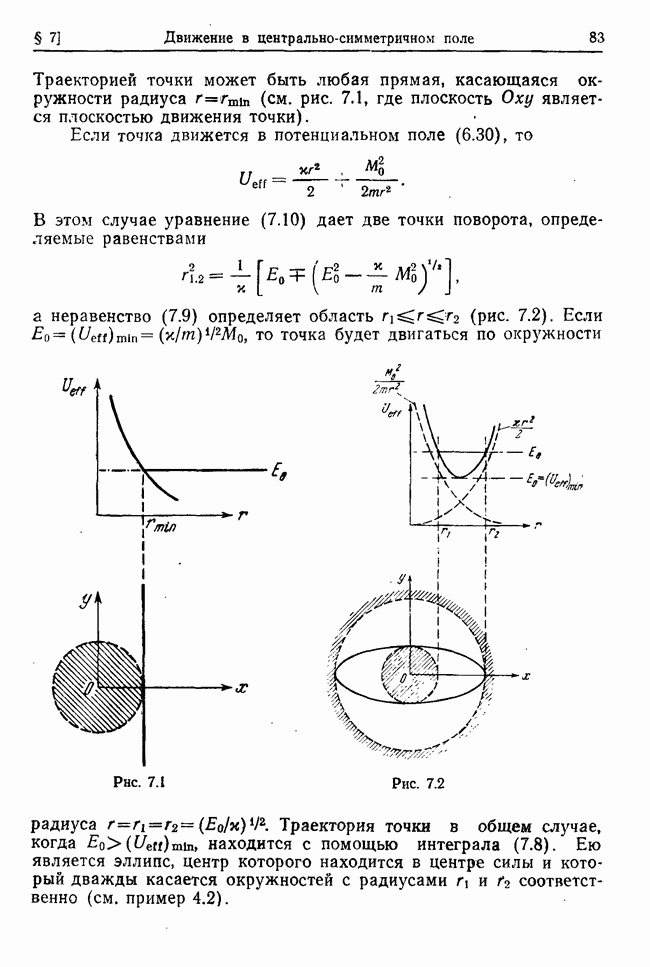
Ввиду потенциальности заданных сил характеристическое уравнение (32.7) и все дополнения характеристического детерминанта содержат только степени квадрата X. Поэтому в рассматриваемом случае дополнения будут действительными величинами, которые удовлетворяют соотношениям (см. (32.10))

Используя эти соотношения и учитывая, что

(здесь  — действительные произвольные постоянные), найдем, общее решение системы дифференциальных уравнений (32.4) в виде
— действительные произвольные постоянные), найдем, общее решение системы дифференциальных уравнений (32.4) в виде

где 
Итак, собственные колебания системы, описываемые координатами  представляют собой наложение гармонических колебаний с собственными частотами системы. Функции
представляют собой наложение гармонических колебаний с собственными частотами системы. Функции  являются строго периодическими функциями времени, а
являются строго периодическими функциями времени, а  в общем случае не являются таковыми (например, при несоизмеримости собственных частот координата никогда не примет начального значения
в общем случае не являются таковыми (например, при несоизмеримости собственных частот координата никогда не примет начального значения  Подчеркнем также, что нельзя отождествлять какую-либо собственную частоту
Подчеркнем также, что нельзя отождествлять какую-либо собственную частоту  с частотой колебаний какой-либо определенной точки системы. Такое представление верно лишь в предельном случае невзаимодействующих точек системы, если каждая из них обладает одной степенью свободы. Вообще говоря, собственные частоты характеризуют движение системы в целом; всегда можно задать начальные условия так, чтобы все координаты гармонически изменялись со временем с одной из собственных частот системы. Действительно, в силу произвольности амплитуд а начальные условия можно выбрать так, чтобы все
с частотой колебаний какой-либо определенной точки системы. Такое представление верно лишь в предельном случае невзаимодействующих точек системы, если каждая из них обладает одной степенью свободы. Вообще говоря, собственные частоты характеризуют движение системы в целом; всегда можно задать начальные условия так, чтобы все координаты гармонически изменялись со временем с одной из собственных частот системы. Действительно, в силу произвольности амплитуд а начальные условия можно выбрать так, чтобы все
амплитуды, кроме одной, равнялись нулю. Например, пусть  тогда из (32.17) получим частное решение
тогда из (32.17) получим частное решение

В этом случае все координаты гармонически изменяются с одной собственной частотой  в фазе или противофазе в зависимости от знака
в фазе или противофазе в зависимости от знака  Во многих простых случаях такое выделение гармонических колебаний из собственных колебаний системы помогает сразу определить соответствующую частоту.
Во многих простых случаях такое выделение гармонических колебаний из собственных колебаний системы помогает сразу определить соответствующую частоту.
Из общего решения (32.17) следует, что в качестве независимых координат можно взять величины  Действительно, это решение определяет линейное преобразование от координат
Действительно, это решение определяет линейное преобразование от координат  к координатам
к координатам  . Координаты
. Координаты  называются главными (или нормальными) координатами. Соответственно гармонические колебания с собственными частотами системы называются главными (или нормальными) колебаниями. Очевидно, что координаты 0 удовлетворяют уравнениям
называются главными (или нормальными) координатами. Соответственно гармонические колебания с собственными частотами системы называются главными (или нормальными) колебаниями. Очевидно, что координаты 0 удовлетворяют уравнениям

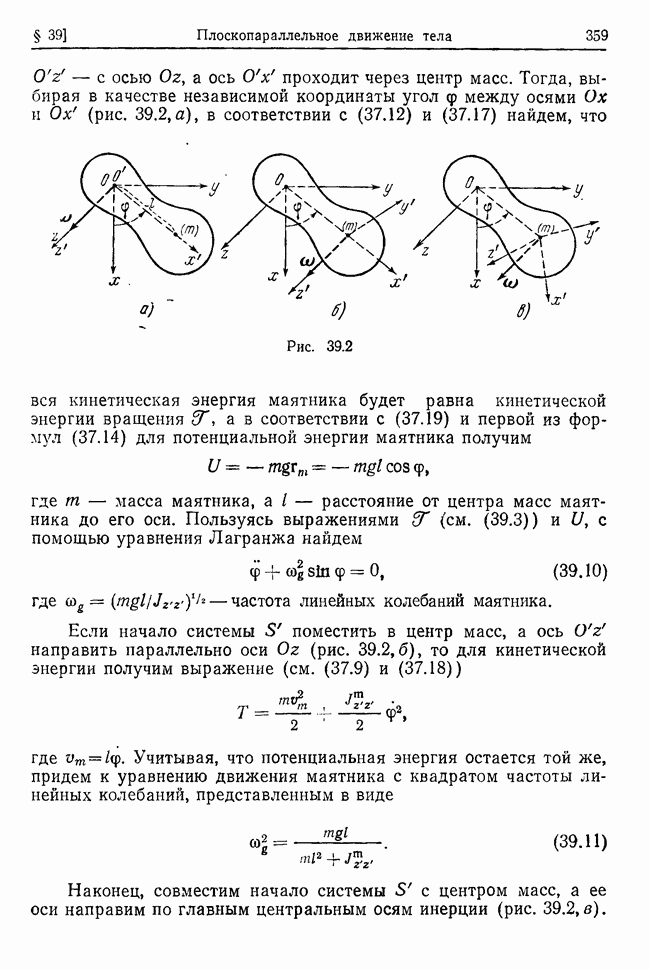
Эта система представляет собой уравнения Лагранжа в главных координатах  Каждое из этих уравнений является уравнением относительно лишь одной главной координаты. Поэтому системе (32.19) соответствует функция Лагранжа, равная сумме функций каждая из которых зависит только от соответствующей главной координаты
Каждое из этих уравнений является уравнением относительно лишь одной главной координаты. Поэтому системе (32.19) соответствует функция Лагранжа, равная сумме функций каждая из которых зависит только от соответствующей главной координаты  и ее производной
и ее производной  , т. е. лагранжиан системы в главных координатах должен иметь вид
, т. е. лагранжиан системы в главных координатах должен иметь вид

где

Введение главных координат равносильно одновременному приведению двух квадратичных форм Т и  к каноническому виду. Действительно, Т и
к каноническому виду. Действительно, Т и  в случае произвольных независимых координат задаются с помощью двух симметричных матгшн
в случае произвольных независимых координат задаются с помощью двух симметричных матгшн

Если одна из двух квадратичных форм определенно положительна, то некоторым линейным преобразованием обе формы всегда можно привести к каноническому виду [43, гл. VI, § 3, п. 95, теорема 2];. при этом матрицы преобразуются к диагональным матрицам

Соответственно для систем с идеальными голономными связями и, консервативными потенциальными силами всегда можно ввести главные координаты.
В заключение остановимся на случаях кратных и нулевых корней характеристического уравнения. Если некоторый корень этого уравнения является кратным, то в качестве общего решения следует опять-таки взять решение вида (32.17). Однако в этом случае коэффициенты  , соответствующие кратному корню, не являются алгебраическими дополнениями характеристического детерминанта и должны быть определены из уравнений (32.8). Нужно также иметь в виду, что кратному корню соответствуют главные колебания, одинаковые по частоте, но различные в общем случае по амплитуде и фазе (см. пример 32.4).
, соответствующие кратному корню, не являются алгебраическими дополнениями характеристического детерминанта и должны быть определены из уравнений (32.8). Нужно также иметь в виду, что кратному корню соответствуют главные колебания, одинаковые по частоте, но различные в общем случае по амплитуде и фазе (см. пример 32.4).
Если какая-нибудь собственная частота  то, как видно из (31.19),
то, как видно из (31.19),

«Нулевая частота» возникает, например, в том случае, когда потенциальная энергия системы достигает минимума не в одной «точке», а в некоторой области, т. е. в том случае, когда потенциальная энергия не обладает изолированным минимумом (см. примеры 32.5 и 32.6).
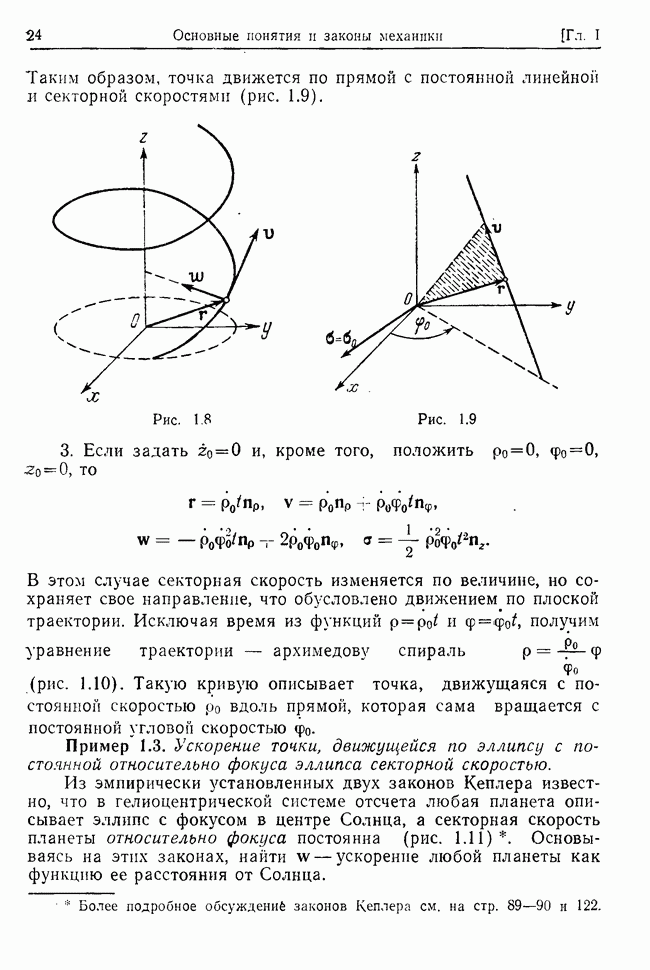
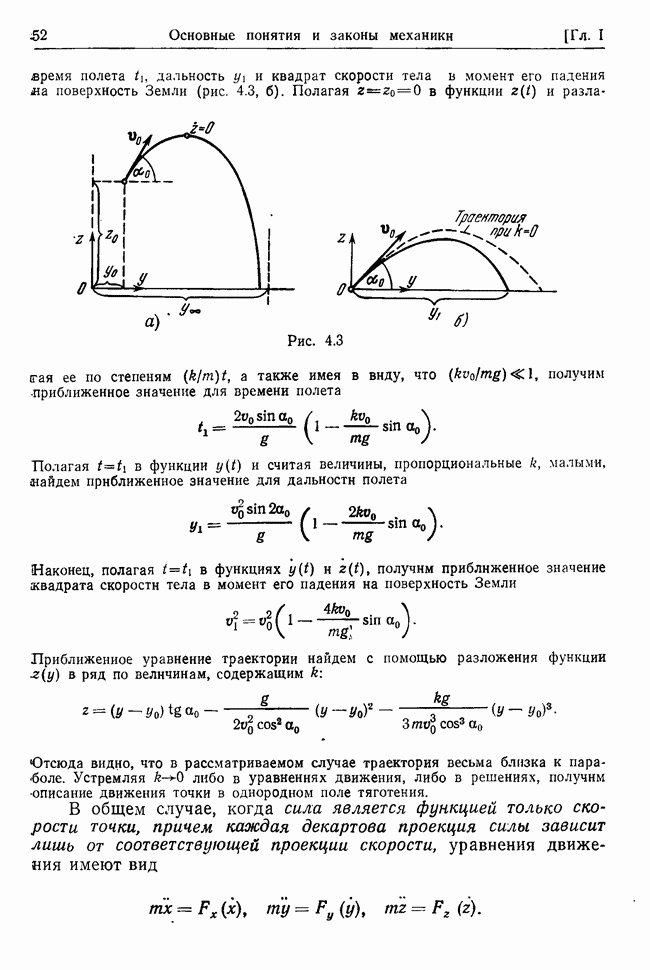
Пример 32.1. Плоские колебания материальной точки, подвешенной на пружине.
Положение устойчивого равновесия точки, подвешенной на пружине, а именно положение

было определено в примере 31.1. Там же были найдены значения вторых производных потенциальной энергии в рассматриваемом положении. Используя эти результаты, найдем общее решение, описывающее линейные колебания точки в вертикальной плоскости.
Разлагая кинетическую и потенциальную энергии точки в положении устойчивого равновесия, получим

где  . Отсюда видно, что координаты
. Отсюда видно, что координаты  являются главными координатами (см. (32.20)). Используя выражения Т и V, получим уравнения колебаний (см. (32.19))
являются главными координатами (см. (32.20)). Используя выражения Т и V, получим уравнения колебаний (см. (32.19))

и значения квадратов двух собственных частот

Общим решением уравнений будут функции

Таким образом, колебание точки слагается из гармонического колебания вдоль оси пружины с частотой, равной  и гармонического колебания математического маятника длины ред с частотой, равной
и гармонического колебания математического маятника длины ред с частотой, равной 
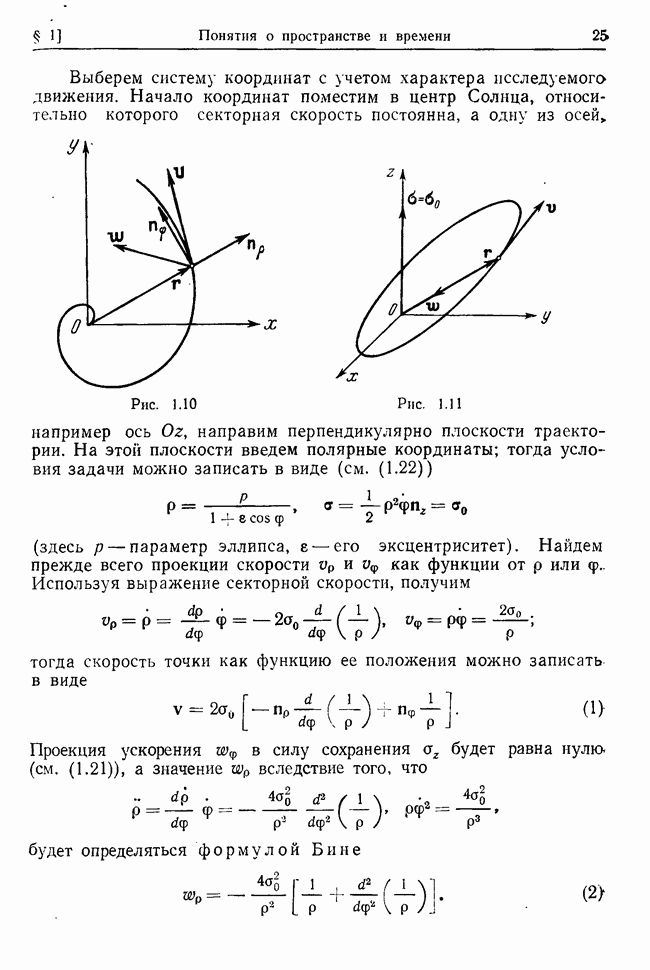
Пример 32.2. Колебания системы двух точек на горизонтальном стержне.

Рис. 32.1
Две точки одинаковой массы  находятся на неподвижном гладком и горизонтальном стержне длины
находятся на неподвижном гладком и горизонтальном стержне длины  . Эти точки соединены друг с другом и с концами стержня тремя пружинами, подчиненными закону Гука (жесткость каждой из пружин и длина в ненапряженном состоянии соответственно равны х и а). Найти закон движения системы вблизи ее положения устойчивого равновесия.
. Эти точки соединены друг с другом и с концами стержня тремя пружинами, подчиненными закону Гука (жесткость каждой из пружин и длина в ненапряженном состоянии соответственно равны х и а). Найти закон движения системы вблизи ее положения устойчивого равновесия.
Направим ось  вдоль стержня и совместим начало отсчета, с одним из кондов стержня. Выбирая в качестве независимых координат декартовы координаты точек
вдоль стержня и совместим начало отсчета, с одним из кондов стержня. Выбирая в качестве независимых координат декартовы координаты точек  , для. кинетической энергии системы получим выражение
, для. кинетической энергии системы получим выражение

Потенциальная энергия  системы слагается из энергии упругой деформации всех пружин, т. е.
системы слагается из энергии упругой деформации всех пружин, т. е.

где  - удлинения пружин, соответственно равные
- удлинения пружин, соответственно равные

В данном случае положение устойчивого равновесия очевидно и определяется координатами

Кинетическая и потенциальная энергии как функции отклонений от этого положения и обобщенных скоростей будут соответственно равны

где 
Соответственно уравнения движения (32.4) примут вид

где  .
.
Повторяя общую процедуру решения уравнений, запишем уравнения для амплитуд (см. (32.6))

и характеристическое уравнение (см. 32.7))

Последнее уравнение распадается на два квадратных уравнения, решение которых приводит к четырем собственным значениям X:


где

Подставляя  в первое из уравнений для амплитуд, найдем
в первое из уравнений для амплитуд, найдем 
Аналогично получим, что

Используя эти соотношения, находим общее решение (см. (32.9))

Итак, колебания системы двух точек в общем случае характеризуются двумя собственными частотами  и слагаются из двух главных колебаний. Главное колебание
и слагаются из двух главных колебаний. Главное колебание  осуществляется (см. рис. 32.1, б), если в начальный момент времени средняя пружина не растянута, обе точки одинаково отклонены в одну сторону и имеют одинаковые начальные скорости (по величине и направлению). В этом случае средняя пружина в любой момент времени не напряжена и, следовательно, не влияет на колебания точек; соответственно частота этого колебания равна
осуществляется (см. рис. 32.1, б), если в начальный момент времени средняя пружина не растянута, обе точки одинаково отклонены в одну сторону и имеют одинаковые начальные скорости (по величине и направлению). В этом случае средняя пружина в любой момент времени не напряжена и, следовательно, не влияет на колебания точек; соответственно частота этого колебания равна  Главное колебание
Главное колебание  осуществляется, если в начальный момент боковые пружины одинаково сжаты (или растянуты), а скорости точек одинаковы по величине и противоположно направлены (рис. 32.1, в). Соответственно частота второго колебания больше частоты первого гколебания и равна
осуществляется, если в начальный момент боковые пружины одинаково сжаты (или растянуты), а скорости точек одинаковы по величине и противоположно направлены (рис. 32.1, в). Соответственно частота второго колебания больше частоты первого гколебания и равна  .
.
Пример 32.3. Маятник с кратными собственными частотами.

Рис. 32.2
Две материальные точки 1 и 2 с одинаковыми массами  соединены невесомым стержнем длины 21. Центр этого маятника движется по горизонтальному гладкому и неподвижному стержню длины
соединены невесомым стержнем длины 21. Центр этого маятника движется по горизонтальному гладкому и неподвижному стержню длины  (рис. 32.2). Каждая из точек 1 и 2 соединена с двумя одинаковыми пружинами жесткости х и длины а в ненапряженном состоянии. Неподвижные концы пружин закреплены на расстоянии
(рис. 32.2). Каждая из точек 1 и 2 соединена с двумя одинаковыми пружинами жесткости х и длины а в ненапряженном состоянии. Неподвижные концы пружин закреплены на расстоянии  от горизонтального стержня. Найти общее решение для линейных колебаний маятника в вертикальной плоскости (плоскости рисунка).
от горизонтального стержня. Найти общее решение для линейных колебаний маятника в вертикальной плоскости (плоскости рисунка).
Выберем систему координат так, как это показано на рис. 32.2. В качестве независимых координат возьмем координату
11 центра маятника и угол  его наклона относительно вертикали. Тогда координаты точек 1 и 2 будут соответственно равны
его наклона относительно вертикали. Тогда координаты точек 1 и 2 будут соответственно равны

Подставляя в общее выражение для потенциальной энергии маятника

.приближенные значения удлинений пружин

получим

Кинетическая энергия маятника в тех же обобщенных переменных  с той же точностью будет равна
с той же точностью будет равна

Из выражений для Т и  следует, что у и
следует, что у и  являются главными координатами, удовлетворяющими уравнениям Лагранжа:
являются главными координатами, удовлетворяющими уравнениям Лагранжа:

где  . Корни характеристического уравнения этой системы кратны, соответственно чему общее решение определяется двумя главными колебаниями с одинаковыми частотами и с различными, вообще говоря, амплитудами и фазами;
. Корни характеристического уравнения этой системы кратны, соответственно чему общее решение определяется двумя главными колебаниями с одинаковыми частотами и с различными, вообще говоря, амплитудами и фазами;

Эти колебания можно осуществить, задавая «симметричные» и «антисимметричные» начальные условия (см. предыдущий пример).
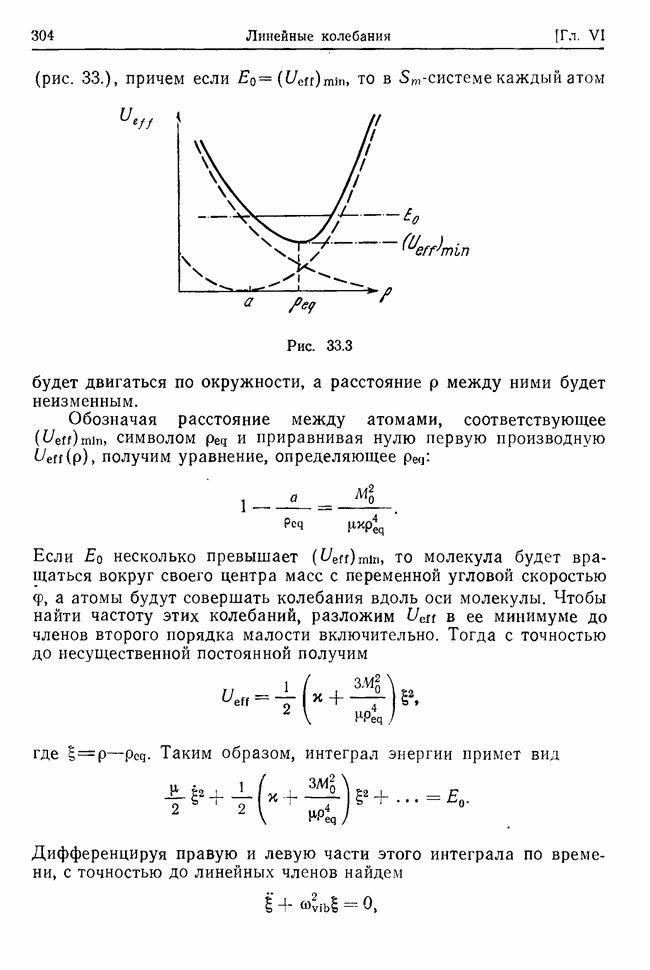
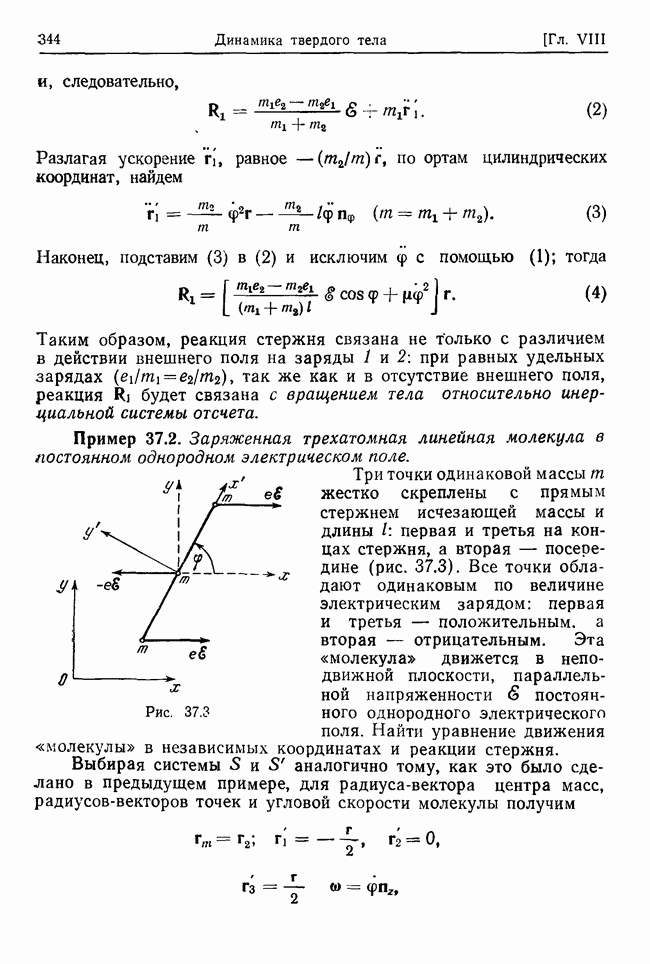
Пример 32.4. Продольные колебания невращающейся двухатомной молекулы.
Известно, что внутренняя энергия двухатомной молекулы с хорошей степенью точности описывается потенциалом как функцией расстояния  между атомами [39, стр. 225]:
между атомами [39, стр. 225]:

где  — постоянные, характеризующие молекулу (например, а является расстоянием между атомами, при котором потенциальная энергия минимальна).
— постоянные, характеризующие молекулу (например, а является расстоянием между атомами, при котором потенциальная энергия минимальна).
Если отклонение  достаточно мало, то энергию взаимодействия атомов можно приближенно записать в виде
достаточно мало, то энергию взаимодействия атомов можно приближенно записать в виде

(здесь опущена несущественная постоянная). Поэтому двухатомную молекулу можно представлять как систему двух материальных точек с массами  соединенных между собой пружиной жесткости у. и длины а в ненапряженном состоянии. Предполагая, что такая молекула движется только вдоль своей оси, т. е. вдоль оси пружины, найти закон движения молекулы.
соединенных между собой пружиной жесткости у. и длины а в ненапряженном состоянии. Предполагая, что такая молекула движется только вдоль своей оси, т. е. вдоль оси пружины, найти закон движения молекулы.
Совмещая декартову ось  с осью молекулы, получим выражения для кинетической и потенциальной энергий молекулы:
с осью молекулы, получим выражения для кинетической и потенциальной энергий молекулы:

Отсюда видно, что  обращается в нуль не только в некотором фиксированном положении
обращается в нуль не только в некотором фиксированном положении  но и в любом другом положении, соответствующем требованию
но и в любом другом положении, соответствующем требованию  Следовательно,
Следовательно,  не имеет, изолированного минимума в положении
не имеет, изолированного минимума в положении  Несмотря на это, применим метод решения, изложенный в настоящем параграфе (оправданность этого шага будет видна в дальнейшем).
Несмотря на это, применим метод решения, изложенный в настоящем параграфе (оправданность этого шага будет видна в дальнейшем).
Введем отклонения от положения равновесия

где  связаны отношением
связаны отношением 
Выражая  через отклонения, получим
через отклонения, получим

Соответственно уравнения движения, уравнения для амплитуд и частот будут иметь вид

(здесь  - приведенная масса). Из этих уравнений находим частоты и отношение амплитуд
- приведенная масса). Из этих уравнений находим частоты и отношение амплитуд

Используя эти результаты, получим общее решение

где  — действительные константы, а коэффициенты при
— действительные константы, а коэффициенты при  выбраны в соответствии с решением задачи двух тел (см. (12.7)). Выражая
выбраны в соответствии с решением задачи двух тел (см. (12.7)). Выражая  через начальные значения
через начальные значения  найдем общее решение для
найдем общее решение для 

или

Используя систему центра масс молекулы, ту же задачу можно решить короче. В этой системе кинетическая и потенциальная энергии молекулы выражаются формулами

где  (см. (12.7)). Отсюда можно найти уравнение Лагранжа
(см. (12.7)). Отсюда можно найти уравнение Лагранжа

где  а затем, используя соотношения задачи двух тел, получить решение
а затем, используя соотношения задачи двух тел, получить решение

где

Из обоих решений видно, что движение молекулы слагается из движения молекулы как целого со скоростью  (с чем связа
(с чем связа
на нулевая частота, появившаяся в первом решении) и колебаний атомов с частотой  которые совершаются в системе центра масс около положения устойчивого равновесия
которые совершаются в системе центра масс около положения устойчивого равновесия

Колебания первого и второго атомов совершаются в противофазе с отношением амплитуд, равным 
Пример 32.5. Продольные колебания линейной трехатомной симметричной молекулы.
Рассмотрим трехатомную молекулу как систему, состоящую из трех точек с массами  расположенных на одной прямой и соединенных между собой одинаковыми пружинами (длина в ненапряженном состоянии и жесткость каждой из пружин соответственно равны а их). Найти собственные частоты колебаний невращающейся молекулы и закон ее движения.
расположенных на одной прямой и соединенных между собой одинаковыми пружинами (длина в ненапряженном состоянии и жесткость каждой из пружин соответственно равны а их). Найти собственные частоты колебаний невращающейся молекулы и закон ее движения.

Рис. 32.3
Решая задачу в произвольной инерциальной системе отсчета, мы, так же как и в предыдущем примере, получим нулевую частоту, связанную с поступательным движением молекулы как целого. Однако проще с самого начала исключить эту частоту и рассматривать колебания молекулы в системе ее центра масс.
Направим декартову ось  по оси молекулы (рис. 32.3, а). Тогда кинетическая и потенциальная энергии будут соответственно равны
по оси молекулы (рис. 32.3, а). Тогда кинетическая и потенциальная энергии будут соответственно равны

Здесь координаты точек связаны соотношением (см. (21.4))

с помощью которого из выражений для Т и  можно исключить, например,
можно исключить, например,  . В результате получим
. В результате получим


Имея в виду, что положение устойчивого равновесия в системе  определяется равенствами
определяется равенствами

и вводя в качестве переменных отклонения от этого положения

в независимых координатах  найдем
найдем

Используя эти функции, придем к уравнениям движения, уравнениям для амплитуд и характеристическому уравнению:

где

Характеристическому уравнению удовлетворяют

где

 — масса всей молекулы. Соответственно из уравнений для амплитуд вытекают соотношения
— масса всей молекулы. Соответственно из уравнений для амплитуд вытекают соотношения

Таким образом, общее решение будет иметь вид

где

Возвращаясь к переменным  и учитывая соотношения между ними, окончательно найдем
и учитывая соотношения между ними, окончательно найдем

Из этого решения видно, что продольные колебания трехатомной симметричной молекулы сводятся к наложению двух главных колебаний. Главное колебание  совершается с частотой
совершается с частотой  и осуществляется, если в начальный момент времени отклонения и скорости двух крайних атомов одинаковы по величине и направлены в разные стороны, средний атом в этом случае все время находится в центре масс молекулы (рис. 32.3, б). Второе главное колебание
и осуществляется, если в начальный момент времени отклонения и скорости двух крайних атомов одинаковы по величине и направлены в разные стороны, средний атом в этом случае все время находится в центре масс молекулы (рис. 32.3, б). Второе главное колебание  с частотой
с частотой  асимметрично; для его осуществления нужно задать одинаковые начальные условия для крайних атомов; что касается атома 2, то его начальные отклонения и скорость должны относиться к отклонениям и скоростям крайних атомов как
асимметрично; для его осуществления нужно задать одинаковые начальные условия для крайних атомов; что касается атома 2, то его начальные отклонения и скорость должны относиться к отклонениям и скоростям крайних атомов как  (рис. 32.3, в).
(рис. 32.3, в).
Пример 32.6. Теплоемкость кристалла.
При сравнительно невысоких температурах атомы кристалла совершают линейные колебания около узлов кристаллической решетки, т. е. около положений устойчивого равновесия. Поэтому энергия атомов кристалла будет равна (см. (32.2) и (32.3))

где  проекции отклонения первого атома от «своего» узла и т. д. Выражение (1) в главных координатах
проекции отклонения первого атома от «своего» узла и т. д. Выражение (1) в главных координатах  имеет вид
имеет вид

где

Отсюда ясно, что полную энергию кристалла можно представить как сумму энергий  независимых осцилляторов
независимых осцилляторов
Согласно теореме о вириале сил (см. (6.37))  . Полагая далее, что энергия Е в среднем равнораспределена по всем осцилляторам,из (2) найдем
. Полагая далее, что энергия Е в среднем равнораспределена по всем осцилляторам,из (2) найдем

где  — средняя кинетическая энергия любого
— средняя кинетическая энергия любого  -ого осциллятора. Далее определим абсолютную температуру Т системы как величину, пропорциональную средней кинетической энергии
-ого осциллятора. Далее определим абсолютную температуру Т системы как величину, пропорциональную средней кинетической энергии  , т. е. положим
, т. е. положим  (здесь множитель
(здесь множитель  — постоянная Больцмана — имеет размерность энергии, деленной на градус). Тогда средняя энергия кристалла запишется в виде
— постоянная Больцмана — имеет размерность энергии, деленной на градус). Тогда средняя энергия кристалла запишется в виде  а теплоемкость с кристалла, т. е. отношение приращения средней энергии к приращению температуры, будет равна
а теплоемкость с кристалла, т. е. отношение приращения средней энергии к приращению температуры, будет равна  (закон Дюлонга — Пти).
(закон Дюлонга — Пти).
Приложение 32.1. Общие соотношения, которым подчинены собственные значения X для систем с идеальными голономными стационарными связями и потенциальными стационарными силами.
Умножая каждое из уравнений системы (32.8) на соответствующую комплексно сопряженную амплитуду  и складывая все результаты умножения, получим
и складывая все результаты умножения, получим

Входящие в это соотношение билинейные формы от амплитуд  соответствуют квадратичным формам Т и
соответствуют квадратичным формам Т и  Действительно, выполняя в (32.2) замену
Действительно, выполняя в (32.2) замену

найдем билинейную форму  Производя аналогичную [замену в (32.3), получим билинейную форму
Производя аналогичную [замену в (32.3), получим билинейную форму  Используя эти обозначения, запишем соотношение (1) в виде
Используя эти обозначения, запишем соотношение (1) в виде

Квадратичные формы Т и  являются положительно определенными формами с действительными симметричными коэффициентами. Следовательно, билинейные формы
являются положительно определенными формами с действительными симметричными коэффициентами. Следовательно, билинейные формы  являются действительными положительными величинами при любом а. Чтобы убедиться в этом, представим амплитуды С в виде
являются действительными положительными величинами при любом а. Чтобы убедиться в этом, представим амплитуды С в виде

где коэффициенты и  вещественны. Тогда для билинейной формы Т получим
вещественны. Тогда для билинейной формы Т получим

Мнимая часть формы  равна нулю в силу симметрии коэффициентов
равна нулю в силу симметрии коэффициентов  и антисимметрии множителей
и антисимметрии множителей  Действительная часть той же формы равна сумме билинейных форм от вещественных амплитуд и
Действительная часть той же формы равна сумме билинейных форм от вещественных амплитуд и  , т. е.
, т. е.

Если хотя бы один из коэффициентов и или  отличен от нуля (а нас интересует именно такой случай нетривиального решения), то
отличен от нуля (а нас интересует именно такой случай нетривиального решения), то  Аналогично найдем, что
Аналогично найдем, что  . Таким образом, из соотношения (2) действительно вытекает свойство (32.10).
. Таким образом, из соотношения (2) действительно вытекает свойство (32.10).
Приложение 32.2. Уравнения Лагранжа в главных координатах.
Чтобы получить уравнения (32.19), найдем, исходя из (32.2) и (32.3), кинетическую и потенциальную энергии в главных координатах. Например, подставляя (32.17) и (32.3), получим

Эта форма зависит только от квадратов 0, поскольку коэффициенты при произведениях  равны нулю:
равны нулю:

Действительно, умножая каждое из уравнений (32.8) на амплитуду и складывая все результаты умножения, найдем соотношения, аналогичные соотношениям (2) приложения 32.1:

Таким же образом получим соотношение для Я:

Ввиду симметрии коэффициентов  билинейные формы, входящие в (3) и (4), также симметричны относительно индексов а и
билинейные формы, входящие в (3) и (4), также симметричны относительно индексов а и  т. е.
т. е.

Используя это свойство, из соотношений (3) и (4) найдем

Отсюда, предполагая отсутствие кратных корней, получим

и, следоватетьно (см. (3)),

Представляя билинейную форму

в виде (см. (32.12))

(здесь  отличны от нуля) и используя соотношения (7), убеждаемся в справедливости (2).
отличны от нуля) и используя соотношения (7), убеждаемся в справедливости (2).
Учитывая эти соотношения, найдем потенциальную энергию в главных координатах

где

Аналогично для кинетической энергии получим выражение

где

С помощью (8) и (9) нетрудно убедиться, что уравнения Лагранжа в главных координатах имеют вид (32.19).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ЧАСТЬ I. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
- Глава I. ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ МЕХАНИКИ
- § 1. Понятия о материальной точке, о пространстве и времени
- § 2. Понятия о силе и массе
- § 3. Понятие об инерциальной системе отсчета и законы Ньютона. Принцип относительности Галилея
- § 4. Решение уравнений движения и начальные условия
- Глава II. ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ ИМПУЛЬСА, КИНЕТИЧЕСКОГО МОМЕНТА И ЭНЕРГИИ
- § 5. Законы изменения и сохранения импульса и момента импульса материальной точки
- § 6. Законы изменения и сохранения энергии материальной точки
- § 7. Движение в центрально-симметричном поле
- § 8. Движение под действием силы, обратно пропорциональной квадрату расстояния до центра силы. Законы Кеплера
- § 9. Движение центра масс; законы изменения и сохранения импульса системы
- § 10. Законы изменения и сохранения кинетического момента системы
- § 11. Законы изменения и сохранения энергии системы
- Глава III. ЗАДАЧА ДВУХ ТЕЛ И ТЕОРИЯ РАССЕЯНИЯ ЧАСТИЦ
- § 12. Задача двух тел
- § 13. Упругое рассеяние частиц
- § 14. Поперечные сечения рассеяния
- § 15. Распад частиц
- Глава IV. ДВИЖЕНИЕ ОТНОСИТЕЛЬНО НЕИНЕРЦИАЛЬНЫХ СИСТЕМ ОТСЧЕТА
- § 16. Положение системы отсчета (твердого тела)
- § 17. Поступательное движение и изменение ориентации системы отсчета (твердого тела)
- § 18. Общий случай движения системы отсчета (твердого тела)
- § 19. Положение, скорость и ускорение материальной точки относительно разных систем отсчета
- § 20. Уравнение движения материальной точки относительно неинерциальной системы отсчета; силы инерции
- § 21. Законы изменения кинетического момента и кинетической энергии относительно поступательно движущейся системы центра масс
- § 22. Законы изменения и сохранения импульса, кинетического момента и энергии относительно произвольных неинерциальных систем отсчета
- Глава V. УРАВНЕНИЯ ЛАГРАНЖА
- § 23. Основная задача динамики несвободной системы и понятие о связях
- § 24. Действительные, возможные и виртуальные перемещения; идеальные связи
- § 25. Уравнения Лагранжа с реакциями связей; законы изменения импульса, кинетического момента и энергии для систем со связями
- § 26. Уравнения Лагранжа в независимых координатах и общее уравнение механики; циклические координаты и симметрия силового поля и связей
- § 27. Структура уравнений движения в независимых координатах и функция Лагранжа
- § 28. Законы сохранения обобщенного импульса и обобщенной энергии
- § 29. Ковариантность уравнений Лагранжа в независимых координатах
- Глава VI. ЛИНЕЙНЫЕ КОЛЕБАНИЯ
- § 30. Собственные одномерные колебания
- § 31. Положение устойчивого равновесия
- § 32. Собственные и главные колебания системы под действием потенциальных сил
- § 33. Собственные колебания системы под действием потенциальных, гироскопических и диссипативных сил
- § 34. Вынужденные колебания
- Глава VII. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
- § 35. Собственные колебания и метод Крылова — Боголюбова
- § 36. Вынужденные колебания и резонанс
- Глава VIII. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 37. Уравнения движения твердого тела
- § 38. Тензор инерции
- § 39. Плоскопараллельное движение твердого тела
- § 40. Движение твердого тела с одной неподвижной точкой. Уравнения Эйлера
- § 41. Линейные неголономные связи
- Глава IX. УРАВНЕНИЯ ГАМИЛЬТОНА
- § 42. Канонические уравнения
- § 43. Фазовое пространство и теорема Лиувилля
- § 44. Скобки Пуассона
- § 45. Уравнение Гамильтона — Якоби
- § 46. Метод разделения переменных
- § 47. Движение материальной точки и волновой процесс
- § 48. Интегральный инвариант Пуанкаре — Картана
- § 49. Канонические преобразования
- § 50. Переменные «действие — угол» и адиабатические инварианты
- § 51. Уравнения движения и интегральные вариационные принципы
- ЧАСТЬ II. ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
- § 52. Физически бесконечно малая частица
- § 53. Деформация малой частицы
- § 54. Законы сохранения массы, изменения импульса и кинетического момента
- § 55. Уравнение изменения кинетической энергии. Законы термодинамики
- Глава XI. ИДЕАЛЬНАЯ ЖИДКОСТЬ
- § 56. Уравнения движения идеальной жидкости
- § 57. Основные теоремы динамики идеальной жидкости
- § 58. Потоки импульса и энергии
- § 59. Несжимаемая жидкость
- § 60. Звуковые волны
- § 61. Ударные волны
- § 62. Магнитогидродинамика идеальной жидкости
- Глава XII. ВЯЗКАЯ ЖИДКОСТЬ
- § 63. Тензор напряжений и уравнения движения
- § 64. Уравнение Навье—Стокса
- § 65. Малые колебания
- § 66. Магнитогидродинамика вязкой жидкости
- ПРИЛОЖЕНИЕ К ГЛАВЕ XII
- Глава XIII. ИДЕАЛЬНО УПРУГОЕ ТЕЛО
- § 67. Закон Гука и уравнения изменения импульса
- § 68. Равновесие изотропных тел
- § 69. Упругие волны
- ПРИЛОЖЕНИЕ К ГЛАВЕ XIII
- ЛИТЕРАТУРА