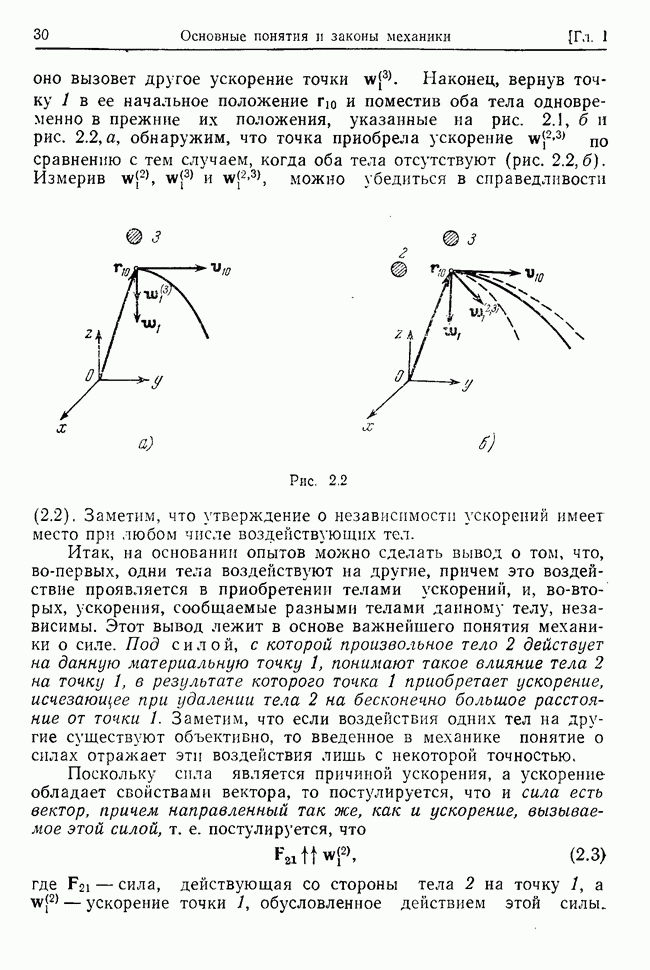
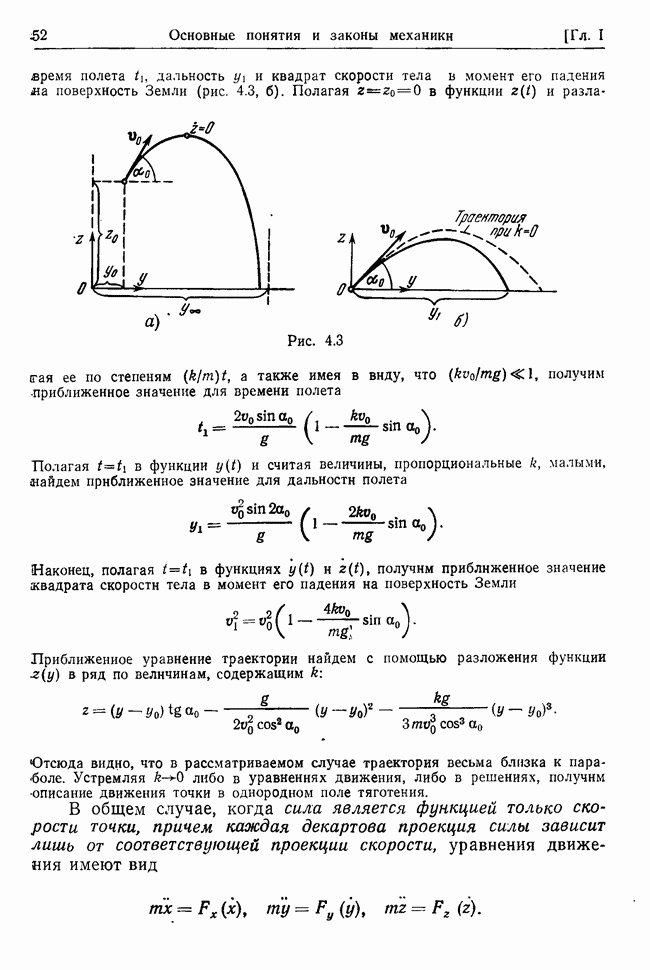
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 33. Собственные колебания системы под действием потенциальных, гироскопических и диссипативных сил
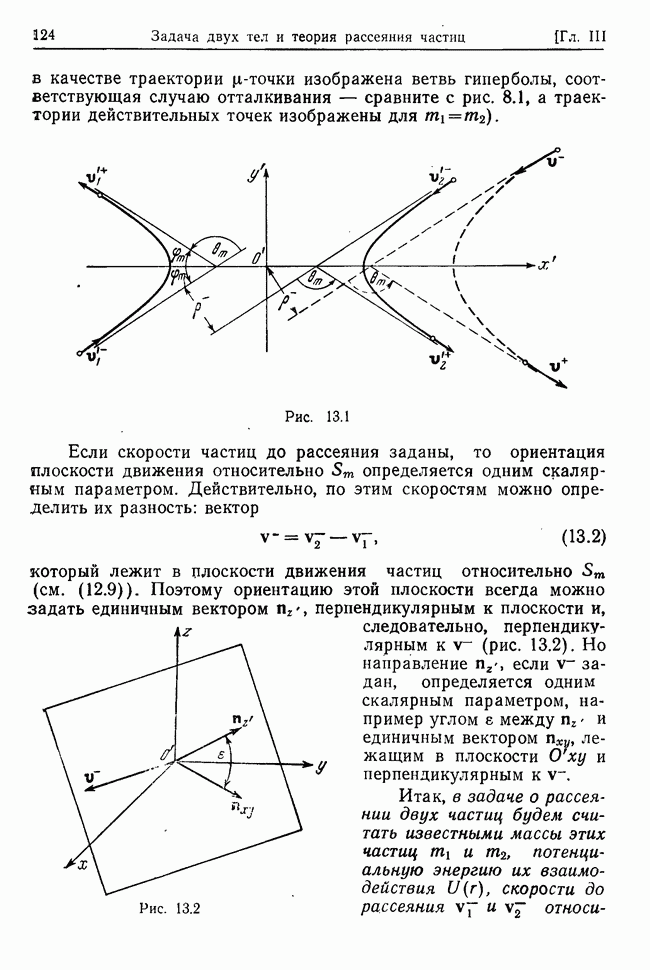
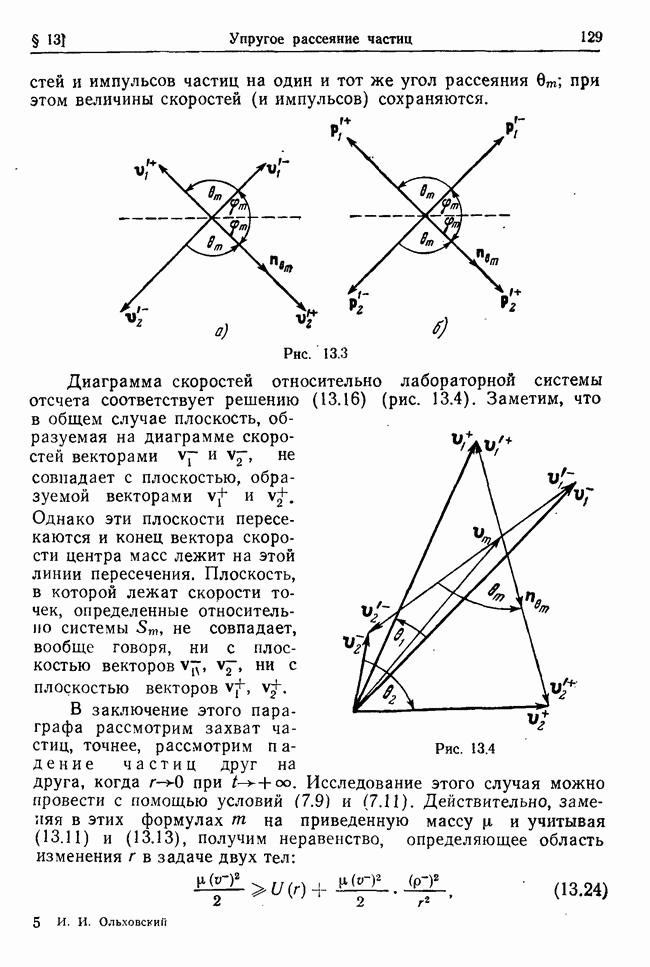
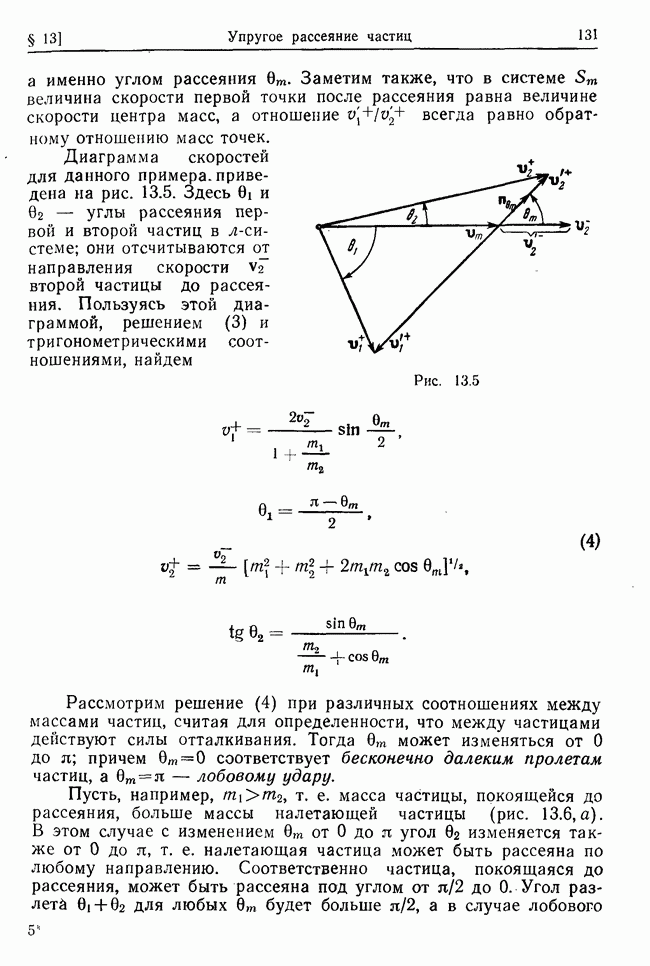
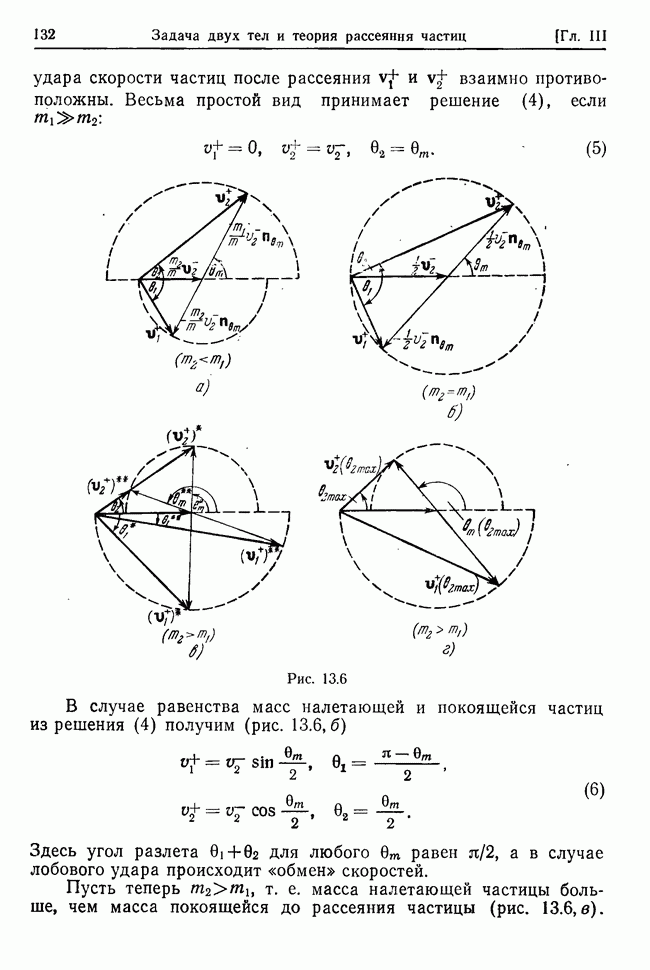
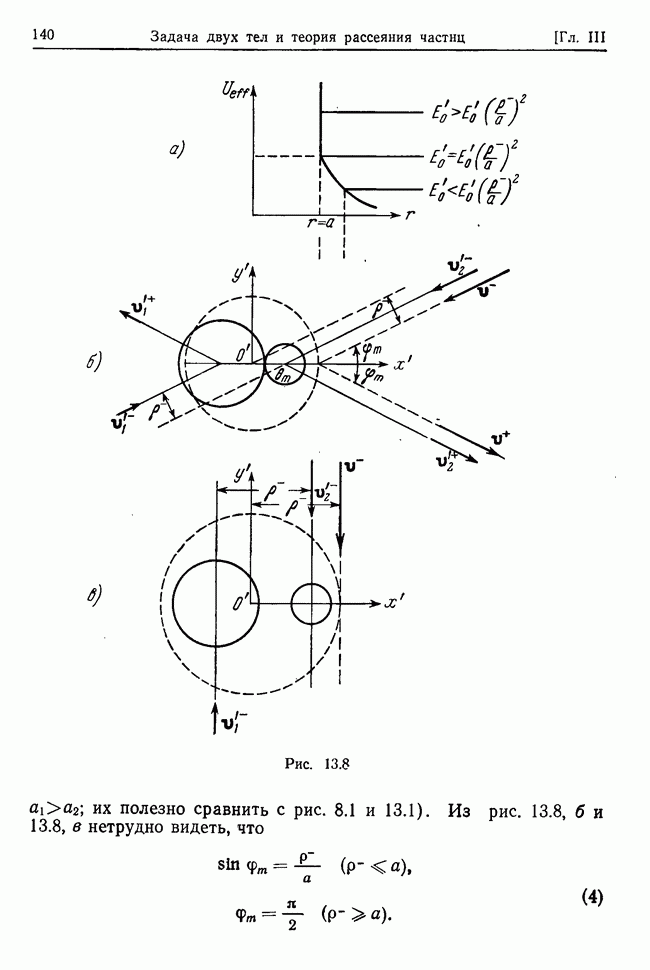
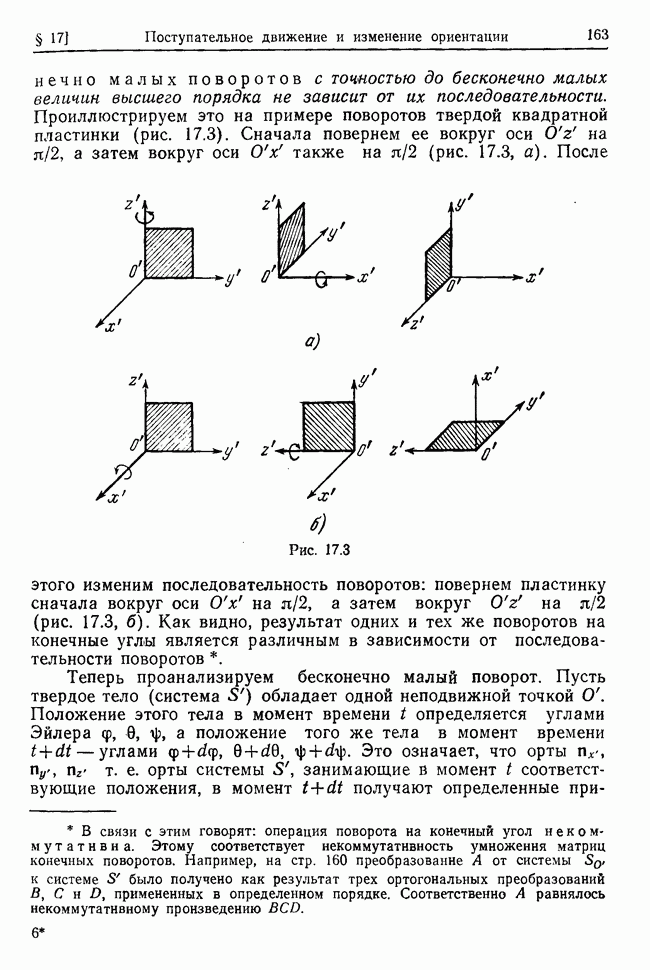
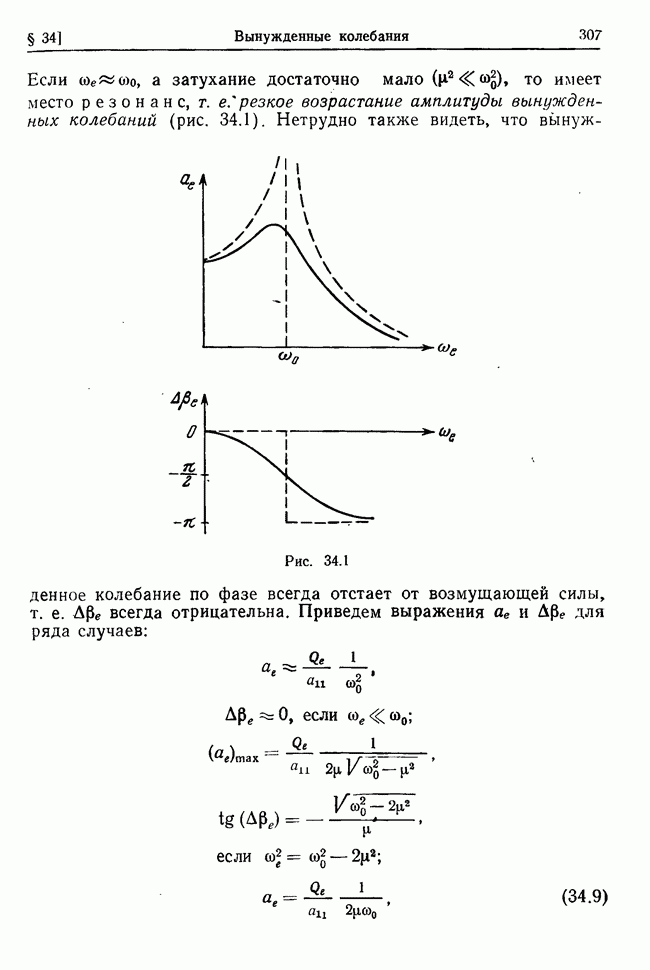
Рассмотрим колебания системы при наличии потенциальных и гироскопических сил, а также диссипативных сил, линейных
относительно скоростей точек. В остальном сохраним предположения о силах и связях, сформулированные в предыдущем параграфе. Тогда кинетическая энергия Т, обобщенный потенциал  и диссипативная функция
и диссипативная функция  будут иметь вид (см. (32.1), (27.21), (27.27))
будут иметь вид (см. (32.1), (27.21), (27.27))

где все функции  зависят только от координат, поскольку силы и связи стационарны; кроме того, коэффициенты
зависят только от координат, поскольку силы и связи стационарны; кроме того, коэффициенты  симметричны относительно перестановок индексов.
симметричны относительно перестановок индексов.
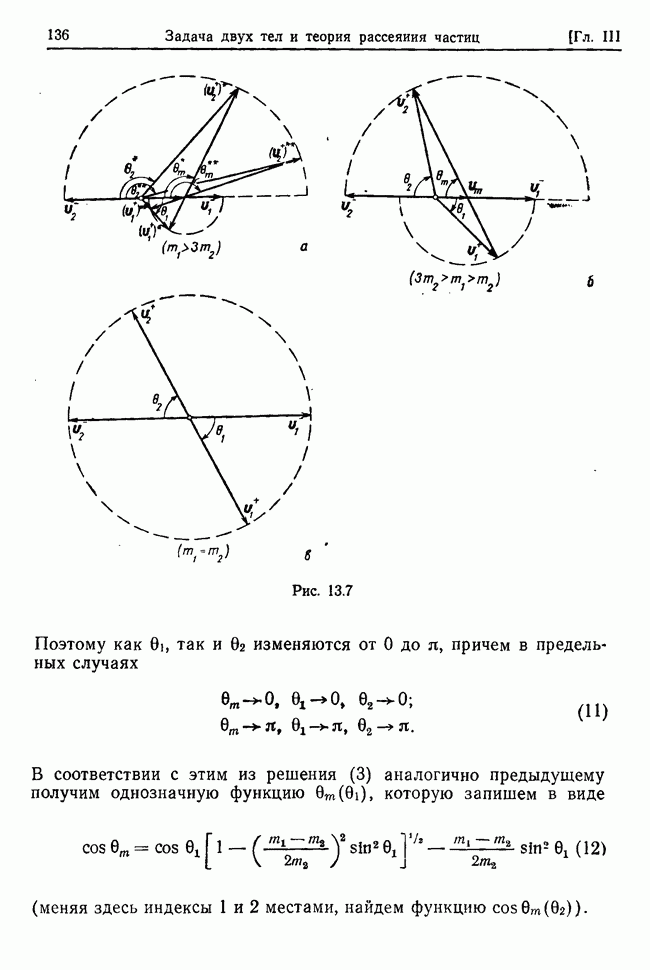
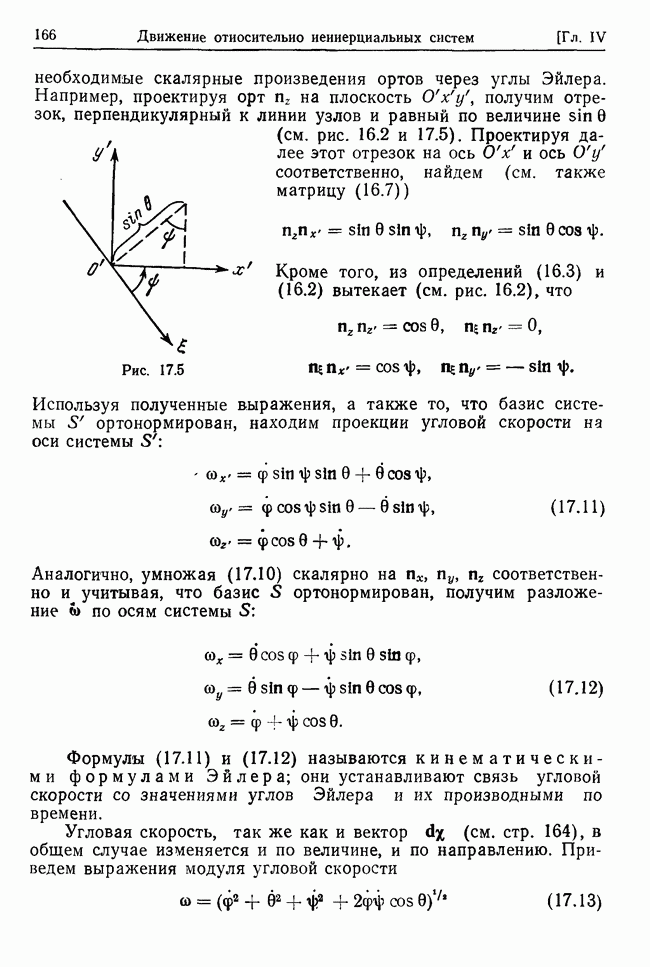
Разлатая  в положении устойчивого равновесия с точностью до членов второго порядка малости включительно, можно получить линейные уравнения движения. Однако эти уравнения легче получить, проводя разложение обеих частей уравнений Лагранжа (27.23) с точностью до членов первого порядка.
в положении устойчивого равновесия с точностью до членов второго порядка малости включительно, можно получить линейные уравнения движения. Однако эти уравнения легче получить, проводя разложение обеих частей уравнений Лагранжа (27.23) с точностью до членов первого порядка.
Запишем исходные уравнения (27.23) с учетом (27.26)

Используя выражение для кинетической энергии (см. (33.1)), представим левые части системы (33.2) в виде

Затем, учитывая, что производные от обобщенного потенциала соответственно равны

для обобщенно-потенциальной силы получим выражения

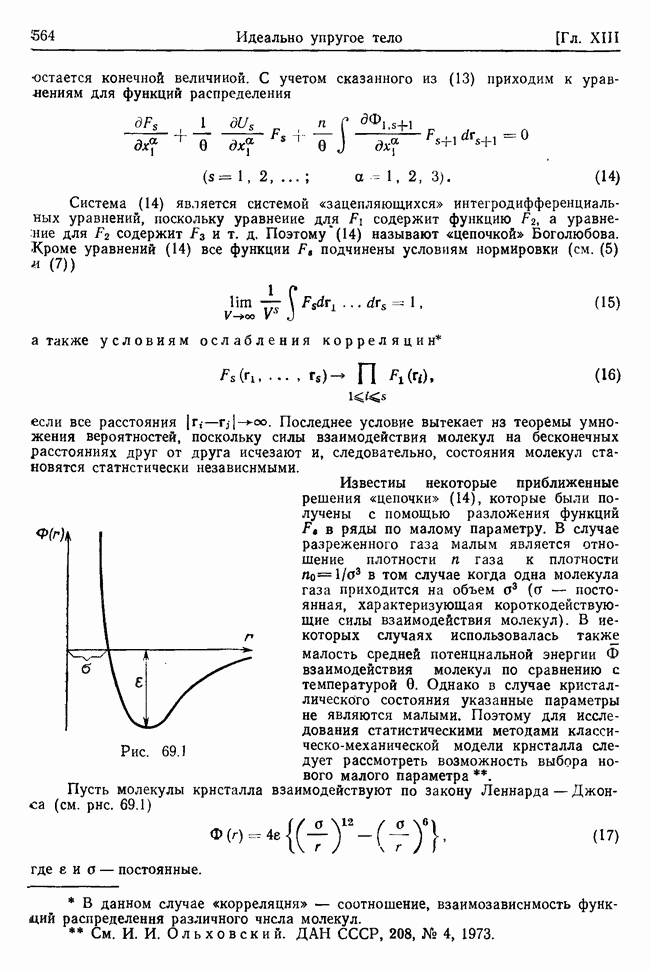
где  - коэффициенты, антисимметричные по индексам. Для обобщенных диссипативных сил соответственно найдем
- коэффициенты, антисимметричные по индексам. Для обобщенных диссипативных сил соответственно найдем

Теперь разложим все члены, входящие в уравнения Лагранжа, в положении устойчивого равновесия, т. е. в положении изолированного минимума обычной потенциальной энергии (см. достаточный признак устойчивости на стр. 268). Это положение определяется из уравнений

Разложение доведем до членов первого порядка малости включительно по степеням отклонений  и обобщенных скоростей
и обобщенных скоростей  . В результате из (33.3), (33.4) и (33.5) с учетом (33.6) получим
. В результате из (33.3), (33.4) и (33.5) с учетом (33.6) получим

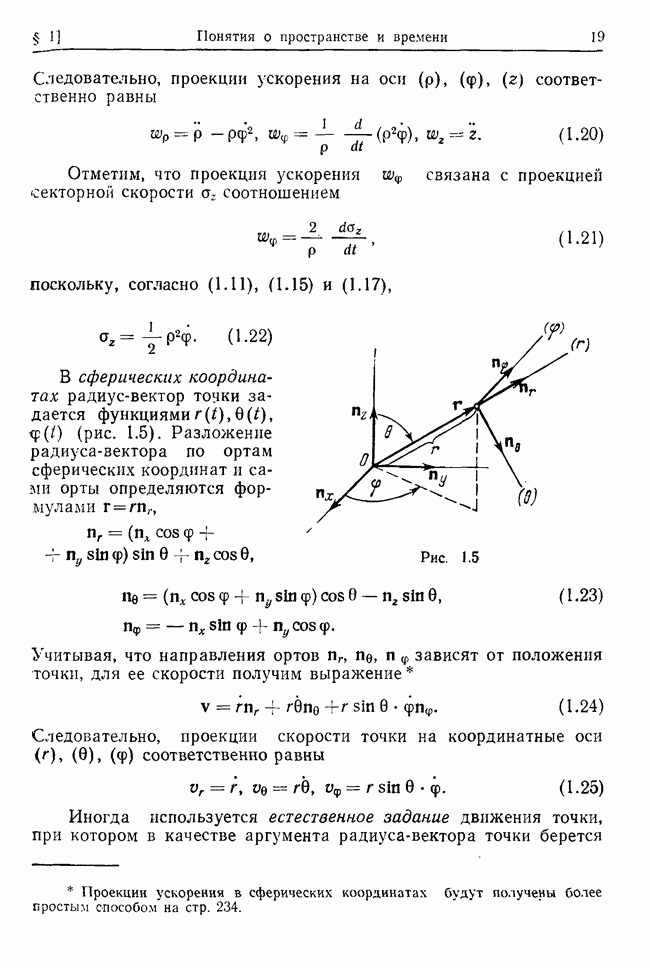
где 
Подставляя (33.7) в (33.2) и опуская для простоты записи знак равновесия  найдем интересующие нас уравнения
найдем интересующие нас уравнения

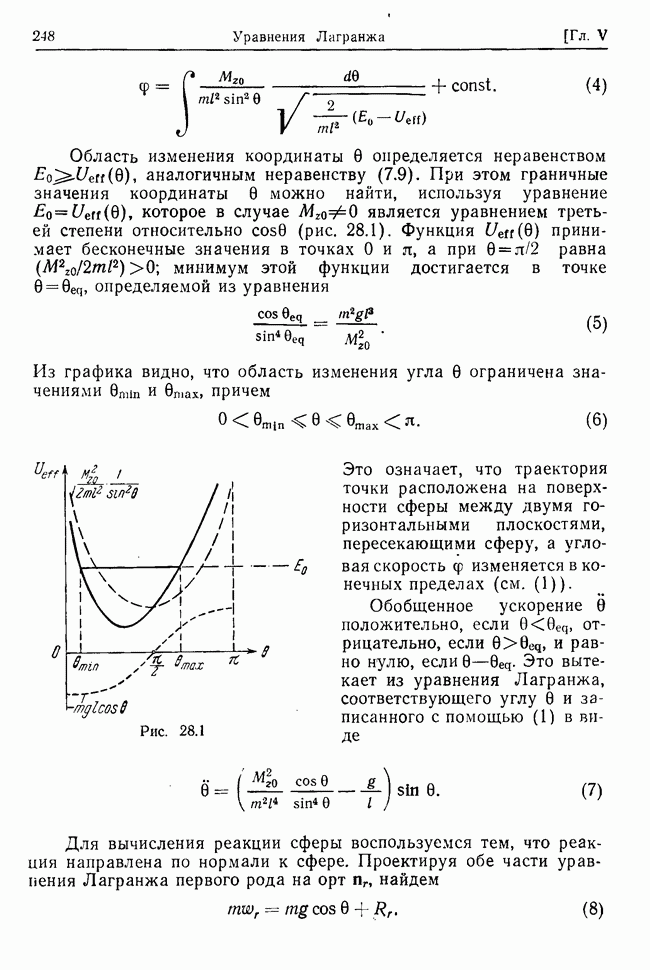
В этой системе уравнений коэффициенты  симметричны,
симметричны,  антисимметричны относительно перестановки индексов.
антисимметричны относительно перестановки индексов.
Общая процедура решения системы (33.8) аналогична методу решения системы (32.4). Поэтому сразу приведем соответствующее характеристическое уравнение и уравнения для амплитуд:

Общее решение системы (33.8) имеет вид (32.9), где  определяются из (33.9), а отношения амплитуд — из (33.10).
определяются из (33.9), а отношения амплитуд — из (33.10).
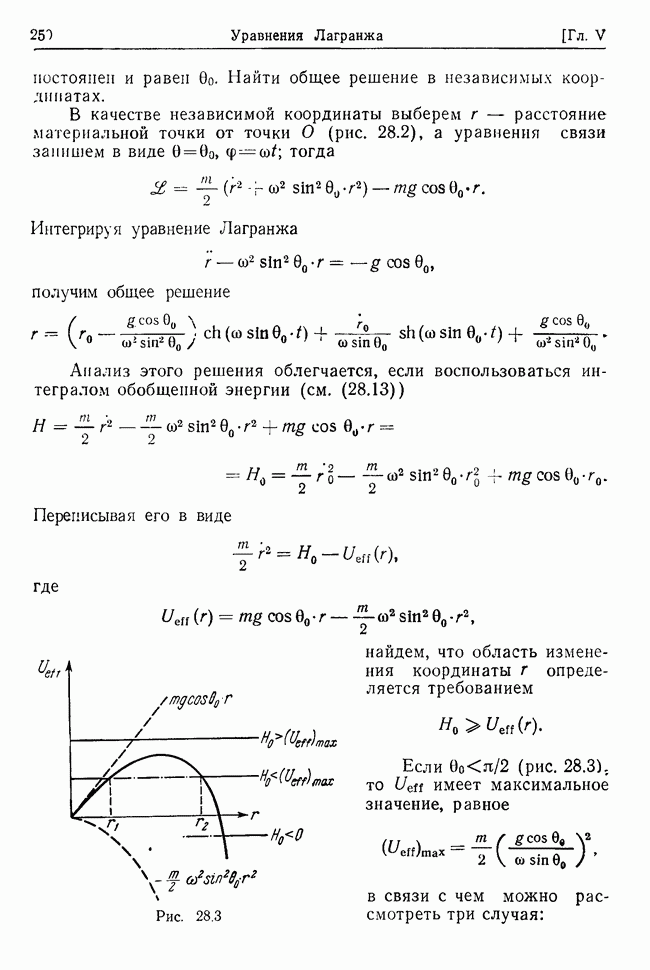
Каждое из собственных значений  может быть либо комплексным (и тогда сопряженное ему число также будет корнем характеристического уравнения), либо вещественным. Таким образом, каждое из собственных значений
может быть либо комплексным (и тогда сопряженное ему число также будет корнем характеристического уравнения), либо вещественным. Таким образом, каждое из собственных значений  можно записать в одной из форм
можно записать в одной из форм

где  — действительные величины. Это следует из известной теоремы о корнях алгебраического уравнения с действительными коэффициентами [45, стр. 159—161]. Кроме того, можно утверждать, что все коэффициенты затухания
— действительные величины. Это следует из известной теоремы о корнях алгебраического уравнения с действительными коэффициентами [45, стр. 159—161]. Кроме того, можно утверждать, что все коэффициенты затухания  положительны. Действительно, согласно закону (28.15), энергия системы со стационарными силами и связями убывает за счет работы диссипативных сил. Ввиду того, что в решении (32.9) имеются экспоненциальные множители, это возможно только в случае положительности коэффициентов затухания.
положительны. Действительно, согласно закону (28.15), энергия системы со стационарными силами и связями убывает за счет работы диссипативных сил. Ввиду того, что в решении (32.9) имеются экспоненциальные множители, это возможно только в случае положительности коэффициентов затухания.
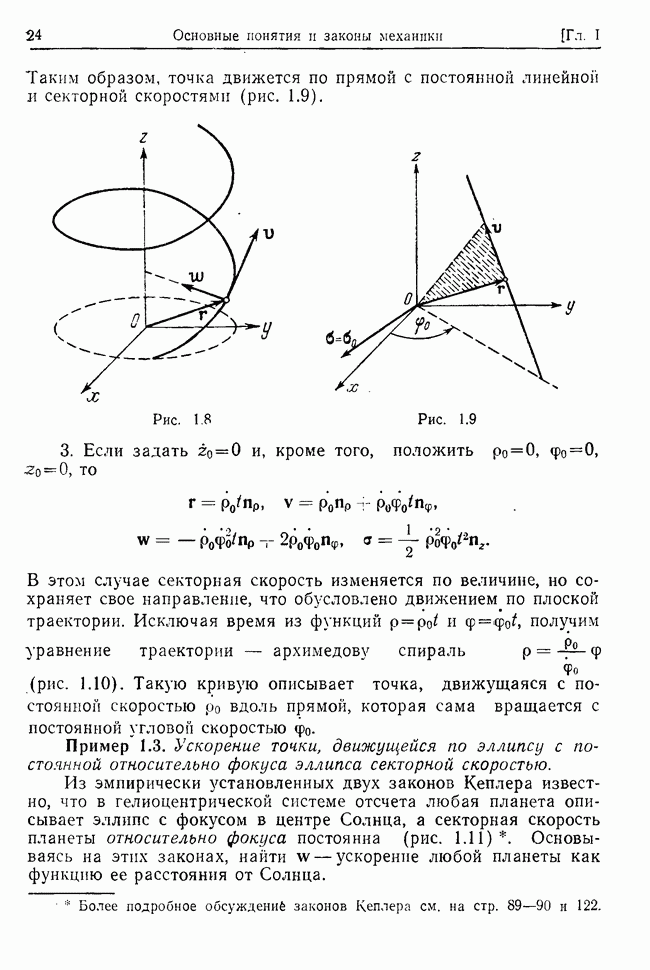
Если диссипация энергии достаточно мала, то все корни к можно разбить на пары комплексно сопряженных корней, а общее решение имеет вид

и описывает затухающие колебания системы. Если диссипация энергии отсутствует (т. е. все коэффициенты  ), то корни будут чисто мнимыми, коэффициенты затухания равны нулю, а система совершает незатухающие колебания. Наконец, если все коэффициенты
), то корни будут чисто мнимыми, коэффициенты затухания равны нулю, а система совершает незатухающие колебания. Наконец, если все коэффициенты  достаточно велики, то все корни к вещественны.
достаточно велики, то все корни к вещественны.
В этом случае система совершает апериодическое движение, которое описывается решением

Если среди всех корней характеристического уравнения часть корней является комплексной, а часть действительной, то соответствующую форму общего решения нетрудно получить из (32.9).
В общем случае при наличии диссипативных и гироскопических сил алгебраические дополнения, определяющие отношение амплитуд в решении (32.9), не удовлетворяют требованию (32.15), т. е. имеют место неравенства

Однако в частных случаях и при наличии диссипативных сил возможно выполнение требований (32.15) и введение «главных» координат (в том смысле, что каждое из уравнений (33.8), записанное в таких переменных, будет уравнением относительно какой-либо одной переменной).
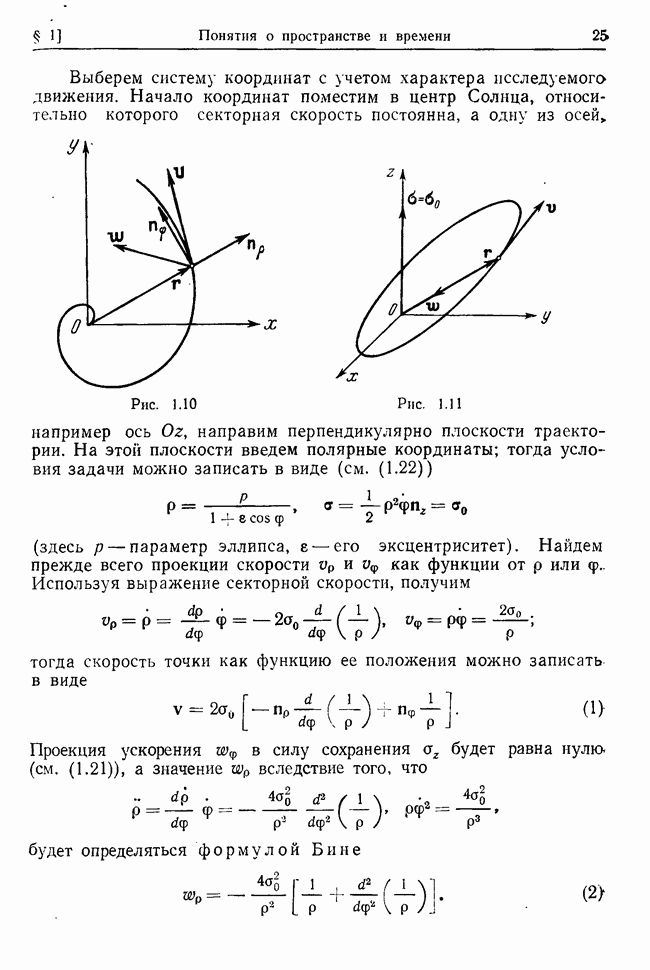
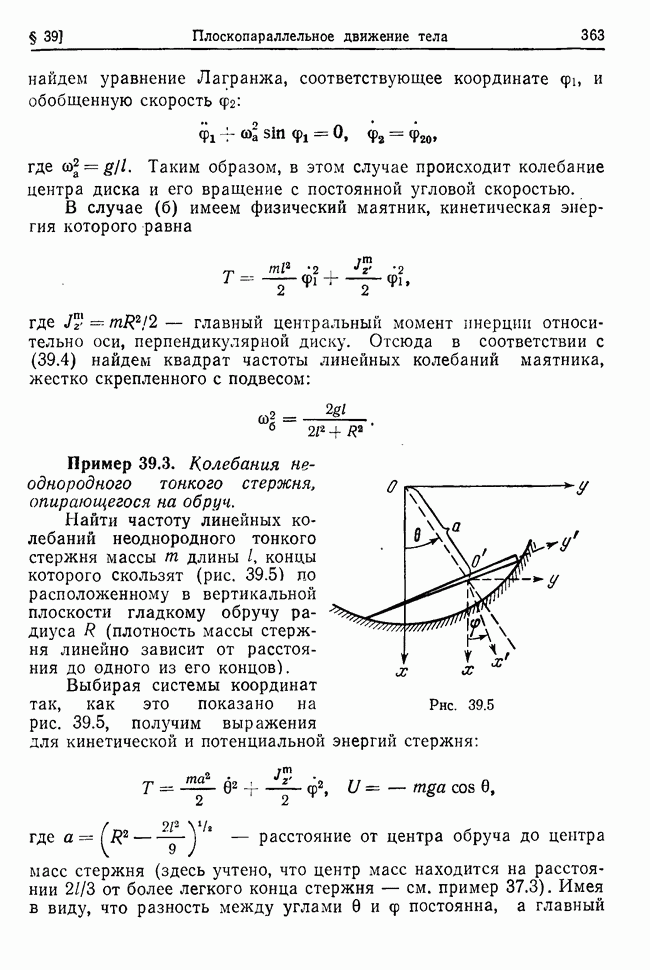
Пример 33.1. Движение маятников, соединенных пружиной, в среде с сопротивлением.
Точки подвеса двух одинаковых математических маятников длины  и массы
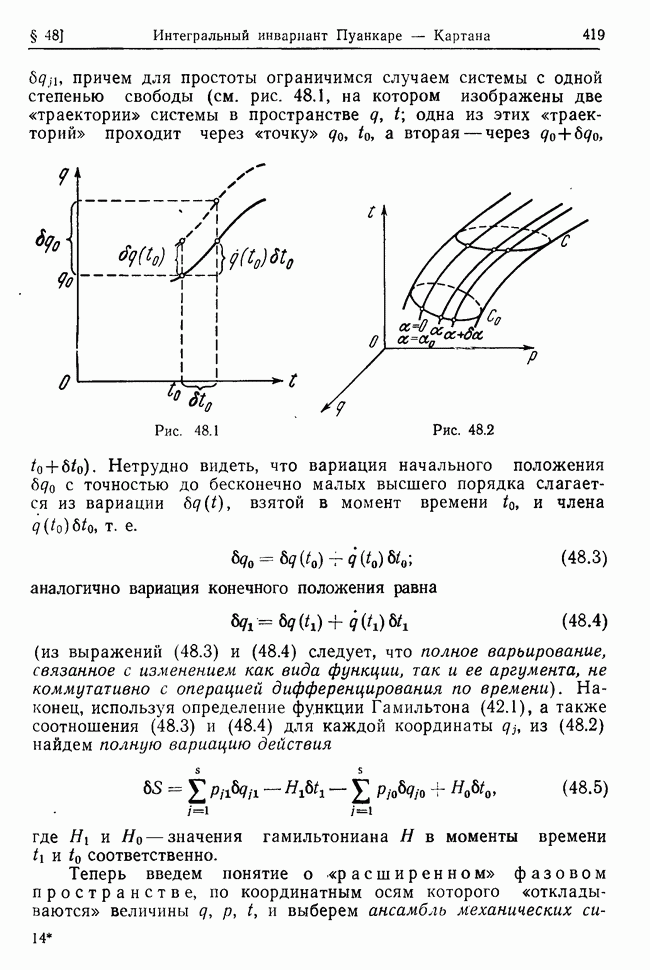
и массы  находятся на расстоянии а друг от друга и расположены на одной горизоитали.
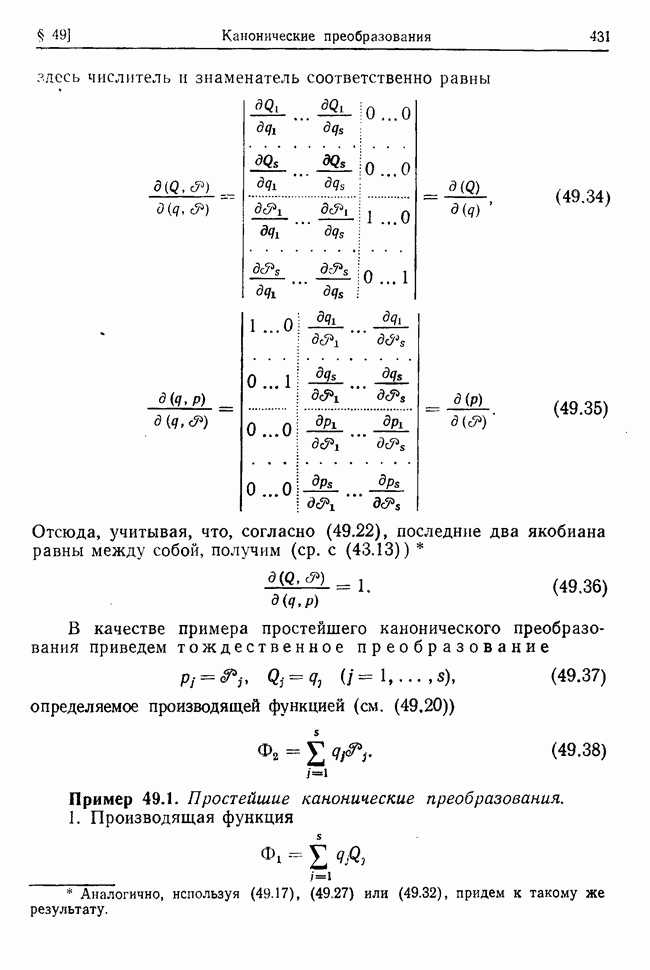
находятся на расстоянии а друг от друга и расположены на одной горизоитали.
Точки соединены между собой пружиной жесткости х и длины а в ненапряженном состоянии. Вся система помещена в среду с сопротивлением, пропорциональным первой степени скорости тела (коэффициент сопротивления  Найти закон движения маятников в вертикальной плоскости, проходящей через точки подвеса, вблизи положения устойчивого равновесия системы.
Найти закон движения маятников в вертикальной плоскости, проходящей через точки подвеса, вблизи положения устойчивого равновесия системы.
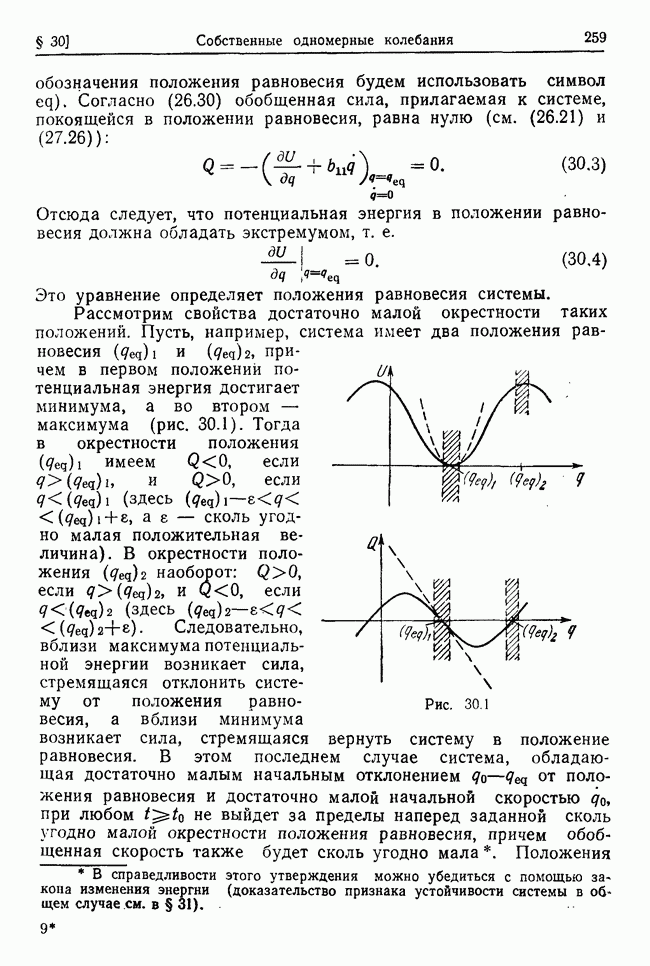
Выберем систему координат так, как это показано на рис. 33.1, а в качестве независимых координат возьмем  — углы
— углы

Рис. 33.1
отклонения каждого маятника от положения устойчивого равновесия:  Тогда удлинение пружины для малых отклонений и энергия ее упругой деформации с точностью до величин второго порядка малости будут соответственно равны
Тогда удлинение пружины для малых отклонений и энергия ее упругой деформации с точностью до величин второго порядка малости будут соответственно равны

С той же точностью для потенциальной энергии обоих маятников в поле тяжести получим выражение

Следовательно, потенциальная энергия системы будет равна

(здесь опущена несущественная постоянная). Выражения для кинетической энергии и диссипативной функции будут иметь вид

Квадратичные формы  могут быть заданы с помощью матриц
могут быть заданы с помощью матриц

где

Записывая линейные уравнения движения в форме (33.8)

найдем характеристическое уравнение

Учитывая, что  это уравнение можно записать в виде
это уравнение можно записать в виде

или в виде двух квадратных уравнений

с коэффициентами

Таким образом, решение характеристического уравнения приводит к четырем собственным значениям К:

где

Общее решение уравнений движения запишем в виде (33.12)

Затем получим значения алгебраических дополнений

характеристического детерминанта при различных корнях  , характеристического уравнения. Нетрудно убедиться, что
, характеристического уравнения. Нетрудно убедиться, что

а дополнение  как видно, не зависит от X. В связи с этим общее решение может быть записано в виде
как видно, не зависит от X. В связи с этим общее решение может быть записано в виде

Здесь  соответственно равны
соответственно равны


Таким образом, функция  описывает либо затухающее колебание с частотой он и коэффициентом затухания
описывает либо затухающее колебание с частотой он и коэффициентом затухания  либо апериодическое движение с коэффициентами затухания
либо апериодическое движение с коэффициентами затухания  Функция
Функция  соответственно характеризуется частотой
соответственно характеризуется частотой  и затуханием
и затуханием  или двумя коэффициентами затухания
или двумя коэффициентами затухания 
Величины  являются главными координатами системы. Действительно, эти независимые координаты подчинены уравнениям Лагранжа
являются главными координатами системы. Действительно, эти независимые координаты подчинены уравнениям Лагранжа

каждое из которых является уравнением относительно одной из этих координат. Соответственно  и
и  выраженные через главные координаты, будут содержать только квадраты переменных, т. е. коэффициенты этих форм будут образовывать диагональные матрицы:
выраженные через главные координаты, будут содержать только квадраты переменных, т. е. коэффициенты этих форм будут образовывать диагональные матрицы:

Главное «колебание»  осуществляется, если начальные отклонения обоих маятников и их скорости соответственно равны между собой (рис. 33.2, а). Если же начальные отклонения обоих маятников и их скорости соответственно равны по величине, но противоположны по знаку, то реализуется второе главное «колебание»
осуществляется, если начальные отклонения обоих маятников и их скорости соответственно равны между собой (рис. 33.2, а). Если же начальные отклонения обоих маятников и их скорости соответственно равны по величине, но противоположны по знаку, то реализуется второе главное «колебание»  (рис. 33.2, б).
(рис. 33.2, б).
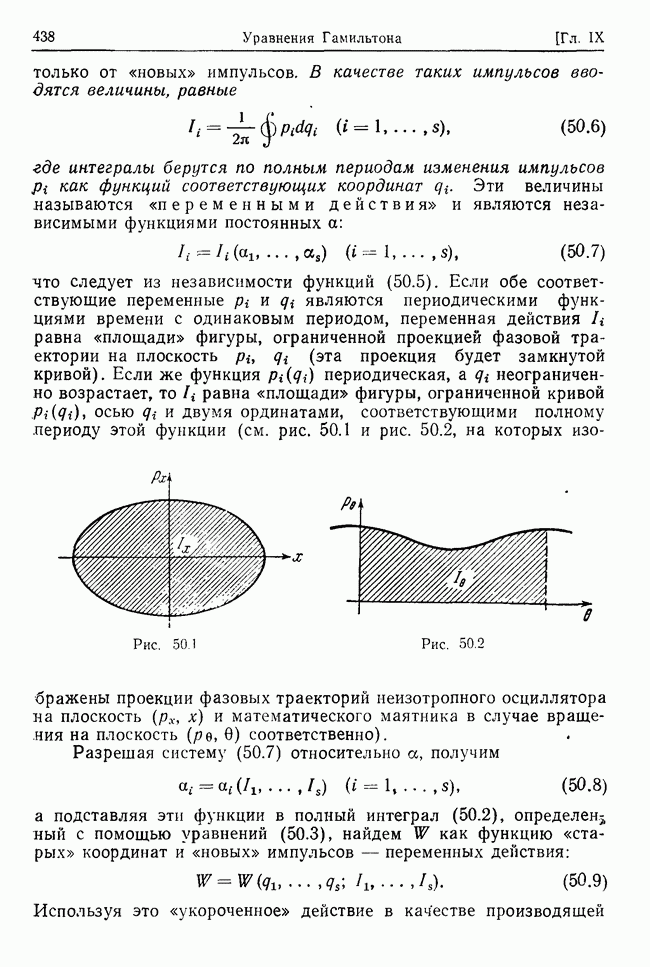
В заключение отметим частные случаи. Пусть, например, сопротивление достаточно мало, т. е.  . Тогда функции
. Тогда функции  описывают затухающие гармонические колебания. Если же маятники помещены в достаточно вязкую среду
описывают затухающие гармонические колебания. Если же маятники помещены в достаточно вязкую среду

Рис. 33.2
 то
то  изменяется апериодически, а
изменяется апериодически, а  совершает затухающее колебание. Наконец, в весьма вязкой среде, когда
совершает затухающее колебание. Наконец, в весьма вязкой среде, когда  обе главные координаты описывают апериодические движения.
обе главные координаты описывают апериодические движения.
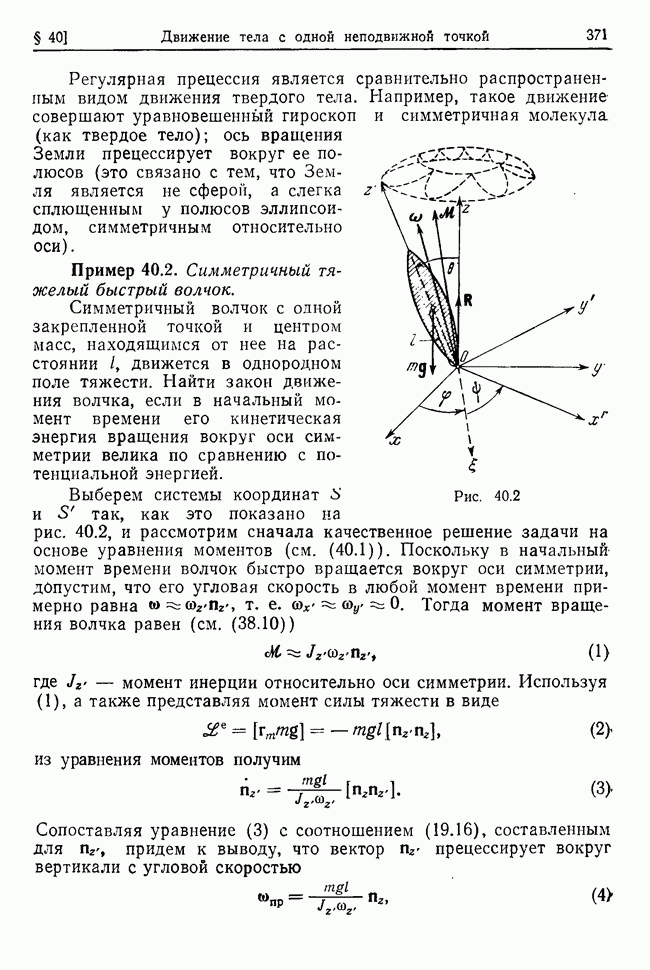
Пример 33.2. Линейный заряженный осциллятор в магнитном поле.
Точка массы  с зарядом
с зарядом  движется в постоянном однородном магнитном поле напряженности
движется в постоянном однородном магнитном поле напряженности  . На материальную точку также действует сила притяжения, пропорциональная расстоянию до центра силы О (коэффициент пропорциональности х). Найти частоты колебаний осциллятора и закон его движения.
. На материальную точку также действует сила притяжения, пропорциональная расстоянию до центра силы О (коэффициент пропорциональности х). Найти частоты колебаний осциллятора и закон его движения.
Выбирая систему декартовых координат с началом в точке О и осью  направленной вдоль
направленной вдоль  и проектируя правую и левую части уравнения движения точки
и проектируя правую и левую части уравнения движения точки

на координатные оси, получим систему дифференциальных уравнений

где

Эти же уравнения можно получить, используя уравнения Лагранжа. Действительно, обобщенный потенциал в рассматриваемой задаче равен (см. (27.11) и 

где А — вектор-потенциал магнитного поля. Выбор А диктуется (хотя и неоднозначно) условиями задачи. Например, если положить

то мы сможем удовлетворить условию (см. (27.12))

Используя выражение для А, найдем функцию Лагранжа в декартовых координатах

которая приведет к полученным выше линейным уравнениям движения.
Соответствующие им уравнения для амплитуд и характеристическое уравнение имеют вид

Из последнего уравнения находим собственные значения Я:

где

a  — ларморова частота.
— ларморова частота.
Последовательно подставляя собственные значения к в уравнения для амплитуд, найдем соотношения между амплитудами:

Используя эти соотношения, придем к общему решению в виде

откуда окончательно находим

где все  — постоянные, определяемые начальными условиями.
— постоянные, определяемые начальными условиями.
Итак, колебание проекции заряженной точки на плоскость, перпендикулярную  характеризуется частотами
характеризуется частотами  отличными от
отличными от  — собственной частоты, осциллятора в отсутствие магнитного поля. Интересно отметить, что первое частное решение описывает движение проекций точки по окружности с угловой скоростью
— собственной частоты, осциллятора в отсутствие магнитного поля. Интересно отметить, что первое частное решение описывает движение проекций точки по окружности с угловой скоростью  по часовой стрелке; второе частное решение описывает аналогичное движение с угловой скоростью
по часовой стрелке; второе частное решение описывает аналогичное движение с угловой скоростью  против часовой стрелки. Колебание заряда в направлении
против часовой стрелки. Колебание заряда в направлении  происходит с собственной частотой со. В случае малой напряженности магнитного поля частоты
происходит с собственной частотой со. В случае малой напряженности магнитного поля частоты  сводятся к сумме и разности собственной частоты осциллятора и ларморовой частоты:
сводятся к сумме и разности собственной частоты осциллятора и ларморовой частоты:

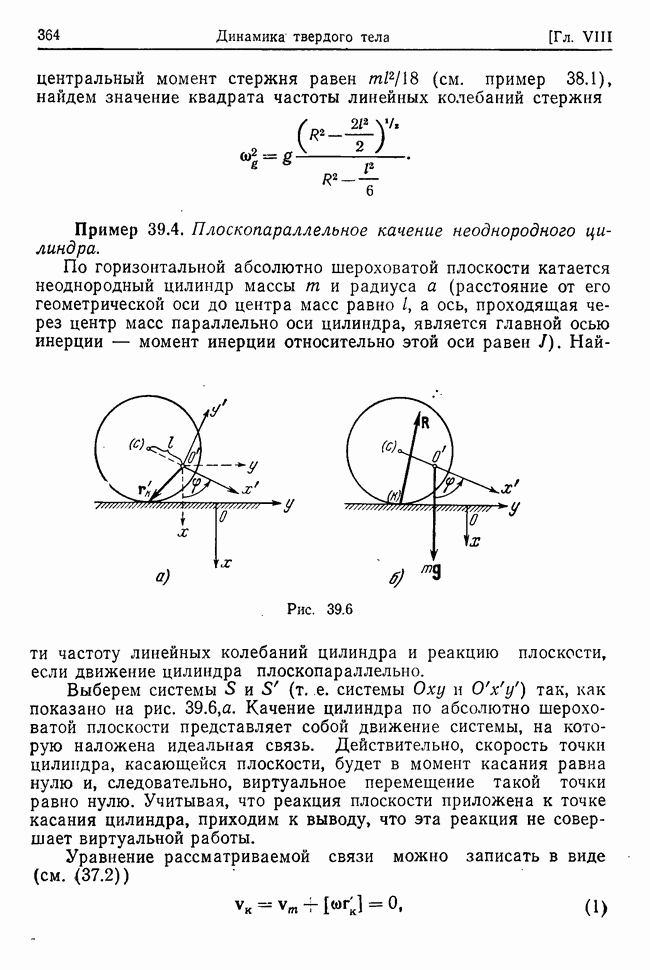
Пример 33.3. Линейные колебания вращающейся двухатомной молекулы.
Исходя из той же модели молекулы, что и в примере 32.5, и допуская, что внешние силы отсутствуют, определить частоту линейных колебаний вращающейся молекулы.
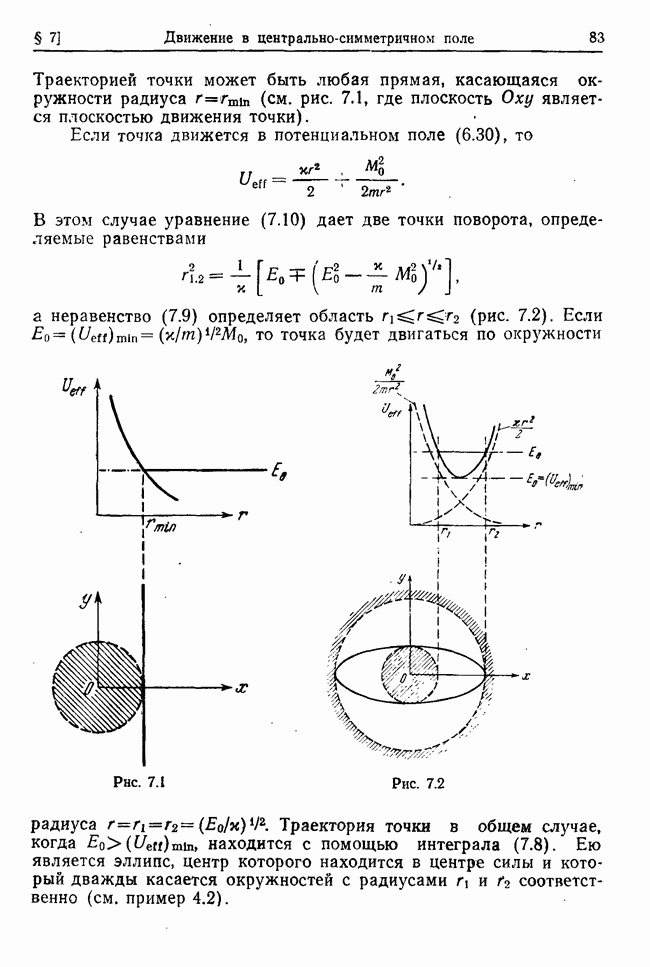
Применяя законы сохранения момента и энергии относительно системы центра масс молекулы, получим два интеграла движения в полярных координатах в плоскости движения молекулы (см. (7.2) и 

где  — полярные координаты вектора
— полярные координаты вектора  — момент и энергия молекулы относительно
— момент и энергия молекулы относительно  -системы.
-системы.
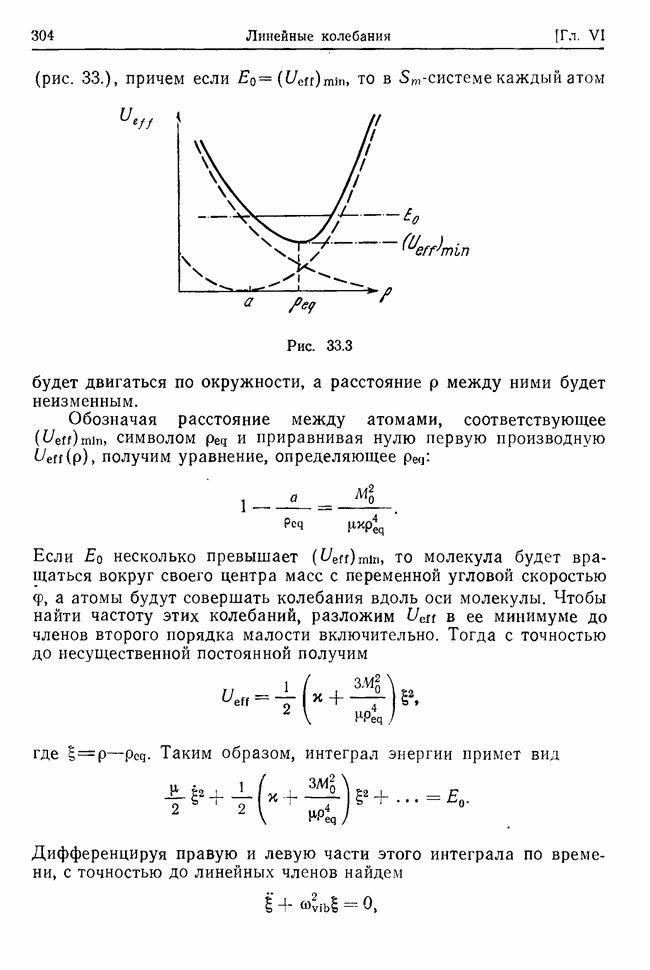
Исключая из интеграла энергии с помощью интеграла момента угловую скорость  найдем
найдем

где  Функция
Функция  имеет минимум
имеет минимум
(рис. 33.), причем если  то в
то в  -системе каждый атом будет двигаться по окружности, а расстояние
-системе каждый атом будет двигаться по окружности, а расстояние  между ними будет неизменным.
между ними будет неизменным.

Рис. 33.3
Обозначая расстояние между атомами, соответствующее  символом
символом  и приравнивая нулю первую производную
и приравнивая нулю первую производную  получим уравнение, определяющее
получим уравнение, определяющее 

Если  несколько превышает
несколько превышает  , то молекула будет вращаться вокруг своего центра масс с переменной угловой скоростью Ф, а атомы будут совершать колебания вдоль оси молекулы. Чтобы найти частоту этих колебаний, разложим
, то молекула будет вращаться вокруг своего центра масс с переменной угловой скоростью Ф, а атомы будут совершать колебания вдоль оси молекулы. Чтобы найти частоту этих колебаний, разложим  в ее минимуме до членов второго порядка малости включительно. Тогда с точностью до несущественной постоянной получим
в ее минимуме до членов второго порядка малости включительно. Тогда с точностью до несущественной постоянной получим

где  Таким образом, интеграл энергии примет вид
Таким образом, интеграл энергии примет вид

Дифференцируя правую и левую части этого интеграла по времени, с точностью до линейных членов найдем

где 
Замечая, что величина  равна угловой скорости
равна угловой скорости  в «равновесии» (когда
в «равновесии» (когда  ), приходим к выводу, что квадрат частоты линейных колебаний вращающейся двухатомной молекулы равен сумме квадрата частоты колебаний невращающейся молекулы и утроенного квадрата угловой скорости вращения молекулы в «равновесии», т. е.
), приходим к выводу, что квадрат частоты линейных колебаний вращающейся двухатомной молекулы равен сумме квадрата частоты колебаний невращающейся молекулы и утроенного квадрата угловой скорости вращения молекулы в «равновесии», т. е.

где  . Влияние колебаний молекулы на ее угловую скорость вращения можно определить, используя интеграл момента. Тогда с точностью до членов первого порядка включительно найдем, что
. Влияние колебаний молекулы на ее угловую скорость вращения можно определить, используя интеграл момента. Тогда с точностью до членов первого порядка включительно найдем, что

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- ЧАСТЬ I. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
- Глава I. ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ МЕХАНИКИ
- § 1. Понятия о материальной точке, о пространстве и времени
- § 2. Понятия о силе и массе
- § 3. Понятие об инерциальной системе отсчета и законы Ньютона. Принцип относительности Галилея
- § 4. Решение уравнений движения и начальные условия
- Глава II. ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ ИМПУЛЬСА, КИНЕТИЧЕСКОГО МОМЕНТА И ЭНЕРГИИ
- § 5. Законы изменения и сохранения импульса и момента импульса материальной точки
- § 6. Законы изменения и сохранения энергии материальной точки
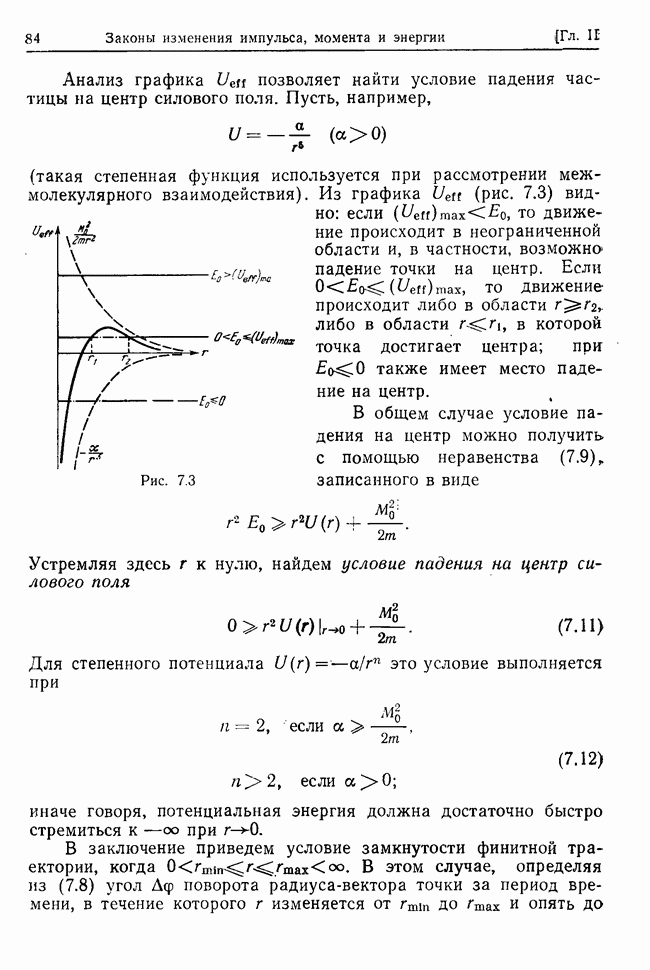
- § 7. Движение в центрально-симметричном поле
- § 8. Движение под действием силы, обратно пропорциональной квадрату расстояния до центра силы. Законы Кеплера
- § 9. Движение центра масс; законы изменения и сохранения импульса системы
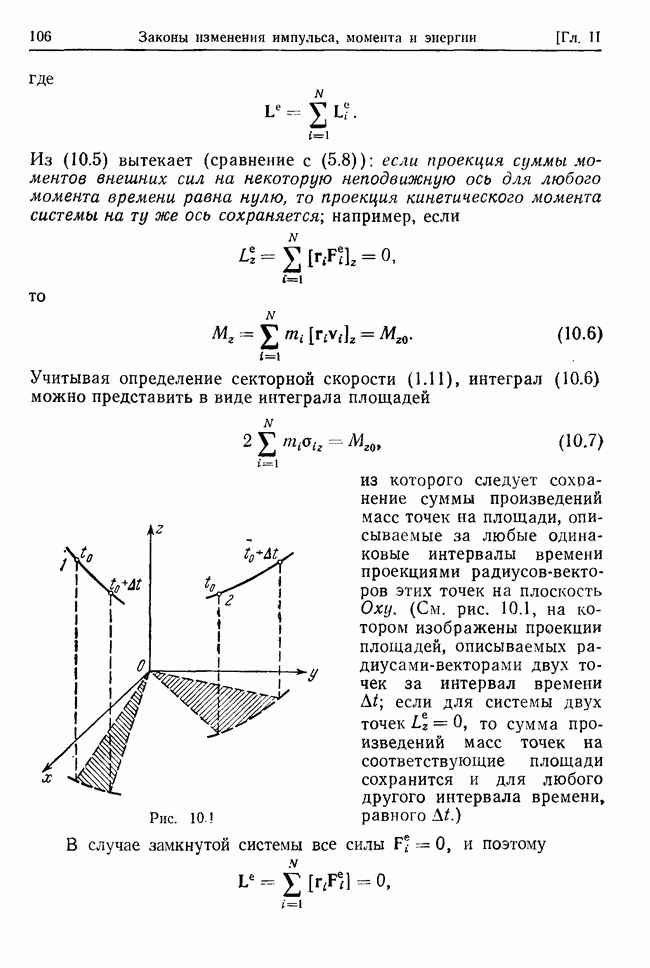
- § 10. Законы изменения и сохранения кинетического момента системы
- § 11. Законы изменения и сохранения энергии системы
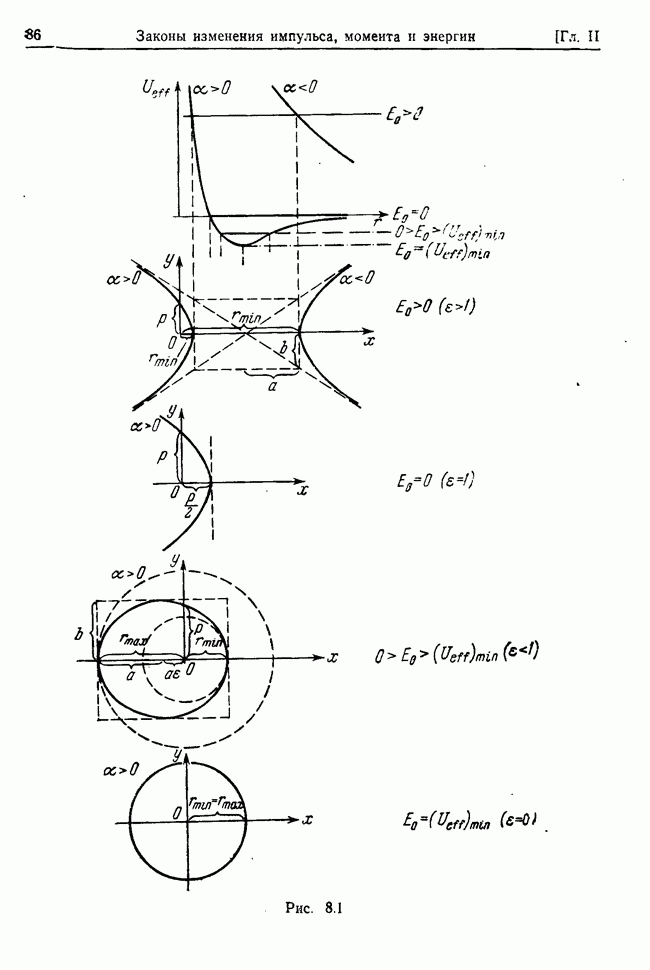
- Глава III. ЗАДАЧА ДВУХ ТЕЛ И ТЕОРИЯ РАССЕЯНИЯ ЧАСТИЦ
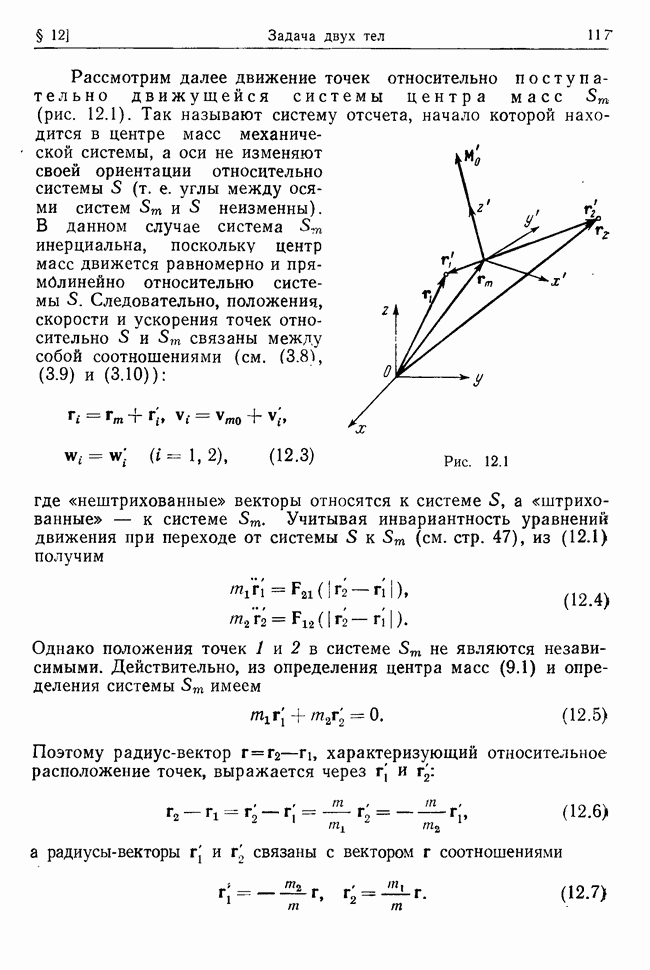
- § 12. Задача двух тел
- § 13. Упругое рассеяние частиц
- § 14. Поперечные сечения рассеяния
- § 15. Распад частиц
- Глава IV. ДВИЖЕНИЕ ОТНОСИТЕЛЬНО НЕИНЕРЦИАЛЬНЫХ СИСТЕМ ОТСЧЕТА
- § 16. Положение системы отсчета (твердого тела)
- § 17. Поступательное движение и изменение ориентации системы отсчета (твердого тела)
- § 18. Общий случай движения системы отсчета (твердого тела)
- § 19. Положение, скорость и ускорение материальной точки относительно разных систем отсчета
- § 20. Уравнение движения материальной точки относительно неинерциальной системы отсчета; силы инерции
- § 21. Законы изменения кинетического момента и кинетической энергии относительно поступательно движущейся системы центра масс
- § 22. Законы изменения и сохранения импульса, кинетического момента и энергии относительно произвольных неинерциальных систем отсчета
- Глава V. УРАВНЕНИЯ ЛАГРАНЖА
- § 23. Основная задача динамики несвободной системы и понятие о связях
- § 24. Действительные, возможные и виртуальные перемещения; идеальные связи
- § 25. Уравнения Лагранжа с реакциями связей; законы изменения импульса, кинетического момента и энергии для систем со связями
- § 26. Уравнения Лагранжа в независимых координатах и общее уравнение механики; циклические координаты и симметрия силового поля и связей
- § 27. Структура уравнений движения в независимых координатах и функция Лагранжа
- § 28. Законы сохранения обобщенного импульса и обобщенной энергии
- § 29. Ковариантность уравнений Лагранжа в независимых координатах
- Глава VI. ЛИНЕЙНЫЕ КОЛЕБАНИЯ
- § 30. Собственные одномерные колебания
- § 31. Положение устойчивого равновесия
- § 32. Собственные и главные колебания системы под действием потенциальных сил
- § 33. Собственные колебания системы под действием потенциальных, гироскопических и диссипативных сил
- § 34. Вынужденные колебания
- Глава VII. НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
- § 35. Собственные колебания и метод Крылова — Боголюбова
- § 36. Вынужденные колебания и резонанс
- Глава VIII. ДИНАМИКА ТВЕРДОГО ТЕЛА
- § 37. Уравнения движения твердого тела
- § 38. Тензор инерции
- § 39. Плоскопараллельное движение твердого тела
- § 40. Движение твердого тела с одной неподвижной точкой. Уравнения Эйлера
- § 41. Линейные неголономные связи
- Глава IX. УРАВНЕНИЯ ГАМИЛЬТОНА
- § 42. Канонические уравнения
- § 43. Фазовое пространство и теорема Лиувилля
- § 44. Скобки Пуассона
- § 45. Уравнение Гамильтона — Якоби
- § 46. Метод разделения переменных
- § 47. Движение материальной точки и волновой процесс
- § 48. Интегральный инвариант Пуанкаре — Картана
- § 49. Канонические преобразования
- § 50. Переменные «действие — угол» и адиабатические инварианты
- § 51. Уравнения движения и интегральные вариационные принципы
- ЧАСТЬ II. ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
- § 52. Физически бесконечно малая частица
- § 53. Деформация малой частицы
- § 54. Законы сохранения массы, изменения импульса и кинетического момента
- § 55. Уравнение изменения кинетической энергии. Законы термодинамики
- Глава XI. ИДЕАЛЬНАЯ ЖИДКОСТЬ
- § 56. Уравнения движения идеальной жидкости
- § 57. Основные теоремы динамики идеальной жидкости
- § 58. Потоки импульса и энергии
- § 59. Несжимаемая жидкость
- § 60. Звуковые волны
- § 61. Ударные волны
- § 62. Магнитогидродинамика идеальной жидкости
- Глава XII. ВЯЗКАЯ ЖИДКОСТЬ
- § 63. Тензор напряжений и уравнения движения
- § 64. Уравнение Навье—Стокса
- § 65. Малые колебания
- § 66. Магнитогидродинамика вязкой жидкости
- ПРИЛОЖЕНИЕ К ГЛАВЕ XII
- Глава XIII. ИДЕАЛЬНО УПРУГОЕ ТЕЛО
- § 67. Закон Гука и уравнения изменения импульса
- § 68. Равновесие изотропных тел
- § 69. Упругие волны
- ПРИЛОЖЕНИЕ К ГЛАВЕ XIII
- ЛИТЕРАТУРА