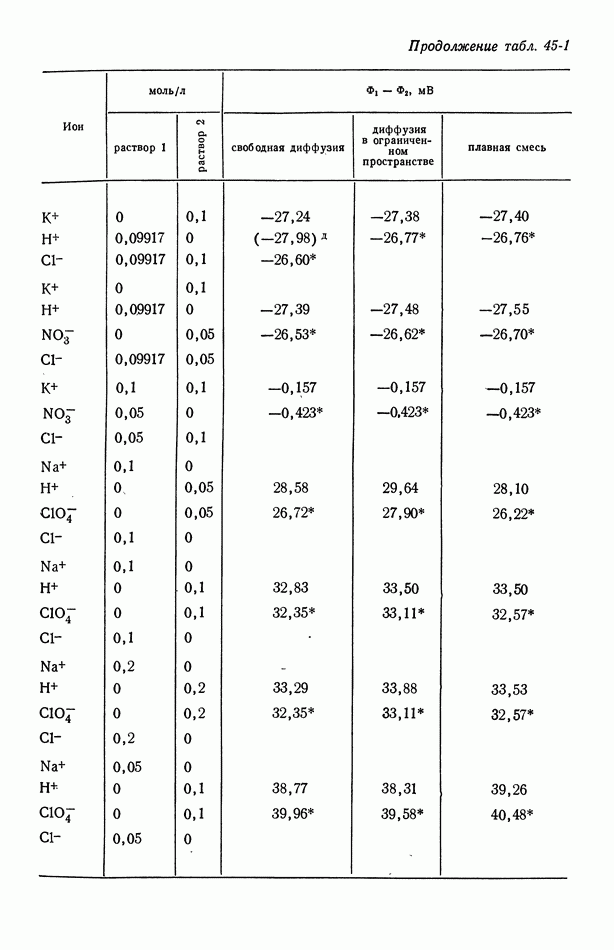
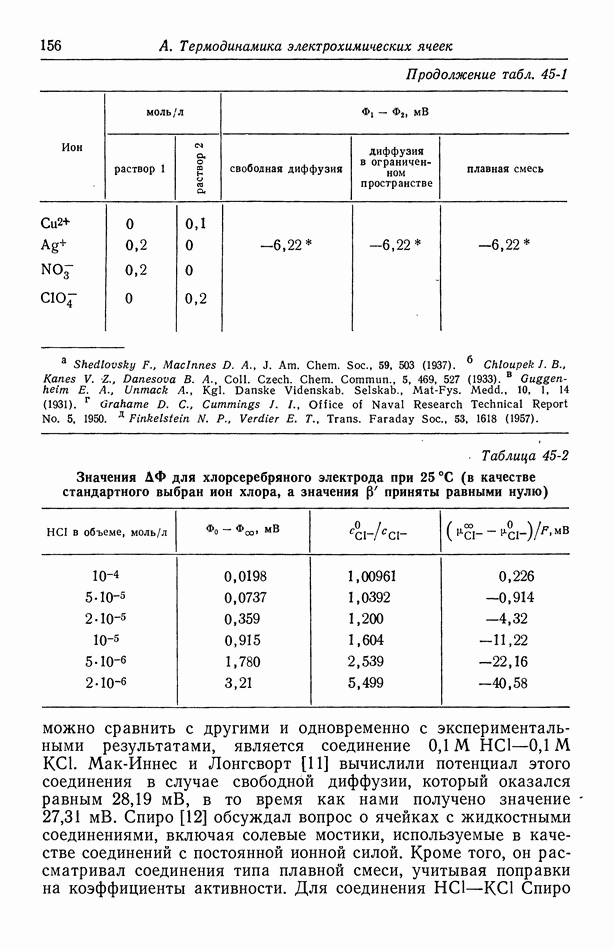
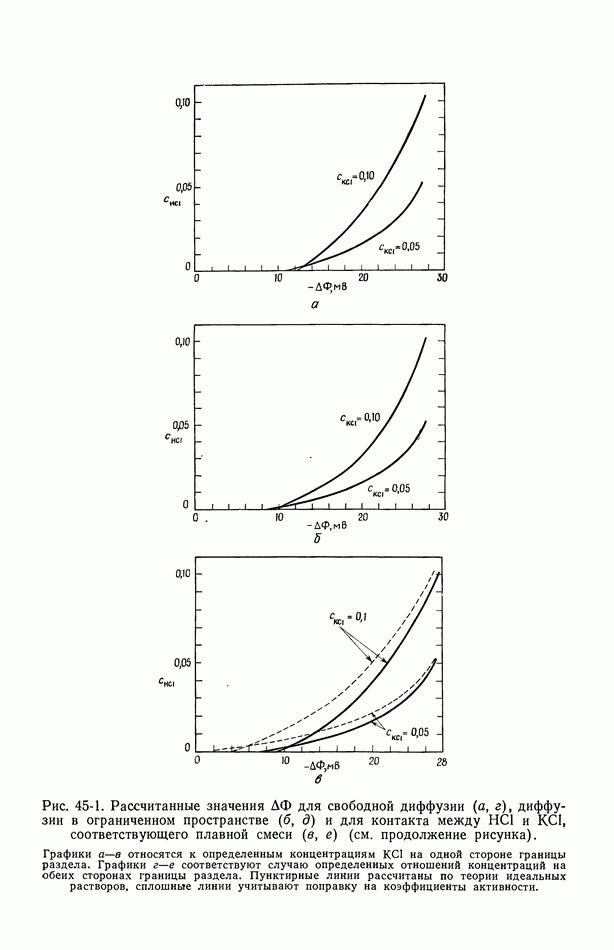
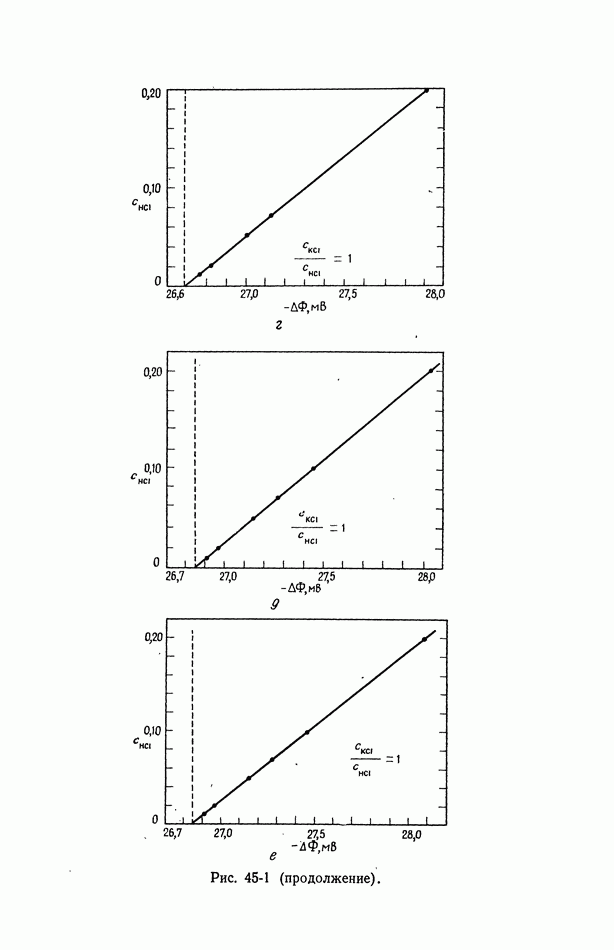
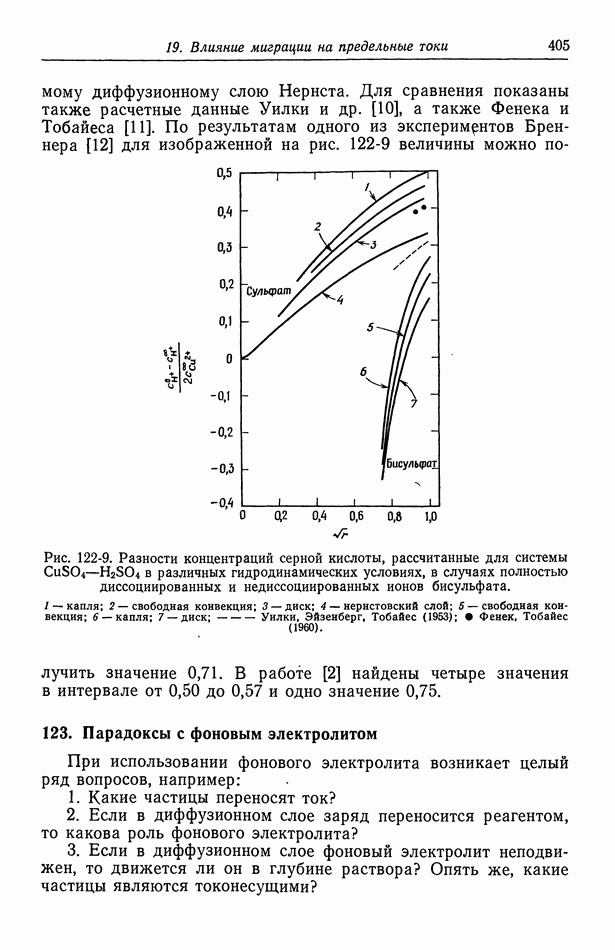
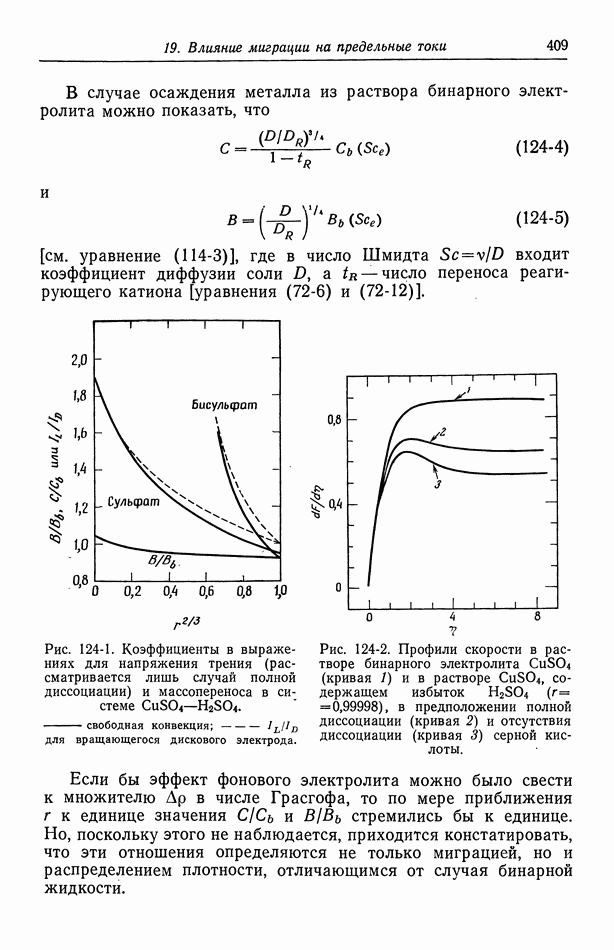
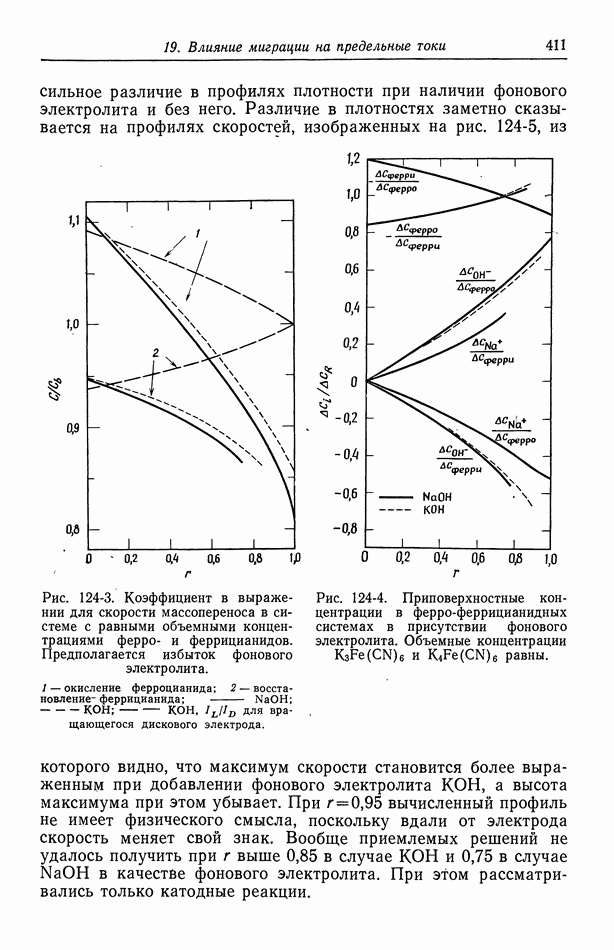
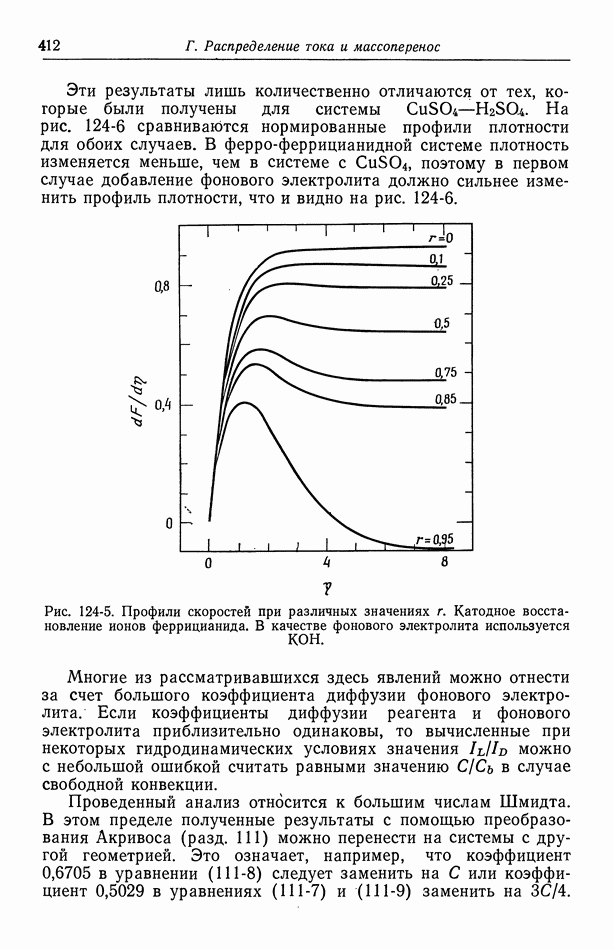
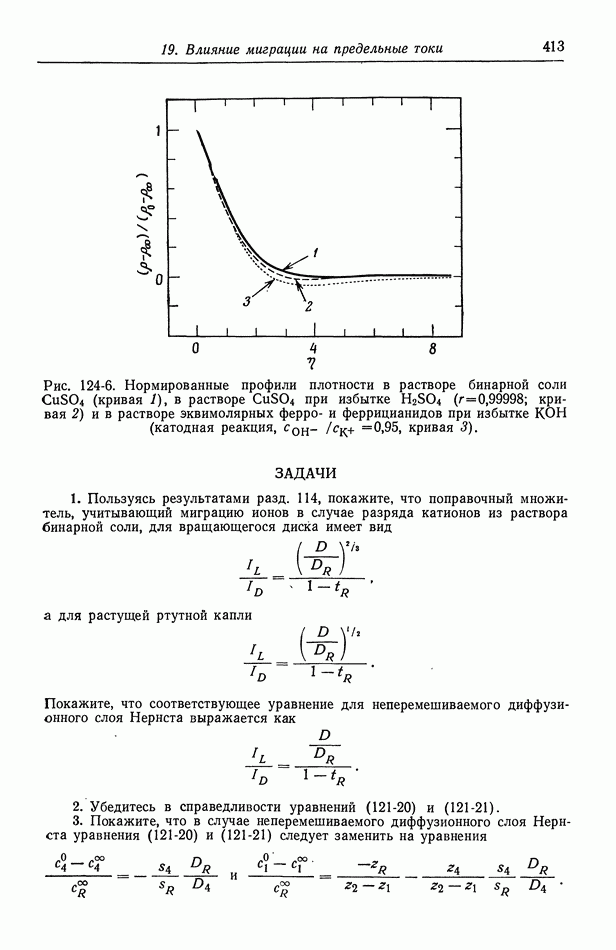
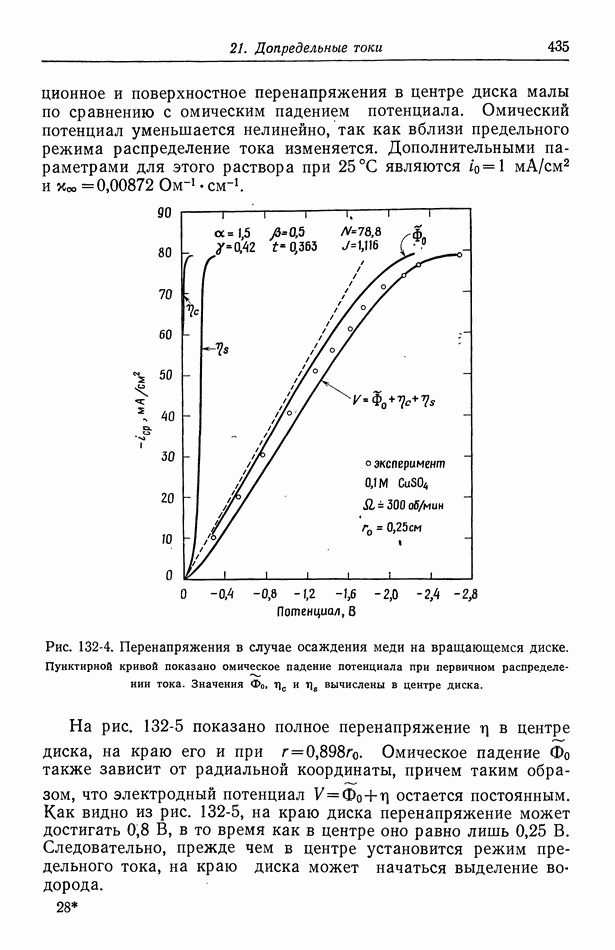
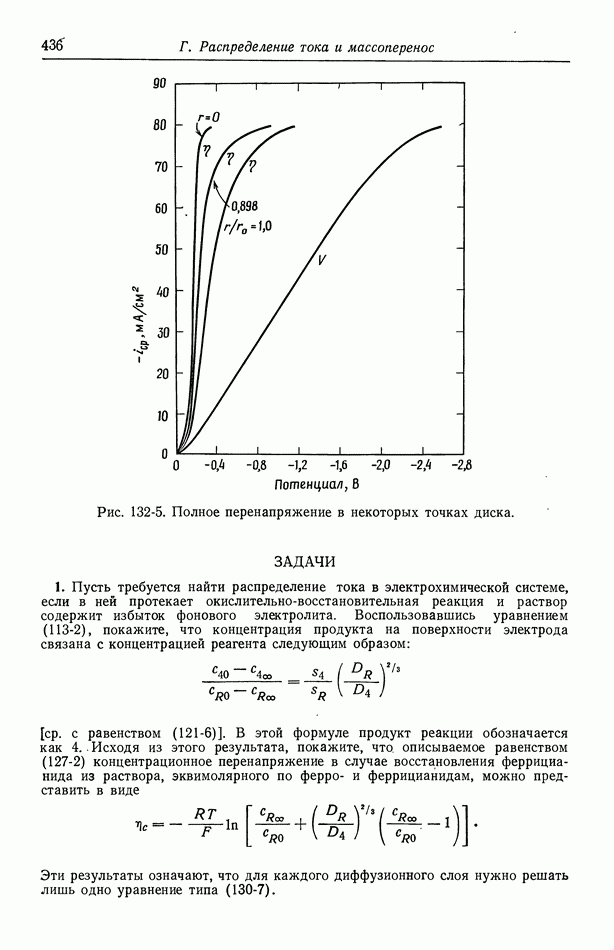
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
98. Турбулентное течение
Турбулентное течение характеризуется быстрыми и случайными флуктуациями скорости, давления и концентрации около их средних значений. Этими флуктуациями, как правило, интересуются лишь при статистическом описании систем. Поэтому в качестве первого шага при изучении турбулентного течения обычно рассматривают уравнения для средних величин, которые, как считается, описывают течение. При этом для некоторых средних величин получаются дифференциальные уравнения, в которые входят моменты высших порядков. Таким образом, этот метод не позволяет непосредственно вычислить любую среднюю величину. Задача о турбулентном течении имеет прямую аналогию в кинетической теории газов, где детали случайного движения молекул несущественны, и интерес представляют лишь некоторые средние измеримые величины.
Во многих случаях можно найти простое решение уравнения движения (94-4), описывающее ламинарное течение, однако наблюдаемое течение при этом турбулентно. Это обстоятельство привело к исследованиям устойчивости ламинарного течения. Вопрос об устойчивости течения формулируется следующим образом: если течение возмущается на бесконечно малую величину, то будет ли возмущение возрастать в пространстве и времени или же оно затухнет и течение останется ламинарным? Этот вопрос обычно решается путем линеаризации задачи вблизи основного, ламинарного решения. Получаемые результаты иногда согласуются с экспериментально наблюдаемыми условиями перехода к турбулентности или к более сложному ламинарному течению, как в случае вихрей Тейлора при течении между вращающимися цилиндрами (разд. 4). Иногда имеется
значительное расхождение с экспериментом, как в случае пуазейлевского течения в трубе.
Для турбулентного течения средние значения можно определить как средние по времени, например

Период времени  по которому проводится усреднение, должен быть большим по сравнению с периодом флуктуаций, который можно оценить как 0,01 с.
по которому проводится усреднение, должен быть большим по сравнению с периодом флуктуаций, который можно оценить как 0,01 с.
Для ламинарного течения напряжение дается равенством (94-1), определяющим закон Ньютона для вязкого течения. Однако в турбулентном течении имеется дополнительный механизм переноса импульса, обусловленный тем фактом, что случайные флуктуации скорости стремятся передавать импульс в область с меньшим количеством движения. Таким образом, полное среднее напряжение, или лоток импульса, равно сумме вязкого и турбулентного потоков импульса:

где вязкий поток импульса  определяется усредненным по времени уравнением (94-1), а турбулентный поток импульса
определяется усредненным по времени уравнением (94-1), а турбулентный поток импульса  будет получен в настоящем разделе несколько позднее.
будет получен в настоящем разделе несколько позднее.
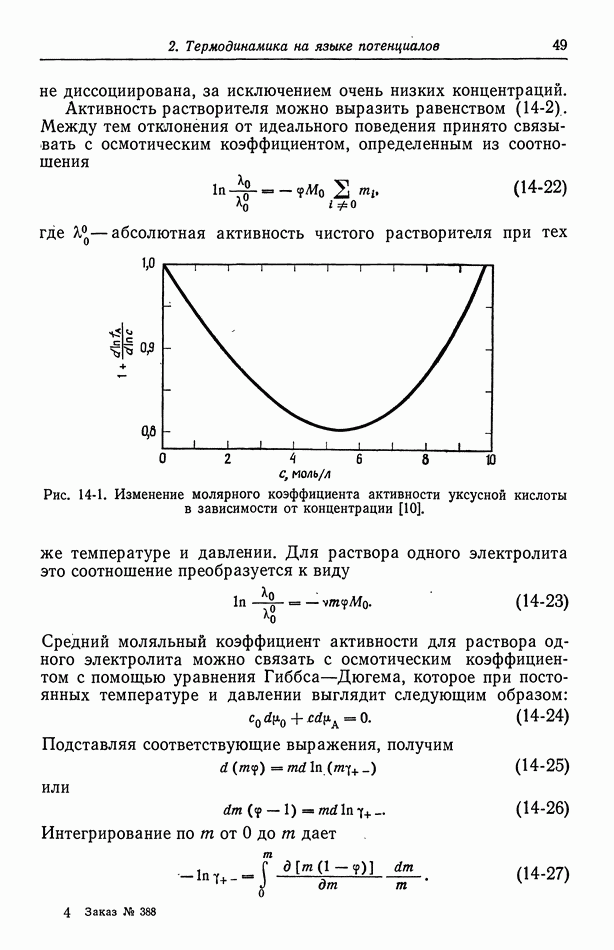
Вдали от твердой стенки преобладает перенос импульса по турбулентному механизму. Однако вблизи твердой поверхности турбулентные флуктуации гасятся, вследствие чего доминирует вязкий перенос импульса. Поэтому напряжение трения на стенке по-прежнему определяется равенством

относящимся к течению в трубе радиуса  Затухание флуктуаций вблизи твердой поверхности вполне естественно, поскольку жидкость не может пересечь границу раздела с твердым телом.
Затухание флуктуаций вблизи твердой поверхности вполне естественно, поскольку жидкость не может пересечь границу раздела с твердым телом.
Природу турбулентного потока импульса можно выяснить, усредняя по времени уравнение движения (93-4):

Здесь через  обозначен тот же тензор напряжений, который раньше обозначался
обозначен тот же тензор напряжений, который раньше обозначался  Этот тензор для ньютоновских жидкостей задается равенством (94-1).
Этот тензор для ньютоновских жидкостей задается равенством (94-1).
Введем отклонение от средних по времени значений скорости и давления:

Назовем  флуктуацией скорости или флуктуирующей частью скорости. Несколько правил усреднения по времени следует непосредственно из определения (98-1). Так, временное среднее суммы равно сумме средних по времени:
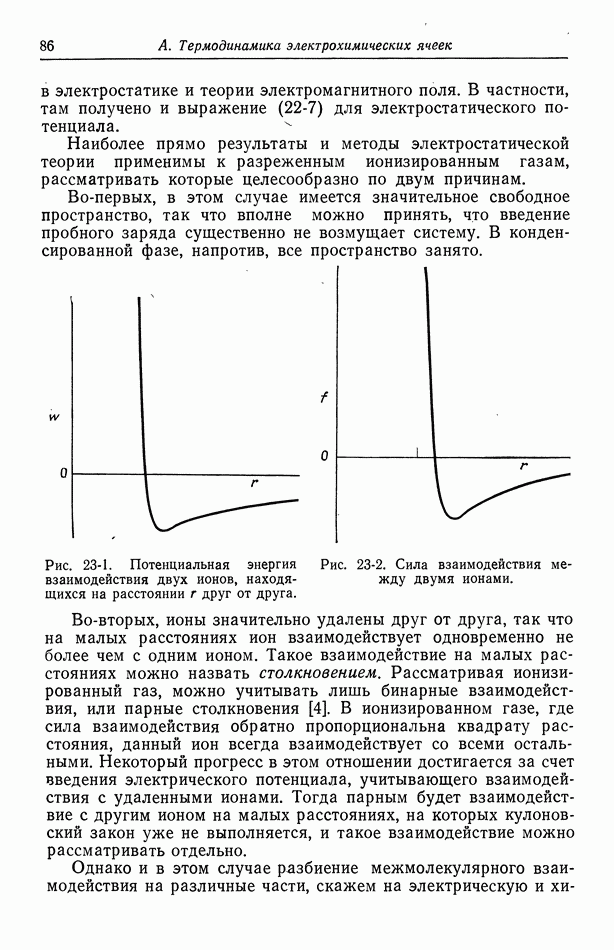
флуктуацией скорости или флуктуирующей частью скорости. Несколько правил усреднения по времени следует непосредственно из определения (98-1). Так, временное среднее суммы равно сумме средних по времени:

Среднее значение производной равно производной от среднего по времени:  В общем случае среднее по времени от нелинейного члена даст более одного члена. Например,
В общем случае среднее по времени от нелинейного члена даст более одного члена. Например,  Конечно, среднее по времени от флуктуации равно нулю:
Конечно, среднее по времени от флуктуации равно нулю: 
Мы считаем, что характеристики жидкости, например  д., постоянны, поскольку даже при таких допущениях задача о турбулентном течении остается трудной и поскольку несжимаемые жидкости также подвержены турбулентному течению. В действительности сжимаемый ламинарный пограничный слой может быть более устойчивым, чем несжимаемый. С учетом этих замечаний усреднение по времени уравнения движения (98-4) дает
д., постоянны, поскольку даже при таких допущениях задача о турбулентном течении остается трудной и поскольку несжимаемые жидкости также подвержены турбулентному течению. В действительности сжимаемый ламинарный пограничный слой может быть более устойчивым, чем несжимаемый. С учетом этих замечаний усреднение по времени уравнения движения (98-4) дает

Усредненное по времени уравнение непрерывности (93-3) имеет вид

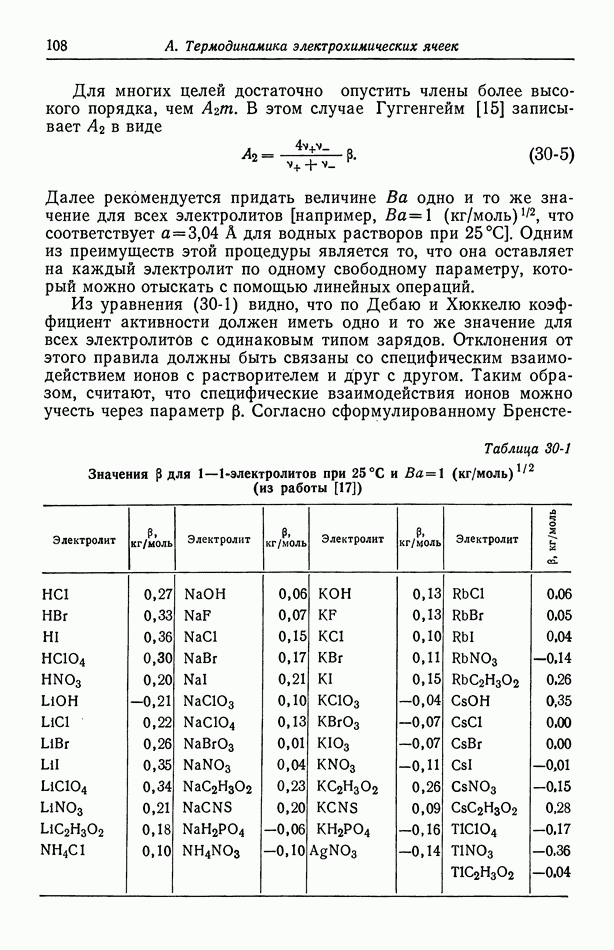
Среднее вязкое напряжение находится усреднением по времени равенства (94-1):

Эти уравнения совпадают с уравнениями, имевшимися до усреднения, за исключением того, что в уравнении движения (98-6) появляется член  Если выразить турбулентный поток импульса как
Если выразить турбулентный поток импульса как

и записать полное среднее напряжение в соответствии с равенством (98-2), то уравнение движения приобретает вид

Это уравнение весьма похоже на то, каким оно было до усреднения.
Эти выкладки иллюстрируют происхождение турбулентного потока импульса или так называемого напряжения Рейнольдса, определяемого равенством (98-9). Турбулентный механизм переноса импульса до некоторой степени аналогичен механизму переноса импульса в газах, с той лишь разницей, что в газах перенос осуществляется за счет случайного движения молекул, а в жидкостях — за счет случайного движения больших молекулярных агрегатов.
Видно, что процесс усреднения не позволяет надежно предсказать напряжение Рейнольдса. Не располагая фундаментальной теорией, многие авторы с переменным успехом писали эмпирические выражения для  Возможно, стоит подчеркнуть, что между турбулентным напряжением и производными скорости нет простого соотношения, как это имеет место для вязкого напряжения в ньютоновской жидкости, где является характеристикой состояния, зависящей лишь от температуры, давления и состава.
Возможно, стоит подчеркнуть, что между турбулентным напряжением и производными скорости нет простого соотношения, как это имеет место для вязкого напряжения в ньютоновской жидкости, где является характеристикой состояния, зависящей лишь от температуры, давления и состава.
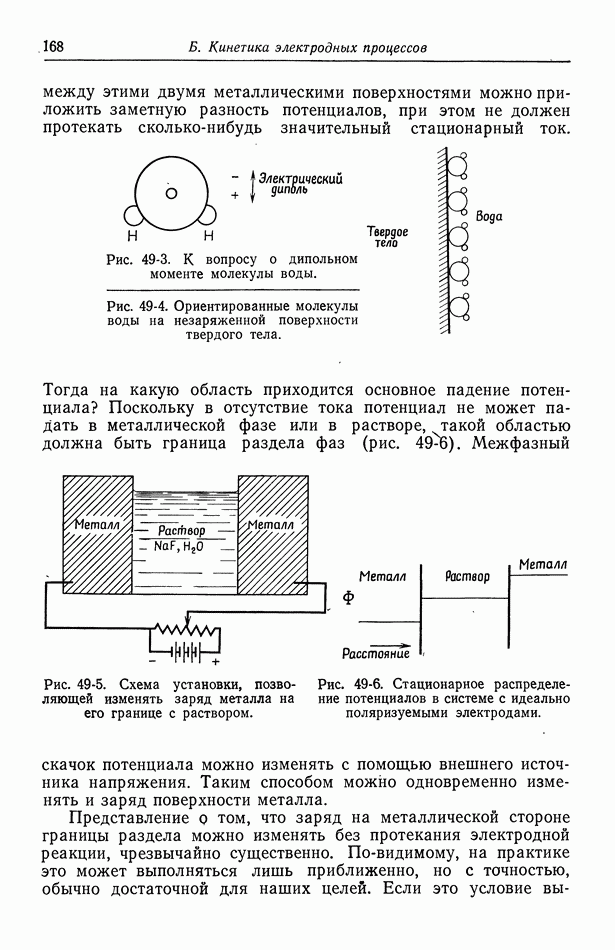
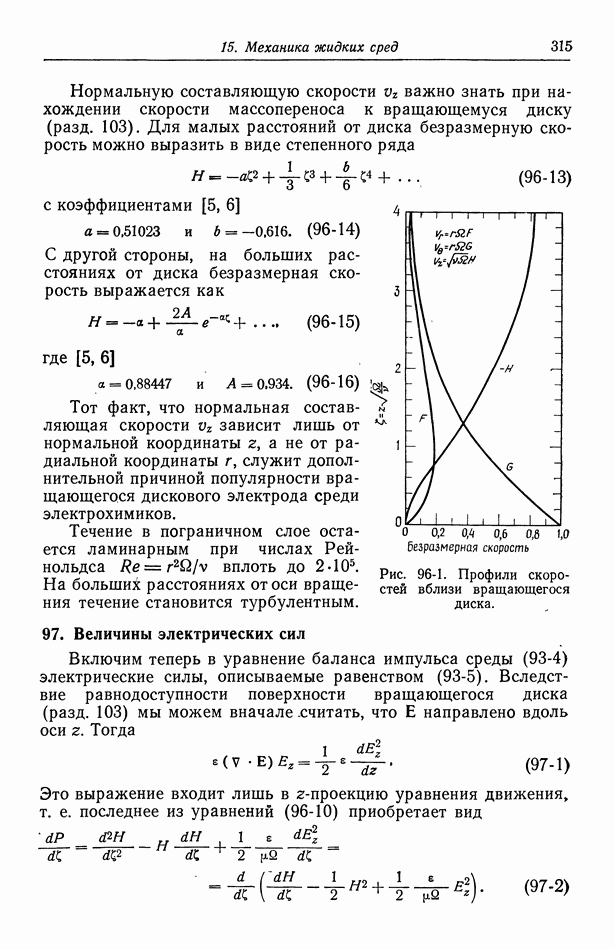
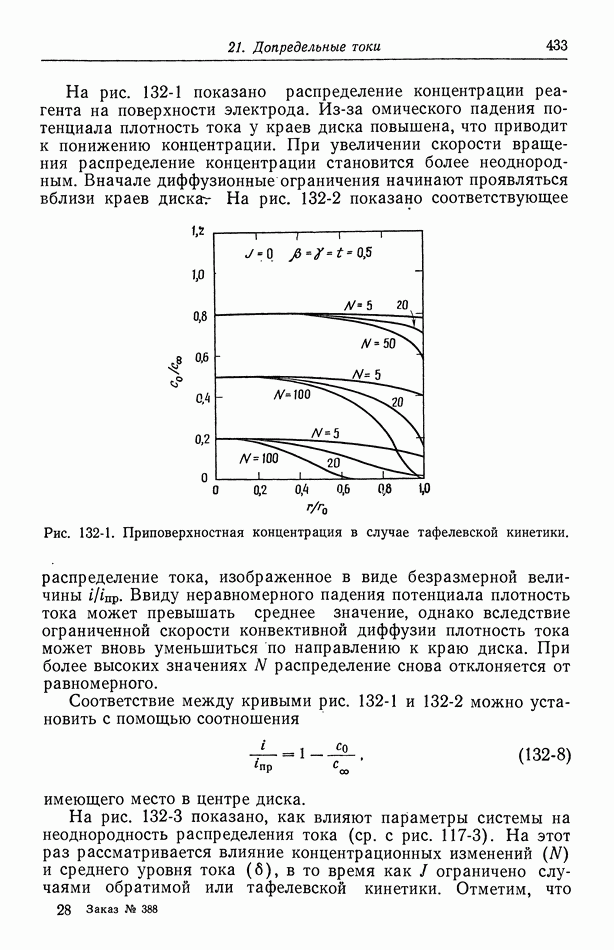
Многие практические задачи по турбулентности включают область вблизи твердой поверхности, поскольку по своему смыслу именно эта область служит местом зарождения турбулентности и поскольку именно в этой области требуется вычислять напряжения трения и скорости массопереноса. Делалось много попыток изучить экспериментальные данные с целью обобщения свойств разных характеристик турбулентного переноса вблизи поверхности. К таким характеристикам относятся средние высших порядков, например напряжение Рейнольдса, вытекающие из усреднения уравнений движения и конвективной диффузии. Это обобщение имеет вид универсального закона распределения скоростей вблизи поверхности. Тот же результат можно выразить с помощью турбулентной вязкости и турбулентной кинематической вязкости — коэффициентов, связывающих турбулентный перенос с градиентами скорости. Эти коэффициенты существенно зависят от расстояния до стенки и потому не являются фундаментальными характеристиками жидкости. Такого рода информация часто получается при изучении полностью развитого течения в трубе или некоторых простых пограничных слоев.
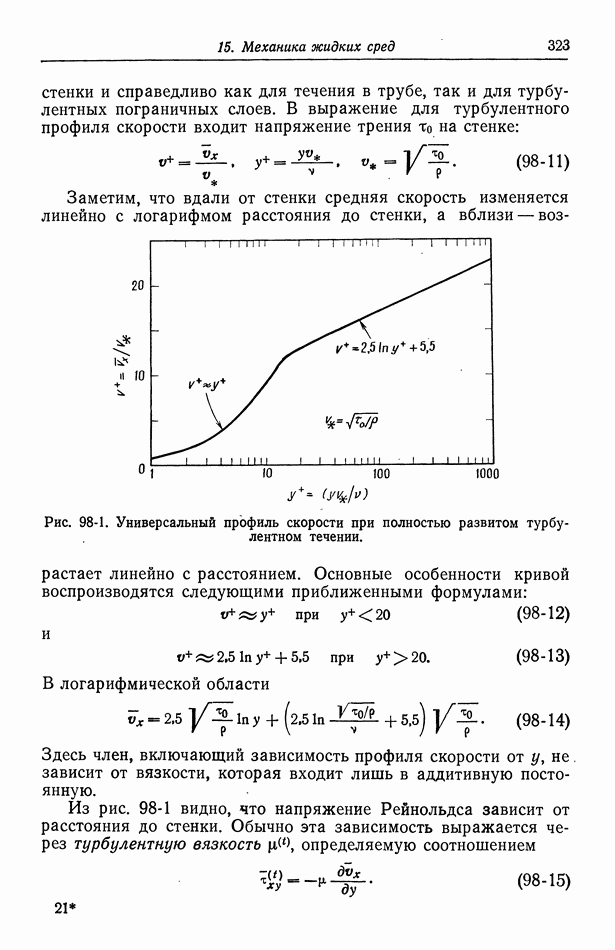
При изучении турбулентного течения вблизи поверхности твердого тела показано, что соотношение, называемое универсальным профилем скорости, справедливо для средней тангенциальной скорости, зависимость которой от расстояния до твердой поверхности изображена на рис. 98-1. Это соотношение описывает полностью развитое турбулентное течение вблизи гладкой
стенки и справедливо как для течения в трубе, так и для турбулентных пограничных слоев. В выражение для турбулентного профиля скорости входит напряжение трения То на стенке:

Заметим, что вдали от стенки средняя скорость изменяется линейно с логарифмом расстояния до стенки, а вблизи — возрастает линейно с расстоянием.

Рис. 98-1. Универсальный профиль скорости при полностью развитом турбулентном течении.
Основные особенности кривой воспроизводятся следующими приближенными формулами:

и

В логарифмической области

Здесь член, включающий зависимость профиля скорости от у, не, зависит от вязкости, которая входит лишь в аддитивную постоянную.
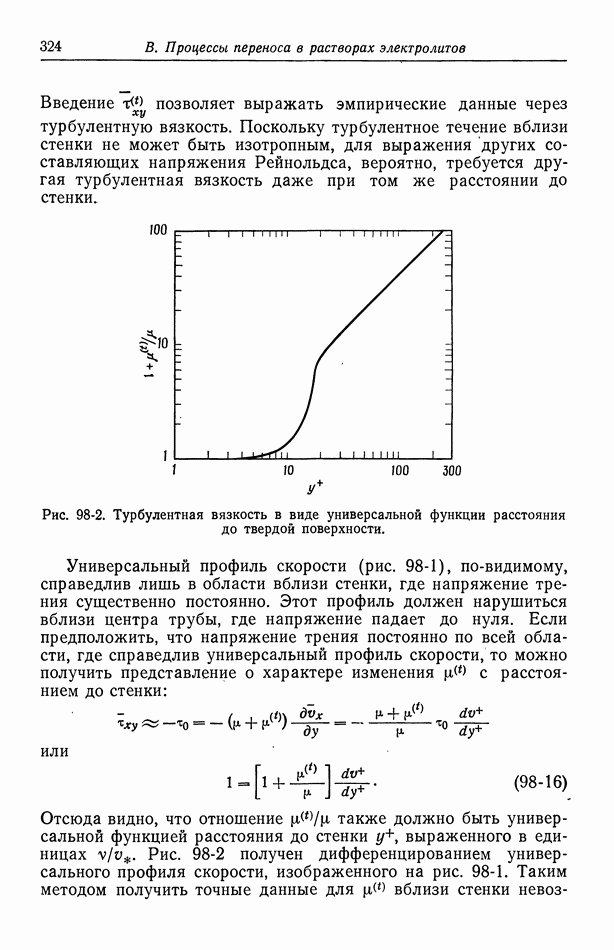
Из рис. 98-1 видно, что напряжение Рейнольдса зависит от расстояния до стенки. Обычно эта зависимость выражается через турбулентную вязкость  определяемую соотношением
определяемую соотношением

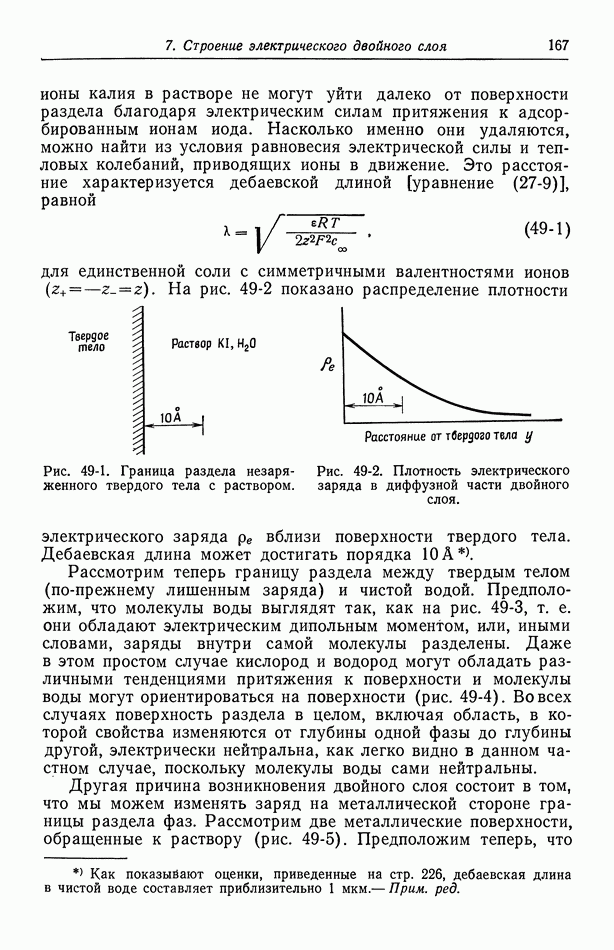
Введение  позволяет выражать эмпирические данные через
позволяет выражать эмпирические данные через

турбулентную вязкость. Поскольку турбулентное течение вблизи стенки не может быть изотропным, для выражения других составляющих напряжения Рейнольдса, вероятно, требуется другая турбулентная вязкость даже при том же расстоянии до стенки.

Рис. 98-2. Турбулентная вязкость в виде универсальной функции расстояния до твердой поверхности.
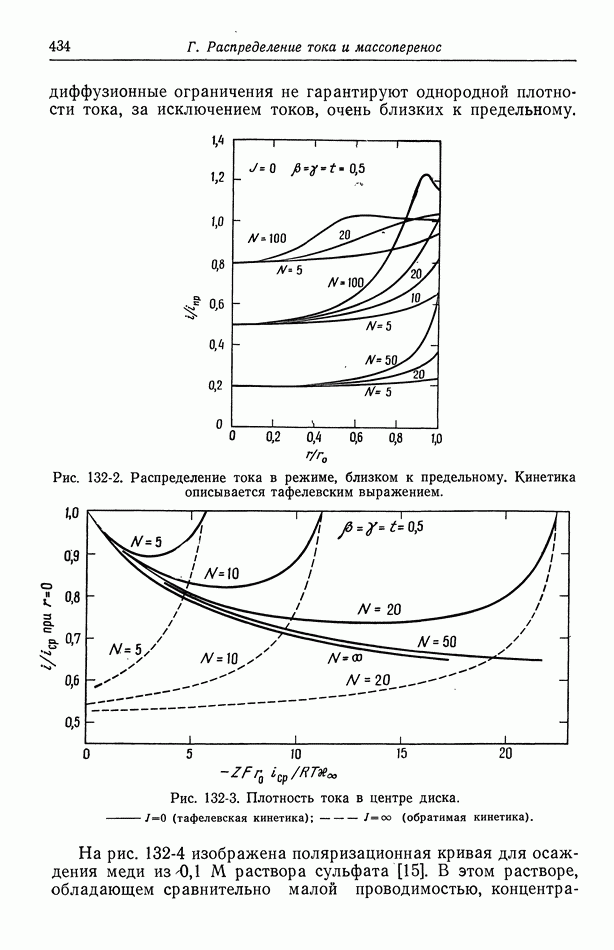
Универсальный профиль скорости (рис. 98-1), по-видимому, справедлив лишь в области вблизи стенки, где напряжение трения существенно постоянно. Этот профиль должен нарушиться вблизи центра трубы, где напряжение падает до нуля. Если предположить, что напряжение трения постоянно по всей области, где справедлив универсальный профиль скорости, то можно получить представление о характере изменения с расстоянием до стенки:

или
Отсюда видно, что отношение  также должно быть универсальной функцией расстояния до стенки
также должно быть универсальной функцией расстояния до стенки  выраженного в единицах
выраженного в единицах  Рис. 98-2 получен дифференцированием универсального профиля скорости, изображенного на рис. 98-1. Таким методом получить точные данные для вблизи стенки
Рис. 98-2 получен дифференцированием универсального профиля скорости, изображенного на рис. 98-1. Таким методом получить точные данные для вблизи стенки
невозможно, поскольку в этой области  Однако эта задача не имеет особого значения, так как в задачи гидродинамики входит лишь сумма
Однако эта задача не имеет особого значения, так как в задачи гидродинамики входит лишь сумма 
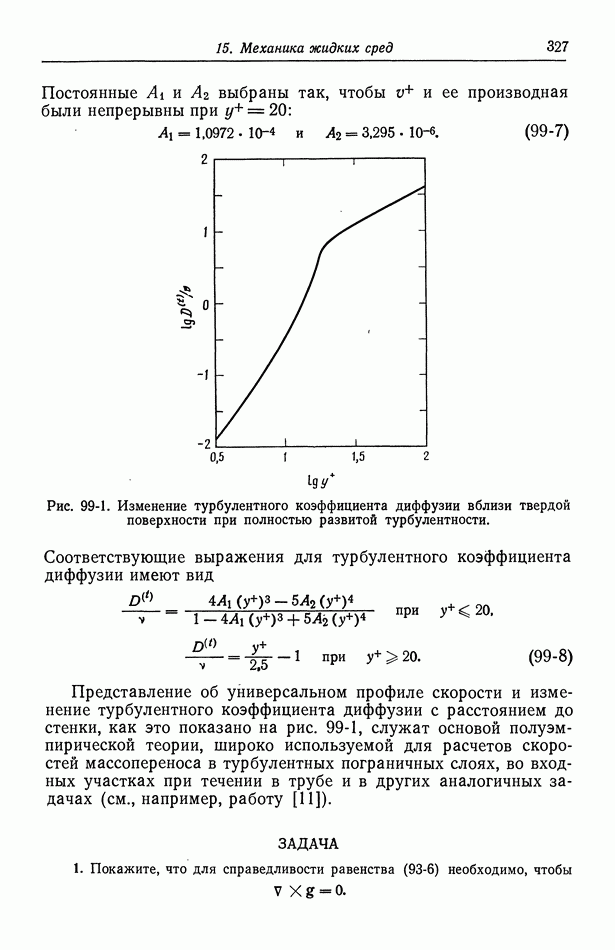
Универсальный профиль скорости — один из немногих выводов, полученных в теории турбулентного течения вблизи стенки. Этот профиль широко используется в тех случаях, когда экспериментальные наблюдения невозможны. Таким образом, универсальный профиль служит основой полуэмпирической теории турбулентного течения, которая применяется к гидродинамике турбулентных пограничных слоев, к массопереносу в турбулентных пограничных слоях, а также во входной области в случае полностью развитого течения в трубе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
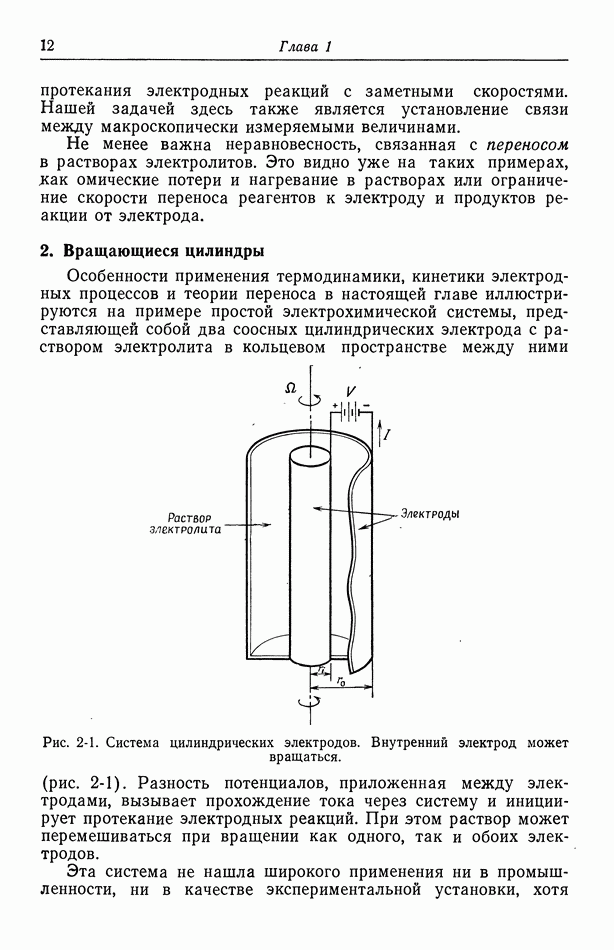
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
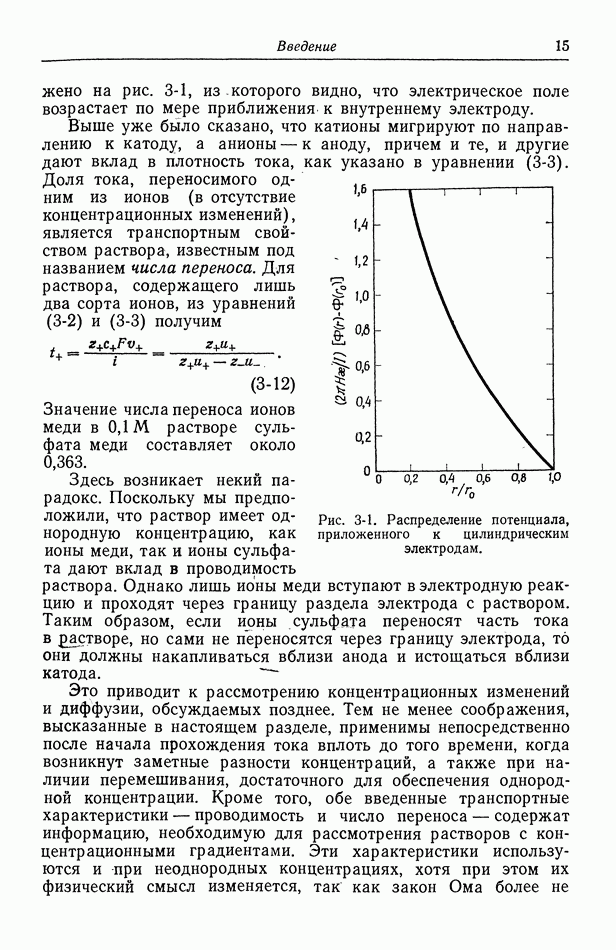
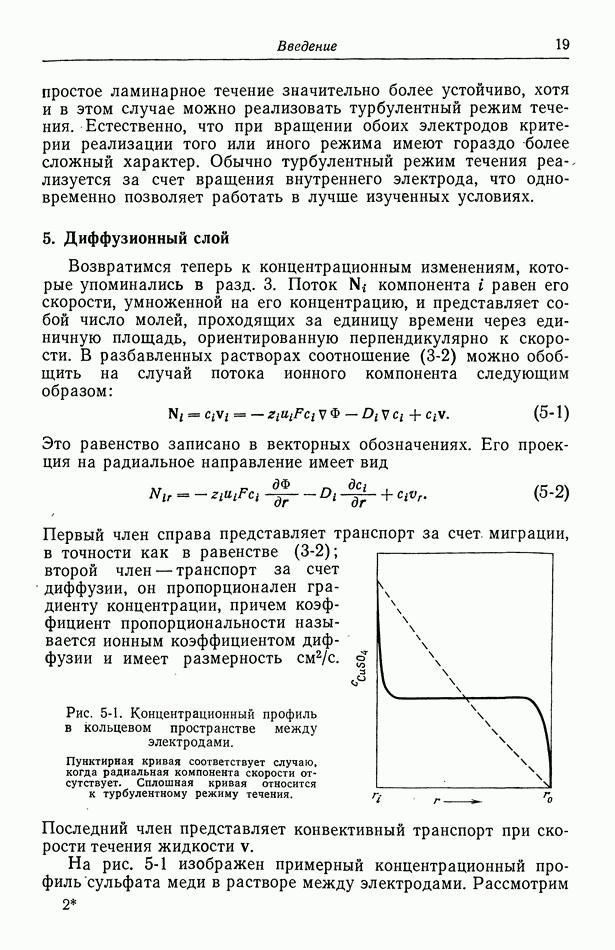
- 5. Диффузионный слой
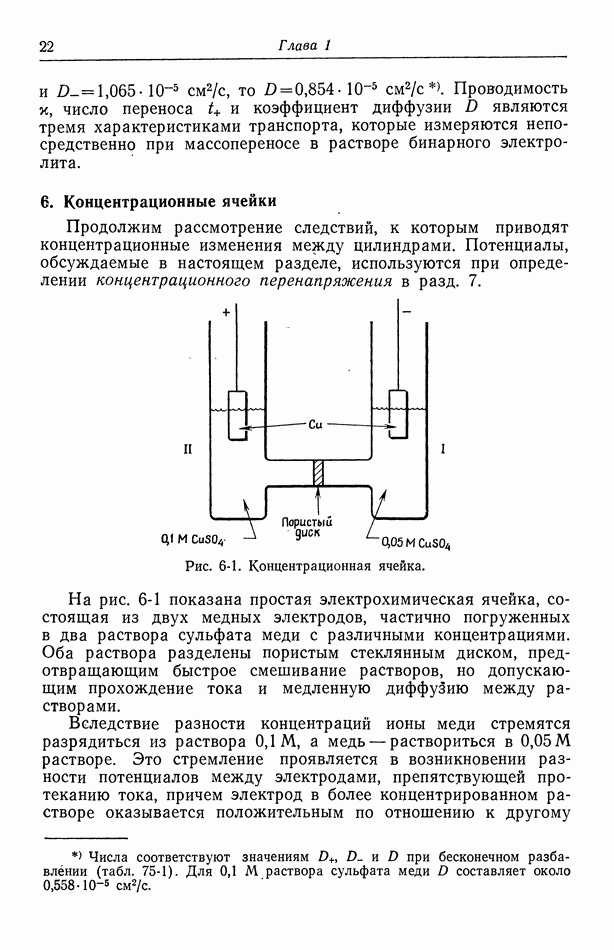
- 6. Концентрационные ячейки
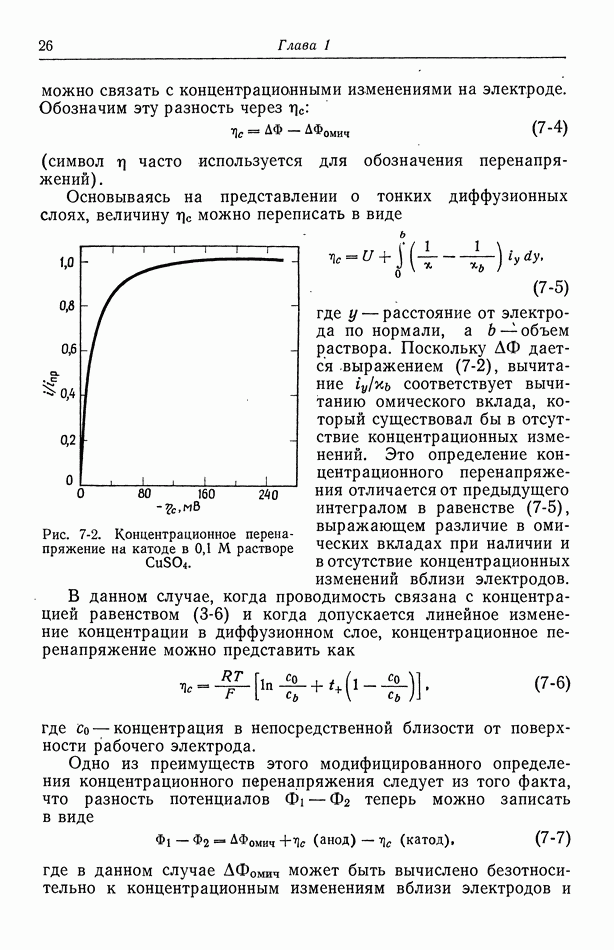
- 7. Концентрационное перенапряжение
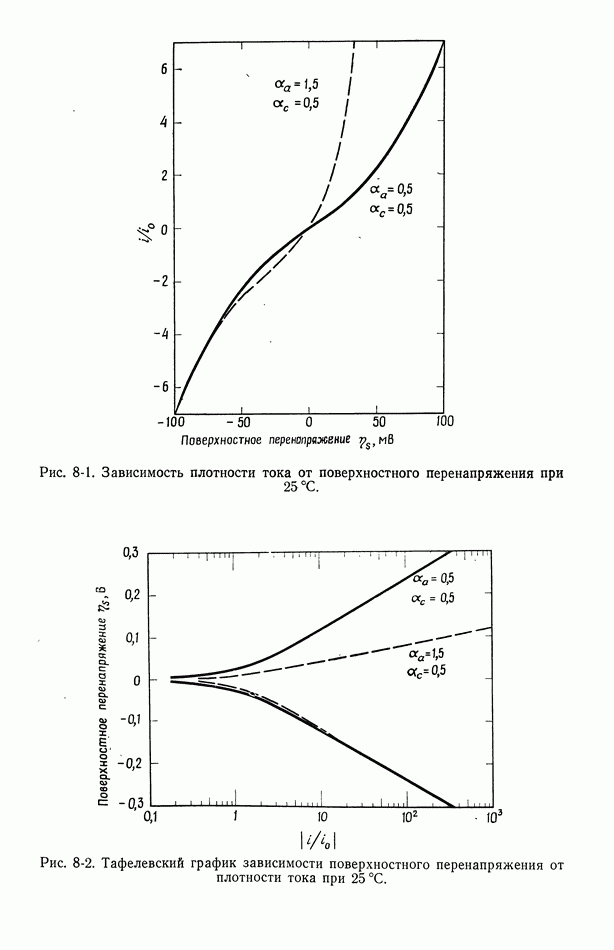
- 8. Поверхностное перенапряжение
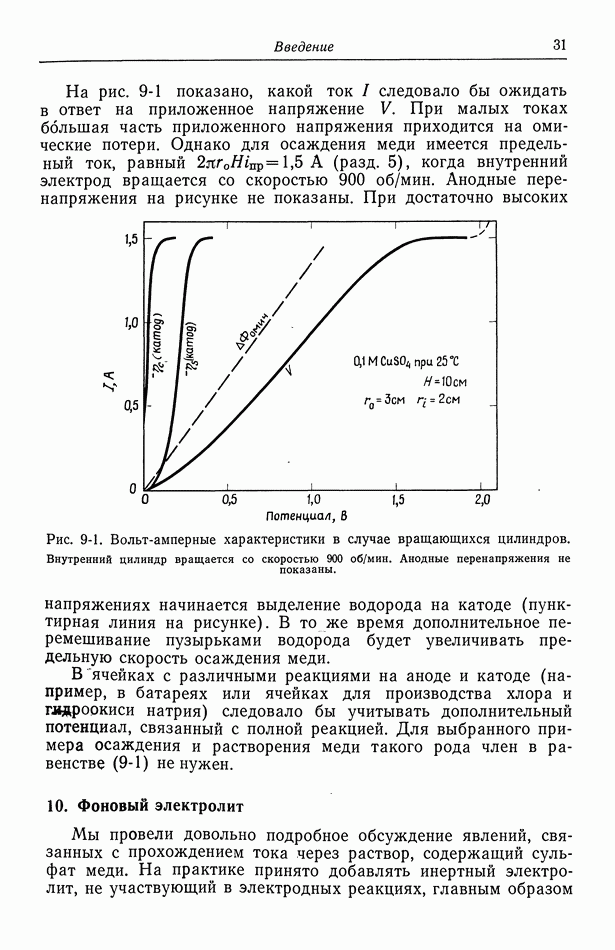
- 9. Потенциал ячейки
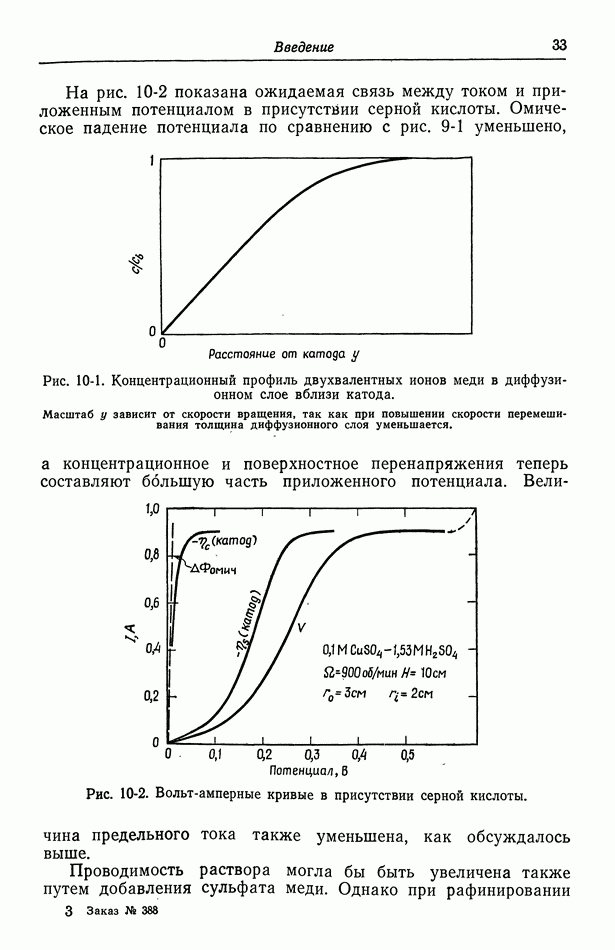
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
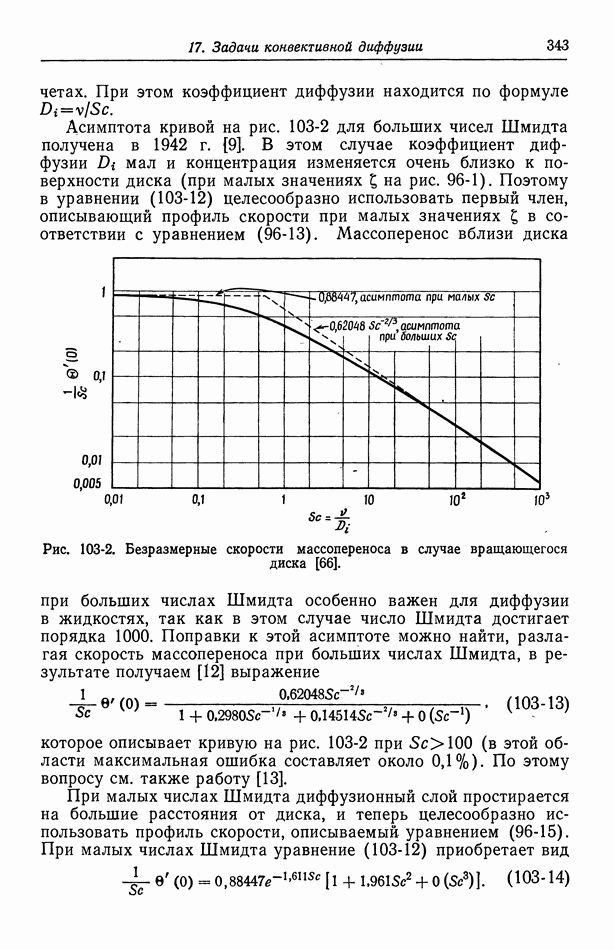
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
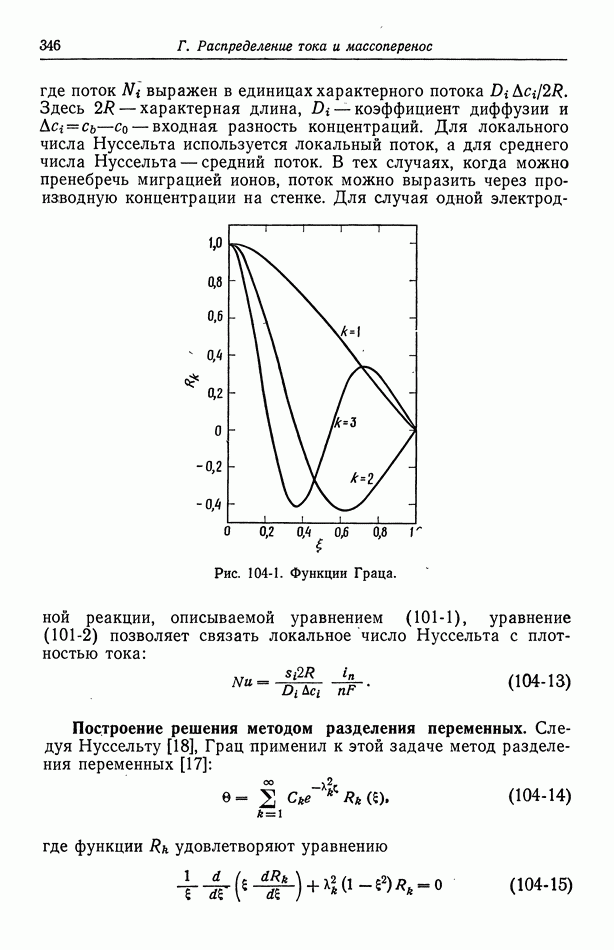
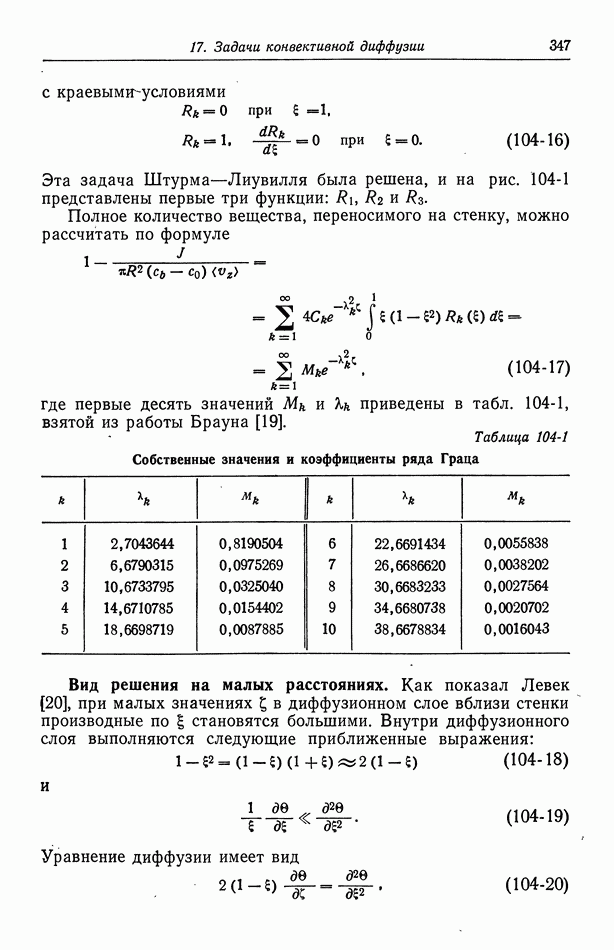
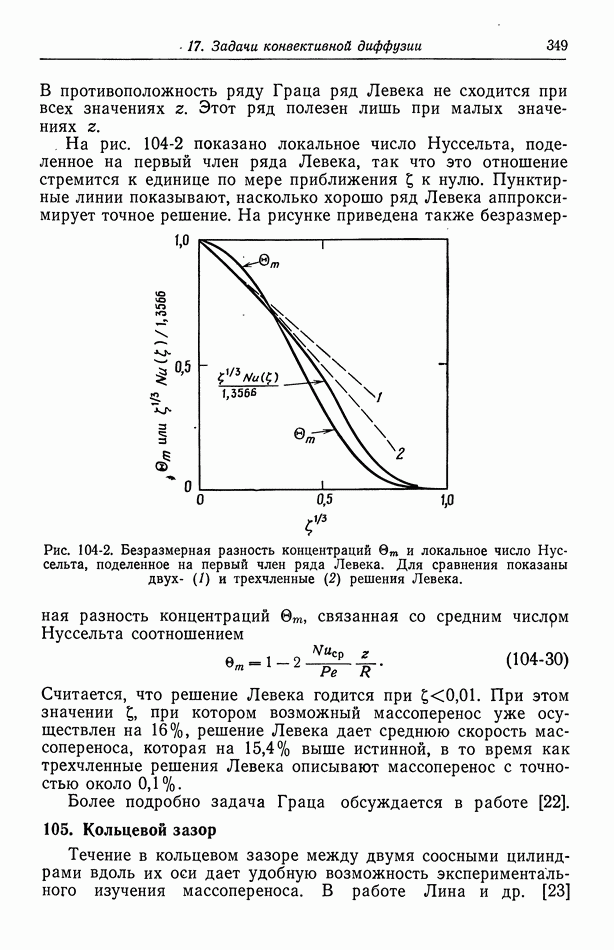
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
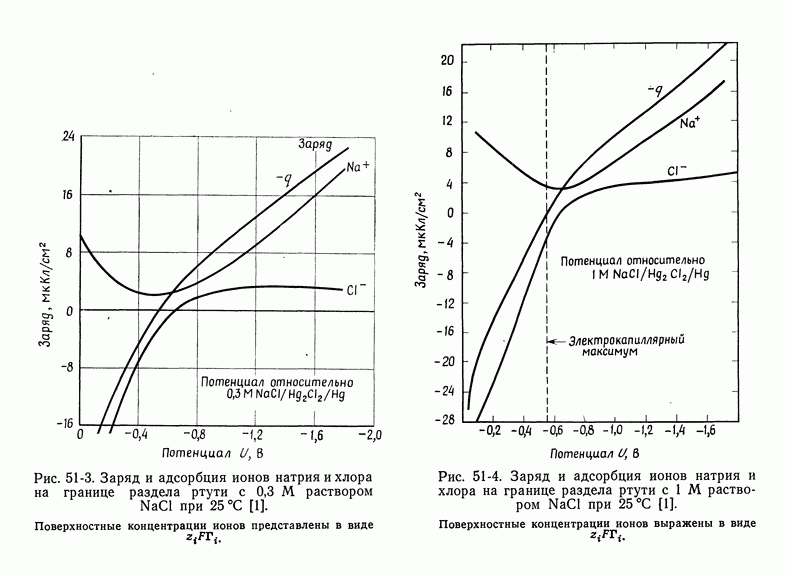
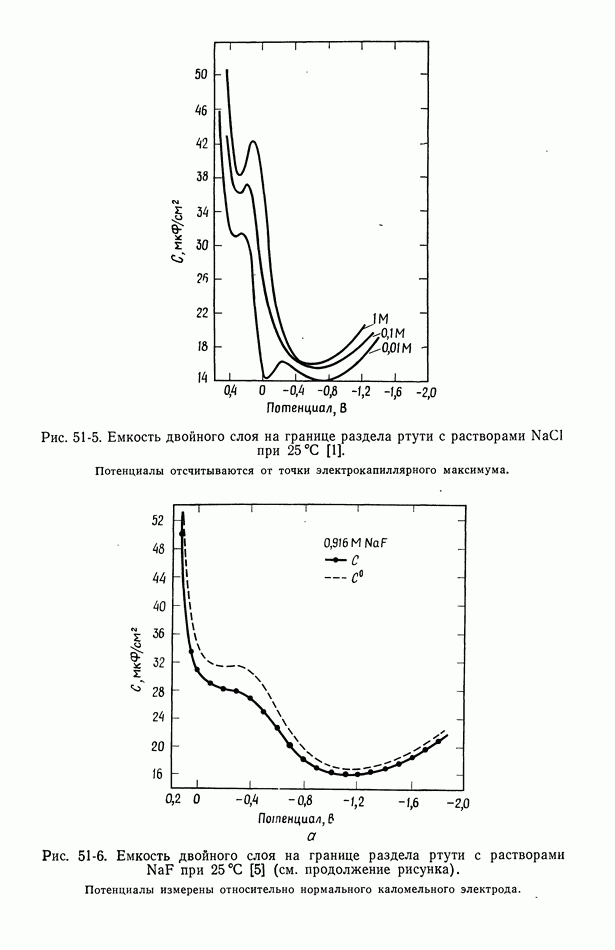
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
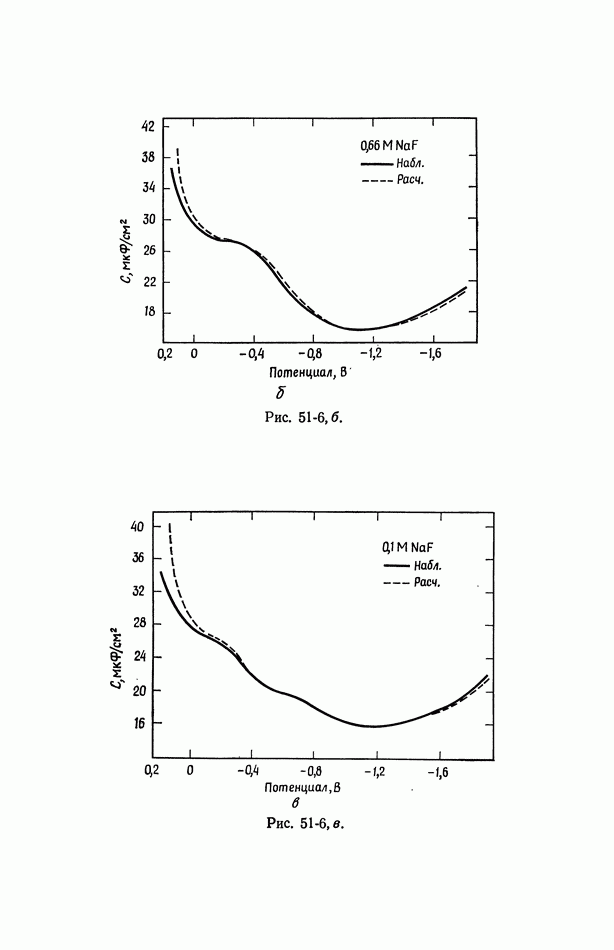
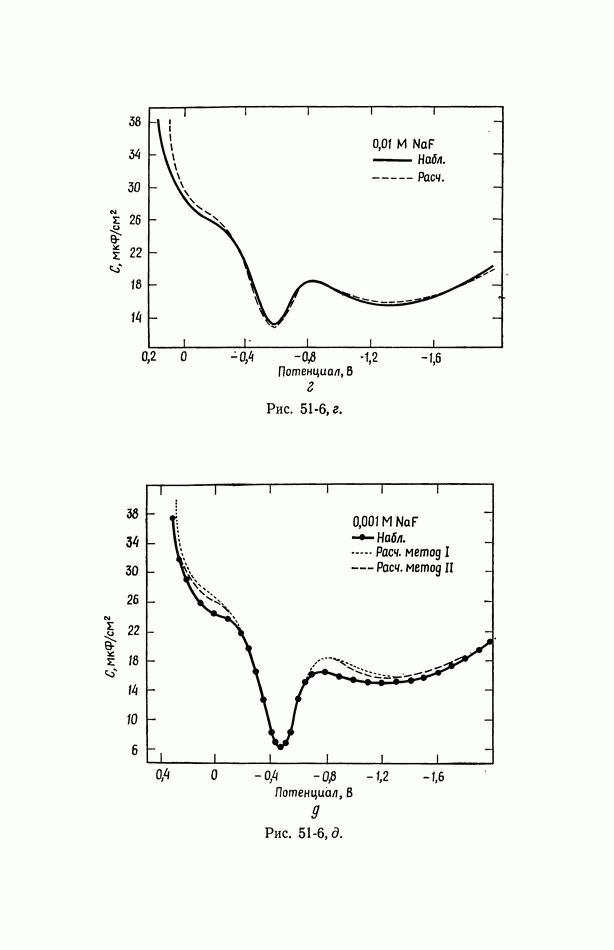
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
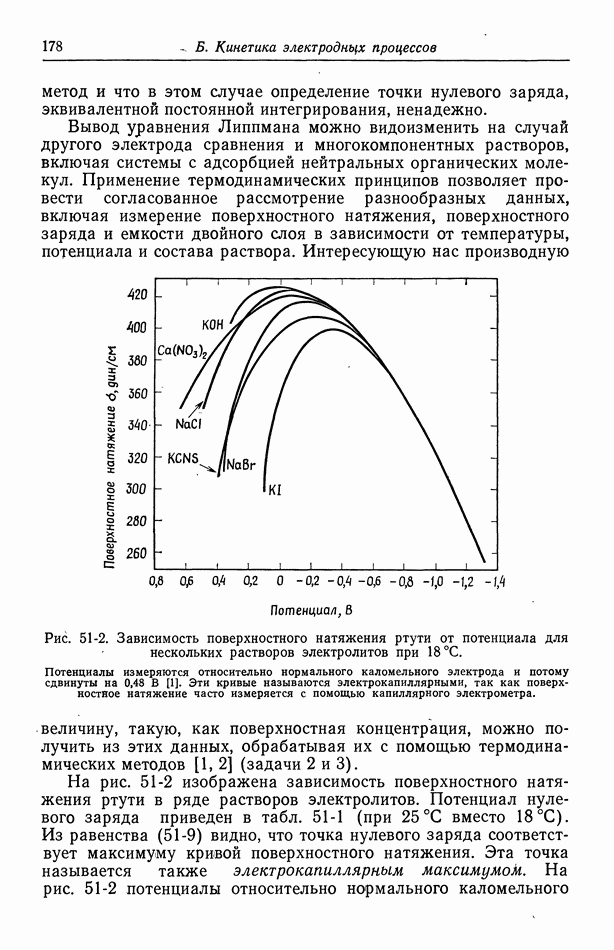
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
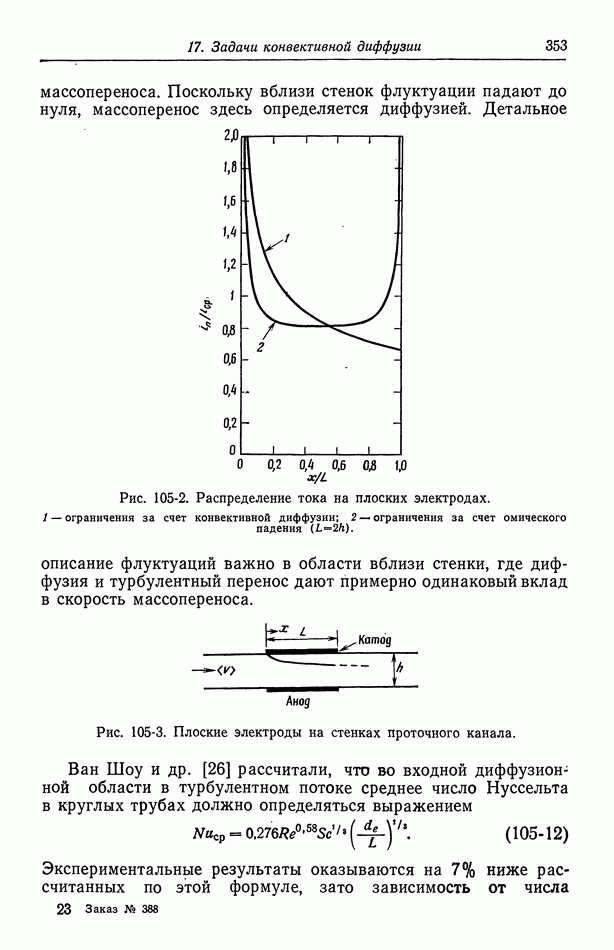
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
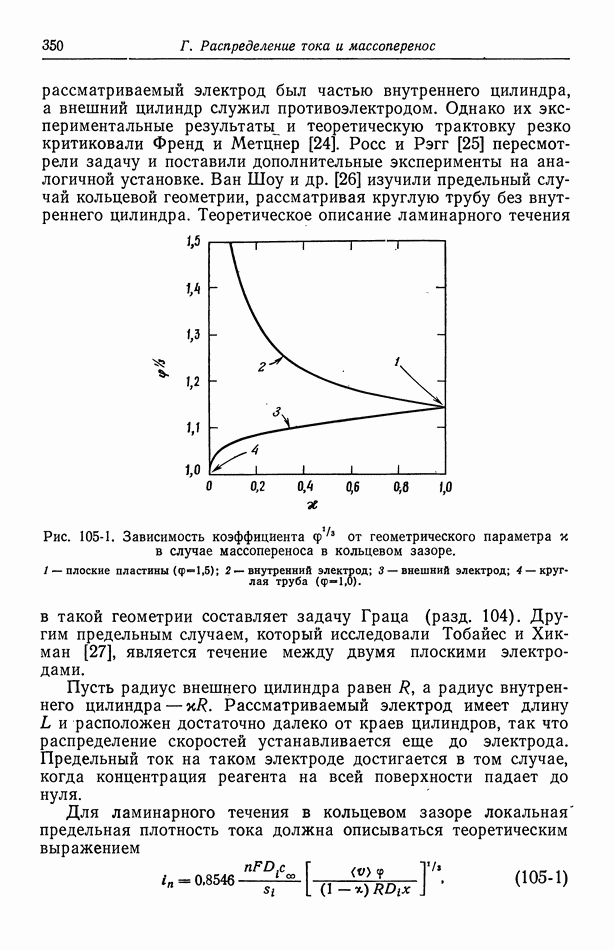
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
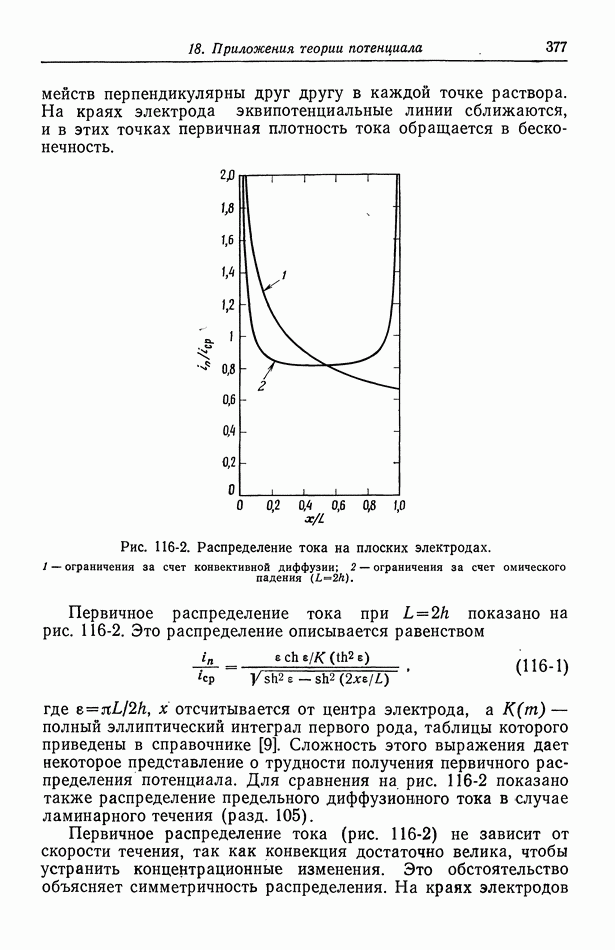
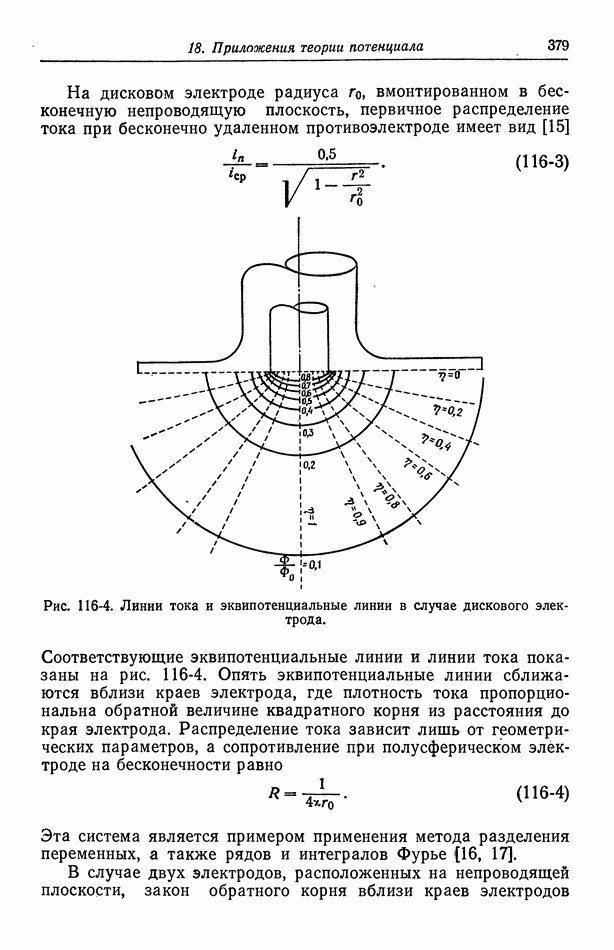
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
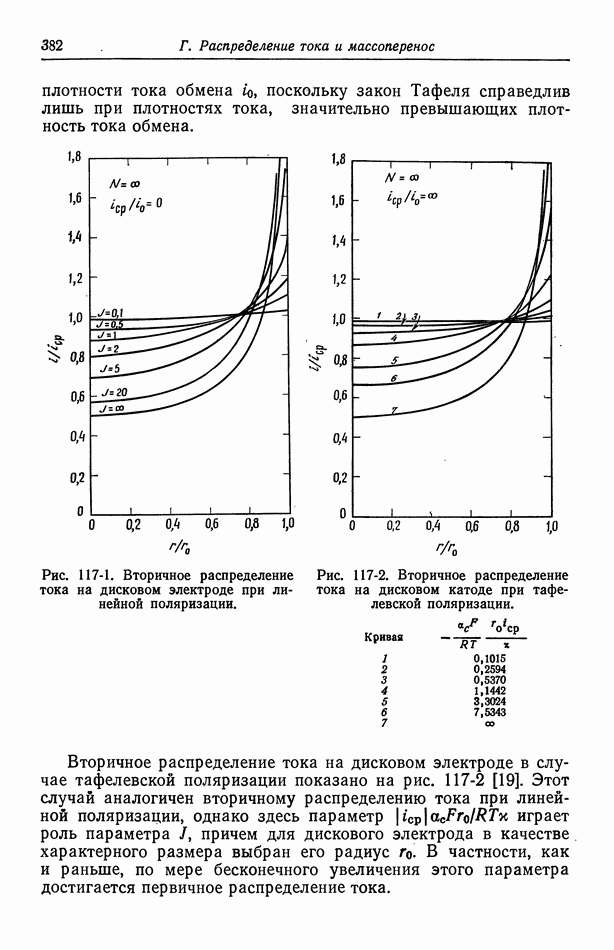
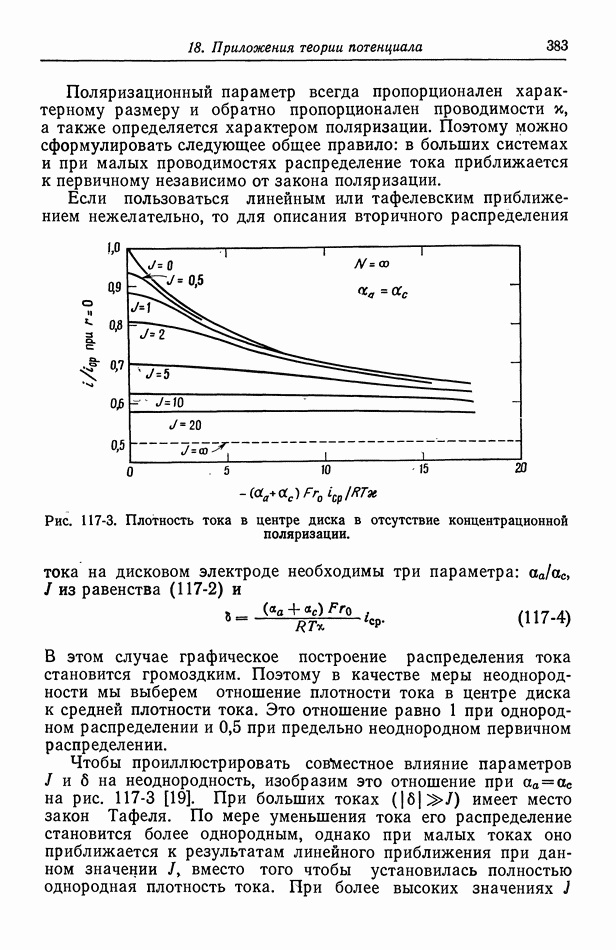
- 117. Вторичное распределение тока
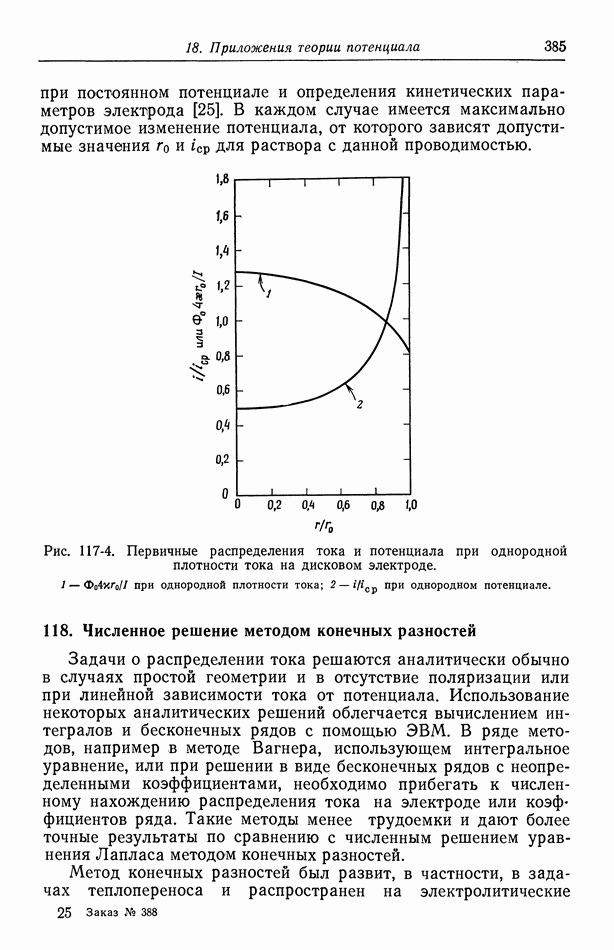
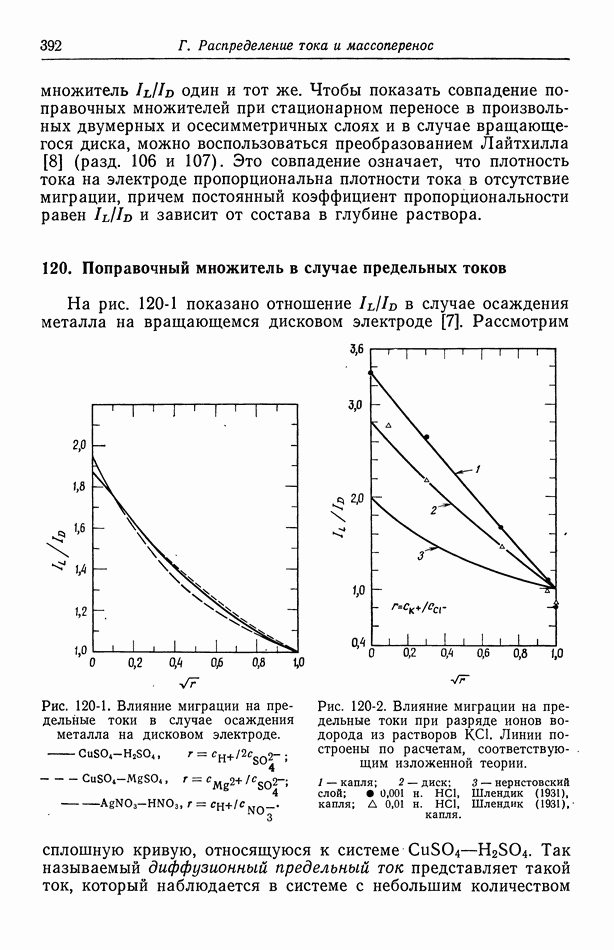
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
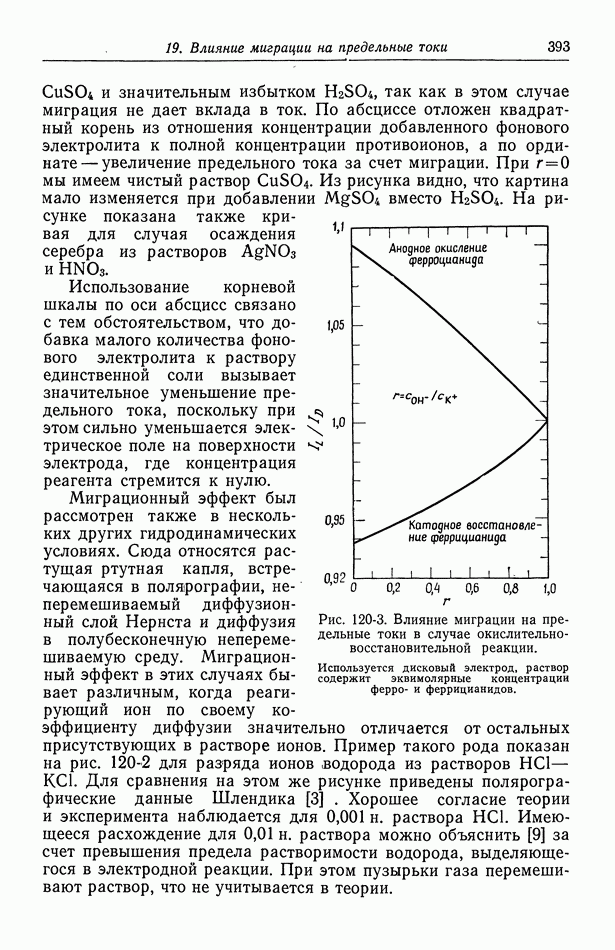
- 120. Поправочный множитель в случае предельных токов
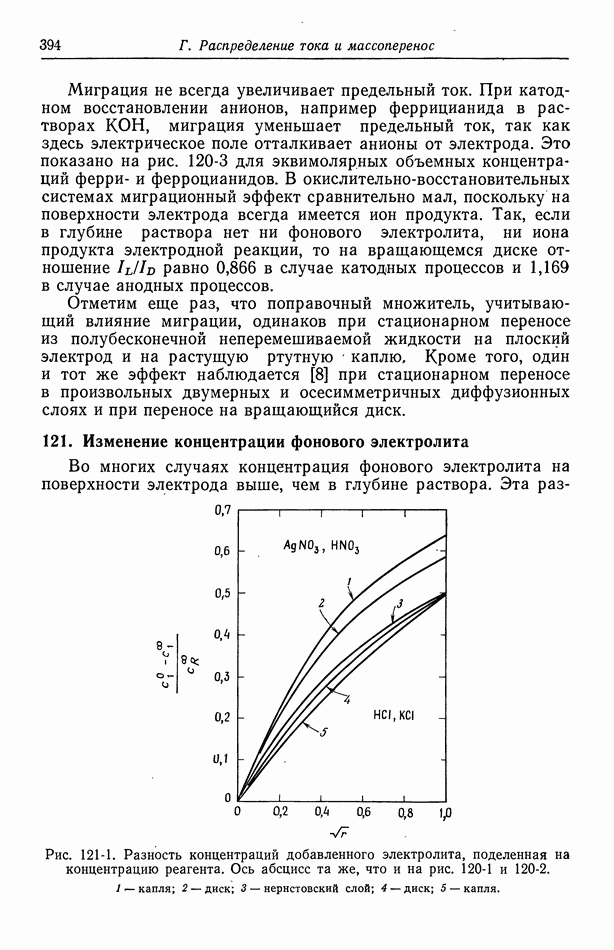
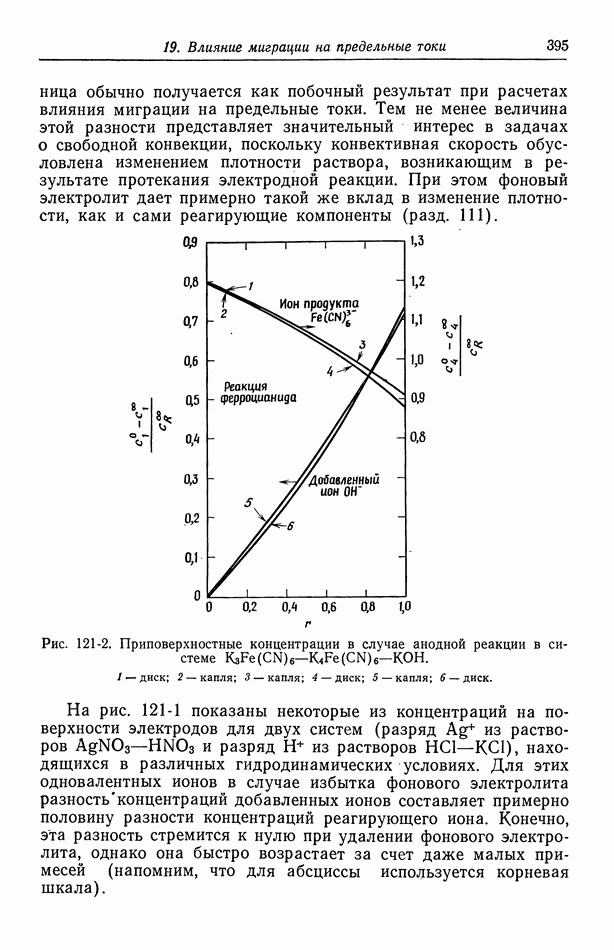
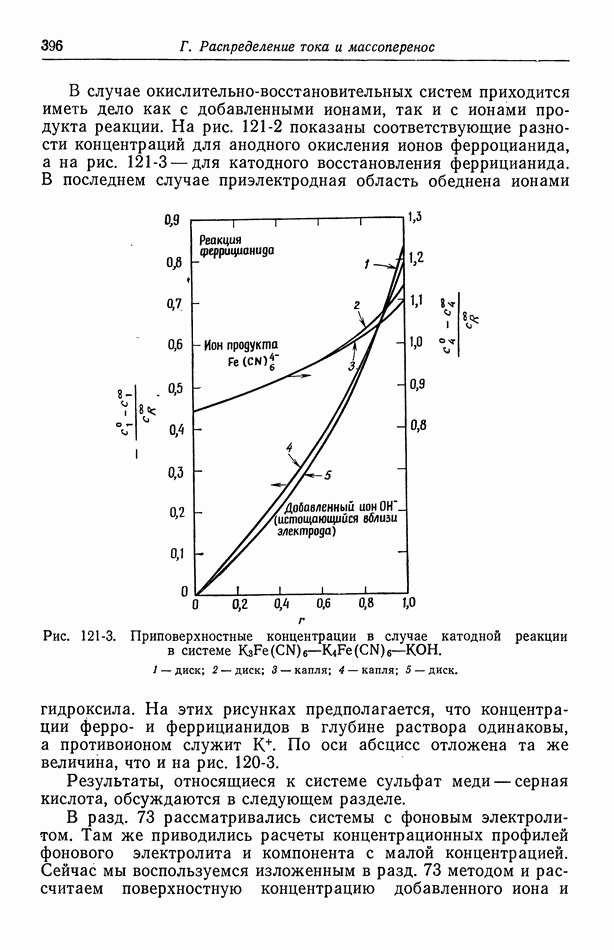
- 121. Изменение концентрации фонового электролита
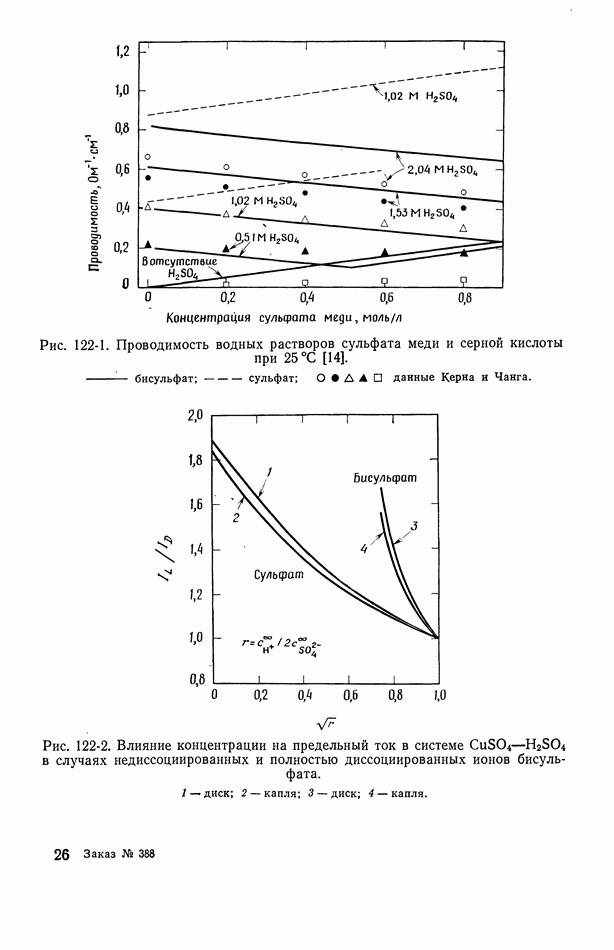
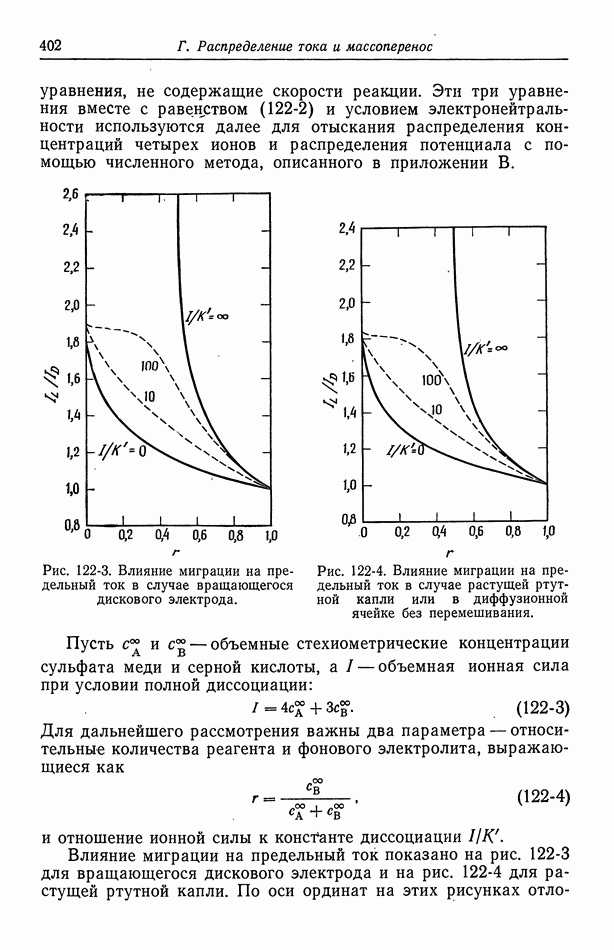
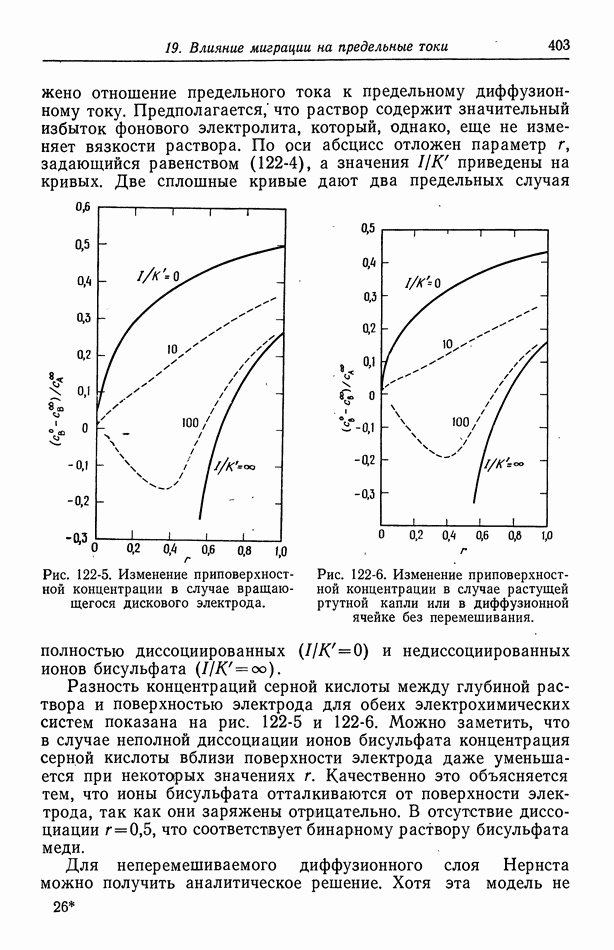
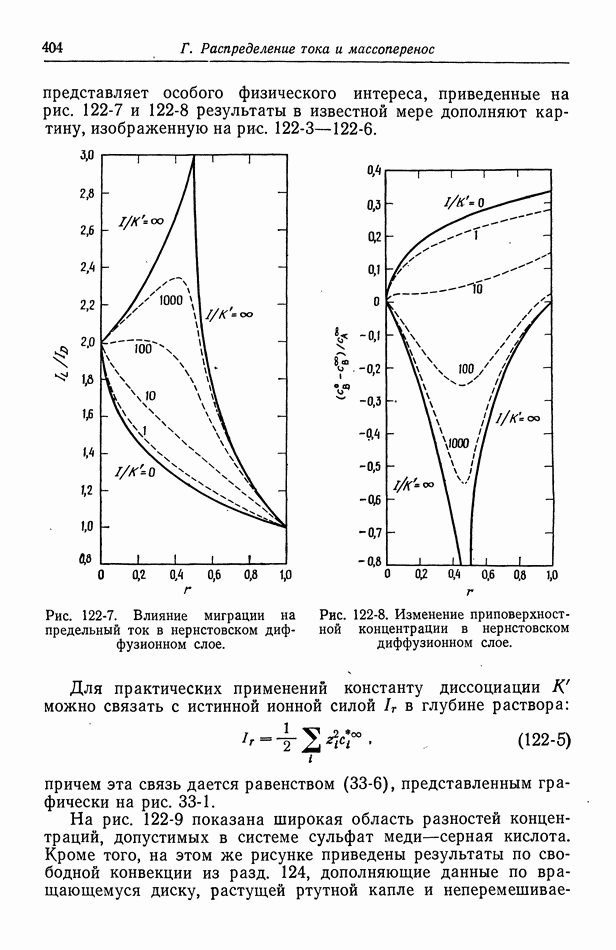
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ