| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
В гл. 17 рассматривались задачи конвективной диффузии. Большинство из них относилось к случаю предельного тока и избытка фонового электролита. Сравнительно простая задача получается и тогда, когда поддерживается предельное значение тока, а концентрация фонового электролита уменьшена по сравнению с концентрацией реагирующих ионов. Поскольку ток имеет предельное значение, омическим падением потенциала в растворе по-прежнему можно пренебречь, и распределение тока определяется массопереносом в диффузионном слое. Наличие электрического поля в диффузионном слое может привести к увеличению или уменьшению предельного тока, обусловленному. миграцией реагирующих ионов.
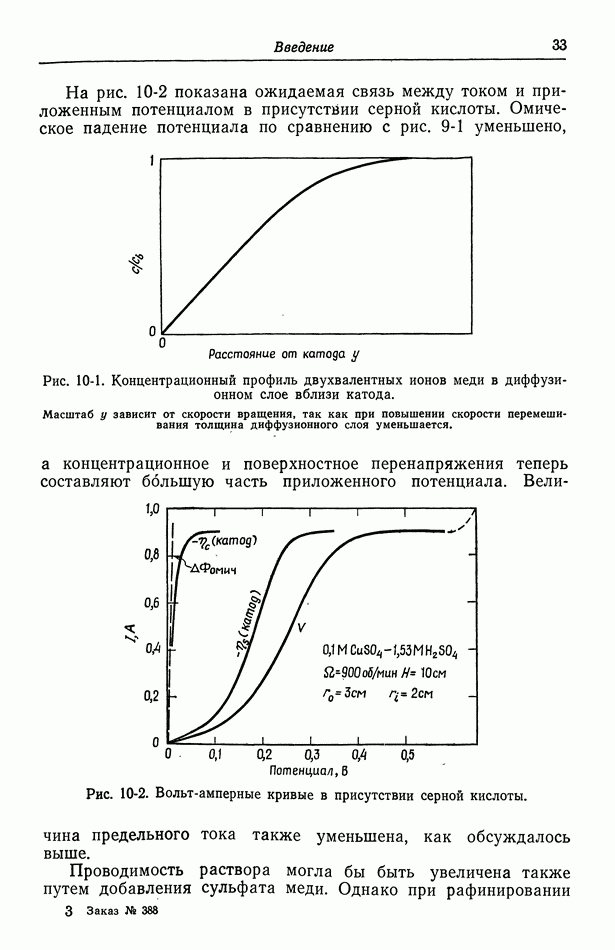
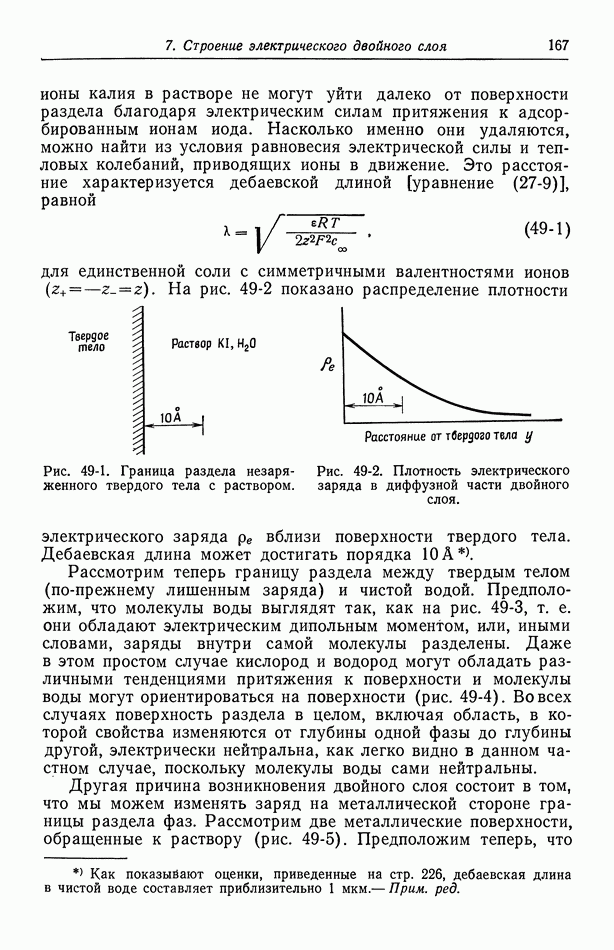
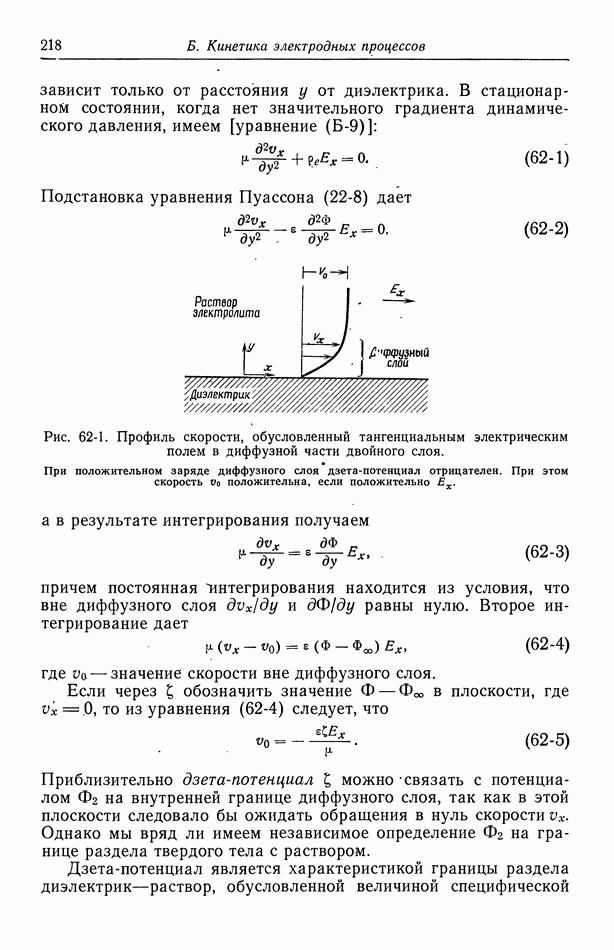
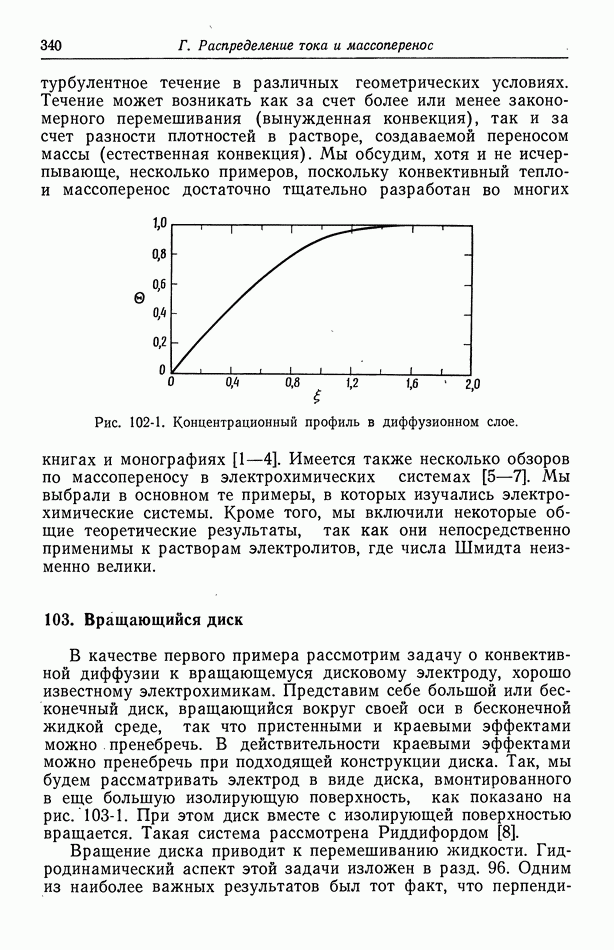
Пусть на рис. 102-1 изображен концентрационный профиль  при осаждении меди в режиме предельного тока. Внутри диффузионного слоя частицы переносятся за счет миграции и диффузии. Тогда на поверхности электрода электрическое поле велико, так как концентрация здесь равна нулю. Если добавить теперь инертный электролит, например
при осаждении меди в режиме предельного тока. Внутри диффузионного слоя частицы переносятся за счет миграции и диффузии. Тогда на поверхности электрода электрическое поле велико, так как концентрация здесь равна нулю. Если добавить теперь инертный электролит, например  то электрическое поле значительно уменьшится, особенно на поверхности электрода. Вклад миграции в перенос уменьшается, и предельный ток снижается.
то электрическое поле значительно уменьшится, особенно на поверхности электрода. Вклад миграции в перенос уменьшается, и предельный ток снижается.
Согласно условию электронейтральности (100-3), растворы, содержащие лишь два типа ионов, также удовлетворяют уравнению конвективной диффузии (102-2), в котором  заменено на коэффициент диффузии электролита
заменено на коэффициент диффузии электролита  (разд. 72). Поэтому для таких растворов задачи конвективной диффузии в случае предельного тока решаются сравнительно легко (разд. 114). Здесь предельный ток увеличивается по сравнению со случаем тех же разряжающихся ионов в растворе с избытком инертного электролита, что можно объяснить влиянием миграции в диффузионном слое.
(разд. 72). Поэтому для таких растворов задачи конвективной диффузии в случае предельного тока решаются сравнительно легко (разд. 114). Здесь предельный ток увеличивается по сравнению со случаем тех же разряжающихся ионов в растворе с избытком инертного электролита, что можно объяснить влиянием миграции в диффузионном слое.
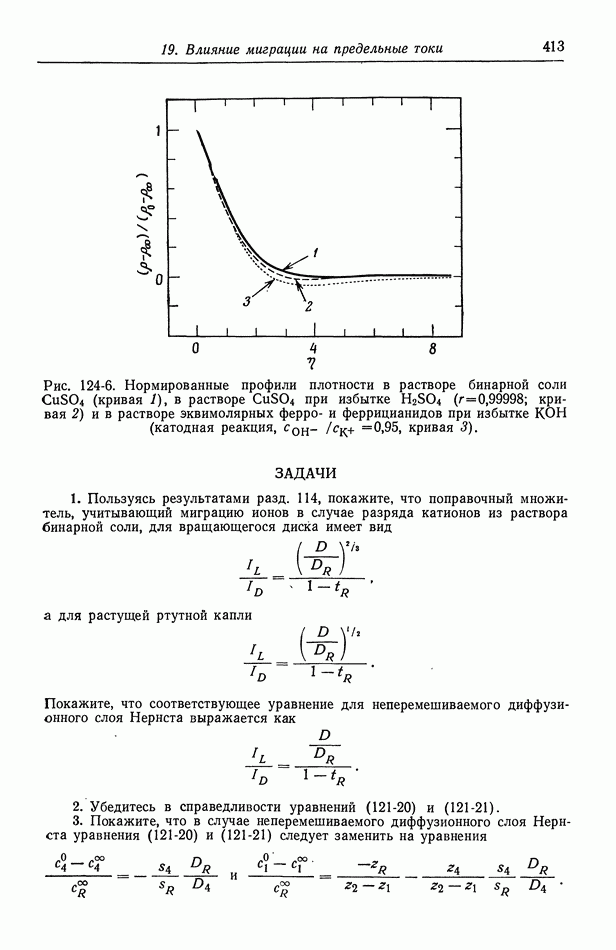
Некоторый интерес представляет расчет предельного тока в промежуточных случаях, когда инертный электролит присутствует не в избыточном количестве. Эта задача была решена Эйкеном [1] для случая ионов трех типов в системах, которые можно представлять с помощью неперемешиваемого диффузионного слоя Нернста (см. также работу [2]). Поскольку экспериментальные данные [3] по разряду ионов водорода на растущей ртутной капле не описывались формулой Эйкена, Гейровский [4] отказался от его метода и ввел поправочный множитель, содержащий число переноса разряжающегося иона. Эта поправка утвердилась в электрохимической литературе, хотя она и не имела количественного обоснования.
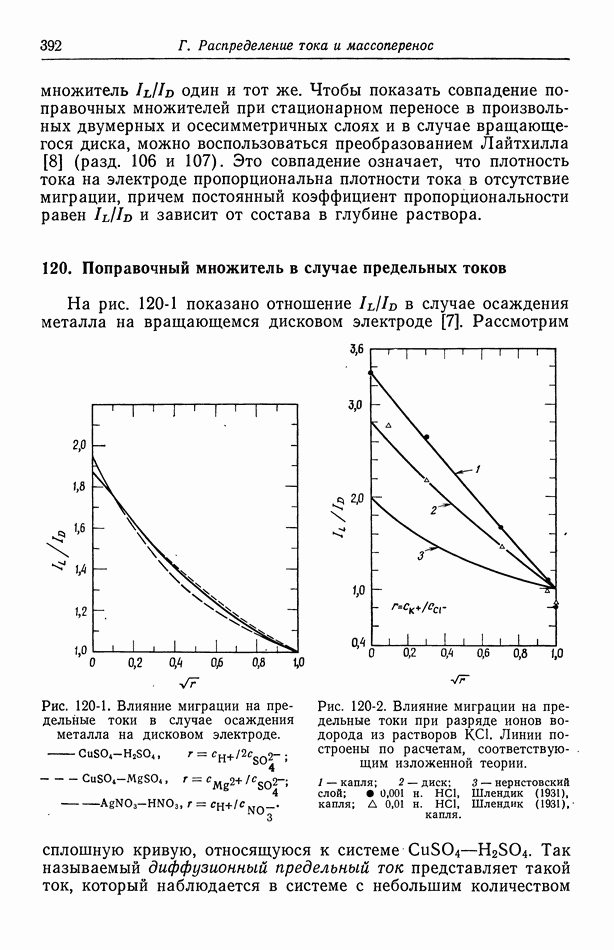
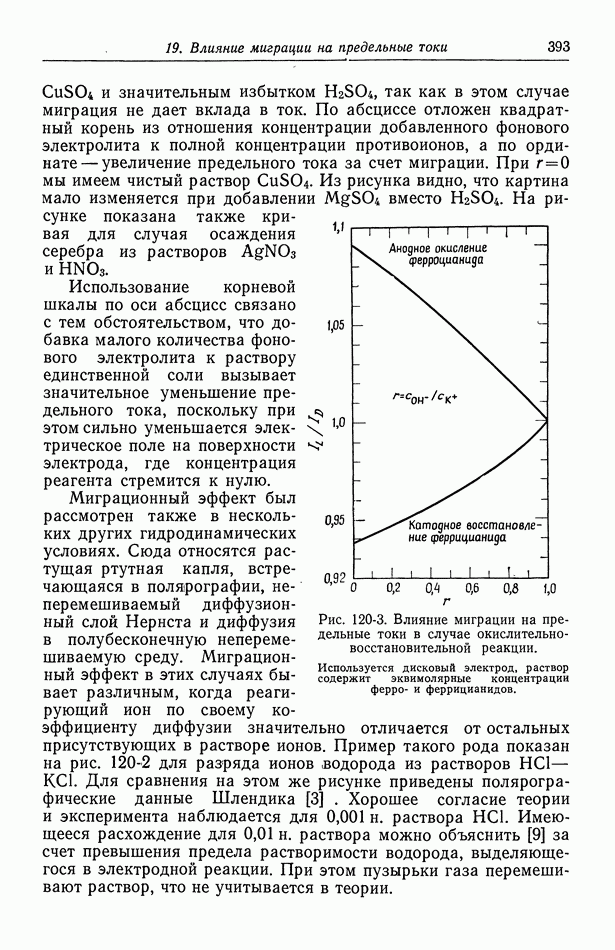
Окада и др. [5] рассмотрели влияние ионной миграции на предельные токи в случае растущей ртутной капли, а Гордон и др. [6] — в случае вращающегося дискового электрода. Ньюмен [7] изучил этот эффект для четырех случаев: вращающегося диска, растущей ртутной капли, диффузии в полубесконечную среду и неперемешиваемого диффузионного слоя Нернста. Удобной мерой влияния миграции служит отношение предельного тока к предельному диффузионному току  рассчитанное в гл. 17 в задачах о конвективной диффузии при избытке фонового электролита. Эта величина зависит от отношения концентраций в глубине раствора.
рассчитанное в гл. 17 в задачах о конвективной диффузии при избытке фонового электролита. Эта величина зависит от отношения концентраций в глубине раствора.
Влияние миграции на предельный ток — явление, не имеющее аналогии в неэлектролитических системах, в противоположность задачам конвективной диффузии, во многом аналогичным переносу тепла и массопереносу в неэлектролитических системах.
119. Решение задачи
В случае вращающегося диска нормальная составляющая скорости зависит лишь от расстояния до поверхности диска у (разд. 96). Следовательно,  диффузионном слое также зависят только от у, а предельная плотность тока однородна по всей поверхности диска. Объединяя равенства (100-1) и (100-2), получаем
диффузионном слое также зависят только от у, а предельная плотность тока однородна по всей поверхности диска. Объединяя равенства (100-1) и (100-2), получаем

Далее, представим скорость с помощью первого члена ее разложения в ряд по степеням у:

где  Это приближение справедливо в диффузионном
Это приближение справедливо в диффузионном
слое при больших числах Шмидта. Вводя новую переменную

где  коэффициент диффузии скорость-определяющего реагента, перепишем уравнение (119-1) в виде
коэффициент диффузии скорость-определяющего реагента, перепишем уравнение (119-1) в виде

Здесь штрихи обозначают дифференцирование по 
Для каждого типа растворенных компонентов имеется уравнение вида (119-4). Эти уравнения следует решать относительно концентраций  и потенциала
и потенциала  вместе с условием электронейтральности (100-3).
вместе с условием электронейтральности (100-3).
В качестве граничных условий можно записать

где точку обращения потенциала в нуль,  можно выбирать произвольно. Пусть электродная реакция описывается уравнением (101-1). Тогда нормальные составляющие потока компонентов на электроде и плотности тока связаны равенством (101-2). Поскольку плотность тока заранее не известна, вместо этого равенства мы воспользуемся соотношением между потоком компонентов и потоком скорость определяющего реагента:
можно выбирать произвольно. Пусть электродная реакция описывается уравнением (101-1). Тогда нормальные составляющие потока компонентов на электроде и плотности тока связаны равенством (101-2). Поскольку плотность тока заранее не известна, вместо этого равенства мы воспользуемся соотношением между потоком компонентов и потоком скорость определяющего реагента:

в котором  Записывая соотношение (119-6) через переменную
Записывая соотношение (119-6) через переменную  получим
получим

Граничное условие для скорость определяющего реагента при установлении предельного тока имеет вид

Этих граничных условий достаточно для решения данной задачи. Равенства (119-4) и (100-3) составляют систему нелинейных обыкновенных дифференциальных уравнений с граничными условиями в нуле и на бесконечности. Такие уравнения легко решаются с помощью численного метода, изложенного в приложении В. Получаемые при этом результаты обсуждаются в следующих разделах. После вычисления профилей концентрации и потенциала предельную плотность тока можно найти по потоку скорость определяющего реагента, причем удобной
мерой влияния миграции является отношение предельного тока к предельному диффузионному току 
В данном случае влияние миграции примерно такое же, как и в других гидродинамических условиях. Для ртутной капли, растущей в растворе с первоначально однородным составом, уравнения переноса в переходном режиме можно свести к уравнению

если воспользоваться теми же приближениями, что и при выводе уравнения Ильковича (110-2), не содержащего поправочного члена. Уравнение (119-9) играет здесь ту же роль, что и уравнение (119-4)  вращающегося диска. В случае ртутной капли, растущей с постоянной объемной скоростью, величина
вращающегося диска. В случае ртутной капли, растущей с постоянной объемной скоростью, величина  определена следующим образом:
определена следующим образом:

хотя наш анализ и не ограничивается этим случаем.
Для плоского электрода в бесконечной неперемешиваемой среде уравнения переноса также сводятся, к уравнению (119-9), где  теперь определено несколько иначе:
теперь определено несколько иначе:

При стационарном переносе в неперемешиваемом диффузионном слое Нернста уравнения переноса можно записать в виде

где

и  толщина диффузионного слоя.
толщина диффузионного слоя.
Эти случаи весьма похожи друг на друга, и в каждом из них можно использовать одну и ту же вычислительную программу. Это обстоятельство обусловлено, в частности, тем, что в режиме предельного тока граничные условия (119-5), (119-7) и (119-8) имеют место во всех случаях, за исключением того, что условие (119-5) записано для точки  диффузионного слоя Нернста.
диффузионного слоя Нернста.
Поскольку математическая постановка задач о растущей ртутной капле и диффузии в бесконечную неперемешиваемую среду одинакова, для обоих этих процессов поправочный
множитель  один и тот же. Чтобы показать совпадение поправочных множителей при стационарном переносе в произвольных двумерных и осесимметричных слоях и в случае вращающегося диска, можно воспользоваться преобразованием Лайтхилла [8] (разд. 106 и 107). Это совпадение означает, что плотность тока на электроде пропорциональна плотности тока в отсутствие миграции, причем постоянный коэффициент пропорциональности равен
один и тот же. Чтобы показать совпадение поправочных множителей при стационарном переносе в произвольных двумерных и осесимметричных слоях и в случае вращающегося диска, можно воспользоваться преобразованием Лайтхилла [8] (разд. 106 и 107). Это совпадение означает, что плотность тока на электроде пропорциональна плотности тока в отсутствие миграции, причем постоянный коэффициент пропорциональности равен  и зависит от состава в глубине раствора.
и зависит от состава в глубине раствора.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
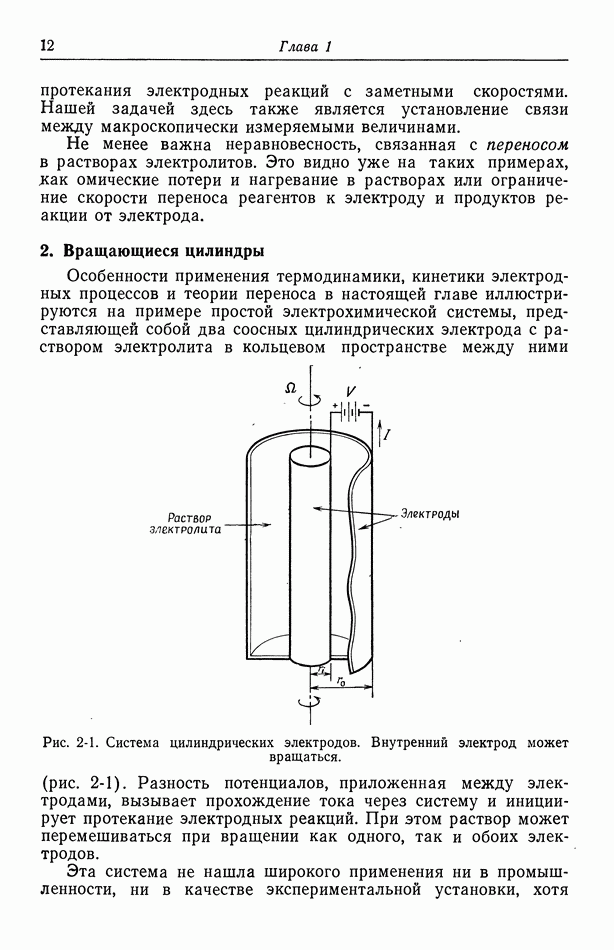
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
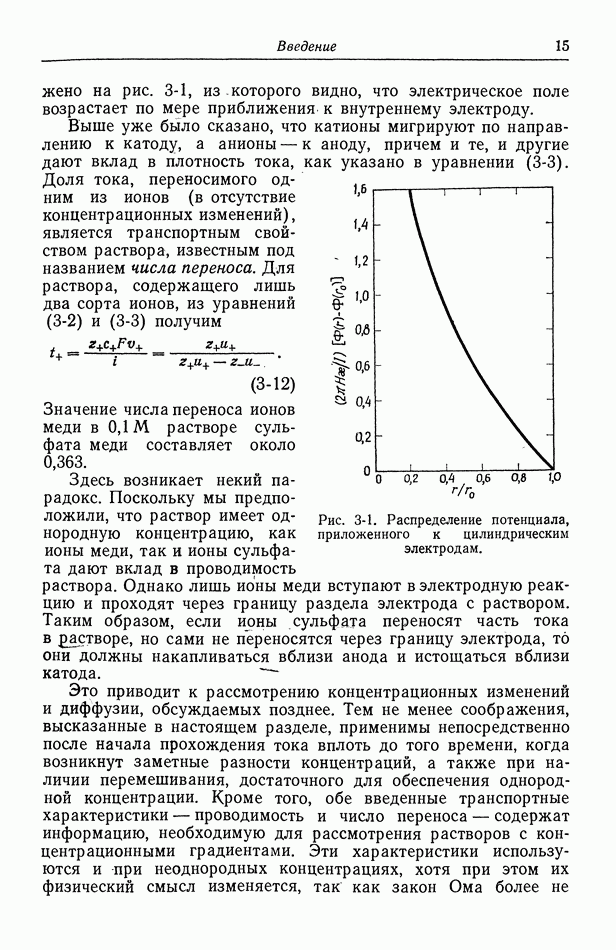
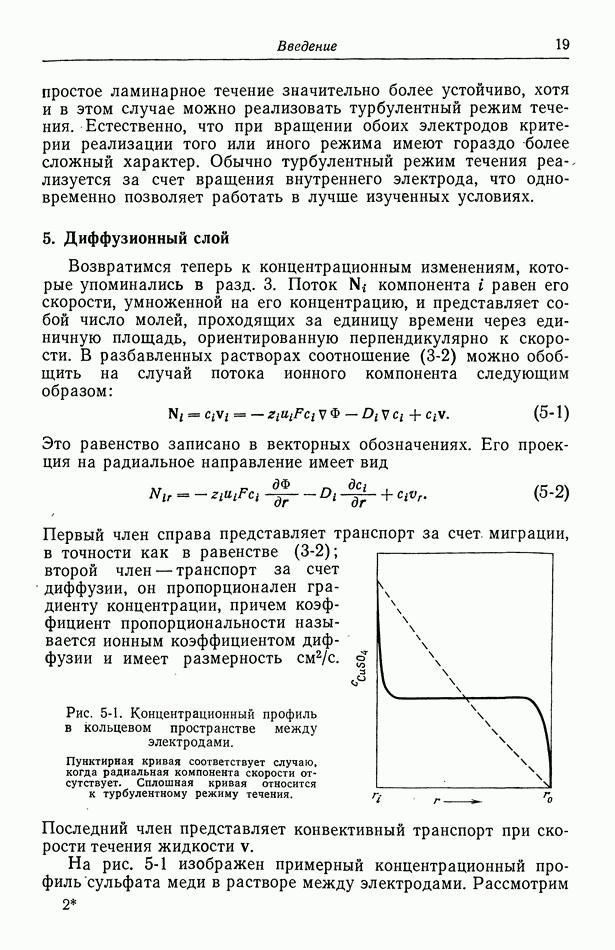
- 5. Диффузионный слой
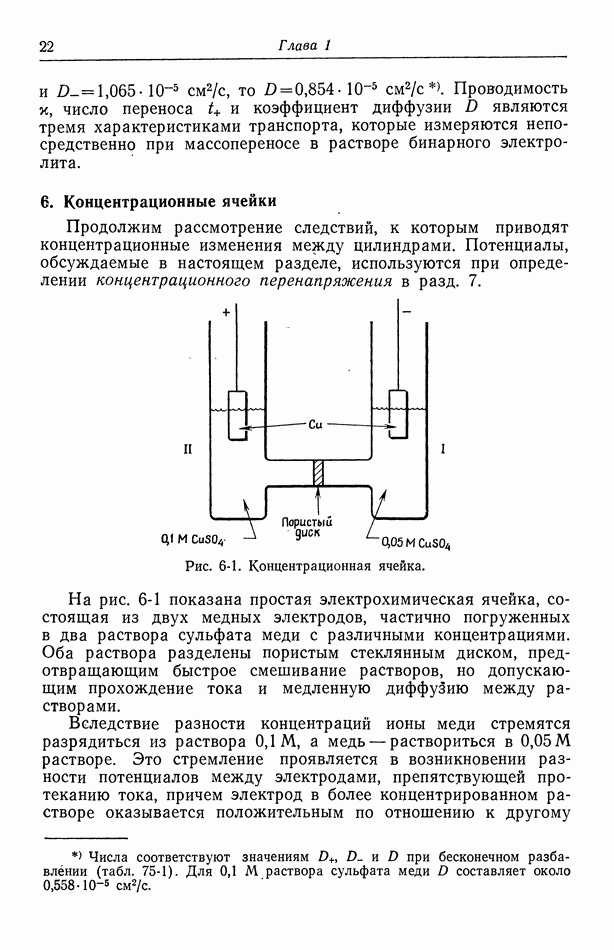
- 6. Концентрационные ячейки
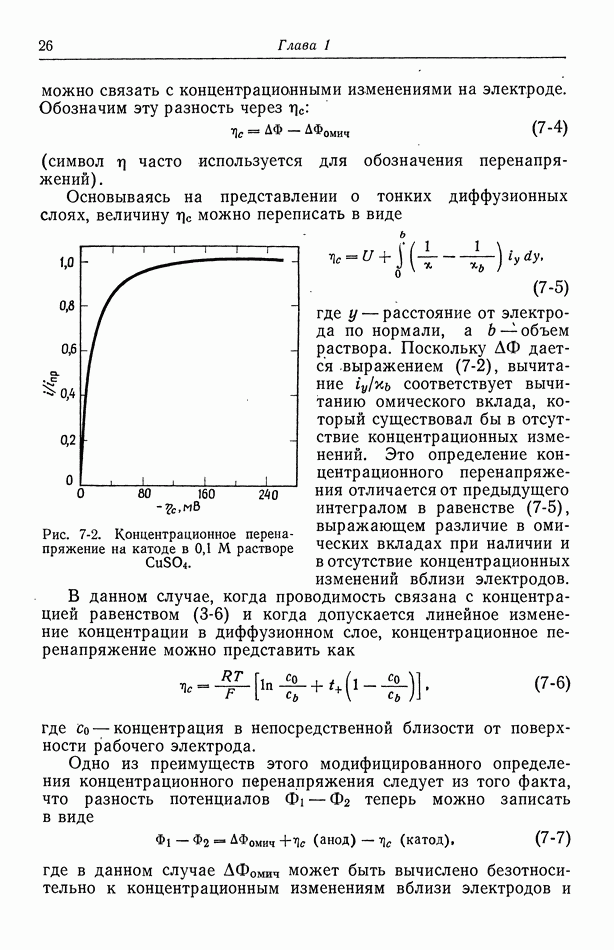
- 7. Концентрационное перенапряжение
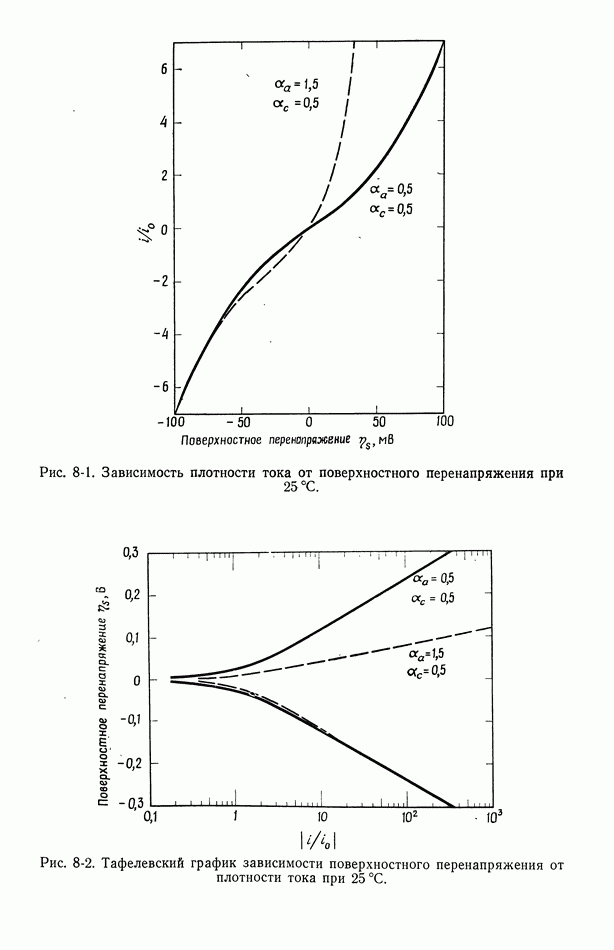
- 8. Поверхностное перенапряжение
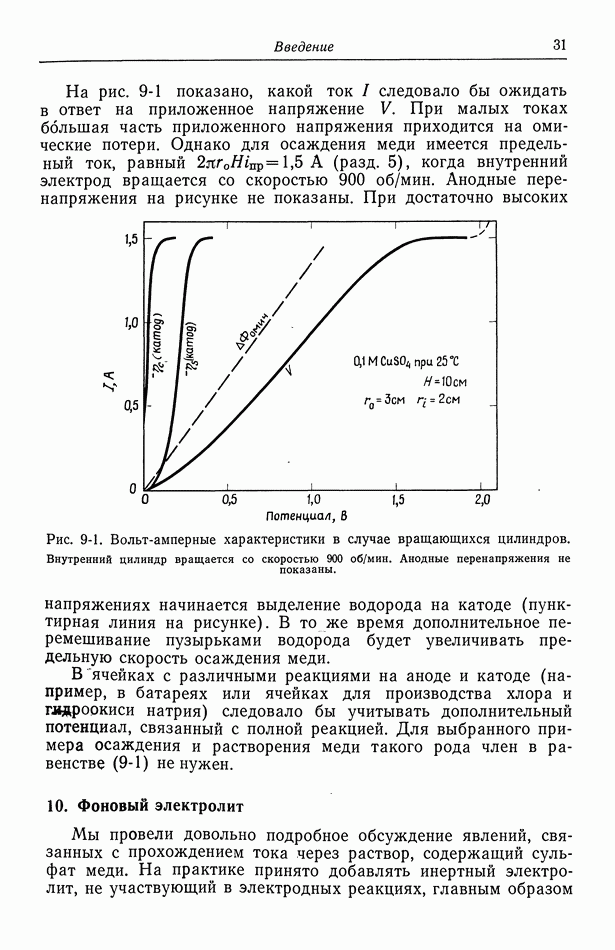
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
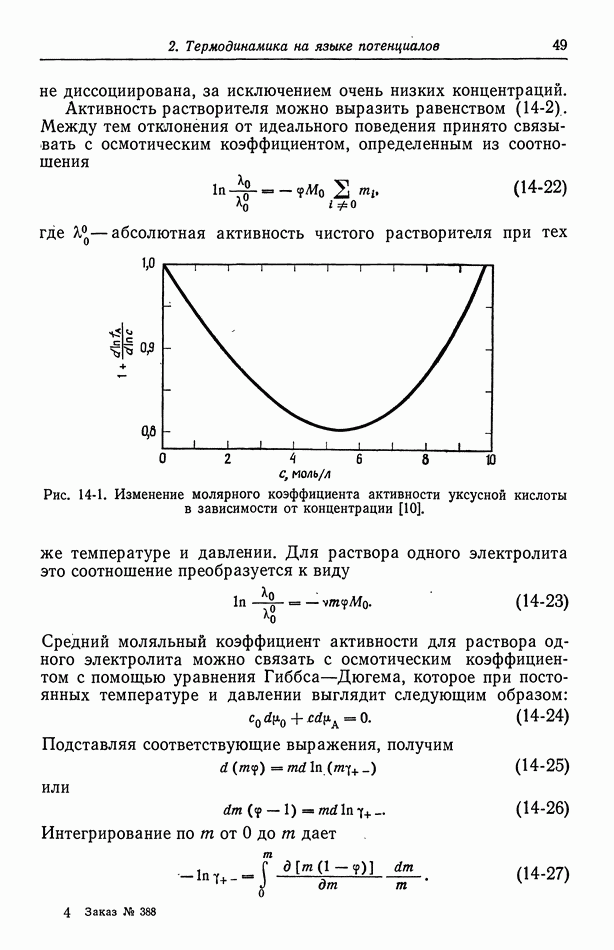
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
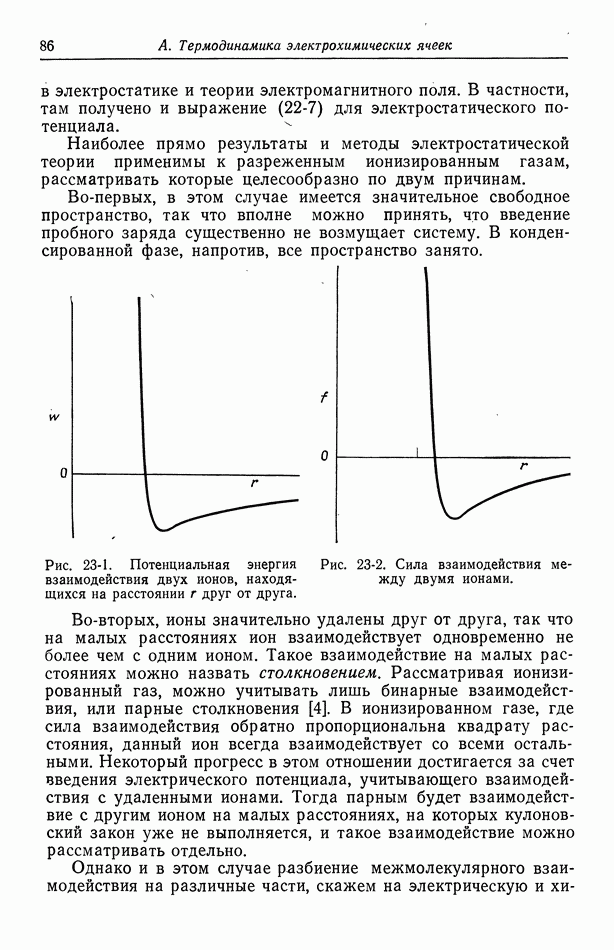
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
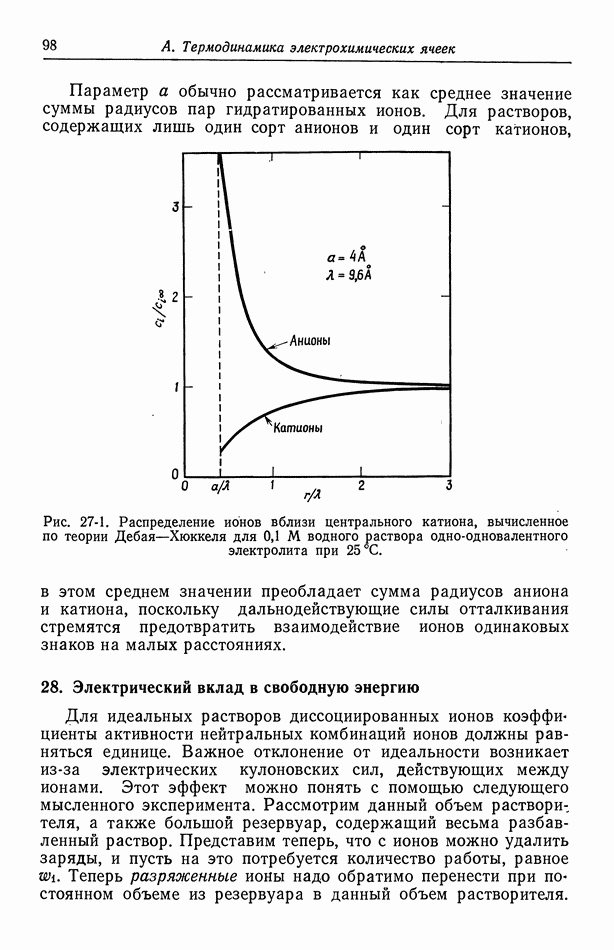
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
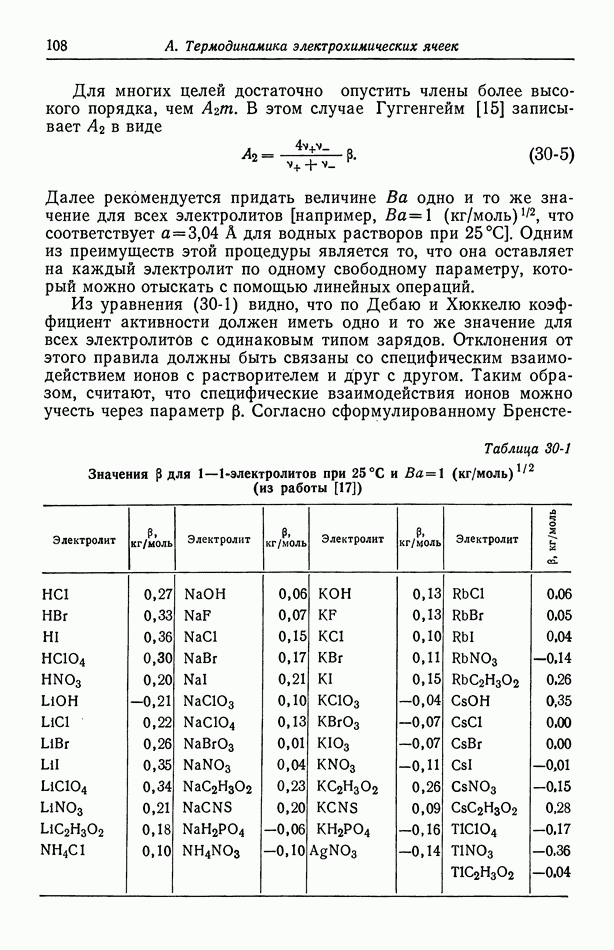
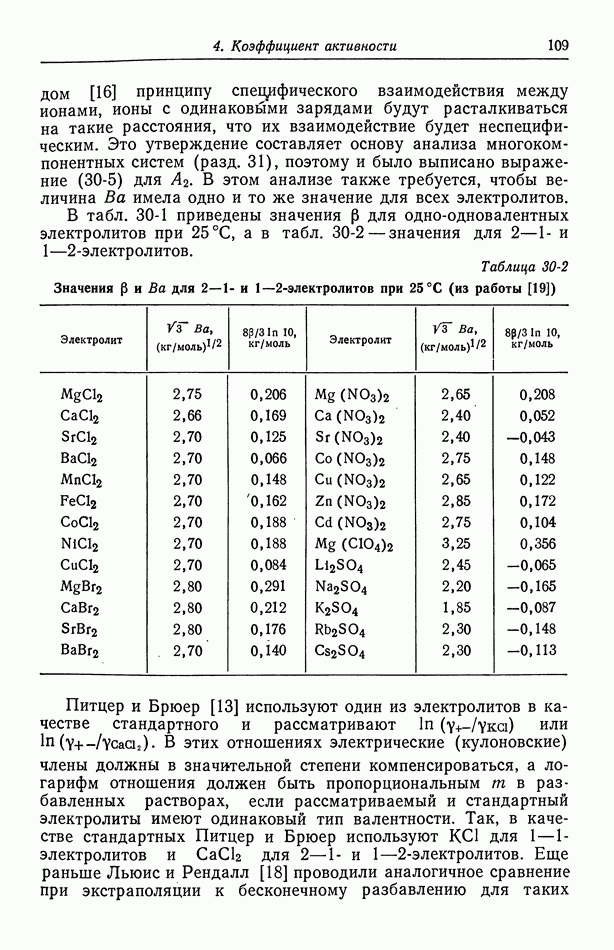
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
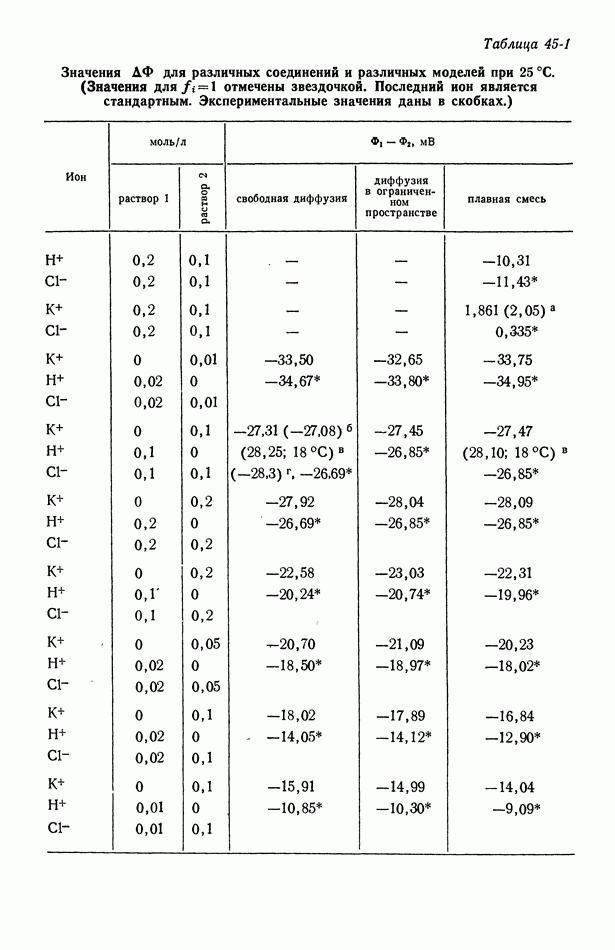
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
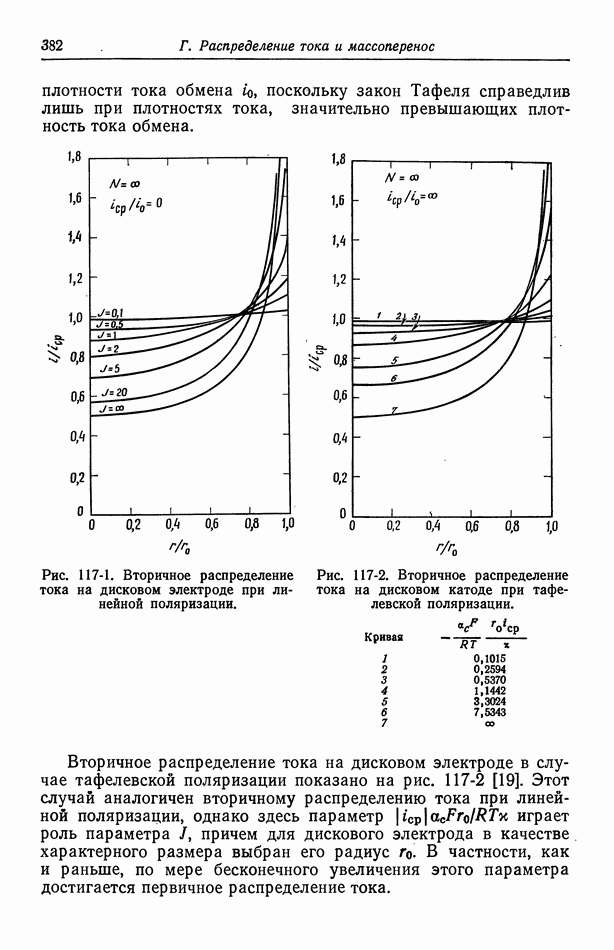
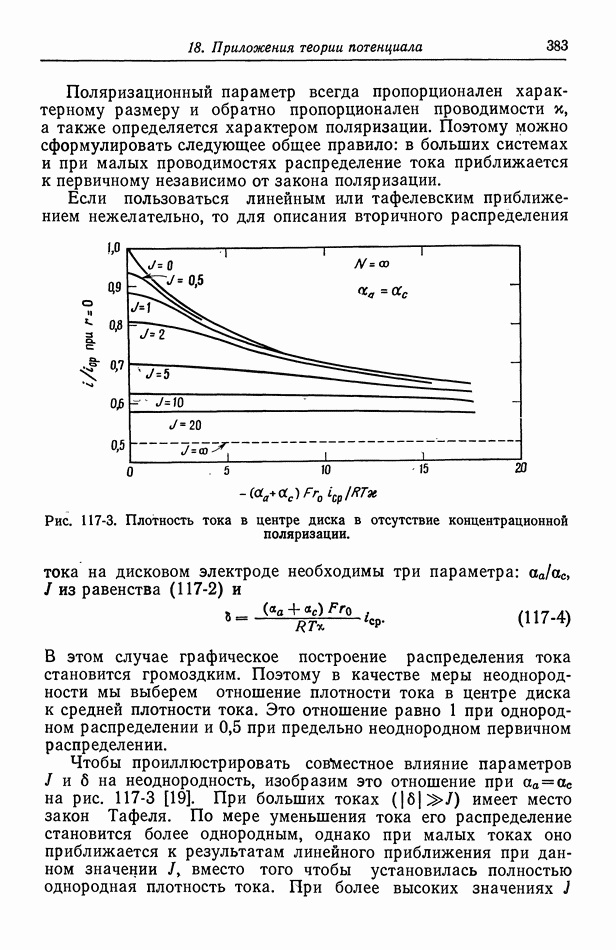
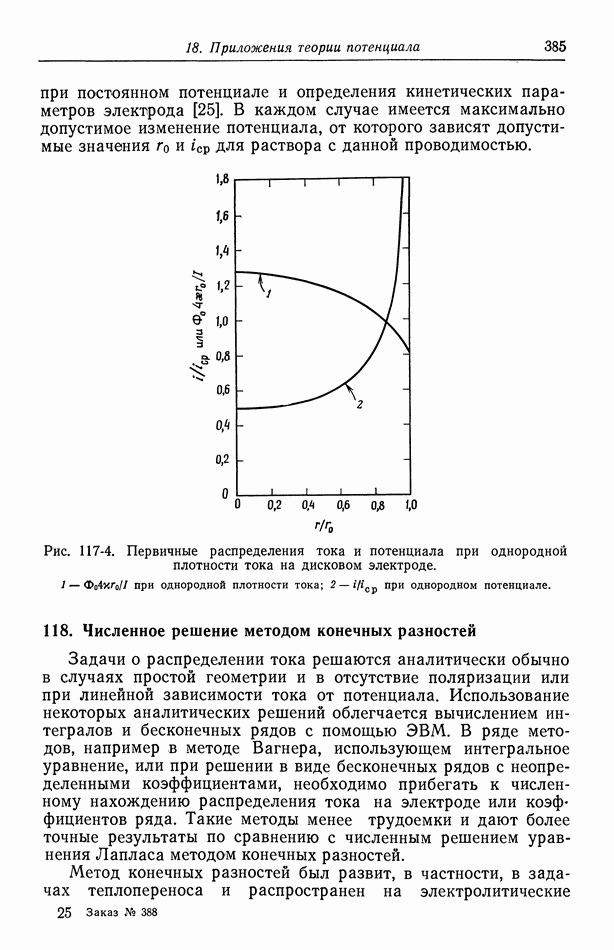
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
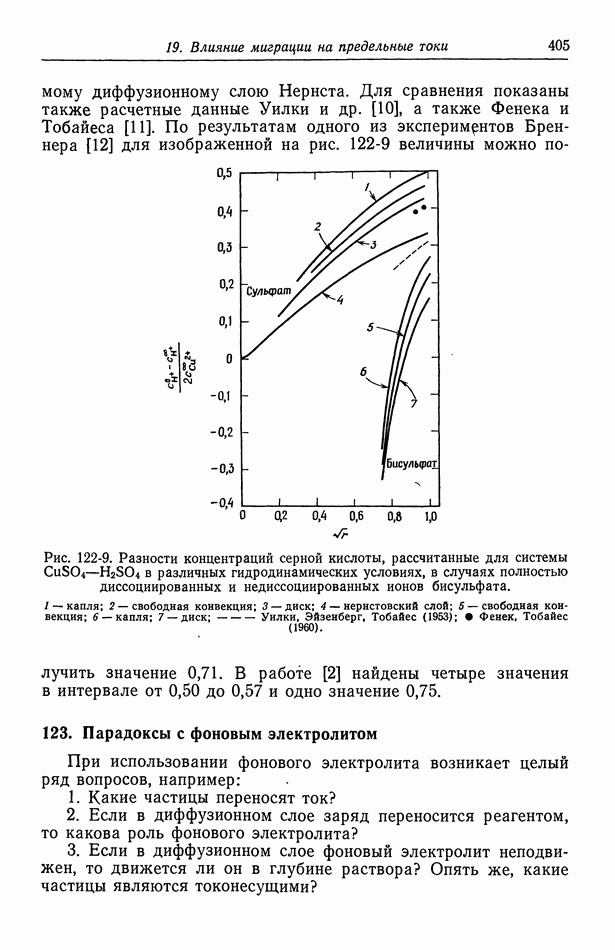
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
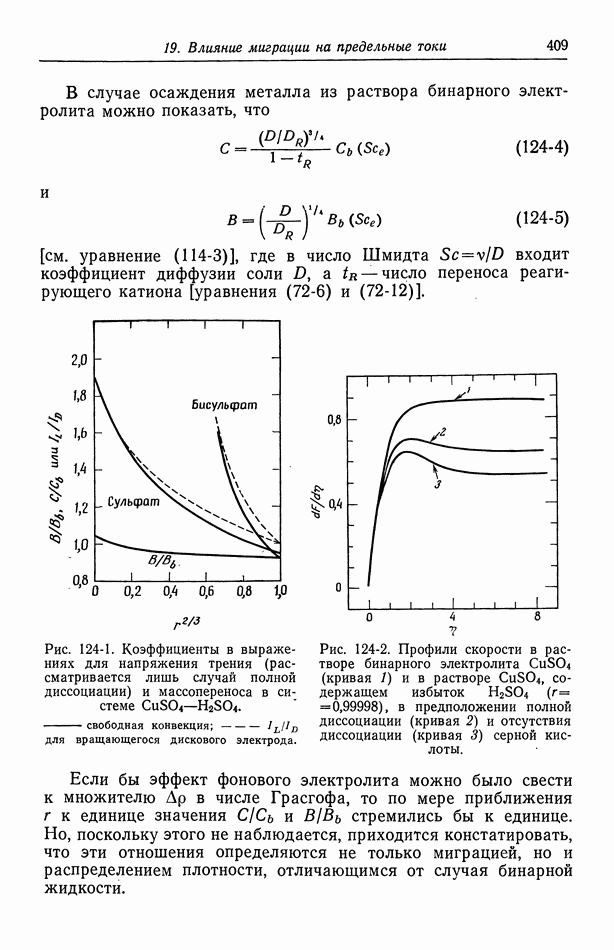
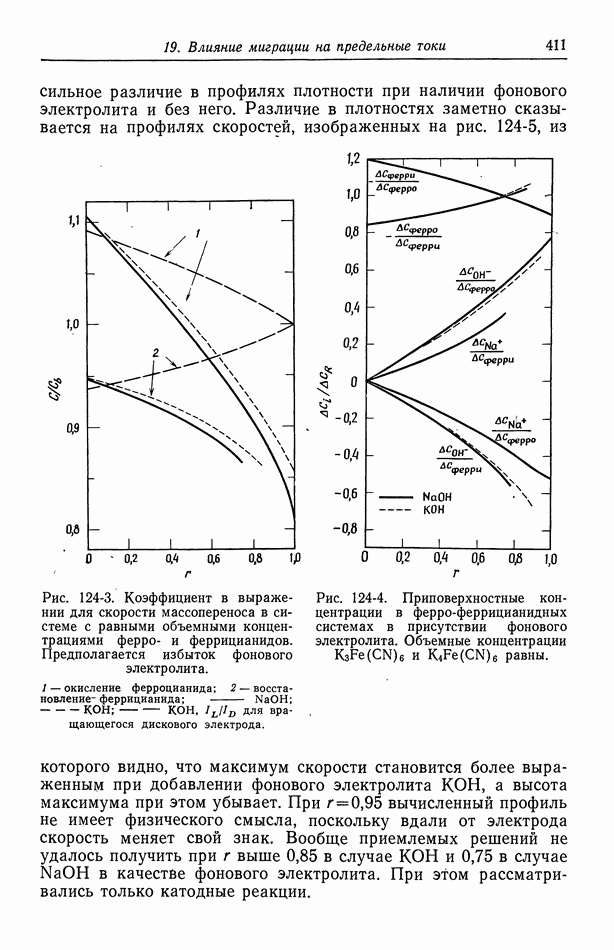
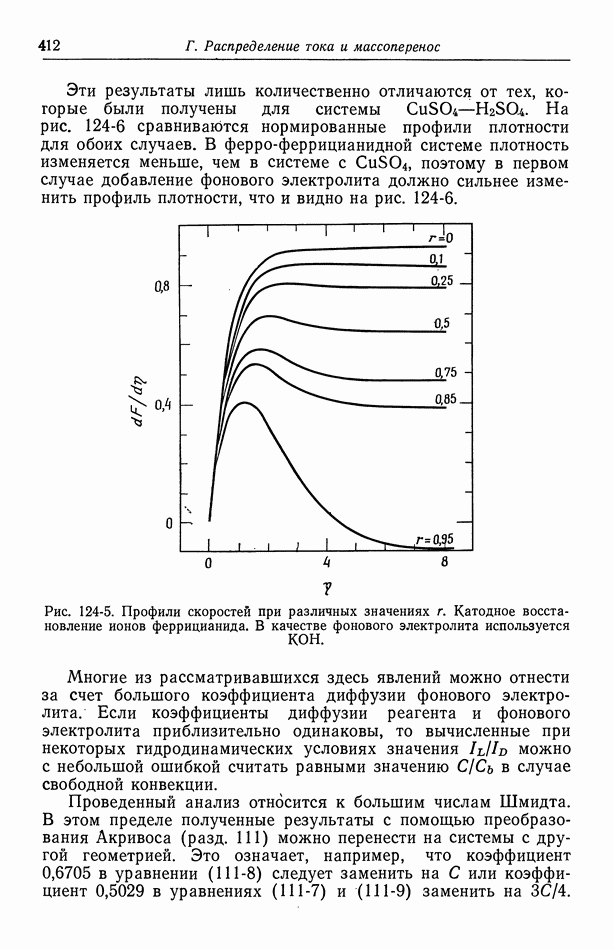
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ