| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
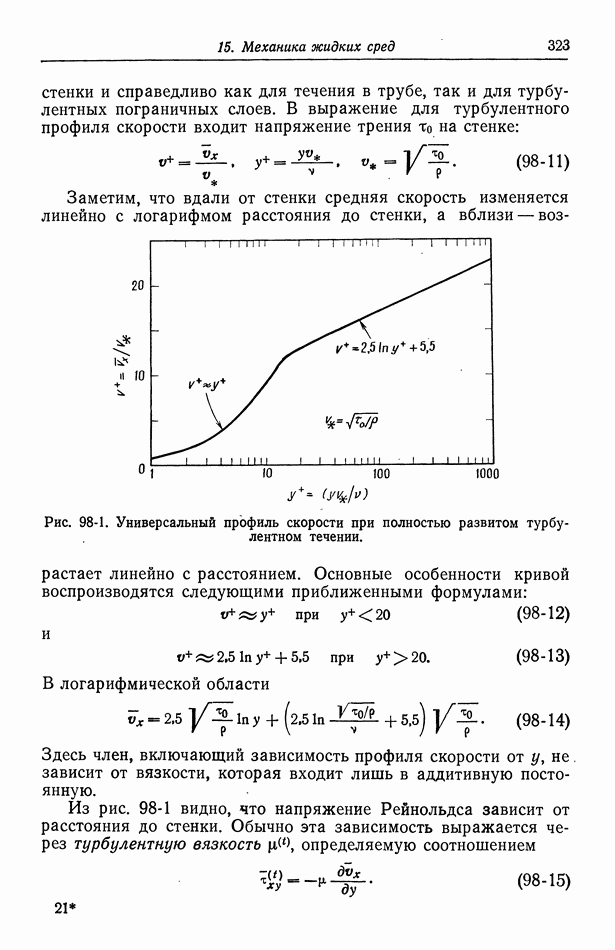
117. Вторичное распределение тока
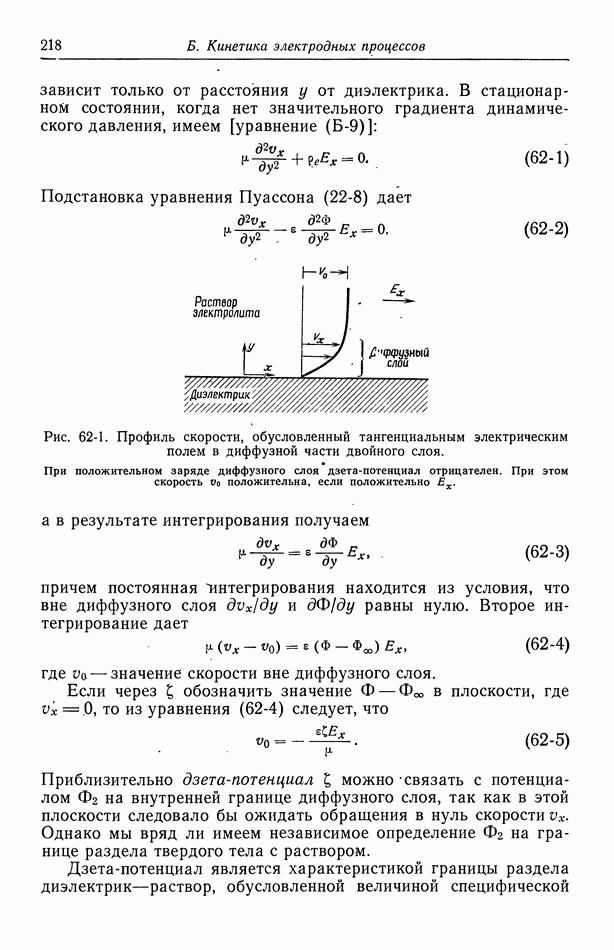
Если рассматривать случай замедленной электродной реакции, то раствор электролита вблизи электрода больше нельзя считать эквипотенциальным, и в результате вычислений получается так называемое вторичное распределение тока. Влияние электродной поляризации в общем случае сводится к сглаживанию первичного распределения тока и, в частности, к устранению бесконечной плотности тока на краях электрода. Это можно рассматривать как результат включения дополнительного сопротивления на поверхности электрода. Математически задача сводится к решению уравнения Лапласа с более сложными, быть может даже нелинейными, граничными условиями.
Для электродной поляризации использовался большой набор различных математических выражений, что обусловлено как разнообразием кинетики электродных процессов, так и различием используемых приближений. На практике кинетическое уравнение часто заменяют на линейное или логарифмическое (тафелевское) соотношение между поверхностным перенапряжением и производной потенциала на электроде. Во всяком случае, для отыскания распределения тока требуются, помимо геометрических, и другие параметры. Преимущество линейного или логарифмического приближения состоит в том, что оно вносит лишь один новый параметр. Таким образом, достаточно близкие к реальности ситуации можно рассматривать без излишних усложнений.
При достаточно малых поверхностных перенапряжениях уравнение (101-4) можно линеаризовать, в результате чего получается

Это равенство служит краевым условием для уравнения Лапласа; оно нередко встречалось в литературе, поскольку возникающую при этйм линейную краевую задачу часто удается решить. Кроме того, если область плотностей тока на электроде достаточно узка, что существенно в гальваностегии, то
вполне оправдана линеаризация поляризационного уравнения вблизи некоторого ненулевого значения перенапряжения. Наконец, в случае линейной поляризации число параметров, необходимых для отыскания распределения тока, сведено до минимума. Это позволяет построить семейство кривых, представляющих распределение тока в случае системы с определенной геометрией.
Вторичное распределение тока  зависит от тех же отношений геометрических параметров, что и первичное распределение, а также, в случае линейной поляризации, еще и от параметра
зависит от тех же отношений геометрических параметров, что и первичное распределение, а также, в случае линейной поляризации, еще и от параметра  где
где  характерный размер системы. С помощью этого параметра Хоар и Агар [18] описывали влияние сопротивления электролита, поляризации и размера ячейки на распределение тока. Если поляризуются оба электрода, то имеется два таких параметра, в которые входят наклоны поляризационных кривых как на катоде, так и на аноде.
характерный размер системы. С помощью этого параметра Хоар и Агар [18] описывали влияние сопротивления электролита, поляризации и размера ячейки на распределение тока. Если поляризуются оба электрода, то имеется два таких параметра, в которые входят наклоны поляризационных кривых как на катоде, так и на аноде.
Для дискового электрода при линейной поляризации дополнительным параметром служит [19]

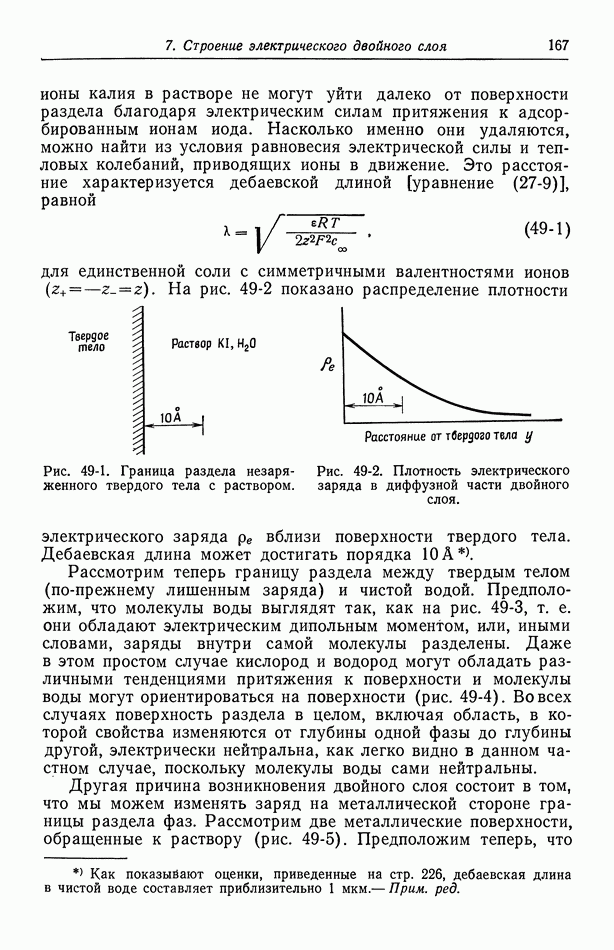
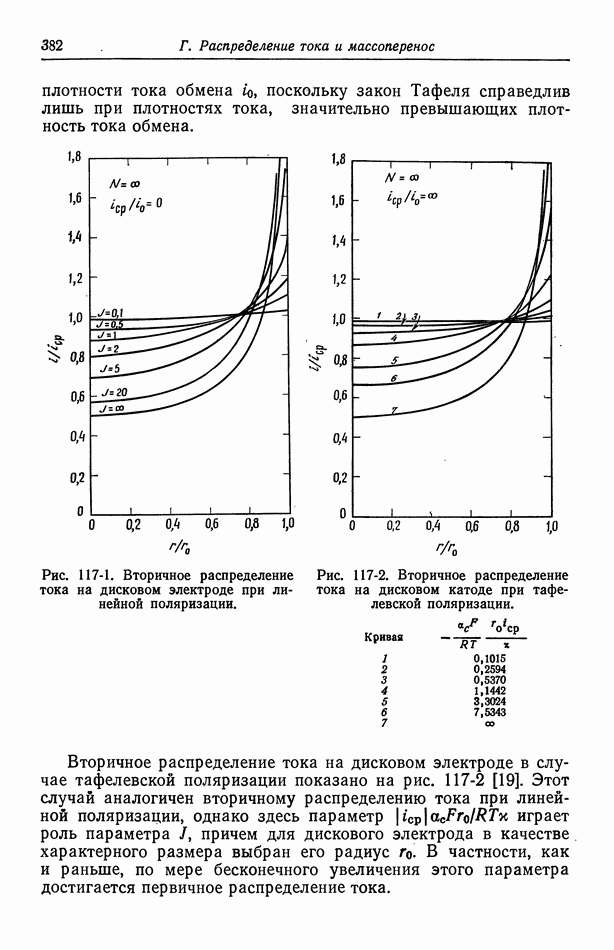
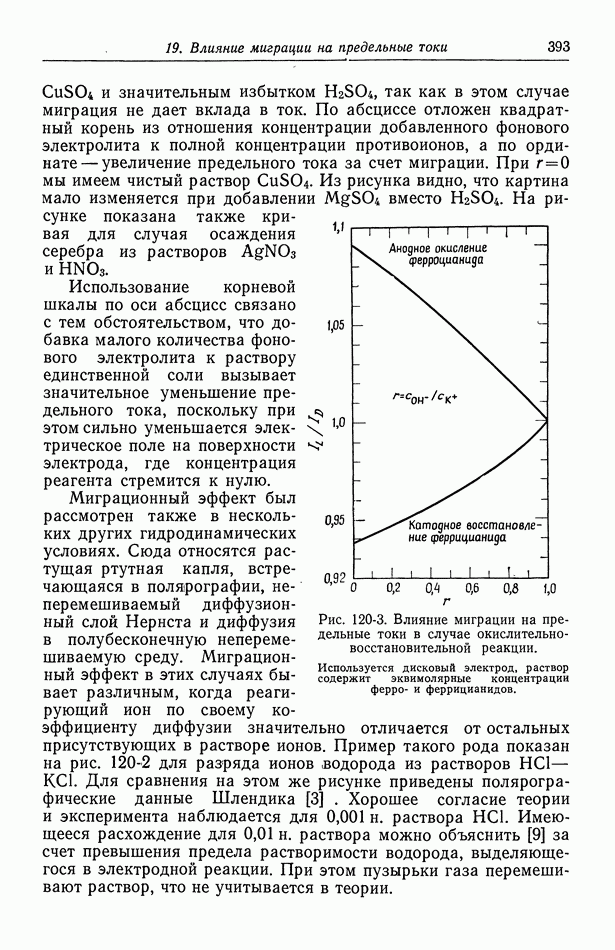
Вторичное распределение тока на дисковом электроде при линейной поляризации показано на рис. 117-1, где  означает такую большую скорость вращения, что изменениями концентрации можно пренебречь.
означает такую большую скорость вращения, что изменениями концентрации можно пренебречь.
При  получается первичное распределение тока. В этом случае омическое сопротивление преобладает над кинетическим сопротивлением границы раздела. При любом конечном значении
получается первичное распределение тока. В этом случае омическое сопротивление преобладает над кинетическим сопротивлением границы раздела. При любом конечном значении  распределение более однородно, и на краях диска плотность тока конечна. При
распределение более однородно, и на краях диска плотность тока конечна. При  распределение становится однородным, однако, чтобы линейный закон по-прежнему сохранял силу, средний ток должен быть малым. За исключением этого случая, распределение тока
распределение становится однородным, однако, чтобы линейный закон по-прежнему сохранял силу, средний ток должен быть малым. За исключением этого случая, распределение тока  не зависит от величины тока.
не зависит от величины тока.
В литературе часто встречается также закон Тафеля, когда в уравнении (101-4) один из экспоненциальных членов пренебрежимо мал. Для катодной реакции имеем

Помимо того что закон Тафеля описывает случай вполне реальной поляризации, его привлекательность состоит еще и в том, что этот закон вносит в задачу минимум дополнительных параметров. Кроме зависимости от тех же геометрических отношений, что и первичное распределение тока, величина  теперь зависит от параметра
теперь зависит от параметра  Соответственно распределение тока зависит от величины тока, но не зависит от величины
Соответственно распределение тока зависит от величины тока, но не зависит от величины
плотности тока обмена  поскольку закон Тафеля справедлив лишь при плотностях тока, значительно превышающих плотность тока обмена.
поскольку закон Тафеля справедлив лишь при плотностях тока, значительно превышающих плотность тока обмена.

Рис. 117-1. Вторичное распределение тока на дисковом электроде при линейной поляризации.

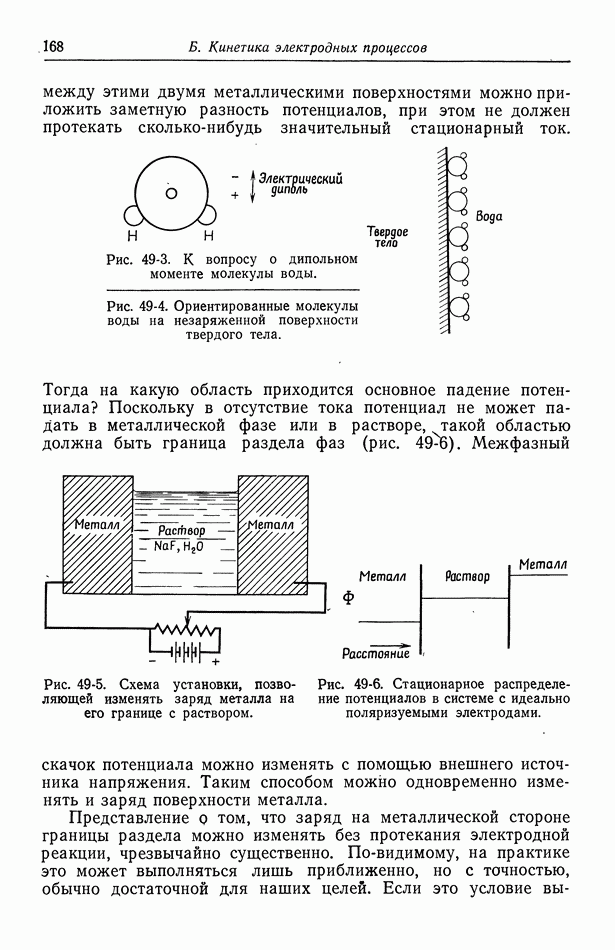
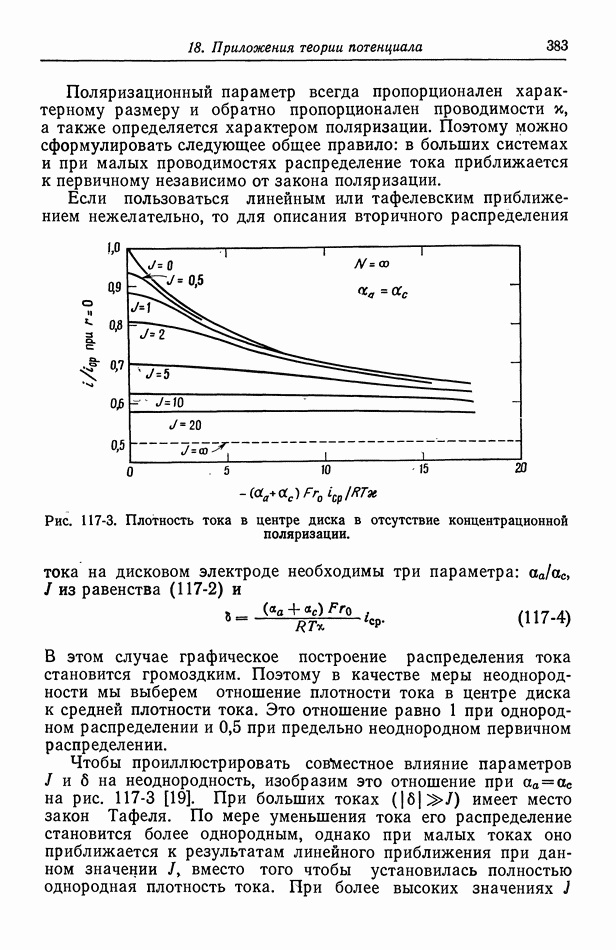
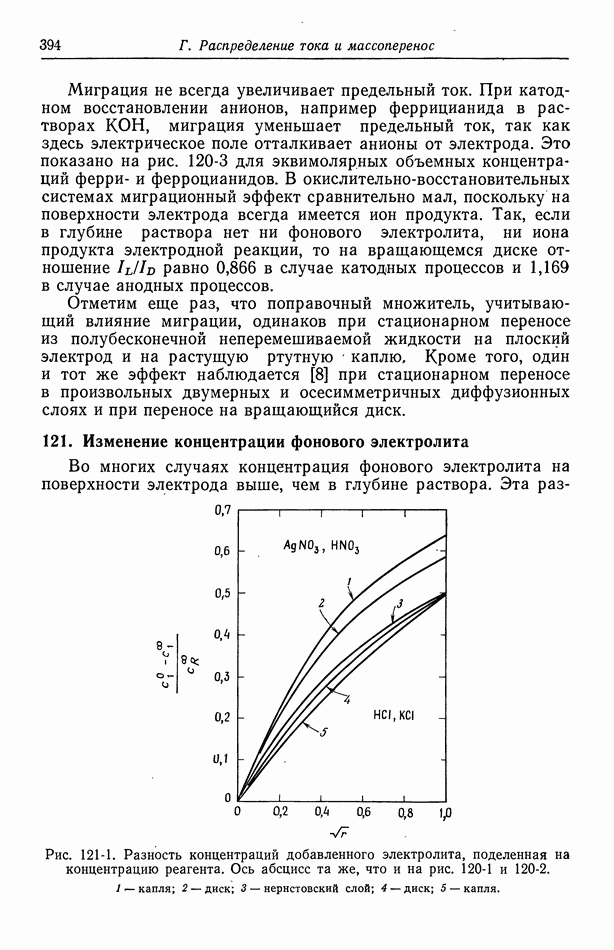
Рис. 117-2. Вторичное распределение тока на дисковом катоде при тафелевской поляризации. 
Вторичное распределение тока на дисковом электроде в случае тафелевской поляризации показано на рис. 117-2 [19]. Этот случай аналогичен вторичному распределению тока при линейной поляризации, однако здесь параметр  играет роль параметра
играет роль параметра  причем для дискового электрода в качестве характерного размера выбран его радиус
причем для дискового электрода в качестве характерного размера выбран его радиус  В частности, как и раньше, по мере бесконечного увеличения этого параметра достигается первичное распределение тока.
В частности, как и раньше, по мере бесконечного увеличения этого параметра достигается первичное распределение тока.
Поляризационный параметр всегда пропорционален характерному размеру и обратно пропорционален проводимости х, а также определяется характером поляризации. Поэтому можно сформулировать следующее общее правило: в больших системах и при малых проводимостях распределение тока приближается к первичному независимо от закона поляризации.
Если пользоваться линейным или тафелевским приближением нежелательно, то для описания вторичного распределения тока на дисковом электроде необходимы три параметра:  из равенства (117-2) и
из равенства (117-2) и


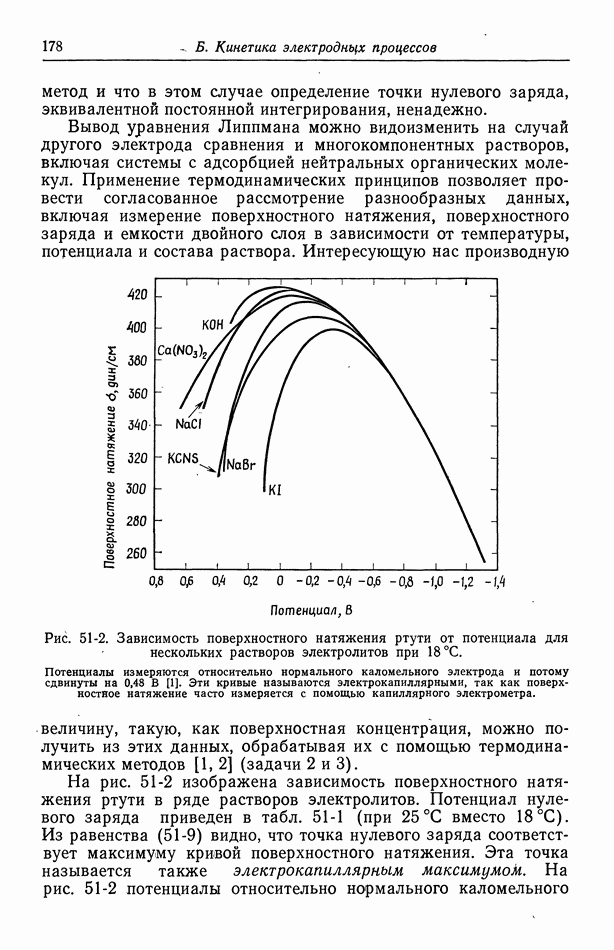
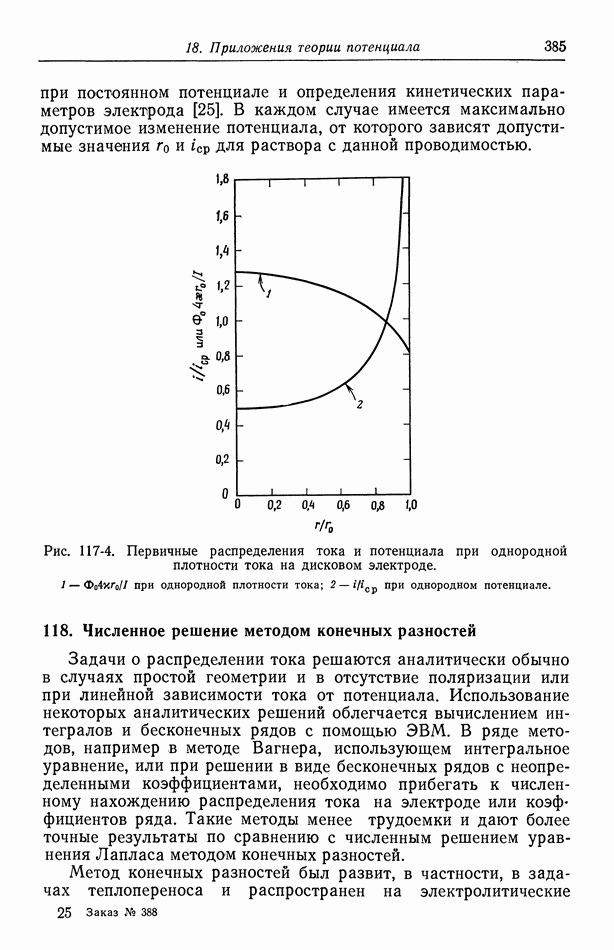
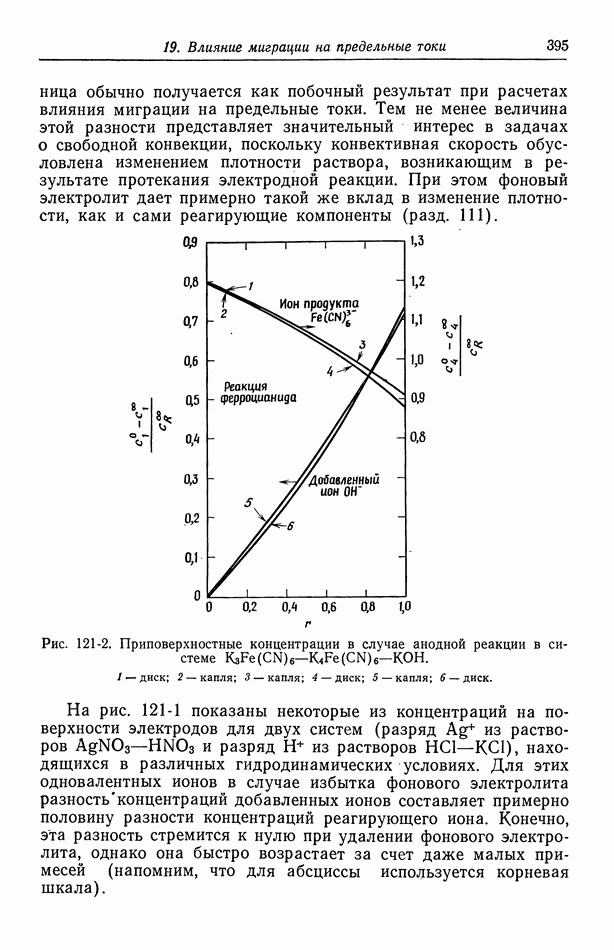
Рис. 117-3. Плотность тока в центре диска в отсутствие концентрационной поляризации.
В этом случае графическое построение распределения тока становится громоздким. Поэтому в качестве меры неоднородности мы выберем отношение плотности тока в центре диска к средней плотности тока. Это отношение равно 1 при однородном распределении и 0,5 при предельно неоднородном первичном распределении.
Чтобы проиллюстрировать совместное влияние параметров  на неоднородность, изобразим это отношение при
на неоднородность, изобразим это отношение при  на рис. 117-3 [19]. При больших токах
на рис. 117-3 [19]. При больших токах  имеет место закон Тафеля. По мере уменьшения тока его распределение становится более однородным, однако при малых токах оно приближается к результатам линейного приближения при данном значении
имеет место закон Тафеля. По мере уменьшения тока его распределение становится более однородным, однако при малых токах оно приближается к результатам линейного приближения при данном значении  вместо того чтобы установилась полностью однородная плотность тока. При более высоких значениях
вместо того чтобы установилась полностью однородная плотность тока. При более высоких значениях 
результаты линейного приближения справедливы при больших плотностях тока.
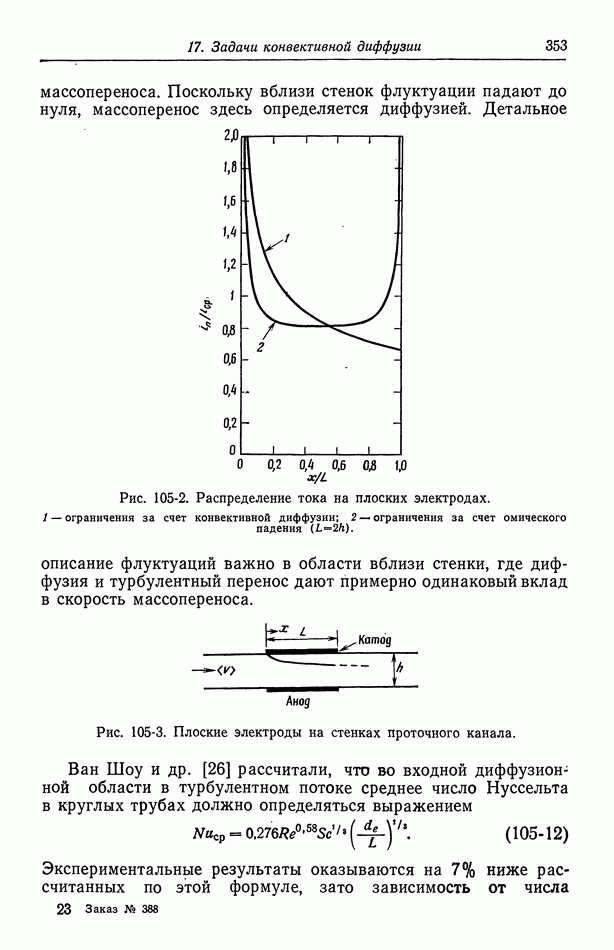
Каспер [10] исследовал влияние линейной поляризации в системе плоских и цилиндрических электродов. Вагнер [12] проанализировал вторичное распределение тока на плоском электроде с двумерной щелью: в двух случаях плоских электродов на стенках канала, состоящих из непроводящего материала, и в случае электрода треугольного профиля [20]. Один из случаев, рассмотренных Вагнером при линейной поляризации, — плоский электрод конечной ширины, помещенный на непроводящую плоскость с противоэлектродом на бесконечности, — рассмотрен Гнусиным и др. [21] для тафелевской поляризации. Эта система, а также случай двух плоских электродов, расположенных на противоположных стенках проточного канала (рис. 105-3), обсуждались Пэрришем и Ньюменом [22, 23].
В некоторых из перечисленных случаев используются распределенные вдоль поверхности электрода источники тока в качестве способа сведения задачи к интегральному уравнению. Получающееся при этом интегральное уравнение, которое бывает линейным или нелинейным в зависимости от используемого закона поляризации, часто решается численными методами.
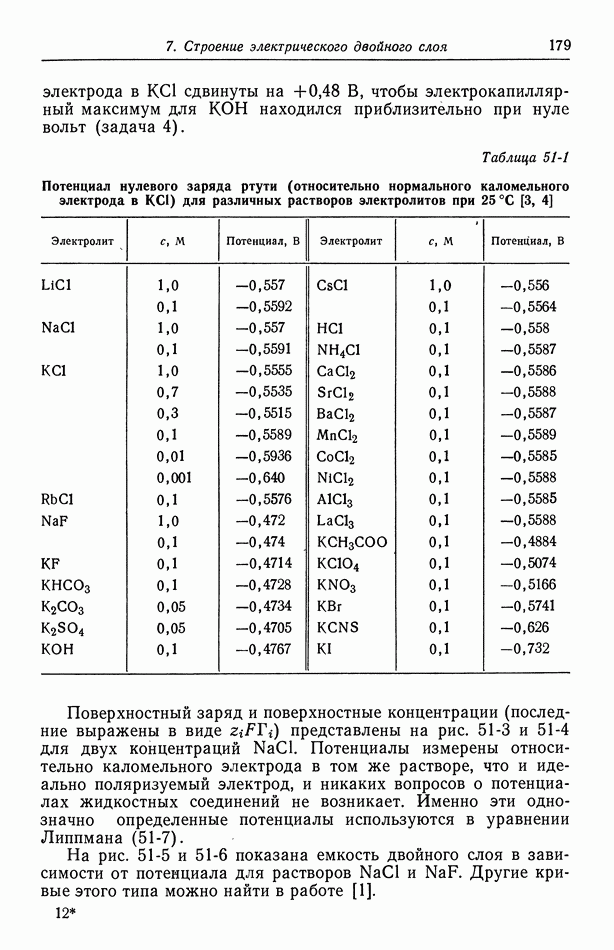
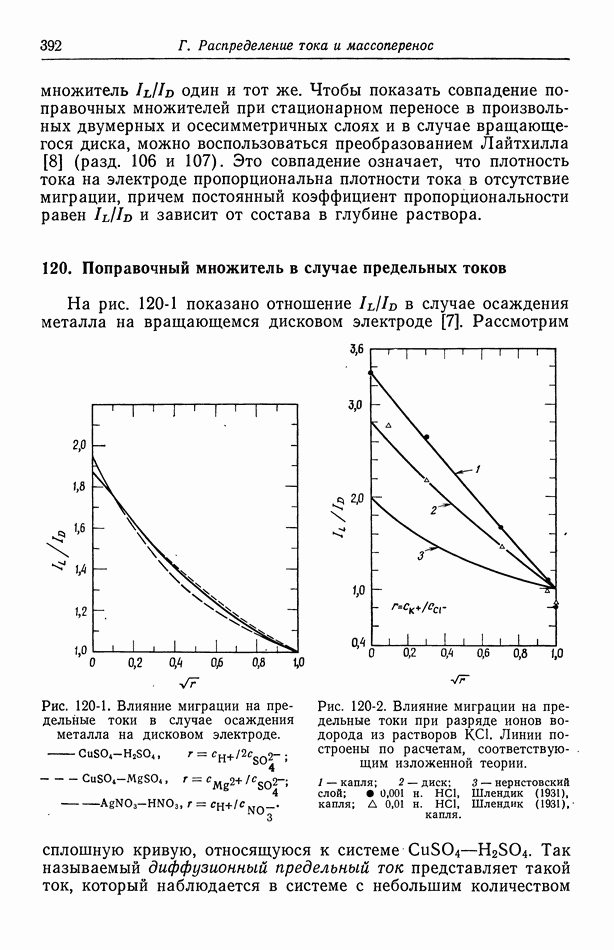
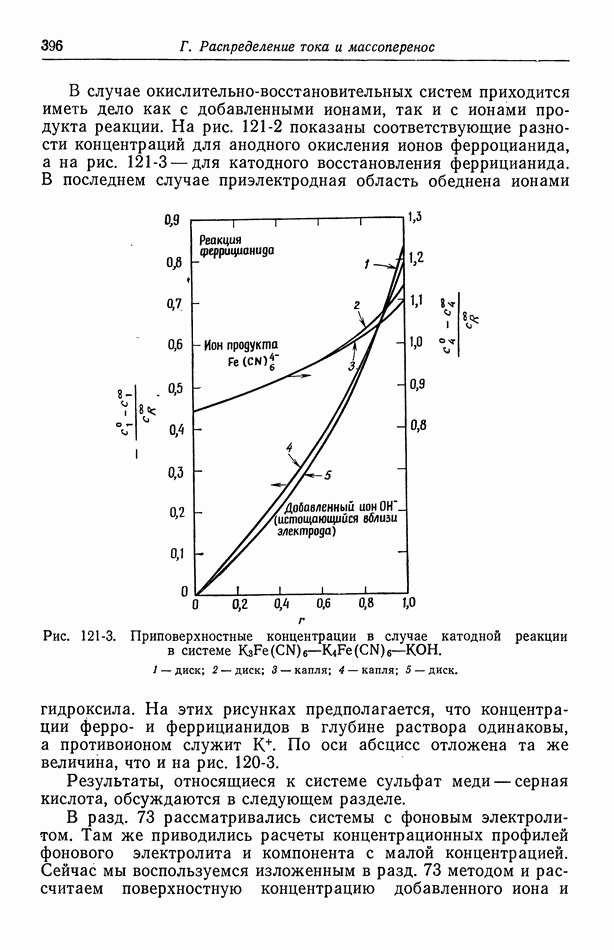
Изображенное на рис. 117-4 первичное распределение тока на дисковом электроде можно сравнить с однородным распределением, найденным в разд. 103 при конвективно-диффузионном контроле. Неоднородное омическое падение потенциала нарушает равнодоступность поверхности диска с точки зрения переноса вещества. Поляризация электрода повышает однородность распределения тока, однако степень неоднородности зависит от параметров  Взаимодействие этих факторов рассматривается в гл. 21. На рис. 117-4 показано также распределение потенциала вблизи диска при однородном распределении тока [19] (см. также работу [24]). Эта кривая нормирована таким образом, чтобы ее удобно было сравнивать с величиной
Взаимодействие этих факторов рассматривается в гл. 21. На рис. 117-4 показано также распределение потенциала вблизи диска при однородном распределении тока [19] (см. также работу [24]). Эта кривая нормирована таким образом, чтобы ее удобно было сравнивать с величиной  для первичного распределения тока. Ясно, что эти предельные случаи однородного потенциала и однородной плотности тока несовместимы.
для первичного распределения тока. Ясно, что эти предельные случаи однородного потенциала и однородной плотности тока несовместимы.
Однородное распределение тока возникает в предельном случае, когда потенциал изменяется в растворе вблизи диска. Максимальная разность потенциалов между центром диска и его краем равна

Из этой формулы следуют важные выводы относительно формы кривых предельного тока, размеров дисков, подвергающихся анодной или катодной защите от коррозии, условий электролиза
при постоянном потенциале и определения кинетических параметров электрода [25]. В каждом случае имеется максимально допустимое изменение потенциала, от которого зависят допустимые значения  для раствора с данной проводимостью.
для раствора с данной проводимостью.

Рис. 117-4. Первичные распределения тока и потенциала при однородной плотности тока на дисковом электроде. 1 —  при однородной плотности тока;
при однородной плотности тока;  при однородном потенциале.
при однородном потенциале.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
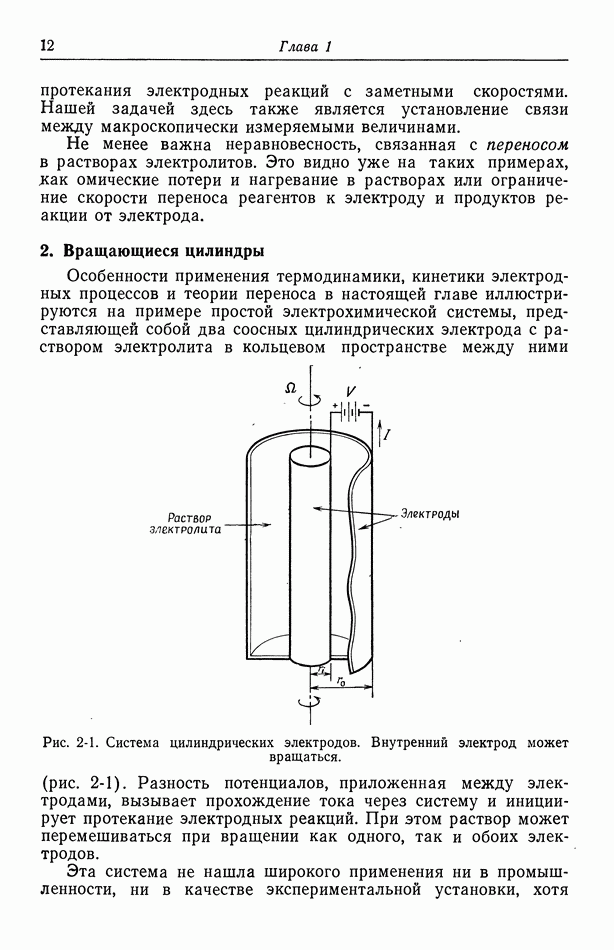
- 2. Вращающиеся цилиндры
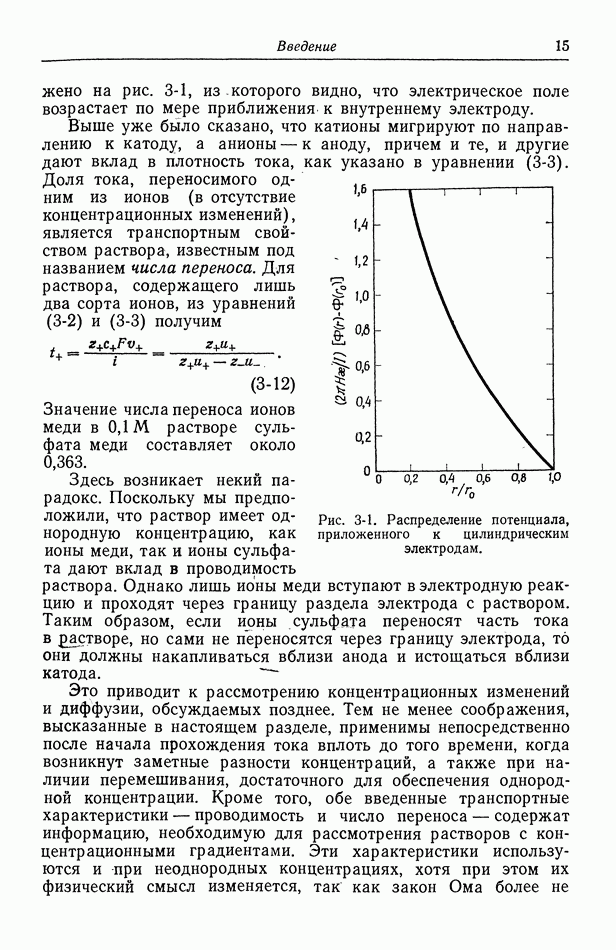
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
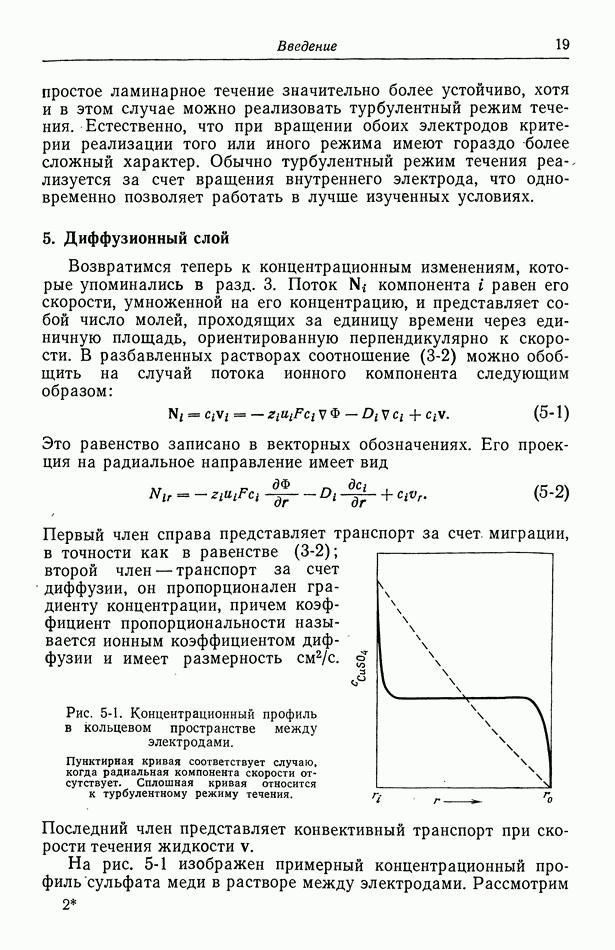
- 5. Диффузионный слой
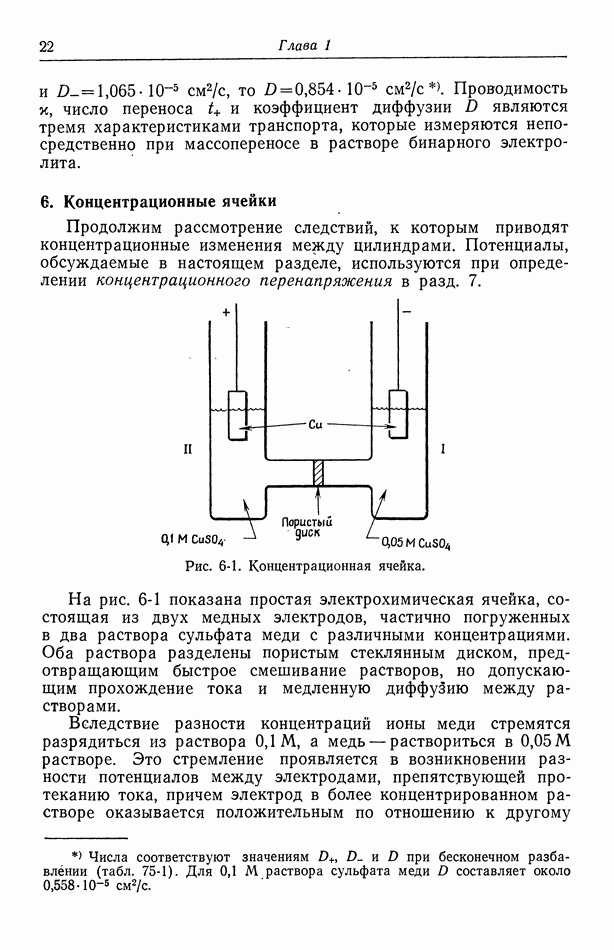
- 6. Концентрационные ячейки
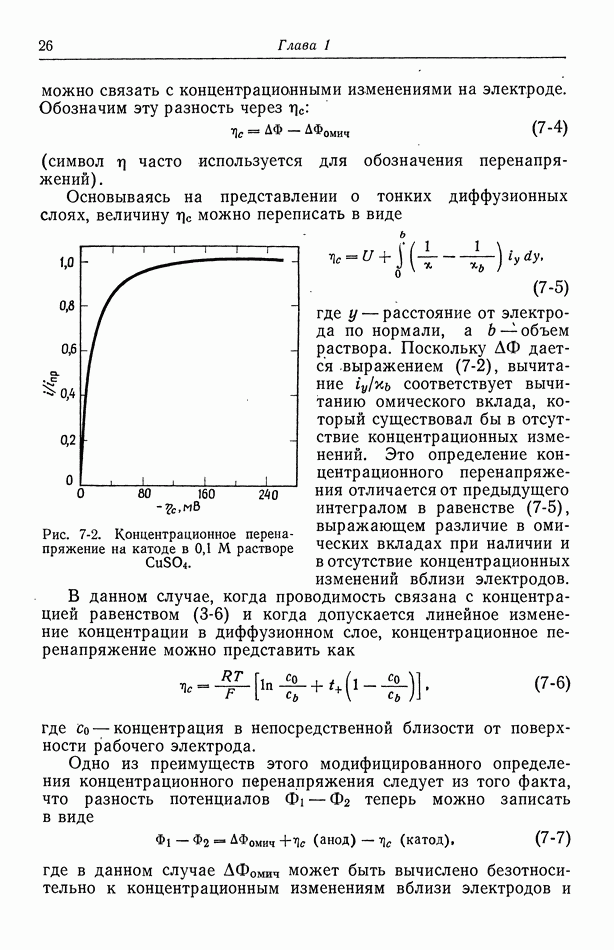
- 7. Концентрационное перенапряжение
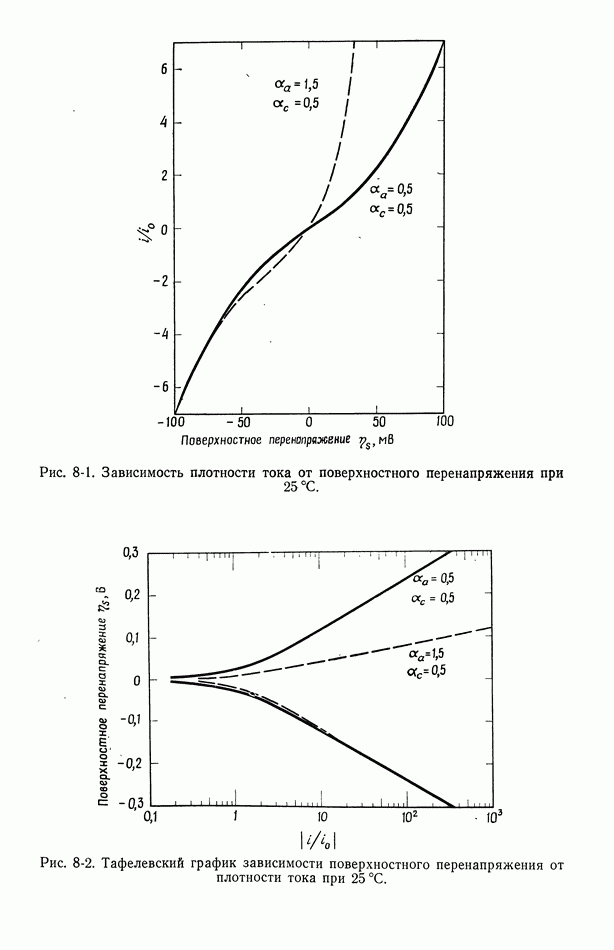
- 8. Поверхностное перенапряжение
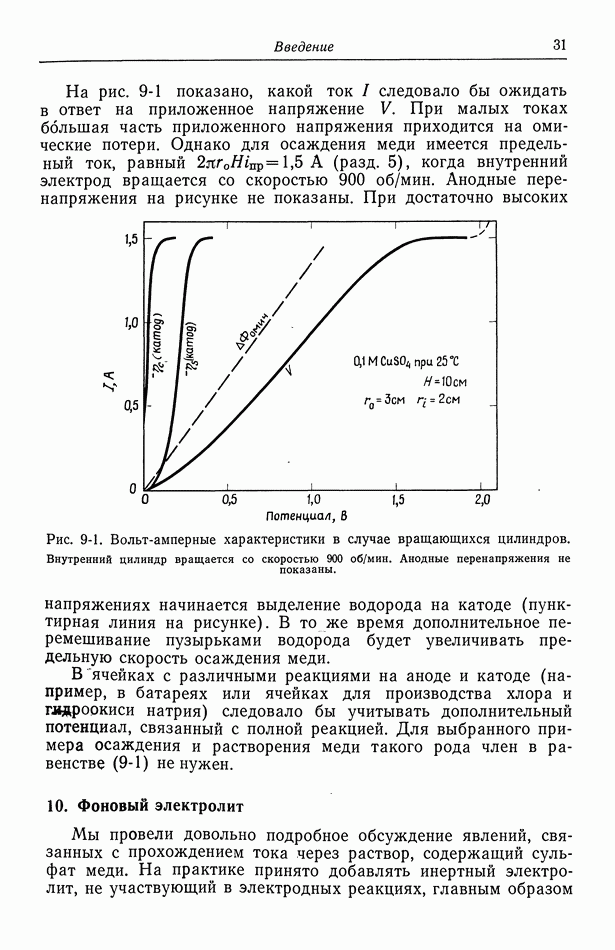
- 9. Потенциал ячейки
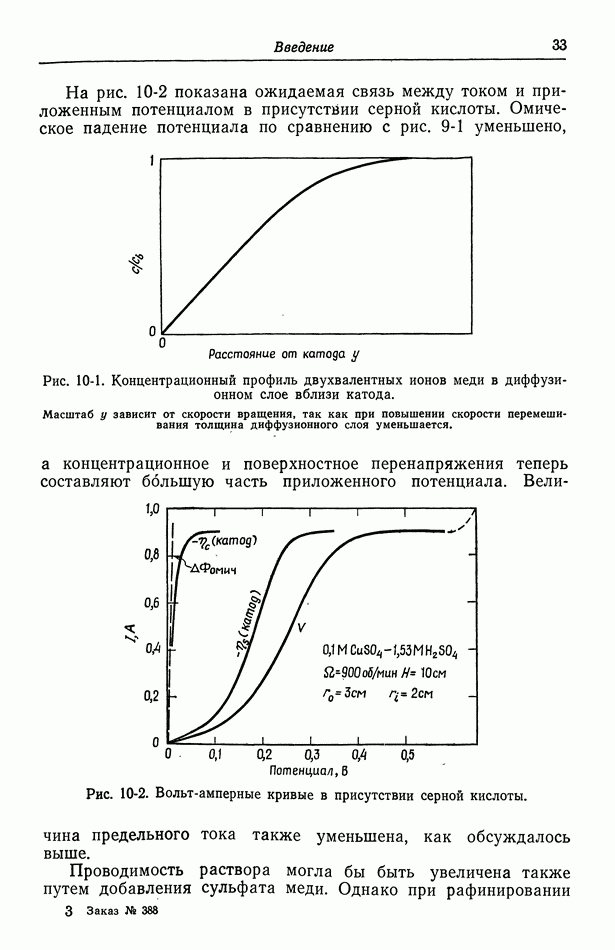
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
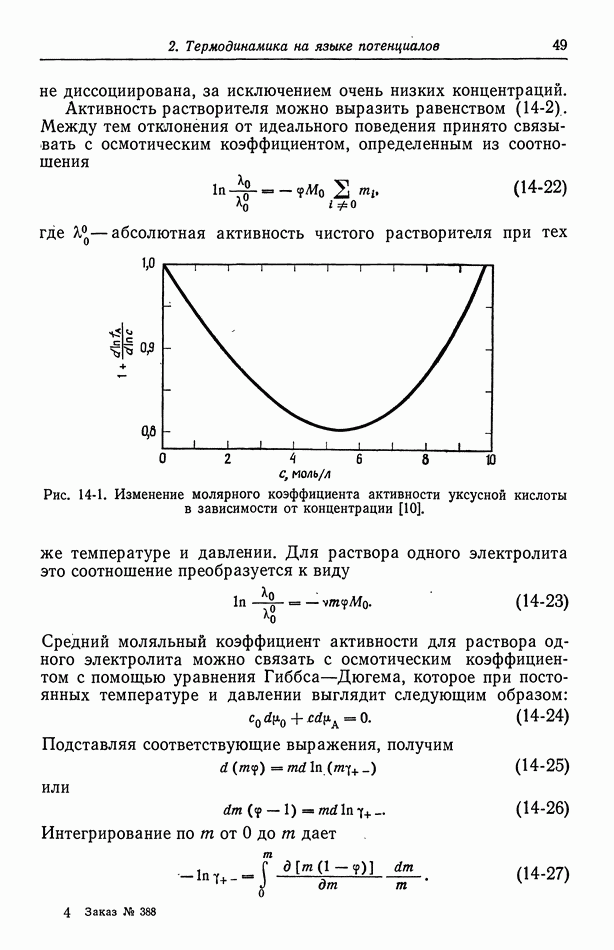
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
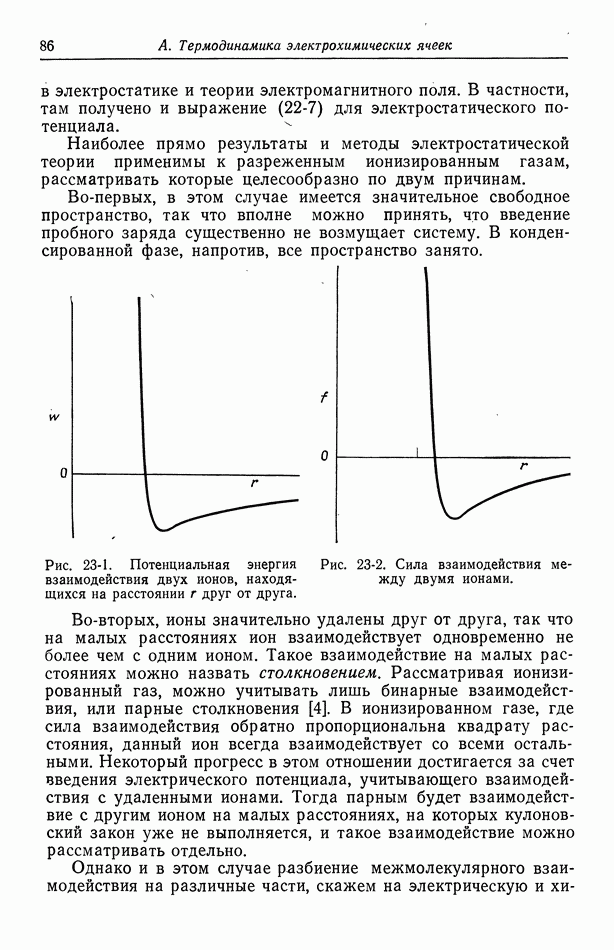
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
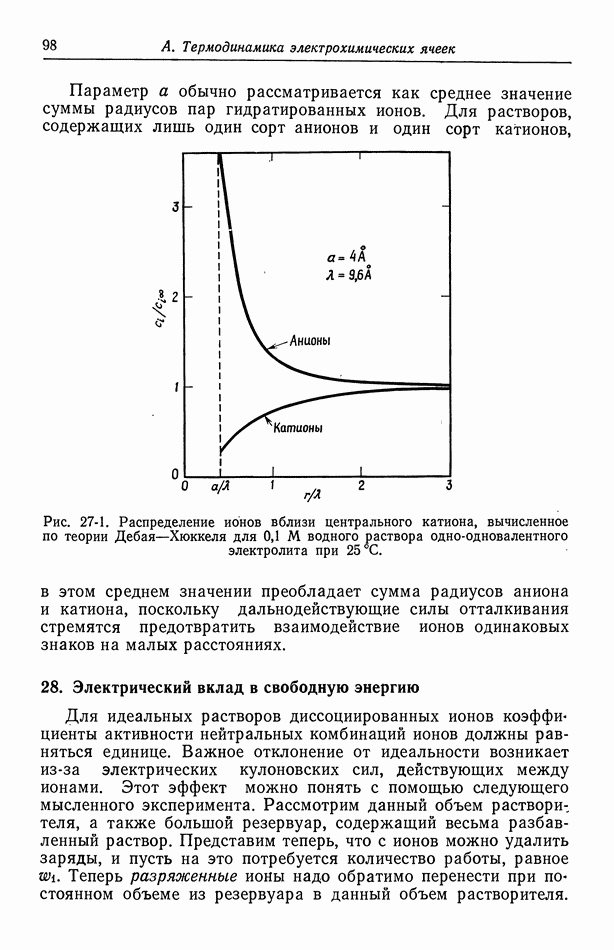
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
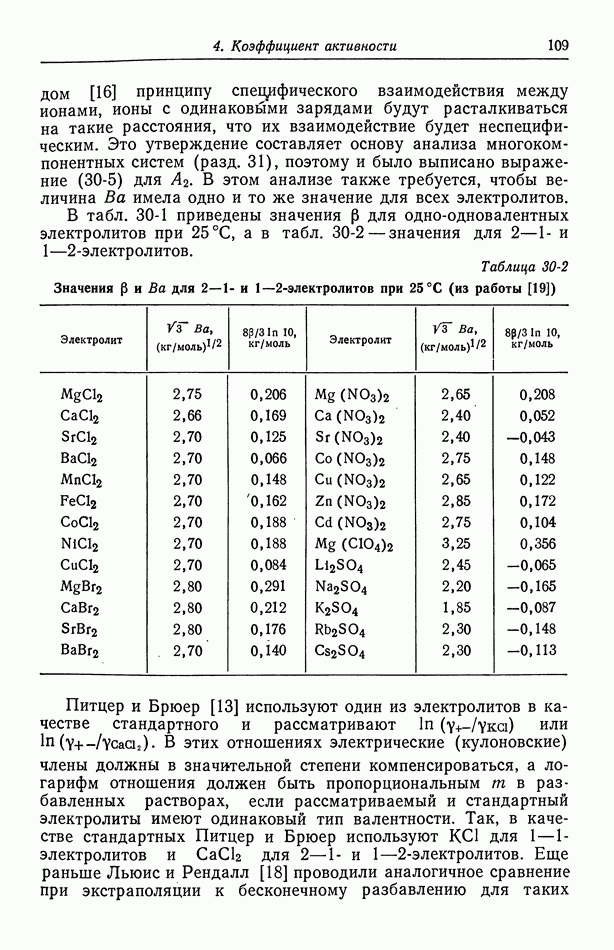
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
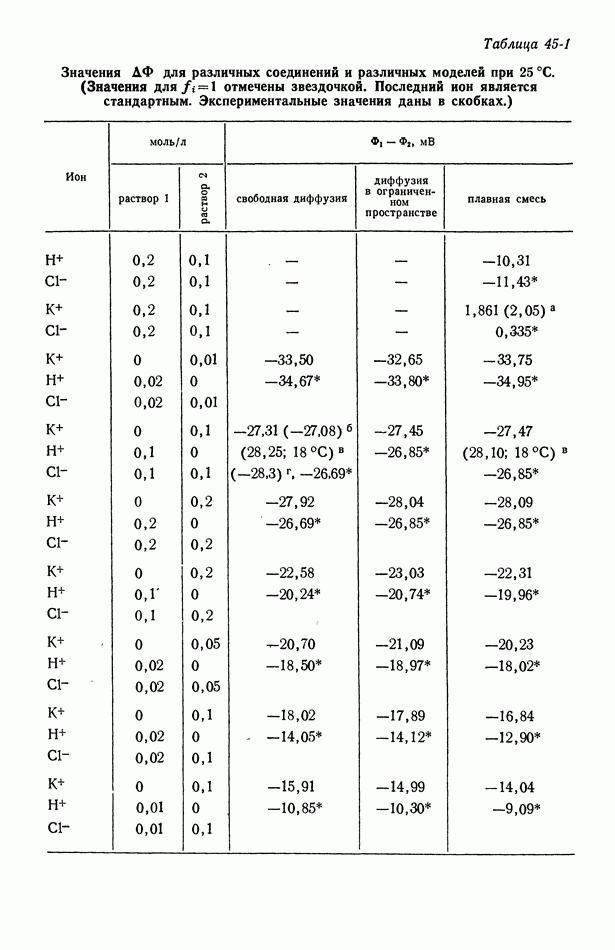
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
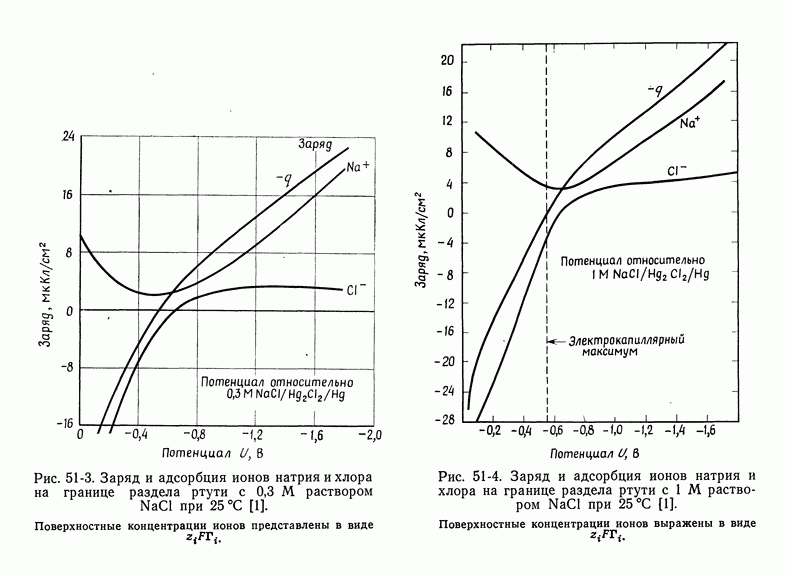
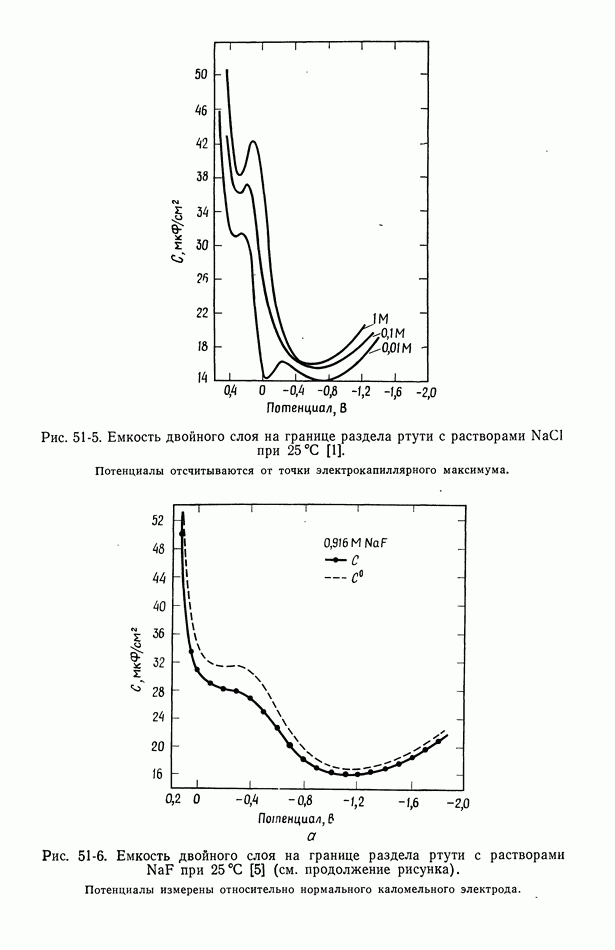
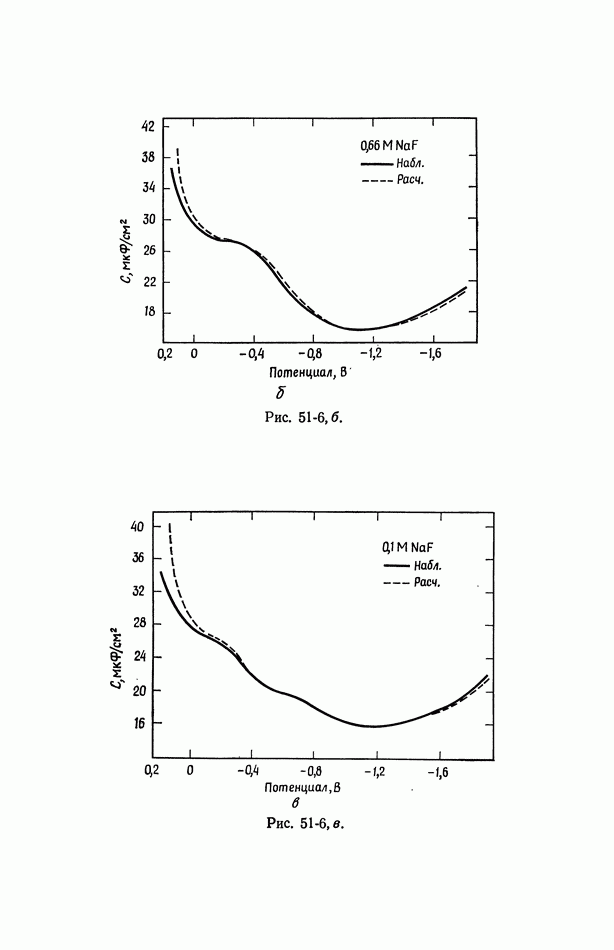
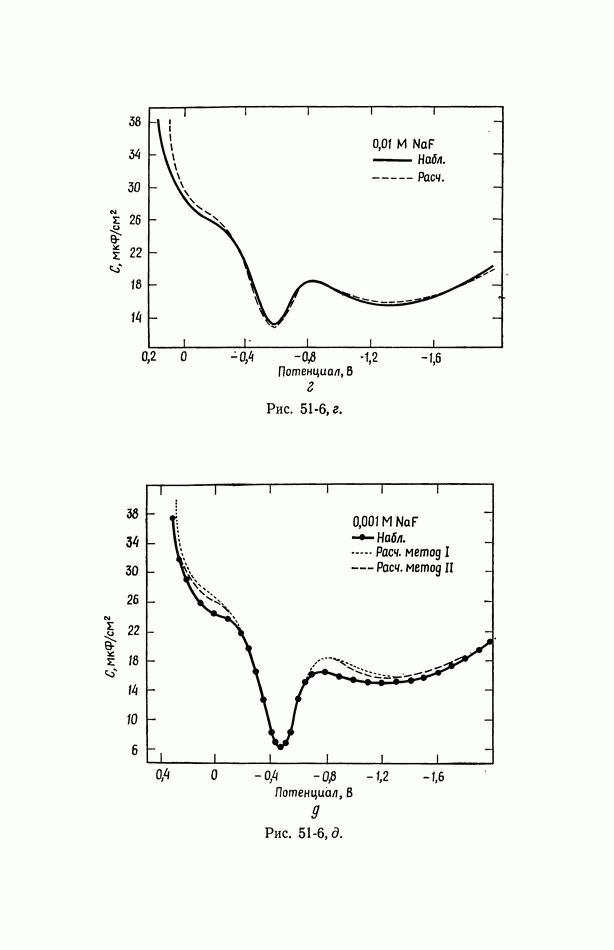
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
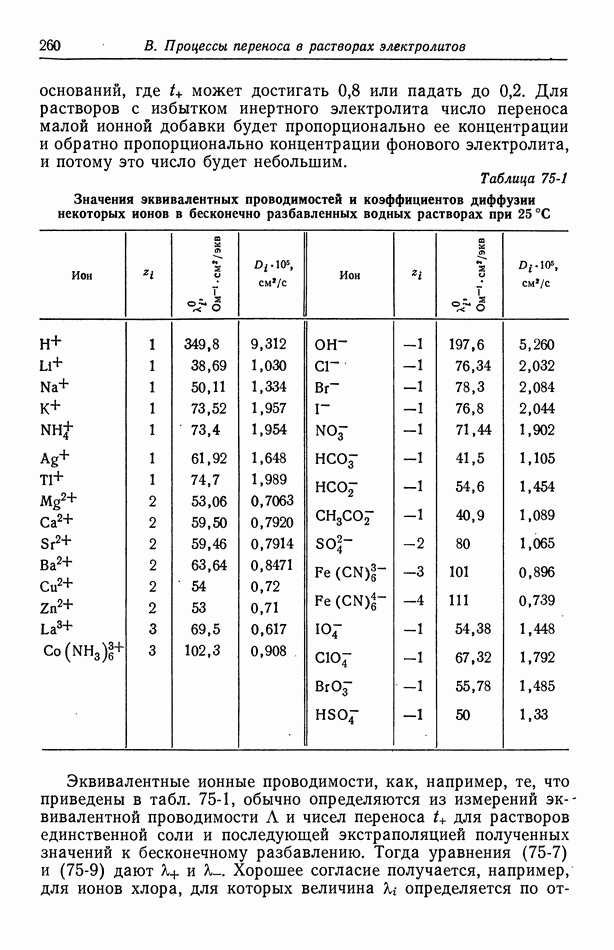
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
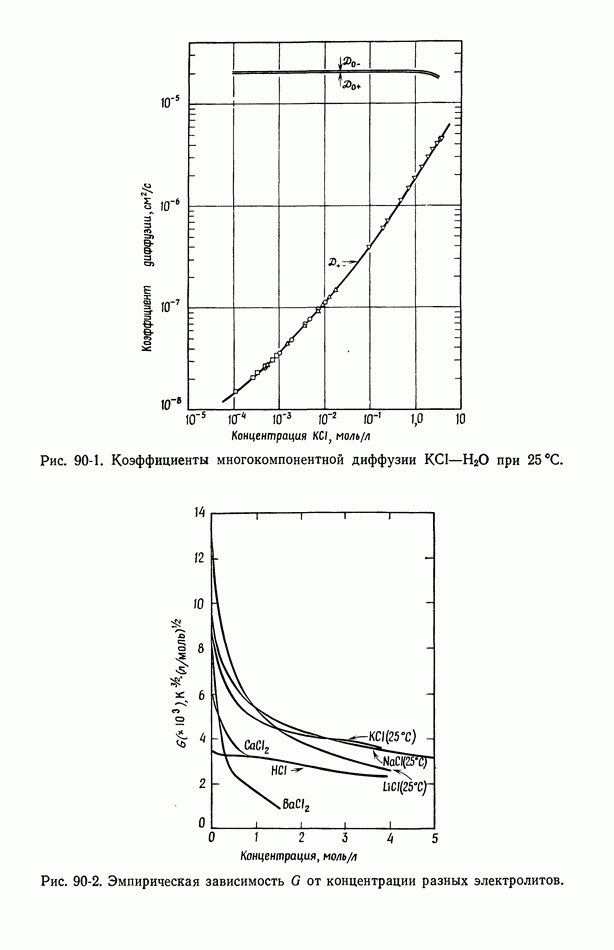
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
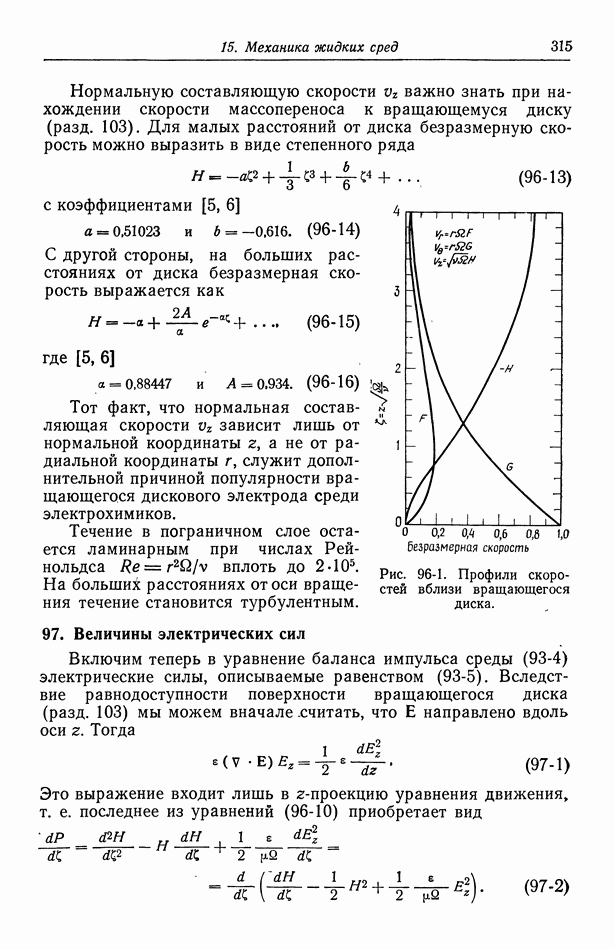
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
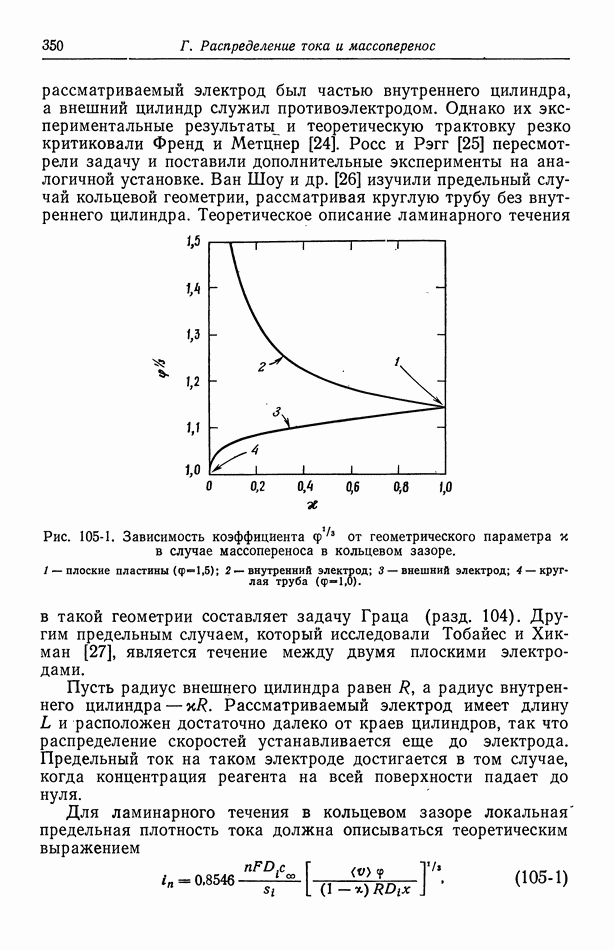
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
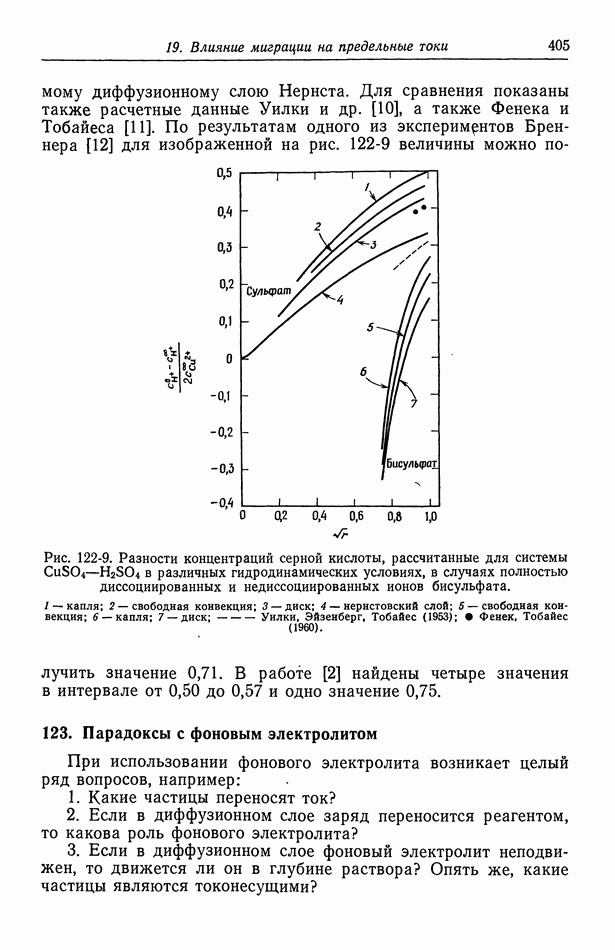
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
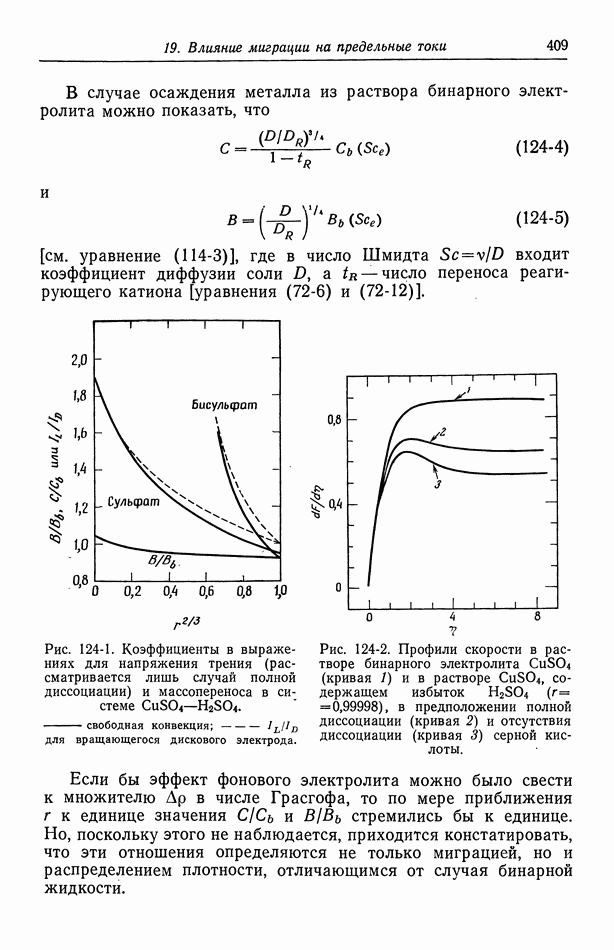
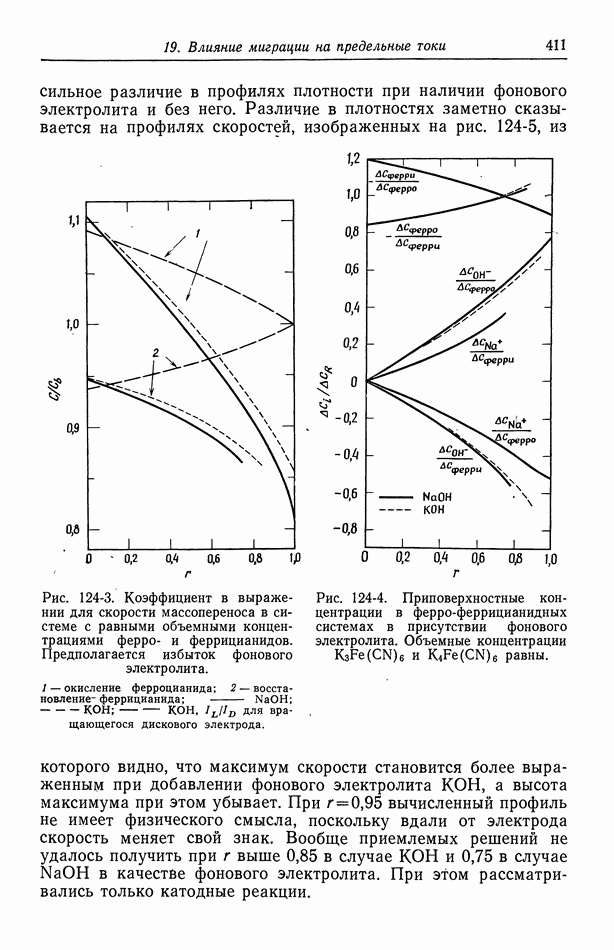
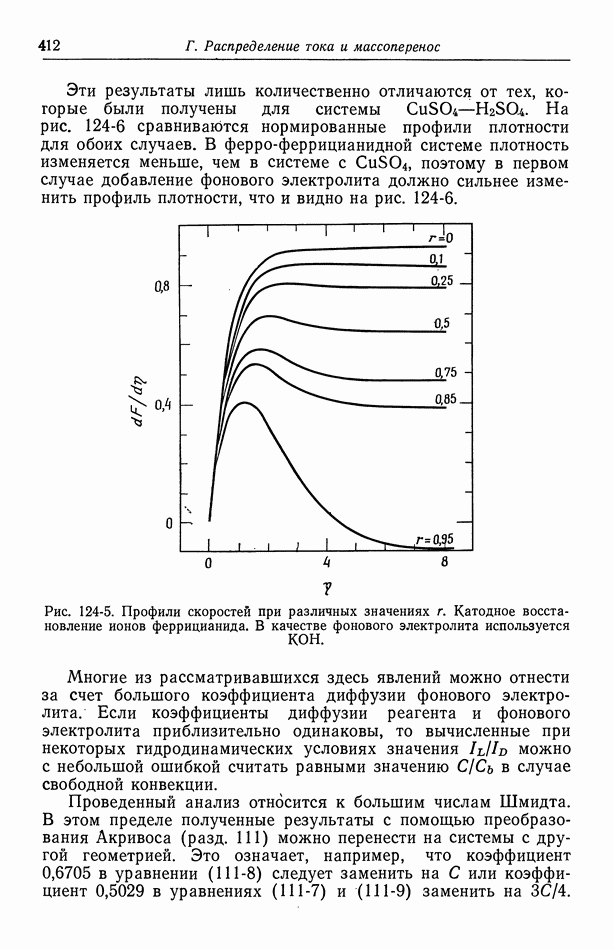
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ