| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
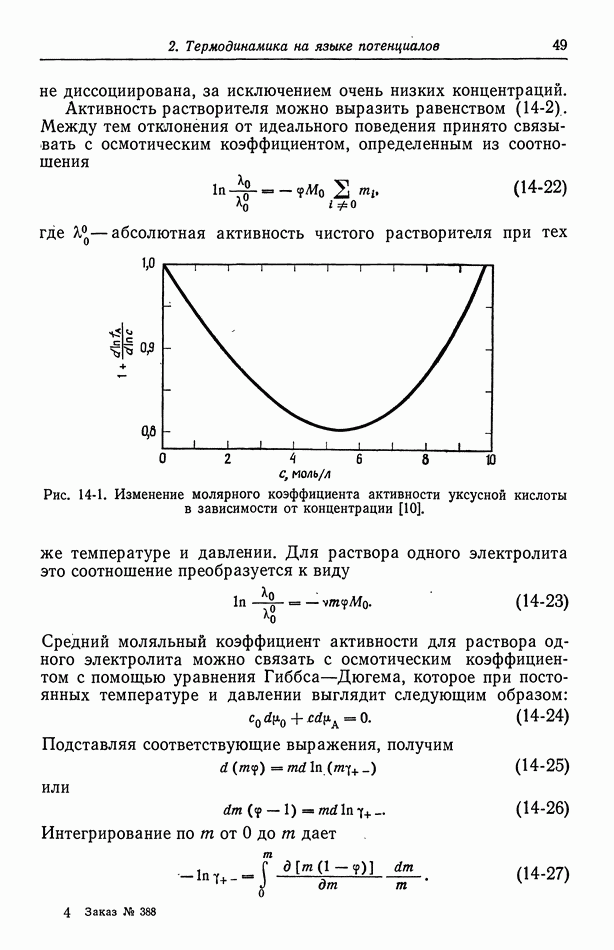
96. Течение жидкости к вращающемуся диску
Вращающийся дисковый электрод весьма популярен в электрохимических исследованиях, частично вследствие того, что гидродинамика здесь хорошо известна, а частично из-за небольших размеров и простоты экспериментального устройства. Вращающийся диск также является одной из немногих систем, для которых возможно нетривиальное решение уравнений механики жидких сред.
Рассмотрим стационарное течение несжимаемой жидкости, вызванное вращением большого диска вокруг оси, проходящей через его центр. Для этой цели воспользуемся цилиндрическими координатами  расстояние по перпендикуляру от диска,
расстояние по перпендикуляру от диска,  радиальное расстояние от оси вращения). На поверхности диска скорость имеет вид
радиальное расстояние от оси вращения). На поверхности диска скорость имеет вид

Последнее условие выражает тот факт, что вращающийся диск увлекает прилегающую к нему жидкость и придает ей угловую скорость 
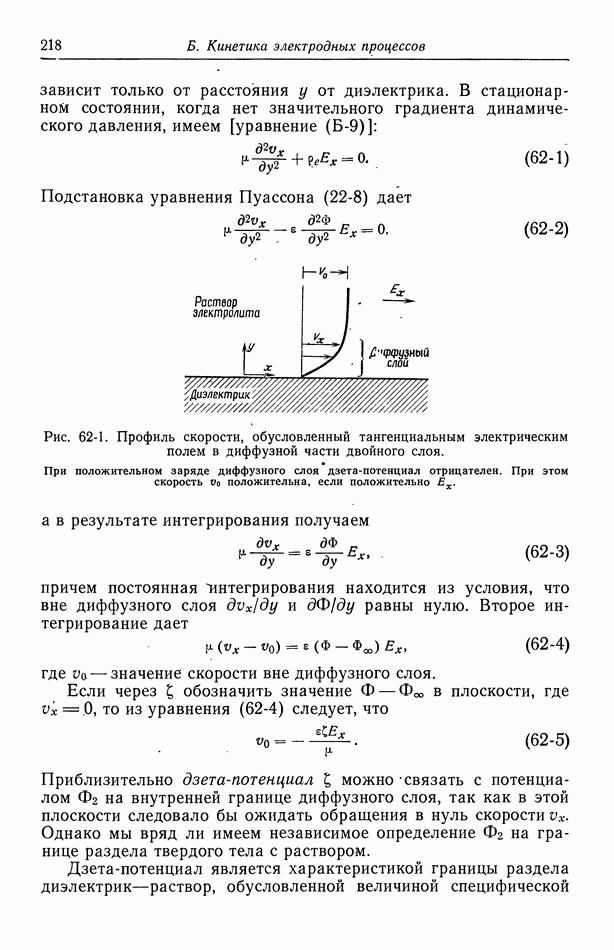
При вращении возникает эффект центрифуги, благодаря которому жидкость стремится двигаться в радиальном направлении. Это приводит к возникновению радиальной составляющей скорости, которая равна нулю на поверхности диска, имеет максимум вблизи поверхности и затем опять устремляется к нулю по мере возрастания расстояния до диска. Для восполнения жидкости, утекающей в направлении  необходимо иметь ненулевую проекцию на оси z скорости, которая приносит жидкость из удаленной части пространства. Такова качественная картина течения, в которой ни одна из составляющих скорости не обращается в нуль.
необходимо иметь ненулевую проекцию на оси z скорости, которая приносит жидкость из удаленной части пространства. Такова качественная картина течения, в которой ни одна из составляющих скорости не обращается в нуль.
В цилиндрических координатах уравнение непрерывности (93-3) приобретает вид [2]

а проекции уравнения движения (94-4) на оси цилиндрической системы координат выглядят следующим образом:

В этих уравнениях мы использовали динамическое давление  введенное в уравнении (93-6). В нашей задаче о стационарном течении, обладающем осевой симметрией, производные по
введенное в уравнении (93-6). В нашей задаче о стационарном течении, обладающем осевой симметрией, производные по  и 0 обращаются в нуль.
и 0 обращаются в нуль.
В 1921 г. фон Карман [3] предложил свести эти уравнения в частных производных к обыкновенным дифференциальным уравнениям, представляя решение в виде

Такое представление решения соответствует разделению переменных.
Подставляя эти выражения в уравнения (96-2) и (96-5), получаем

где штрихи соответствуют дифференцированию по 2.
Граничными условиями служат равенства

Кроме того, требуется определить значение хотя бы в одной точке.
С помощью преобразования фон Кармана задачу удается свести к обыкновенным дифференциальным уравнениям. Однако следует отметить, что в таком решении не учитывается тот факт, что радиус диска может быть конечным. На практике этим краевым эффектом часто можно пренебречь, и получающееся решение оказывается вполне пригодным [4].
Остальные параметры  можно исключить путем введения безразмерных расстояния, скорости и давления с помощью следующих формул:
можно исключить путем введения безразмерных расстояния, скорости и давления с помощью следующих формул:

Дифференциальные уравнения (96-7) приобретают вид

где теперь штрихи обозначают дифференцирование по Граничными условиями служат равенства

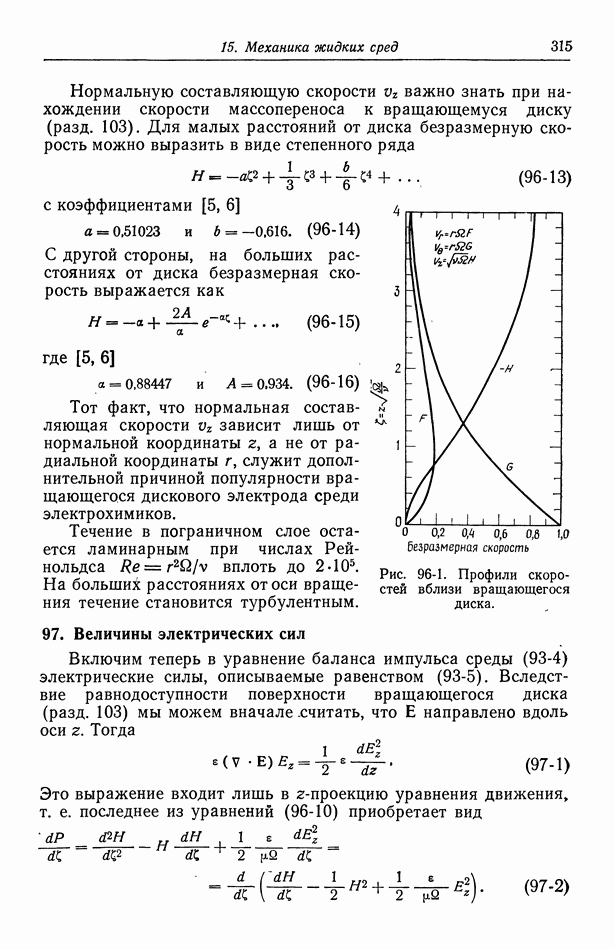
Поскольку эти уравнения нелинейны, их решение приходится искать численными методами. Кочрэн [5] дал оригинальное решение этих уравнений, проводя разложение в ряды при малых и больших значениях Неизвестные коэффициенты разложения определялись из условия согласования получающихся рядов при промежуточных значениях Однако значительно проще решить систему нелинейных дифференциальных уравнений прямыми численными методами (приложение В). Решение уравнений (96-10), удовлетворяющее условиям (96-11), показано на рис. 96-1. После того как профили скоростей уже определены, давление можно получить путем интегрирования последнего из уравнений (96-10):

Нормальную составляющую скорости  важно знать при нахождении скорости массопереноса к вращающемуся диску (разд. 103). Для малых расстояний от диска безразмерную скорость можно выразить в виде степенного ряда
важно знать при нахождении скорости массопереноса к вращающемуся диску (разд. 103). Для малых расстояний от диска безразмерную скорость можно выразить в виде степенного ряда

с коэффициентами [5, 6]

С другой стороны, на больших расстояниях от диска безразмерная скорость выражается как

где


Рис. 96-1. Профили скоростей вблизи вращающегося диска.
Тот факт, что нормальная составляющая скорости  зависит лишь от нормальной координаты
зависит лишь от нормальной координаты  а не от радиальной координаты
а не от радиальной координаты  служит дополнительной причиной популярности вращающегося дискового электрода среди электрохимиков.
служит дополнительной причиной популярности вращающегося дискового электрода среди электрохимиков.
Течение в пограничном слое остается ламинарным при числах Рейнольдса  вплоть до
вплоть до  На больший расстояниях от оси вращения течение становится турбулентным.
На больший расстояниях от оси вращения течение становится турбулентным.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
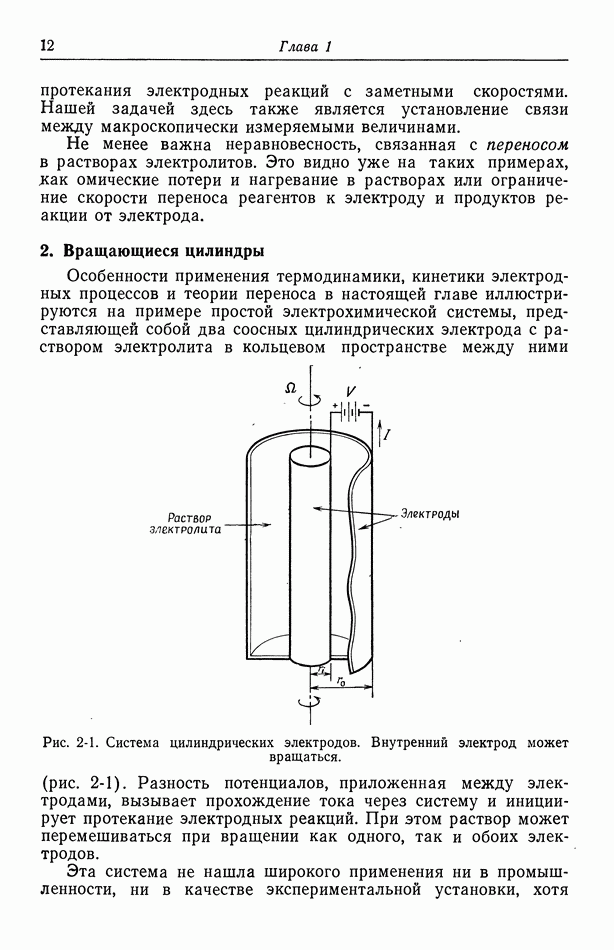
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
- 2. Вращающиеся цилиндры
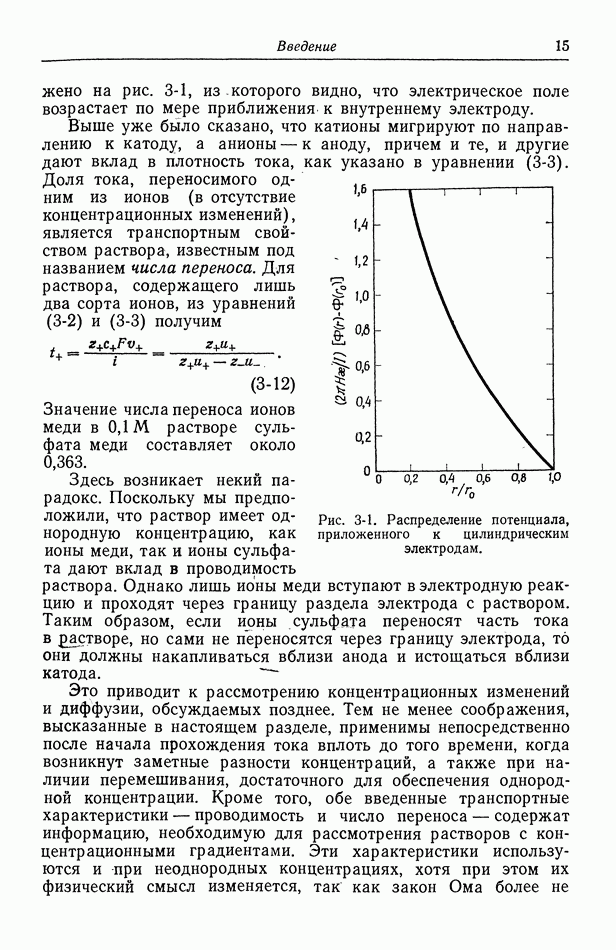
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
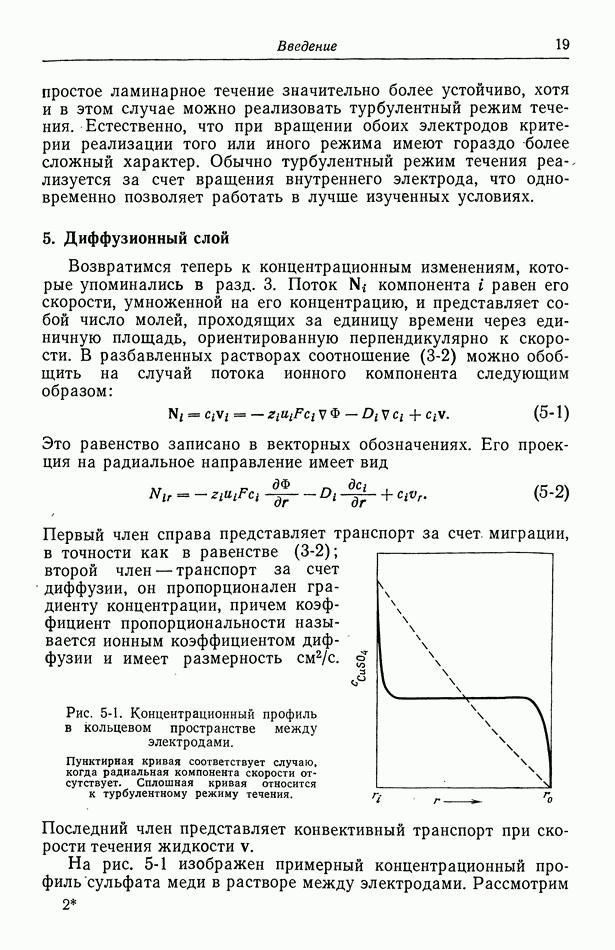
- 5. Диффузионный слой
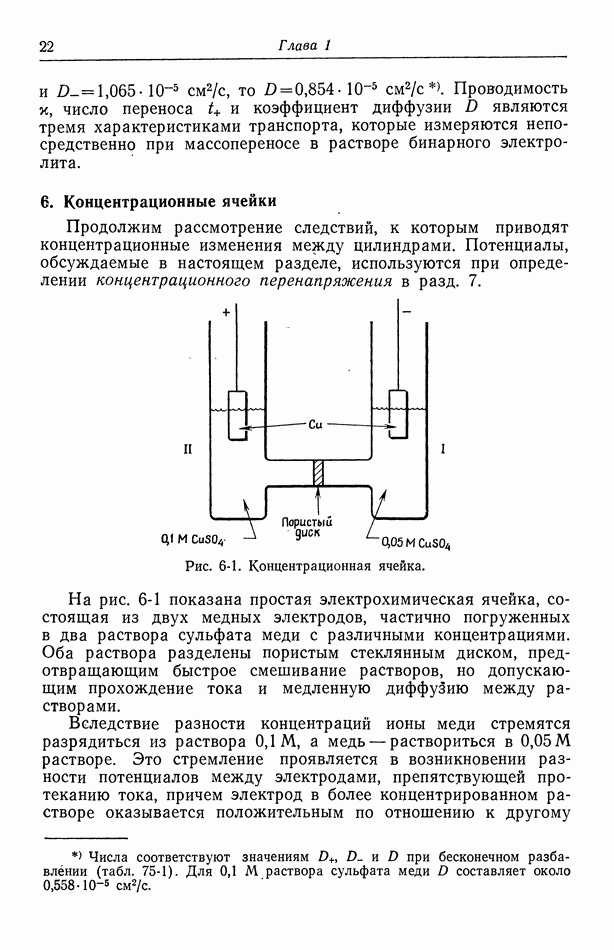
- 6. Концентрационные ячейки
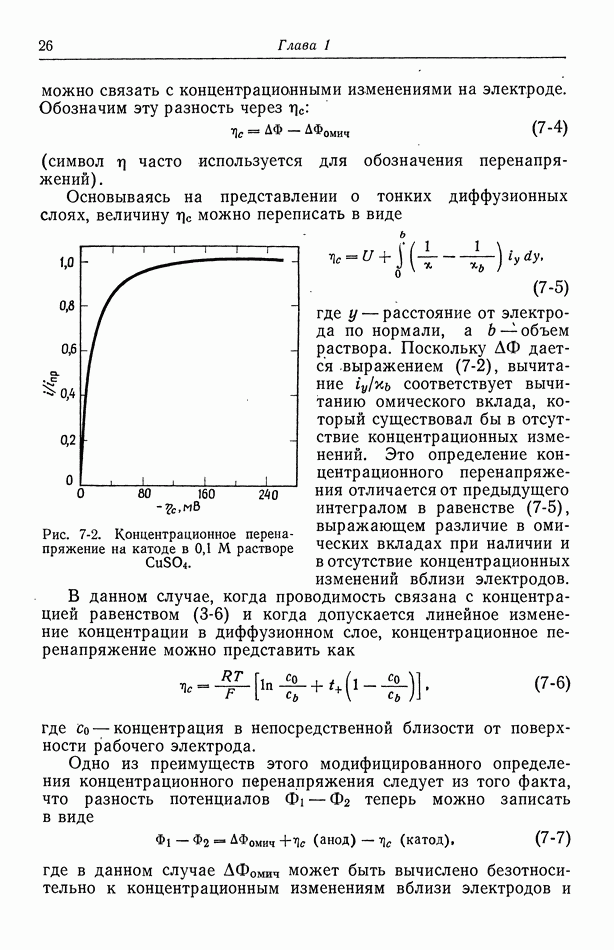
- 7. Концентрационное перенапряжение
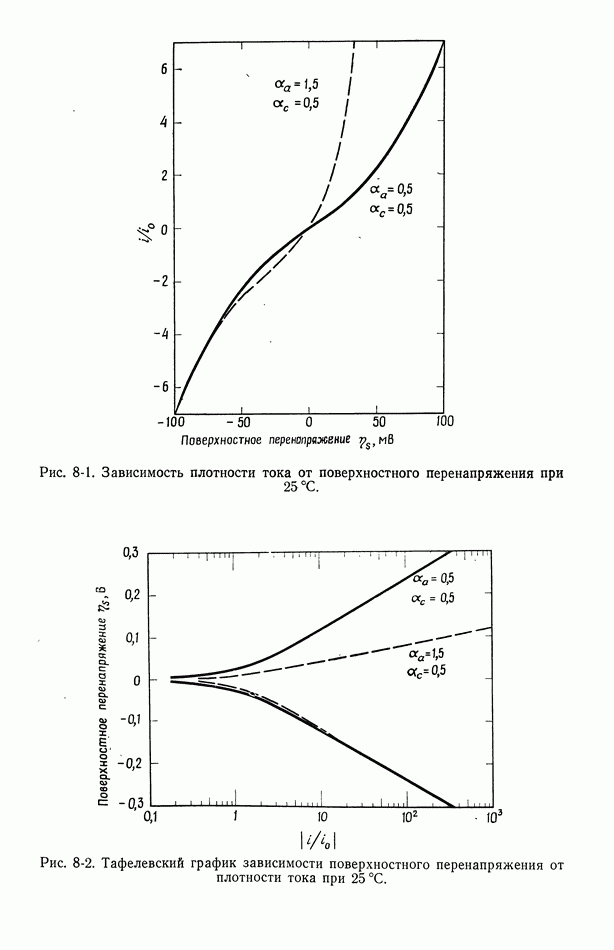
- 8. Поверхностное перенапряжение
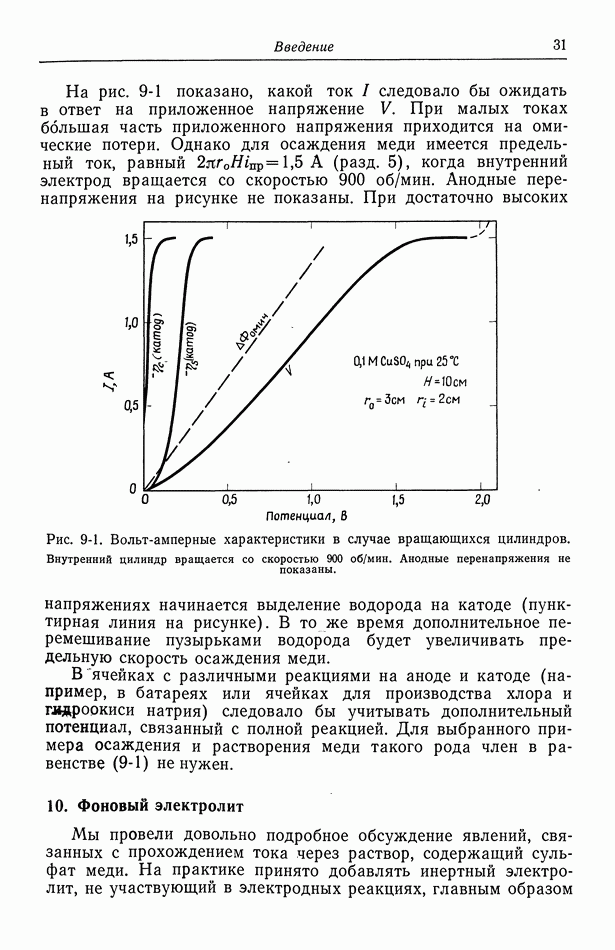
- 9. Потенциал ячейки
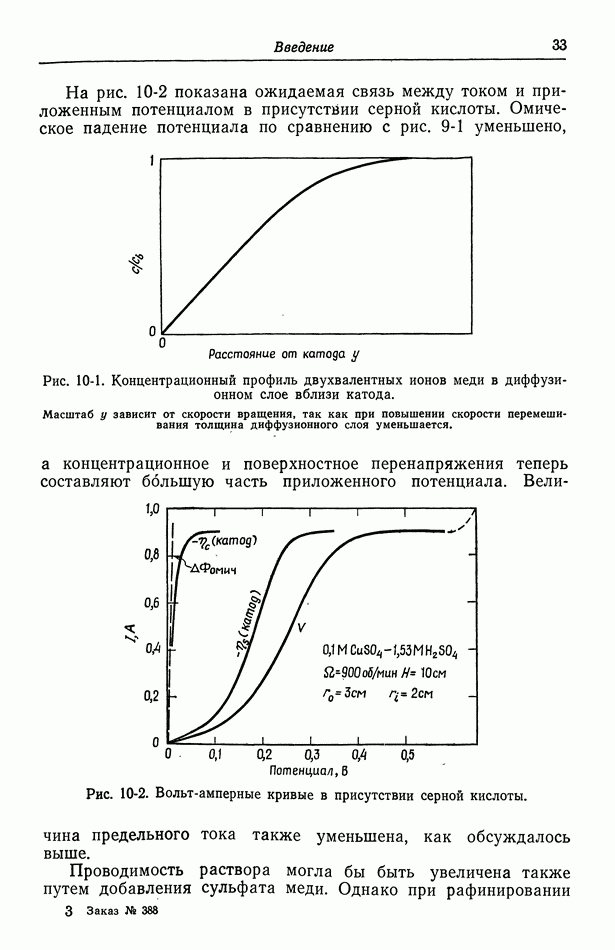
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
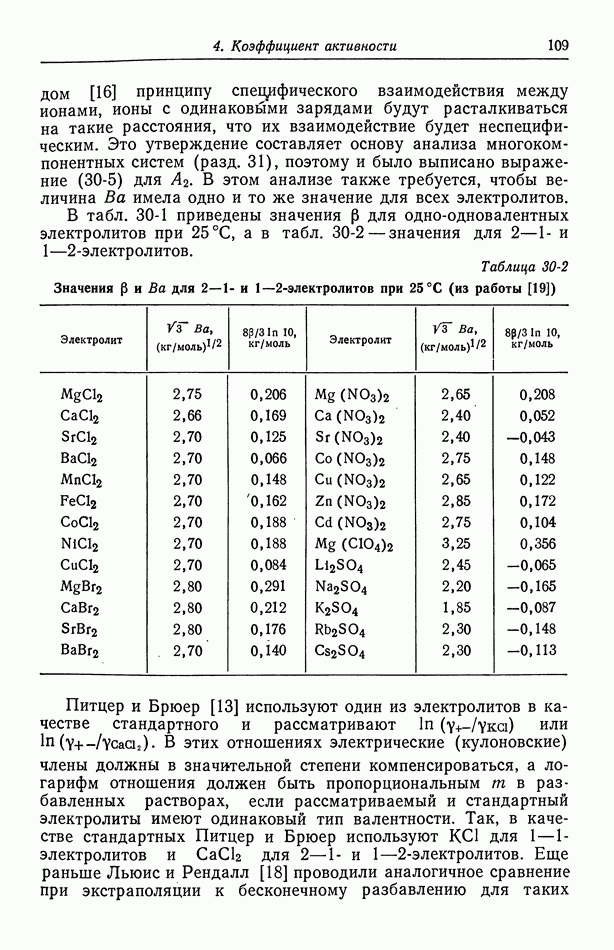
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
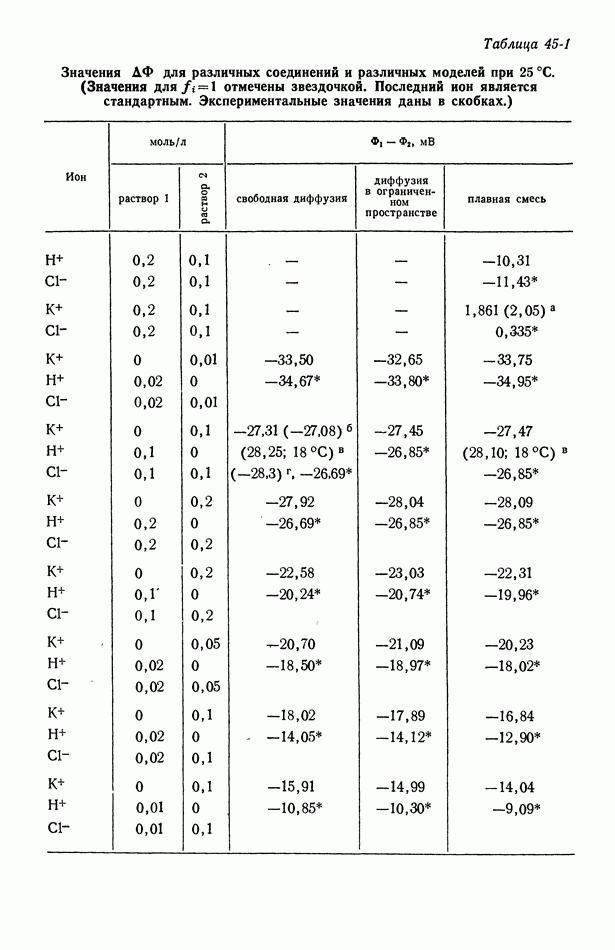
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
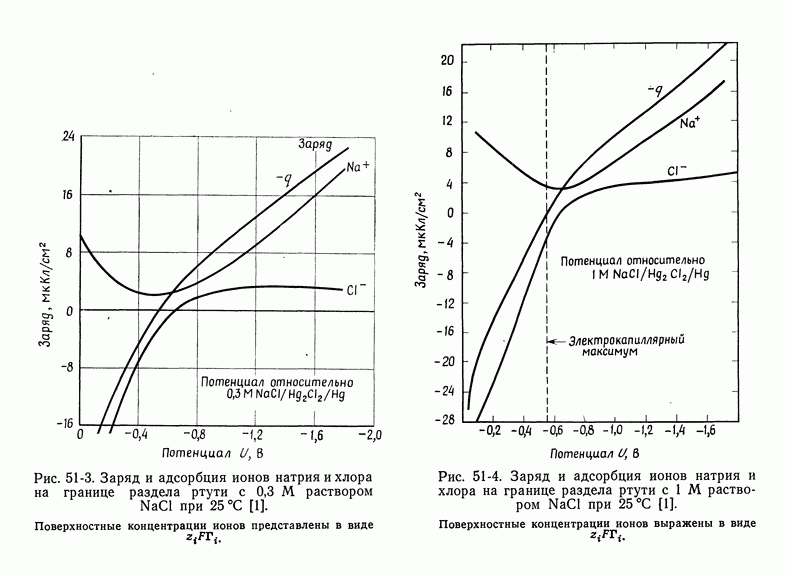
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
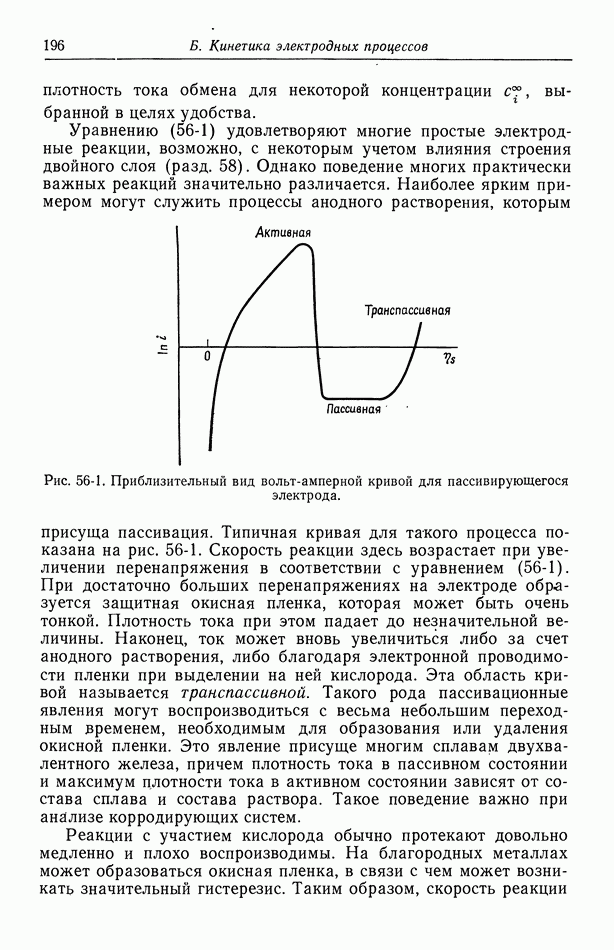
- 56. Зависимость плотности тока от поверхностного перенапряжения
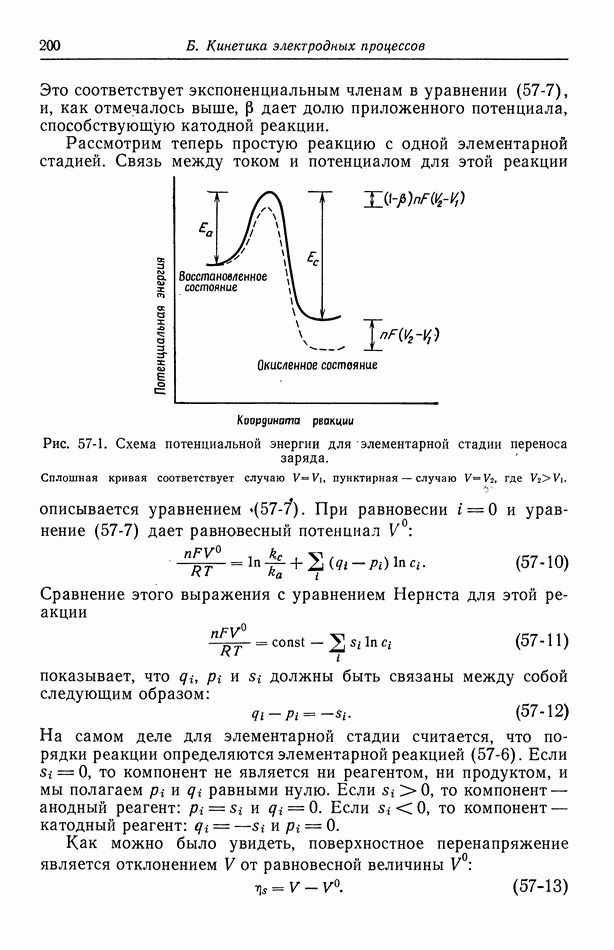
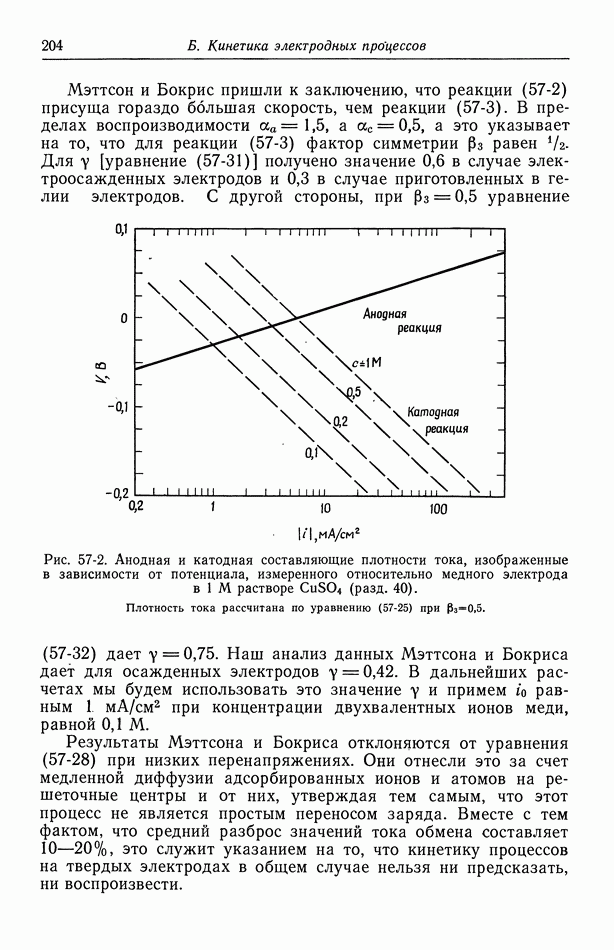
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
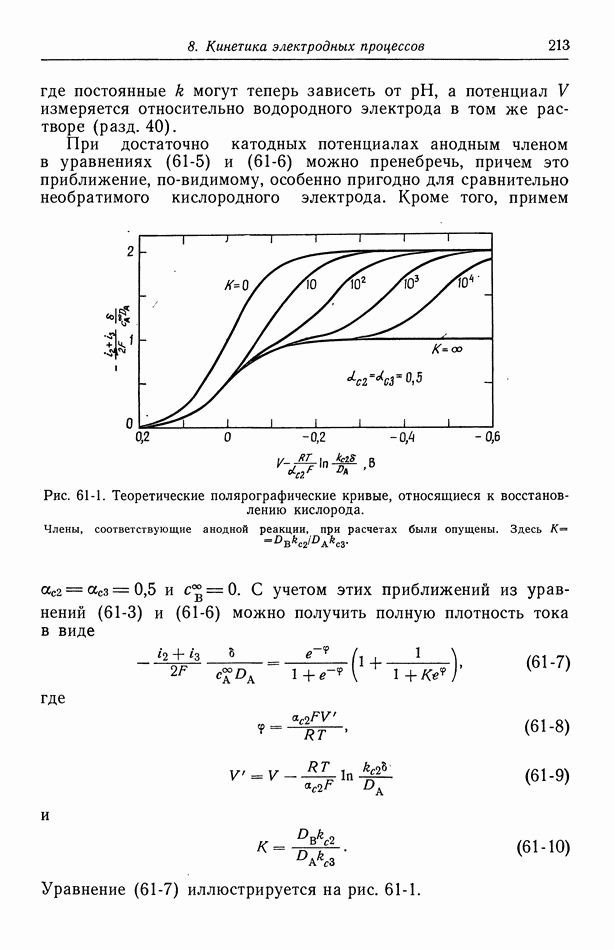
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
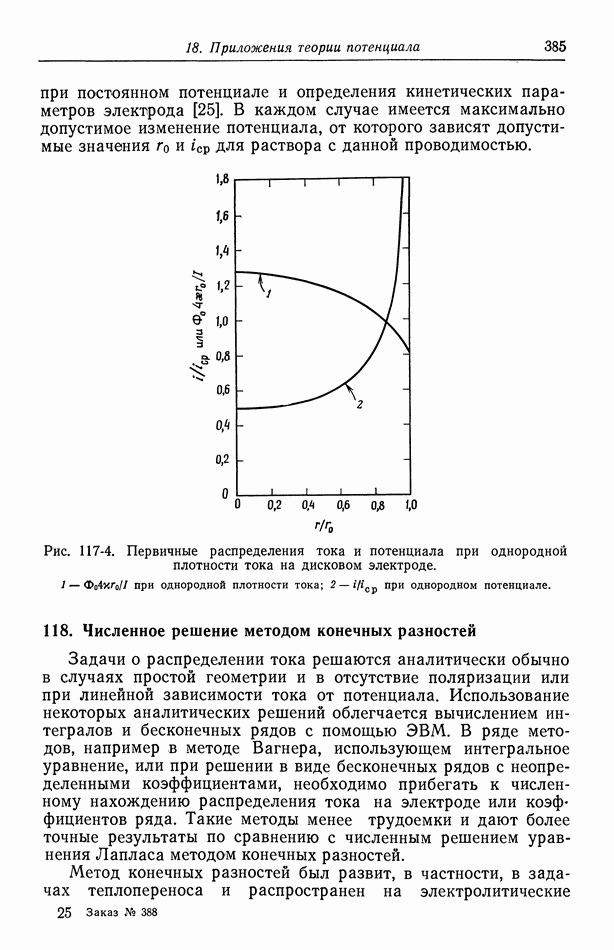
- 116. Первичное распределение тока
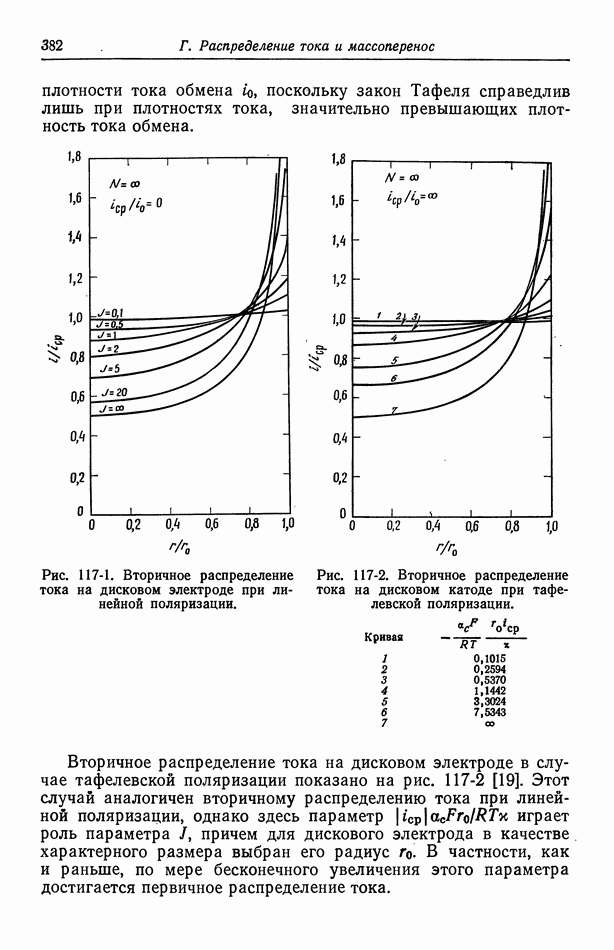
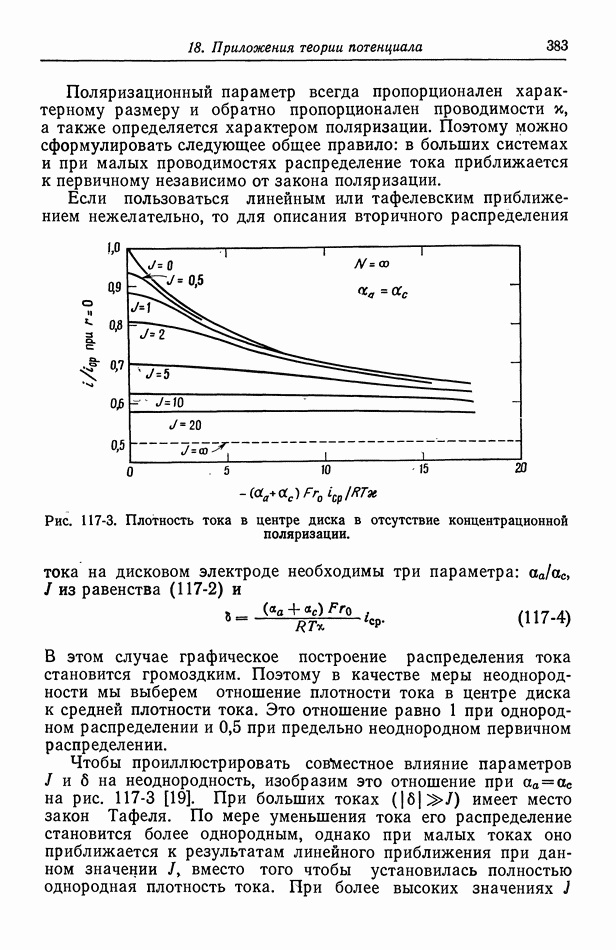
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
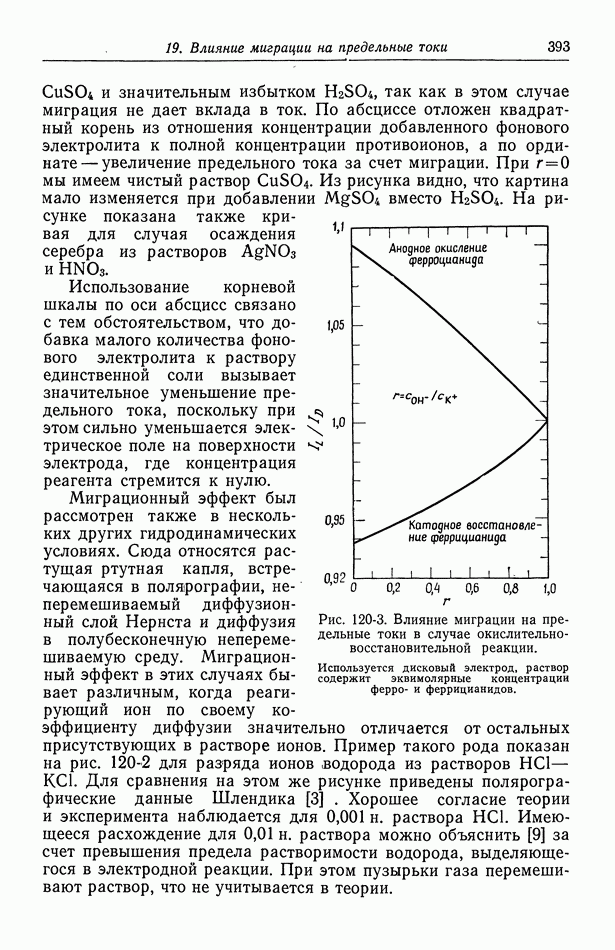
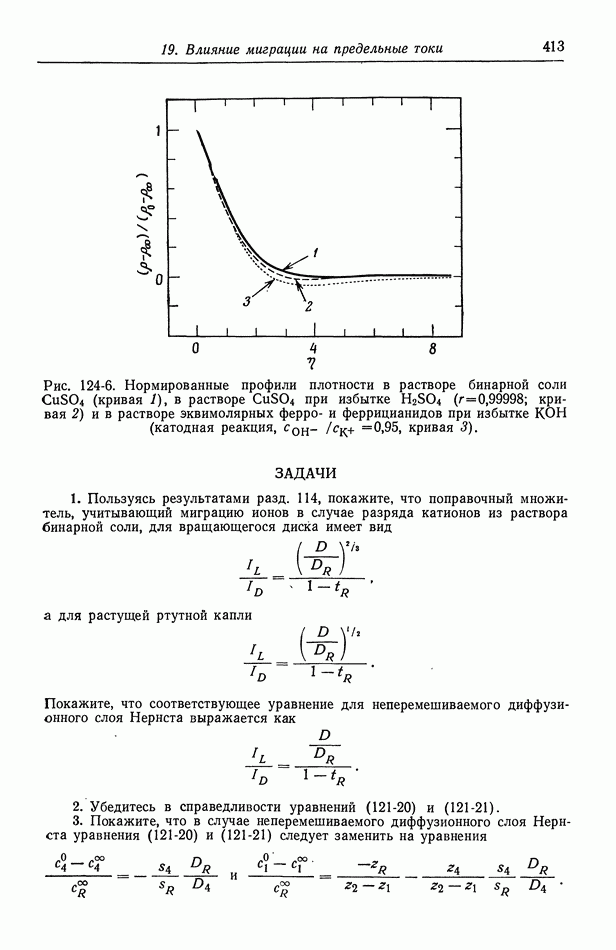
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
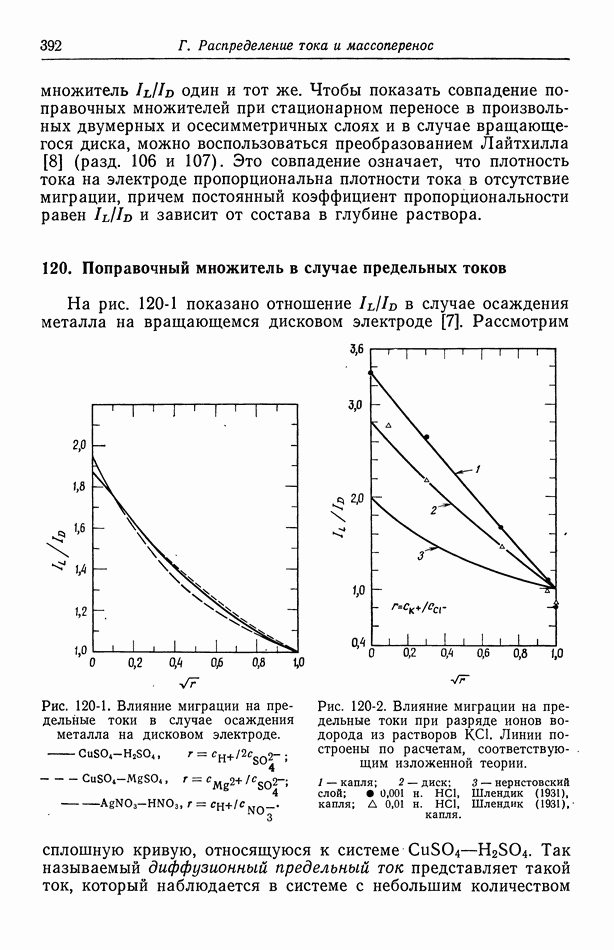
- 120. Поправочный множитель в случае предельных токов
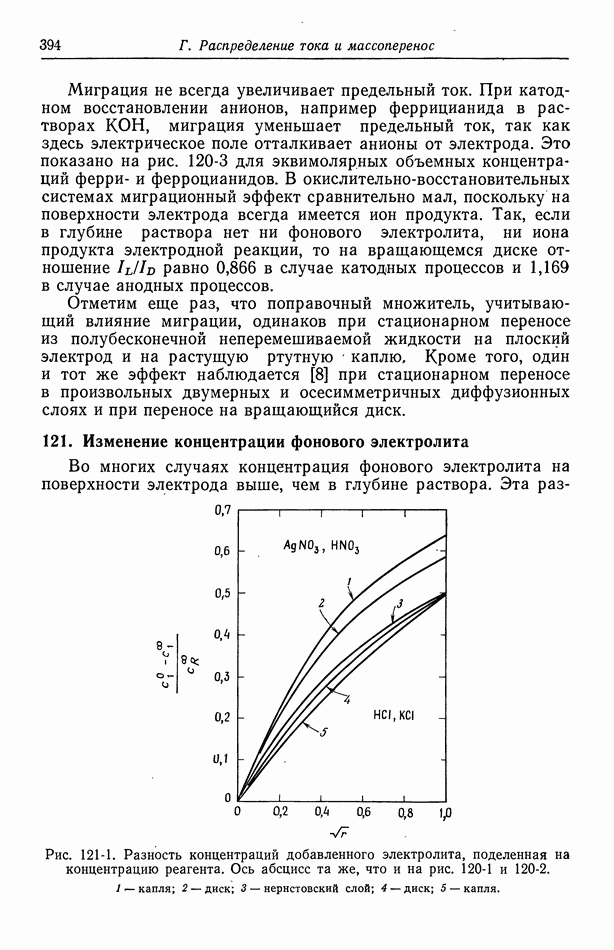
- 121. Изменение концентрации фонового электролита
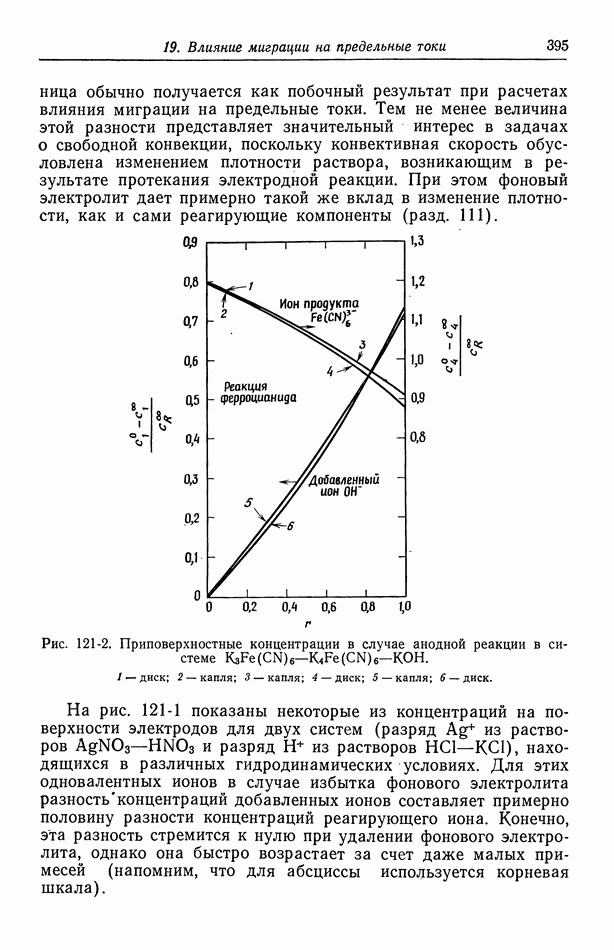
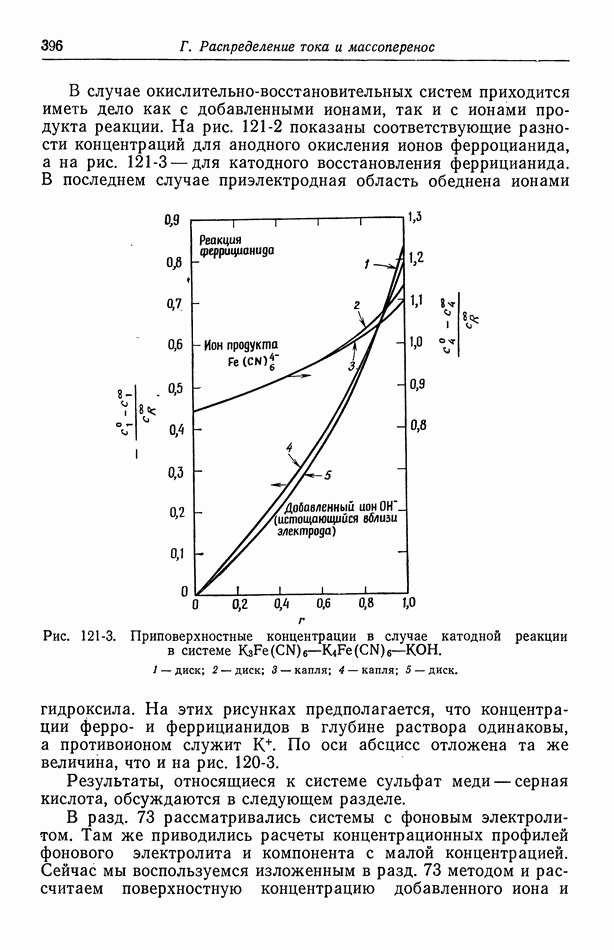
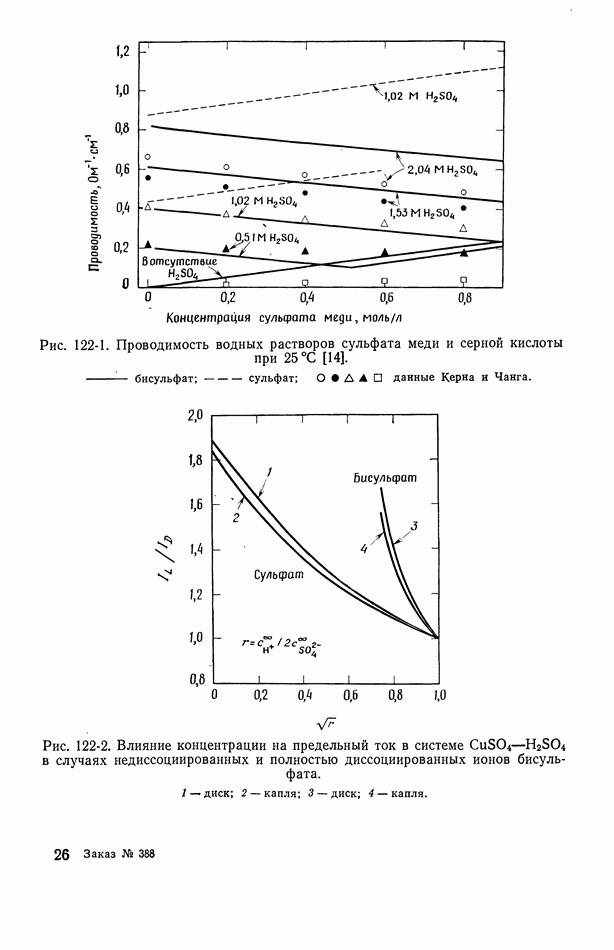
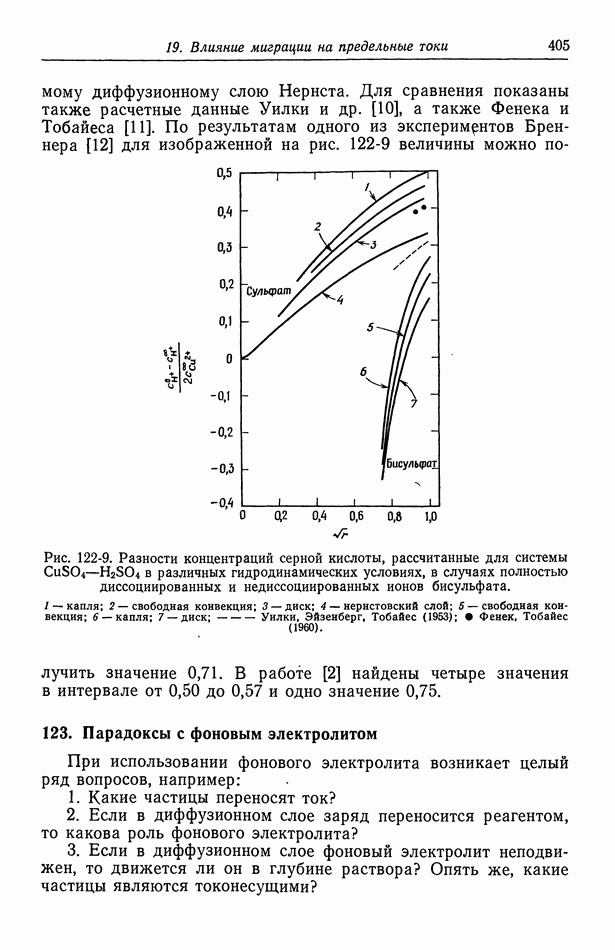
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
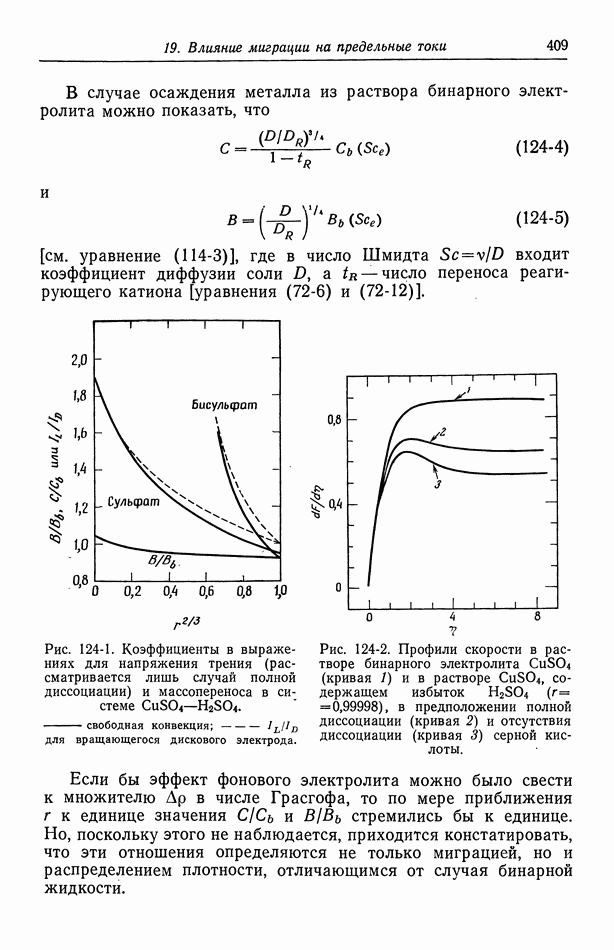
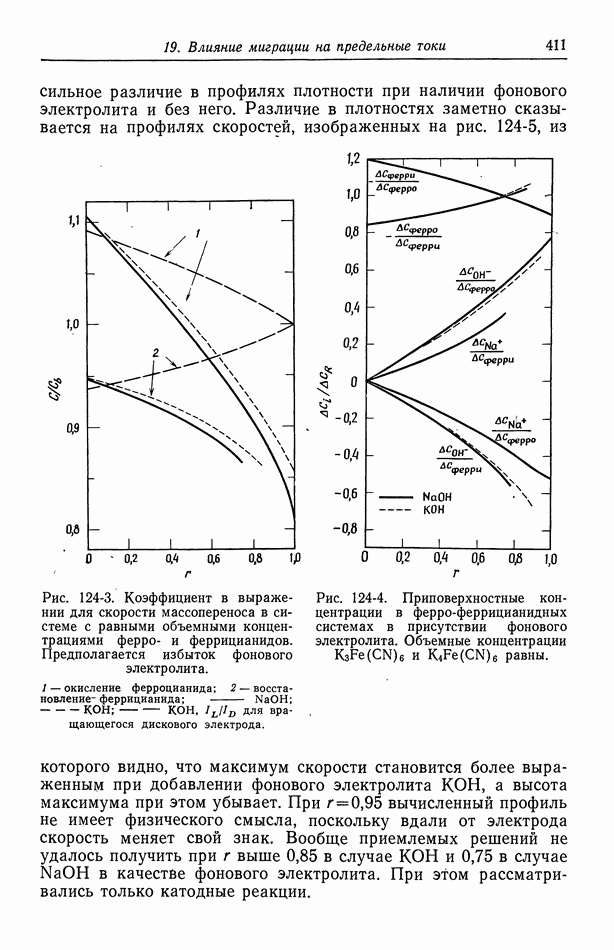
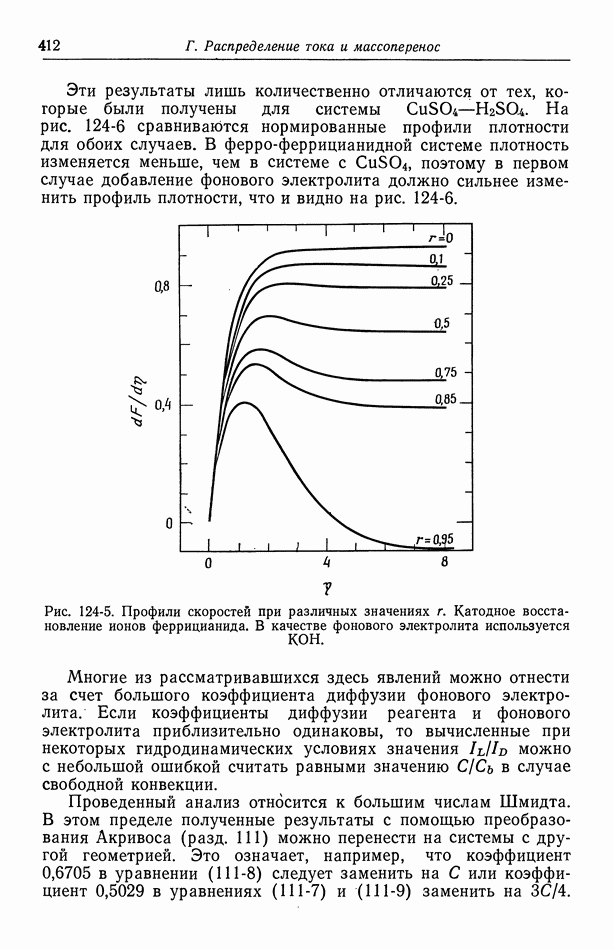
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ