| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
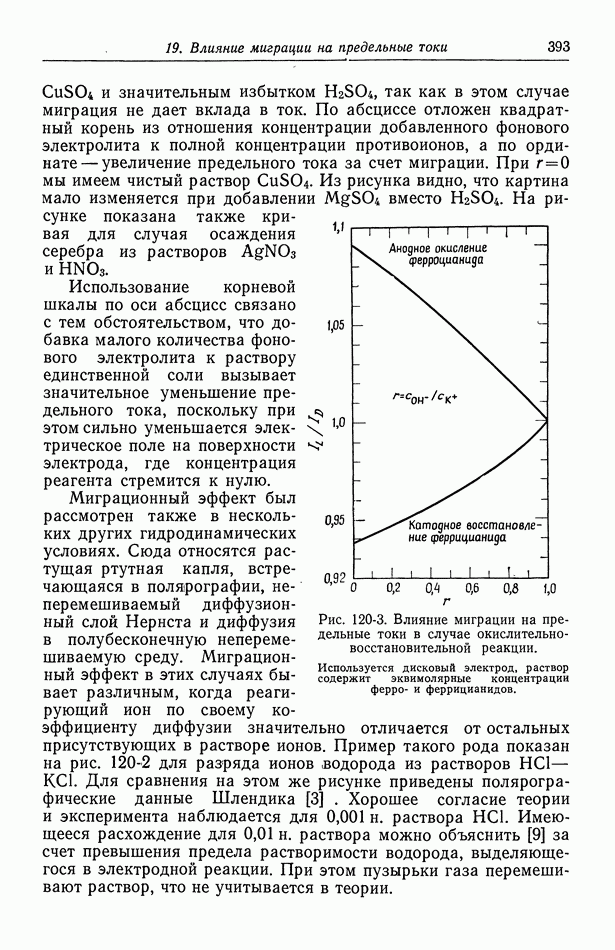
104. Задача Граца
Одна из важнейших задач, решенных в числе первых, — аналитическое описание массопереноса к стенке цилиндрической трубы с установившимся пуазейлевским течением:

Здесь через  обозначены цилиндрические координаты, причем z измеряется вдоль трубы,
обозначены цилиндрические координаты, причем z измеряется вдоль трубы,  радиальное расстояние от центра трубы. Хотя число Рейнольдса может достигать 2000, прежде чем течение станет турбулентным, рассматриваемое течение нельзя относить к типу, характеризующемуся наличием пограничного слоя.
радиальное расстояние от центра трубы. Хотя число Рейнольдса может достигать 2000, прежде чем течение станет турбулентным, рассматриваемое течение нельзя относить к типу, характеризующемуся наличием пограничного слоя.
Уравнением конвективной диффузии является

Мы будем рассматривать массоперенос при постоянной концентрации вблизи поверхности, начиная сточки  где пуазейлевское течение является полностью развитым:
где пуазейлевское течение является полностью развитым:

В случае предельного тока  Другие краевые условия можно записать в виде
Другие краевые условия можно записать в виде

Иными словами, входная концентрация равна  а из условий симметрии следует, что производная концентрации по радиусу в центре трубы равна нулю.
а из условий симметрии следует, что производная концентрации по радиусу в центре трубы равна нулю.
Введем безразмерные переменные:

Уравнение конвективной диффузии приобретает вид

где

есть число Пекле. Рассматривая большие числа Пекле, можно опустить вторую производную по

Полное количество вещества, переносимого к стенке на длине  равно
равно

или

где  среднее число Нуссельта, соответствующее входной разности концентраций.
среднее число Нуссельта, соответствующее входной разности концентраций.
Число Нуссельта является безразмерной скоростью массопереноса:

где поток  выражен в единицах характерного потока
выражен в единицах характерного потока  Здесь
Здесь  характерная длина,
характерная длина,  коэффициент диффузии и
коэффициент диффузии и  входная разность концентраций. Для локального числа Нуссельта используется локальный поток, а для среднего числа Нуссельта — средний поток. В тех случаях, когда можно пренебречь миграцией ионов, поток можно выразить через производную концентрации на стенке.
входная разность концентраций. Для локального числа Нуссельта используется локальный поток, а для среднего числа Нуссельта — средний поток. В тех случаях, когда можно пренебречь миграцией ионов, поток можно выразить через производную концентрации на стенке.

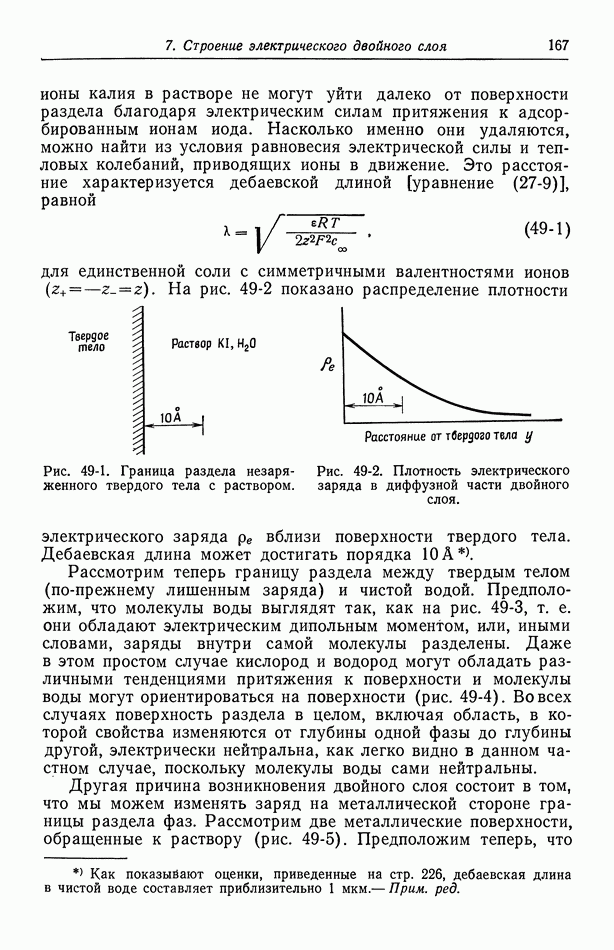
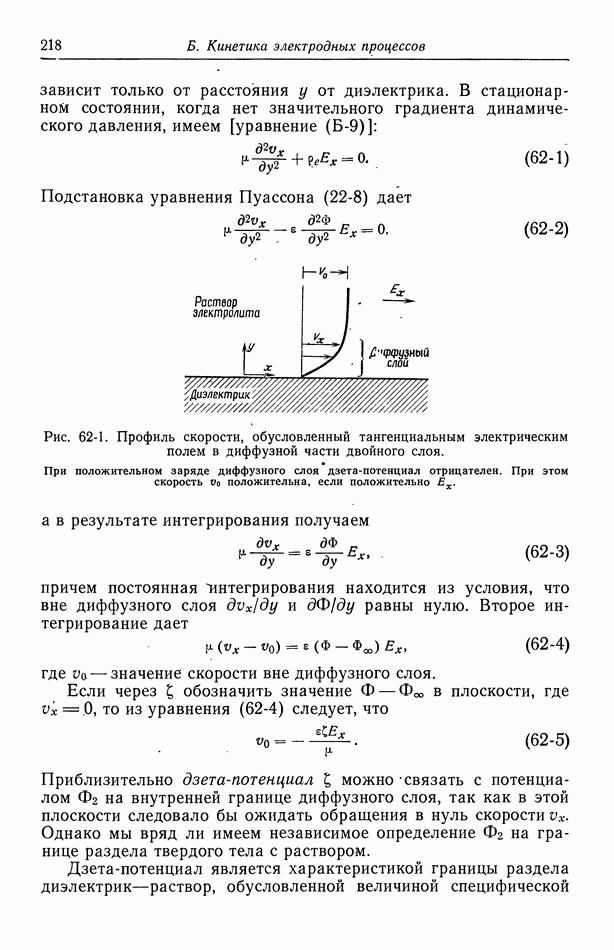
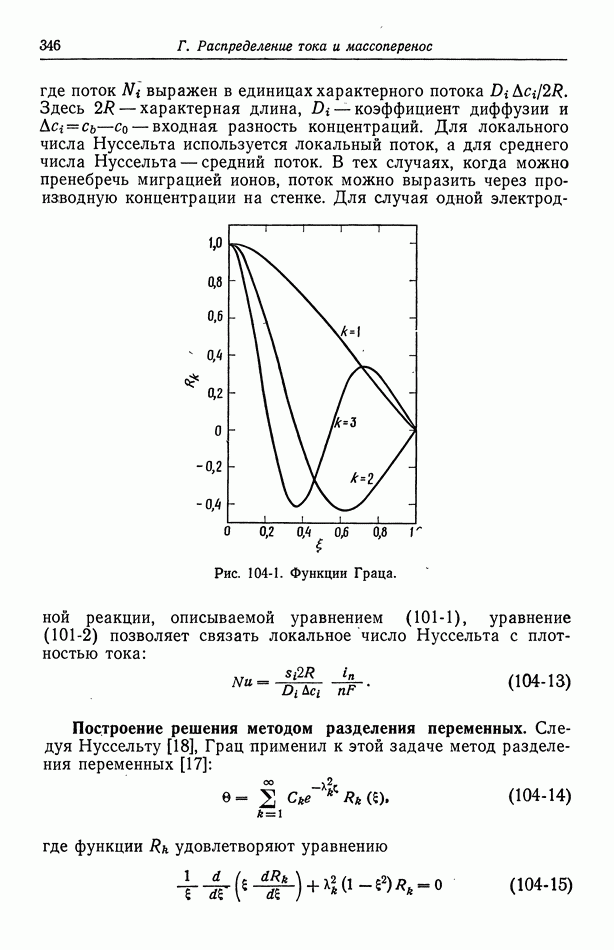
Рис. 104-1. Функции Граца.
Для случая одной электродной реакции, описываемой уравнением (101-1), уравнение (101-2) позволяет связать локальное число Нуссельта с плотностью тока:

Построение решения методом разделения переменных. Следуя Нуссельту [18], Грац применил к этой задаче метод разделения переменных [17]:

где функции  удовлетворяют уравнению
удовлетворяют уравнению

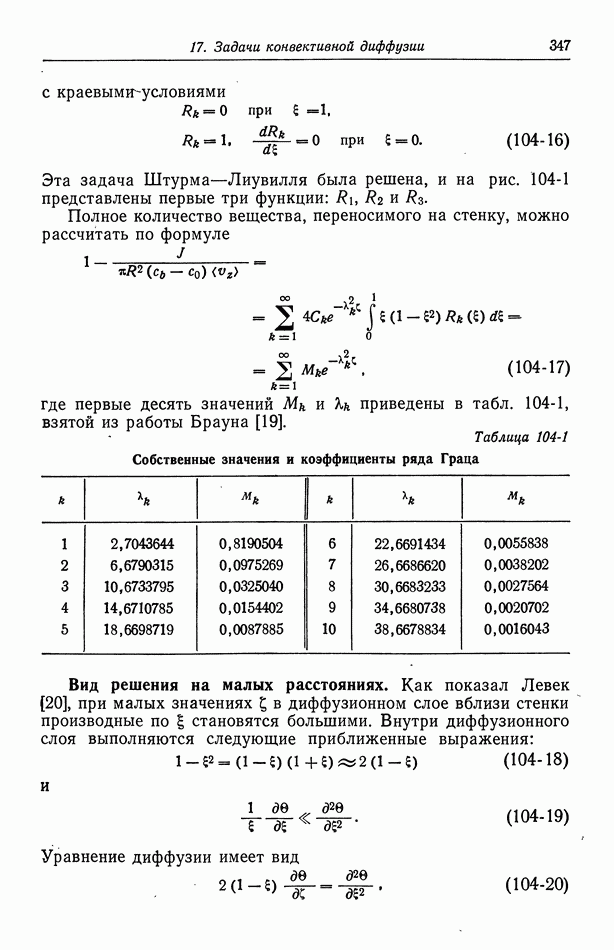
с краевымиусловиями

Эта задача Штурма-Лиувилля была решена, и на рис. 104-1 представлены первые три функции: 
Полное количество вещества, переносимого на стенку, можно рассчитать по формуле

где первые десять значений  приведены в табл. 104-1, взятой из работы Брауна [19].
приведены в табл. 104-1, взятой из работы Брауна [19].
Таблица 104-1 (см. скан) Собственные значения и коэффициенты ряда Граца
Вид решения на малых расстояниях. Как показал Левек [20], при малых значениях  в диффузионном слое вблизи стенки производные по
в диффузионном слое вблизи стенки производные по  становятся большими. Внутри диффузионного слоя выполняются следующие приближенные выражения:
становятся большими. Внутри диффузионного слоя выполняются следующие приближенные выражения:

и

Уравнение диффузии имеет вид

а краевыми условиями служат

Кроме того, вне диффузионного слоя в приближается, к 1. Преобразование подобия

сводит уравнение диффузии к обыкновенному дифференциальному уравнению

решением которого является

Выраженный через физические переменные, параметр подобия можно записать в виде

Здесь

есть расстояние от стенки. Определяемая равенством (104-24) функция изображена на рис. 102-1, где  представлено в виде абсциссы
представлено в виде абсциссы
Полное количество вещества, переносимого на стенку, равно

Из этого выражения видно (лучше, чем из ряда Граца), что скорость массопереноса вблизи начального сечения не ограничена.
Обобщение решения Левека. Имея приближенное решение на малых расстояниях, можно получить [21] поправочные члены, которые учитывают приближения (104-18) и (104-19) и подтверждают их справедливость. Исходя из этого, среднее число Нуссельта, относящееся к разности концентраций на входном участке, можно выразить в виде

Локальное число Нуссельта равно

В противоположность ряду Граца ряд Левека не сходится при всех значениях  Этот ряд полезен лишь при малых значениях
Этот ряд полезен лишь при малых значениях 
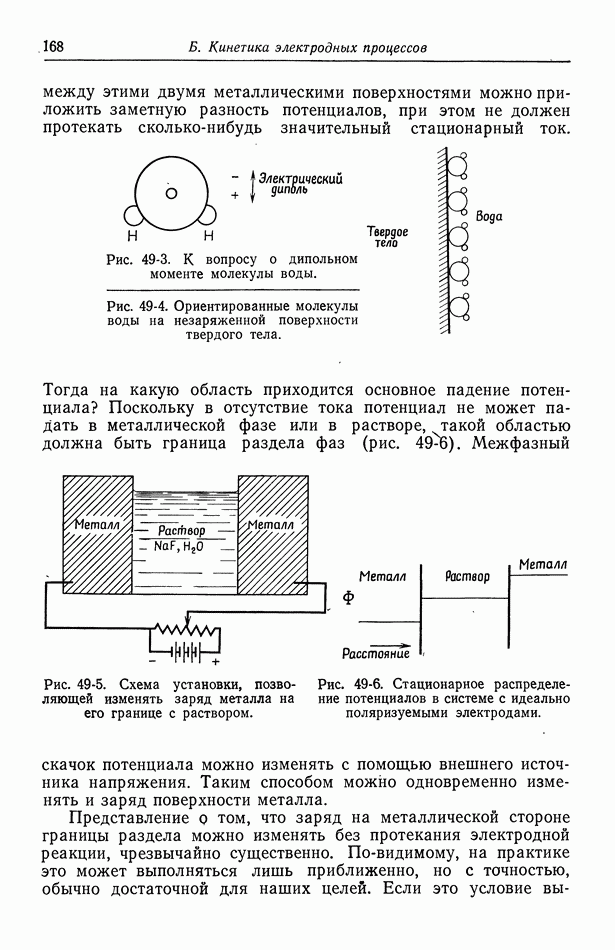
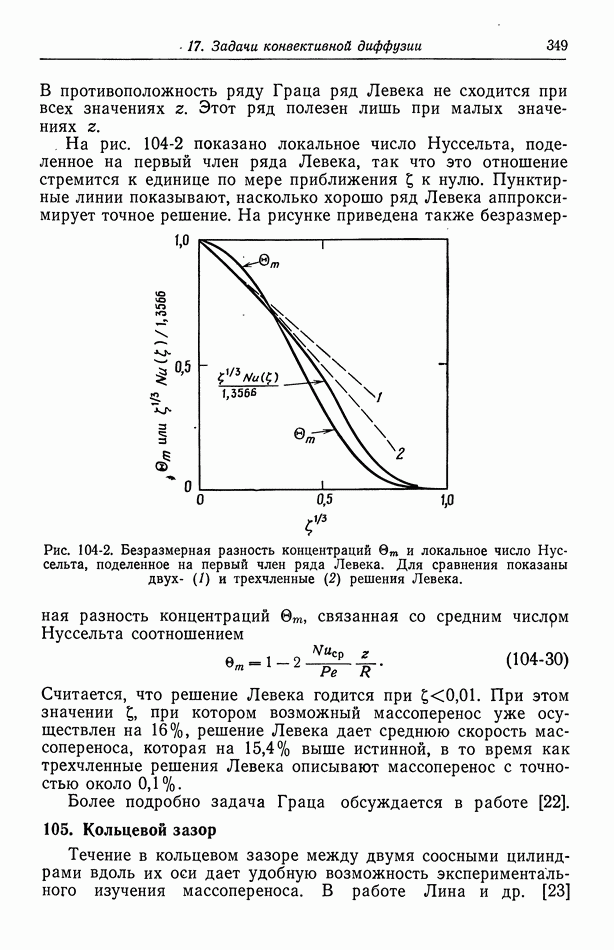
На рис. 104-2 показано локальное число Нуссельта, поделенное на первый член ряда Левека, так что это отношение стремится к единице по мере приближения  к нулю. Пунктирные линии показывают, насколько хорошо ряд Левека аппроксимирует точное решение.
к нулю. Пунктирные линии показывают, насколько хорошо ряд Левека аппроксимирует точное решение.

Рис. 104-2. Безразмерная разность концентраций  и локальное число Нуссельта, поделенное на первый член ряда Левека. Для сравнения показаны двух- (1) и трехчленные (2) решения Левека.
и локальное число Нуссельта, поделенное на первый член ряда Левека. Для сравнения показаны двух- (1) и трехчленные (2) решения Левека.
На рисунке приведена также безразмерная разность концентраций  связанная со средним числрм Нуссельта соотношением
связанная со средним числрм Нуссельта соотношением

Считается, что решение Левека годится при  При этом значении при котором возможный массоперенос уже осуществлен на 16%, решение Левека дает среднюю скорость массопереноса, которая на 15,4% выше истинной, в то время как трехчленные решения Левека описывают массоперенос с точностью около
При этом значении при котором возможный массоперенос уже осуществлен на 16%, решение Левека дает среднюю скорость массопереноса, которая на 15,4% выше истинной, в то время как трехчленные решения Левека описывают массоперенос с точностью около 
Более подробно задача Граца обсуждается в работе [22].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
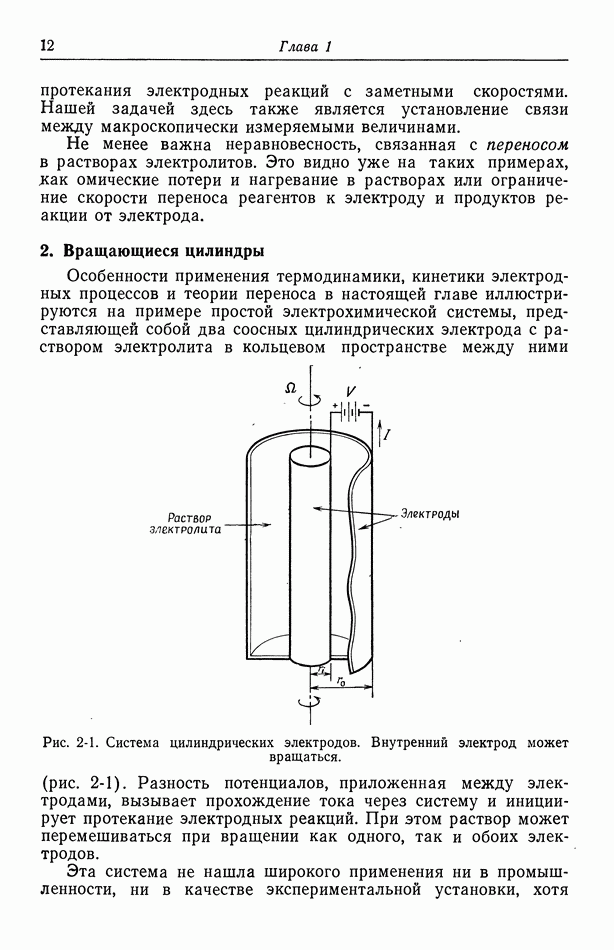
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
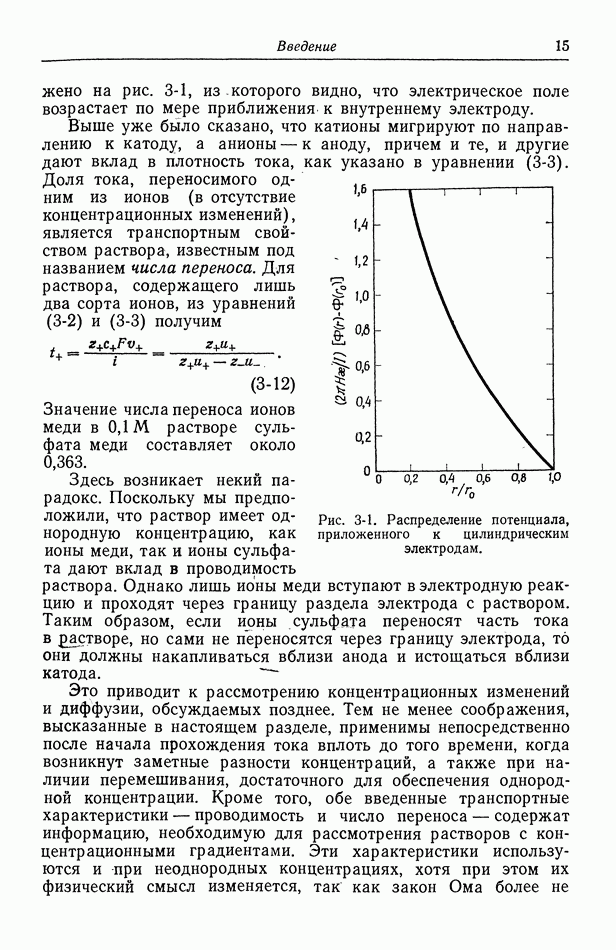
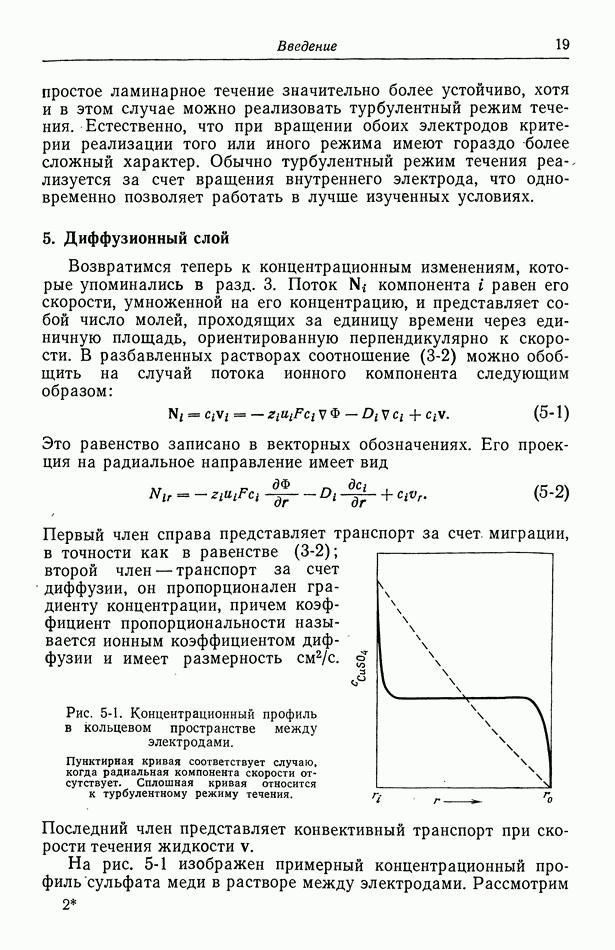
- 5. Диффузионный слой
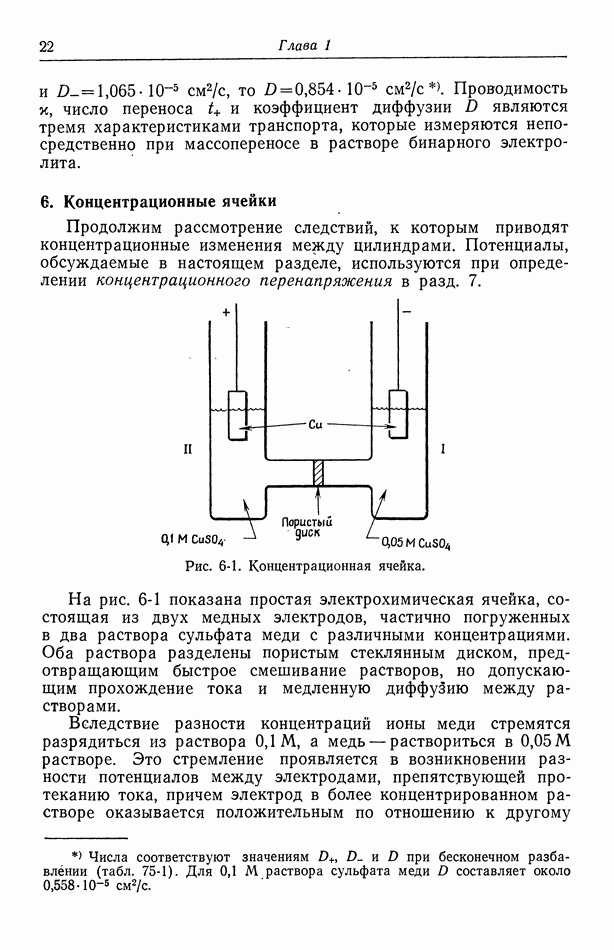
- 6. Концентрационные ячейки
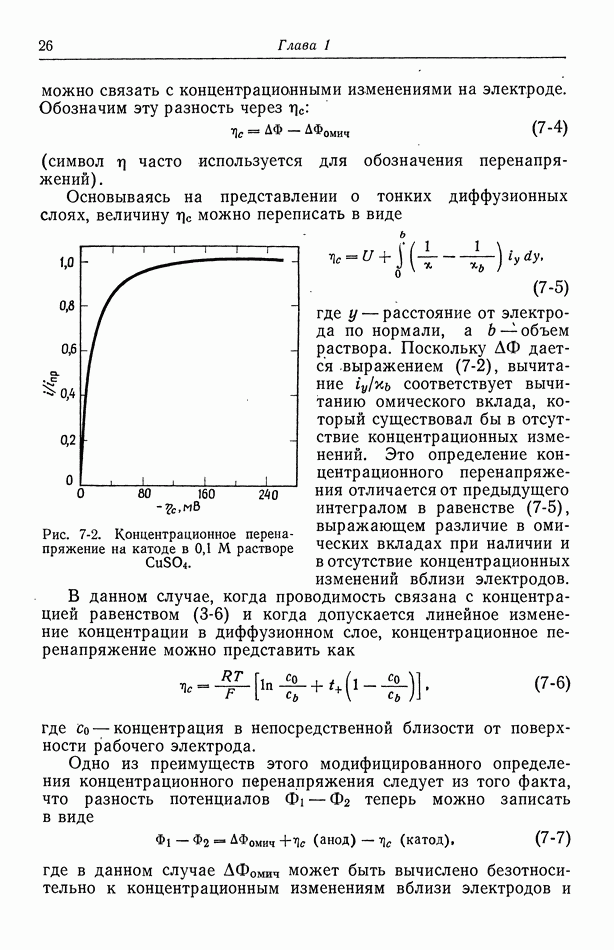
- 7. Концентрационное перенапряжение
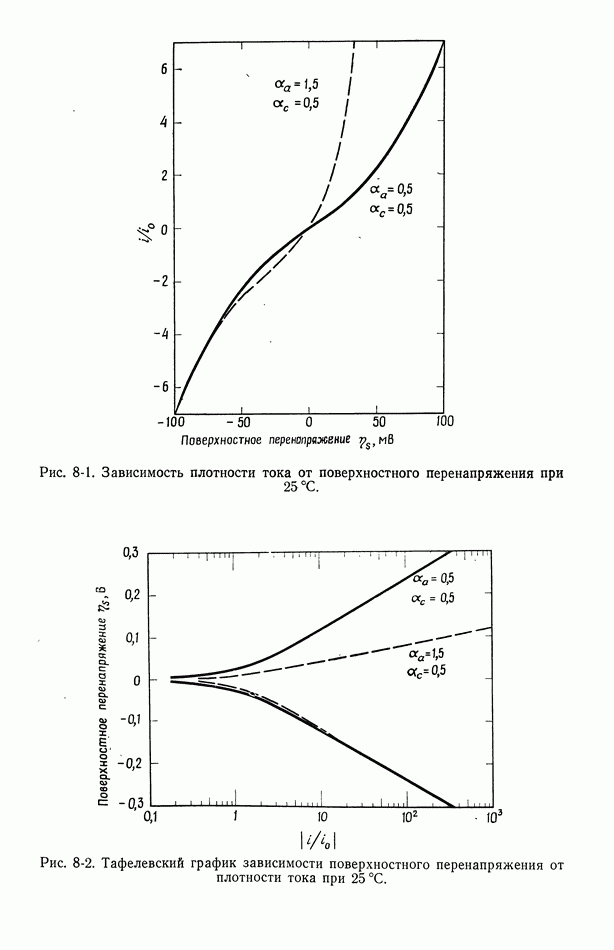
- 8. Поверхностное перенапряжение
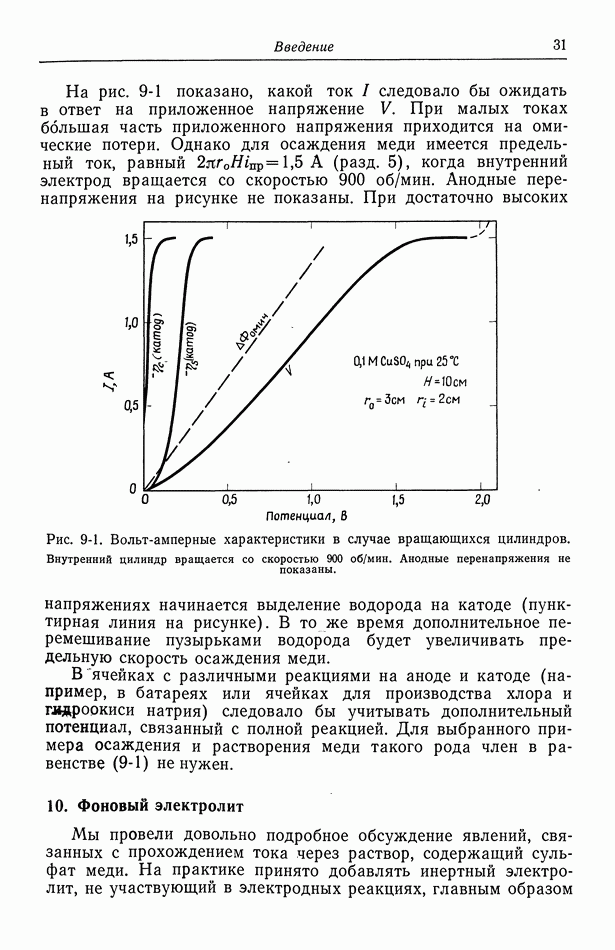
- 9. Потенциал ячейки
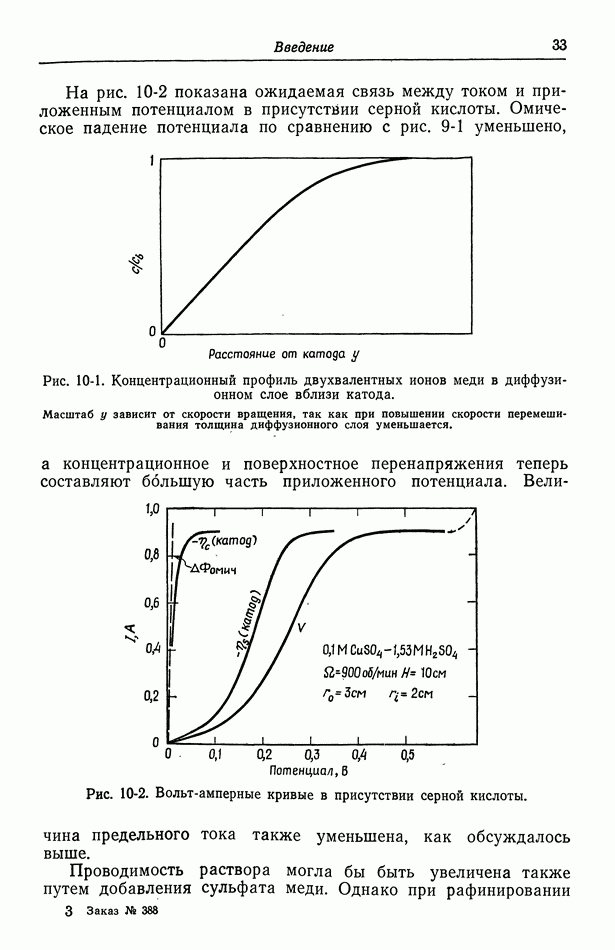
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
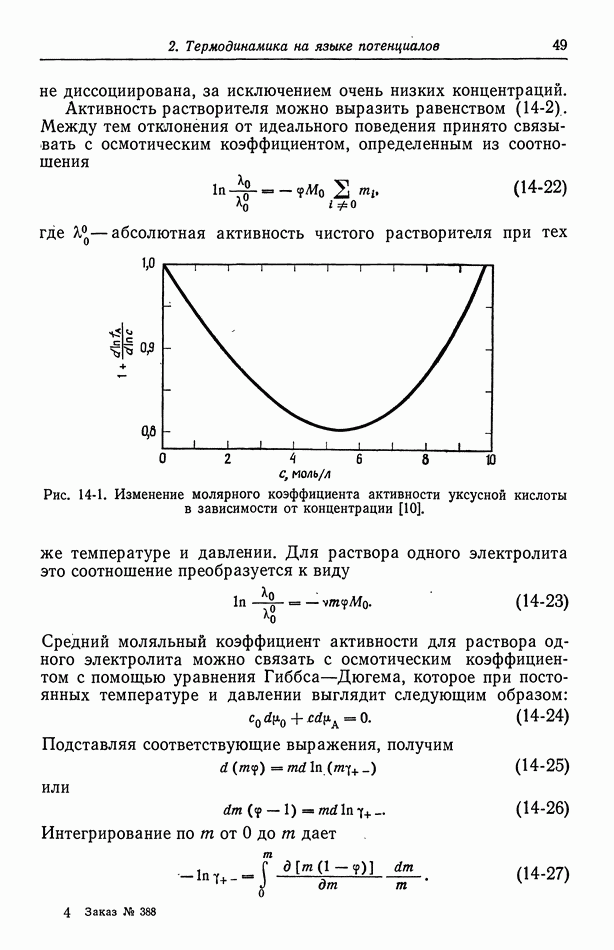
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
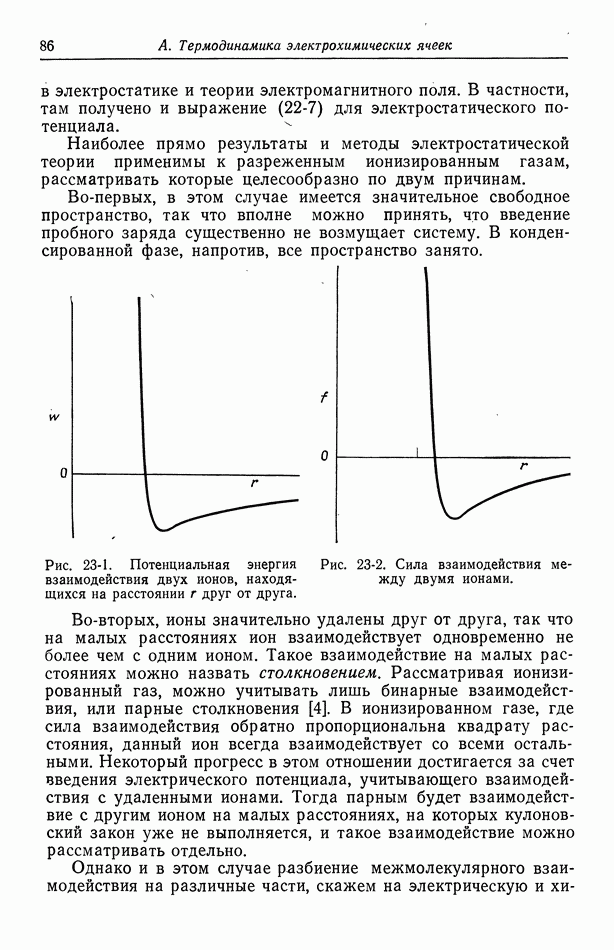
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
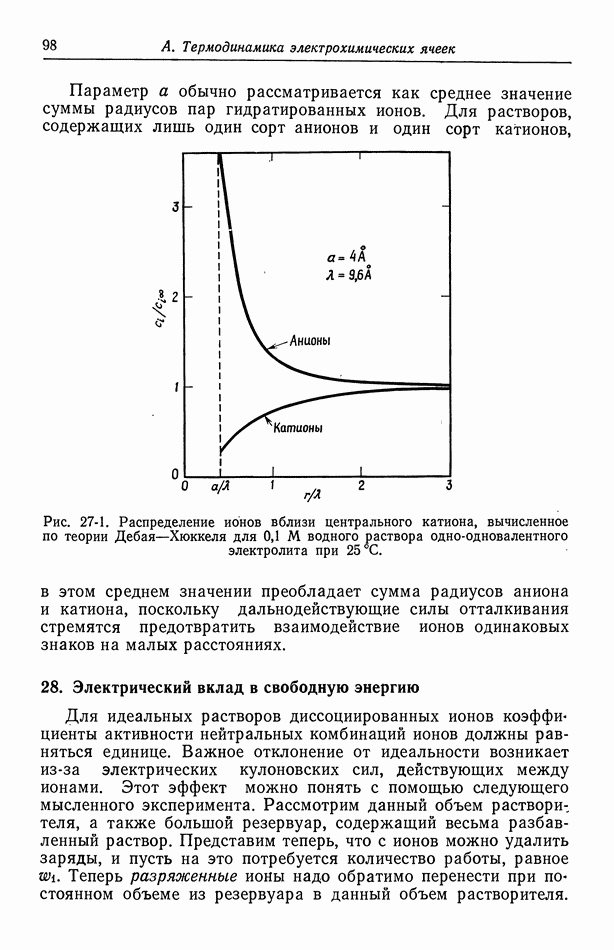
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
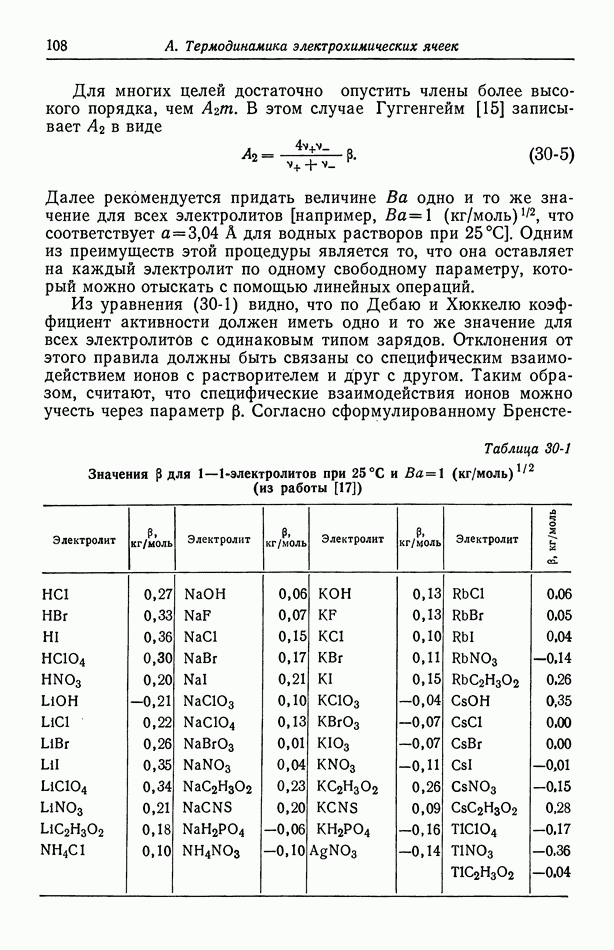
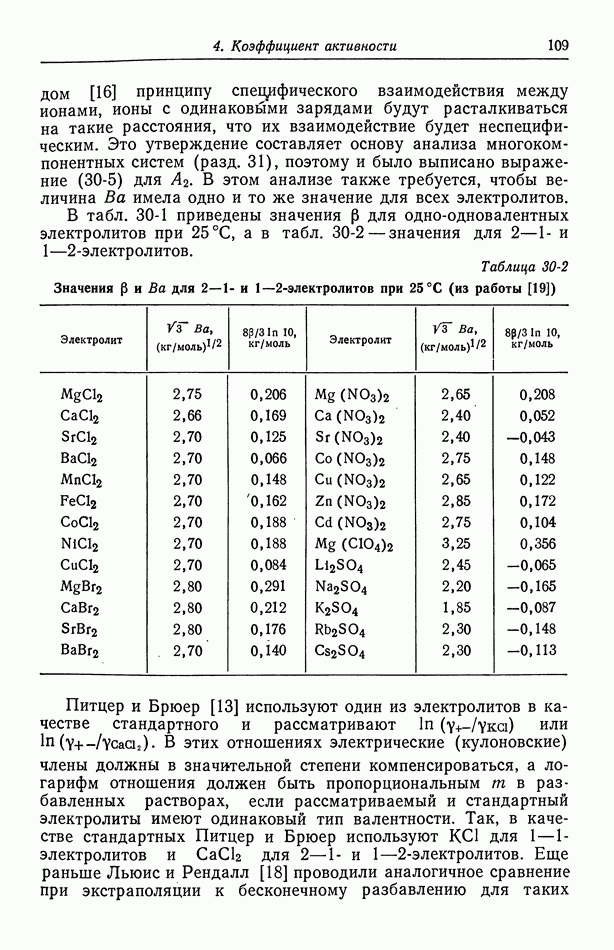
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
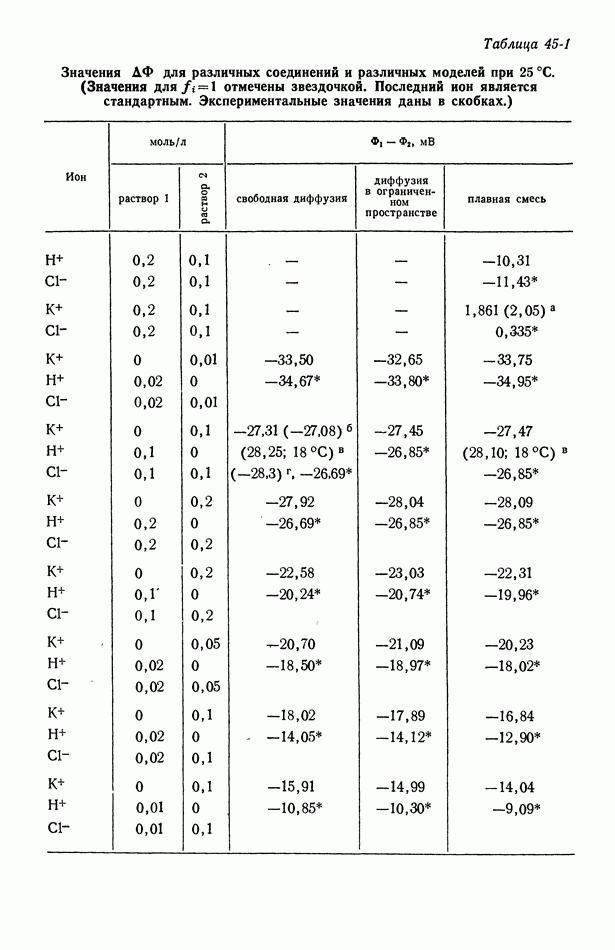
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
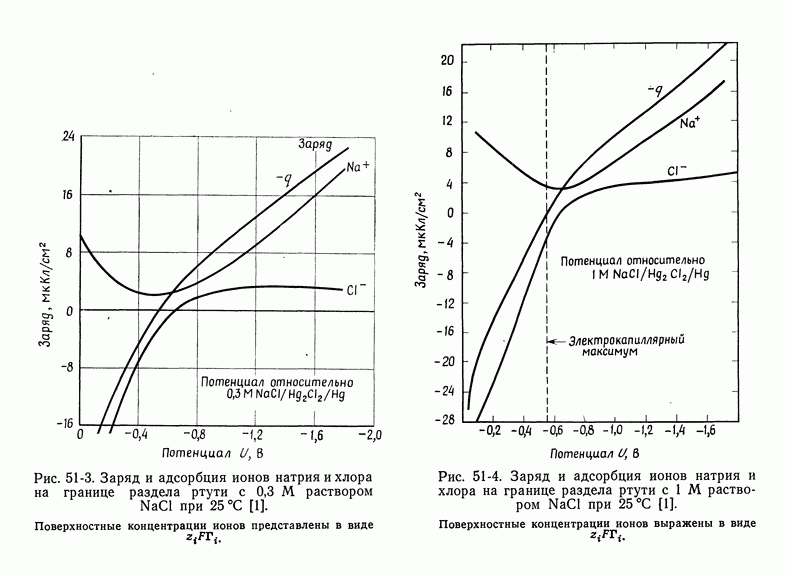
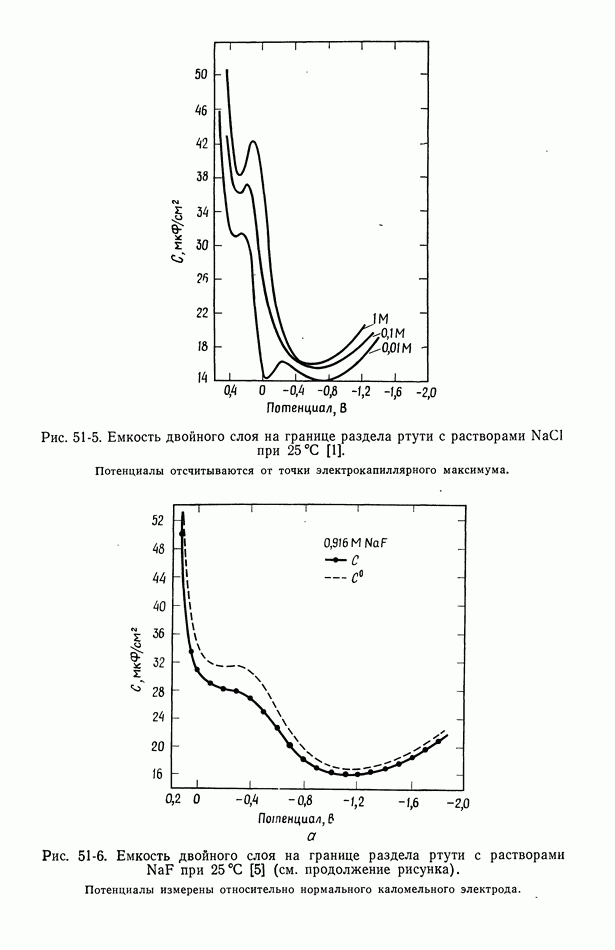
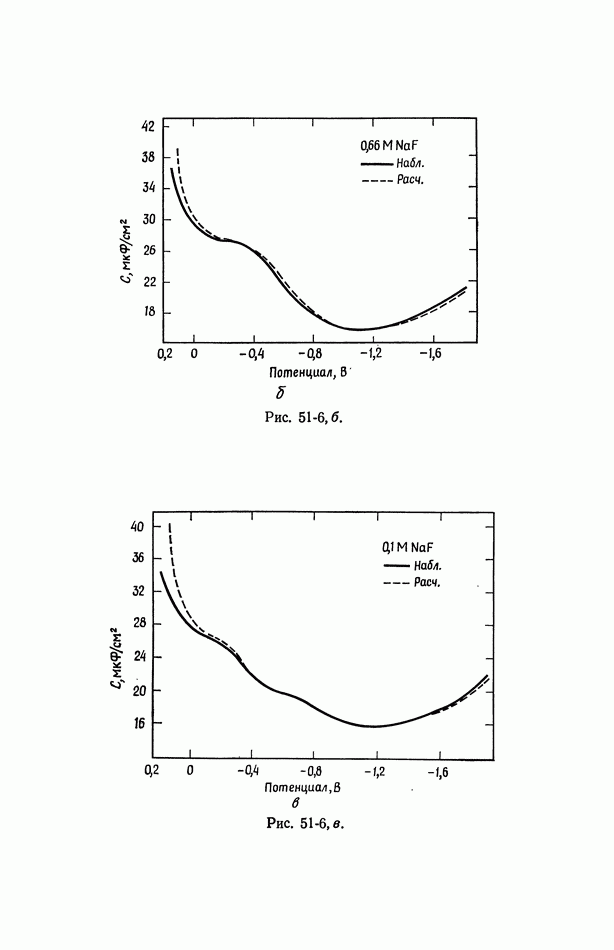
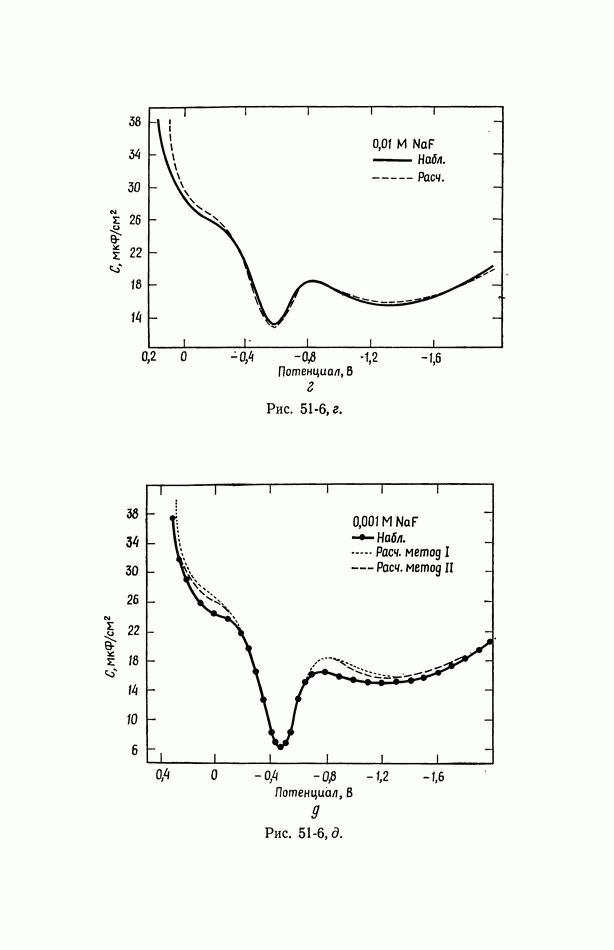
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
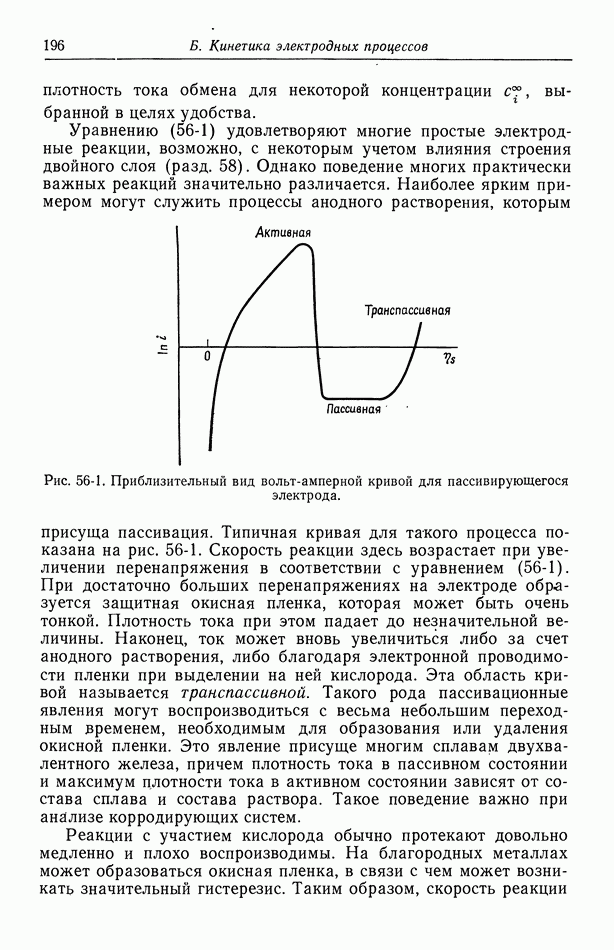
- 56. Зависимость плотности тока от поверхностного перенапряжения
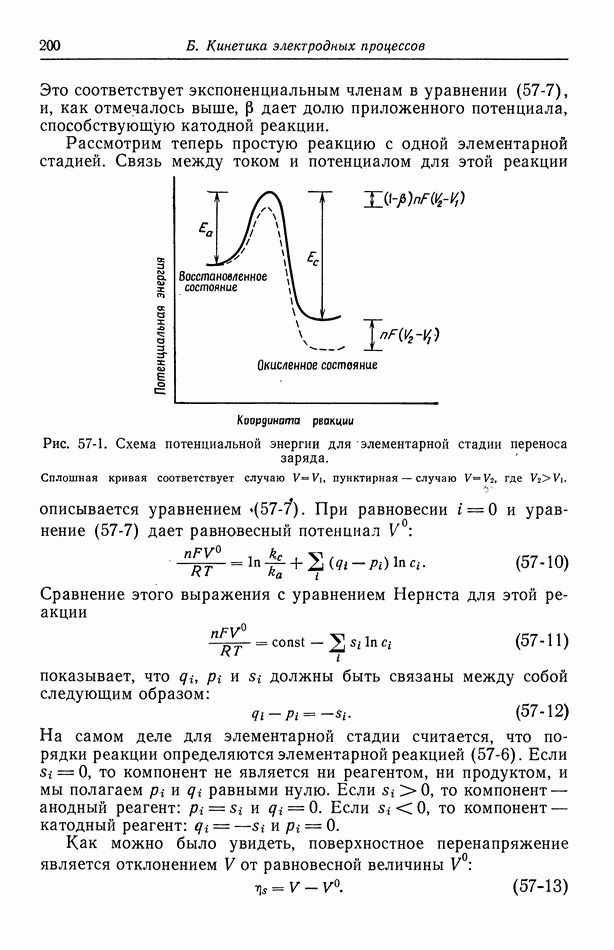
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
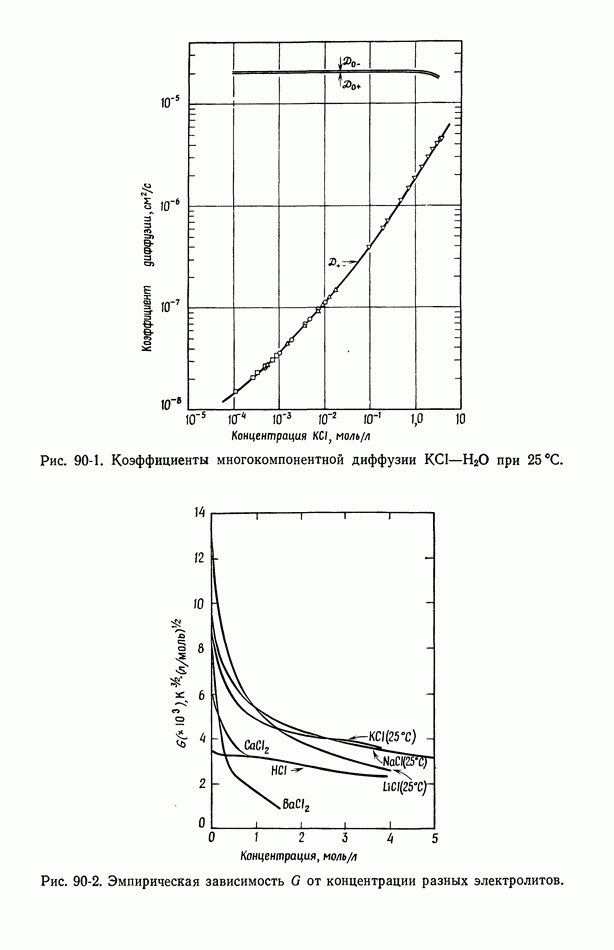
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
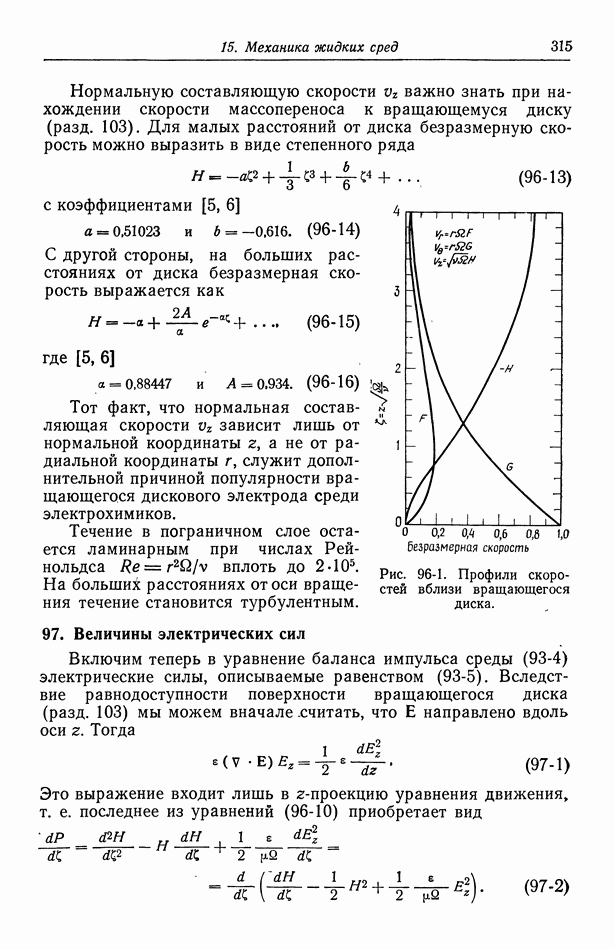
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
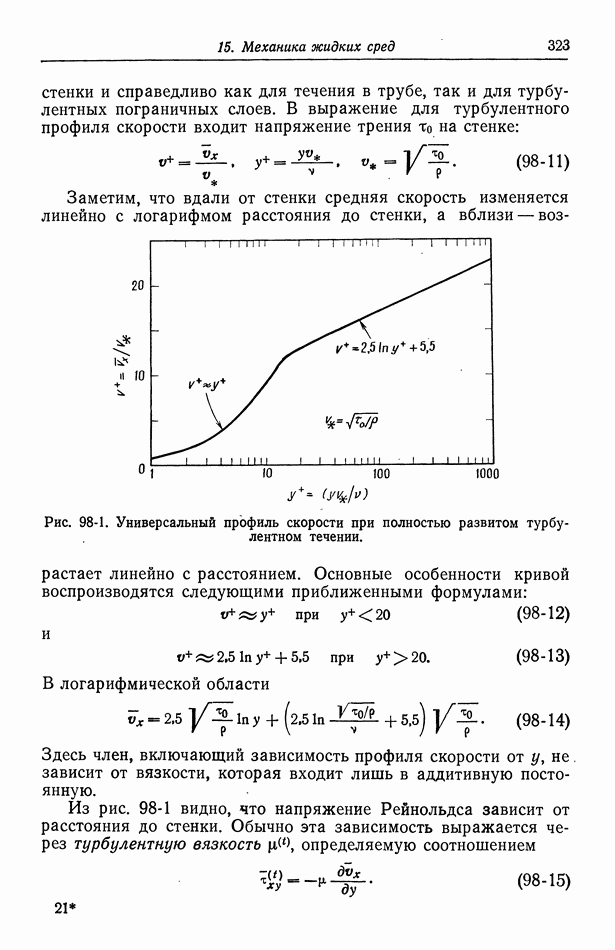
- 98. Турбулентное течение
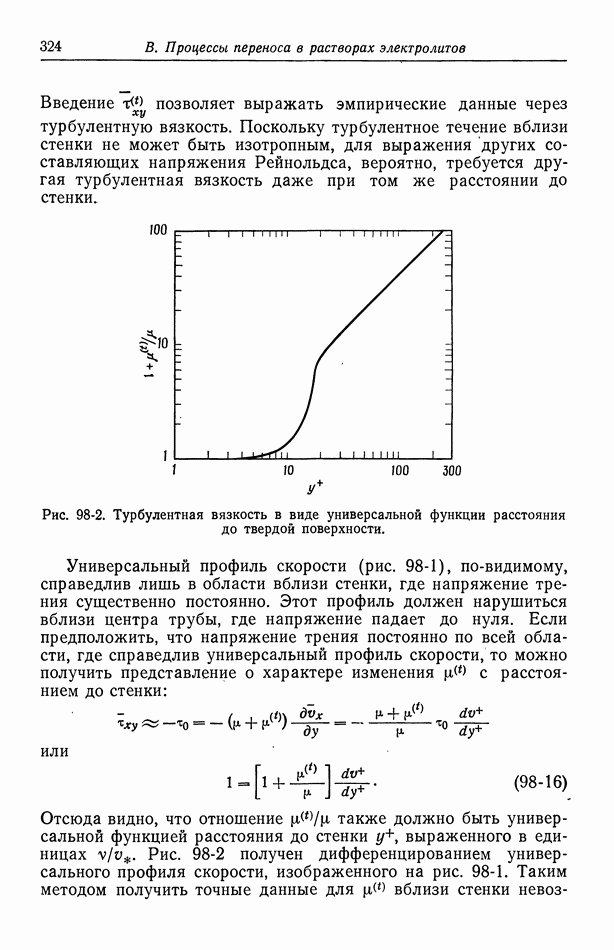
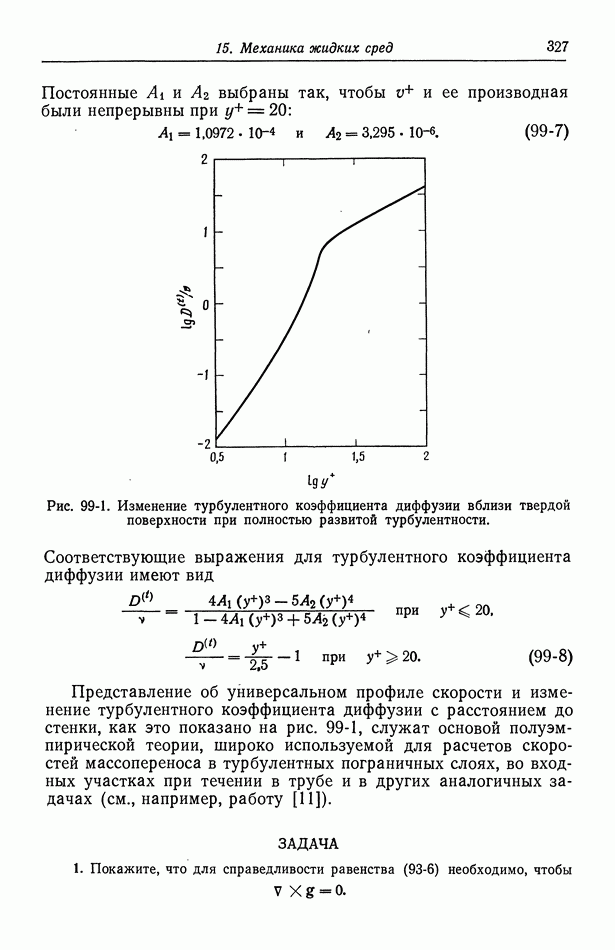
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
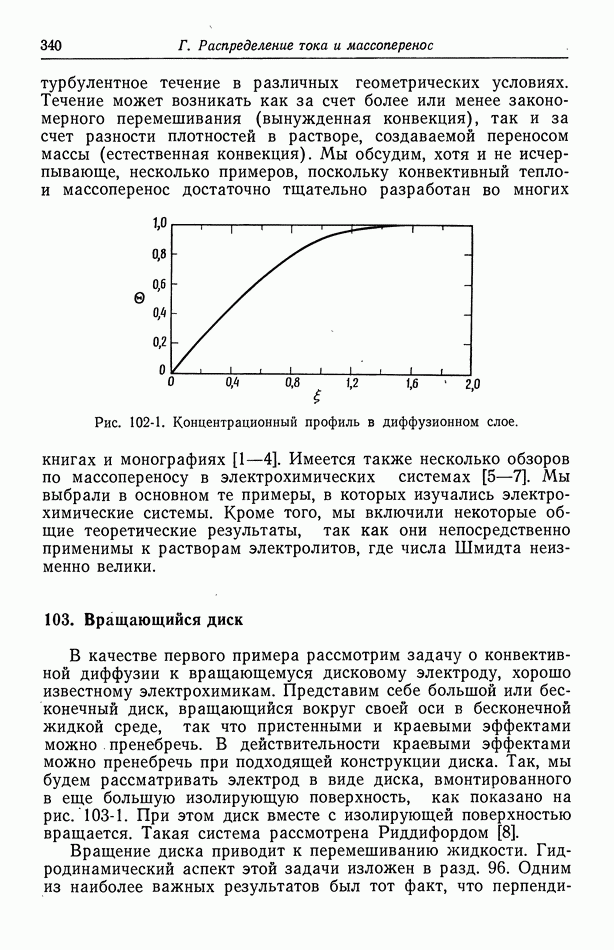
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
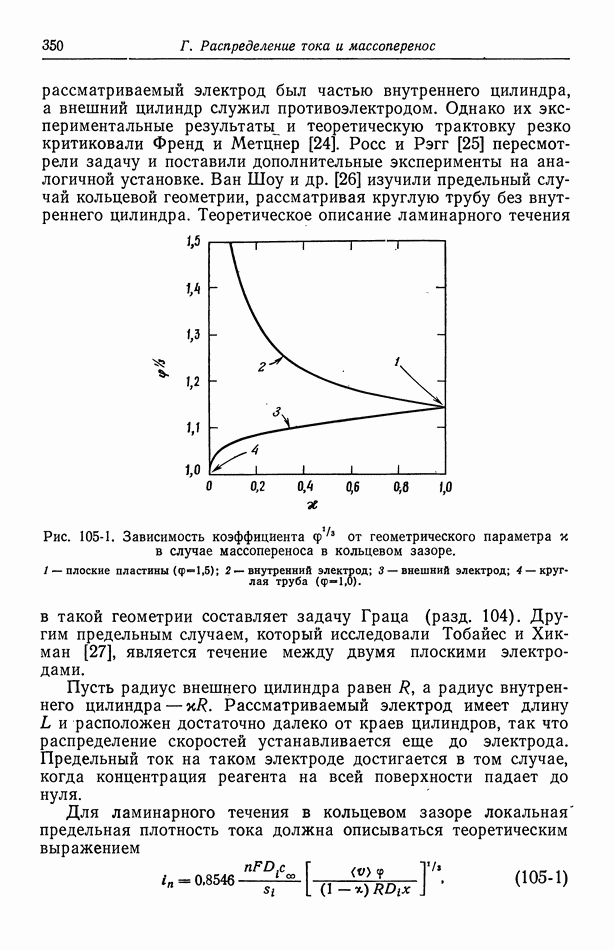
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
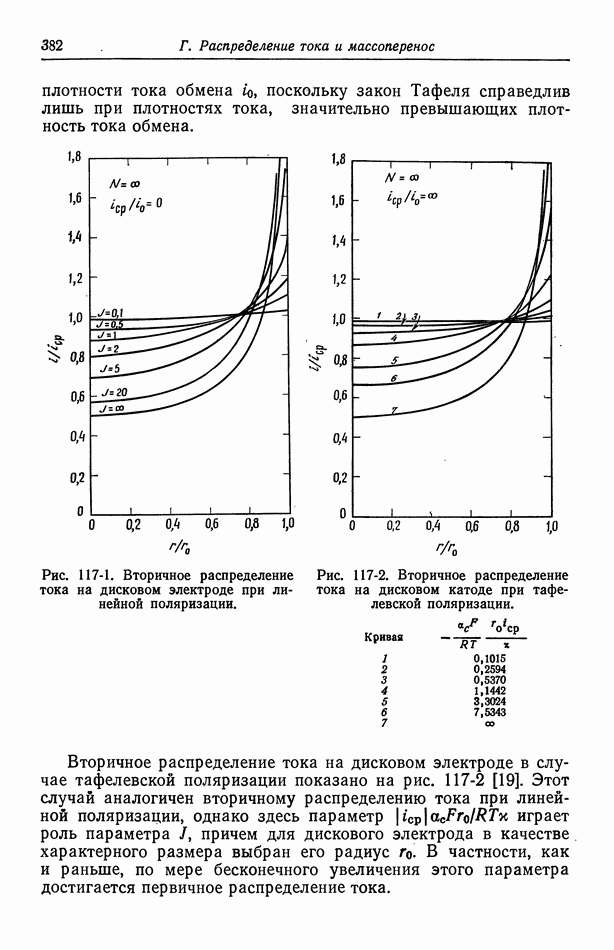
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
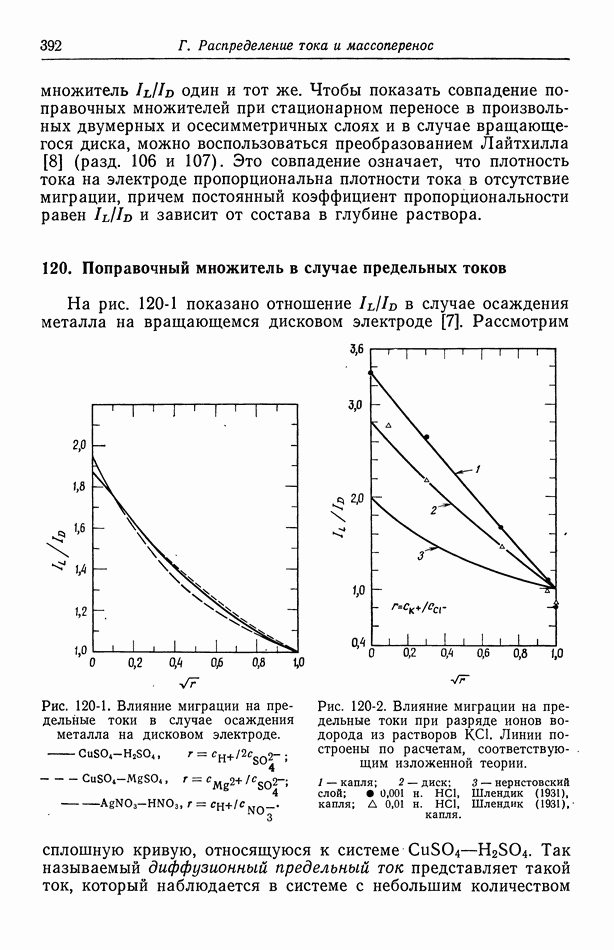
- 120. Поправочный множитель в случае предельных токов
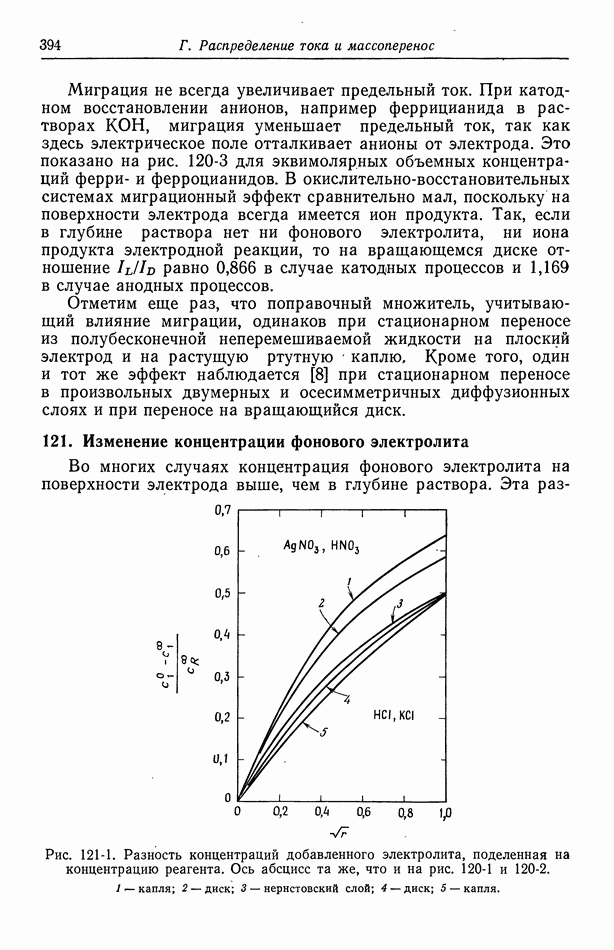
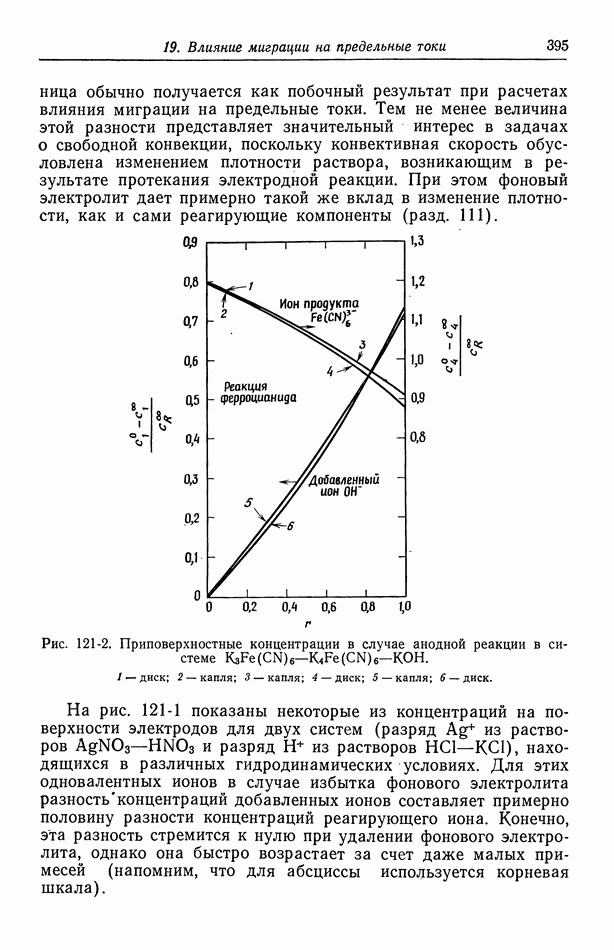
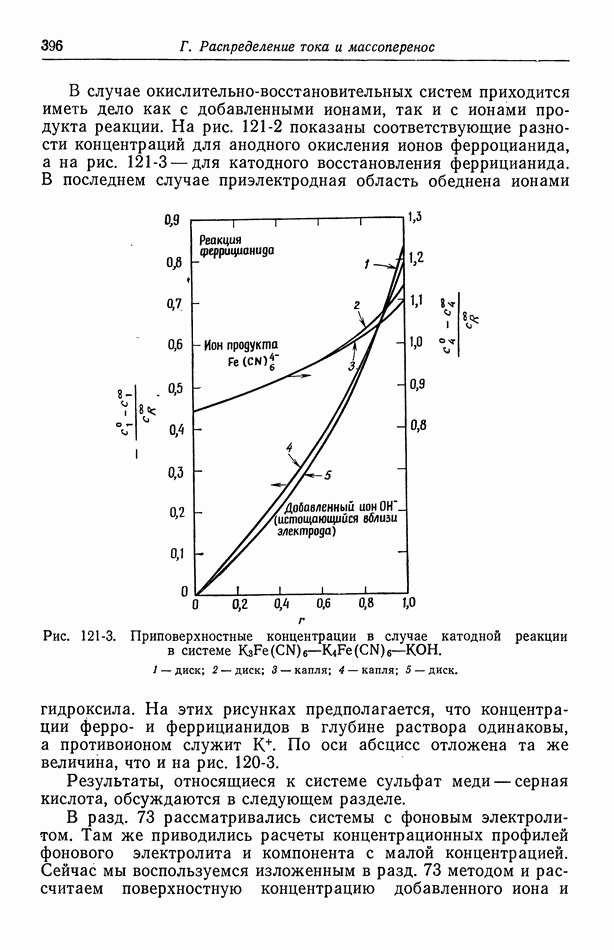
- 121. Изменение концентрации фонового электролита
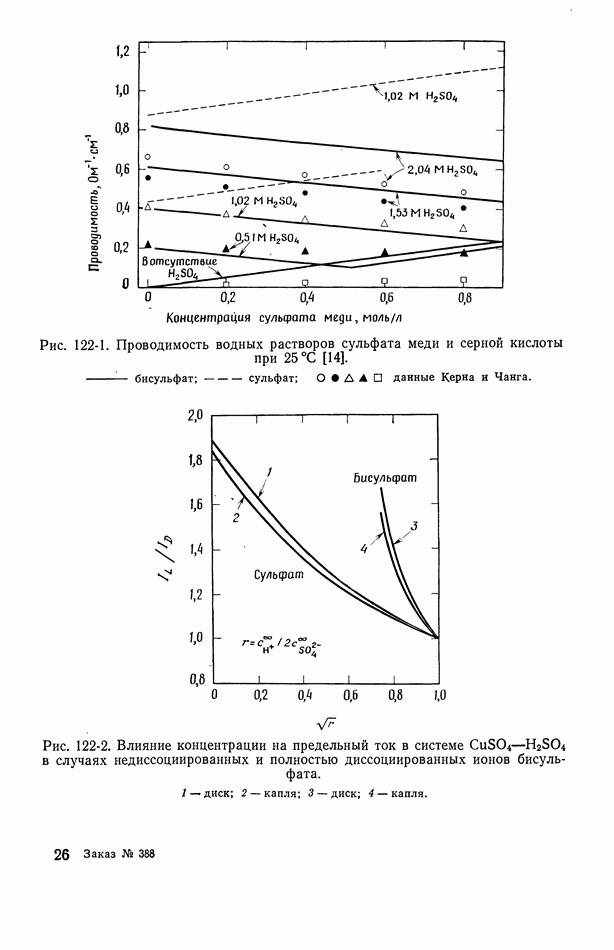
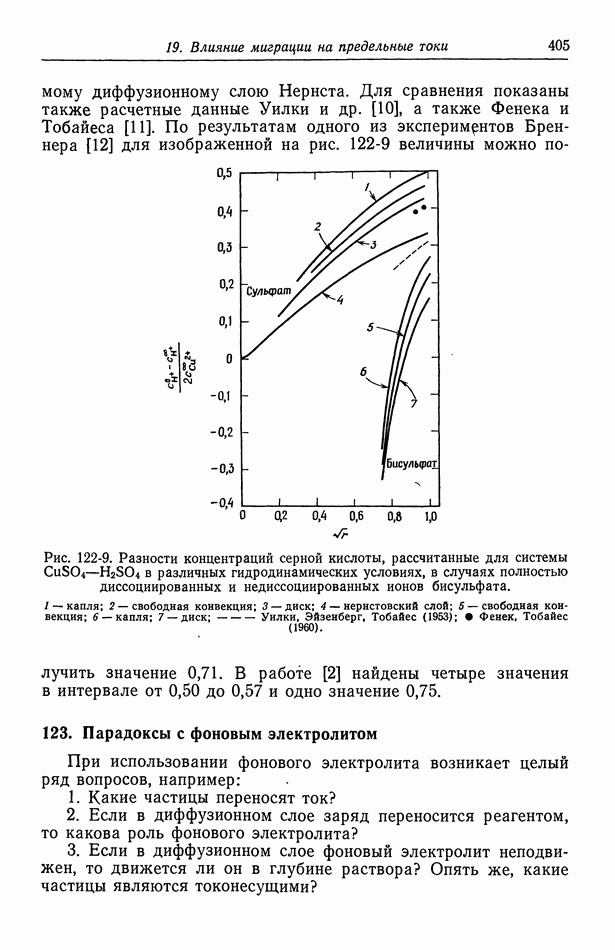
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
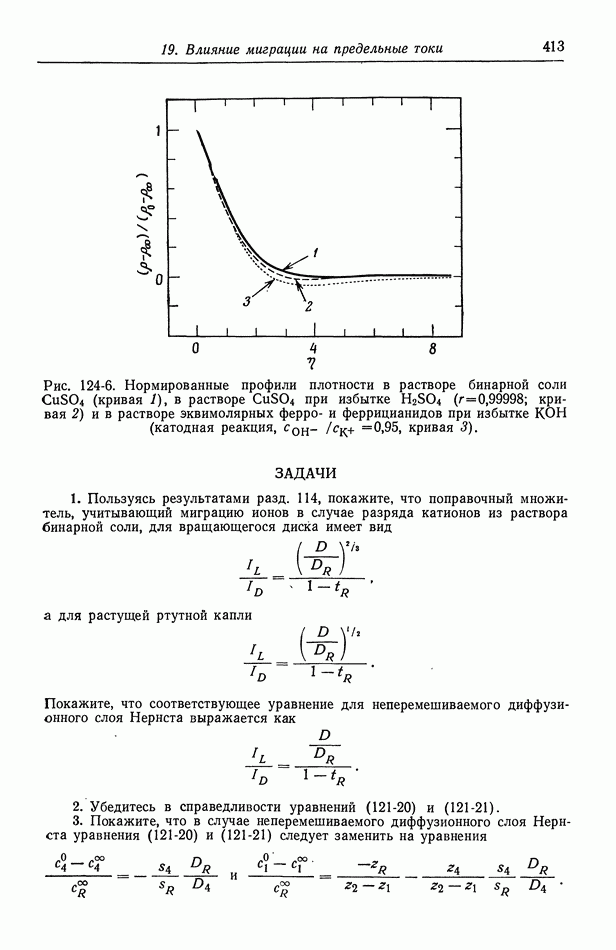
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
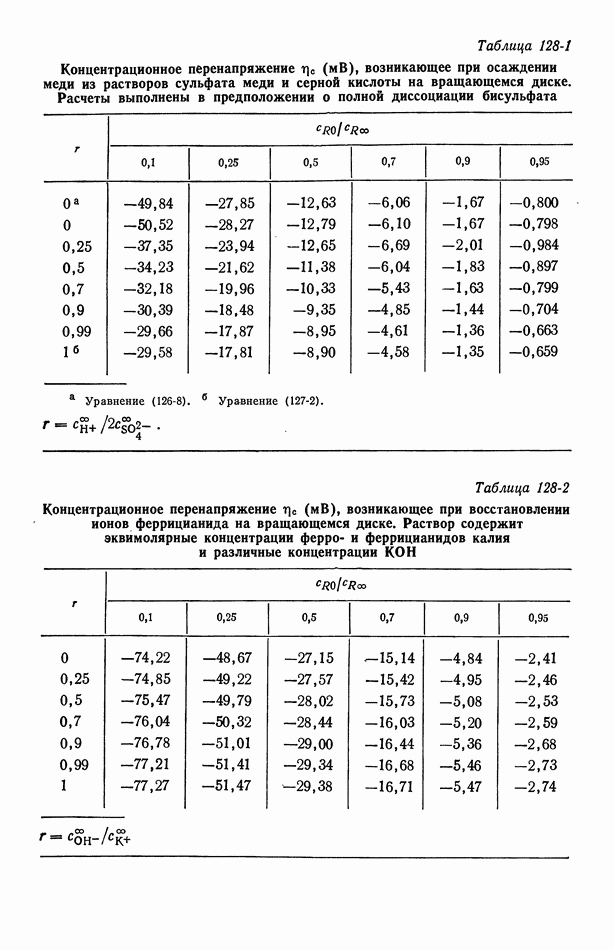
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
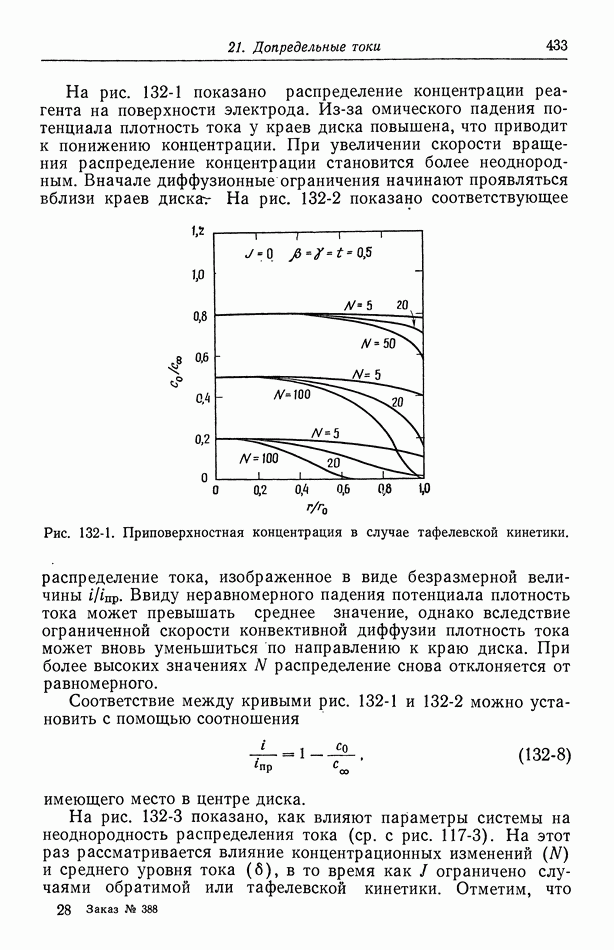
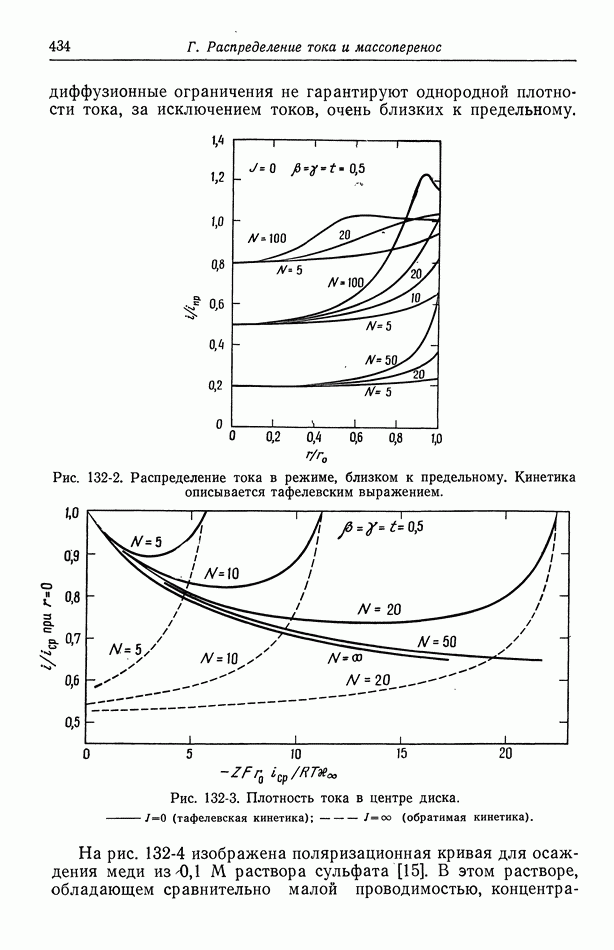
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ