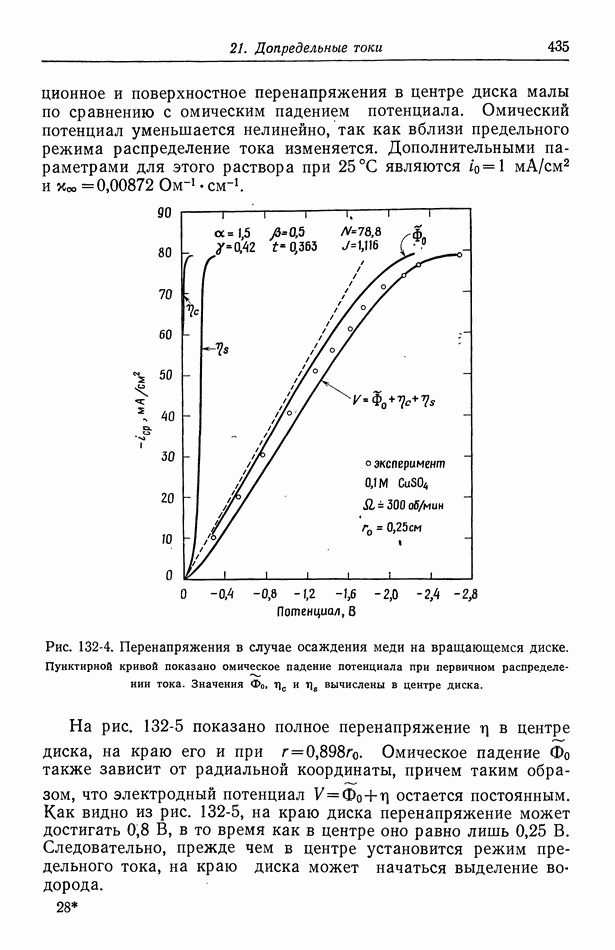
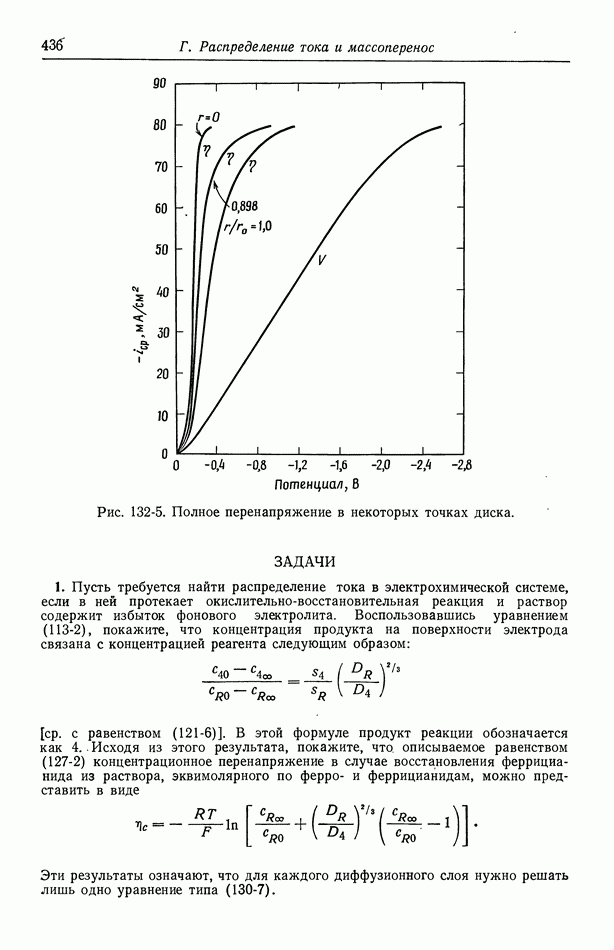
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
26. Электрический потенциал в термодинамике
Рассматриваемый в термодинамике потенциал связан с энергией, необходимой для обратимого переноса ионов из одной фазы в другую. Таким потенциалом, конечно, является электрохимический потенциал ионного компонента. Электростатический потенциал, кроме задач, связанных с его определением в конденсированных фазах, не связан непосредственно с обратимой работой. Хотя в термодинамике можно обойтись без электростатического потенциала за счет использования вместо него электрохимического потенциала, потребность в описании электрического состояния фазы остается.
Часто электрохимический потенциал ионного компонента представляют в виде суммы электрического и «химического» членов:

где  — «электростатический» потенциал, а
— «электростатический» потенциал, а  коэффициент активности, предполагаемый здесь независимым от электрического состояния данной фазы. Заметим прежде всего, что такое разложение не является необходимым, поскольку соответствующие формулы, имеющие значение с точки зрения термодинамики, уже получены в гл. 2.
коэффициент активности, предполагаемый здесь независимым от электрического состояния данной фазы. Заметим прежде всего, что такое разложение не является необходимым, поскольку соответствующие формулы, имеющие значение с точки зрения термодинамики, уже получены в гл. 2.
Электростатический потенциал  можно определить так, что он будет измеримым или неизмеримым. В зависимости от того, как определен
можно определить так, что он будет измеримым или неизмеримым. В зависимости от того, как определен  величина
величина  будет также либо однозначно определена, либо полностью не определена. Развивать теорию можно, даже не имея такого четкого определения электростатического потенциала, какое дает электростатика, и не заботясь о тщательном определении его смысла. Если анализ проводится правильно, то физически осмысленные результаты можно получить в конце, компенсируя неопределенные члены.
будет также либо однозначно определена, либо полностью не определена. Развивать теорию можно, даже не имея такого четкого определения электростатического потенциала, какое дает электростатика, и не заботясь о тщательном определении его смысла. Если анализ проводится правильно, то физически осмысленные результаты можно получить в конце, компенсируя неопределенные члены.
Любое выбранное определение  должно удовлетворять одному условию. Оно должно сводиться к определению (13-2), использованному для разности электрических потенциалов между фазами с одинаковым составом. Так, если фазы
должно удовлетворять одному условию. Оно должно сводиться к определению (13-2), использованному для разности электрических потенциалов между фазами с одинаковым составом. Так, если фазы  имеют одинаковый состав, то
имеют одинаковый состав, то

Таким образом,  является количественной мерой электрического состояния одной фазы относительно другой, имеющей тот же состав. Этому условию удовлетворяет целый ряд возможных определений
является количественной мерой электрического состояния одной фазы относительно другой, имеющей тот же состав. Этому условию удовлетворяет целый ряд возможных определений 
Вместо  может использоваться внешний потенциал, который в принципе измерим. Его недостаток — трудность измерения и использования в термодинамических расчетах. Преимуществом является то, что он придает определенный смысл
может использоваться внешний потенциал, который в принципе измерим. Его недостаток — трудность измерения и использования в термодинамических расчетах. Преимуществом является то, что он придает определенный смысл  и в окончательных результатах этот потенциал не фигурирует, так что нужда в его измерении фактически отпадает.
и в окончательных результатах этот потенциал не фигурирует, так что нужда в его измерении фактически отпадает.
Другая возможность — использование потенциала подходящего электрода сравнения. Поскольку электрод сравнения обратим по некоторому иону, присутствующему в растворе, это эквивалентно использованию электрохимического потенциала иона или  Произвольность этого определения видна из необходимости выбора конкретного электрода сравнения или ионного компонента. Дополнительный недостаток такого выбора состоит в том, что в растворе, не содержащем компонента
Произвольность этого определения видна из необходимости выбора конкретного электрода сравнения или ионного компонента. Дополнительный недостаток такого выбора состоит в том, что в растворе, не содержащем компонента  величина
величина  обращается в минус бесконечность. Таким образом, электрохимический потенциал не согласуется с нашей обычной концепцией электростатического потенциала, что объясняется его связью с обратимой работой. Данный выбор потенциала обладает тем преимуществом, что он связан с измерениями с помощью электродов сравнения, обычно применяемых в электрохимии.
обращается в минус бесконечность. Таким образом, электрохимический потенциал не согласуется с нашей обычной концепцией электростатического потенциала, что объясняется его связью с обратимой работой. Данный выбор потенциала обладает тем преимуществом, что он связан с измерениями с помощью электродов сравнения, обычно применяемых в электрохимии.
Рассмотрим теперь третью возможность. Выберем ионный компонент  и определим потенциал
и определим потенциал  следующим образом:
следующим образом:

Тогда электрохимический потенциал любого другого компонента можно выразить в виде

Следует отметить, что комбинации  в скобках точно определены и не зависят от электрического состояния в соответствии с правилами, изложенными в разд. 14. В таком случае можно записать градиент электрохимического потенциала
в скобках точно определены и не зависят от электрического состояния в соответствии с правилами, изложенными в разд. 14. В таком случае можно записать градиент электрохимического потенциала

Снова видна произвольность этого определения  связанная с необходимостью выбора ионного компонента
связанная с необходимостью выбора ионного компонента  Преимущество такого определения
Преимущество такого определения  состоит в его однозначной связи с электрохимическими потенциалами и согласованности с нашим обычным представлением об электростатическом потенциале. Ввиду наличия члена
состоит в его однозначной связи с электрохимическими потенциалами и согласованности с нашим обычным представлением об электростатическом потенциале. Ввиду наличия члена  в уравнении (26-3) последнее можно использовать для раствора с исчезающей концентрацией компонента
в уравнении (26-3) последнее можно использовать для раствора с исчезающей концентрацией компонента 
В пределе бесконечно разбавленных растворов члены с коэффициентами активности исчезают вследствие выбора вторичного стандартного состояния (14-6). В этом пределе определение  становится независимым от выбора стандартного иона
становится независимым от выбора стандартного иона  Это создает основу того, что следовало бы называть теорией разбавленных растворов электролитов. В то же время уравнения (26-4) и (26-5) показывают, как нужно делать поправки на коэффициент активности в теории разбавленных растворов, не прибегая к коэффициентам активности отдельных ионов. Отсутствие зависимости от типа иона
Это создает основу того, что следовало бы называть теорией разбавленных растворов электролитов. В то же время уравнения (26-4) и (26-5) показывают, как нужно делать поправки на коэффициент активности в теории разбавленных растворов, не прибегая к коэффициентам активности отдельных ионов. Отсутствие зависимости от типа иона  в случае бесконечно разбавленных растворов связано с возможностью измерения разностей электрических потенциалов между фазами с одинаковым составом. Такие растворы имеют существенно одинаковые составы в том смысле, что ион в растворе взаимодействует только с растворителем и даже дальнодействие со стороны остальных ионов им не ощущается.
в случае бесконечно разбавленных растворов связано с возможностью измерения разностей электрических потенциалов между фазами с одинаковым составом. Такие растворы имеют существенно одинаковые составы в том смысле, что ион в растворе взаимодействует только с растворителем и даже дальнодействие со стороны остальных ионов им не ощущается.
Введение такого электрического потенциала полезно при анализе процессов переноса в растворах электролитов [5]. Для, таким образом определенного потенциала Смерл и Ньюмен используют термин квазиэлектростатический потенциал.
Мы обсудили возможные способы использования электрического потенциала в электрохимической термодинамике. Применение потенциала в теории переноса по существу то же, что
и в термодинамике. Работая с электрохимическими потенциалами, можно обойтись без электрического потенциала, хотя его введение может оказаться полезным или удобным. В кинетике электродных процессов в качестве движущей силы реакции может использоваться изменение свободной энергии. Это равносильно использованию поверхностного перенапряжения, определенного в разд. 8.
Электрический потенциал находит применение и в микроскопических моделях, таких, как теория Дебая-Хюккеля, упоминавшаяся выше и излагаемая в следующей главе. Всегда строго определить такой потенциал невозможно. Следует четко различать между теориями макроскопическими — термодинамика, теория процессов переноса и механика жидкостей — и микроскопическими — статистическая механика и кинетическая теория газов и жидкостей. Исходя из свойств молекул или ионов, микроскопические теории позволяют вычислять и связывать между собой такие макроскопические характеристики, как, например, коэффициенты активности и коэффициенты диффузии. При этом редко удается получить удовлетворительные количественные результаты без привлечения дополнительной экспериментальной информации. Макроскопические теории, с одной стороны, создают основу для наиболее экономного измерения и табулирования макроскопических характеристик, а с другой — позволяют использовать эти результаты для предсказания поведения макроскопических систем.
СПИСОК ОБОЗНАЧЕНИЙ
(см. скан)
(см. скан)
СПИСОК ЛИТЕРАТУРЫ
(см. скан)
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
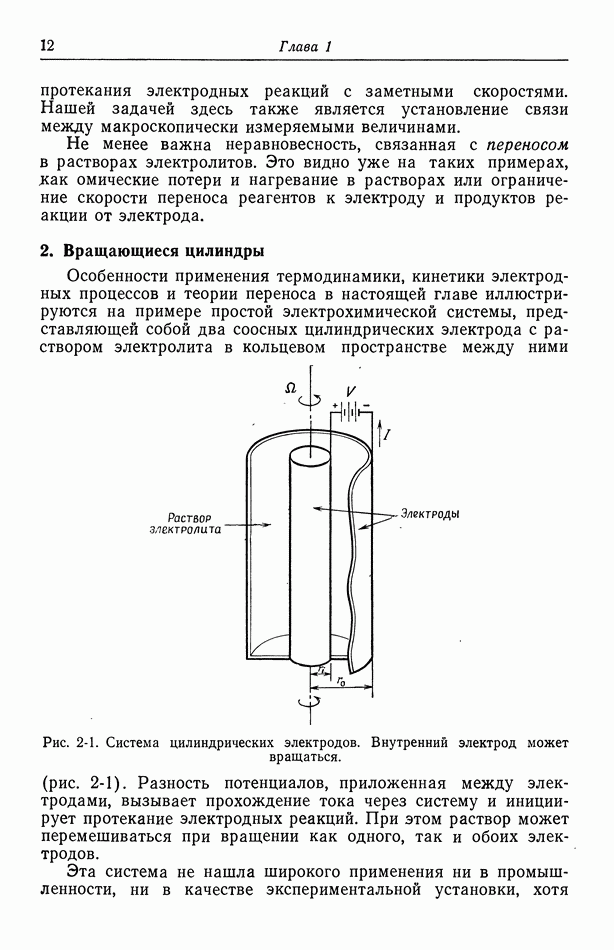
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
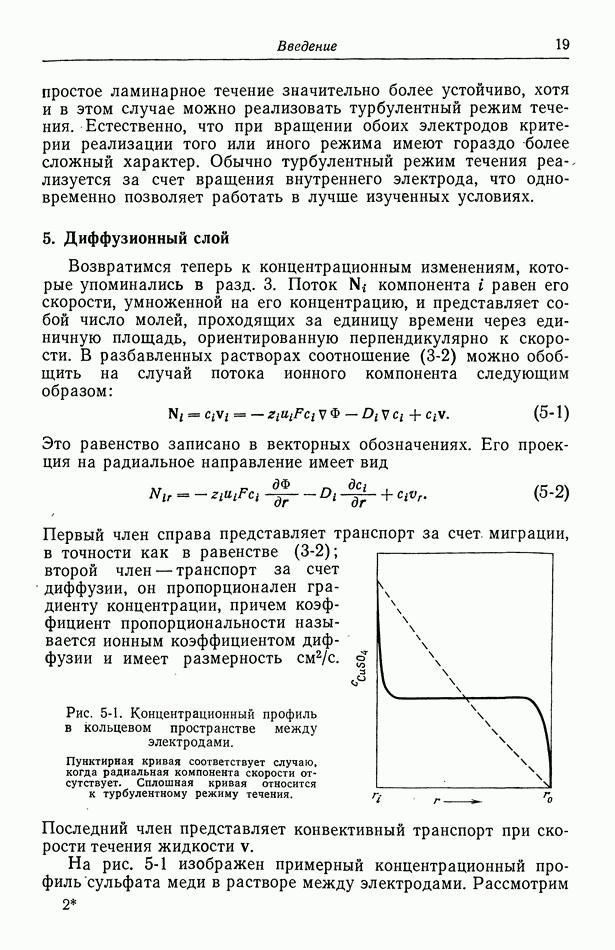
- 5. Диффузионный слой
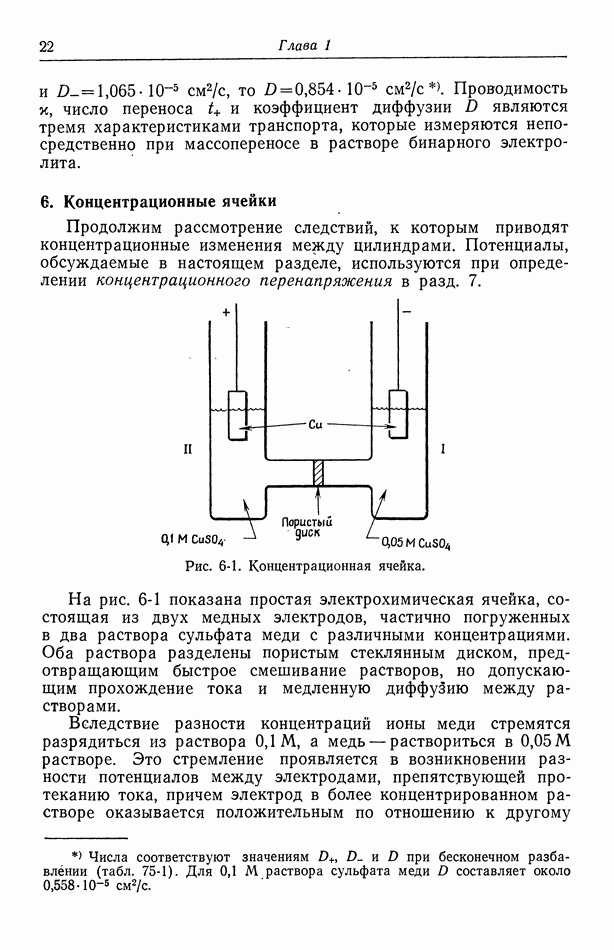
- 6. Концентрационные ячейки
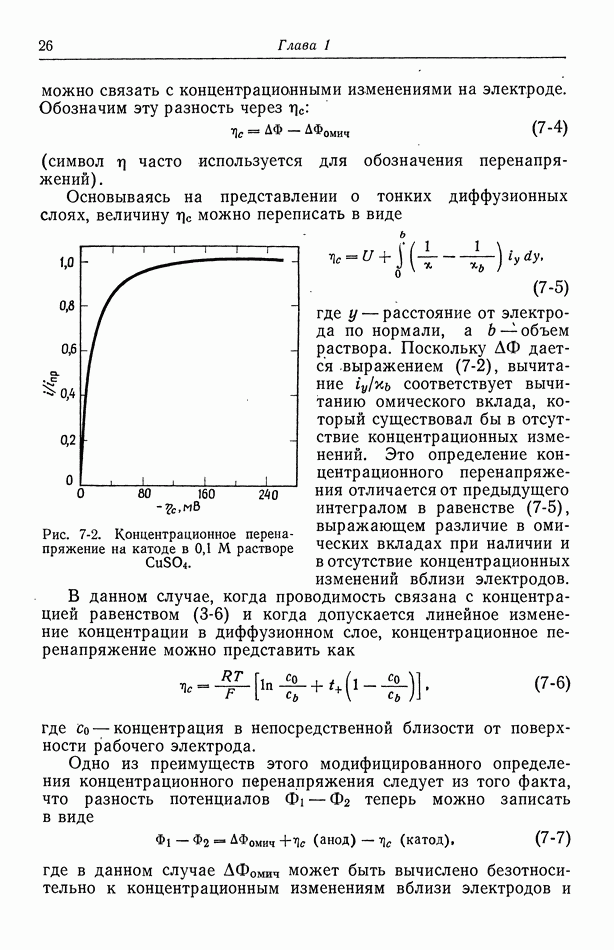
- 7. Концентрационное перенапряжение
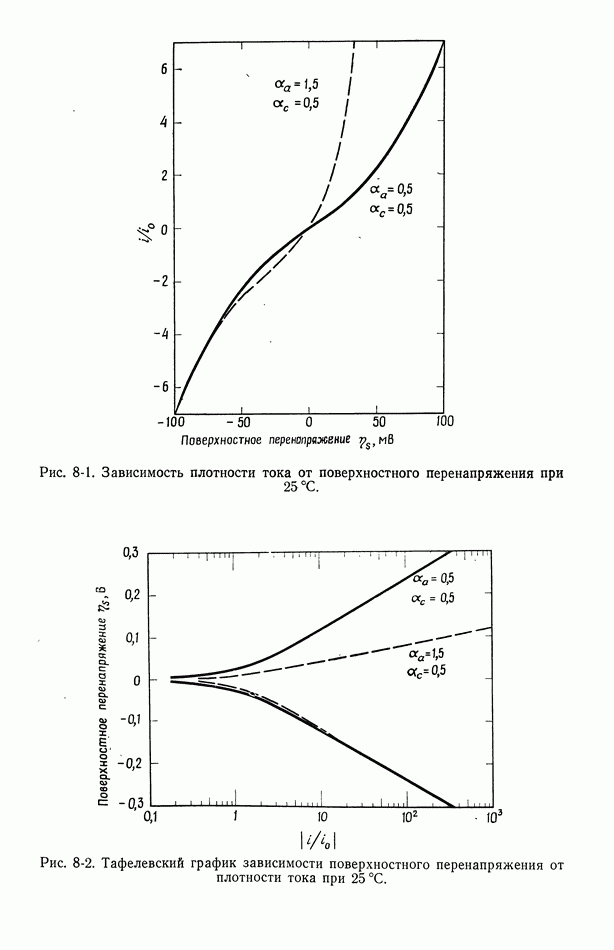
- 8. Поверхностное перенапряжение
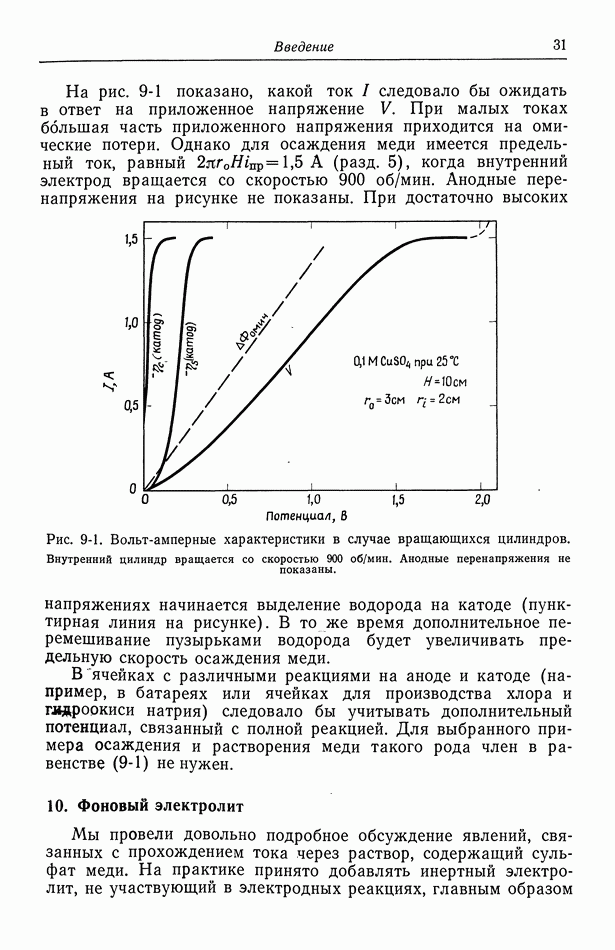
- 9. Потенциал ячейки
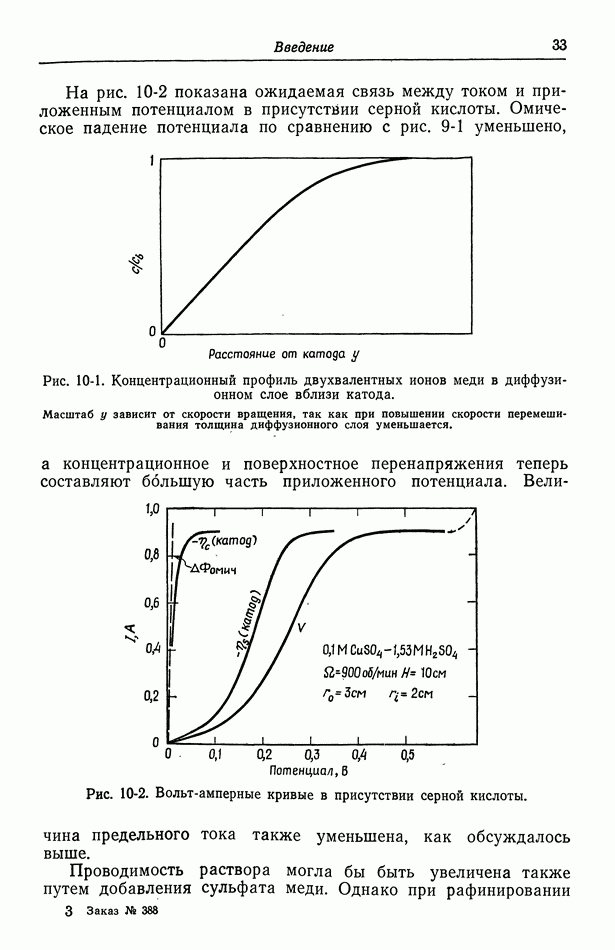
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
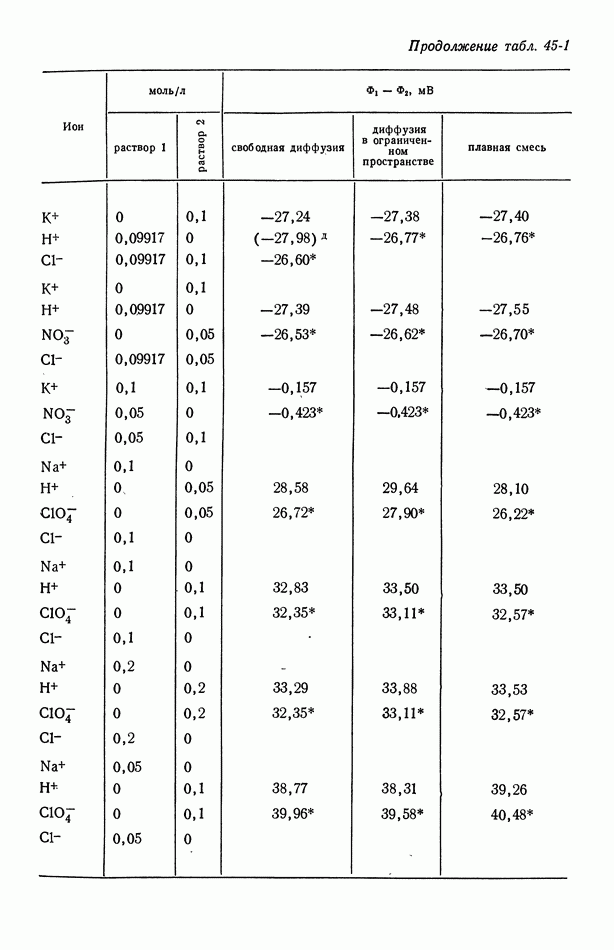
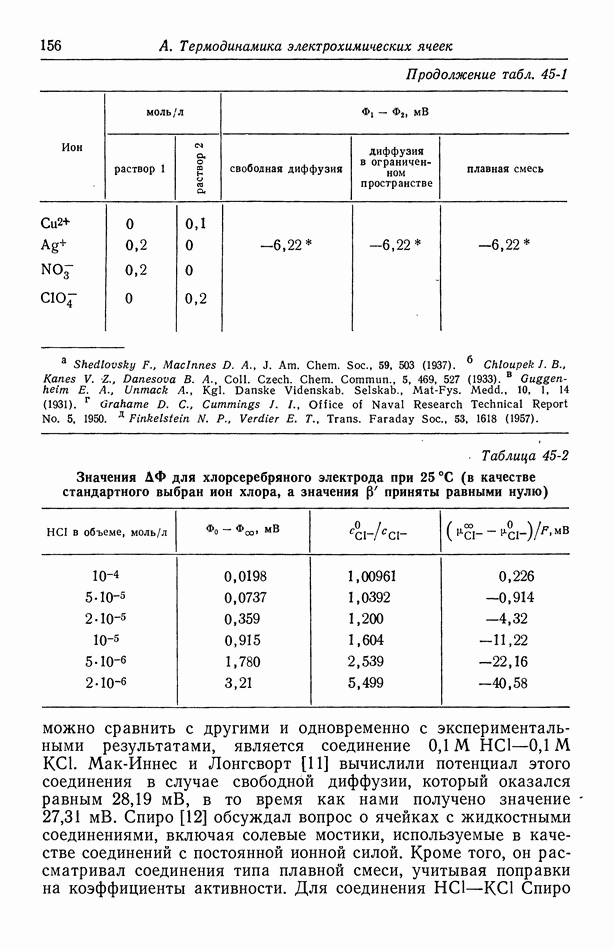
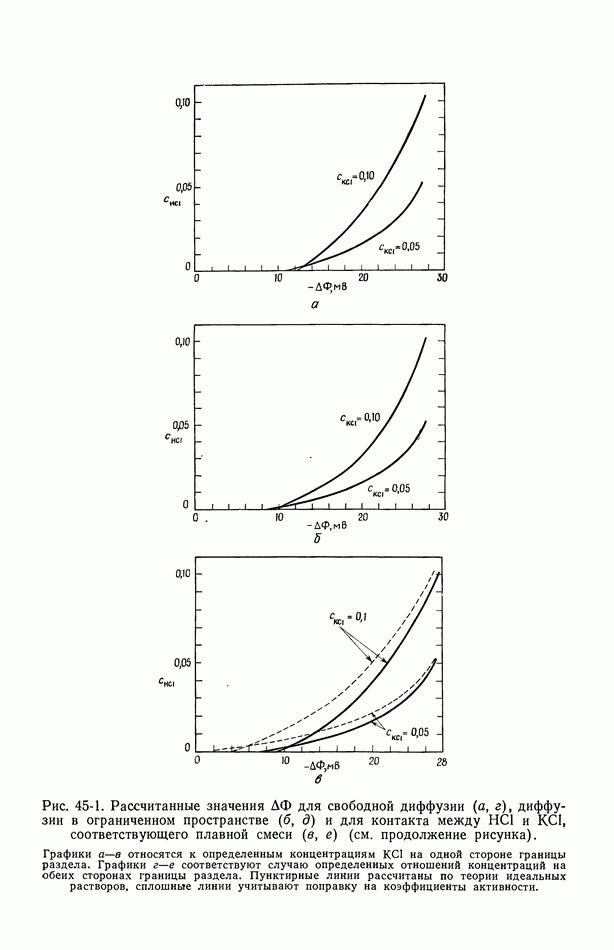
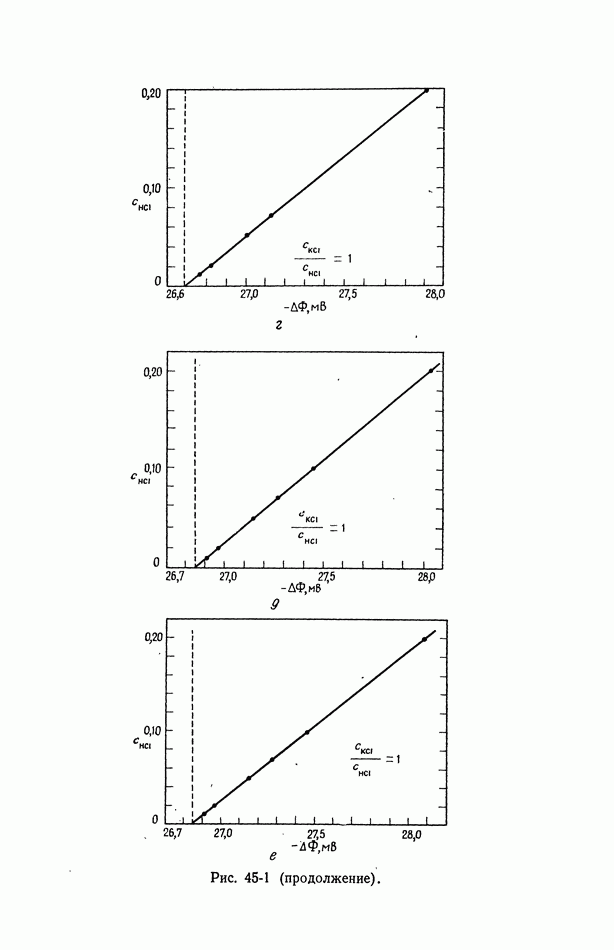
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
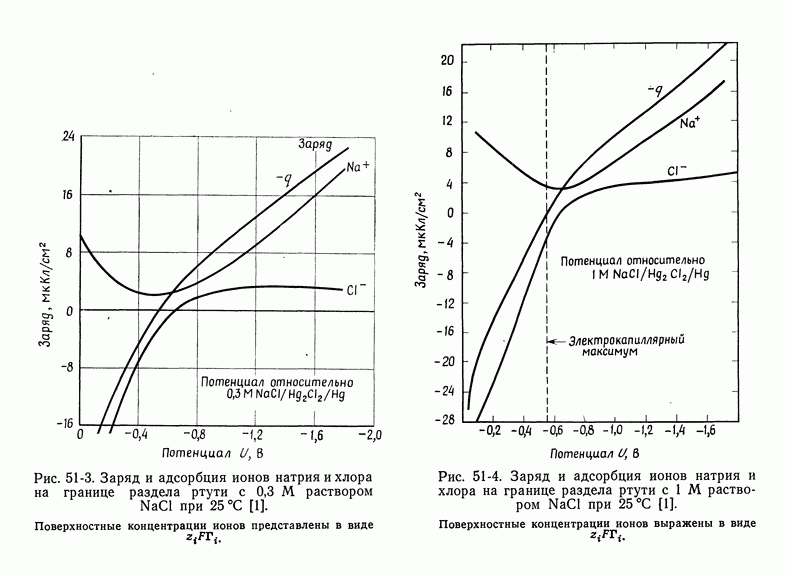
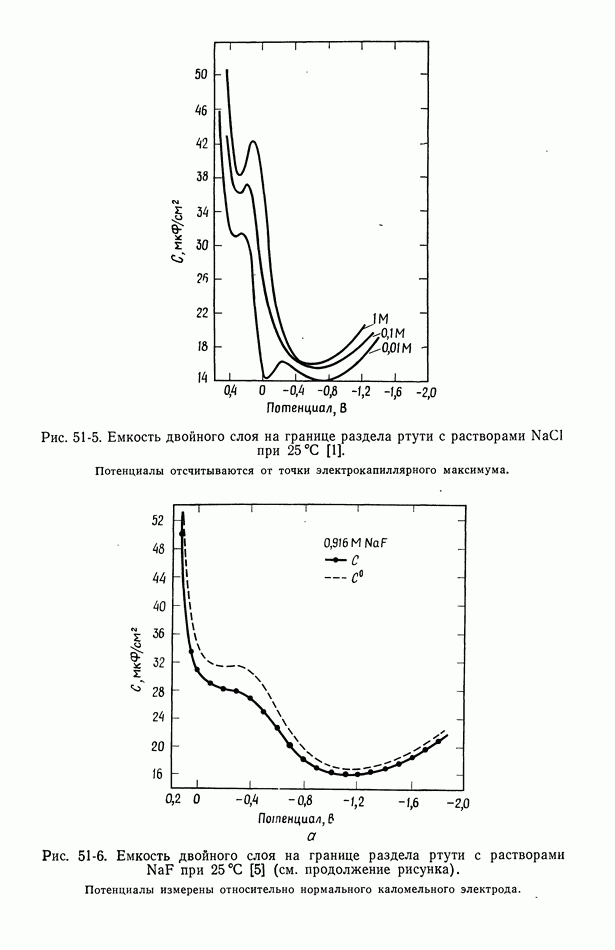
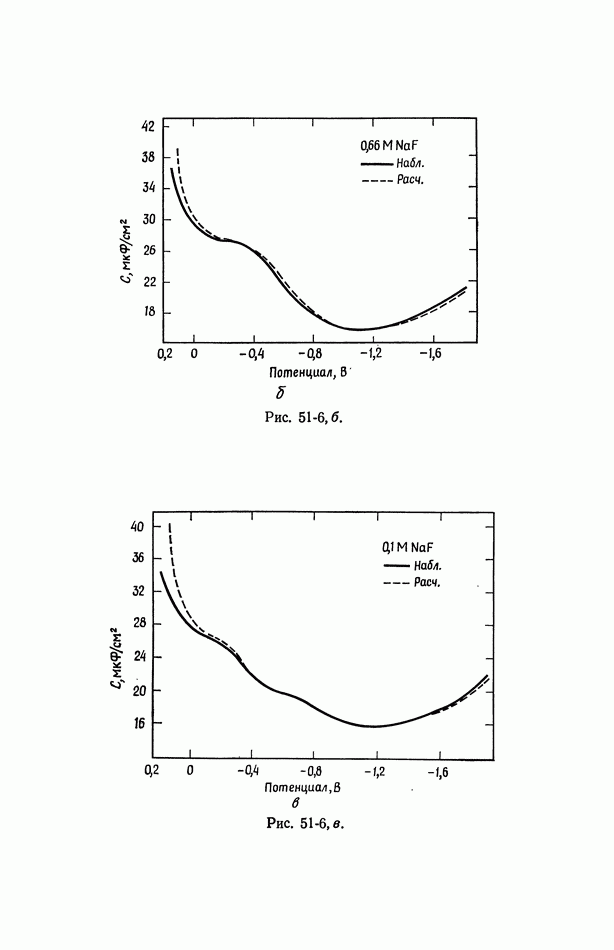
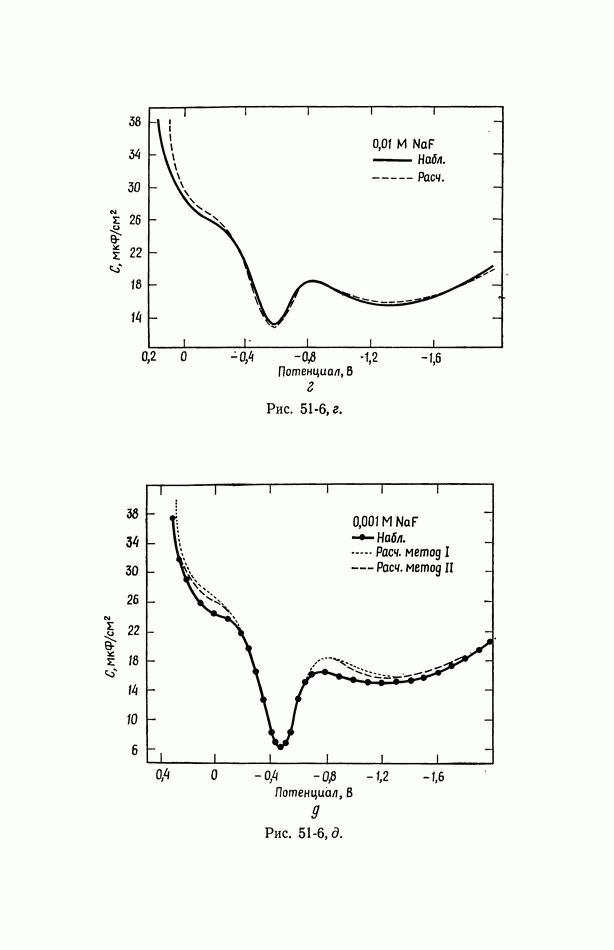
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
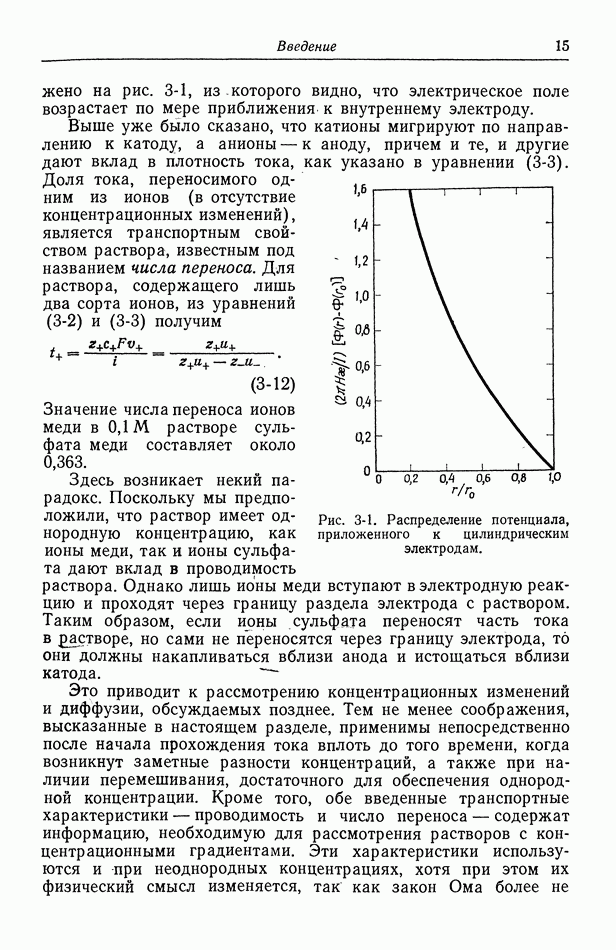
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
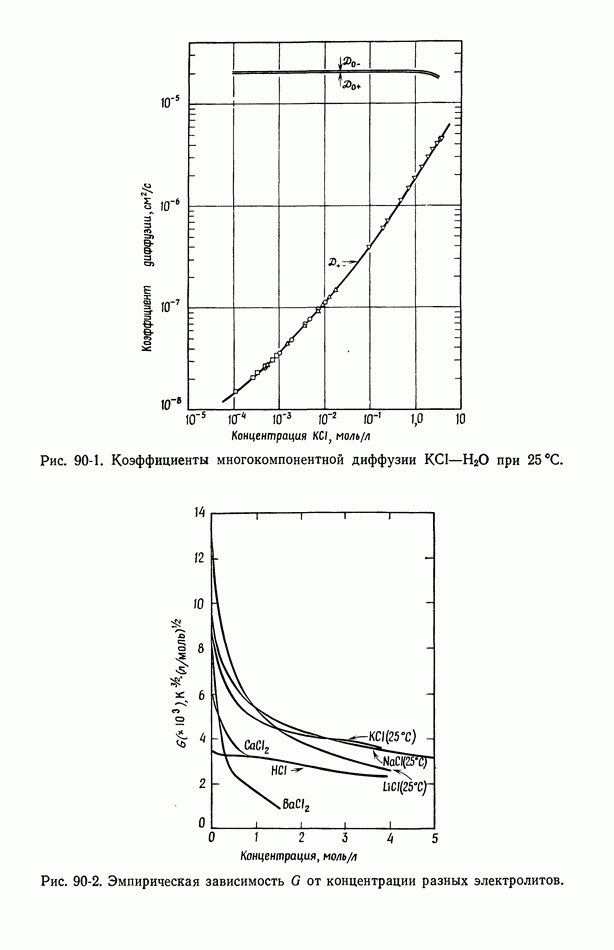
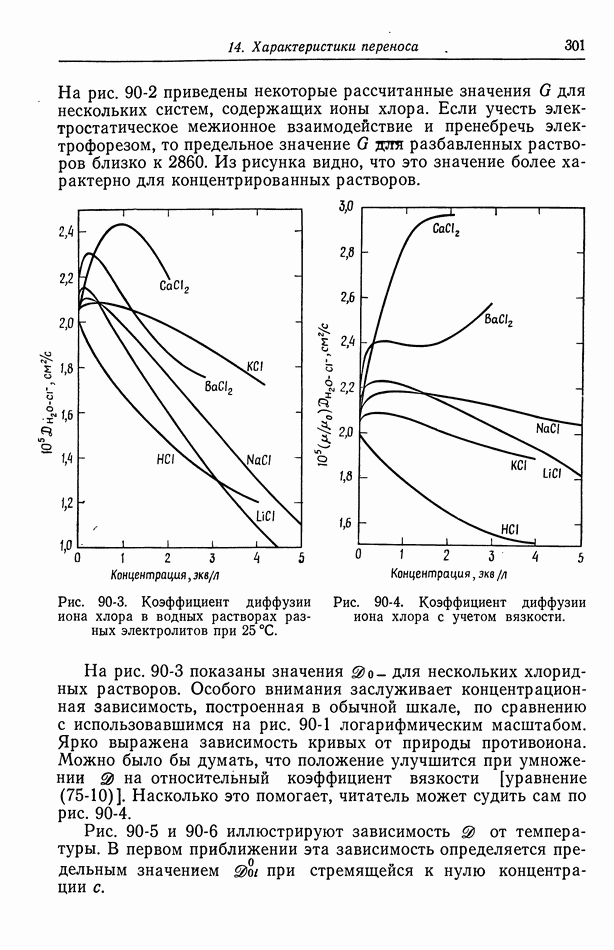
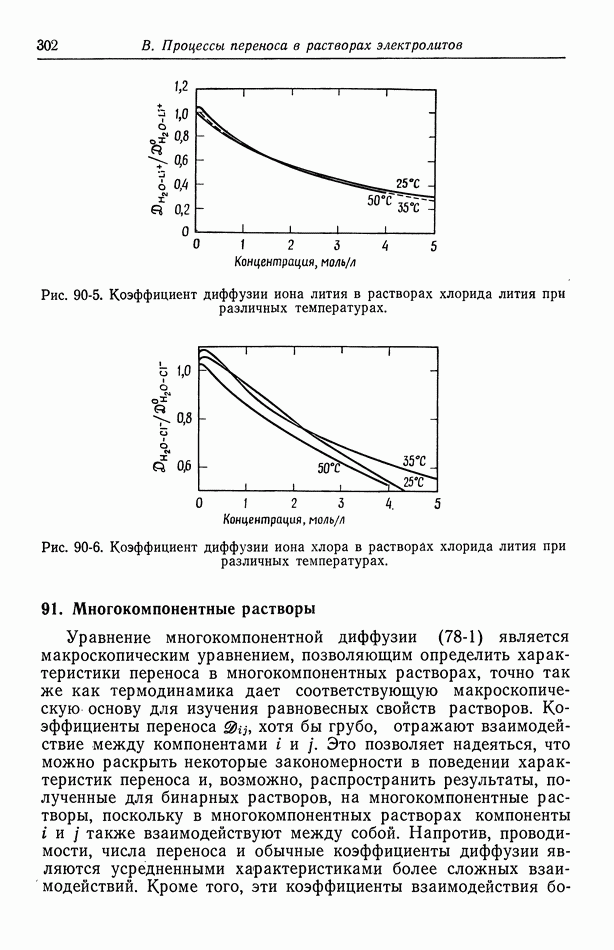
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
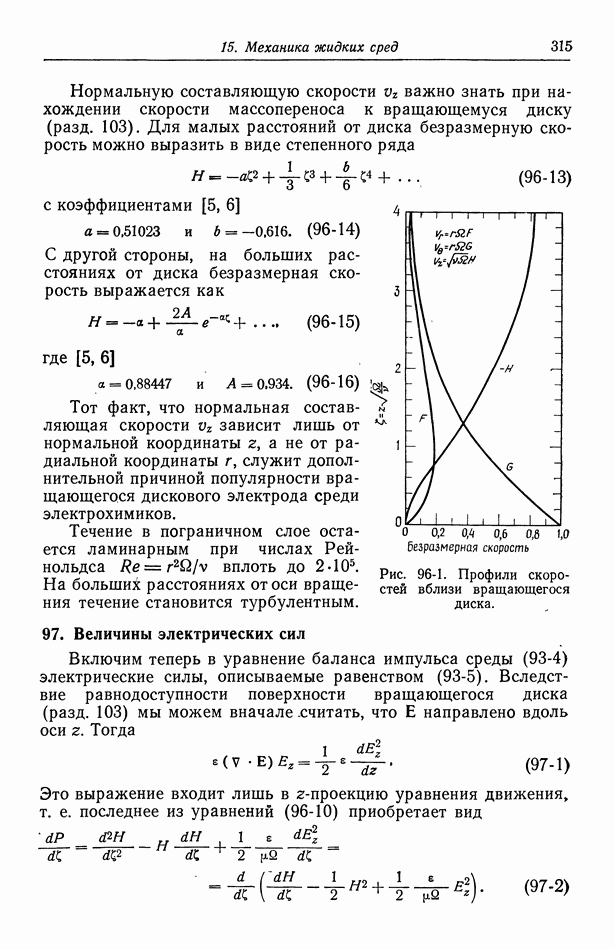
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
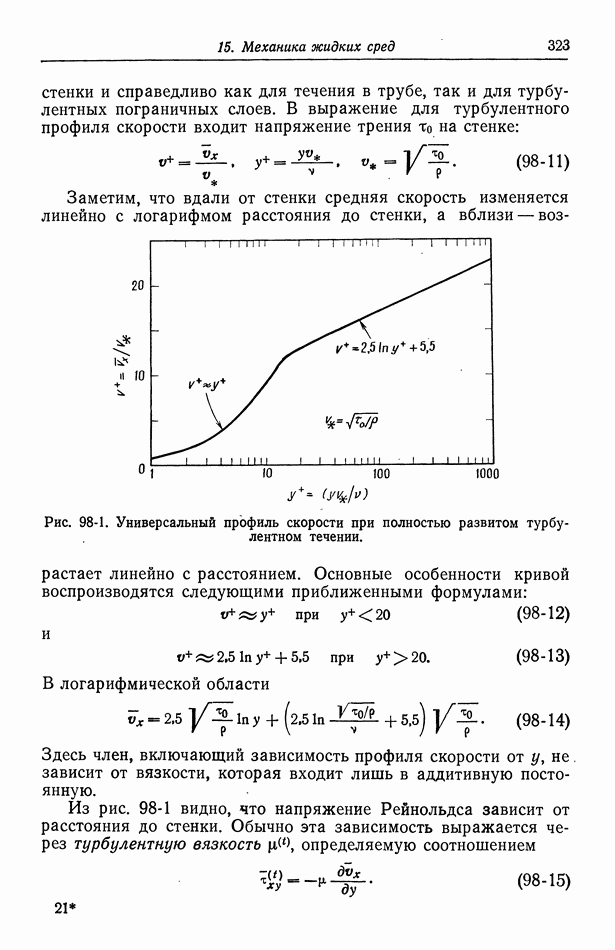
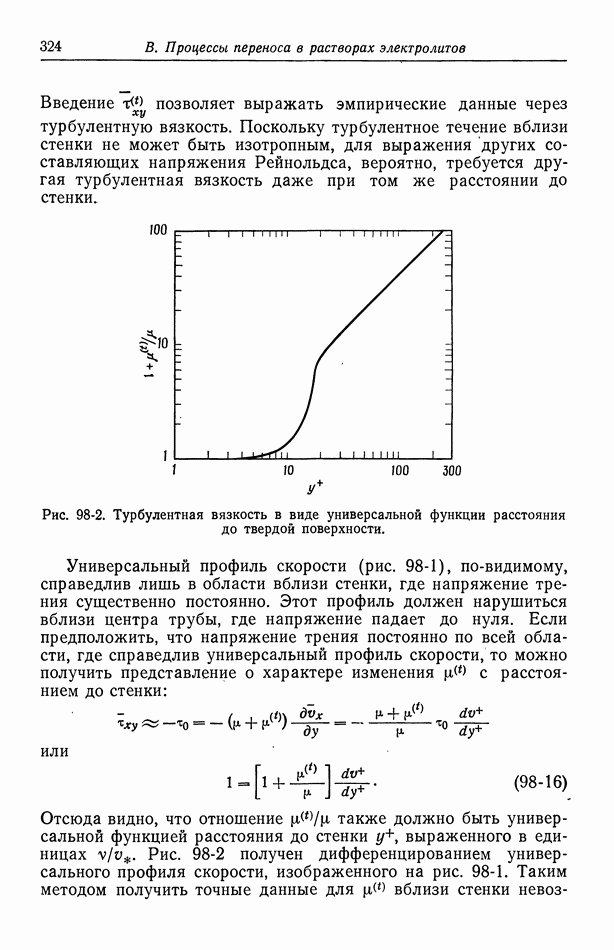
- 98. Турбулентное течение
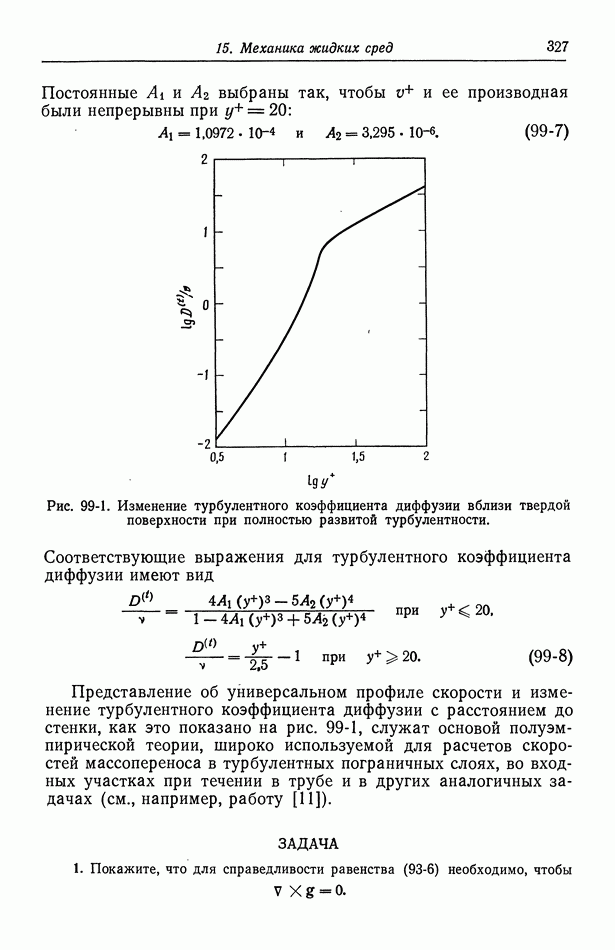
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
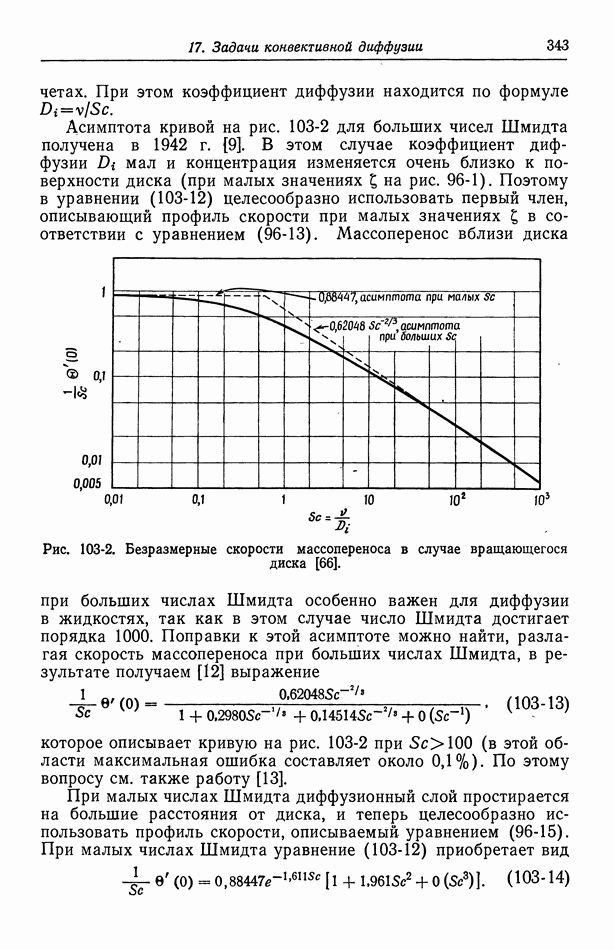
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
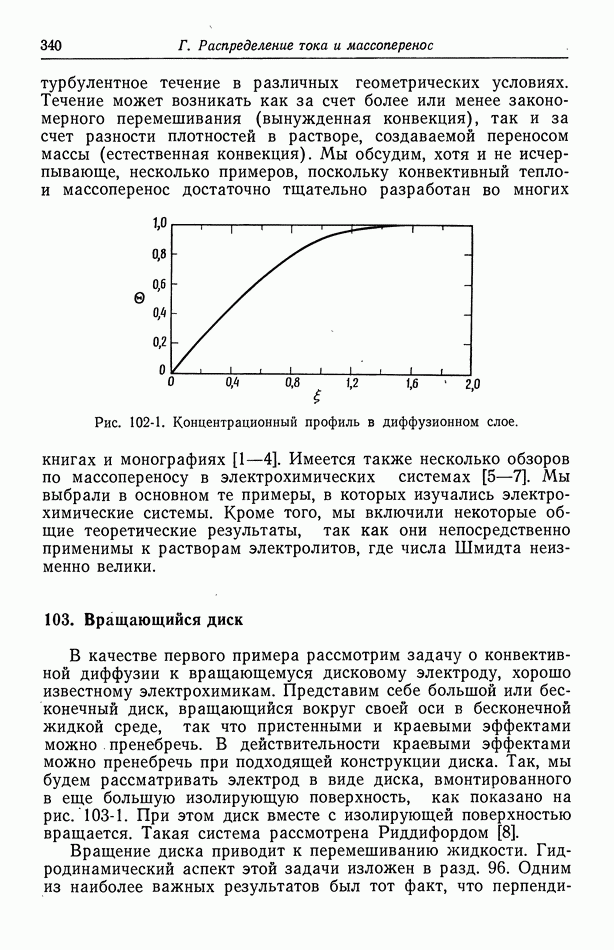
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
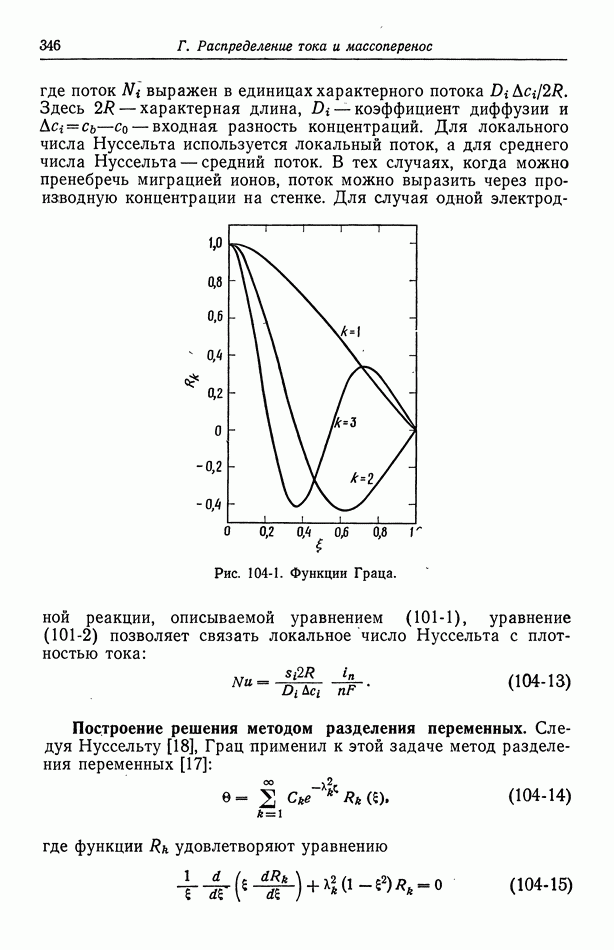
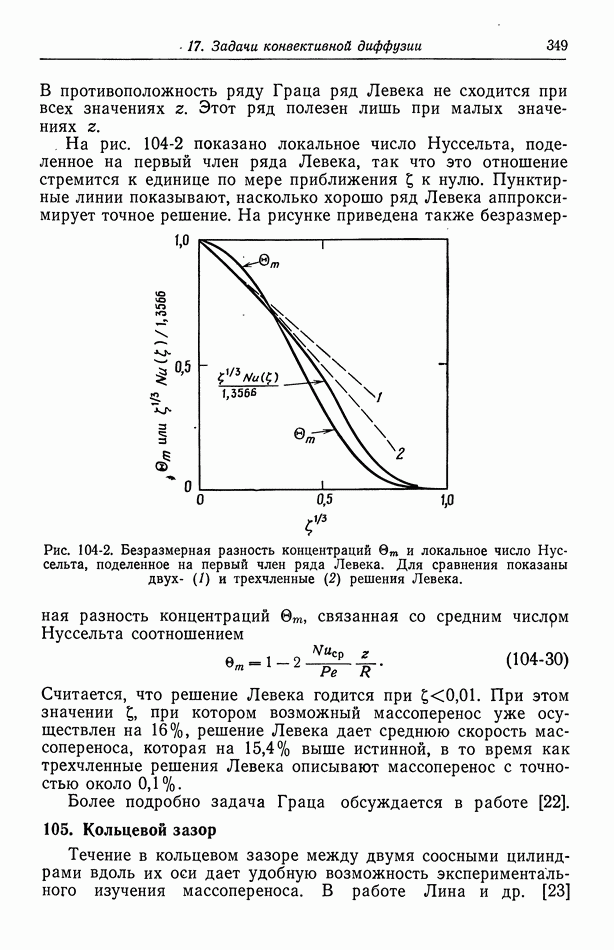
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
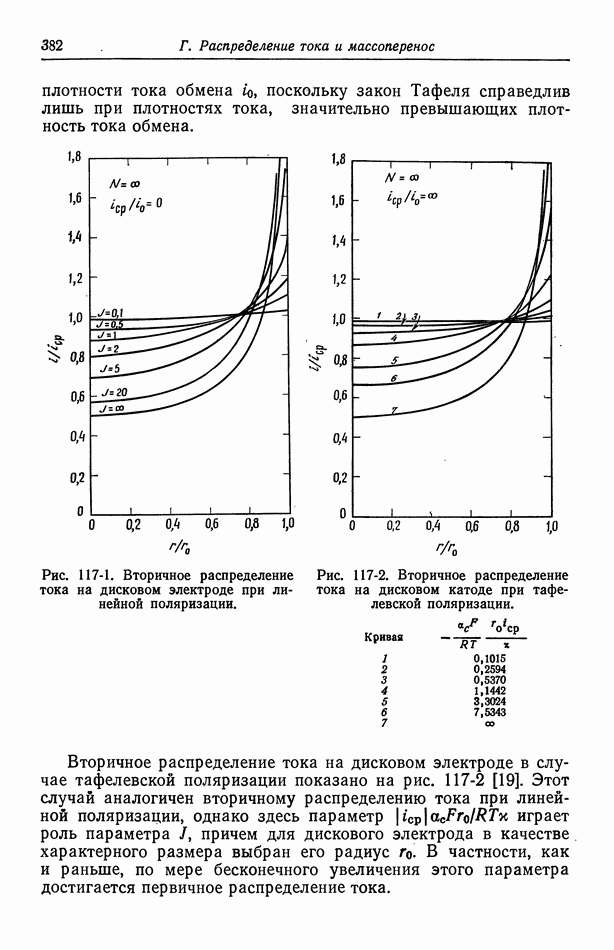
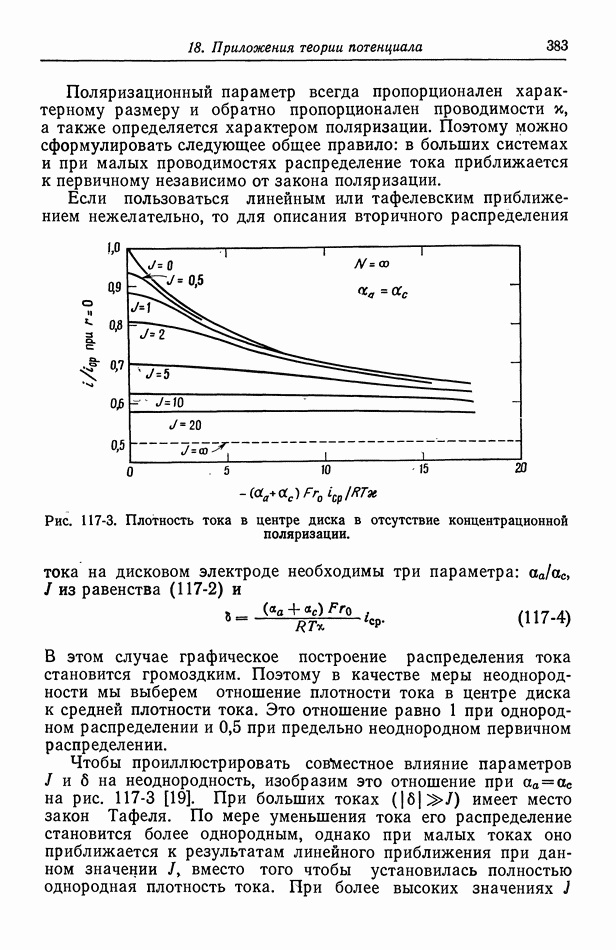
- 117. Вторичное распределение тока
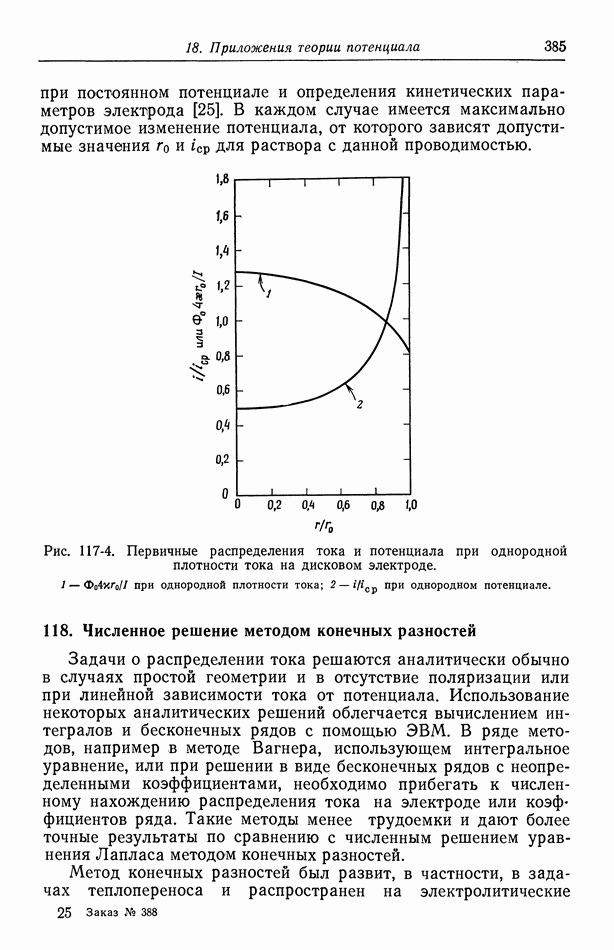
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
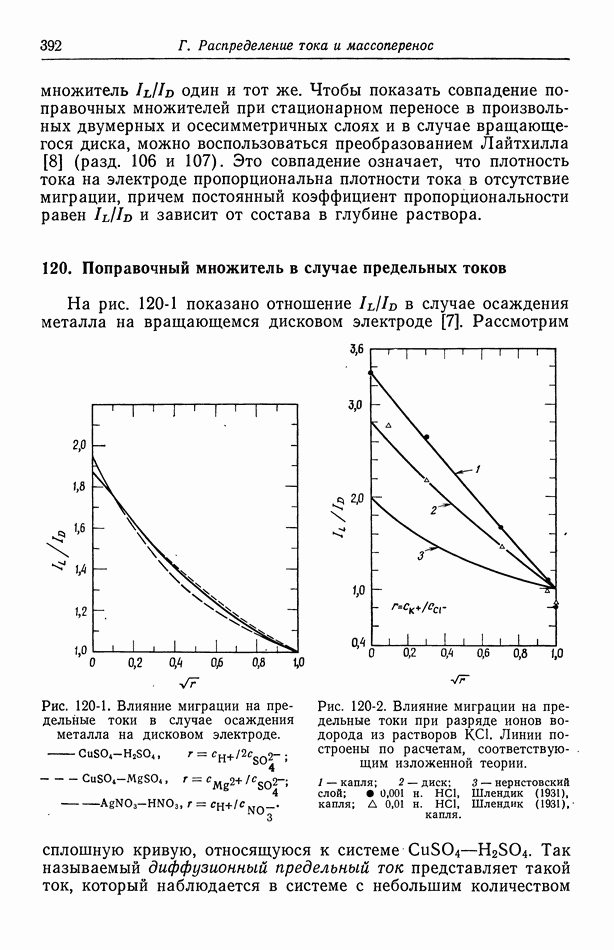
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
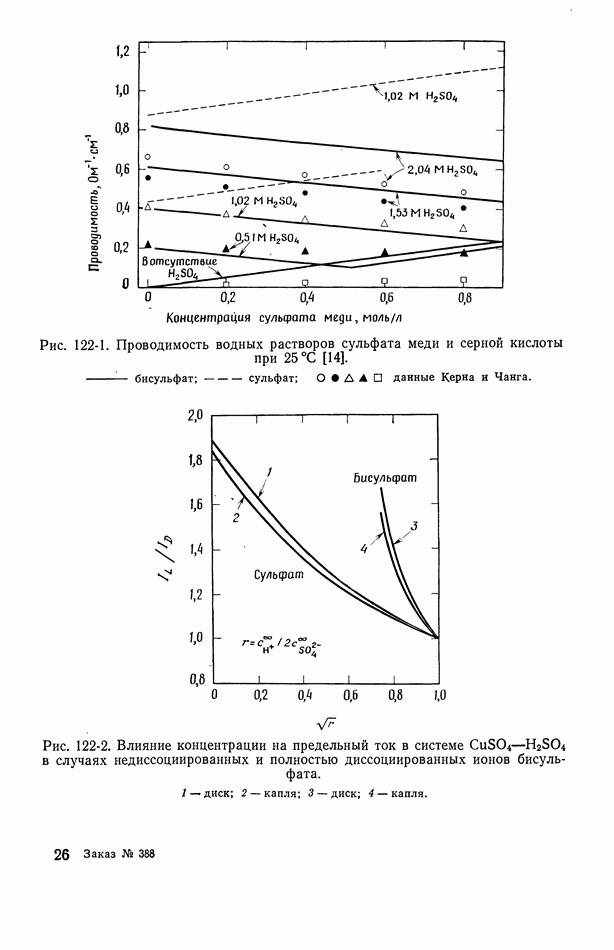
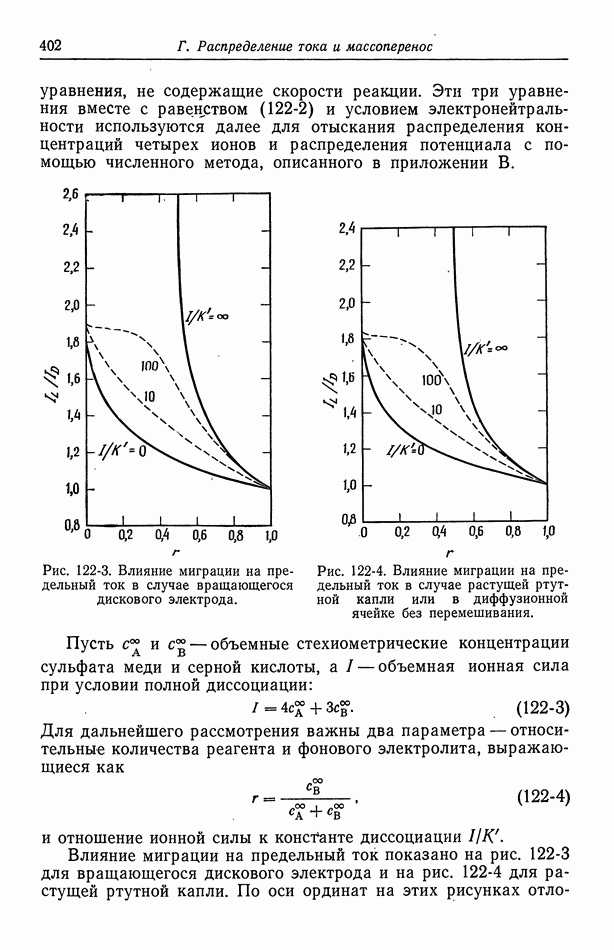
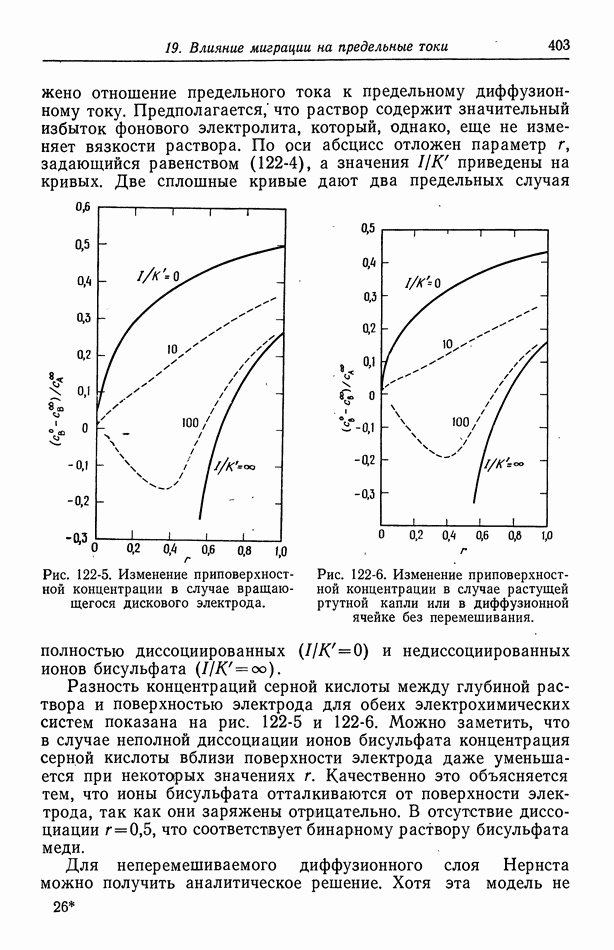
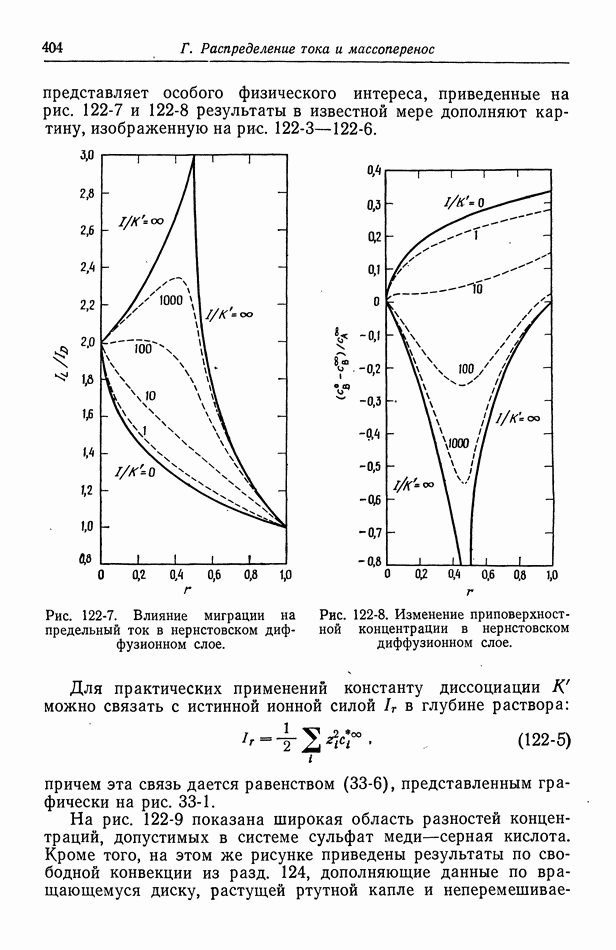
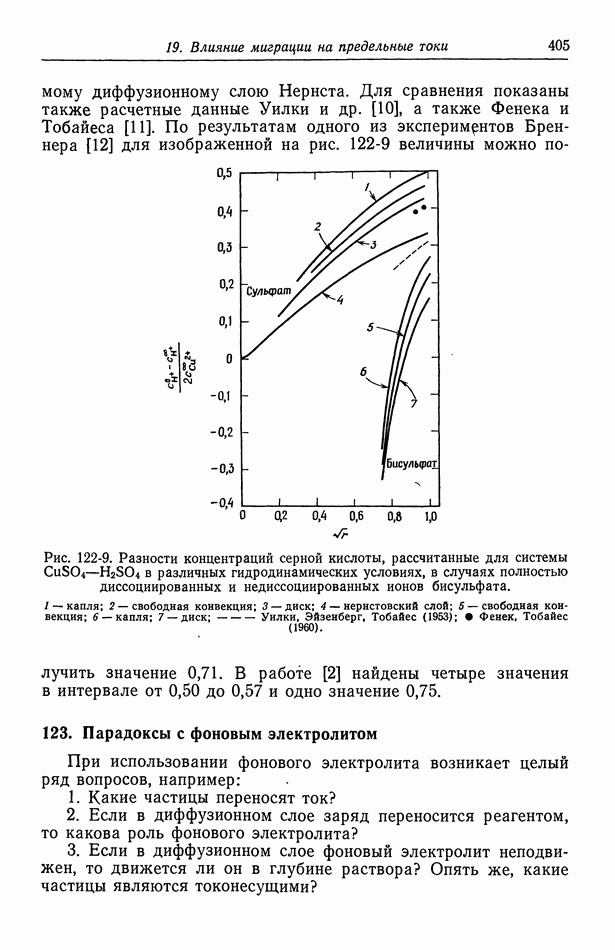
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
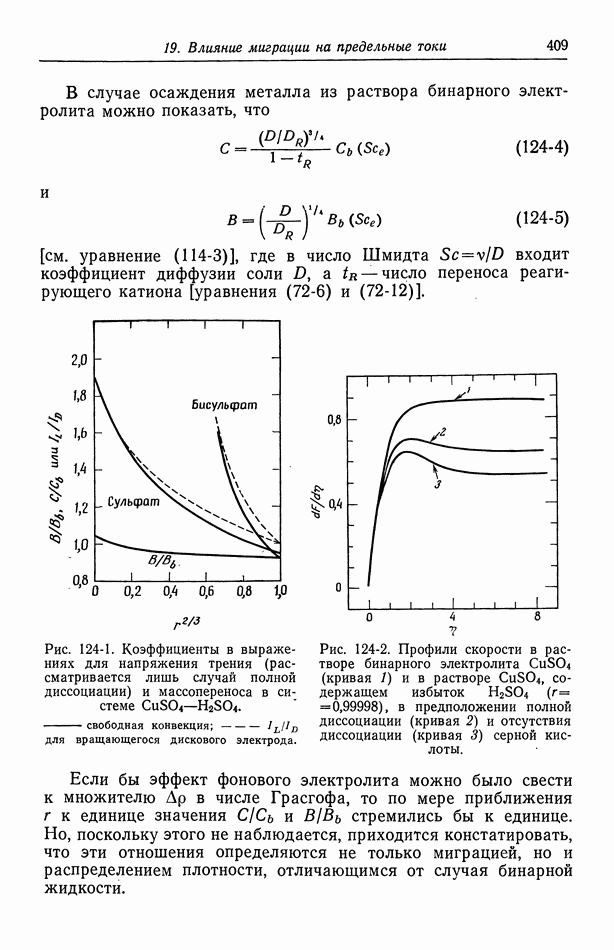
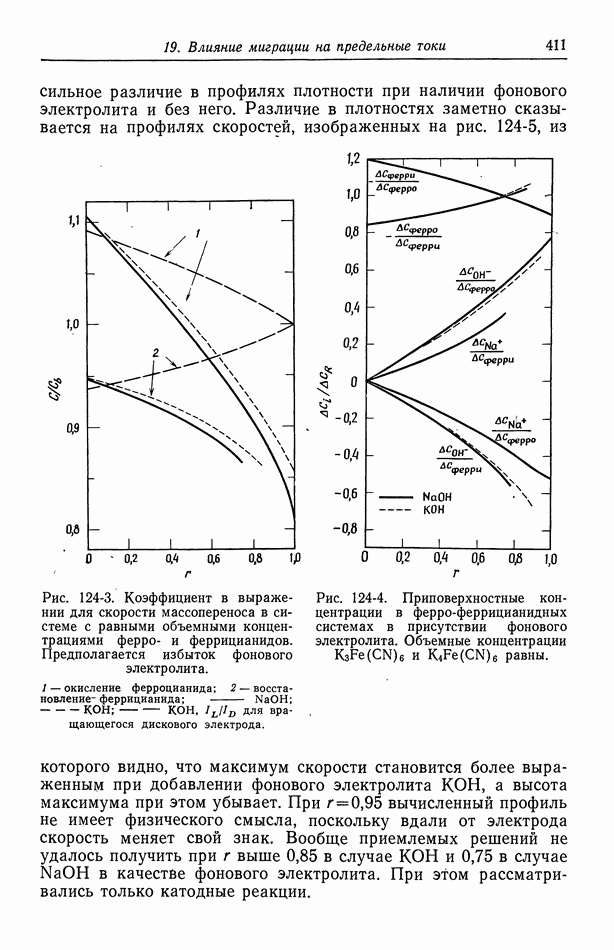
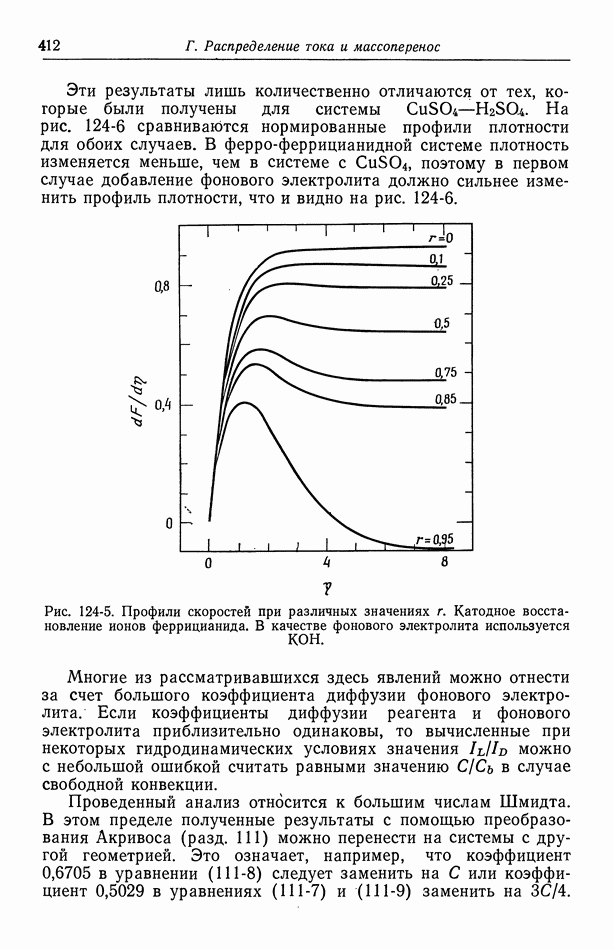
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ