| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
51. Уравнение Липпмана
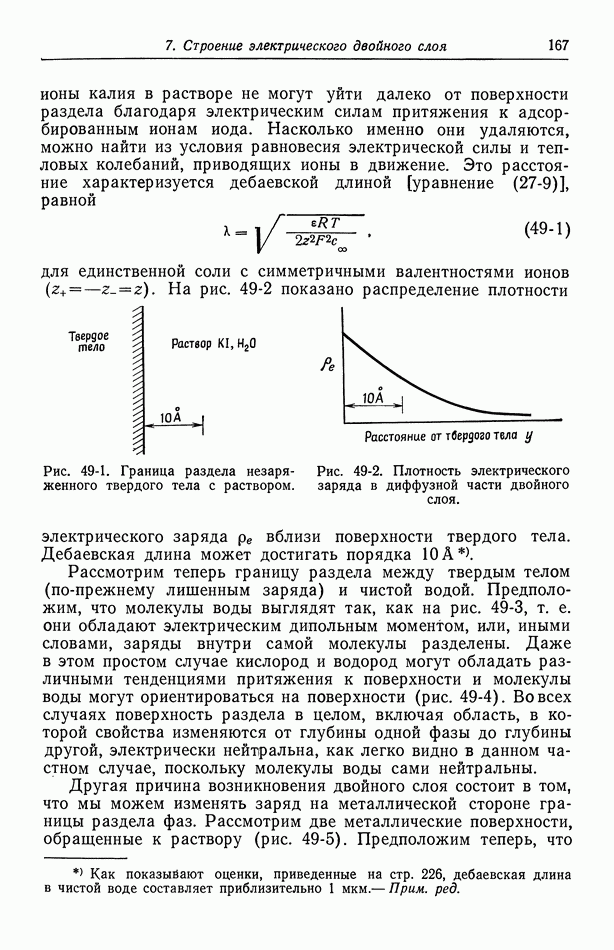
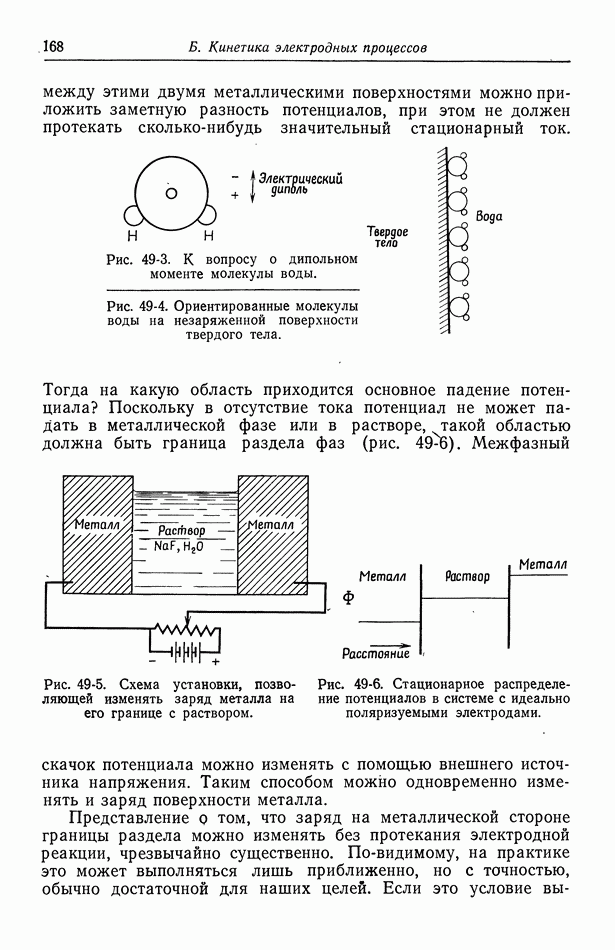
Теперь мы хотим применить изотерму адсорбции Гиббса к границе раздела фаз, включающей идеально поляризуемый электрод. Будем рассматривать систему, изображенную на рис. 51-1.

Рис. 51-1. Система для приложения потенциала к идеально поляризуемому электроду. 1 — водный раствор  противоэлектрод; 3 — электрод сравнения
противоэлектрод; 3 — электрод сравнения 
Противоэлектрод здесь используется для поддержания потенциала ртути, который измеряется относительно хлор-серебряного электрода сравнения. Последнюю цепь можно представить в виде схемы

для которой потенциал, используя методы гл. 2, можно выразить как

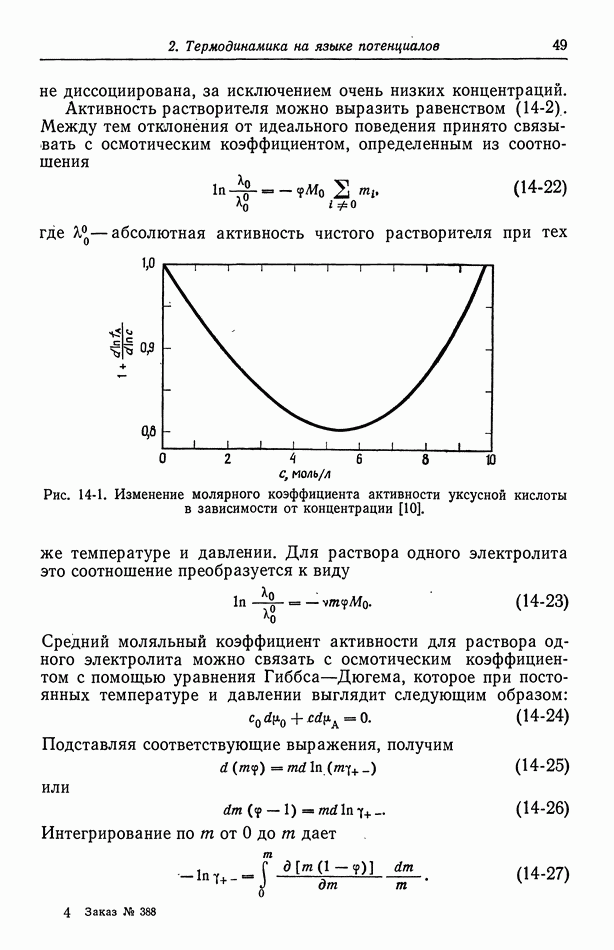
Для изменений поверхностного натяжения ртути при постоянной температуре изотерма адсорбции Гиббса (50-12) принимает вид

Мы считаем, что ртутная фаза К состоит из атомов ртути и электронов. В уравнение (51-3) поверхностная концентрация ртути не входит, так как мы принимаем  Поверхностная концентрация электронов является инвариантом Гиббса, поскольку концентрация электронов в глубине однородных фаз
Поверхностная концентрация электронов является инвариантом Гиббса, поскольку концентрация электронов в глубине однородных фаз  равна нулю [уравнение (50-4)]. Величина
равна нулю [уравнение (50-4)]. Величина  связана с поверхностной плотностью заряда
связана с поверхностной плотностью заряда  обсуждавшейся в разд. 49, соотношением
обсуждавшейся в разд. 49, соотношением

Мы считаем, что водная фаза  состоит из ионов калия, ионов хлора и воды. Поверхность Гиббса мы выбираем так, чтобы
состоит из ионов калия, ионов хлора и воды. Поверхность Гиббса мы выбираем так, чтобы 
Как указывалось ранее, в целом граница раздела электрически нейтральна:

Если воспользоваться равенством (51-5) для исключения  из уравнения (51-3) и равенством (51-4) для введения
из уравнения (51-3) и равенством (51-4) для введения  то получаем
то получаем

Наконец, для введения потенциала  можно использовать равенство (51-2):
можно использовать равенство (51-2):

Это важное соотношение известно под названием уравнения Липпмана. Согласно этому уравнению, измеряя изменение поверхностного натяжения при переменном составе раствора и постоянном потенциале, можно получить поверхностную концентрацию ионов калия, а измеряя изменение поверхностного натяжения при переменном потенциале и постоянном составе, можно получить поверхностный заряд  Все это можно проделать на прочной термодинамической основе без обращения к микроскопическим моделям границы раздела, хотя соответствующие эксперименты требуют значительных усилий для получения точных результатов. Следует иметь в виду, что
Все это можно проделать на прочной термодинамической основе без обращения к микроскопическим моделям границы раздела, хотя соответствующие эксперименты требуют значительных усилий для получения точных результатов. Следует иметь в виду, что  определено при условии
определено при условии 
Приведенный выше вывод уравнения Липпмана отличается от рассмотрения обратимых электродов в гл. 2 в том отношении, что между фазами  нет равновесия по какому-либо компоненту. При наличии таких компонентов их концентрации в одной или другой фазе считаются пренебрежимо малыми. Иной подход состоит в предположении, что имеется непроницаемый для вещества барьер, вследствие чего ток отсутствует. Тогда поверхностный заряд
нет равновесия по какому-либо компоненту. При наличии таких компонентов их концентрации в одной или другой фазе считаются пренебрежимо малыми. Иной подход состоит в предположении, что имеется непроницаемый для вещества барьер, вследствие чего ток отсутствует. Тогда поверхностный заряд  равен поверхностной плотности заряда на электродной стороне этого барьера и никакое вещество не присутствует по обе стороны барьера в сколько-нибудь заметной концентрации. Оба пути приводят к уравнению Липпмана, и различие в исходных положениях практически не имеет последствий.
равен поверхностной плотности заряда на электродной стороне этого барьера и никакое вещество не присутствует по обе стороны барьера в сколько-нибудь заметной концентрации. Оба пути приводят к уравнению Липпмана, и различие в исходных положениях практически не имеет последствий.
Емкость двойного слоя (на единицу площади) С есть производная от заряда двойного слоя  по потенциалу при постоянном составе раствора:
по потенциалу при постоянном составе раствора:

где индекс  означает постоянный состав. Из равенства (51-7) видно, что
означает постоянный состав. Из равенства (51-7) видно, что

Следовательно,

Емкость двойного слоя идеально поляризуемого электрода можно измерить непосредственно на переменном токе. Поскольку двойной слой тонок, он быстро реагирует на переменный ток. Таким образом, за исключением случая адсорбции органических соединений с длинными цепями, емкость на переменном токе не отличается от определенной равенством (51-8) статической емкости вплоть до частот порядка 
Грэм [1] описывает эксперименты, подтверждающие уравнение Липпмана, в которых заряд в зависимости от потенциала определяется тремя независимыми способами:
1. Дифференцированием поверхностного натяжения по потенциалу в соответствии с равенством (51-9).
2. Интегрированием емкости двойного слоя по потенциалу в соответствии с равенством (51-8). Для согласования результата с двумя другими методами необходимо определить постоянную интегрирования.
3. Непосредственным измерением  с помощью прибора типа изображенного на рис. 49-8.
с помощью прибора типа изображенного на рис. 49-8.
Заметим, что к твердым электродам применим лишь второй
метод и что в этом случае определение точки нулевого заряда, эквивалентной постоянной интегрирования, ненадежно.
Вывод уравнения Липпмана можно видоизменить на случай другого электрода сравнения и многокомпонентных растворов, включая системы с адсорбцией нейтральных органических молекул. Применение термодинамических принципов позволяет провести согласованное рассмотрение разнообразных данных, включая измерение поверхностного натяжения, поверхностного заряда и емкости двойного слоя в зависимости от температуры, потенциала и состава раствора.

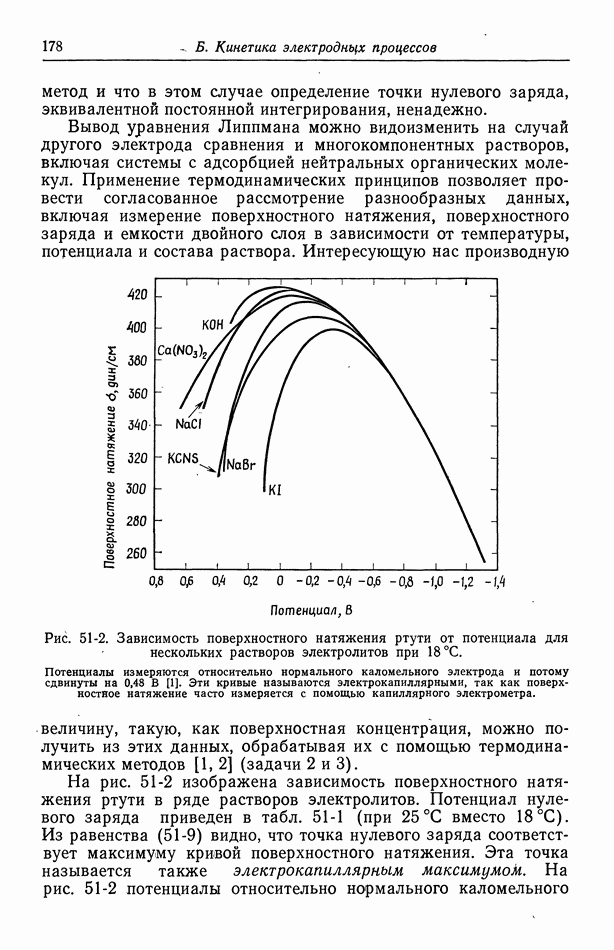
Рис. 51-2. Зависимость поверхностного натяжения ртути от потенциала для нескольких растворов электролитов при 18 °С.
Потенциалы измеряются относительно нормального каломельного электрода и потому сдвинуты на  Эти кривые называются электрокапиллярными, так как поверхностное натяжение часто измеряется с помощью капиллярного электрометра.
Эти кривые называются электрокапиллярными, так как поверхностное натяжение часто измеряется с помощью капиллярного электрометра.
Интересующую нас производную величину, такую, как поверхностная концентрация, можно получить из этих данных, обрабатывая их с помощью термодинамических методов [1, 2] (задачи 2 и 3).
На рис. 51-2 изображена зависимость поверхностного натяжения ртути в ряде растворов электролитов. Потенциал нулевого заряда приведен в табл. 51-1 (при 25°С вместо  Из равенства (51-9) видно, что точка нулевого заряда соответствует максимуму кривой поверхностного натяжения. Эта точка называется также электрокапиллярным максимумом. На рис. 51-2 потенциалы относительно нормального каломельного
Из равенства (51-9) видно, что точка нулевого заряда соответствует максимуму кривой поверхностного натяжения. Эта точка называется также электрокапиллярным максимумом. На рис. 51-2 потенциалы относительно нормального каломельного
электрода в  сдвинуты на
сдвинуты на  чтобы электрокапиллярный максимум для
чтобы электрокапиллярный максимум для  находился приблизительно при нуле вольт (задача 4).
находился приблизительно при нуле вольт (задача 4).
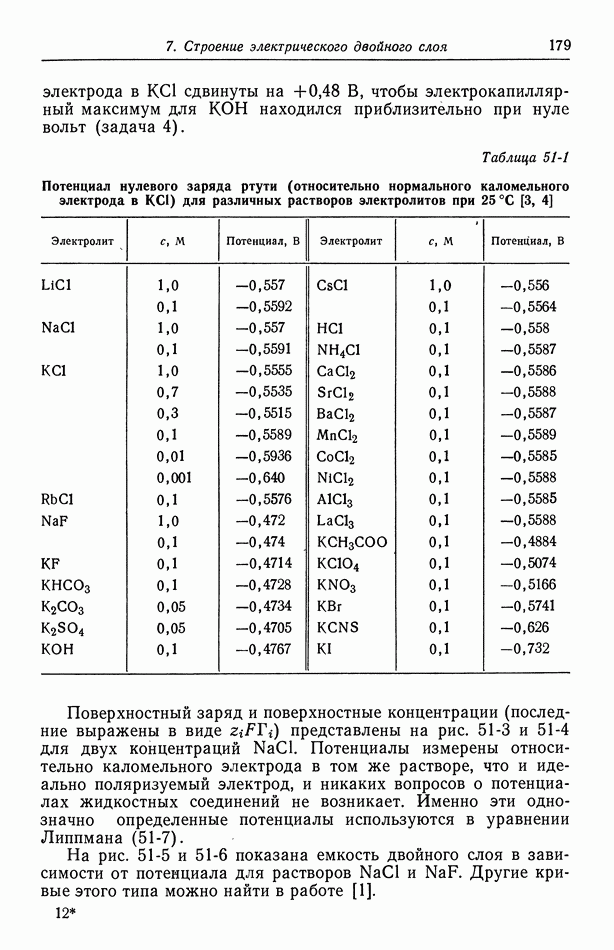
Таблица 51-1 (см. скан) Потенциал нулевого заряда ртути (относительно нормального каломельного электрода в  для различных растворов электролитов при 25 °С [3, 4]
для различных растворов электролитов при 25 °С [3, 4]
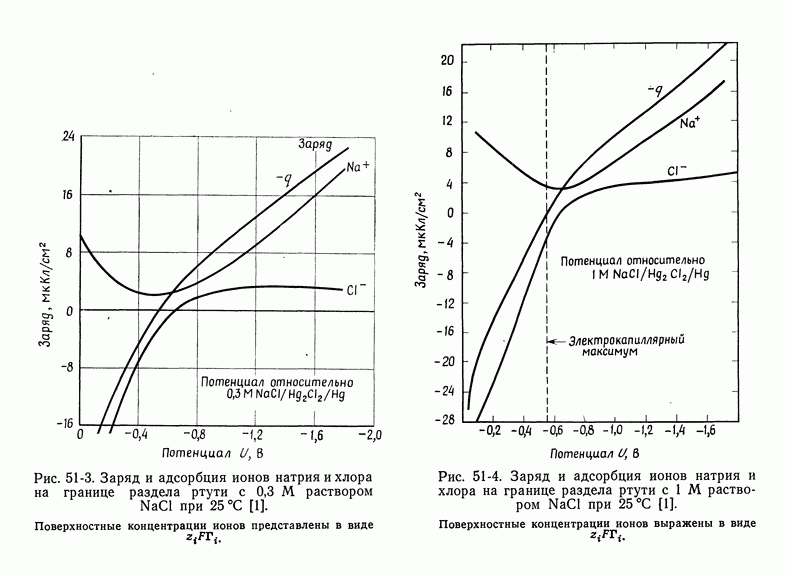
Поверхностный заряд и поверхностные концентрации (последние выражены в виде  представлены на рис. 51-3 и 51-4 для двух концентраций
представлены на рис. 51-3 и 51-4 для двух концентраций  Потенциалы измерены относительно каломельного электрода в том же растворе, что и идеально поляризуемый электрод, и никаких вопросов о потенциалах жидкостных соединений не возникает. Именно эти однозначно определенные потенциалы используются в уравнении Липпмана (51-7).
Потенциалы измерены относительно каломельного электрода в том же растворе, что и идеально поляризуемый электрод, и никаких вопросов о потенциалах жидкостных соединений не возникает. Именно эти однозначно определенные потенциалы используются в уравнении Липпмана (51-7).
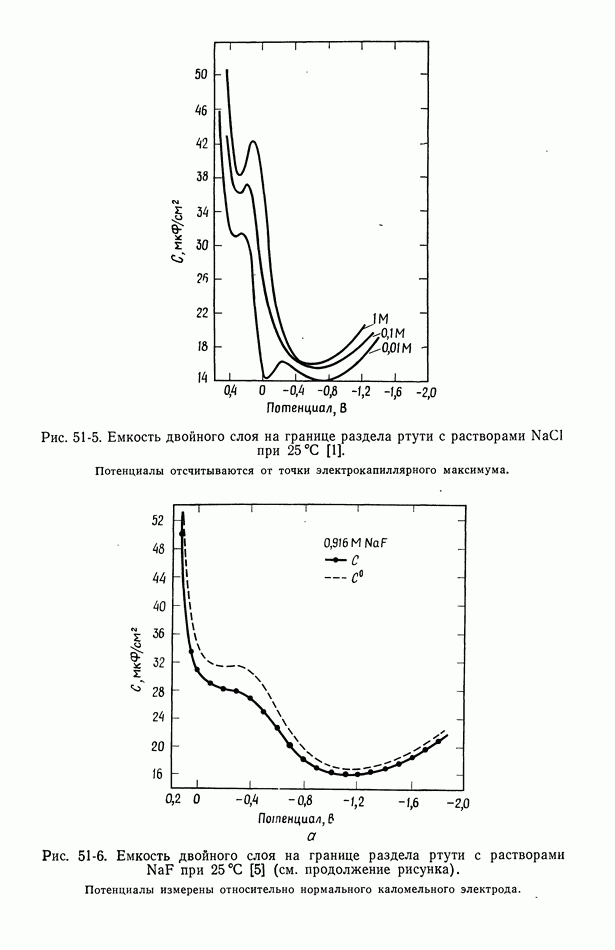
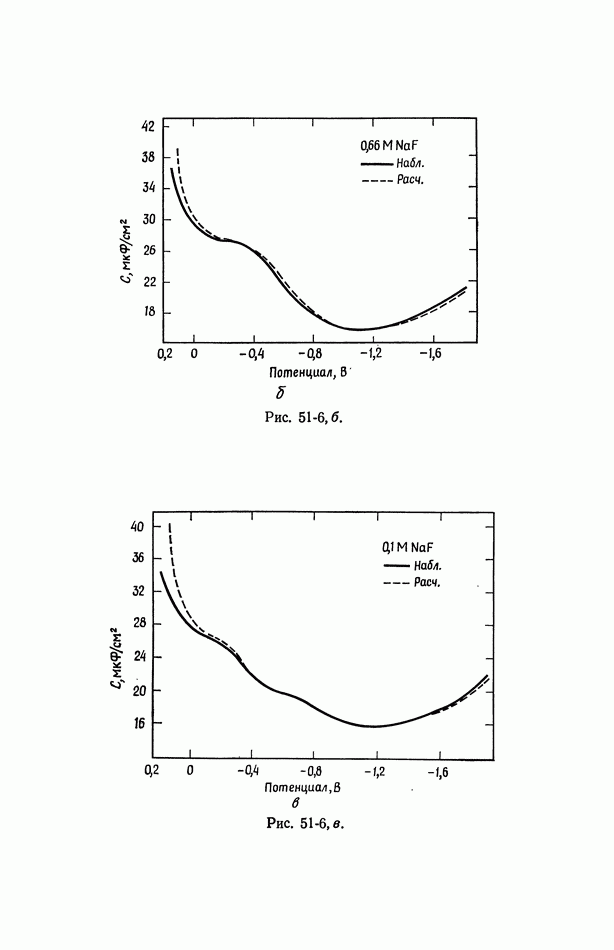
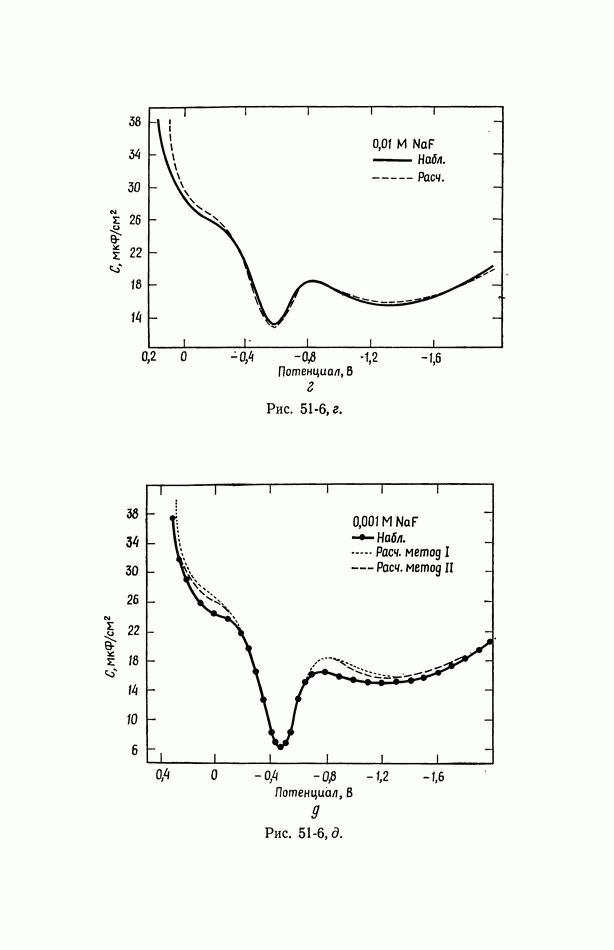
На рис. 51-5 и 51-6 показана емкость двойного слоя в зависимости от потенциала для растворов  Другие кривые этого типа можно найти в работе [1].
Другие кривые этого типа можно найти в работе [1].

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)

(кликните для просмотра скана)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
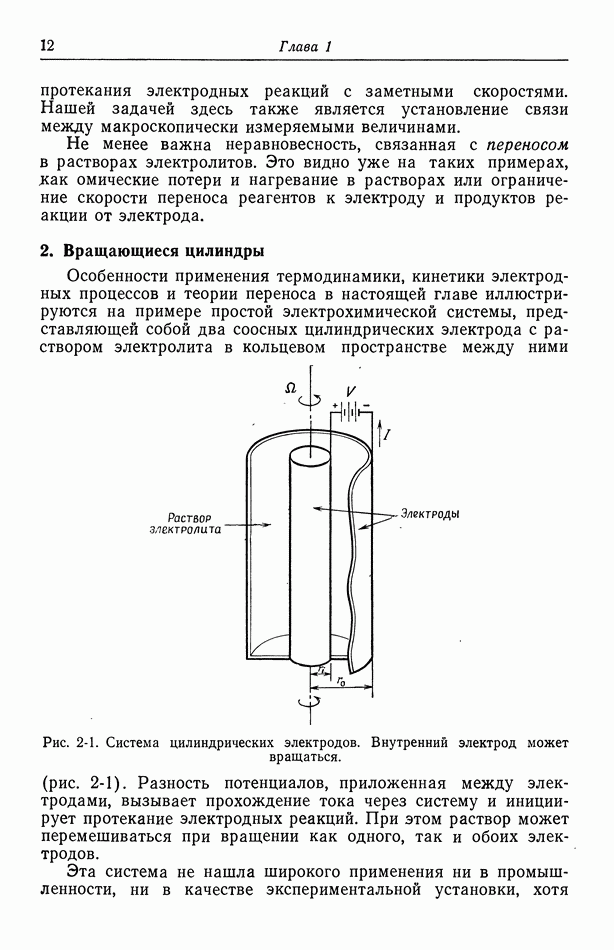
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
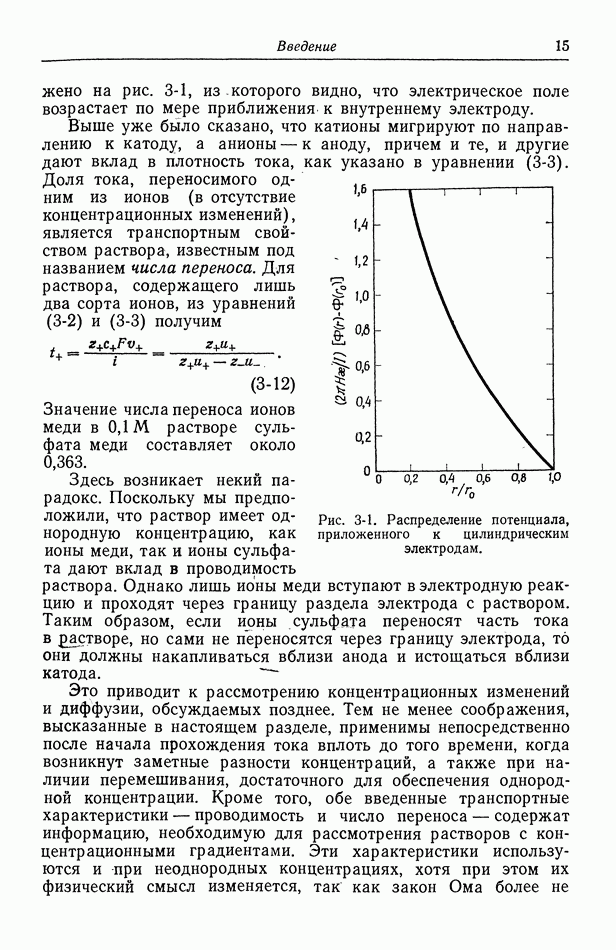
- 5. Диффузионный слой
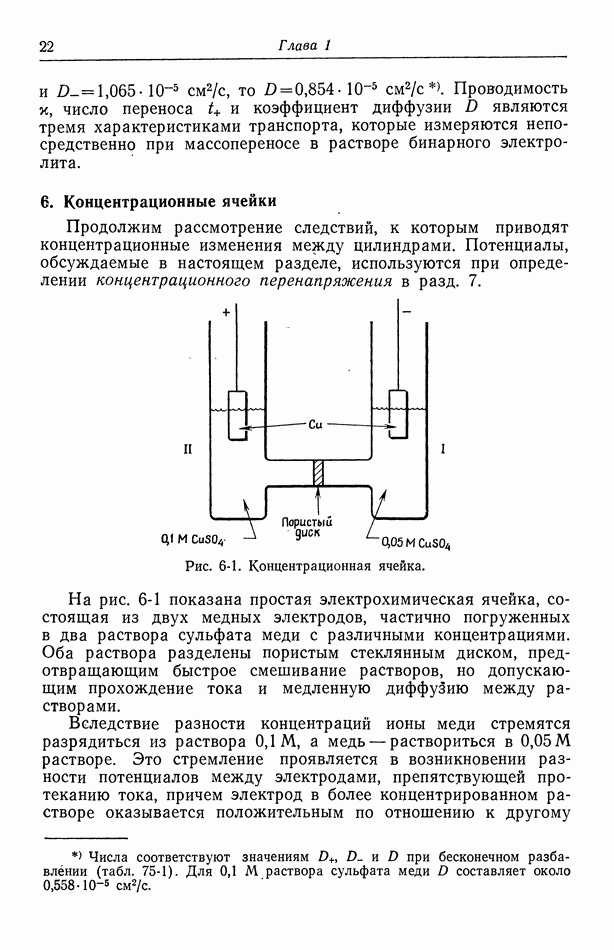
- 6. Концентрационные ячейки
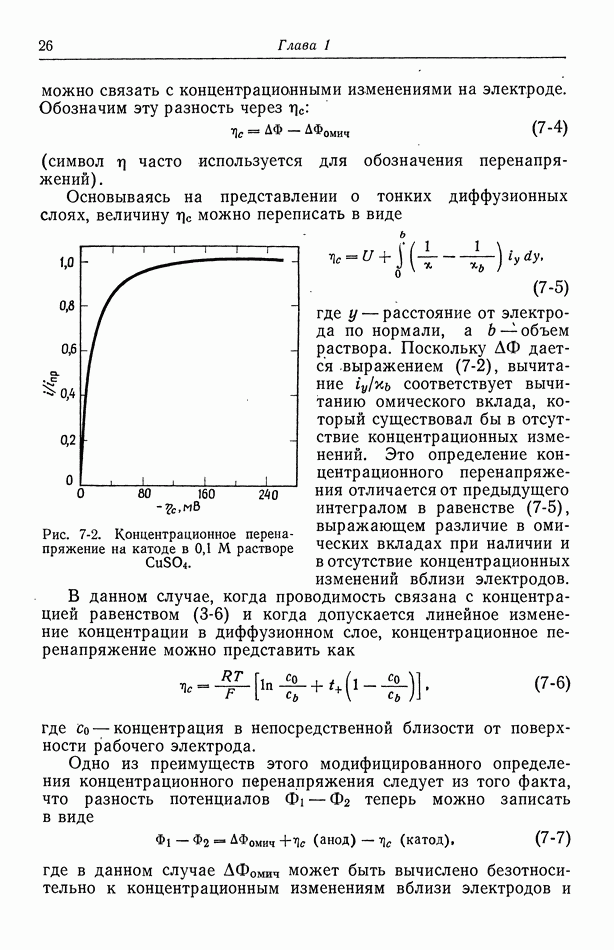
- 7. Концентрационное перенапряжение
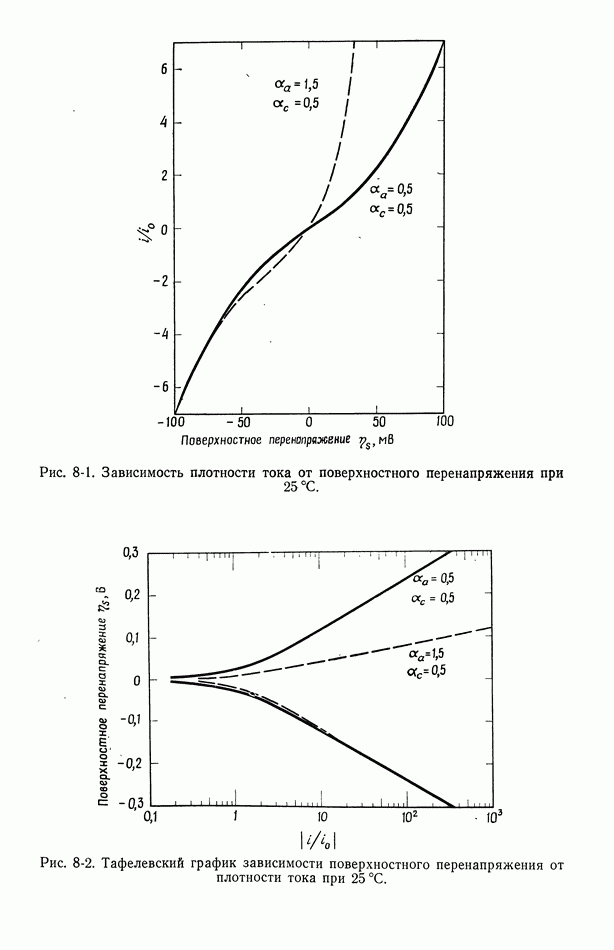
- 8. Поверхностное перенапряжение
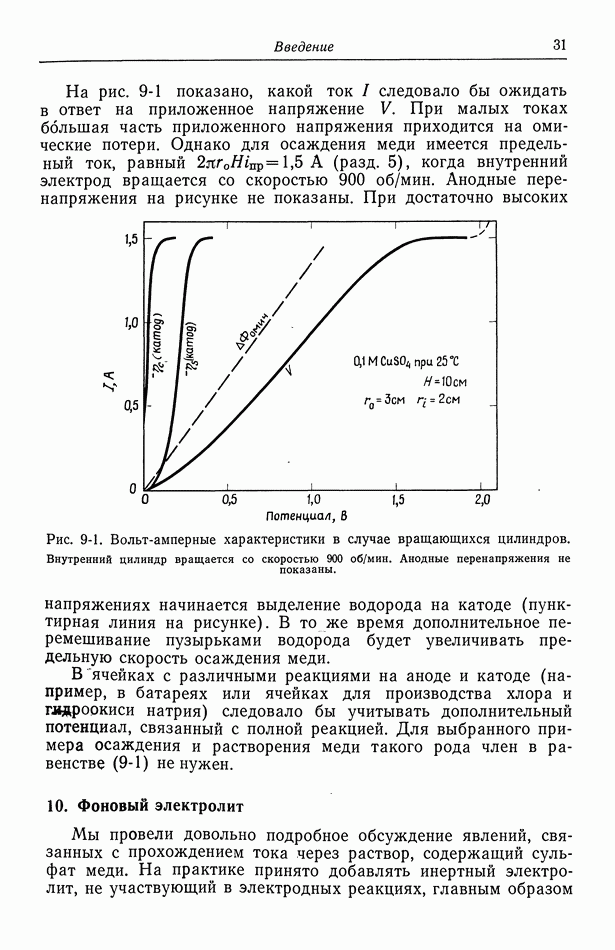
- 9. Потенциал ячейки
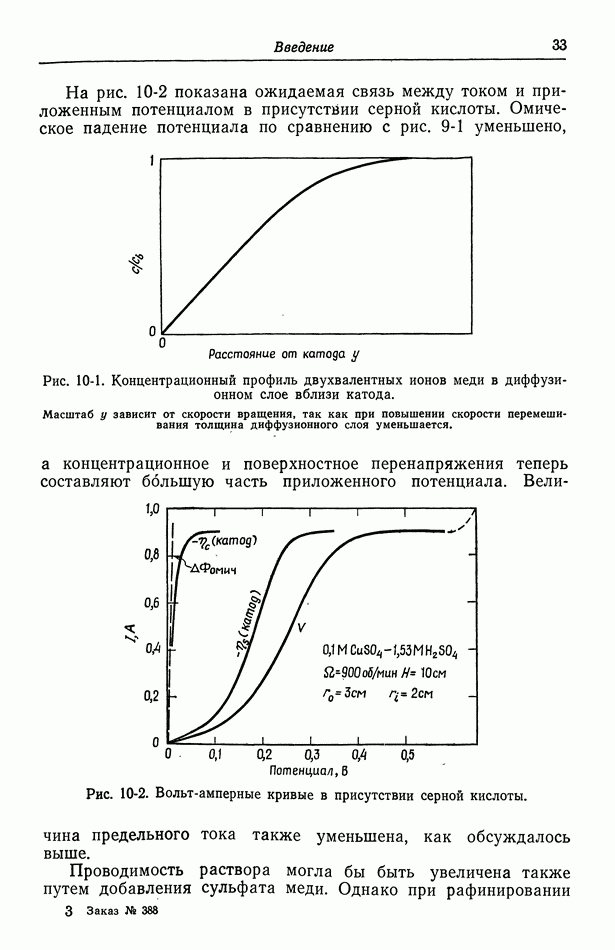
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
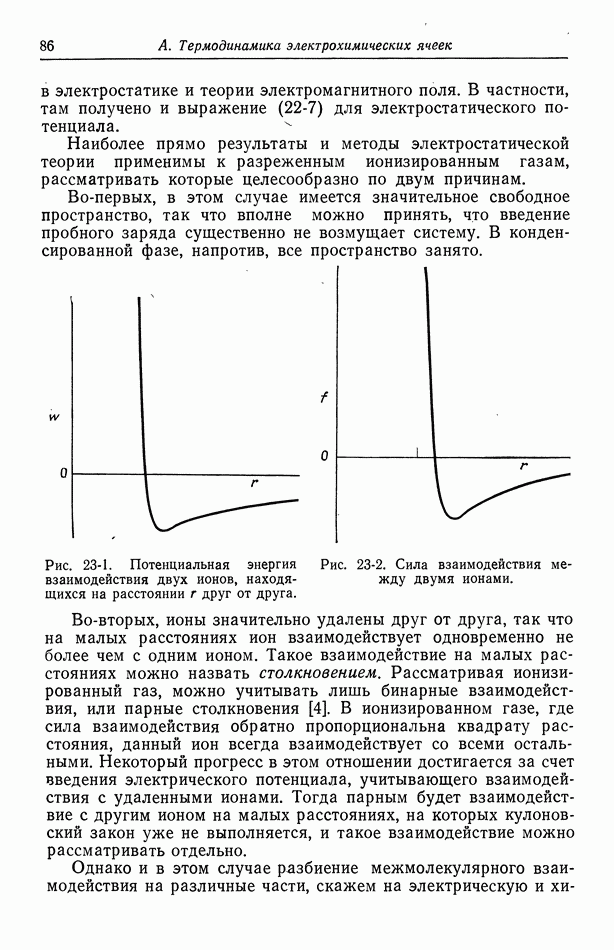
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
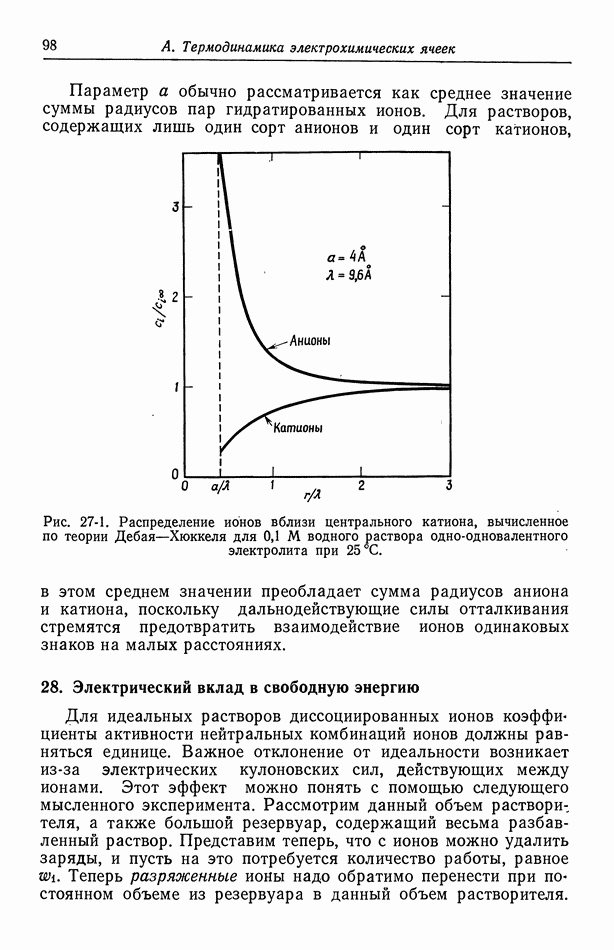
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
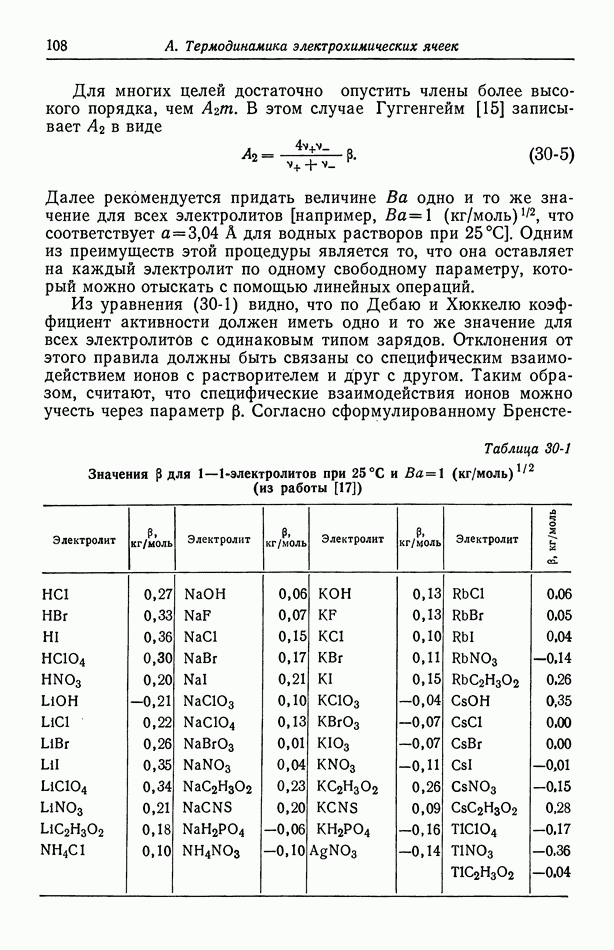
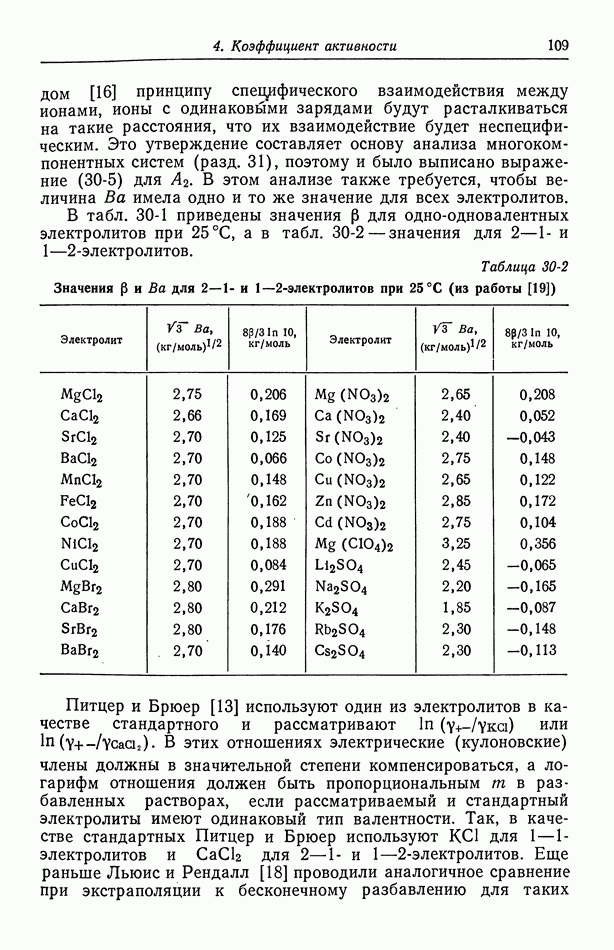
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
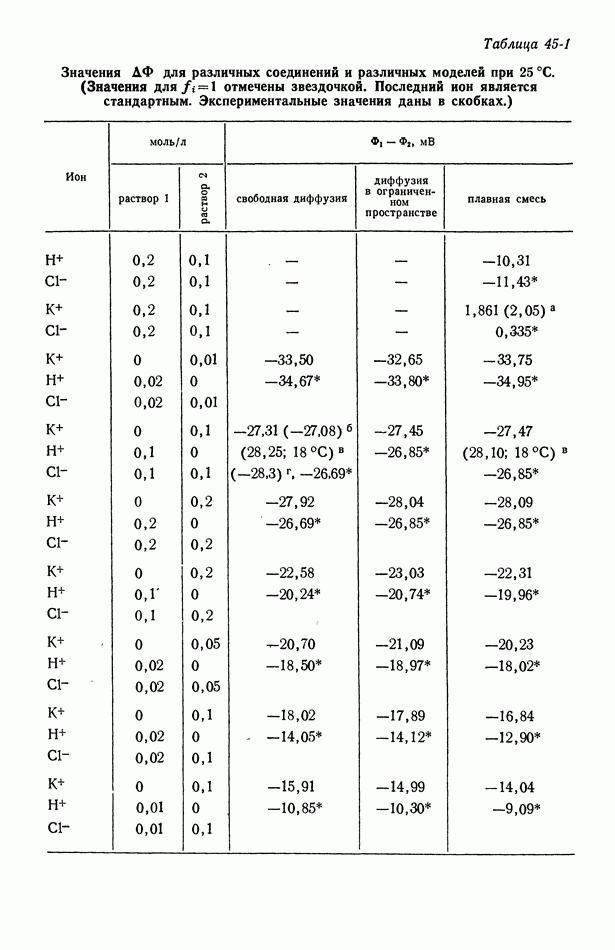
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
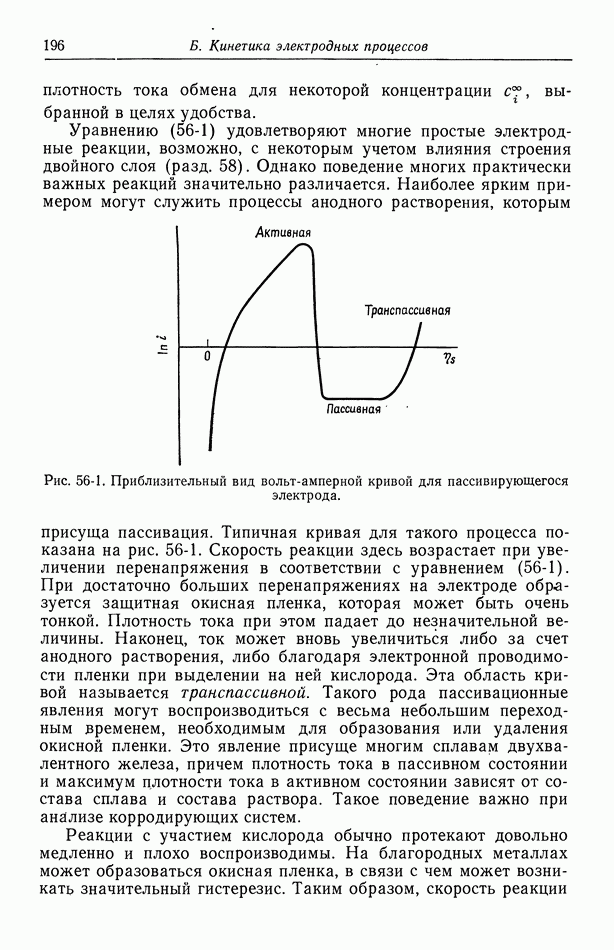
- 56. Зависимость плотности тока от поверхностного перенапряжения
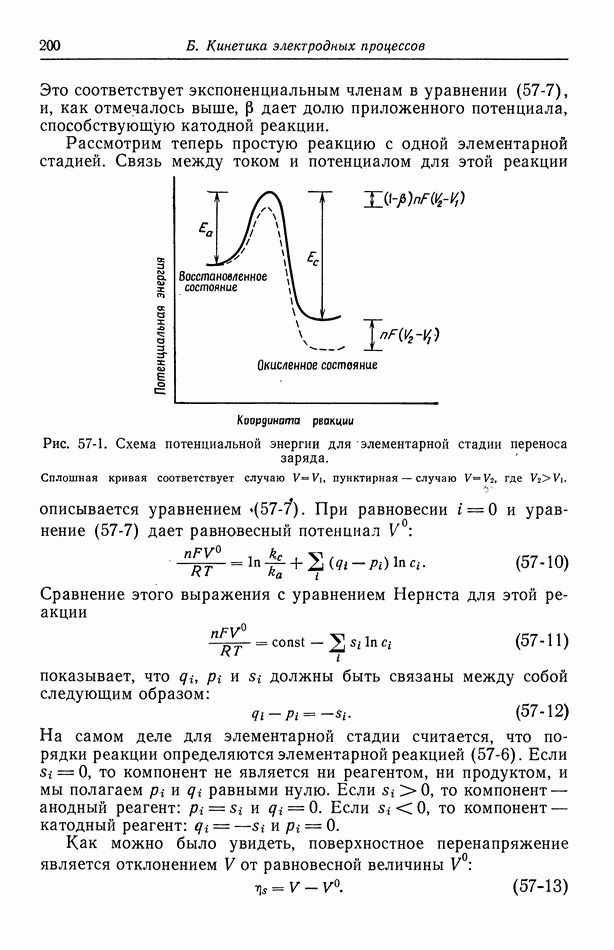
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
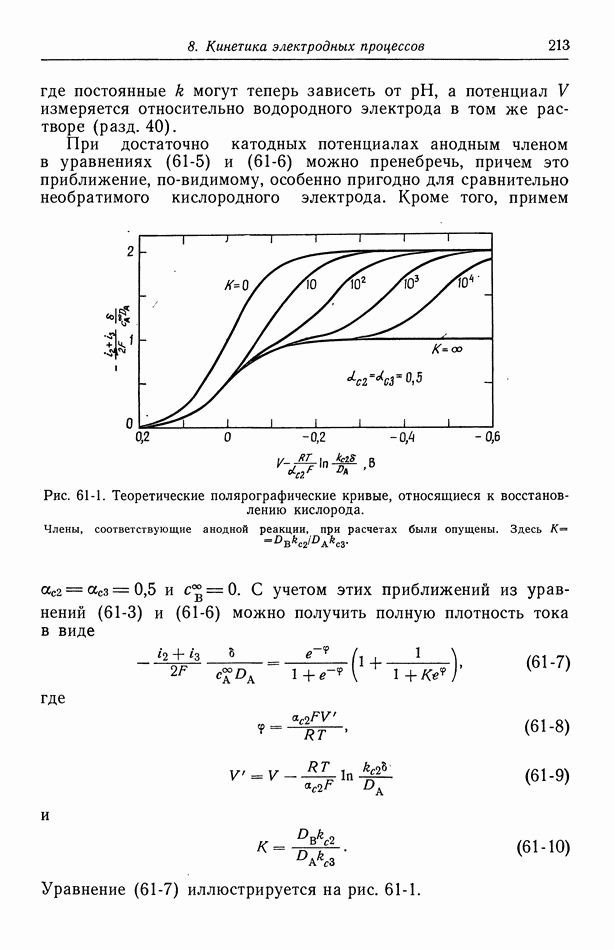
- 59. Кислородный электрод
- 60. Методы измерения
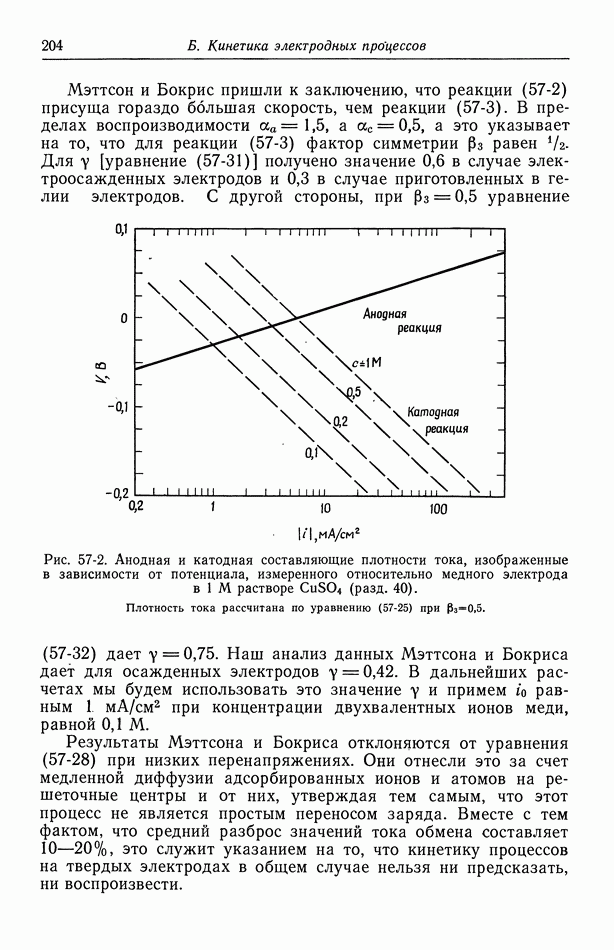
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
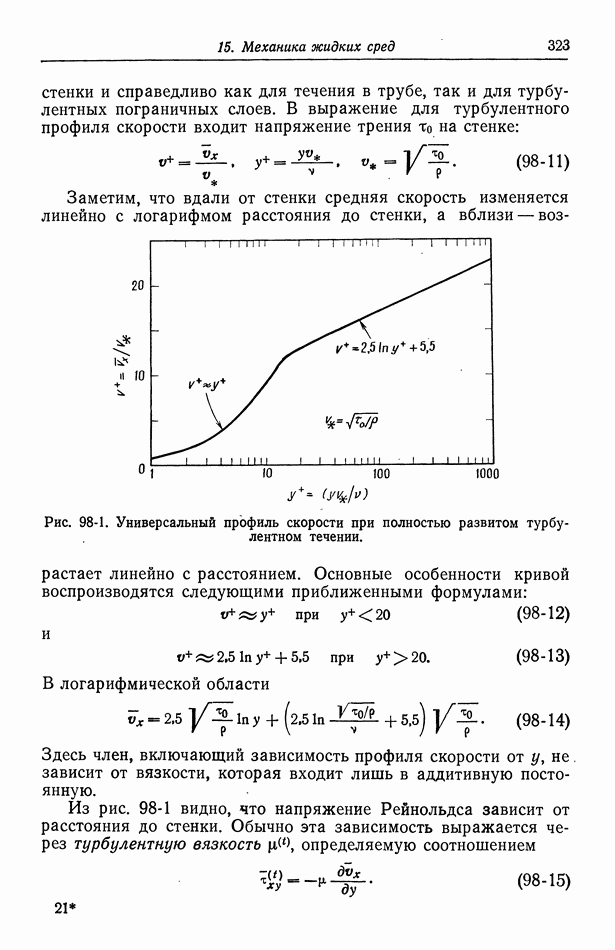
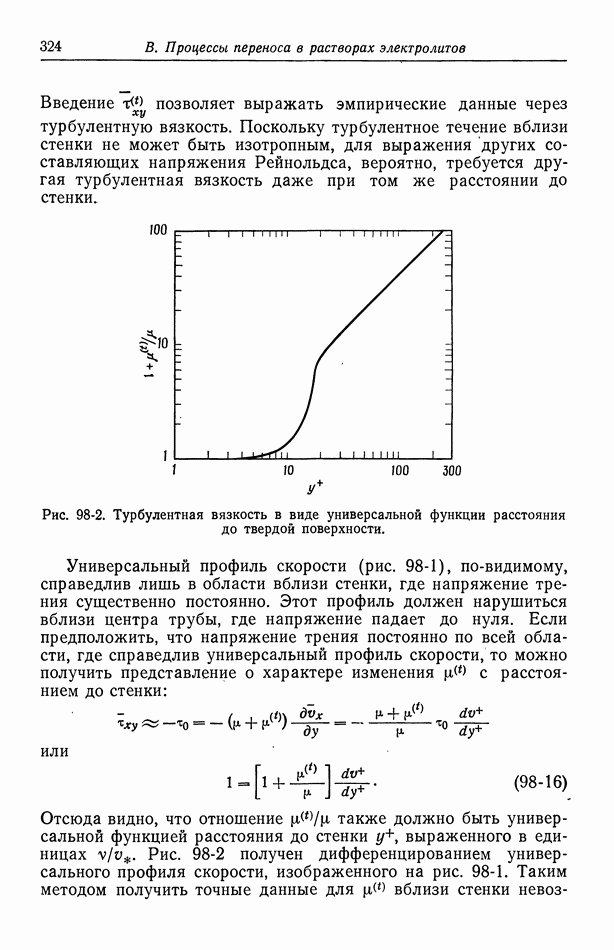
- 98. Турбулентное течение
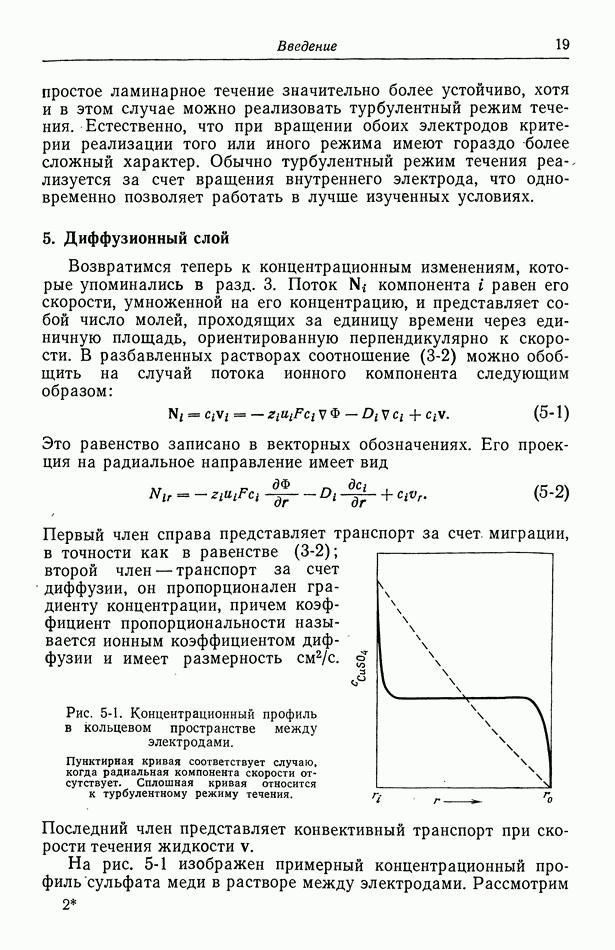
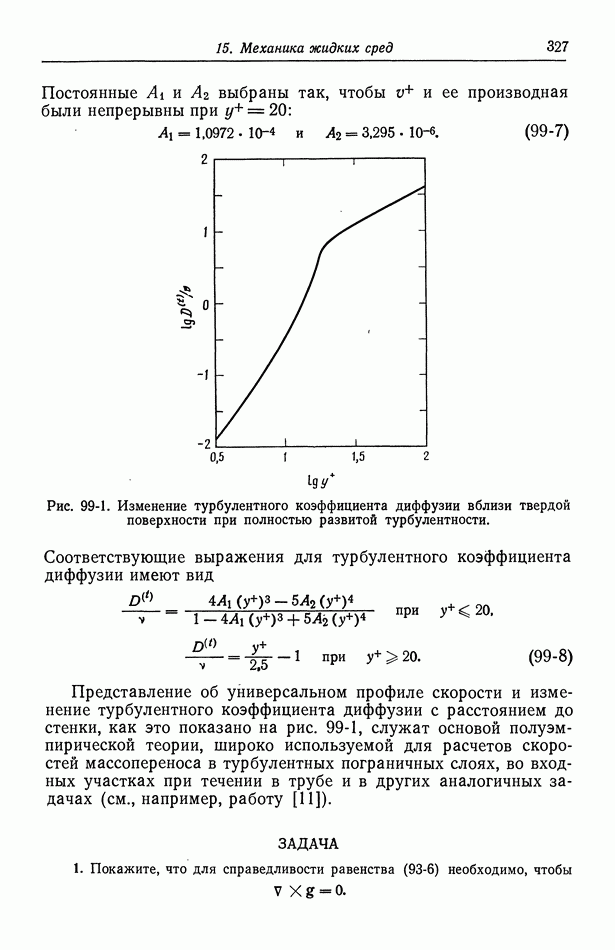
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
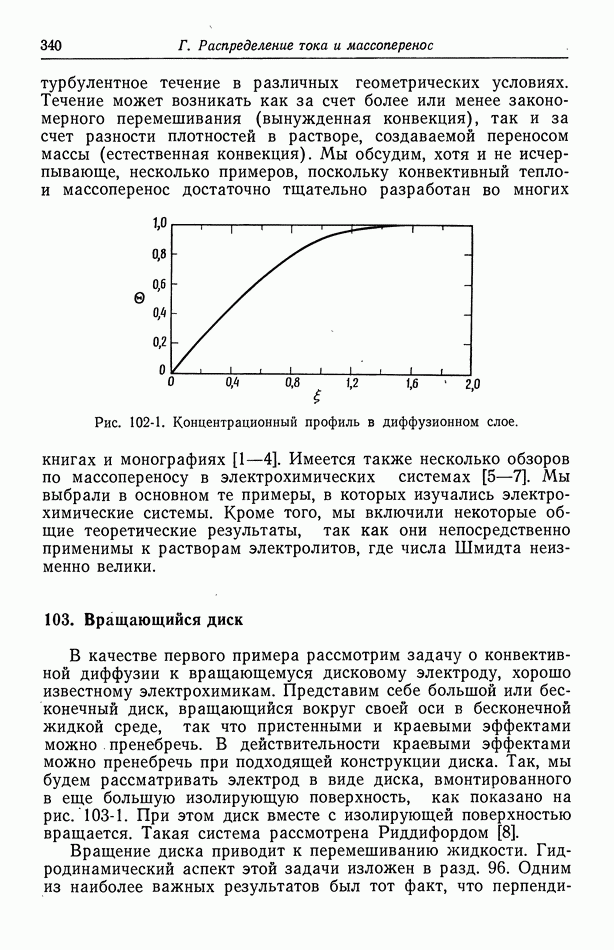
- 102. Упрощенное описание конвективной диффузии
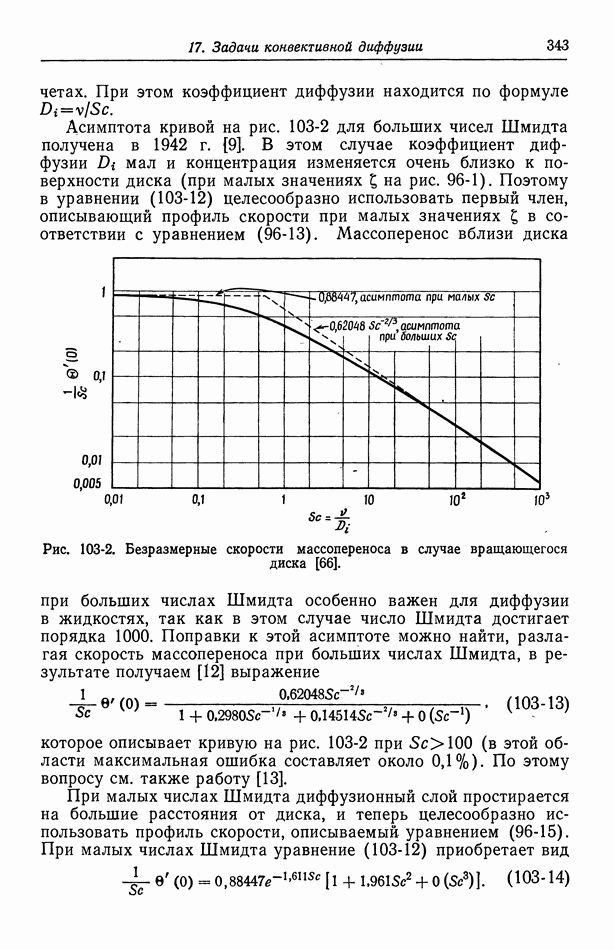
- 103. Вращающийся диск
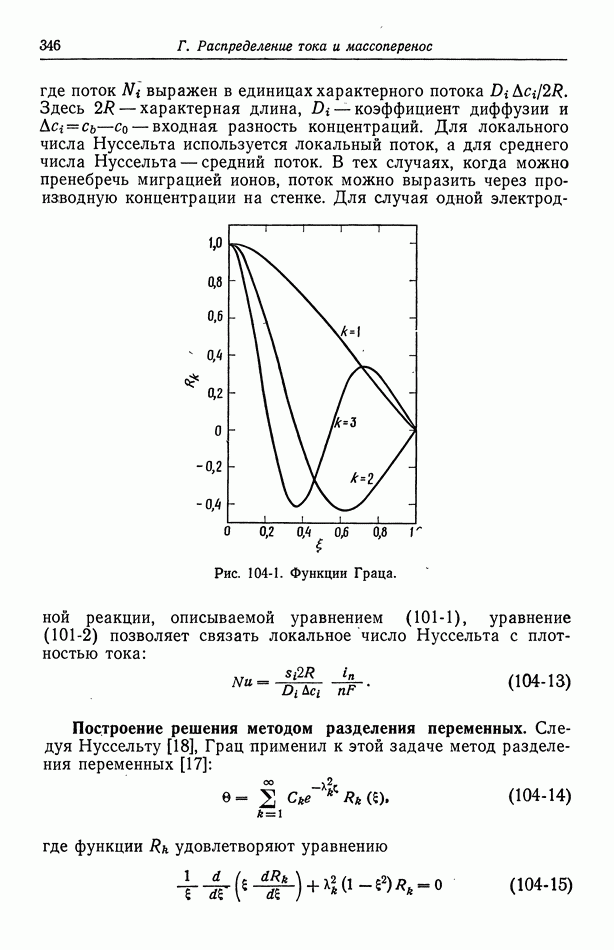
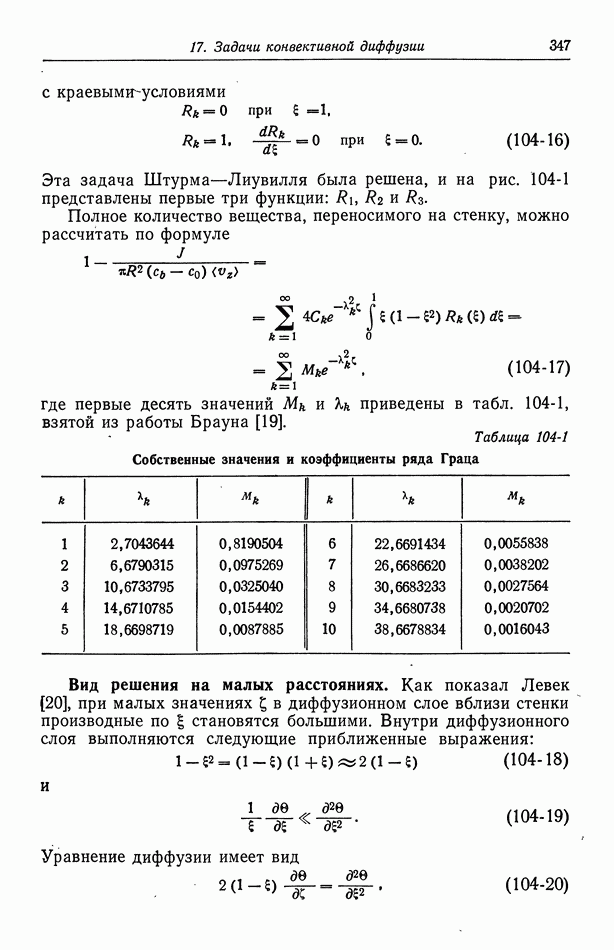
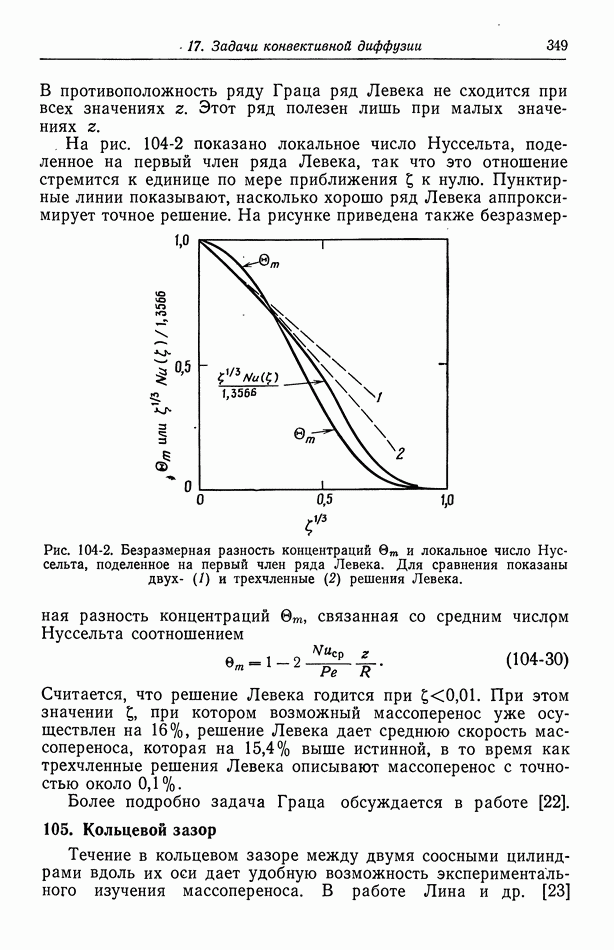
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
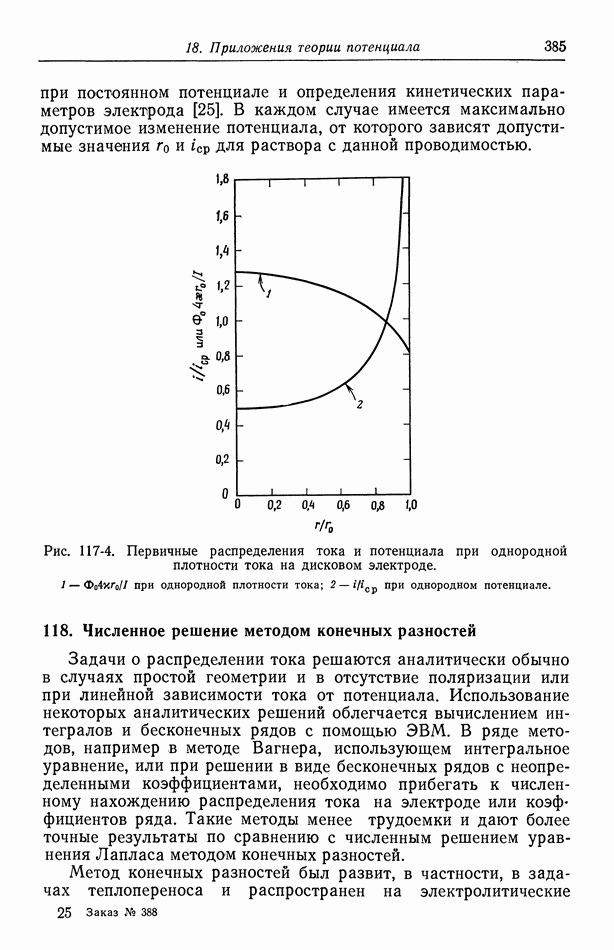
- 116. Первичное распределение тока
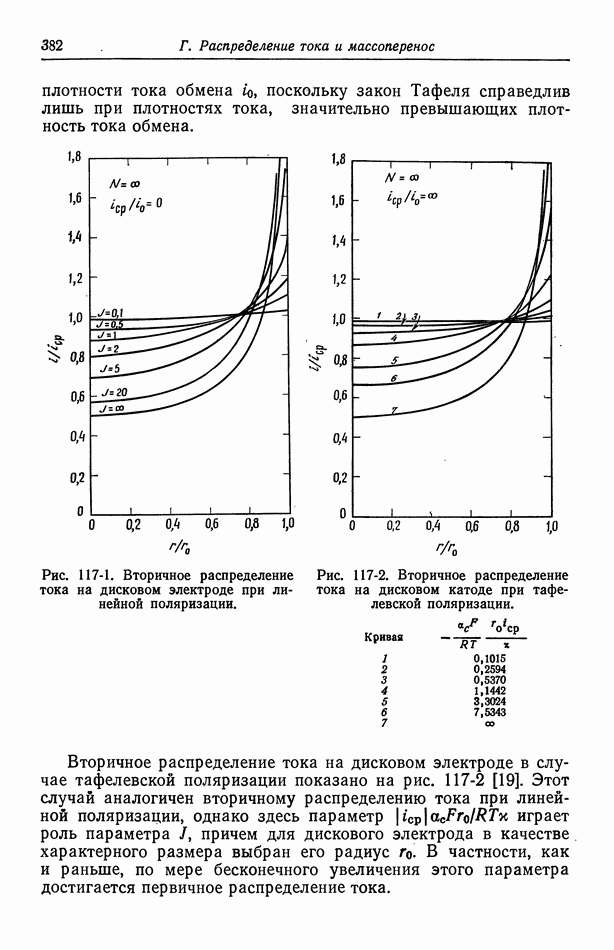
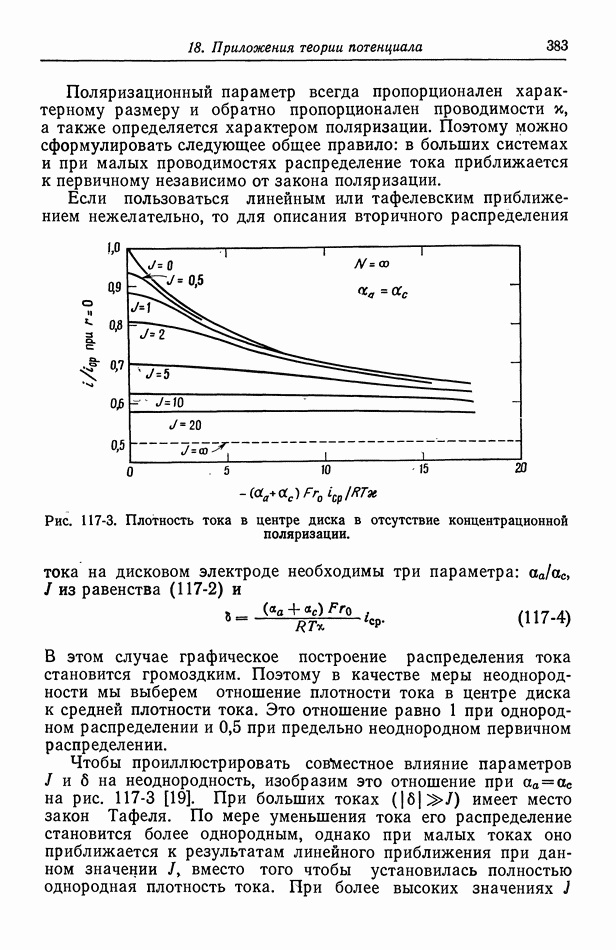
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
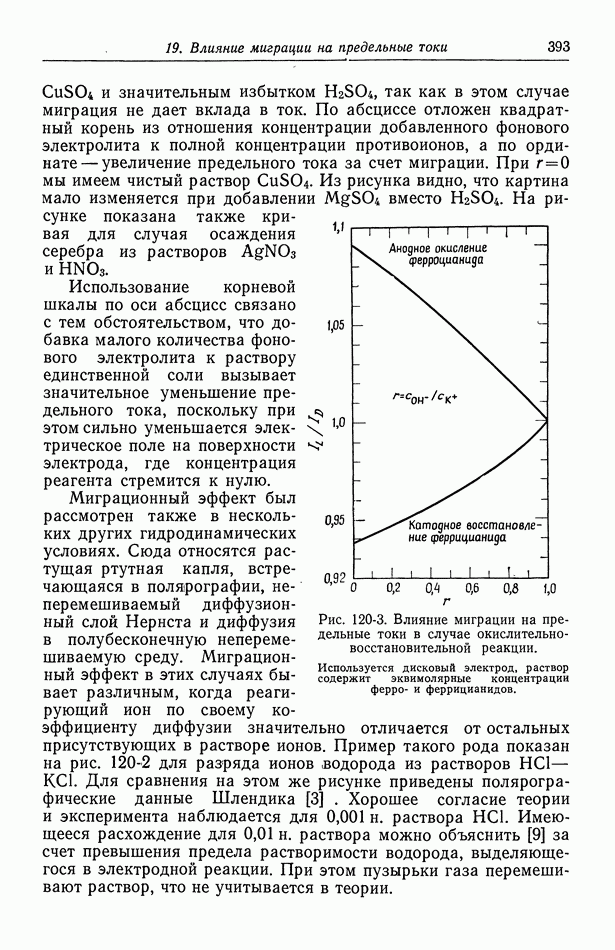
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
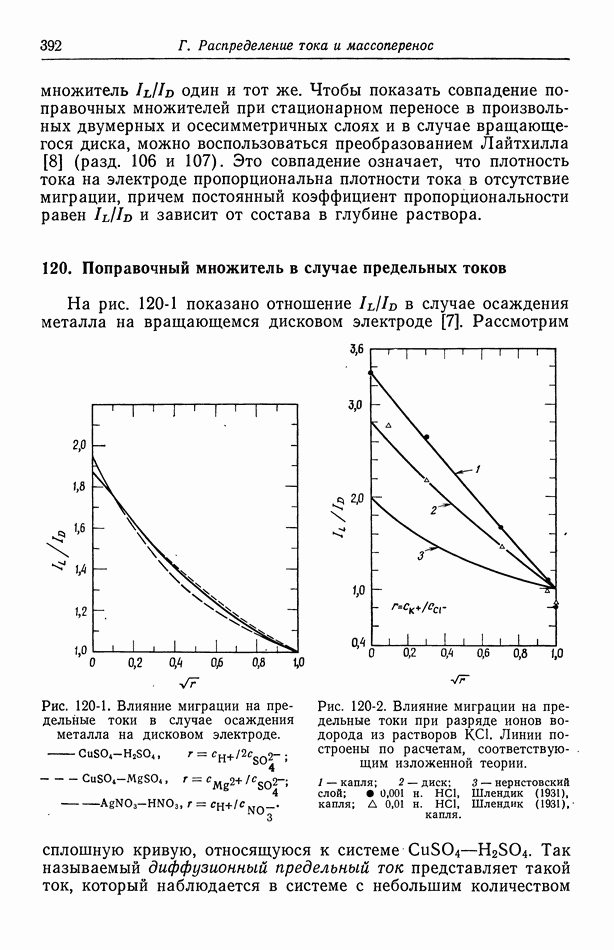
- 120. Поправочный множитель в случае предельных токов
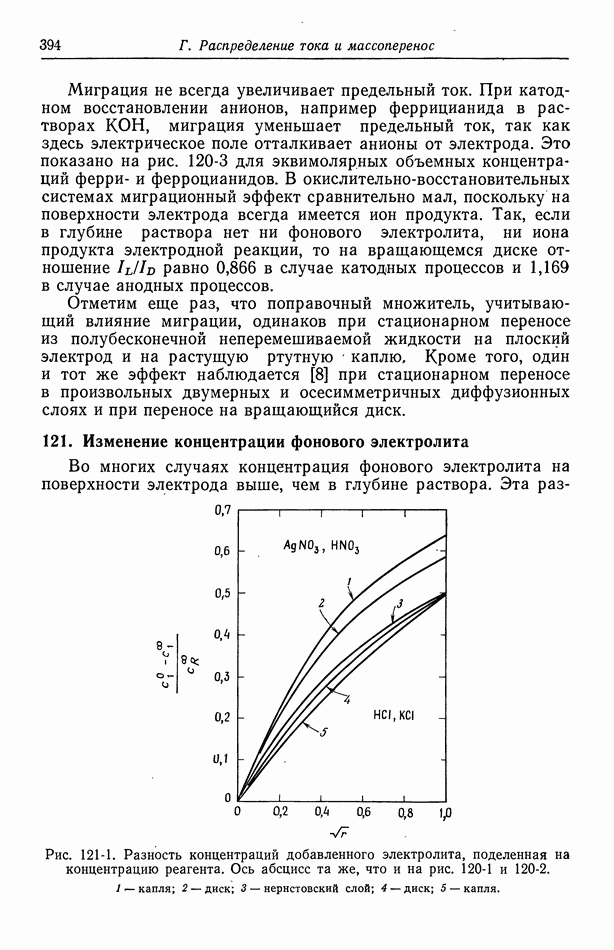
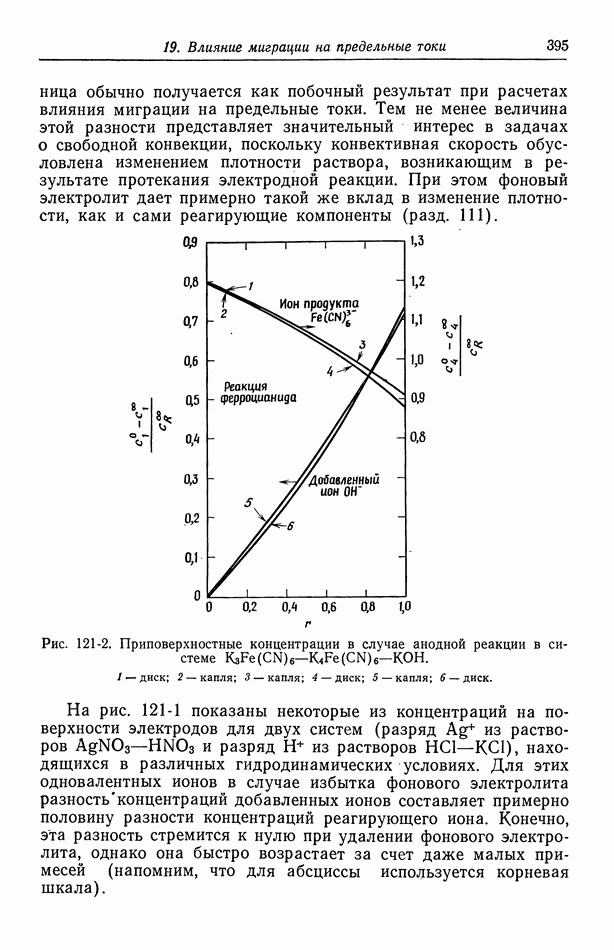
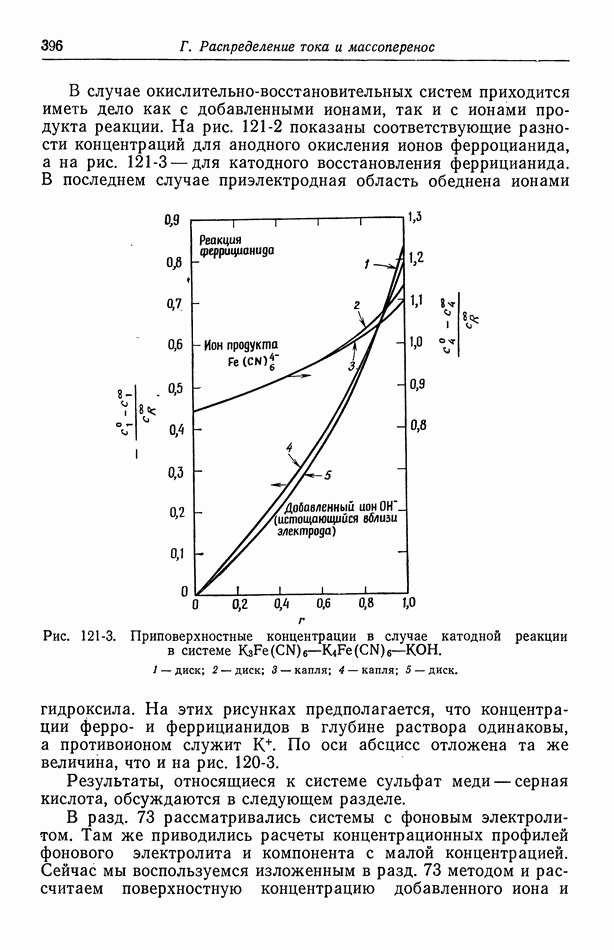
- 121. Изменение концентрации фонового электролита
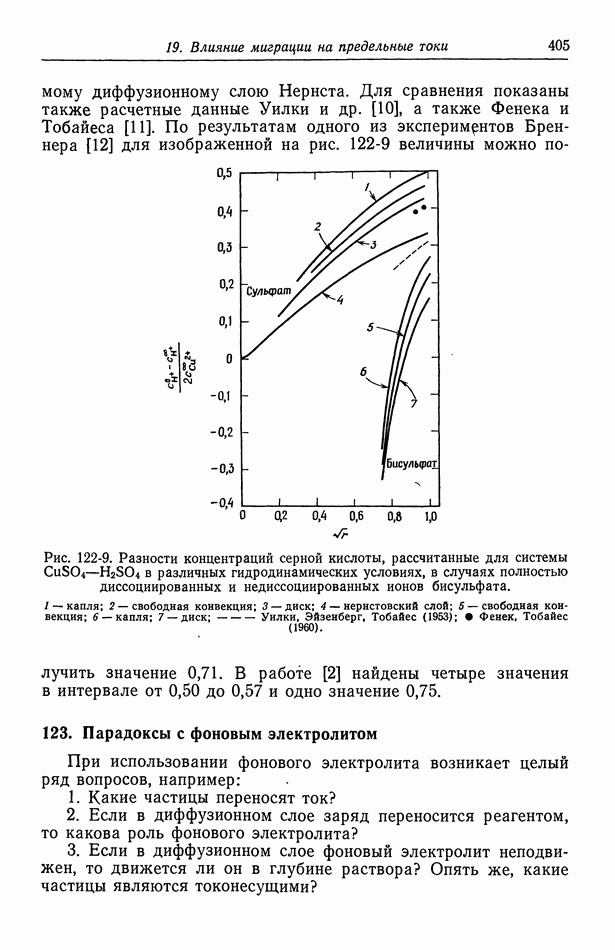
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ