| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
17. Ячейка с одним электролитом переменной концентрации
Ячейка, в которой концентрация одного электролита изменяется от точки к точке, является простейшим примером так называемой ячейки с переносом. Такова ячейка

в которой химический состав обоих проводников из платины одинаков, так же как и обоих литиевых электродов. Концентрация  в фазе
в фазе  отличается от концентрации в фазе
отличается от концентрации в фазе  Переходной является та область, в которой имеется концентрационный градиент; последний обусловлен различием концентраций в фазах
Переходной является та область, в которой имеется концентрационный градиент; последний обусловлен различием концентраций в фазах  Эту область иногда называют жидкостным контактом.
Эту область иногда называют жидкостным контактом.
С помощью условий фазового равновесия [равенство (12-5)] и определения разности потенциалов между фазами с одинаковым составом [равенство (13-2)] потенциал ячейки сводится к

Продвинуться дальше при рассмотрении ячейки с помощью обычной термодинамики невозможно из-за наличия диффузии.
Для оценки разности электрохимических потенциалов, возникающей в равенстве (17-2), можно применить уравнение (16-3). Если положить плотность тока равной нулю и в качестве компонента  принять ионы лития, то уравнение (16-3) приобретает вид
принять ионы лития, то уравнение (16-3) приобретает вид

Последнее равенство можно проинтегрировать по области контакта и подставить результат интегрирования в равенство (17-2), что приводит к

В этом частном случае как  так и
так и  зависят лишь от концентрации
зависят лишь от концентрации  и интеграл в уравнении (17-4) становится независимым от детального вида концентрационного профиля в области контакта:
и интеграл в уравнении (17-4) становится независимым от детального вида концентрационного профиля в области контакта:

Это равенство эквивалентно выражениям, фигурирующим почти в каждом теоретическом анализе ячеек рассматриваемого типа. Однако здесь не использовался прием виртуального пропускания тока, применяемый в большинстве выводов, поскольку такой прием создает впечатление, что обычной термодинамики достаточно для получения потенциала ячейки. Разность потенциалов в равенстве (17-5) не следует называть потенциалом жидкостного контакта; это скорее потенциал ячейки с жидкостным соединением.
Уравнение (17-5) можно обобщить на металлы и электролиты с различными зарядовыми числами, в резулме чего получается

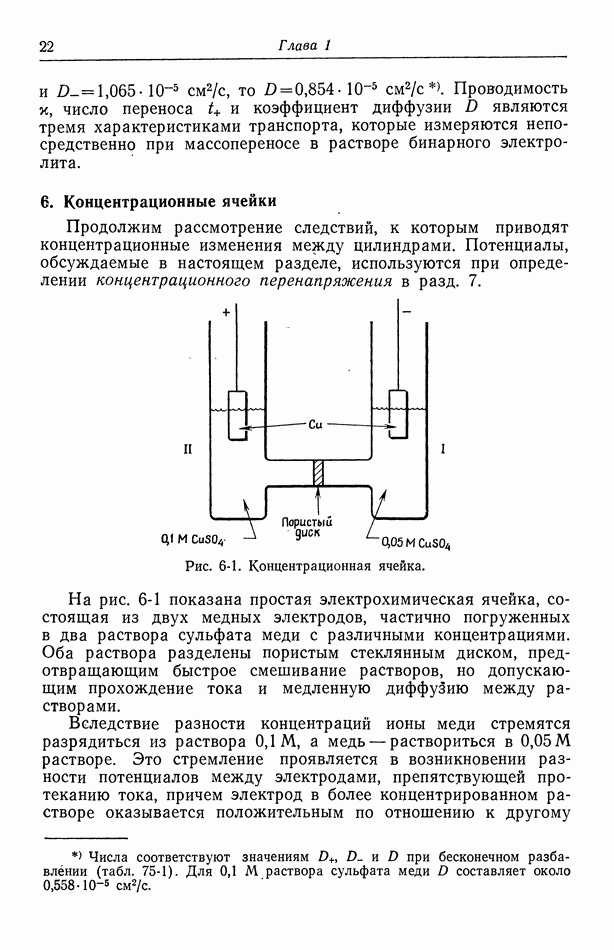
где А обозначает единственный электролит. Предполагается, что в равновесиях между электродами и растворами участвуют лишь катионы, и электроды считаются одинаковыми. Сюда относится также изображенная на рис. 6-1 концентрационная ячейка с сульфатом меди.
После введения коэффициентов активности с помощью равенства (14-15) уравнение (17-6) преобразуется к виду

Если пренебречь концентрационной зависимостью чисел переноса, то получится приближенное выражение

которое послужило основой аппроксимации в уравнении  для потенциала концентрационной ячейки с
для потенциала концентрационной ячейки с  использованной в гл. 1 в качестве примера.
использованной в гл. 1 в качестве примера.
Наконец, можно было бы обобщить эти результаты на произвольную электродную реакцию, когда в растворе имеется единственный электролит А. Представим ячейку в виде

Если «электроды» включают дополнительно газовую фазу или слаборастворимую соль, то химические потенциалы этих нейтральных компонентов принимаются одинаковыми по обе стороны ячейки; кроме того, растворимости принимаются достаточно малыми, чтобы можно было по-прежнему считать, что в растворе содержится лишь один электролит.
Для общей электродной реакции можно принять

где  стехиометрический коэффициент компонента
стехиометрический коэффициент компонента  символ для химической формулы компонента
символ для химической формулы компонента  Для этой реакции обобщением формул, описывающих фазовое равновесие, будет
Для этой реакции обобщением формул, описывающих фазовое равновесие, будет

где следует добавить верхние индексы, означающие фазы, в которых находится соответствующий компонент. Поскольку внешние фазы нейтральны и заряд в них не накапливается, за электроны, производимые или поглощаемые на электродах, ответственны катионы и анионы электролита:

В этом случае мы будем рассматривать ячейку с помощью воображаемого электрода сравнения того же типа, что и основные электроды. Такой электрод может перемещаться через раствор между электродами вместе со своими внешними нейтральными фазами. Чтобы найти изменение потенциала этого
электрода в зависимости от его положения, следует взять градиент от уравнения (17-11)

причем предполагается, что от положения в пространстве зависят лишь свойства раствора. Уравнение (16-3) позволяет связать изменения электрохимических потенциалов ионов с изменениями химического потенциала электролита:

С помощью уравнения Гиббса-Дюгема (14-24) можно связать изменения химических потенциалов растворителя и электролита:

Объединяя уравнения (17-12) — (17-14), получаем

Интегрируя по области контакта, находим

Если  не зависит от концентрации, то это равенство можно записать в виде
не зависит от концентрации, то это равенство можно записать в виде

Отсюда видно, что, когда анион и растворитель не участвуют в электродной реакции, равенства (17-17) и (17-7) совпадают.
Мы рассмотрели здесь концентрационные ячейки, в которых одинаковые электроды помещены в различные растворы одного электролита, соединяющиеся с помощью области контакта с переменной концентрацией. Оказалось, что измеряемый потенциал ячейки зависит не только от термодинамических, но и от транспортных свойств растворов в ячейке. Такие ячейки полезны для
определения коэффициента активности, если известно число переноса, и для определения числа переноса, если известен коэффициент активности. На практике производятся оба типа определений.
Рассмотрим несколько дополнительных примеров. Потенциал ячейки

равен

Это согласуется с уравнением (17-17) при одинаковых парциальных давлениях водорода вблизи обоих платиновых электродов.
Если заменить водородные электроды хлорсеребряными, то получим ячейку

потенциал которой равен

если только серебряные электроды идентичны и твердый хлорид серебра одинаков с обеих сторон ячейки. Потенциалы этой и предыдущей ячеек противоположны по знаку и имеют совершенно разные значения, поскольку  в то время как
в то время как
 . Уравнения (17-22) и (17-17) согласуются, если использовать значения
. Уравнения (17-22) и (17-17) согласуются, если использовать значения  Наконец, для ячейки
Наконец, для ячейки

реакцию на окиснортутных электродах можно записать в виде

Для этой реакции имеем

Следовательно, потенциал ячейки описывается выражением

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
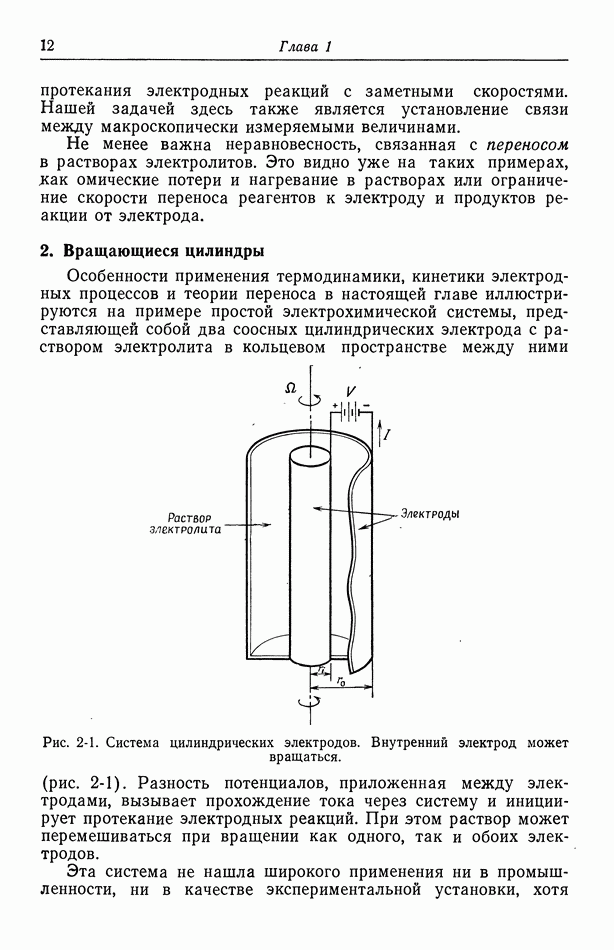
- 2. Вращающиеся цилиндры
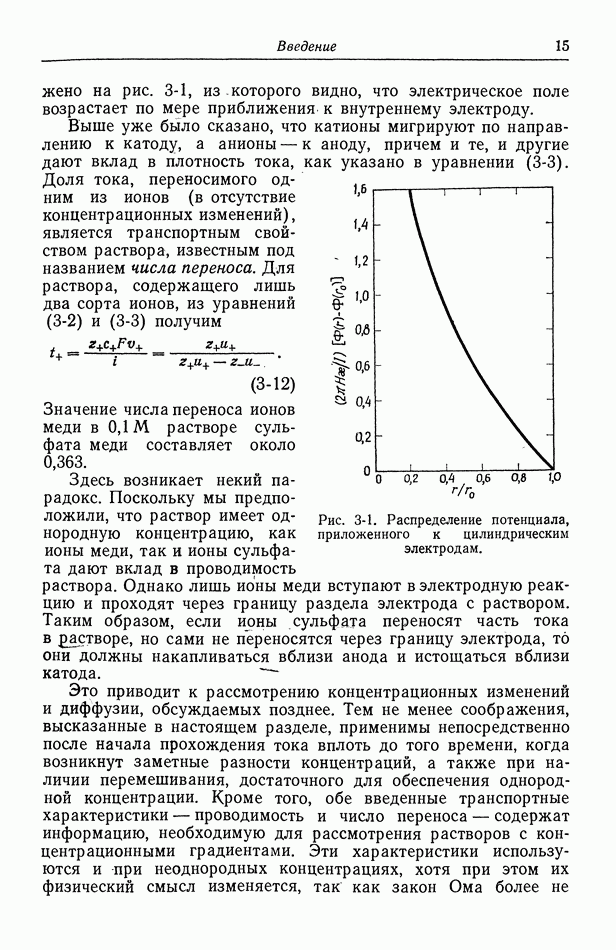
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
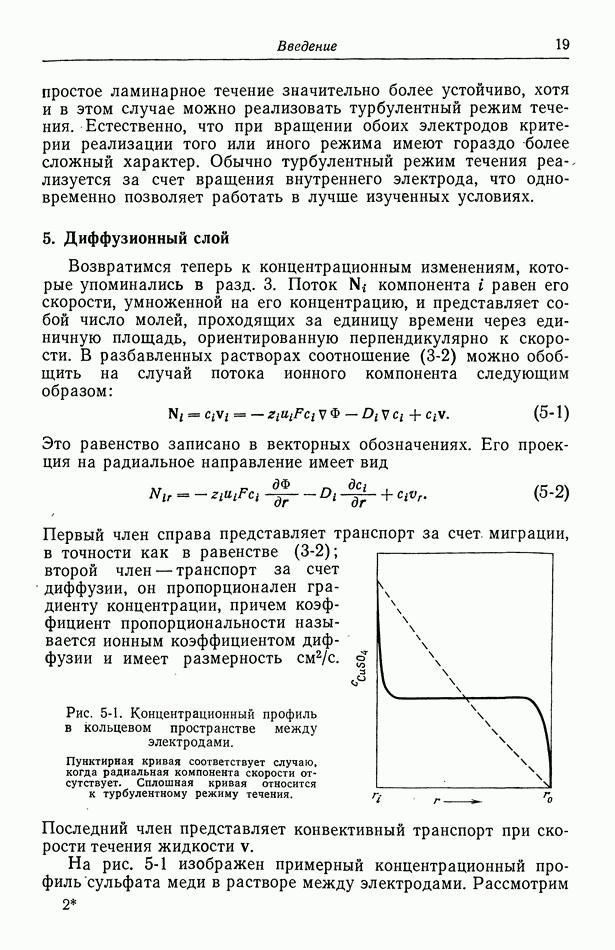
- 5. Диффузионный слой
- 6. Концентрационные ячейки
- 7. Концентрационное перенапряжение
- 8. Поверхностное перенапряжение
- 9. Потенциал ячейки
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ