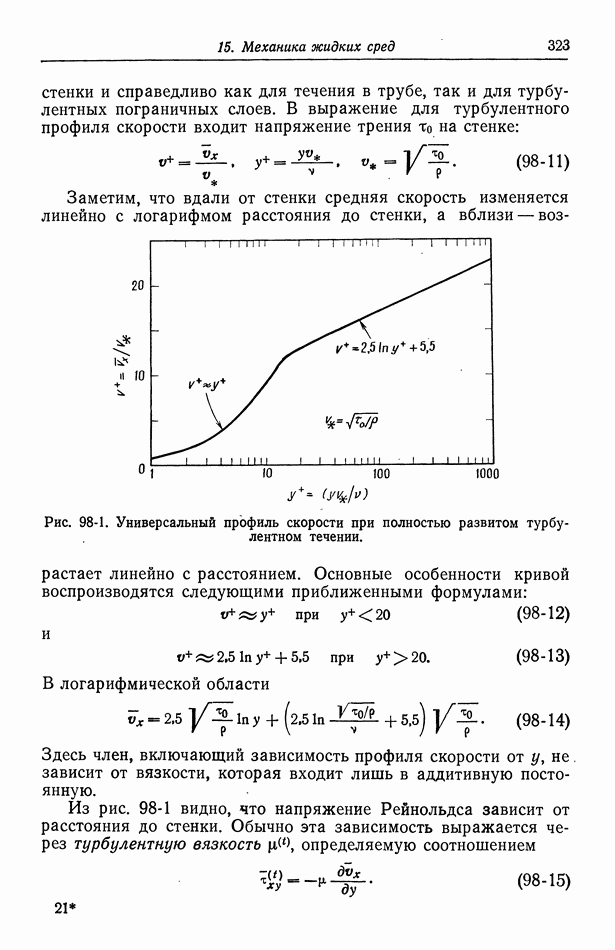
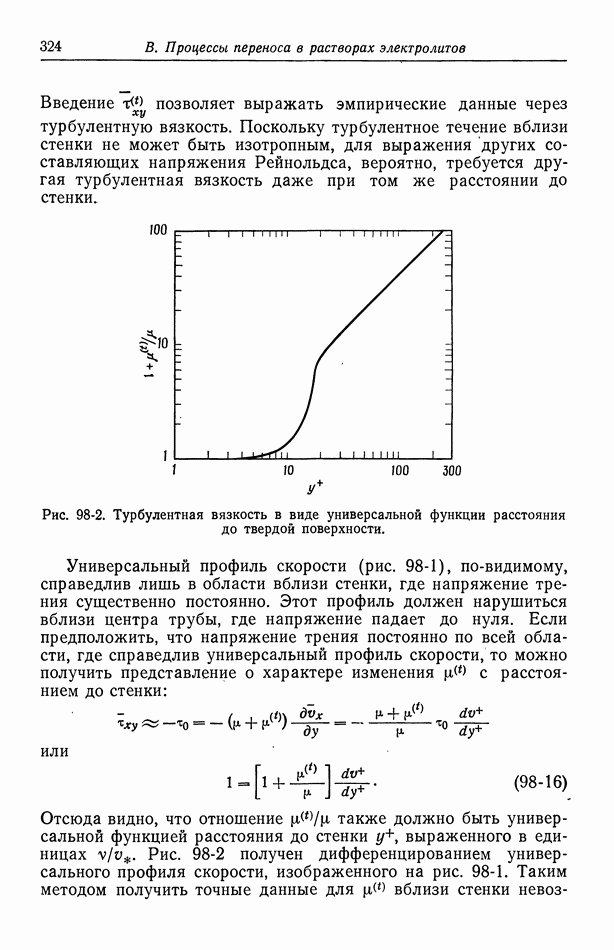
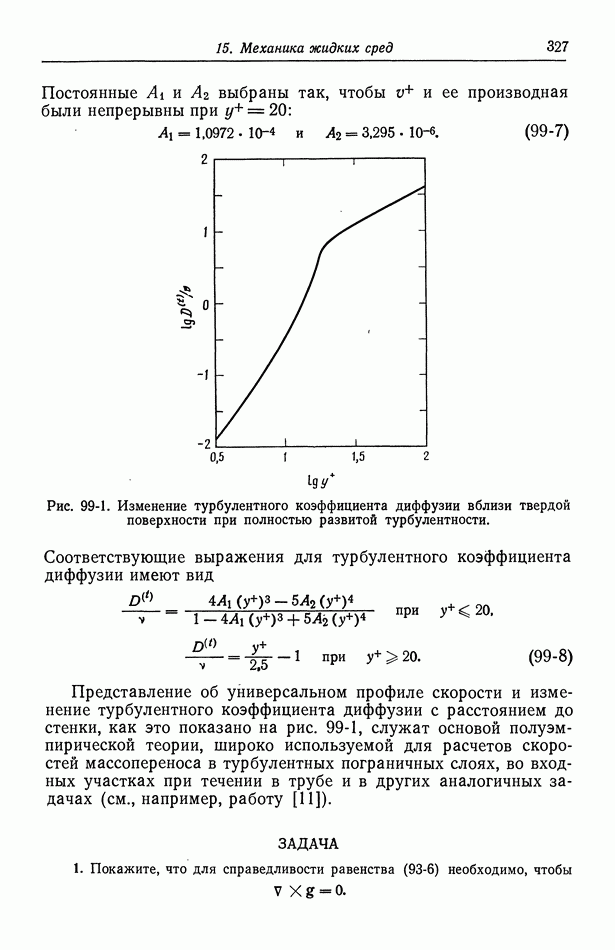
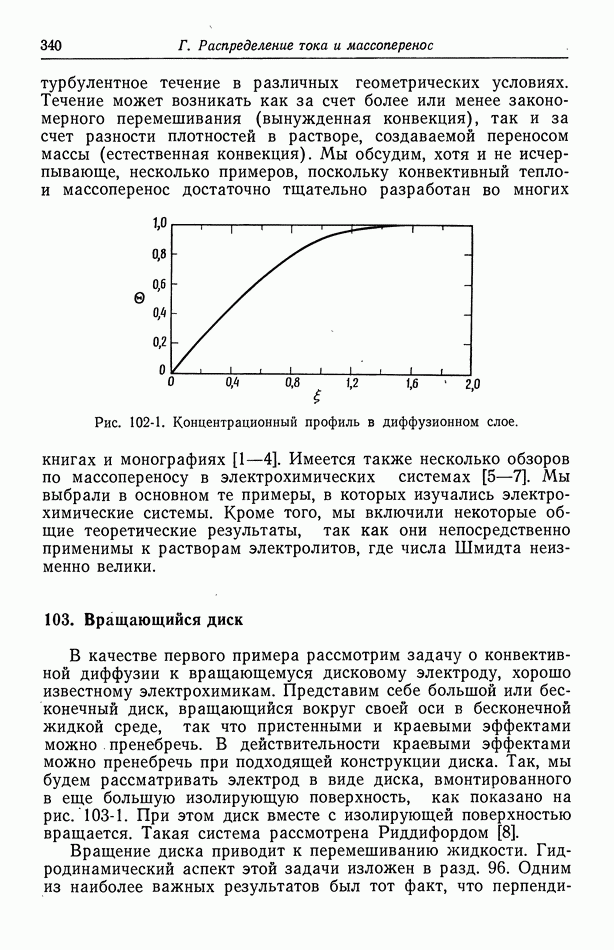
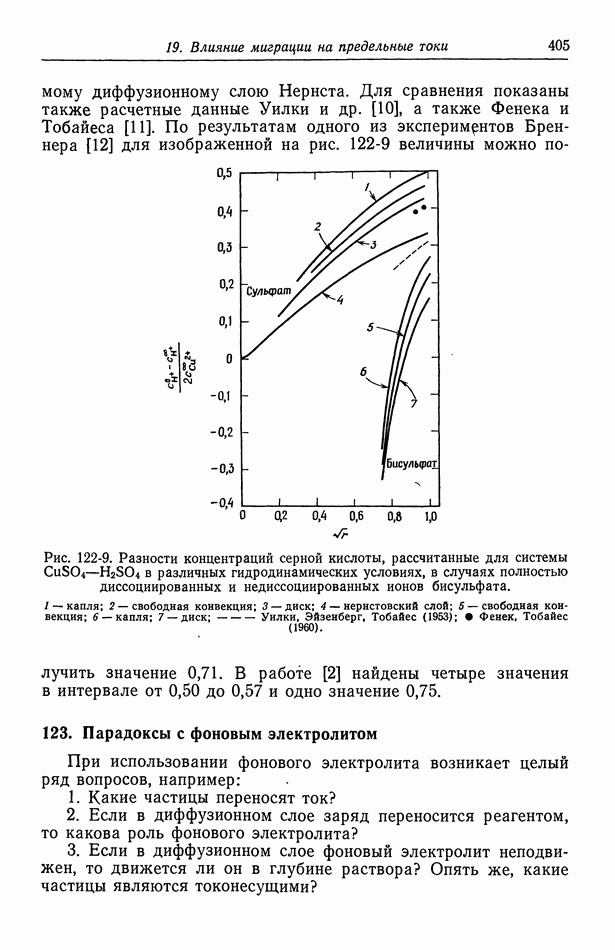
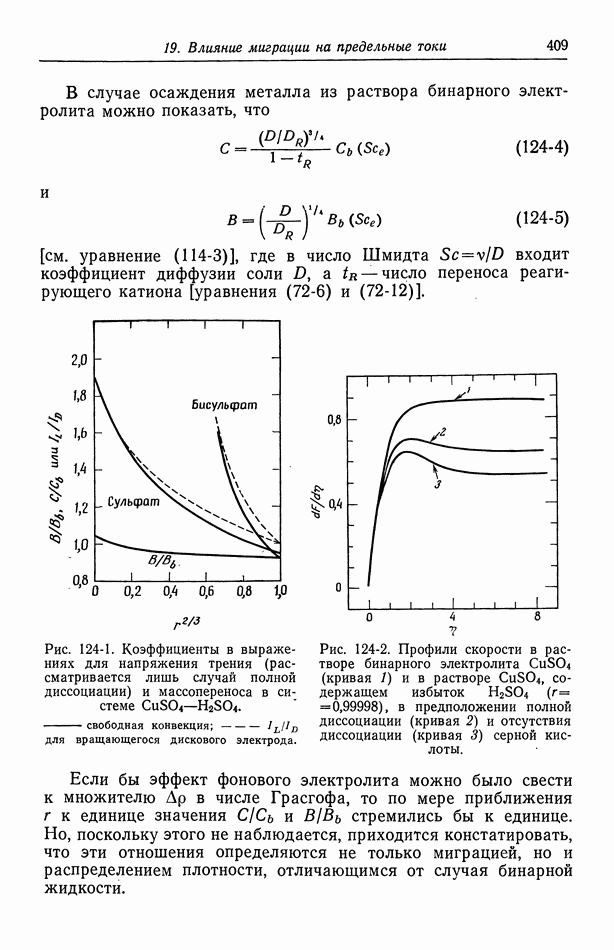
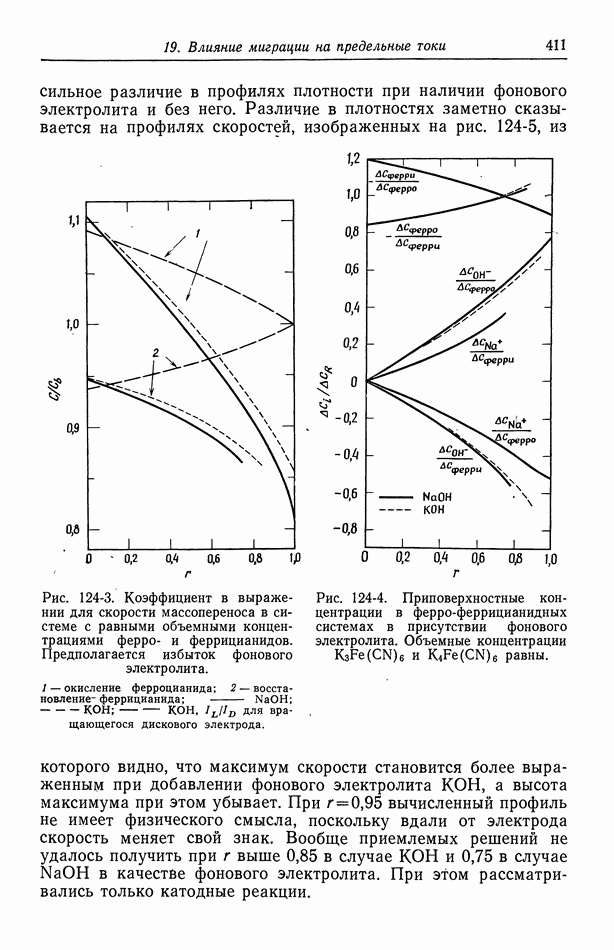
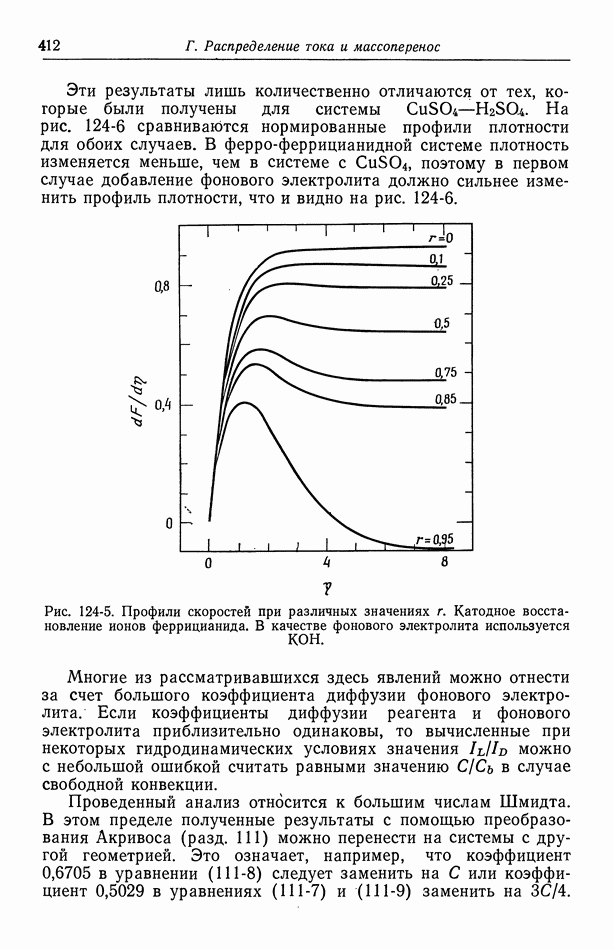
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
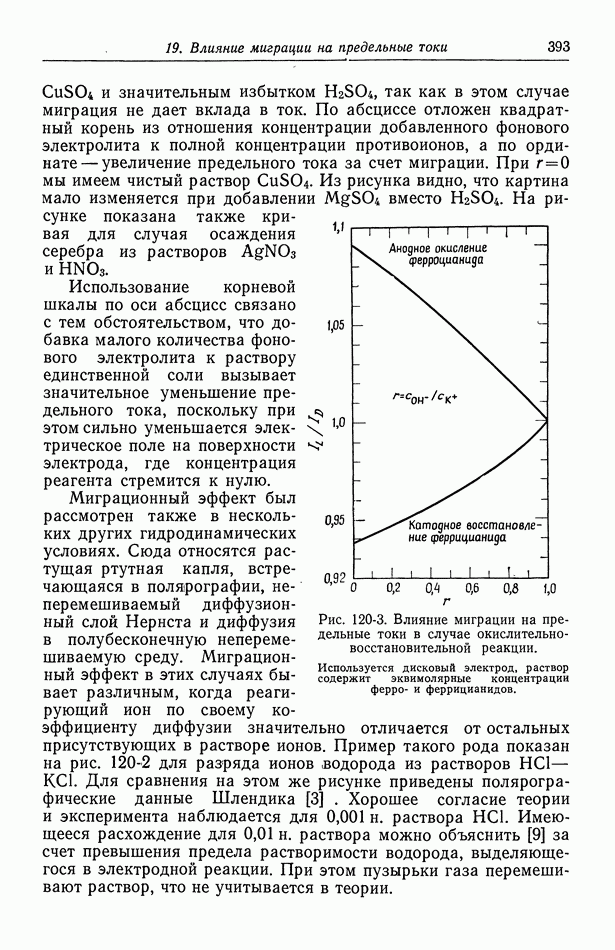
Благодаря кулоновскому взаимодействию между ионами коэффициенты активности электролитов в разбавленных растворах отличаются от коэффициентов активности неэлектролитов, как показано в теории Дебая-Хюккеля. Эта теория является основой для установления эмпирических соотношений между коэффициентами активности в некоторой области концентраций, включая коэффициенты активности растворов нескольких электролитов.
27. Распределение ионов в разбавленных растворах
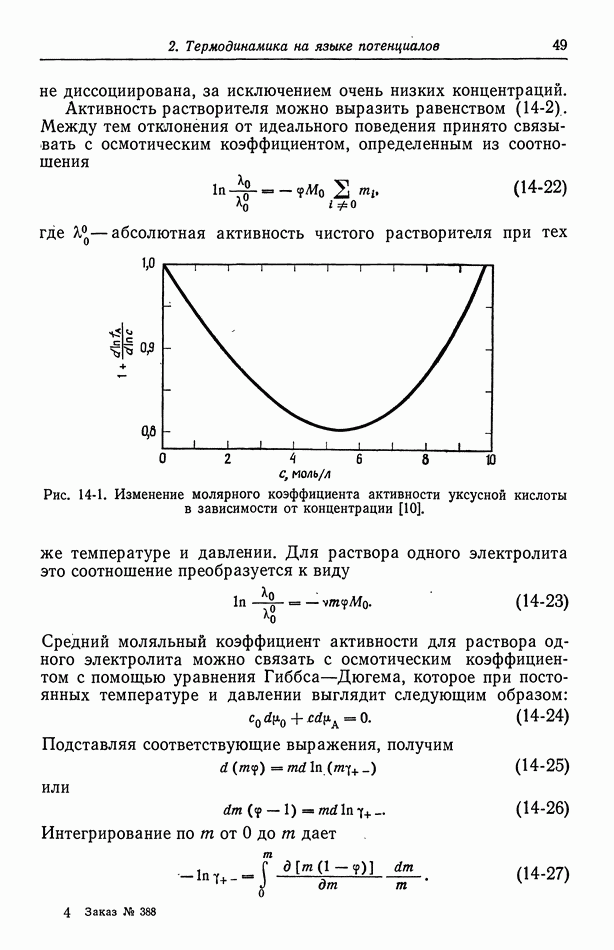
Растворяясь, электролит диссоциирует на катионы и анионы, что порождает электропроводность раствора. Как обсуждалось в разд. 14, диссоциация проявляется также в термодинамических свойствах раствора. Например, она приводит к появлению множителя  в равенстве (14-15) и ответственна за сильное понижение точки замерзания и уменьшение давления паров растворов электролитов.
в равенстве (14-15) и ответственна за сильное понижение точки замерзания и уменьшение давления паров растворов электролитов.
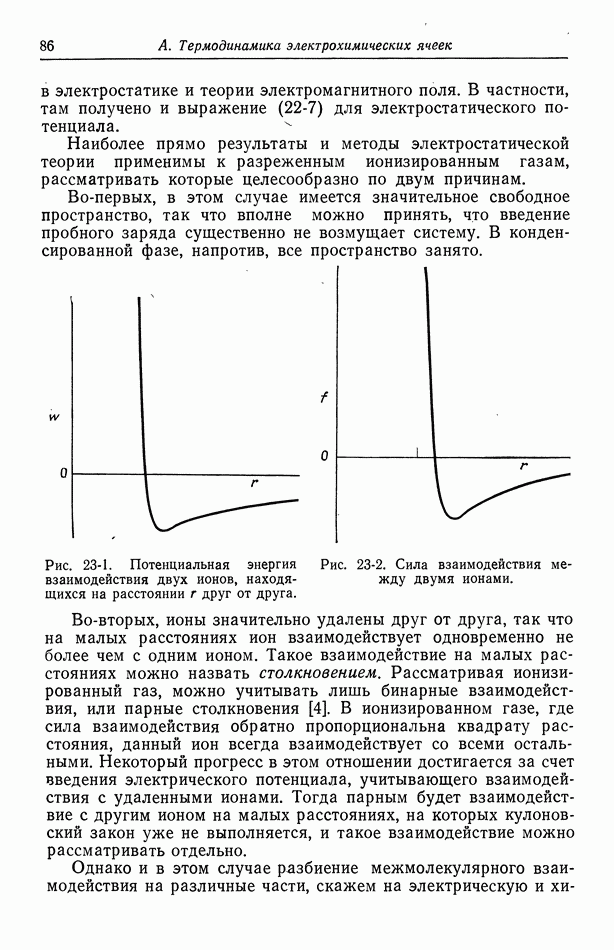
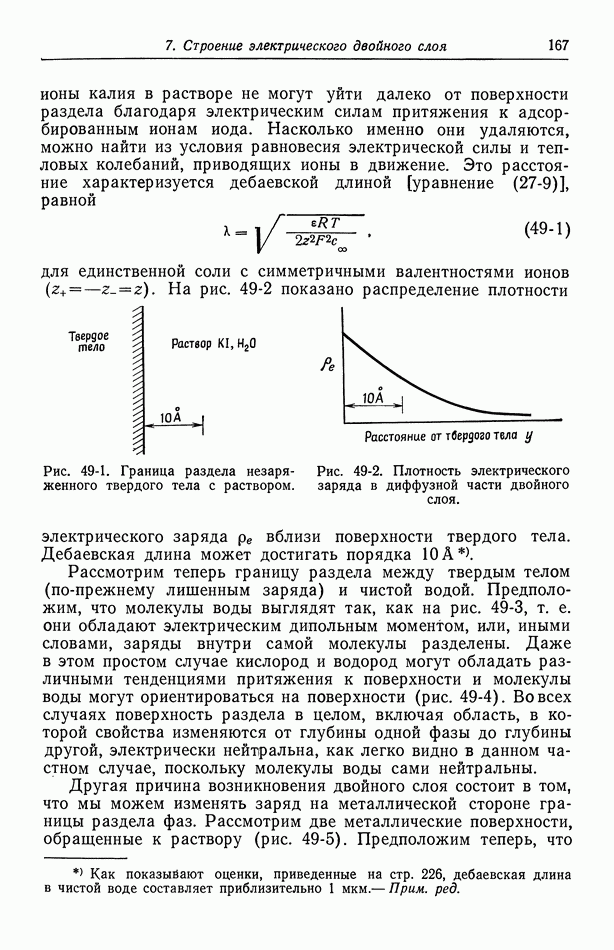
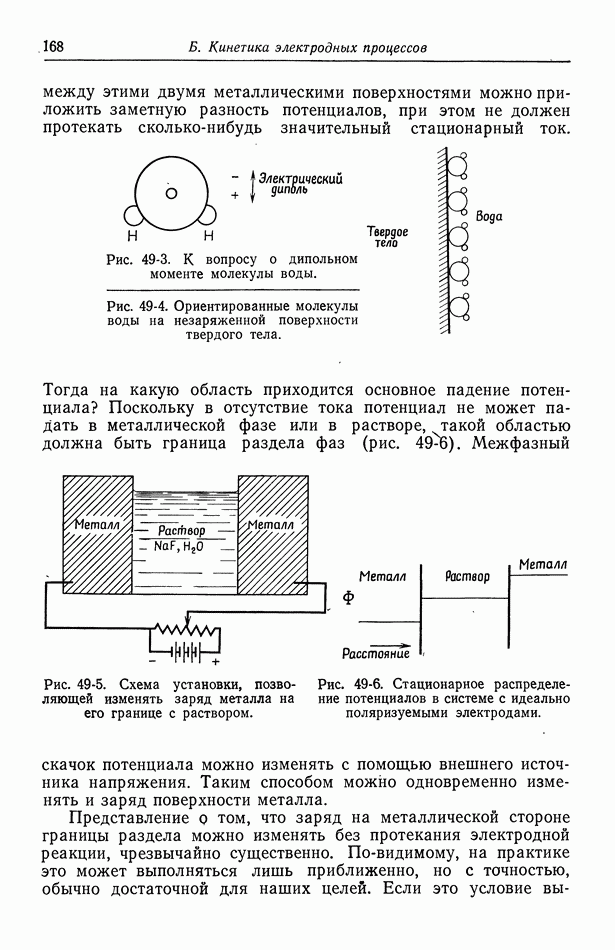
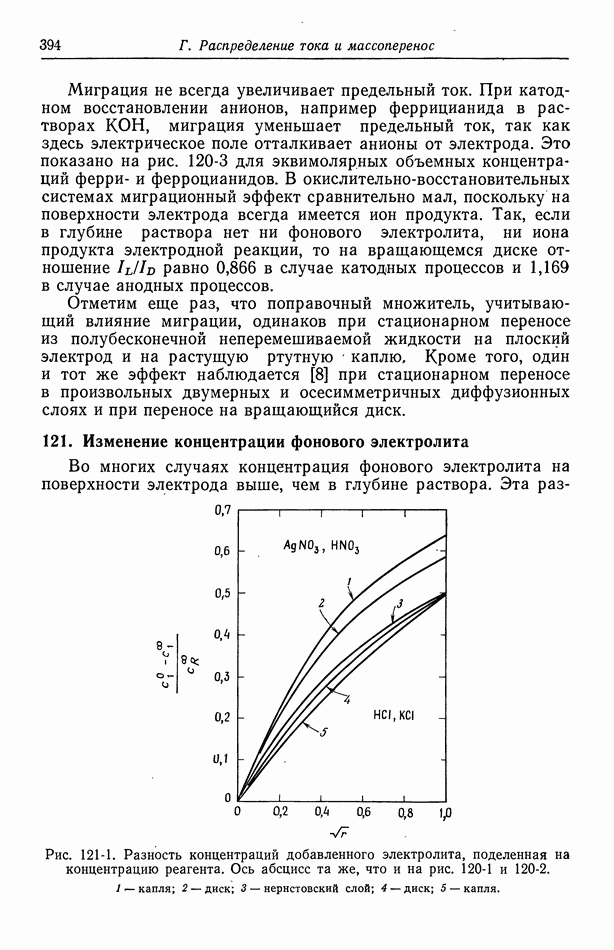
Вследствие электрических сил притяжения и отталкивания между ионами даже в разбавленных растворах распределение ионов не бывает полностью случайным. Это вызывает дальнейшее отклонение термодинамических свойств электролитов от свойств растворов неэлектролитов. Для количественного описания ионных распределений Дебай и Хюккель используют электростатическую модель [1].
Предположим, что в начале координат находится ион валентности  Ионы с зарядом противоположного знака по отношению к этому центральному иону будут притягиваться к началу координат, а ионы с зарядом того же знака — отталкиваться от него. Случайное тепловое движение ионов и молекул растворителя стремится воспрепятствовать этому электрическому эффекту и установить случайное распределение ионов. Равновесие между этими конкурирующими эффектами можно выразить больцмановским распределением ионных концентраций:
Ионы с зарядом противоположного знака по отношению к этому центральному иону будут притягиваться к началу координат, а ионы с зарядом того же знака — отталкиваться от него. Случайное тепловое движение ионов и молекул растворителя стремится воспрепятствовать этому электрическому эффекту и установить случайное распределение ионов. Равновесие между этими конкурирующими эффектами можно выразить больцмановским распределением ионных концентраций:

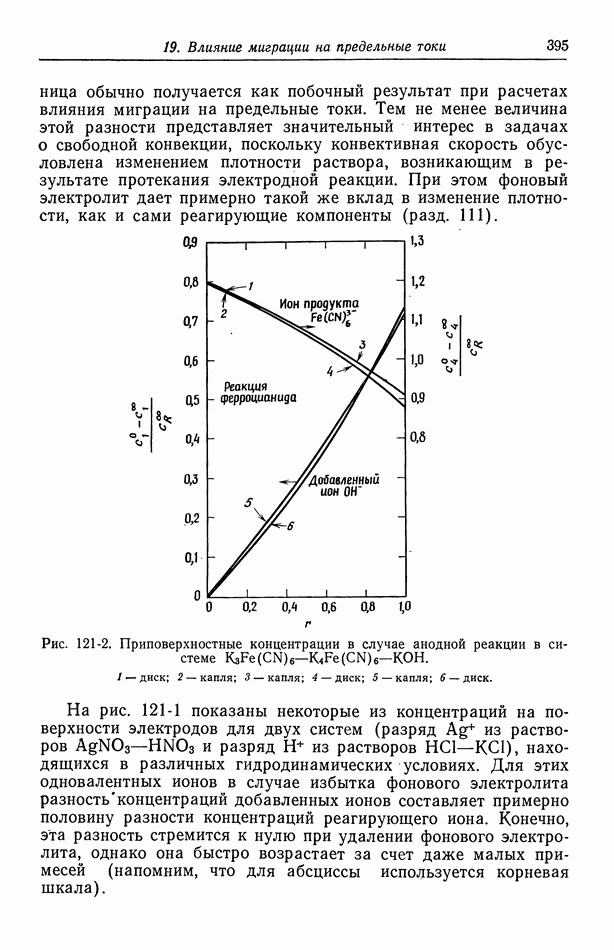
где  средняя концентрация компонента
средняя концентрация компонента  и
и  электростатический потенциал, устанавливающийся вокруг центрального иона. Энергия электрического взаимодействия на моль выражена в виде
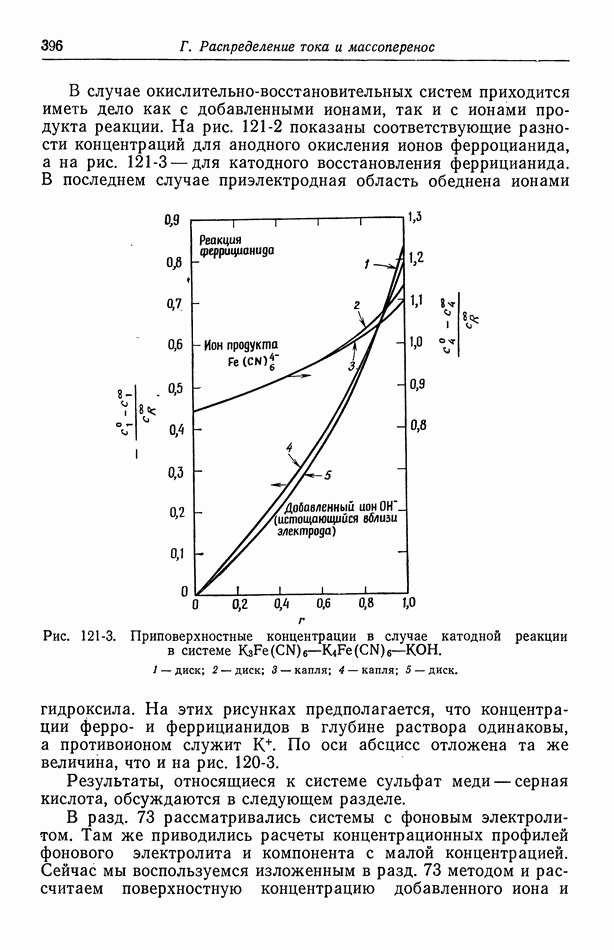
электростатический потенциал, устанавливающийся вокруг центрального иона. Энергия электрического взаимодействия на моль выражена в виде  остальными составляющими энергии взаимодействия можно пренебречь. По мере удаления от центрального иона потенциал
остальными составляющими энергии взаимодействия можно пренебречь. По мере удаления от центрального иона потенциал  приближается к нулю и, следовательно,
приближается к нулю и, следовательно,  приближается к
приближается к 
Потенциал  создается не только центральным, но и другими ионами, которые притягиваются к центральному иону или отталкиваются от него. Распределение потенциала подчиняется уравнению Пуассона (22-8)
создается не только центральным, но и другими ионами, которые притягиваются к центральному иону или отталкиваются от него. Распределение потенциала подчиняется уравнению Пуассона (22-8)

В растворе при равновесии имеет место радиальная симметрия. В сферической системе координат, в начале которой расположен центральный ион, уравнение (27-2) приобретает вид

Предполагается, что центры других ионов не могут приблизиться к центральному иону на расстояние меньше а в связи с короткодействующими силами отталкивания. Таким образом, уравнение (27-1) и, следовательно, уравнение (27-3) применимы лишь при  Краевое условие при
Краевое условие при  можно найти из закона Гаусса (22-10), применяя его к области внутри сферы радиуса
можно найти из закона Гаусса (22-10), применяя его к области внутри сферы радиуса 

Это равенство эквивалентно утверждению, что распределение заряда вокруг центрального иона в точности балансирует заряд этого иона, отличаясь лишь знаком. Так, интегрирование уравнения (27-3) от а до  дает
дает

или

Слева стоит интеграл от плотности заряда  по объему снаружи сферы радиуса
по объему снаружи сферы радиуса  равный взятому с обратным знаком заряду центрального иона.
равный взятому с обратным знаком заряду центрального иона.
Итак, уравнение (27-3) описывает распределение потенциала вблизи центрального иона через средние концентрации  и другие известные параметры. Для получения решений Дебай и Хюккель разложили экспоненциальные члены в уравнении (27-3), считая показатели экспонент малыми:
и другие известные параметры. Для получения решений Дебай и Хюккель разложили экспоненциальные члены в уравнении (27-3), считая показатели экспонент малыми:

Уравнение (27-3) приобретает вид

где  - ебаевская длина, определенная соотношением
- ебаевская длина, определенная соотношением

В этом выражении нет члена с  так как раствор в среднем электрически нейтрален.
так как раствор в среднем электрически нейтрален.
Решением уравнения (27-8), удовлетворяющим краевому условию (27-4) и условию стремления  к нулю по мере бесконечного возрастания
к нулю по мере бесконечного возрастания  является
является

Потенциал, созданный одним лишь центральным ионом, равен  Поэтому равенство (27-10) показывает, что другие ионы, которые притягиваются к началу координат из-за противоположного знака заряда по сравнению с центральным ионом, понижают величину потенциала и приводят к его быстрому исчезновению на больших расстояниях от центрального иона. Таким образом, находящиеся на некотором расстоянии от центрального иона заряженные частицы заэкранированы другими ионами.
Поэтому равенство (27-10) показывает, что другие ионы, которые притягиваются к началу координат из-за противоположного знака заряда по сравнению с центральным ионом, понижают величину потенциала и приводят к его быстрому исчезновению на больших расстояниях от центрального иона. Таким образом, находящиеся на некотором расстоянии от центрального иона заряженные частицы заэкранированы другими ионами.
Дебаевская длина X является важным параметром, описывающим распределение потенциала. Ее величина равна  или
или  в
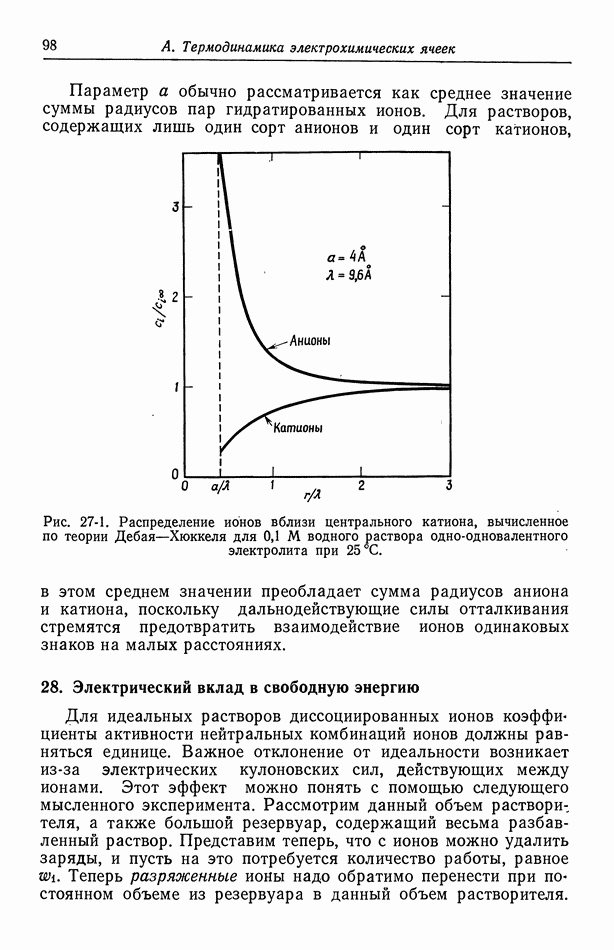
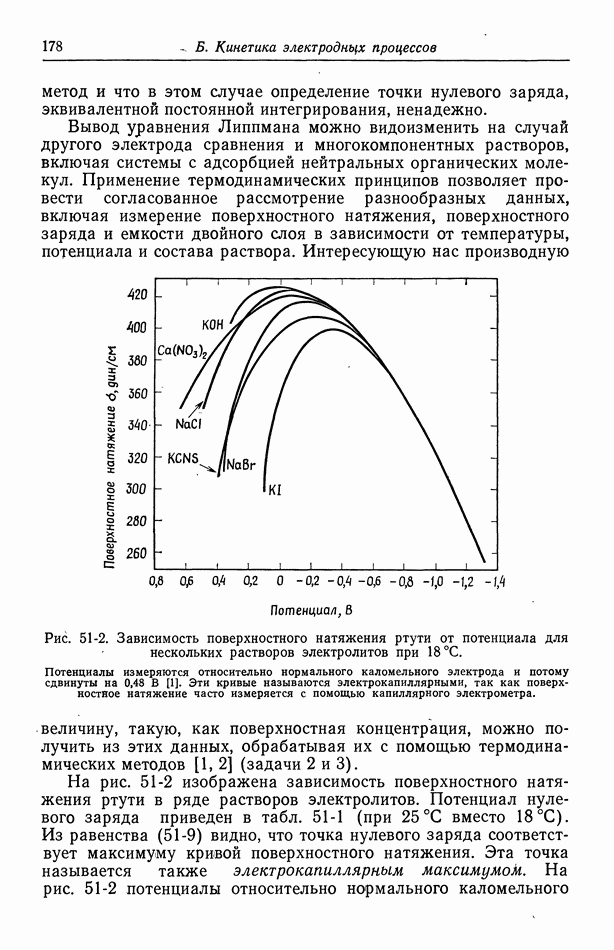
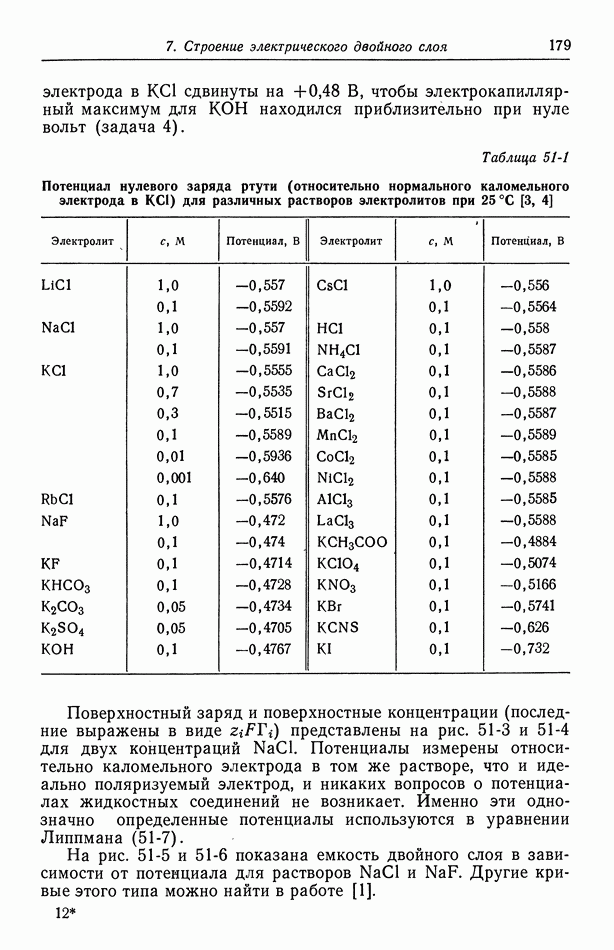
в  водном растворе одно-одновалентного электролита при 25° С. Она обратно пропорциональна зарядам ионов и квадратному корню из концентрации и прямо пропорциональна квадратным корням из диэлектрической проницаемости и абсолютной температуры. На рис. 27-1 показано распределение анионов и катионов вблизи центрального катиона. Кривые вычислены по уравнениям (27-3) и (27-10) для
водном растворе одно-одновалентного электролита при 25° С. Она обратно пропорциональна зарядам ионов и квадратному корню из концентрации и прямо пропорциональна квадратным корням из диэлектрической проницаемости и абсолютной температуры. На рис. 27-1 показано распределение анионов и катионов вблизи центрального катиона. Кривые вычислены по уравнениям (27-3) и (27-10) для  водного раствора одно-одновалентного электролита при
водного раствора одно-одновалентного электролита при  Экранирующие ионы формируют вокруг центрального иона ионное облако толщиной порядка дебаевской длины
Экранирующие ионы формируют вокруг центрального иона ионное облако толщиной порядка дебаевской длины 
Параметр а обычно рассматривается как среднее значение суммы радиусов пар гидратированных ионов.

Рис. 27-1. Распределение ионов вблизи центрального катиона, вычисленное по теории Дебая-Хюккеля для  водного раствора одно-одновалентного электролита при
водного раствора одно-одновалентного электролита при 
Для растворов, содержащих лишь один сорт анионов и один сорт катионов, в этом среднем значении преобладает сумма радиусов аниона и катиона, поскольку дальнодействующие силы отталкивания стремятся предотвратить ззаимодействие ионов одинаковых знаков на малых расстояниях.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
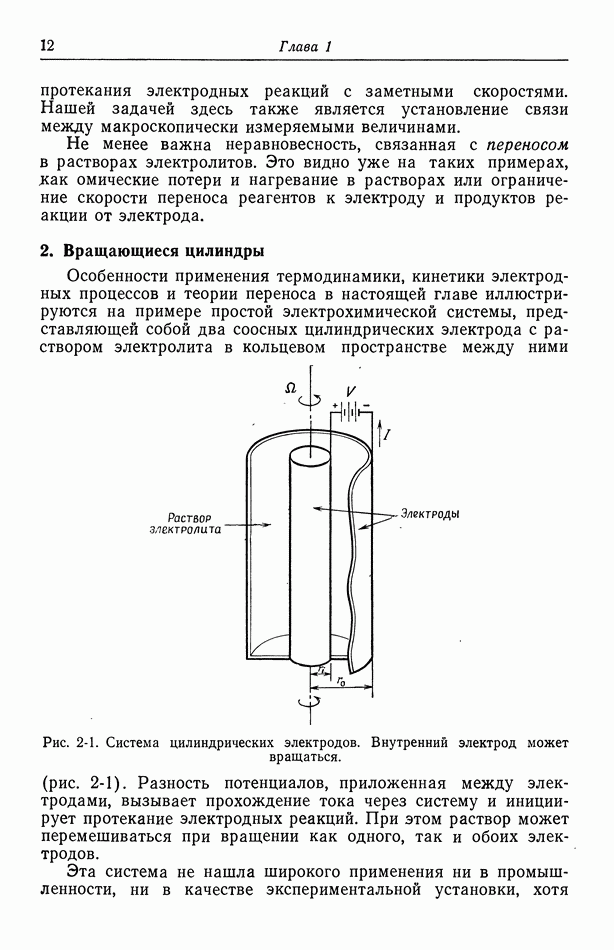
- 2. Вращающиеся цилиндры
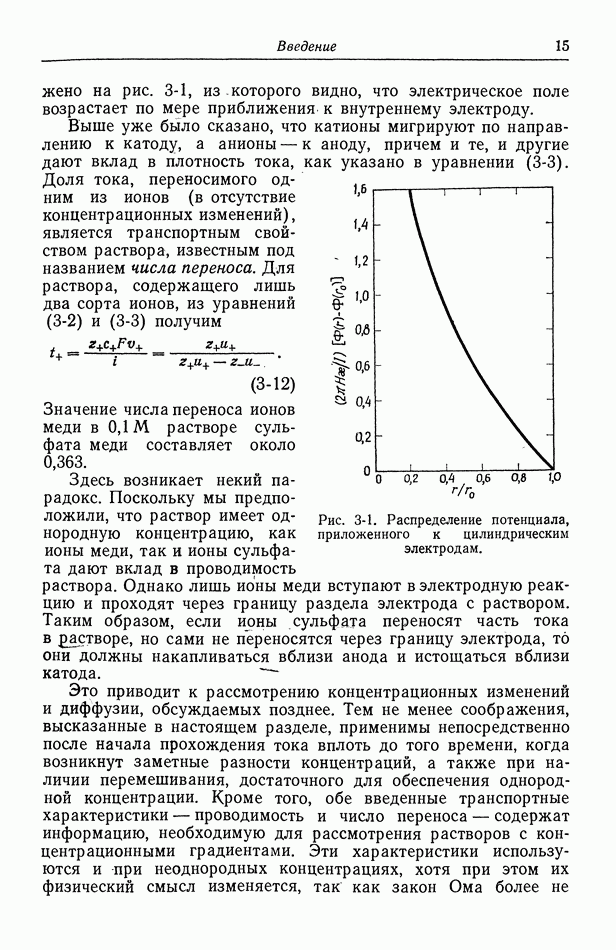
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
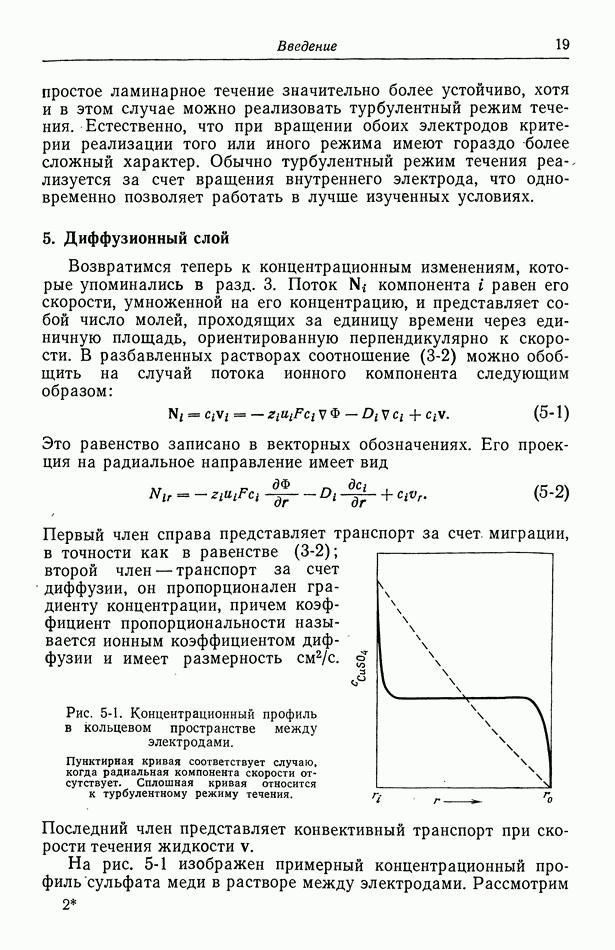
- 5. Диффузионный слой
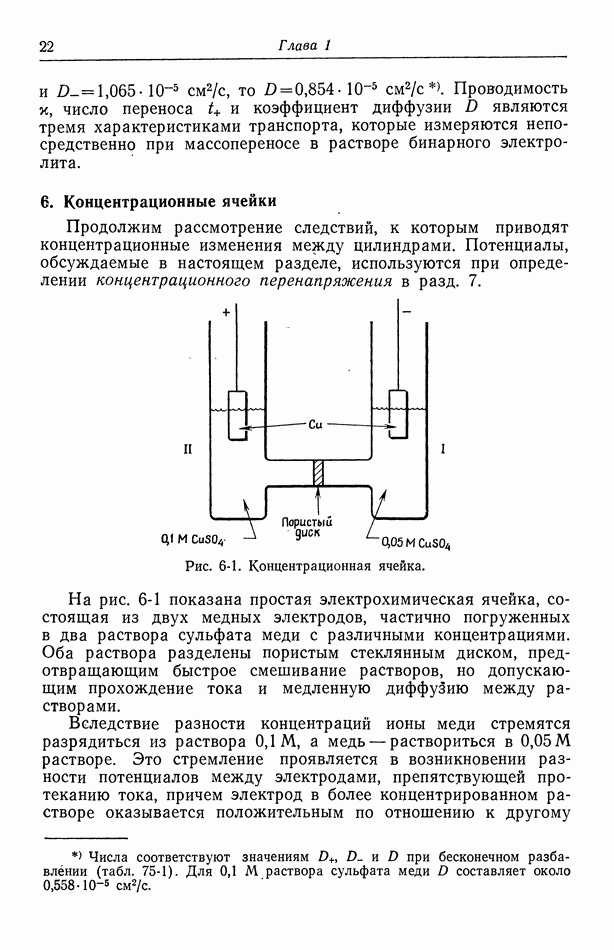
- 6. Концентрационные ячейки
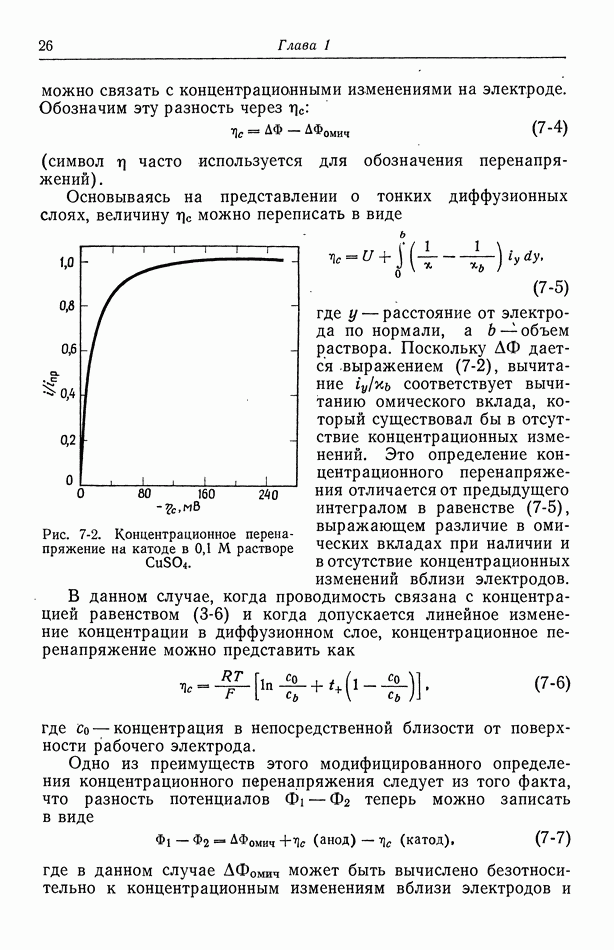
- 7. Концентрационное перенапряжение
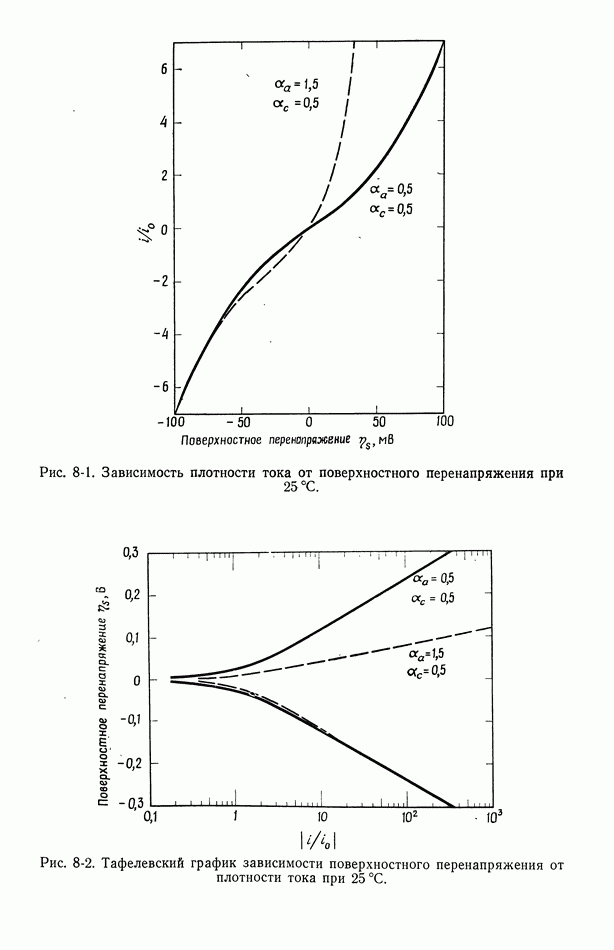
- 8. Поверхностное перенапряжение
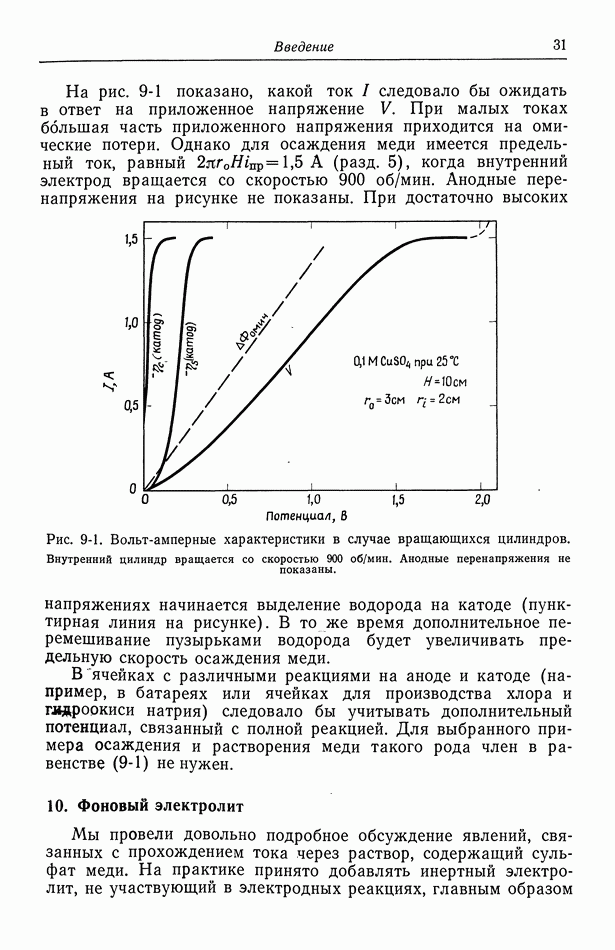
- 9. Потенциал ячейки
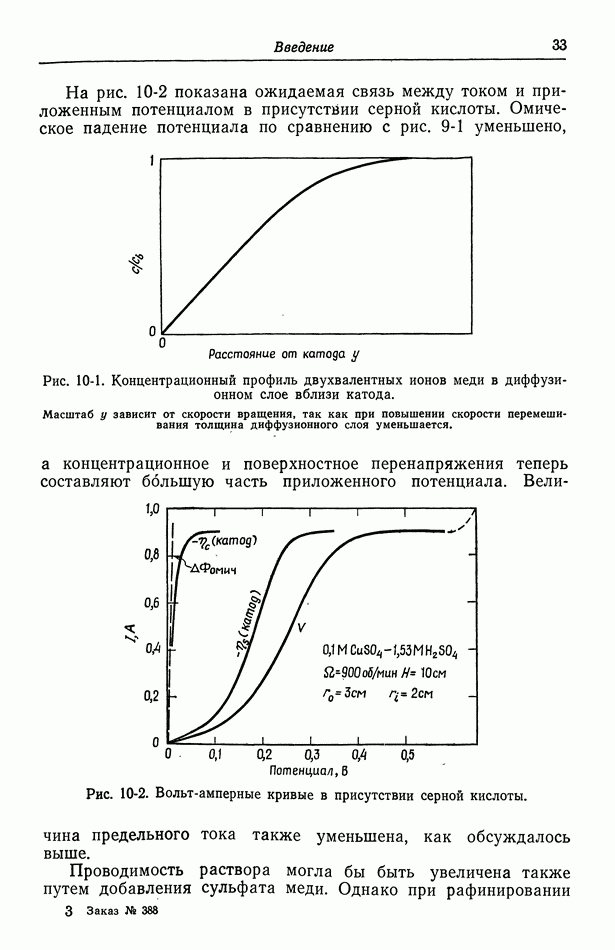
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
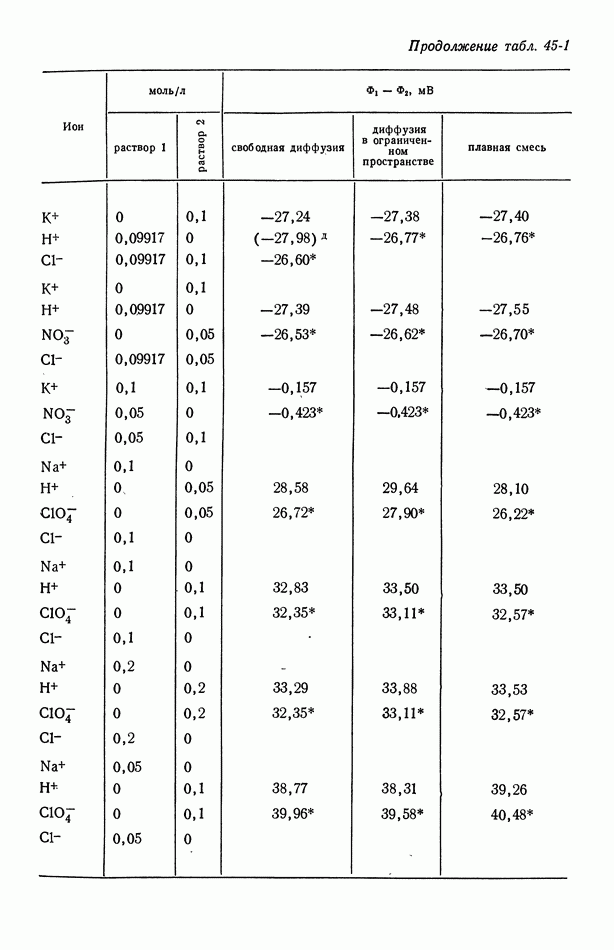
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
- 50. Изотерма адсорбции Гиббса
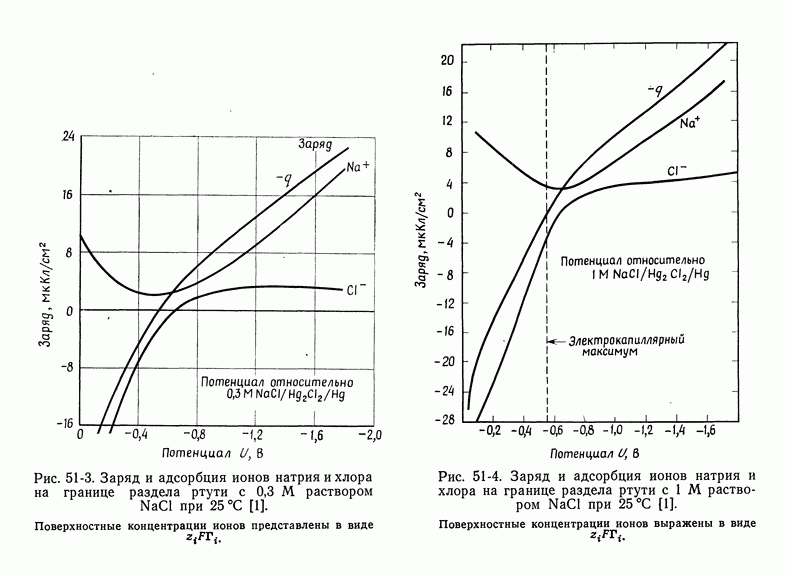
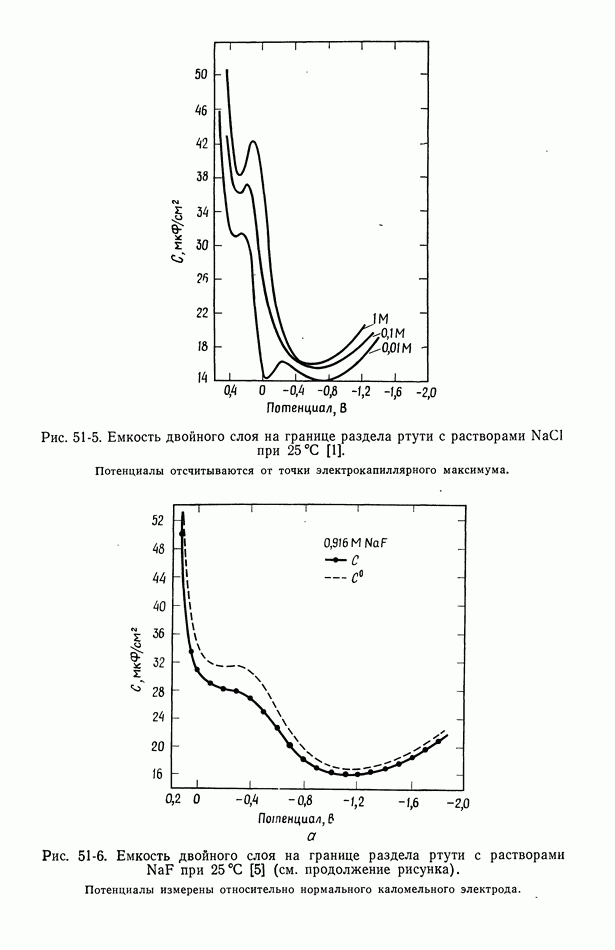
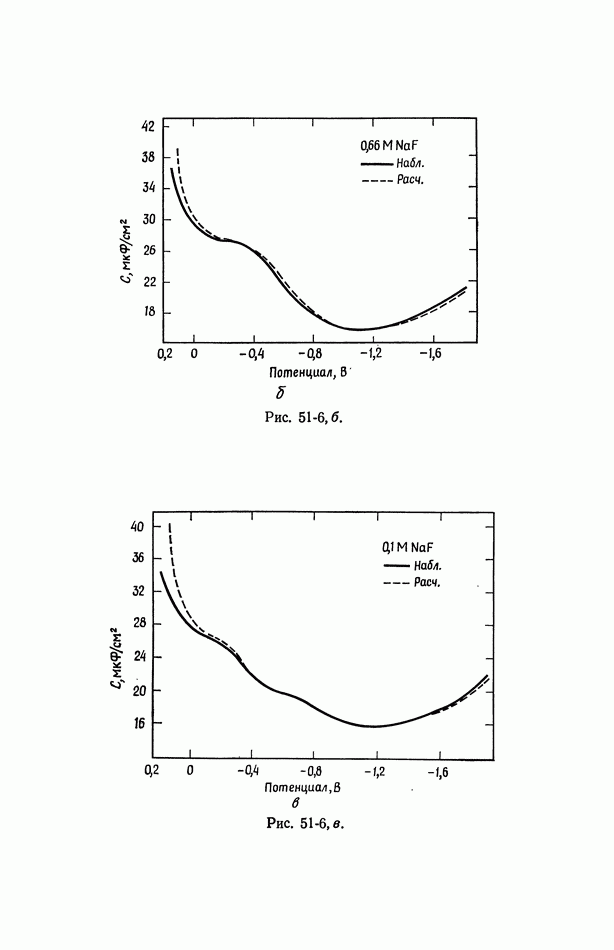
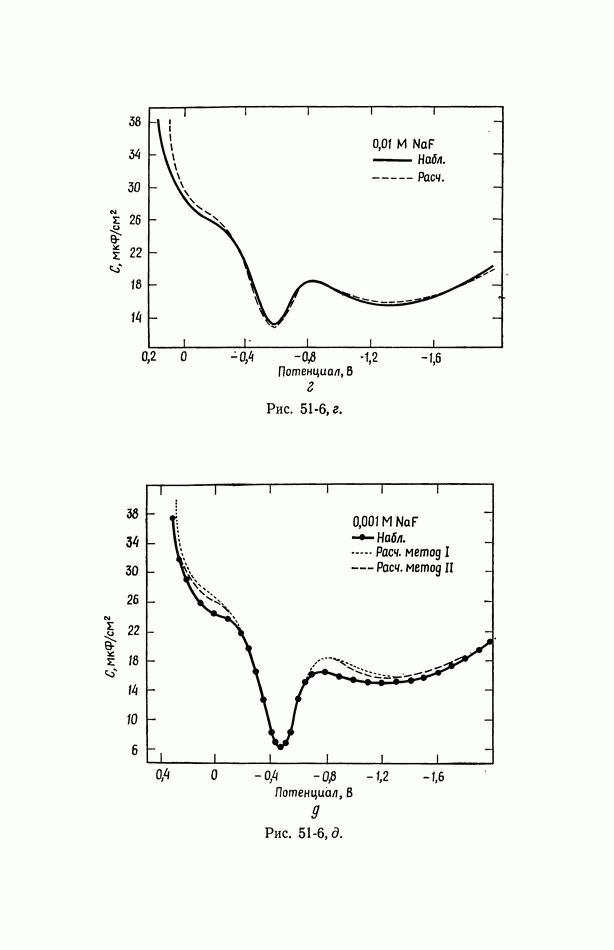
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
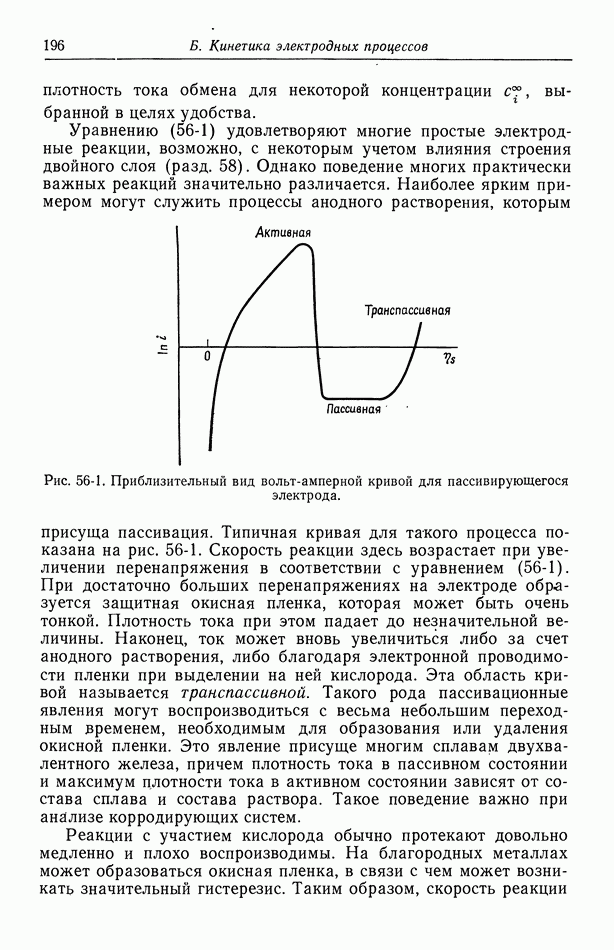
- 56. Зависимость плотности тока от поверхностного перенапряжения
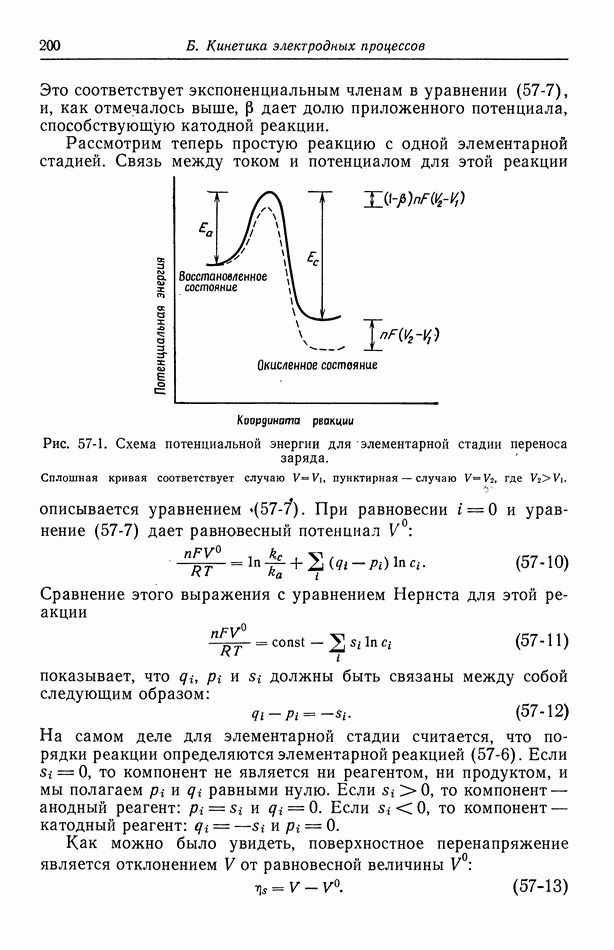
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
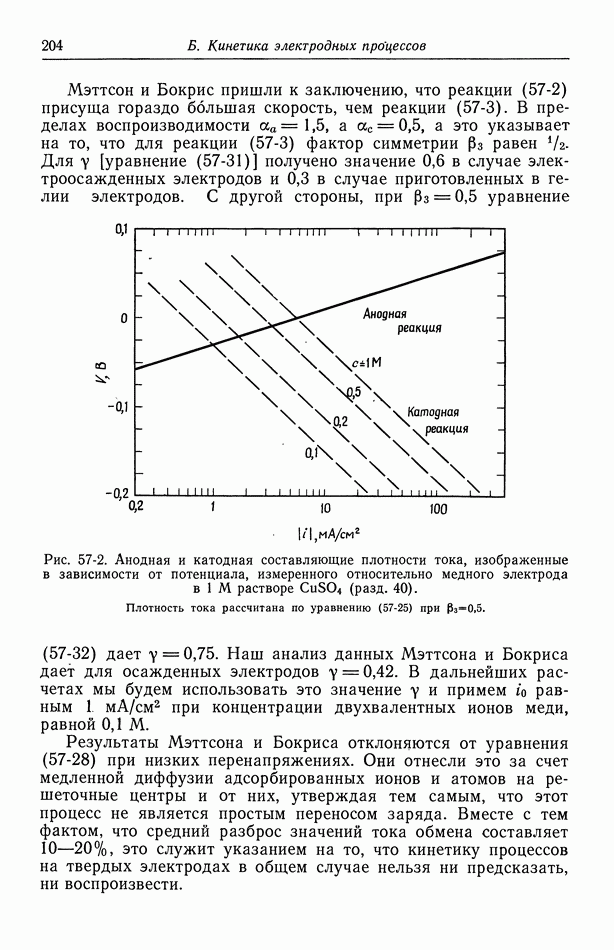
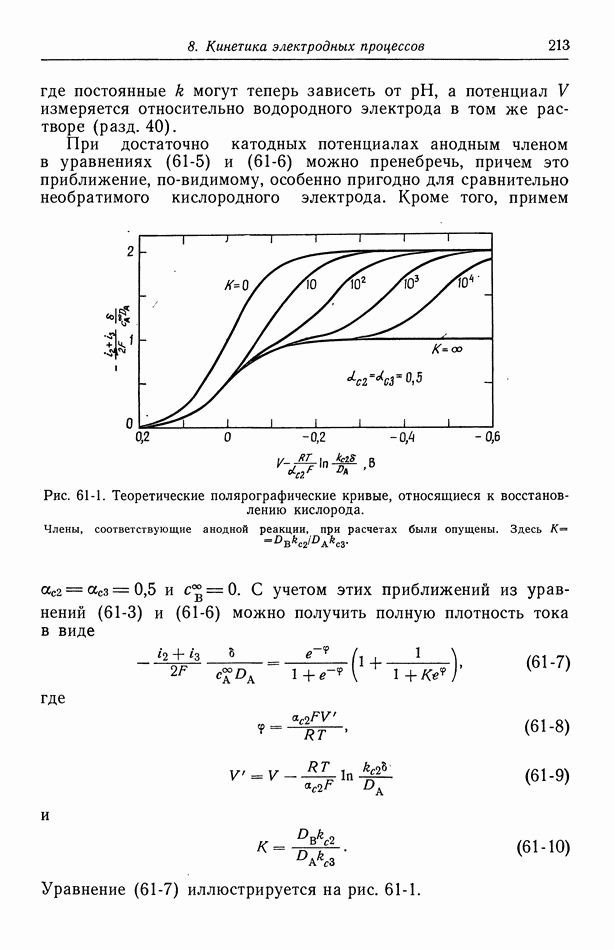
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
- 98. Турбулентное течение
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
- 116. Первичное распределение тока
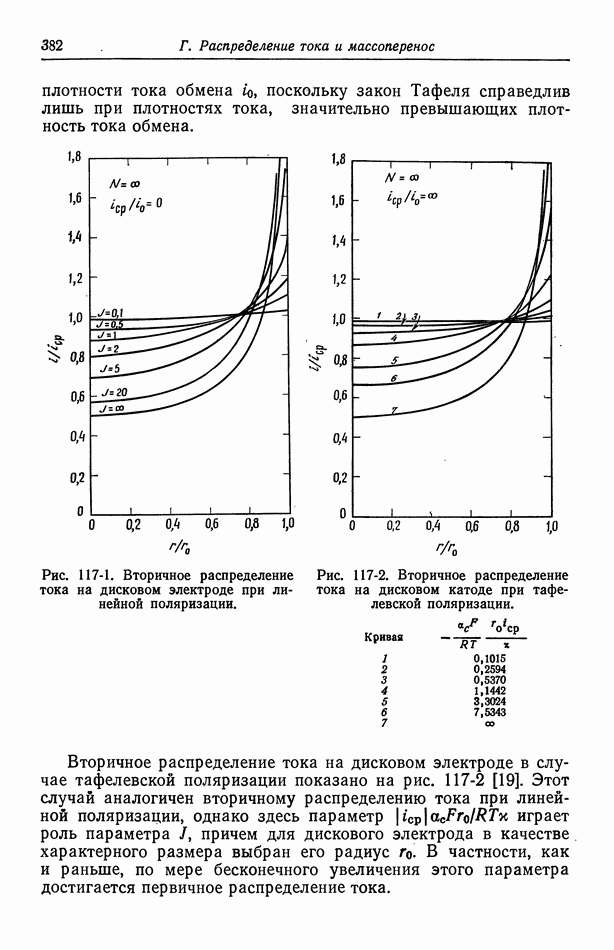
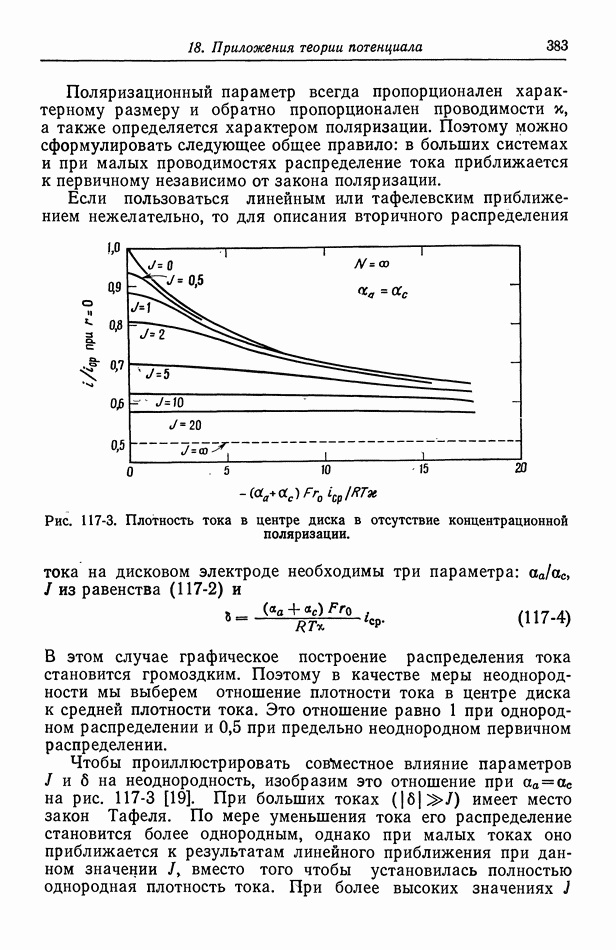
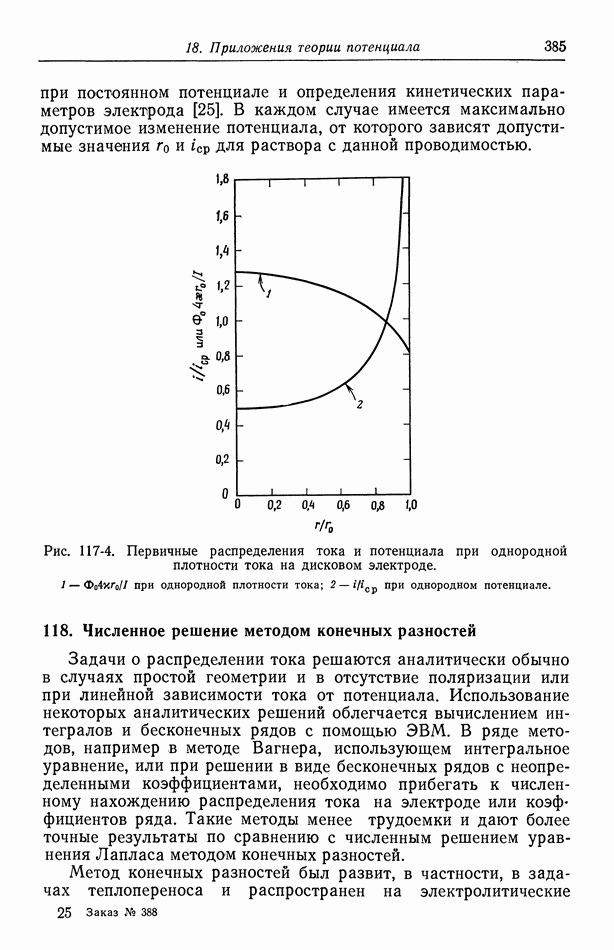
- 117. Вторичное распределение тока
- 118. Численное решение методом конечных разностей
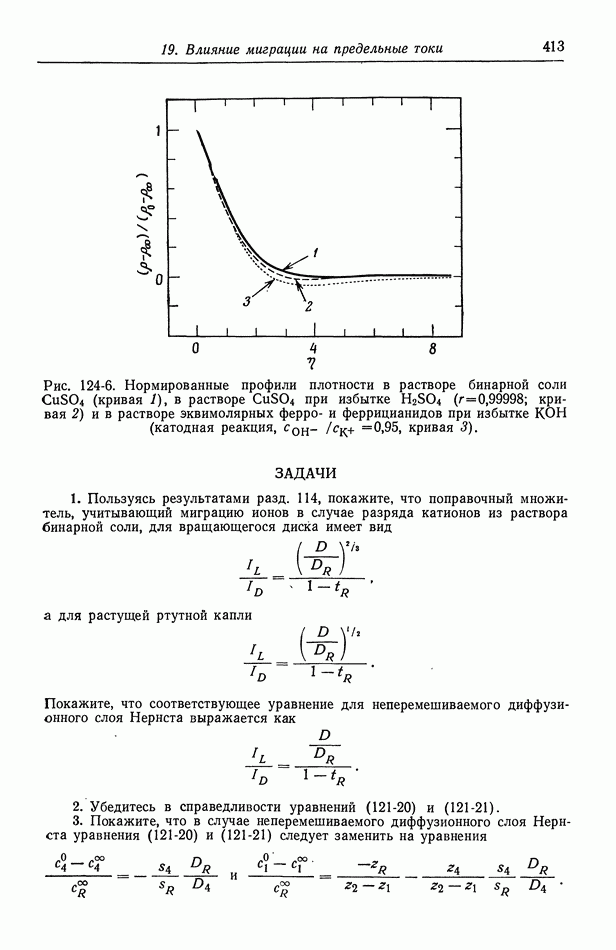
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
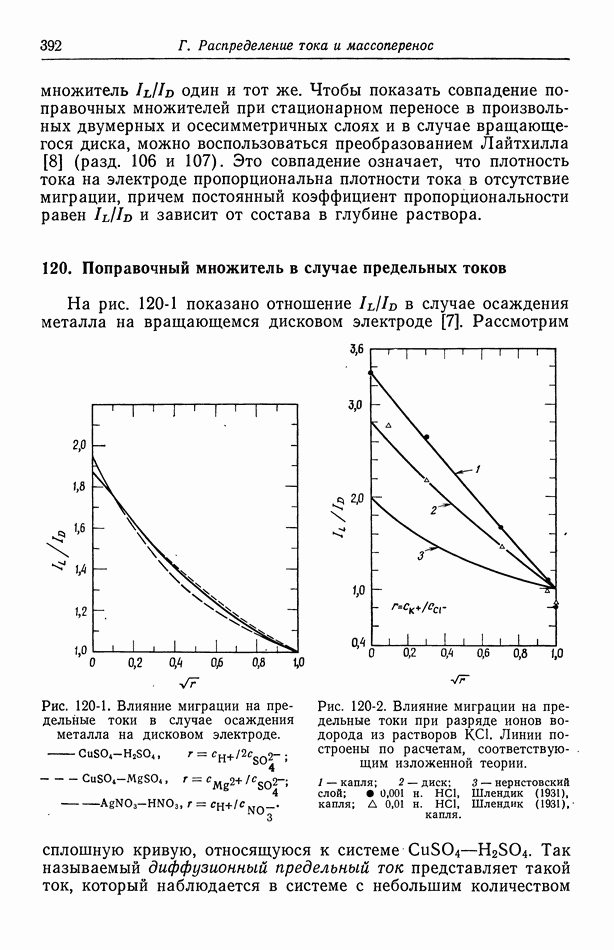
- 120. Поправочный множитель в случае предельных токов
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ