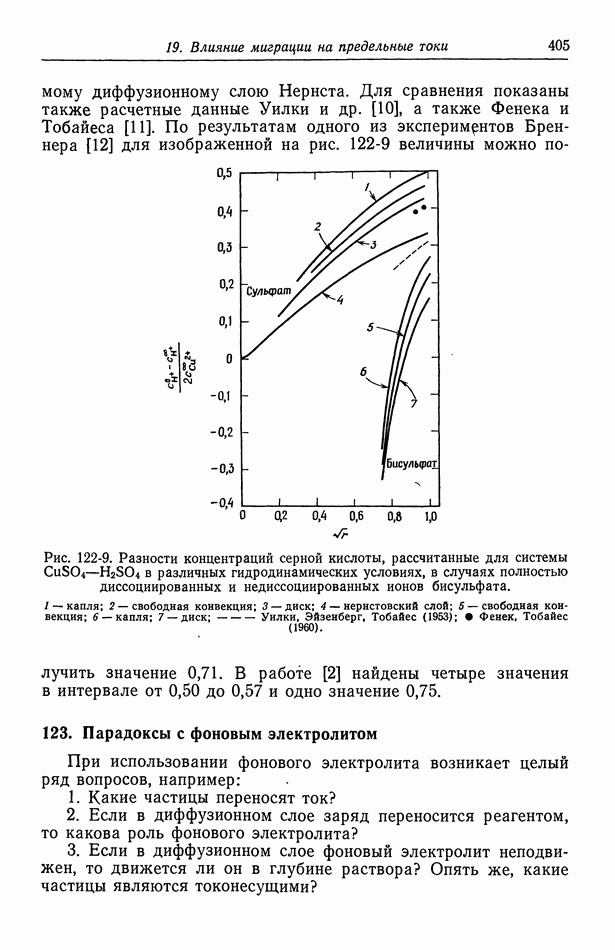
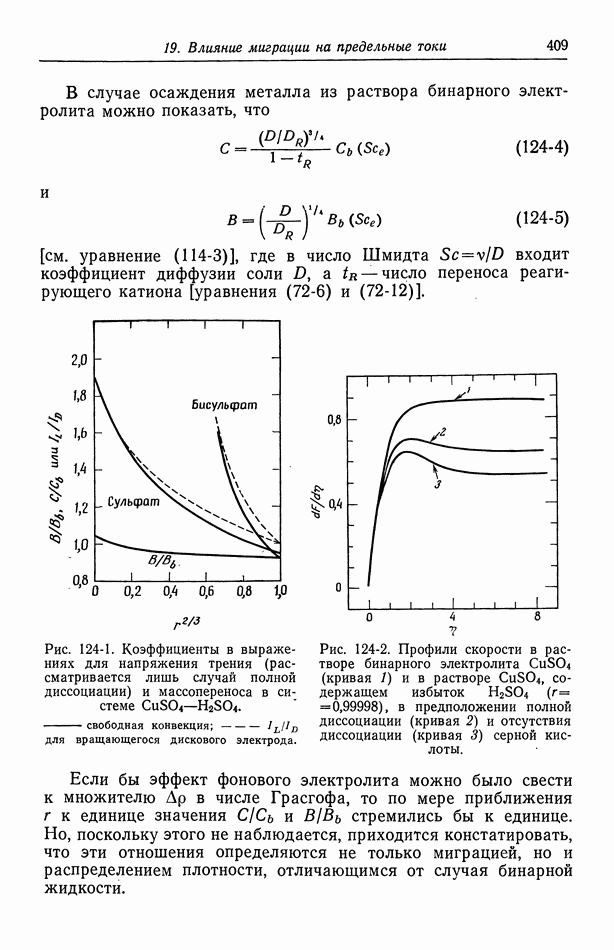
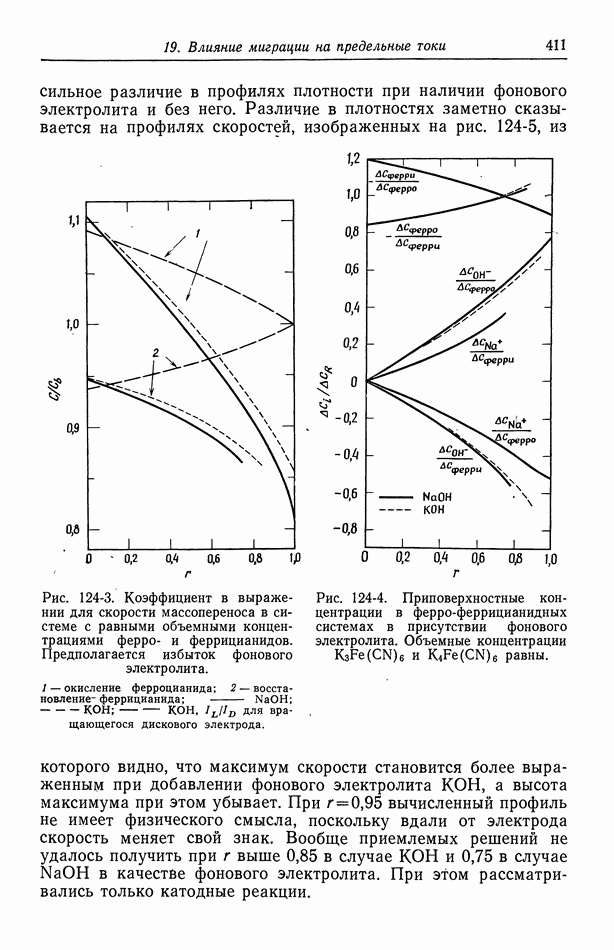
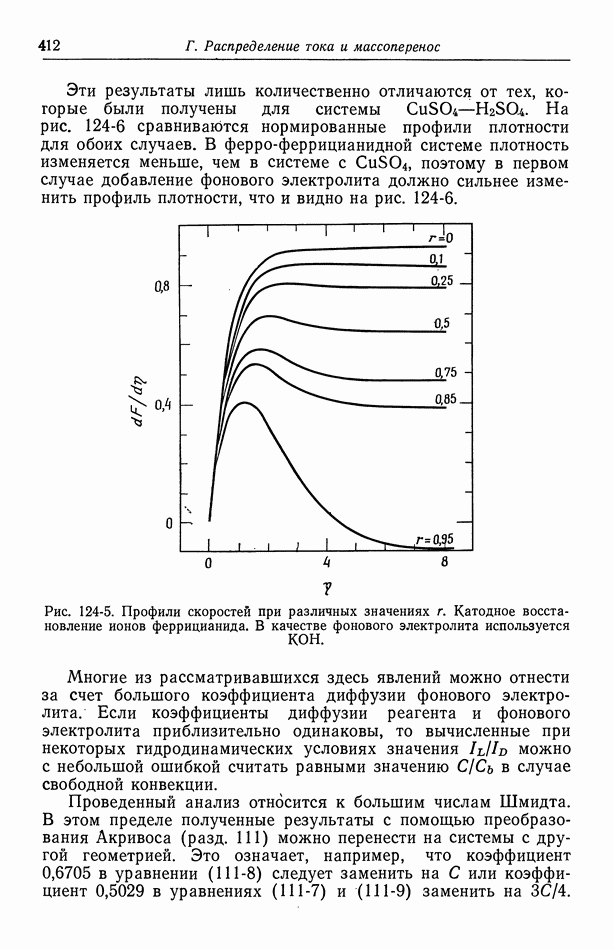
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
14. Определение некоторых термодинамических функций
В настоящем разделе вводятся абсолютная активность, коэффициент активности, средний коэффициент активности и осмотический коэффициент. Два последних коэффициента полезны при табулировании зависимостей термодинамических свойств растворов от их состава, однако их теоретические выражения довольно громоздки.
Абсолютная активность  ионного или нейтрального компонента, широко использовавшаяся Гуггенгеймом [2], определяется из соотношения
ионного или нейтрального компонента, широко использовавшаяся Гуггенгеймом [2], определяется из соотношения

Она обладает тем преимуществом, что обращается в нуль при отсутствии компонента, тогда как химический потенциал обращается в таком случае в минус бесконечность. Кроме того,  безразмерна. Абсолютная активность имеет еще и то преимущество, что с ней можно обращаться как с обычной активностью, и при этом она не зависит от какого-либо вторичного стандартного состояния, которое могло бы быть принято для некоторого раствора или растворителя при определенных температуре и давлении.
безразмерна. Абсолютная активность имеет еще и то преимущество, что с ней можно обращаться как с обычной активностью, и при этом она не зависит от какого-либо вторичного стандартного состояния, которое могло бы быть принято для некоторого раствора или растворителя при определенных температуре и давлении.
Для растворенного компонента величину  можно дальше расписать следующим образом:
можно дальше расписать следующим образом:

где  моляльность, или число молей растворенного вещества на единицу массы растворителя (выражаемая обычно в грамм-молекулах или грамм-ионах на килограмм растворителя),
моляльность, или число молей растворенного вещества на единицу массы растворителя (выражаемая обычно в грамм-молекулах или грамм-ионах на килограмм растворителя),  коэффициент активности компонента
коэффициент активности компонента  постоянный коэффициент пропорциональности, не зависящий от состава и электрического состояния, но определяемый растворенным компонентом и зависящий от температуры и давления. Для конденсированных фаз зависимостью от давления часто пренебрегают.
постоянный коэффициент пропорциональности, не зависящий от состава и электрического состояния, но определяемый растворенным компонентом и зависящий от температуры и давления. Для конденсированных фаз зависимостью от давления часто пренебрегают.
Можно использовать и другие концентрационные шкалы, однако коэффициент активности и постоянный коэффициент меняются так, что  не зависит от используемой концентрационной шкалы. Другой общепринятой концентрационной шкалой является молярность, или число молей на единицу объема раствора (выражается обычно в молях на литр и обозначается
не зависит от используемой концентрационной шкалы. Другой общепринятой концентрационной шкалой является молярность, или число молей на единицу объема раствора (выражается обычно в молях на литр и обозначается  , причем связана с этой шкалой соотношением
, причем связана с этой шкалой соотношением

где а — молярность компонента  коэффициент активности, а
коэффициент активности, а  постоянный коэффициент пропорциональности, аналогичный
постоянный коэффициент пропорциональности, аналогичный
 Моляльность связана с молярностью согласно уравнению
Моляльность связана с молярностью согласно уравнению

где  плотность раствора
плотность раствора  молекулярный вес компонента
молекулярный вес компонента  или
или  , причем в сумму не входит растворитель, обозначенный нижним индексом 0.
, причем в сумму не входит растворитель, обозначенный нижним индексом 0.
Популярность моляльности среди экспериментаторов, работающих в физической химии, видимо, объясняется тем, что ее легко получить непосредственно из масс компонентов в растворе, без отдельного определения плотности. Концентрация в молярной шкале более удобна при анализе процессов транспорта в растворах. Кроме того, моляльность особенно неудобна, если в рассматриваемую область концентраций входит расплавленная соль, поскольку моляльность при этом обращается в бесконечность. Можно использовать шкалу мольных долей, но тогда приходится решать, как рассматривать диссоциированный электролит. Массовая доля имеет то преимущество, что она зависит лишь от масс компонентов и к тому же не зависит от шкалы атомных весов, которая, как известно, изменялась даже в последние годы. Однако шкала массовой доли не позволяет просто рассмотреть взаимосвязанные свойства растворов (понижение точки замерзания, повышение точки кипения, понижение давления пара), а также свойства разбавленных растворов электролитов. Единственной из этих шкал, изменяющейся с температурой при нагревании данного раствора, является молярная концентрация.
Вторичные стандартные состояния, необходимые для нахождения  или
или  рассчитываются из условия обращения в единицу определенной комбинации коэффициентов активности по мере бесконечного разбавления раствора, т. е.
рассчитываются из условия обращения в единицу определенной комбинации коэффициентов активности по мере бесконечного разбавления раствора, т. е.

и

для всех таких комбинаций  в которых значения удовлетворяют уравнению (13-3). В частности, коэффициент активности любого нейтрального недиссоциированного компонента
в которых значения удовлетворяют уравнению (13-3). В частности, коэффициент активности любого нейтрального недиссоциированного компонента
приближается к единице по мере стремления к нулю концентраций всех растворенных веществ. Если принять, что коэффициенты активности безразмерны, то  имеют размерности, обратные размерностям
имеют размерности, обратные размерностям  Учитывая условия (13-5) и (13-6) для определения вторичных стандартных состояний, можно сказать что
Учитывая условия (13-5) и (13-6) для определения вторичных стандартных состояний, можно сказать что  связаны соотношением
связаны соотношением

где  плотность чистого растворителя
плотность чистого растворителя 
Для ионного компонента А, зависит от электрического состояния фазы. Поскольку  приняты независимыми от электрического состояния, заключаем, что от этого состояния зависит
приняты независимыми от электрического состояния, заключаем, что от этого состояния зависит  Аналогичное утверждение применимо к коэффициенту активности
Аналогичное утверждение применимо к коэффициенту активности  . В противоположность этому Гуггенгейм принимает, что
. В противоположность этому Гуггенгейм принимает, что  не зависит, а
не зависит, а  зависит от электрического состояния. Это приводит нас к малоприемлемой ситуации, когда у должен зависеть от состава при постоянном электрическом состоянии. Однако для растворов различного состава еще не было дано определения постоянного электрического состояния.
зависит от электрического состояния. Это приводит нас к малоприемлемой ситуации, когда у должен зависеть от состава при постоянном электрическом состоянии. Однако для растворов различного состава еще не было дано определения постоянного электрического состояния.
Чтобы дополнительно проиллюстрировать природу этих коэффициентов активности, рассмотрим раствор одного электролита А, диссоциирующего на  катионов с зарядовым числом
катионов с зарядовым числом  анионов с зарядовым числом
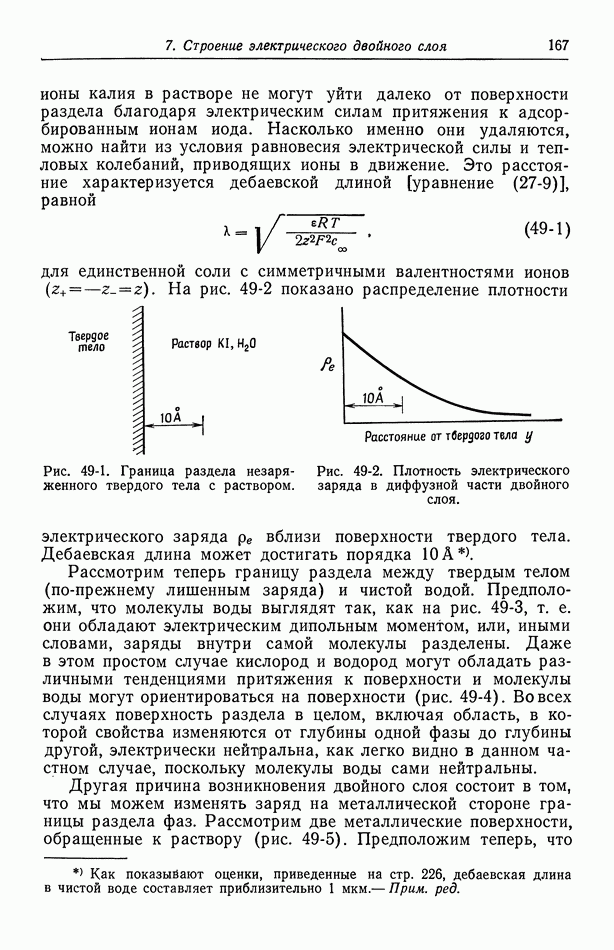
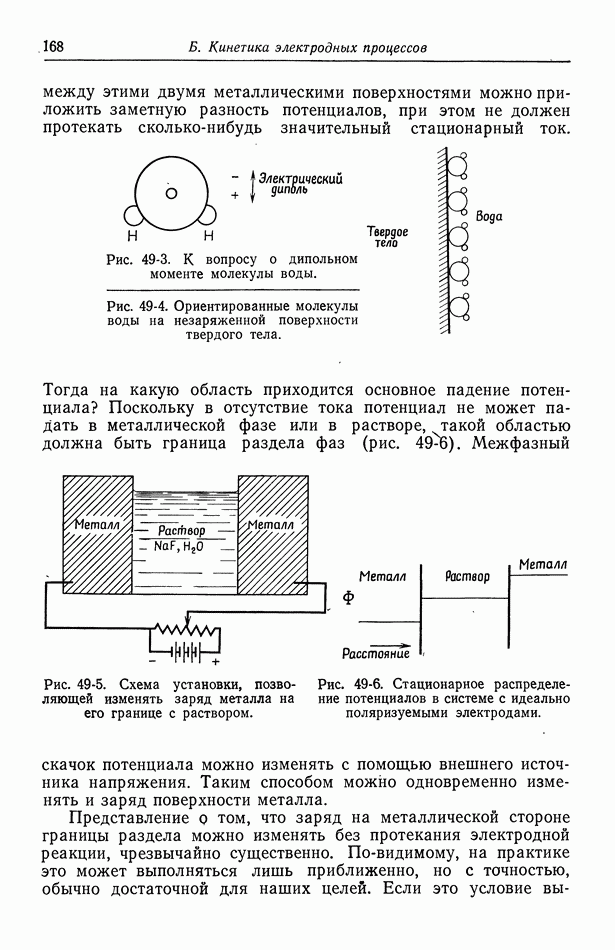
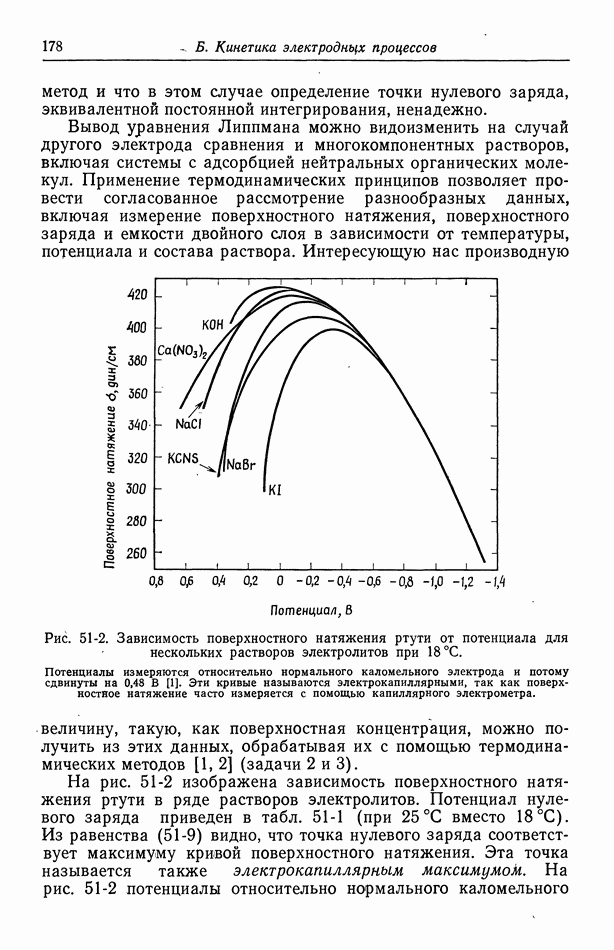
анионов с зарядовым числом  (имеется лишь один электролит, поэтому верхний индекс А у
(имеется лишь один электролит, поэтому верхний индекс А у  опущен). Тогда стехиометрическая концентрация электролита может быть представлена в виде
опущен). Тогда стехиометрическая концентрация электролита может быть представлена в виде

С помощью равенства (12-3) можно выразить химический потенциал А следующим образом:

или

Поскольку А нейтрален, согласно условию (14-5) необходимо, чтобы  Следовательно, такое определение вторичного стандартного состояния приводит к следующей комбинации величин
Следовательно, такое определение вторичного стандартного состояния приводит к следующей комбинации величин 

Этот предельный процесс позволяет отыскать далее произведение
при любом ненулевом значении  с помощью уравнения (14-10).
с помощью уравнения (14-10).
Обобщая эти представления, мы приходим к следующим заключениям:
можно однозначно определить выражение вида

для таких произведений, показатели которых удовлетворяют условию Гуггенгейма

Таким образом, выбор вторичного стандартного состояния в соответствии с условием (14-5) позволяет отдельно определить соответствующие произведения типа

Эти выводы следуют из того факта, что соответствующие произведения электрохимических потенциалов и абсолютных активностей

не зависят от электрического состояния в случае нейтральных комбинаций ионов.
С другой стороны, разности  и отношения взятые в разных фазах, определены однозначно, но зависят от электрических состояний фаз. Их абсолютные значения в отдельной фазе не определены, поскольку в первичном стандартном состоянии (например, при 0°С и 1 атм) не содержится информации об электрическом стандартном состоянии. Соответственно во вторичное стандартное состояние также входят лишь нейтральные комбинации компонентов. Следовательно величины
и отношения взятые в разных фазах, определены однозначно, но зависят от электрических состояний фаз. Их абсолютные значения в отдельной фазе не определены, поскольку в первичном стандартном состоянии (например, при 0°С и 1 атм) не содержится информации об электрическом стандартном состоянии. Соответственно во вторичное стандартное состояние также входят лишь нейтральные комбинации компонентов. Следовательно величины  для ионных компонентов определены не единственно возможным способом, причем эту трудность можно было бы преодолеть путем приписания величине № произвольного значения для одного ионного компонента в каждом растворителе при каждой температуре. Однако в любых приложениях уравнения можно составить так, чтобы всегда требовались только произведения величин
для ионных компонентов определены не единственно возможным способом, причем эту трудность можно было бы преодолеть путем приписания величине № произвольного значения для одного ионного компонента в каждом растворителе при каждой температуре. Однако в любых приложениях уравнения можно составить так, чтобы всегда требовались только произведения величин  (а также
(а также  ), соответствующие нейтральным комбинациям ионов.
), соответствующие нейтральным комбинациям ионов.
Вернемся к раствору одного электролита. По определению, средний коэффициент активности  в моляльной шкале задается выражением
в моляльной шкале задается выражением

где

Проведенное выше обсуждение показывает, что этот средний коэффициент активности определен однозначно и не зависит от электрического состояния раствора. Если также определить из соотношения

то равенство (14-10) можно записать в форме

Для растворов одного электролита измеряется и табулируется именно средний коэффициент активности 
Конечно, термодинамические свойства растворов одного электролита можно изучать неэлектрохимическими средствами и без детального рассмотрения его диссоциации. Например, измеряя давления паров или точки замерзания, можно получить зависимость химического потенциала  от концентрации. В том и состоит достоинство термодинамики, что она позволяет изучать макроскопические характеристики системы, не обращаясь к молекулярным представлениям, если различные компоненты быстро уравновешиваются друг с другом.
от концентрации. В том и состоит достоинство термодинамики, что она позволяет изучать макроскопические характеристики системы, не обращаясь к молекулярным представлениям, если различные компоненты быстро уравновешиваются друг с другом.
Если бы мы применили равенство (14-2) к электролиту А без учета его диссоциации, то получили бы

Это выражение отличается от равенства (14-15) прежде всего отсутствием множителя  Таким образом,
Таким образом,  должны отличаться от
должны отличаться от  причем
причем  должен иметь концентрационную зависимость, значительно отличающуюся от зависимости
должен иметь концентрационную зависимость, значительно отличающуюся от зависимости  Конкретно мы имеем
Конкретно мы имеем

Следовательно,  при 0 и равенство (14-5) неприменимо для определения вторичного стандартного состояния для
при 0 и равенство (14-5) неприменимо для определения вторичного стандартного состояния для  в равенстве (14-16). Мы приходим к выводу, что при
в равенстве (14-16). Мы приходим к выводу, что при
бесконечном разбавлении существенно знать агрегатное состояние растворенного вещества. Эту информацию необходимо учитывать при выборе компонентов раствора, если мы желаем воспользоваться условием (14-5) для определения вторичного стандартного состояния. За исключением этой необходимости выбора другого вторичного стандартного состояния, со строго термодинамической точки зрения вполне законно рассматривать электролит как недиссоциированный, хотя если это и делается, то редко. Таким образом, под коэффициентом активности мы будем подразумевать средний ионный коэффициент активности электролита.
Аналогичные представления могут быть развиты для молярной шкалы концентрации. В этой шкале средний коэффициент активности электролита определяется из соотношения

а если также определить с помощью равенства

то можно выразить химический потенциал электролита в виде

Средние коэффициенты активности в обеих шкалах связаны соотношением

где  молекулярный вес электролита. Это равенство применимо лишь к растворам одного электролита.
молекулярный вес электролита. Это равенство применимо лишь к растворам одного электролита.
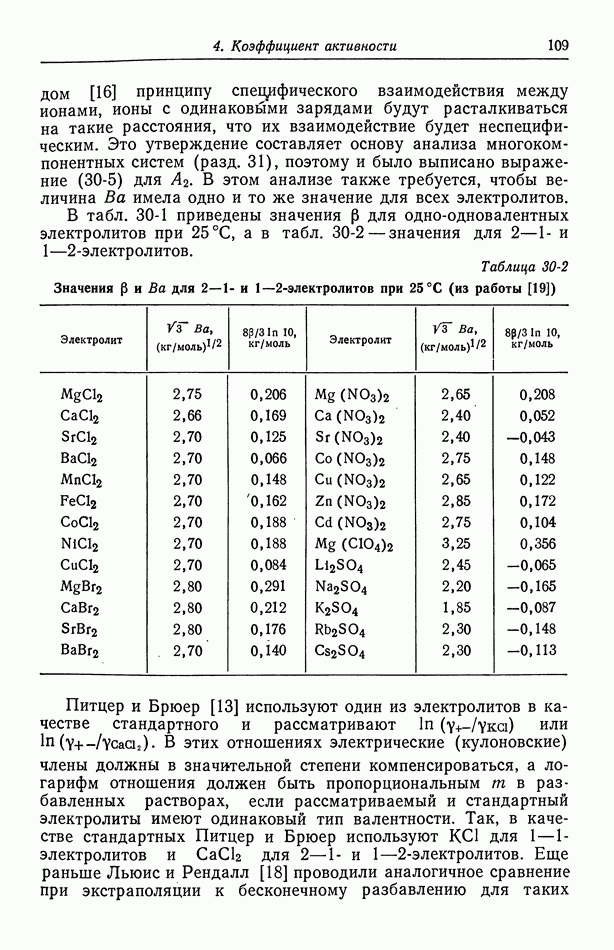
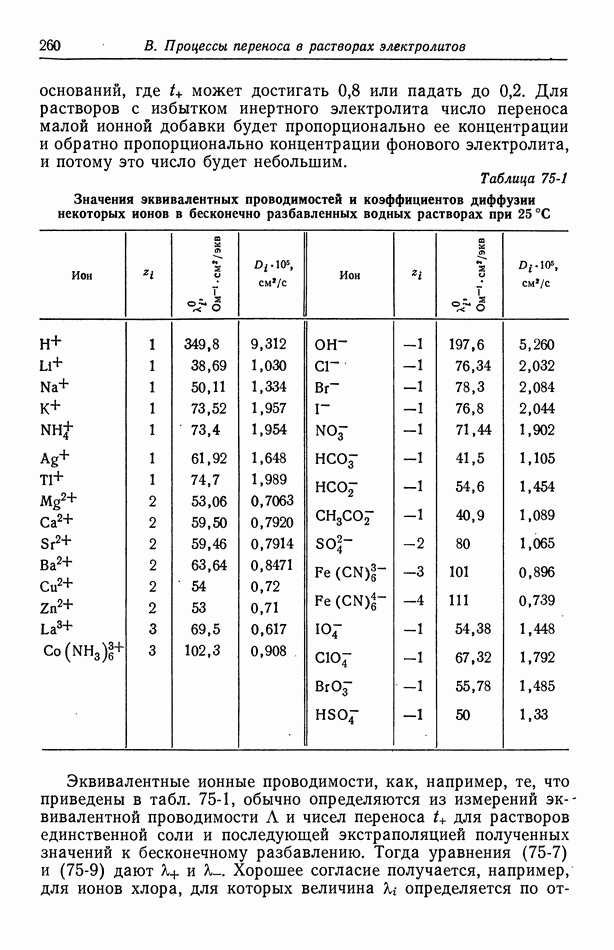
Для иллюстрации последствий ионной диссоциации можно привести разнообразные примеры. Чтобы показать влияние диссоциации соляной кислоты, Льюис и др. [3] построили график зависимости парциального давления  находящейся в равновесии с раствором, как от
находящейся в равновесии с раствором, как от  так и от
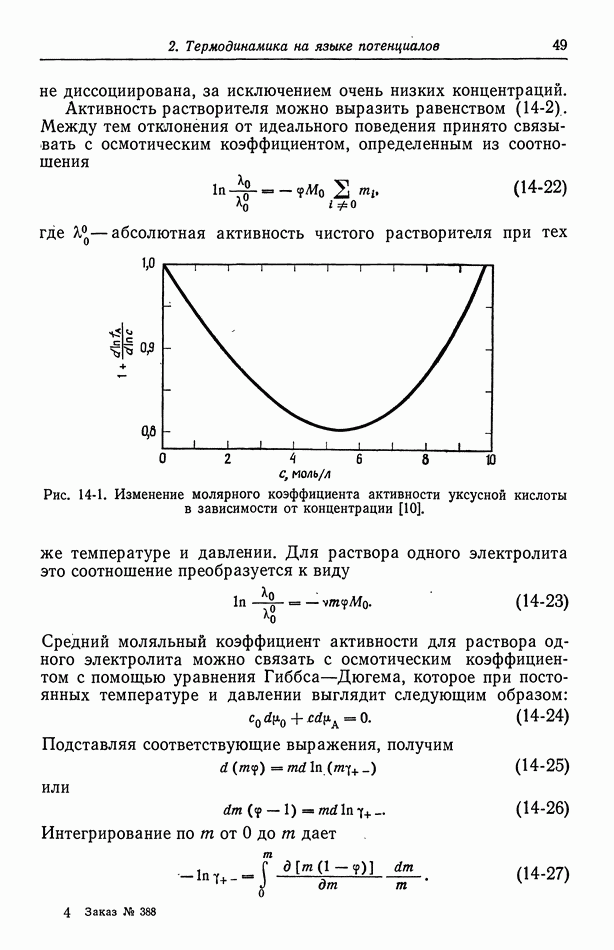
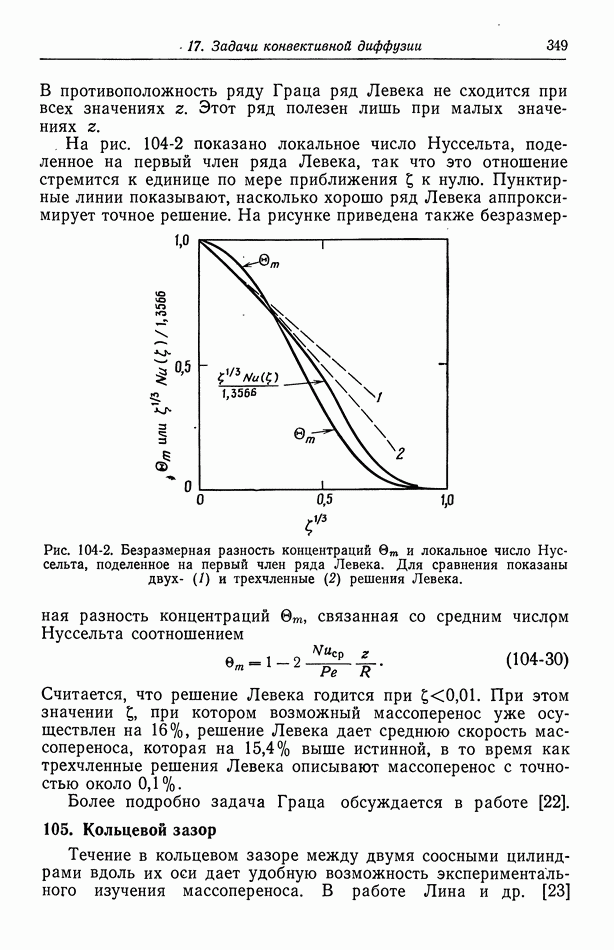
так и от  Они построили также график понижения точки замерзания уксусной кислоты, из которого видно, что уксусная кислота ведет себя как неэлектролит, за исключением очень низких концентраций. То же отмечено на рис. 14-1, показывающем изменение с концентрацией молярного коэффициента активности
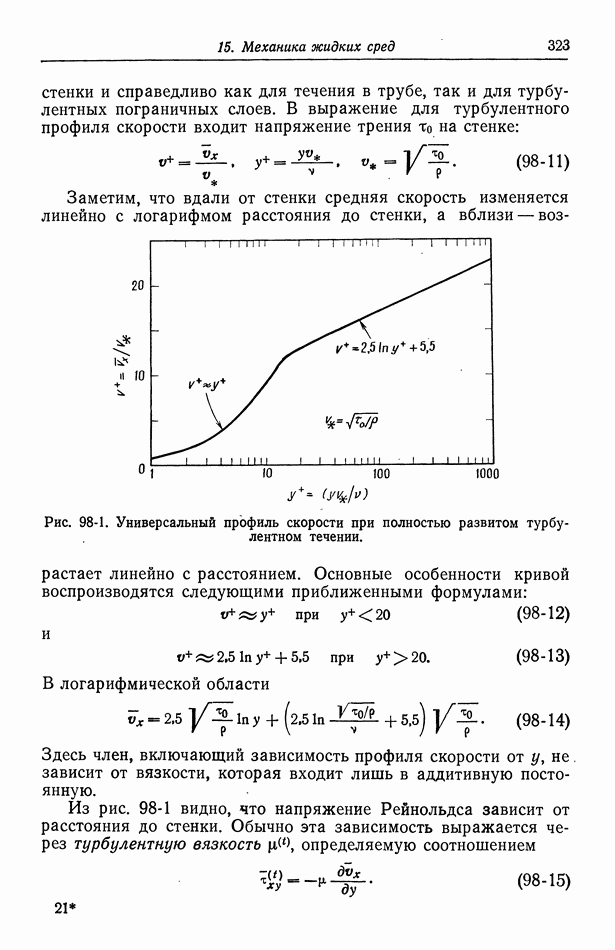
Они построили также график понижения точки замерзания уксусной кислоты, из которого видно, что уксусная кислота ведет себя как неэлектролит, за исключением очень низких концентраций. То же отмечено на рис. 14-1, показывающем изменение с концентрацией молярного коэффициента активности  (определенного аналогично
(определенного аналогично  Его поведение типично для неэлектролитов. Однако, если уксусная кислота действительно диссоциирует на ионы водорода и ацетата при бесконечном разбавлении, величина
Его поведение типично для неэлектролитов. Однако, если уксусная кислота действительно диссоциирует на ионы водорода и ацетата при бесконечном разбавлении, величина  с должна стремиться к 2 по мере приближения с к нулю. Наблюдаемое поведение уксусной кислоты обусловлено ее малой константой диссоциации, вследствие чего уксусная кислота почти
с должна стремиться к 2 по мере приближения с к нулю. Наблюдаемое поведение уксусной кислоты обусловлено ее малой константой диссоциации, вследствие чего уксусная кислота почти
не диссоциирована, за исключением очень низких концентраций.
Активность растворителя можно выразить равенством (14-2). Между тем отклонения от идеального поведения принято связывать с осмотическим коэффициентом, определенным из соотношения же температуре и давлении.

где — абсолютная активность чистого растворителя при тех

Рис. 14-1. Изменение молярного коэффициента активности уксусной кислоты в зависимости от концентрации [10].
Для раствора одного электролита это соотношение преобразуется к виду

Средний моляльный коэффициент активности для раствора одного электролита можно связать с осмотическим коэффициентом с помощью уравнения Гиббса-Дюгема, которое при постоянных температуре и давлении выглядит следующим образом:

Подставляя соответствующие выражения, получим

или

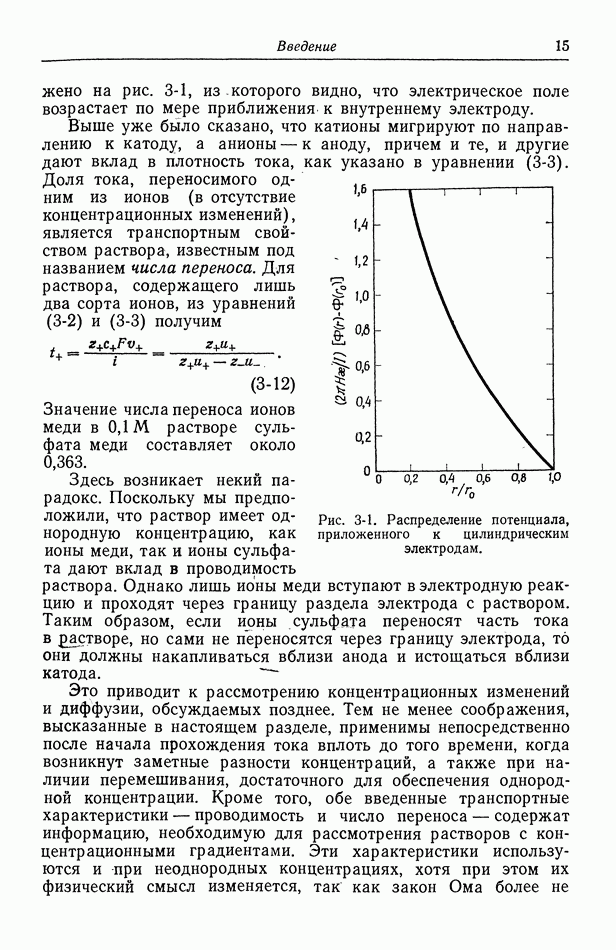
Интегрирование по  от 0 до
от 0 до  дает
дает

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ВВЕДЕНИЕ
- 1. Термодинамика, кинетика электродных процессов и процессы переноса
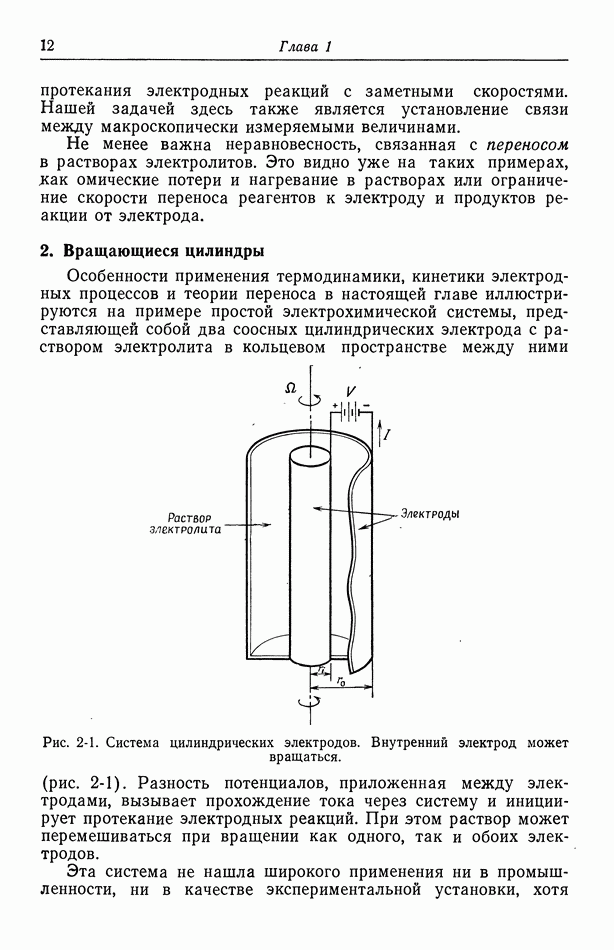
- 2. Вращающиеся цилиндры
- 3. Прохождение тока в электролитах
- 4. Течение жидкости
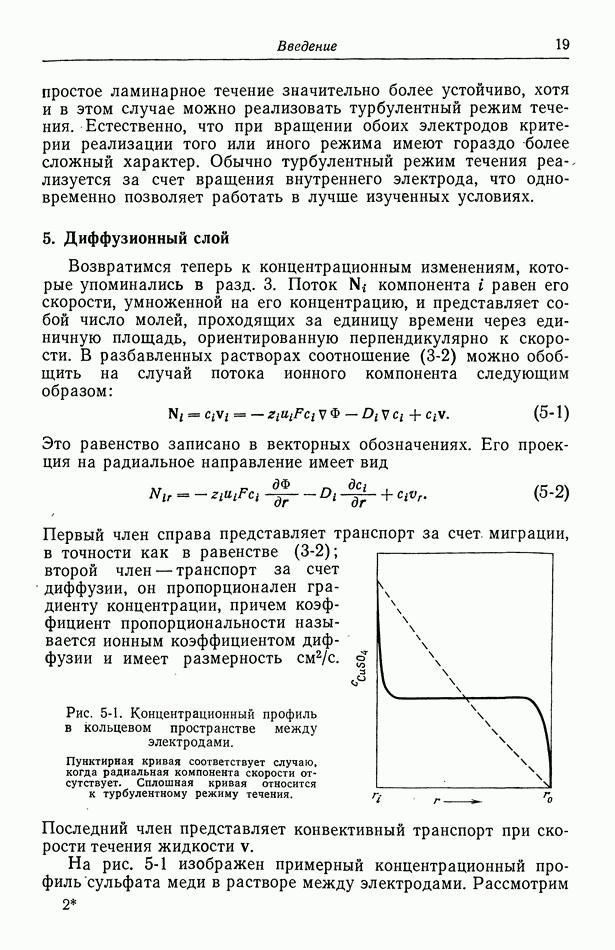
- 5. Диффузионный слой
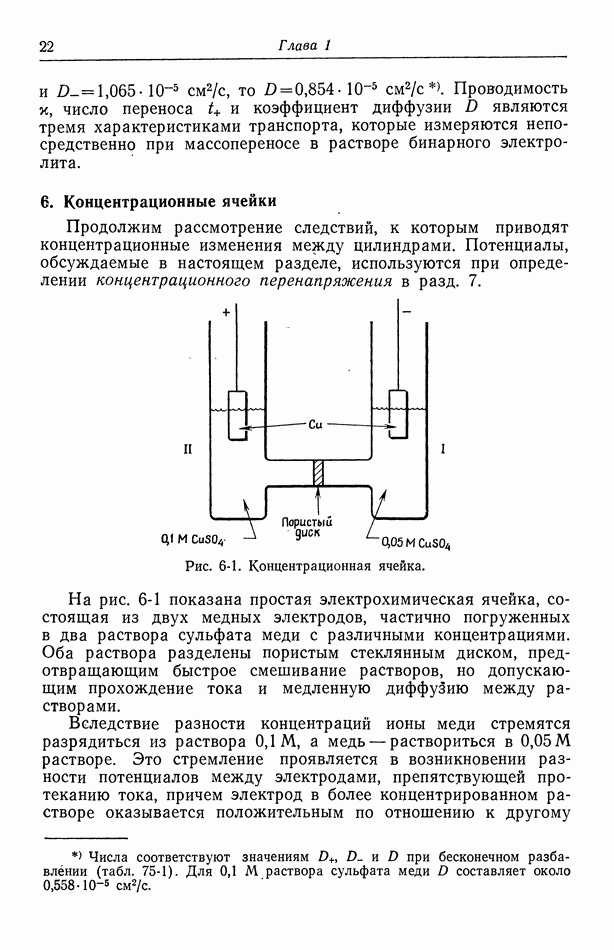
- 6. Концентрационные ячейки
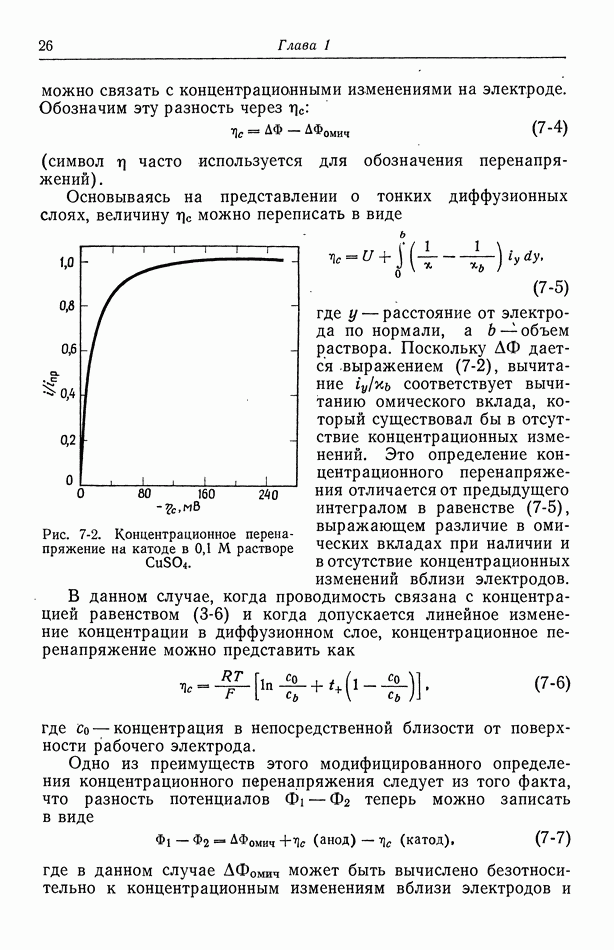
- 7. Концентрационное перенапряжение
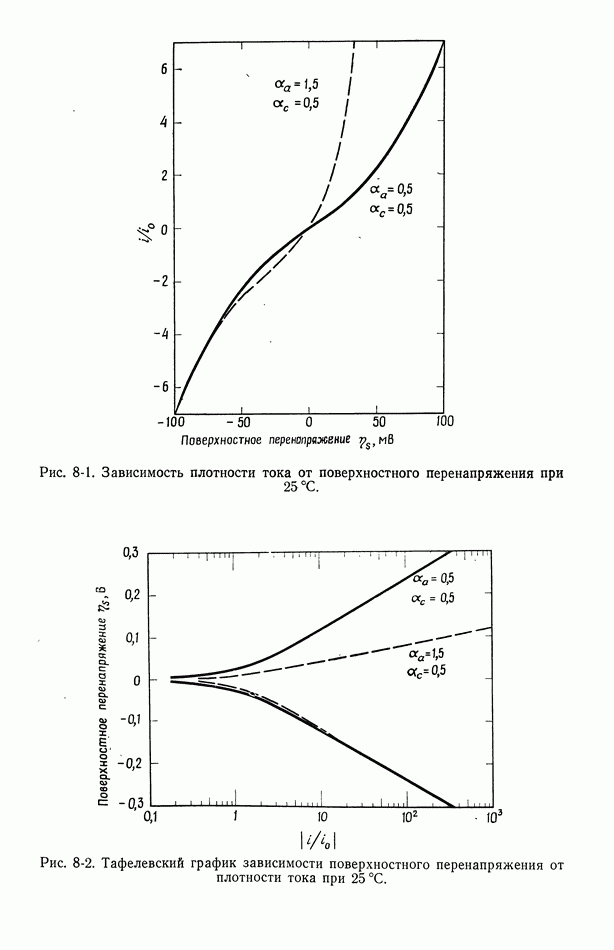
- 8. Поверхностное перенапряжение
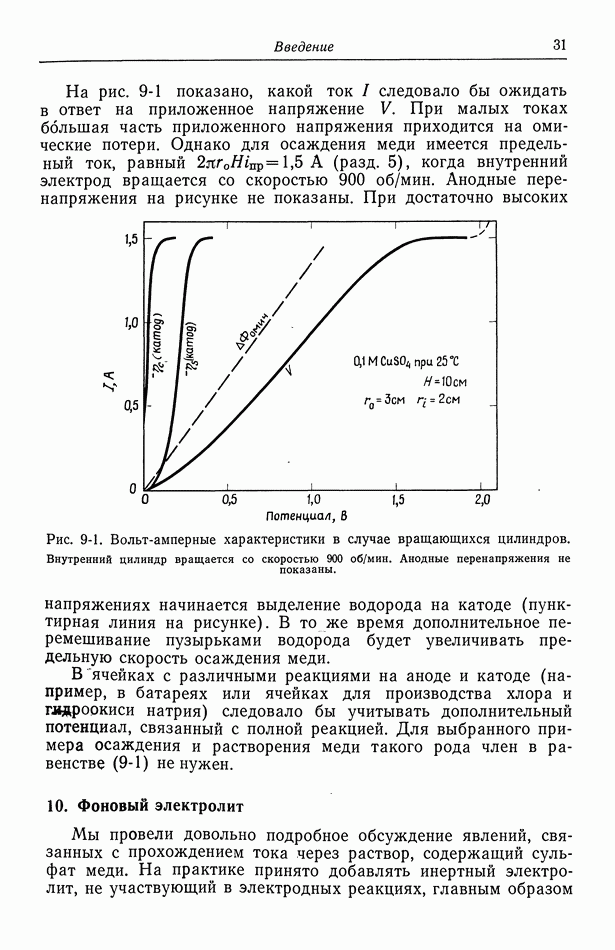
- 9. Потенциал ячейки
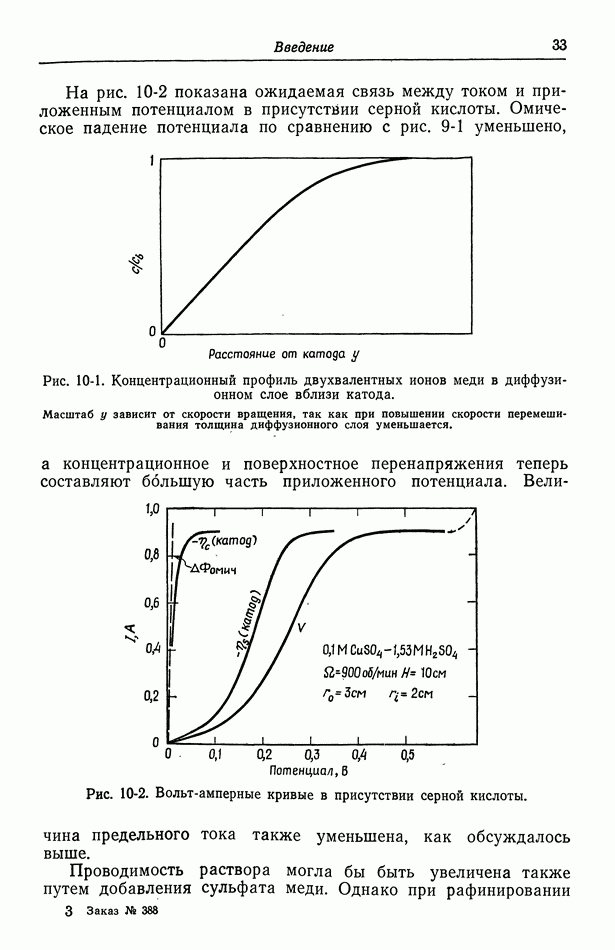
- 10. Фоновый электролит
- 11. Свободная конвекция
- Часть А. ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ ЯЧЕЕК
- Глава 2. ТЕРМОДИНАМИКА НА ЯЗЫКЕ ЭЛЕКТРОХИМИЧЕСКИХ ПОТЕНЦИАЛОВ
- 12. Равновесие фаз
- 13. Химический и электрохимический потенциалы
- 14. Определение некоторых термодинамических функций
- 15. Ячейка с раствором однородной концентрации
- 16. Процессы переноса в областях контакта
- 17. Ячейка с одним электролитом переменной концентрации
- 18. Ячейка с двумя электролитами, концентрация одного из которых почти однородна
- 19. Ячейка с двумя электролитами переменной концентрации
- 20. Стандартный потенциал ячейки и коэффициенты активности
- Глава 3. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ
- 22. Электростатический потенциал
- 23. Межмолекулярные силы
- 24. Внешний и внутренний потенциалы
- 25. Потенциалы электродов сравнения
- 26. Электрический потенциал в термодинамике
- Глава 4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
- 27. Распределение ионов в разбавленных растворах
- 28. Электрический вклад в свободную энергию
- 29. Недостатки модели Дебая-Хюккеля
- 30. Растворы бинарных электролитов
- 31. Многокомпонентные растворы
- 32. Измерение коэффициентов активности
- 33. Слабые электролиты
- Глава 5. ЭЛЕКТРОДЫ СРАВНЕНИЯ
- 34. Критерии выбора электродов сравнения
- 35. Экспериментальные факторы, влияющие на выбор электродов сравнения
- 36. Водородный электрод
- 37. Каломельный электрод и другие электроды типа ртуть—соль ртути
- 38. Окиснортутный электрод
- 39. Электроды типа серебро—галогенид серебра
- 40. Потенциалы относительно данного электрода сравнения
- Глава 6. ПОТЕНЦИАЛЫ ЯЧЕЕК С ПЕРЕНОСОМ
- 41. Уравнение Нернста
- 42. Типы жидкостных соединений
- 43. Формулы для потенциалов жидкостных соединений
- 44. Определение концентрационных профилей
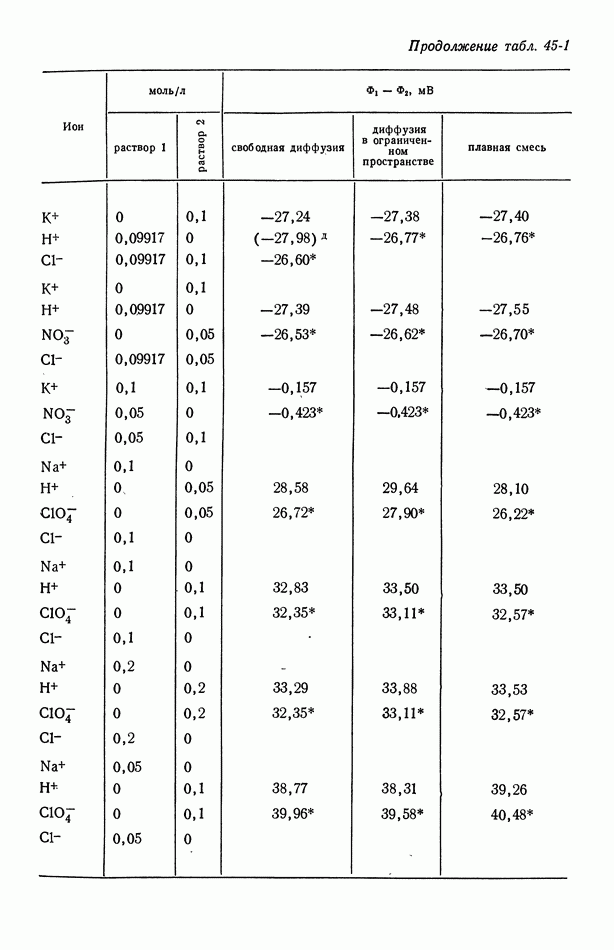
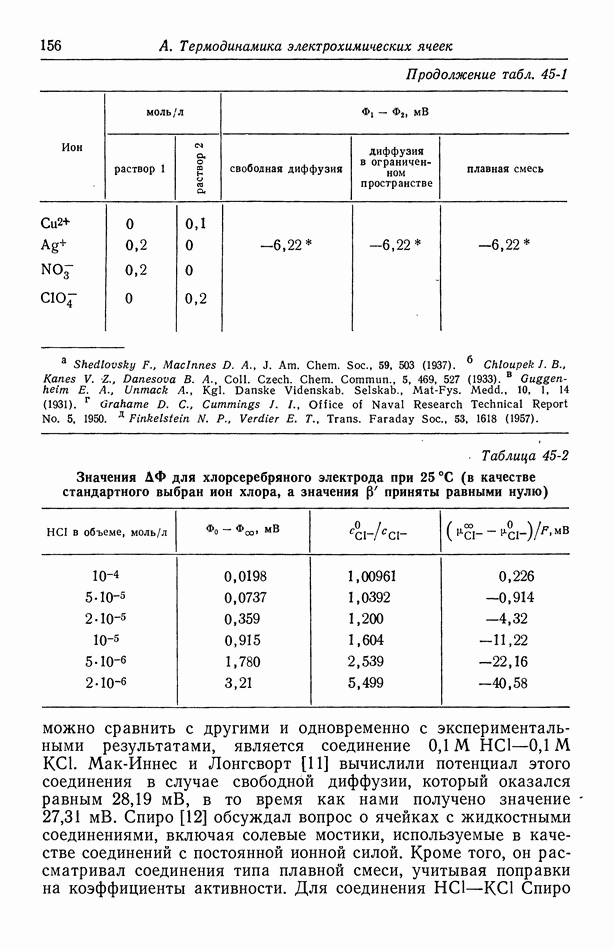
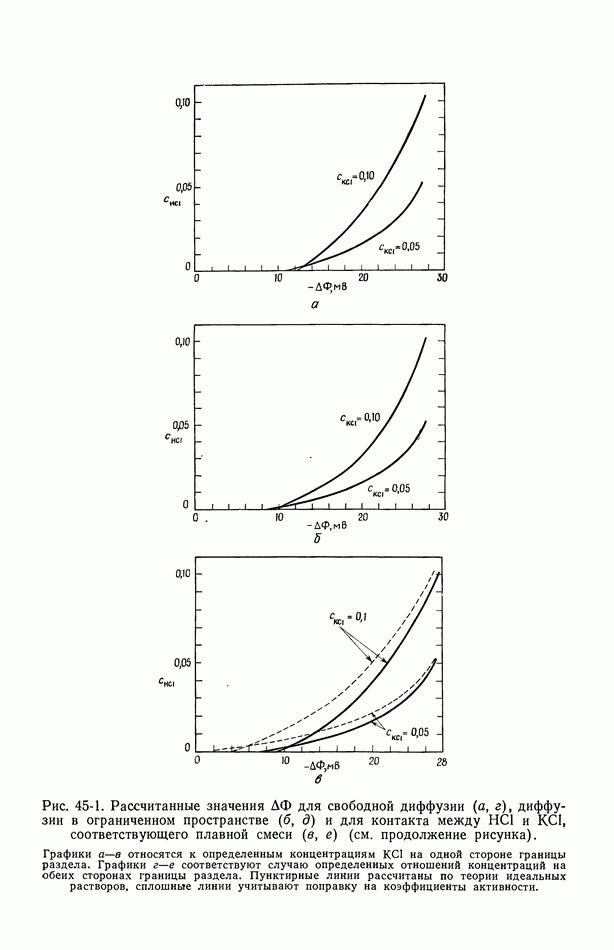
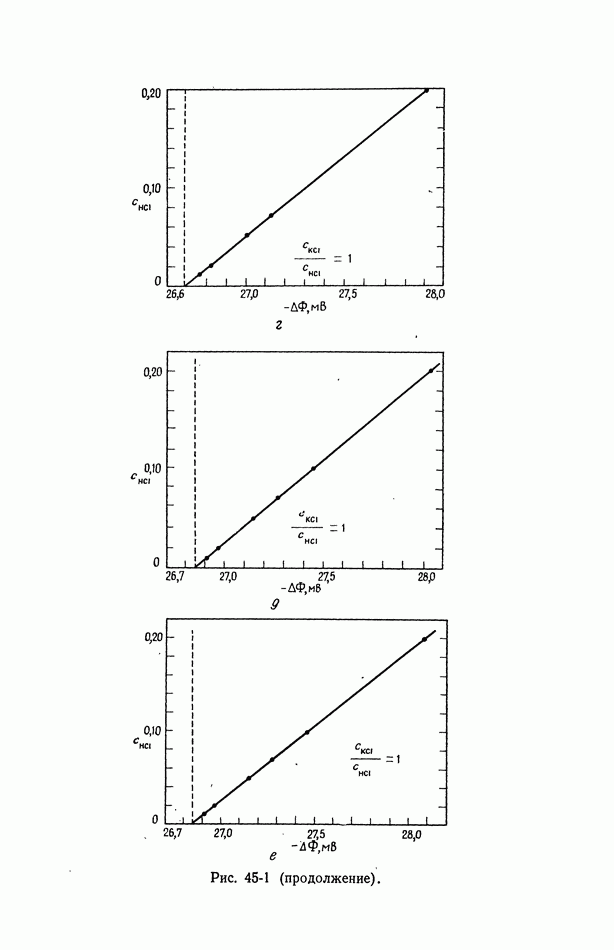
- 45. Численные результаты
- 46. Ячейки с жидкостным соединением
- 47. Поправки к уравнению Нернста
- 48. Мембранные потенциалы
- Часть Б. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ И ДРУГИЕ ПОВЕРХНОСТНЫЕ ЯВЛЕНИЯ
- Глава 7. СТРОЕНИЕ ЭЛЕКТРИЧЕСКОГО ДВОЙНОГО СЛОЯ
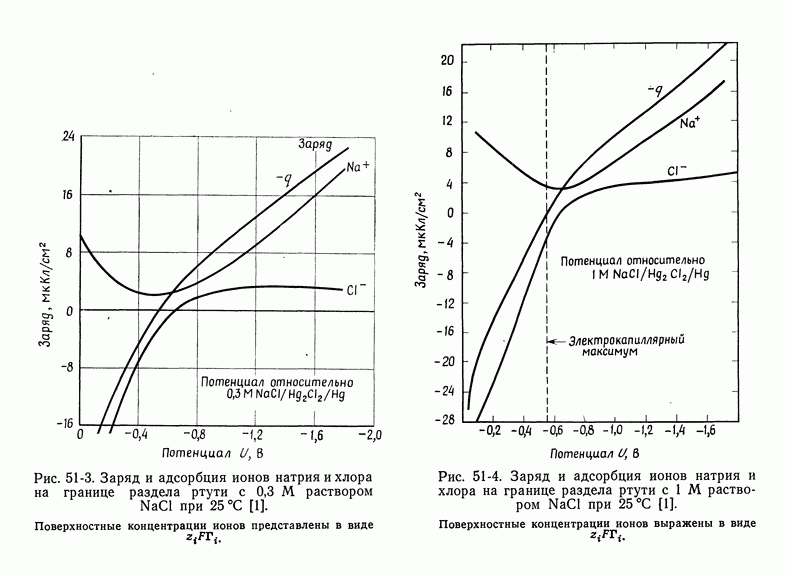
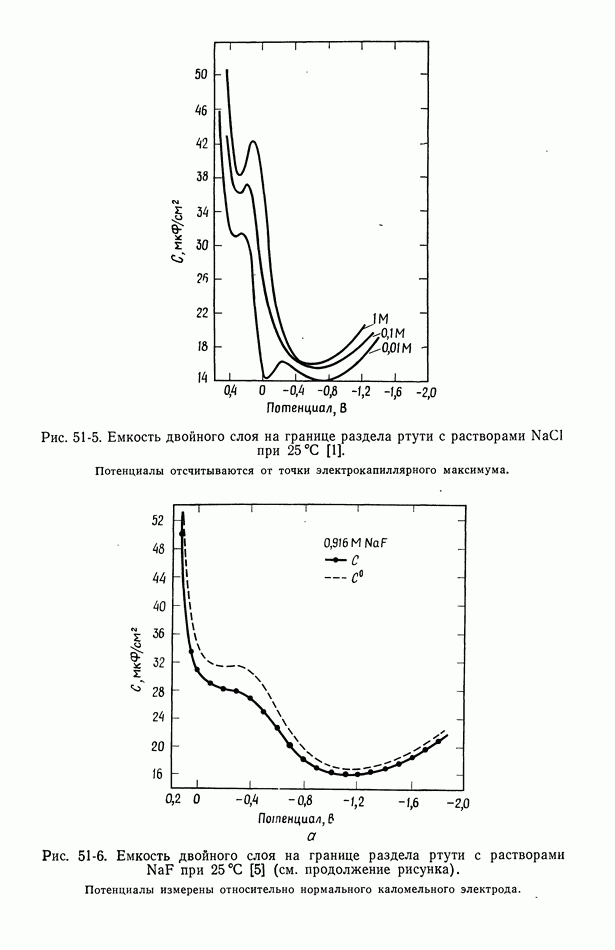
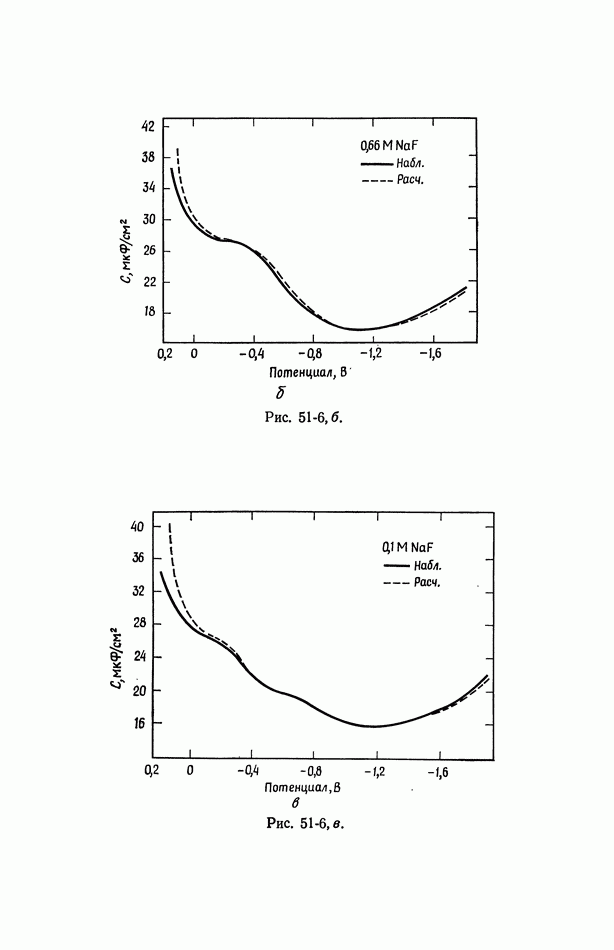
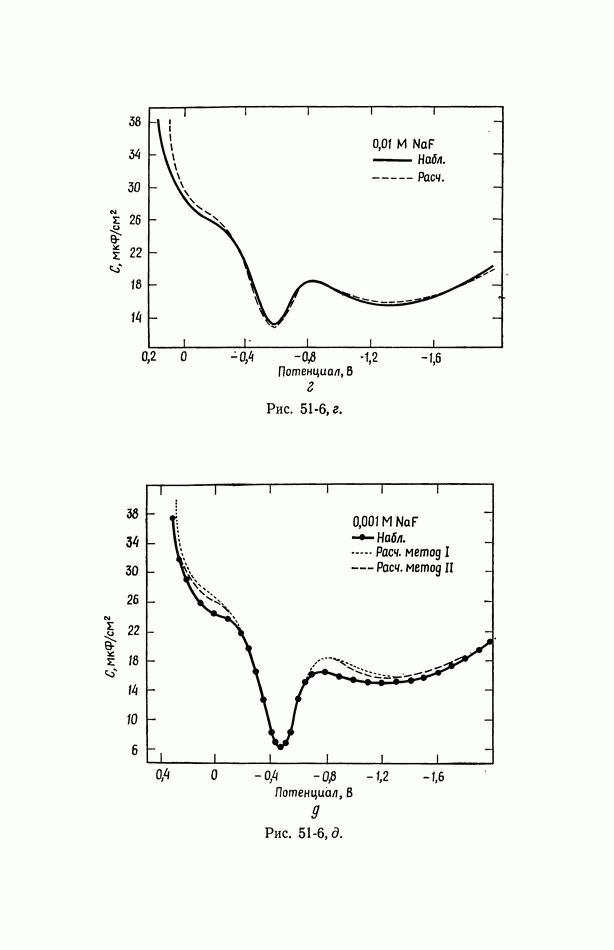
- 50. Изотерма адсорбции Гиббса
- 51. Уравнение Липпмана
- 52. Диффузная часть двойного слоя
- 53. Емкость двойного слоя в отсутствие специфической адсорбции
- 54. Специфическая адсорбция на границе раздела электрод—раствор
- Глава 8. КИНЕТИКА ЭЛЕКТРОДНЫХ ПРОЦЕССОВ
- 55. Гетерогенные электродные реакции
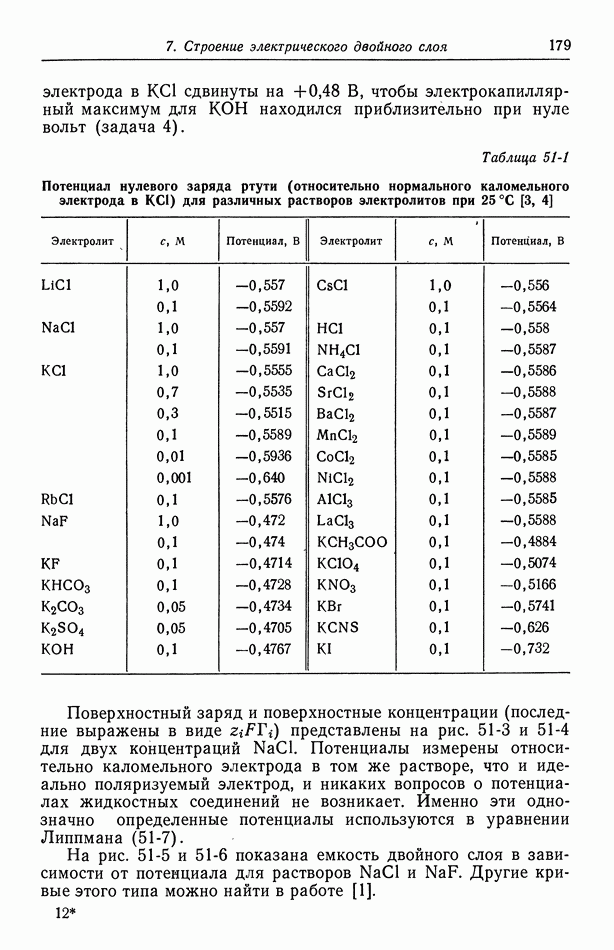
- 56. Зависимость плотности тока от поверхностного перенапряжения
- 57. Модели в кинетике электродных процессов
- 58. Влияние строения двойного слоя
- 59. Кислородный электрод
- 60. Методы измерения
- 61. Одновременно протекающие реакции
- Глава 9. ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
- 62. Разрывная скорость на границе раздела
- 63. Электроосмос и потенциал течения
- 64. Электрофорез
- 65. Потенциал осаждения
- Глава 10. ЭЛЕКТРОКАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- 67. Электрокапиллярное движение ртутных капель
- 68. Потенциалы осаждения для падающих ртутных капель
- Часть В. ПРОЦЕССЫ ПЕРЕНОСА В РАСТВОРАХ ЭЛЕКТРОЛИТОВ
- Глава 11. БЕСКОНЕЧНО РАЗБАВЛЕННЫЕ РАСТВОРЫ
- 70. Проводимость, диффузионные потенциалы и числа переноса
- 71. Сохранение заряда
- 72. Бинарный электролит
- 73. Фоновый электролит
- 74. Многокомпонентная диффузия, возникающая при исключении электрического поля
- 75. Подвижности и коэффициенты диффузии
- 76. Электронейтральность и уравнение Лапласа
- 77. Умеренно разбавленные растворы
- Глава 12. КОНЦЕНТРИРОВАННЫЕ РАСТВОРЫ
- 79. Бинарный электролит
- 80. Стандартные скорости
- 81. Потенциал
- 82. Связь с теорией разбавленных растворов
- 83. Многокомпонентный транспорт
- 84. Потенциалы жидкостного соединения
- Глава 13. ТЕПЛОВЫЕ ЭФФЕКТЫ
- 85. Термодиффузия
- 86. Выделение и перенос тепла
- 87. Тепловыделение на границе раздела фаз
- 88. Термогальванические ячейки
- Глава 14. ХАРАКТЕРИСТИКИ ПЕРЕНОСА
- 89. Бесконечно разбавленные растворы
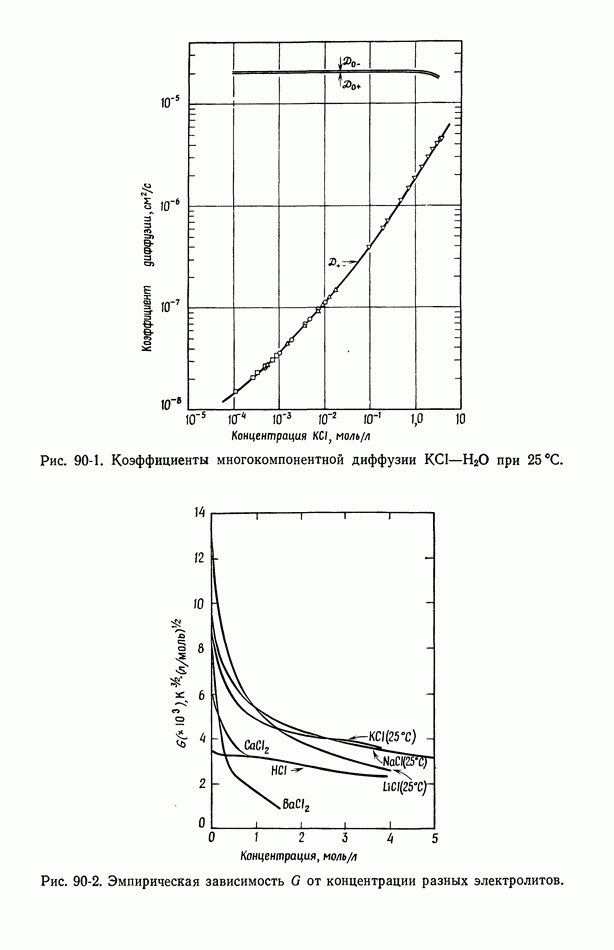
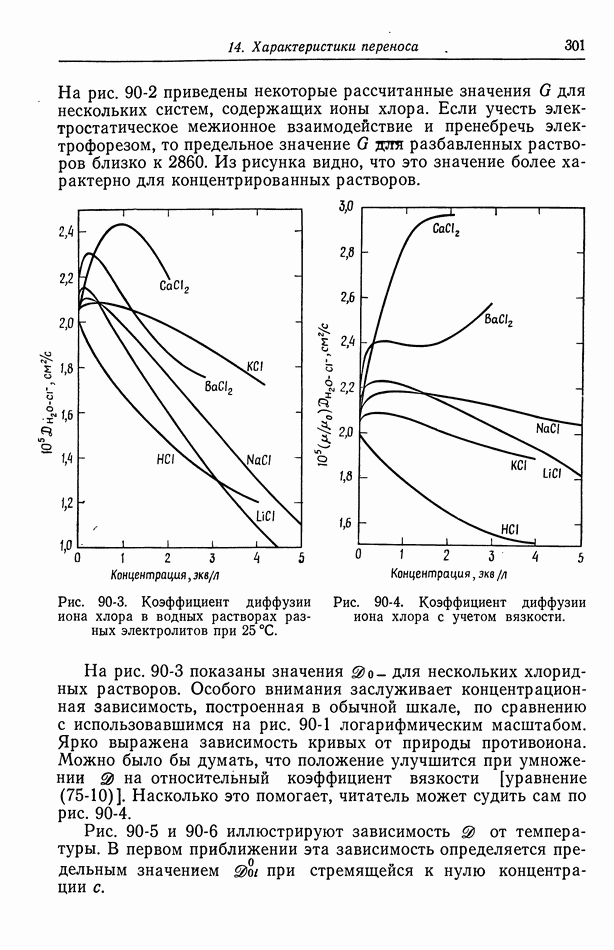
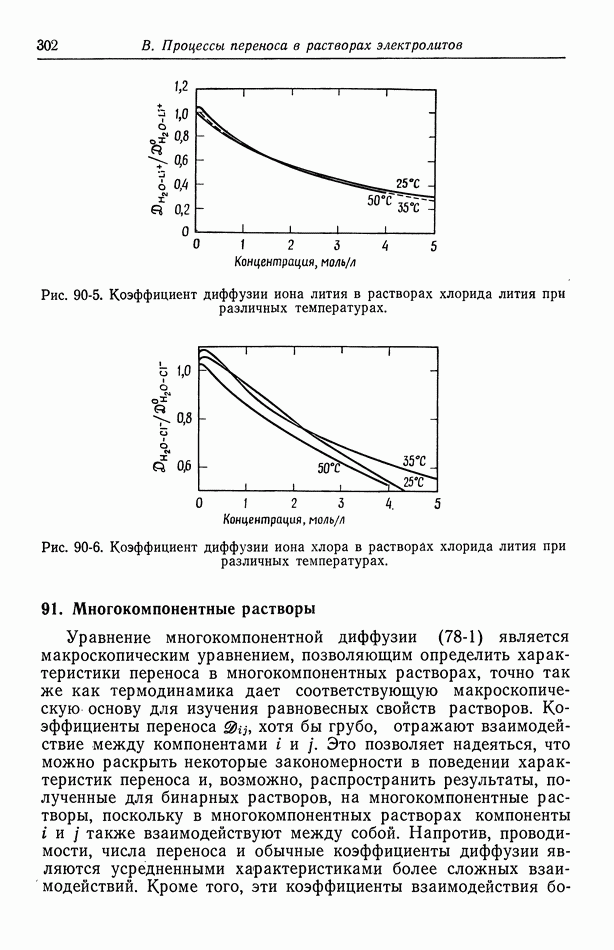
- 90. Растворы, содержащие одну соль
- 91. Многокомпонентные растворы
- 92. Интегральные коэффициенты диффузии
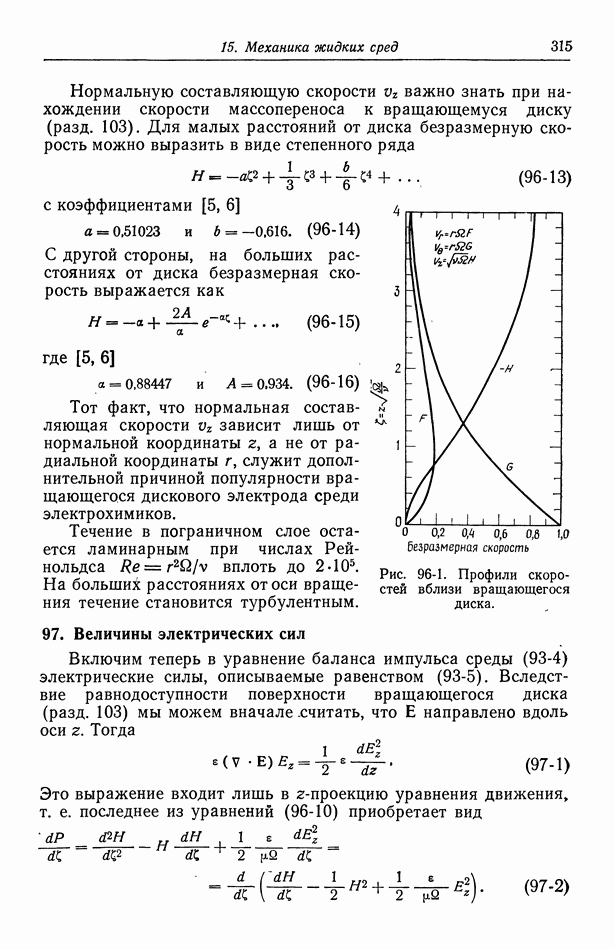
- Глава 15. МЕХАНИКА ЖИДКИХ СРЕД
- 93. Баланс массы и импульса
- 94. Напряжение в ньютоновской жидкости
- 95. Граничные условия
- 96. Течение жидкости к вращающемуся диску
- 97. Величины электрических сил
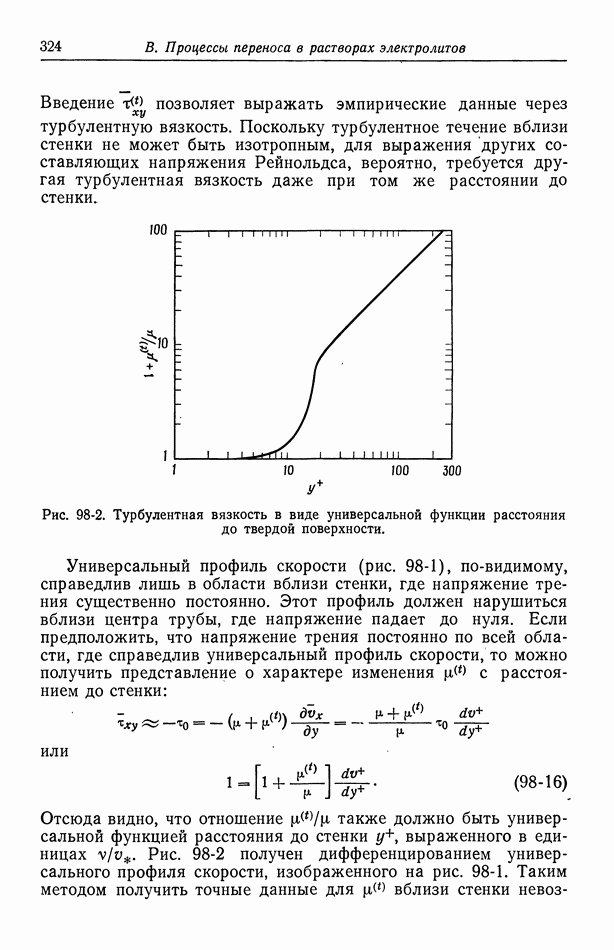
- 98. Турбулентное течение
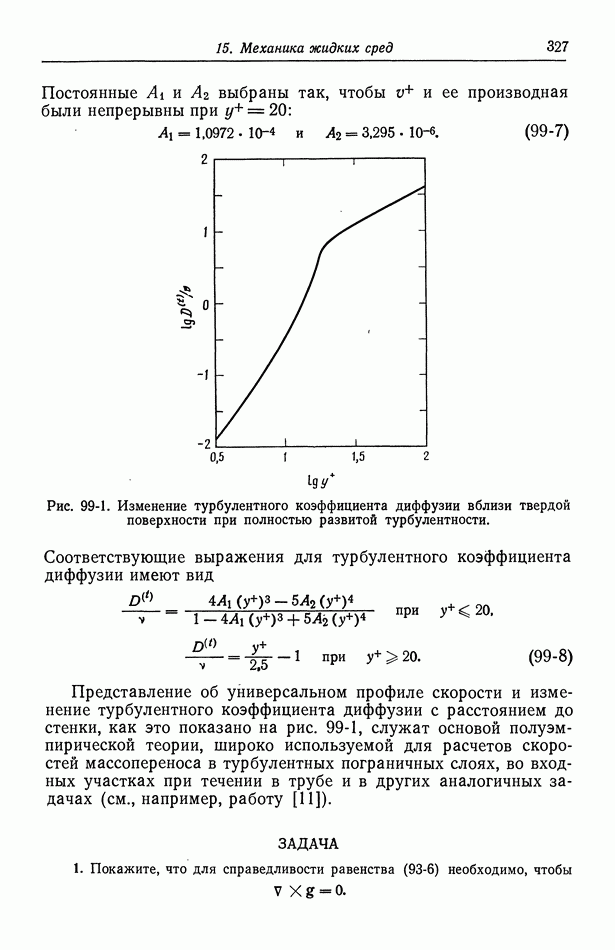
- 99. Массоперенос в турбулентном потоке
- Часть Г. РАСПРЕДЕЛЕНИЕ ТОКА И МАССОПЕРЕНОС В ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМАХ
- Глава 16. ОСНОВНЫЕ УРАВНЕНИЯ
- 100. Перенос в разбавленных растворах
- 101. Кинетика электродных процессов
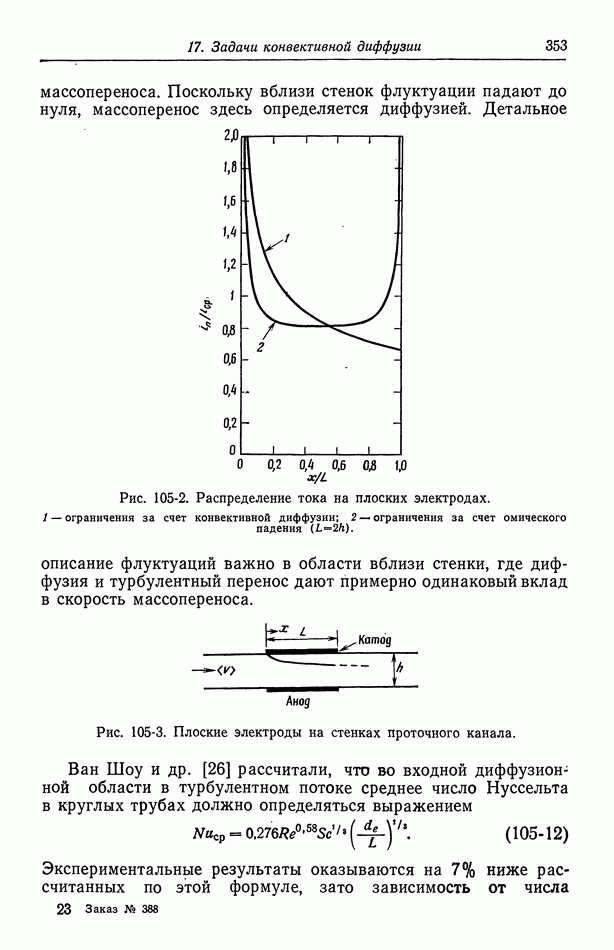
- Глава 17. ЗАДАЧИ КОНВЕКТИВНОЙ ДИФФУЗИИ
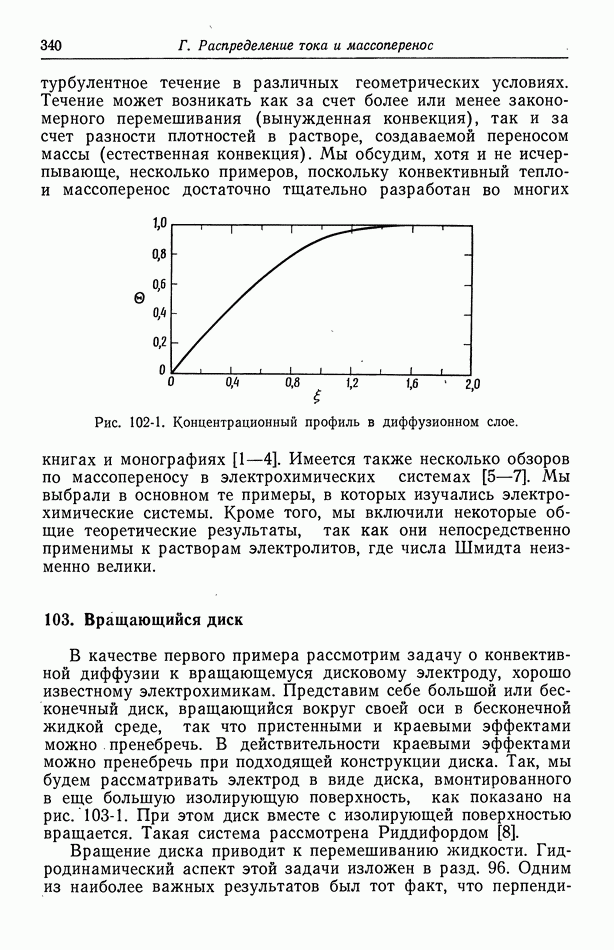
- 102. Упрощенное описание конвективной диффузии
- 103. Вращающийся диск
- 104. Задача Граца
- 105. Кольцевой зазор
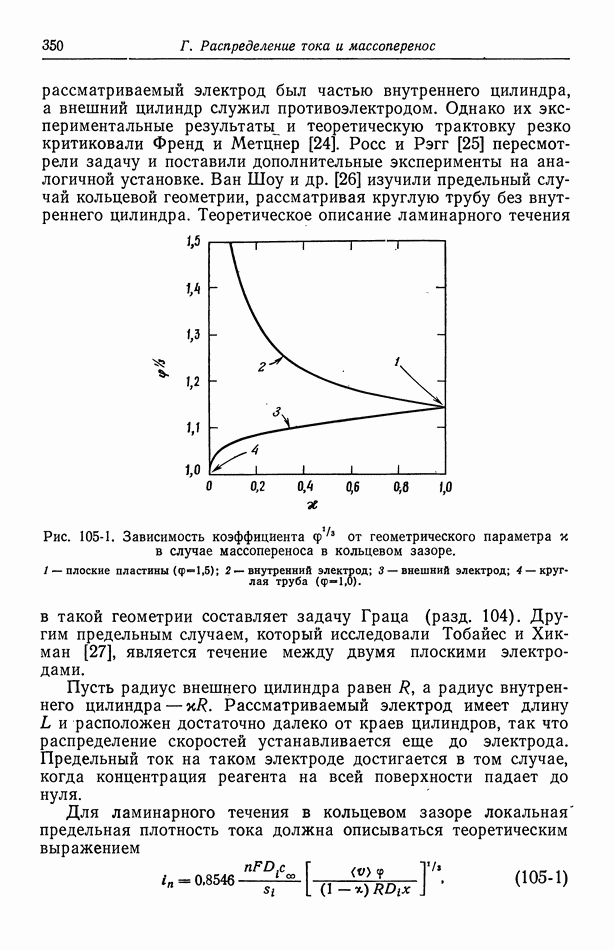
- 106. Двумерные диффузионные слои при вынужденной ламинарной конвекции
- 107. Осесимметричные диффузионные слои при вынужденной ламинарной конвекции
- 108. Плоская пластина в свободном потоке
- 109. Вращающиеся цилиндры
- 110. Растущие ртутные капли
- 112. Наложение свободной и вынужденной конвекции
- 113. Ограничения за счет поверхностных реакций
- 114. Бинарные и концентрированные растворы
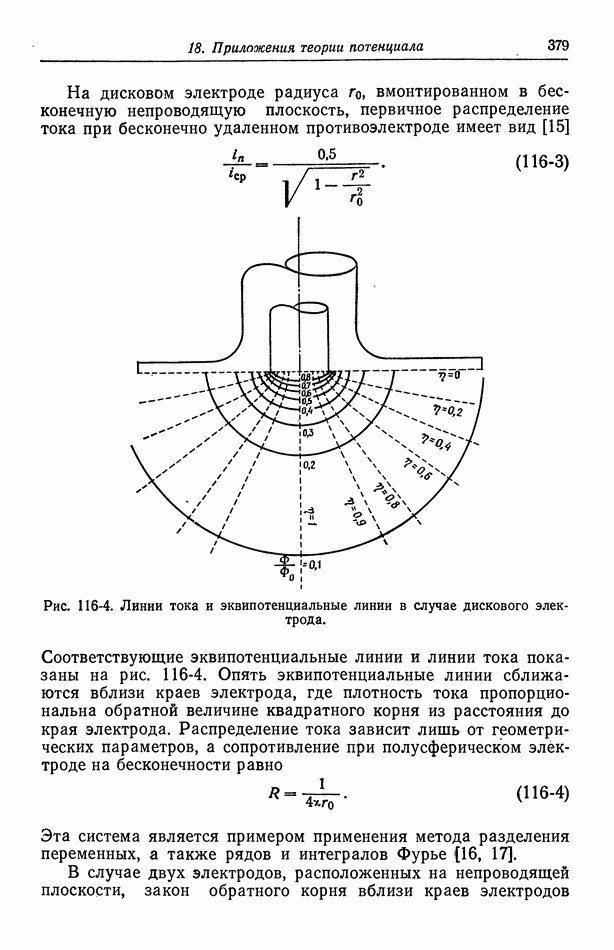
- Глава 18. ПРИЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
- 115. Упрощения в задачах теории потенциала
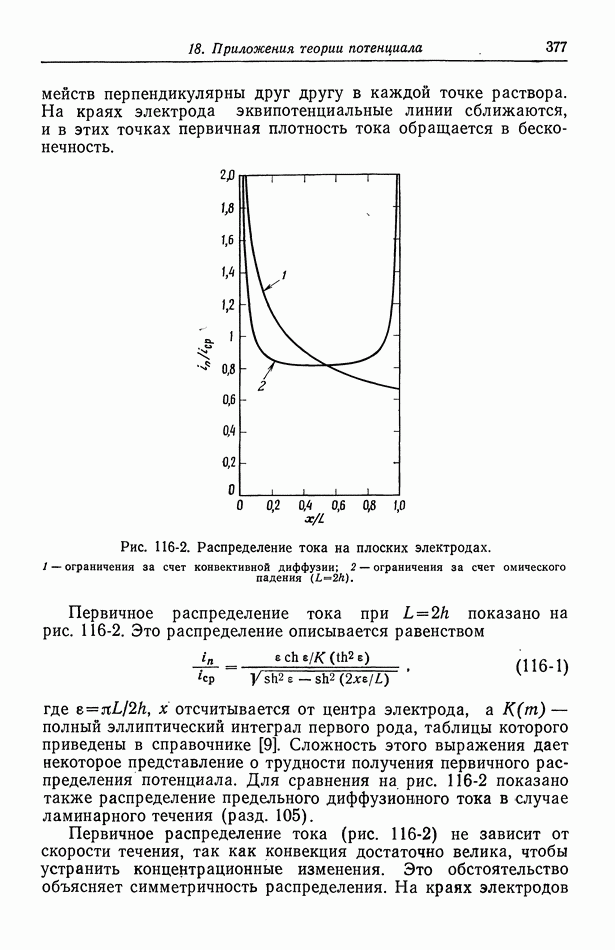
- 116. Первичное распределение тока
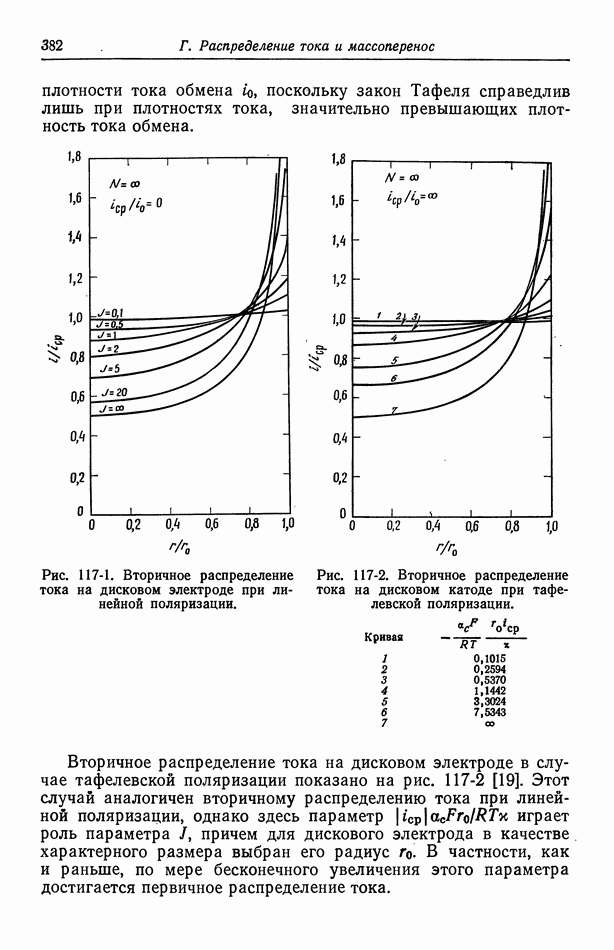
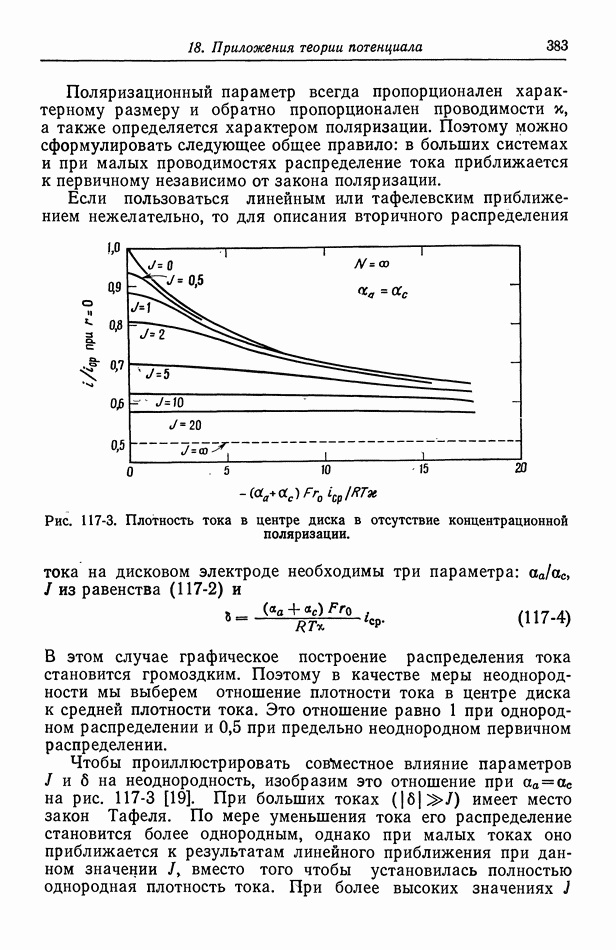
- 117. Вторичное распределение тока
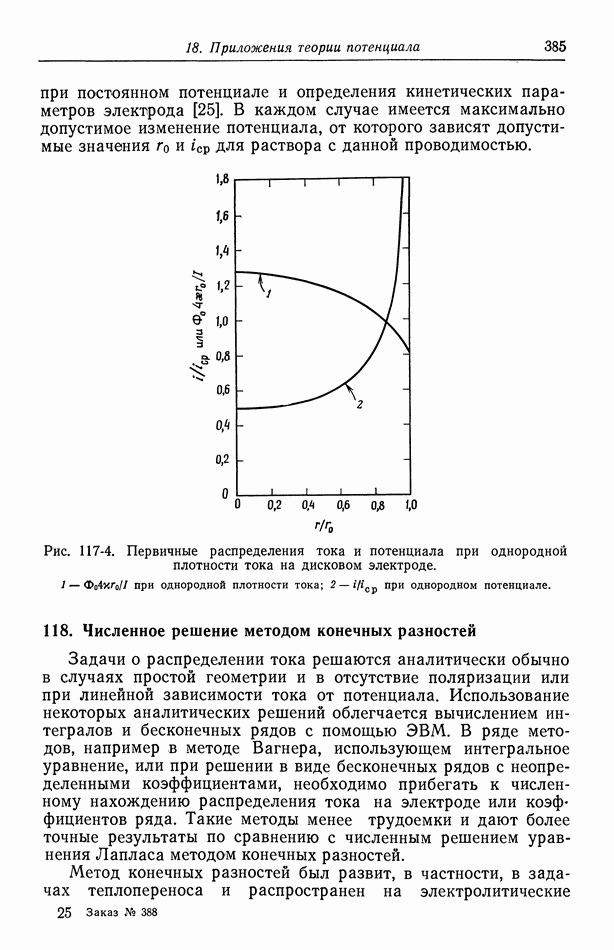
- 118. Численное решение методом конечных разностей
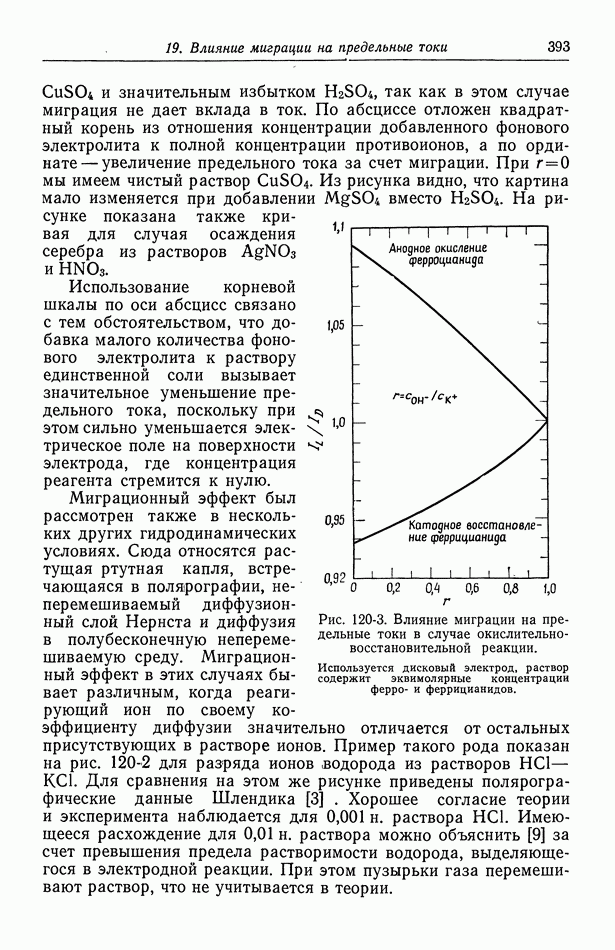
- Глава 19. ВЛИЯНИЕ МИГРАЦИИ НА ПРЕДЕЛЬНЫЕ ТОКИ
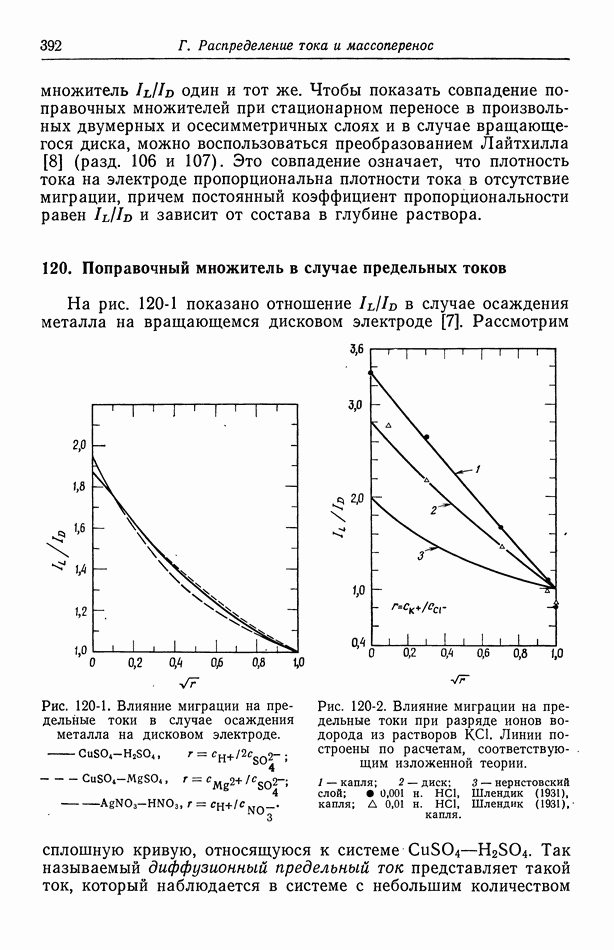
- 120. Поправочный множитель в случае предельных токов
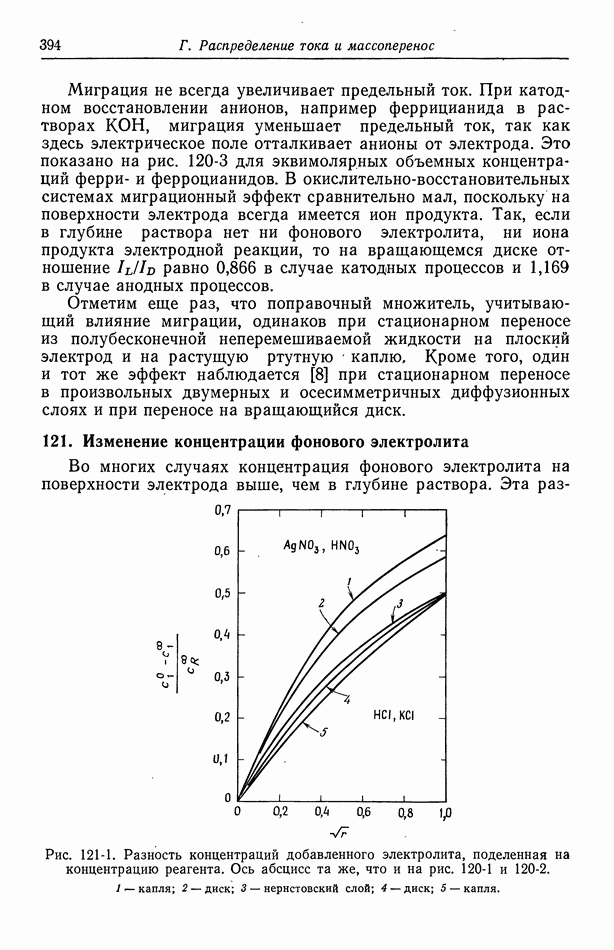
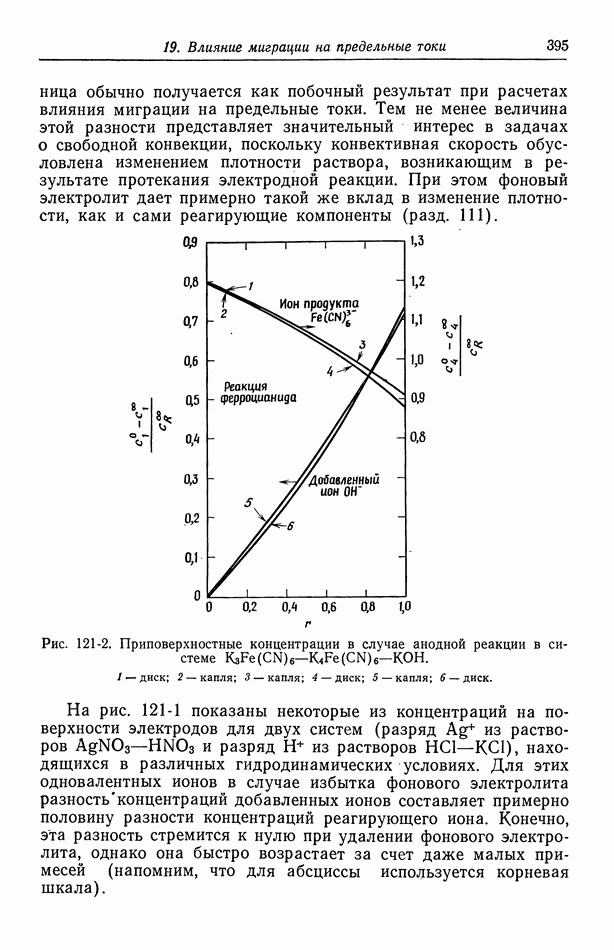
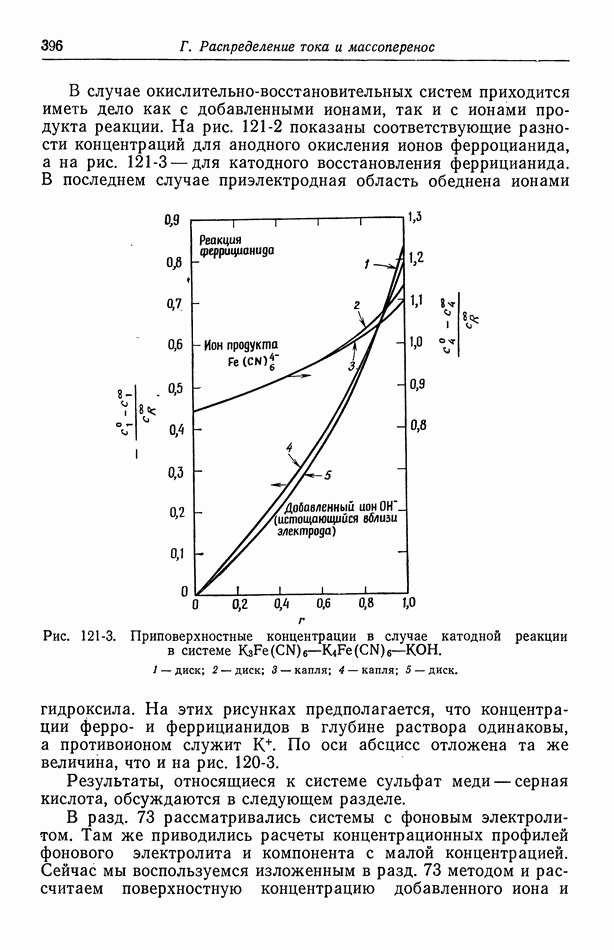
- 121. Изменение концентрации фонового электролита
- 122. Роль ионов бисульфата
- 123. Парадоксы с фоновым электролитом
- 124. Предельные токи в случае свободной конвекции
- Глава 20. КОНЦЕНТРАЦИОННОЕ ПЕРЕНАПРЯЖЕНИЕ
- 126. Бинарный электролит
- 127. Фоновый электролит
- 128. Численные расчеты
- Глава 21. ДОПРЕДЕЛЬНЫЕ ТОКИ
- 129. Объем раствора
- 130. Диффузионные слои
- 131. Граничные условия и метод решения
- 132. Результаты для вращающегося диска
- Приложение А. ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ ОБЪЕМЫ
- Приложение Б. ВЕКТОРЫ И ТЕНЗОРЫ
- Приложение В. ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМЫ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ